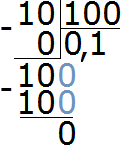Как по известным процентам найти все число

Онлайн калькулятор для вы нахождения числа по его процентам, может решать примеры, сохранять историю вычисления и копировать ссылку на расчет.

Правило: Чтобы найти число по его проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на 100.

Примеры вычисления исходного числа по известному проценту от числа:
Например: число 4 это 5% от неизвестного нам числа, чтобы найти это число нужно 4/5×100=80

Онлайн калькулятор вычисляет 100 процентов зная число и сколько процентов оно составляет от искомого числа. Для вычисления нужно число разделить на процент и умножить на 100.

Значащих цифр:

Вычисление исходного числа по известному проценту от числа

Формула вычисления числа по его проценту.

Если дано число B которое составляет P процентов от числа A и необходимо найти значение числа A, то

Для вывода этого соотношения используем методику решения задач с процентами через пропорции

“все“”часть” =100%”часть в %“   =>  
“все” = “часть” · “100%“часть в %

Примеры вычисления исходного числа по известному проценту от числа

Пример 1.

Найти исходное число, если 5% от этого числа равно 40.

Решение:

Ответ: 800.

Пример 2.

На заводе работает 270 женщины. Это 30% от всех работников. Сколько человек работает на заводе?

Решение:

Ответ: На заводе работает 900.

Пример 3.

Какую сумму нужно положить на депозит под 10% годовых, чтобы через год получить прибыль 1000 рублей.

Решение:

Ответ: на депозит необходимо положить 10000 рублей.

При изучении процентов вам также будут полезны:

Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, который хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.

Содержание урока

Что такое процент?

В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент
. А что означает дробь одна сотая ? Эта дробь означает, что чего-либо разделено на сто частей и оттуда взята одна часть. Значит процентом является одна сотая часть чего-либо.

Процентом называется одна сотая часть чего-либо

Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

От одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% = = 0,01

Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% = = 0,02

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:

Найти от 10 см

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби

Получили 0,1. Теперь 0,1 умножаем на числитель дроби

0,1 × 2 = 0,2

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если , то получим 2 миллиметра:

0,2 см = 2 мм

Значит 2% от 10 см составляют 2 мм.

Пример 2.
Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей 100

300: 100 = 3

Теперь полученный результат умножаем на 50

3 × 50 = 150 руб.

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти от 300 рублей, а решать такие задачи для нас пока проще

300: 100 = 3

3 × 50 = 150

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить и .

Пример 3.
Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

1200: 100 = 12

12 × 32 = 384

Ответ: 384 костюмов нового фасона выпустила фабрика.

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

300 × 0,5 = 150

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000: 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2.
Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35: 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500: 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35
это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35: 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Умение вычисления процента от числа, когда нужно узнать пеню за просрочку, размер переплаты по кредиту или прибыль компании, если известен ее оборот и наценка.

• Как найти число по его проценту?
  

Правило. Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на 100.

Таким вычислением сначала определим, сколько единиц этого числа содержится в 1%, а потом — в целом числе (в 100%).

Например:

Число, 23% которого составляют 52, находится так:
52: 23 * 100 = 226.1

Значит, если число 226,1 равно 100%, то число 52 равно 23% от этого числа.

Число, 125% которого составляют 240, находим так:
240: 125 * 100 = 192.

При определении числа по его проценту следует помнить, что:

— если процент меньше 100%, то число, полученное в результате вычислений, больше заданного числа (если 23% < 100%, то 226,1 > 52);

— если процент больше 100%, то число, полученное в результате вычислений, меньше заданного числа (если 125% > 100%, то 192 < 240).

Следовательно, при вычислении числа по его проценту для самоконтроля нужно проверить:

— заданный в условии процент больше или меньше 100%;
— результат вычисления больше или меньше заданного числа.

• Как узнать процент от суммы в общем случае?
  

После этого есть два варианта:

1. Если нужно узнать, сколько процентов составляет другая сумма от первоначальной, нужно просто разделить ее на размер 1%, полученный ранее.
2. Если же нужен размер суммы, которая составляет, скажем, 27,5% от первоначальной, нужно размер 1% умножить на требуемое количество процентов.

• Как высчитать процент от суммы с помощью пропорции?
  

Для этого придется использовать знания о методе пропорций, который проходят в рамках школьного курса математики. Это будет выглядеть так:

ПустьА — основная сумма, равная 100%, и В — сумма, соотношение которой с А в процентах нам нужно узнать. Записываем пропорцию:

(Х в данном случае — число процентов).

По правилам расчета пропорций мы получаем следующую формулу:

Х = 100 * В / А

Если же нужно узнать, сколько будет составлять сумма В при уже известном числе процентов от суммы А, формула будет выглядеть по-другому:

В = 100 * Х / А

Теперь остается подставить в формулу известные числа — и можно производить расчет.

• Как рассчитать процент от суммы с помощью известных соотношений?
  

Наконец, можно воспользоваться и более простым способом. Для этого достаточно помнить, что 1% в виде десятичной дроби — это 0,01. Соответственно, 20% — это 0,2; 48% — 0,48; 37,5% — это 0,375 и т.д. Достаточно умножить исходную сумму на соответствующее число — и результат будет означать размер процентов.

Кроме того, иногда можно воспользоваться и простыми дробями. Например, 10% — это 0,1, то есть 1/10 следовательно, узнать, сколько составят 10%, просто: нужно всего лишь разделить исходную сумму на 10.

Другими примерами таких соотношений будут:

1. 12,5% — 1/8, то есть нужно делить на 8;
2. 20% — 1/5, то есть нужно разделить на 5;
3. 25% — 1/4, то есть делим на 4;
4. 50% — 1/2, то есть нужно разделить пополам;
5. 75% — 3/4, то есть нужно разделить на 4 и умножить на 3.

Правда, не все простые дроби удобны для расчета процентов. К примеру, 1/3 близка по размерам к 33%, но не равна точно: 1/3 — это 33,(3)% (то есть дробь с бесконечными тройками после запятой).

• Как вычесть процент от суммы без помощи калькулятора?
  

Если же требуется от уже известной суммы отнять неизвестное число, составляющее какое-то количество процентов, можно воспользоваться следующими методами:

1. Вычислить неизвестное число с помощью одного из приведенных выше способов, после чего отнять его от исходного.
2. Сразу рассчитать остающуюся сумму. Для этого от 100% отнимаем то число процентов, которое нужно вычесть, и полученный результат переводим из процентов в число любым из описанных выше способов.

Второй пример удобнее, поэтому проиллюстрируем его. Допустим, надо узнать, сколько останется, если от 4779 отнять 16%. Расчет будет таким:

1. Отнимаем от 100 (общее количество процентов) 16. Получаем 84.
2. Считаем, сколько составит 84% от 4779. Получаем 4014,36.

• Как высчитать (отнять) из суммы процент с калькулятором в руках?
  

Все вышеприведенные вычисления проще делать, используя калькулятор. Он может быть как в виде отдельного устройства, так и в виде специальной программы на компьютере, смартфоне или обычном мобильнике (даже самые старые из ныне используемых устройств обычно имеют эту функцию). С их помощью вопрос, как высчитать процент из суммы,
решается очень просто:

1. Набирается исходная сумма.
2. Нажимается знак «-».
3. Вводится число процентов, которое требуется вычесть.
4. Нажимается знак «%».
5. Нажимается знак «=».

В итоге на экране высвечивается искомое число.

• Как отнять от суммы процент с помощью онлайн-калькулятора?
  

Наконец, сейчас в сети достаточно сайтов, где реализована функция онлайн-калькулятора. В этом случае даже не требуется знания того, как посчитать процент от суммы
: все операции пользователя сводятся к вводу в окошки нужных цифр (или передвижению ползунков для их получения), после чего результат сразу высвечивается на экране.

Особенно эта функция удобна тем, кто рассчитывает не просто абстрактный процент, а конкретный размер налогового вычета или сумму госпошлины. Дело в том, что в этом случае вычисления сложнее: требуется не только найти проценты, но и прибавить к ним постоянную часть суммы. Онлайн-калькулятор позволяет избежать подобных добавочных вычислений. Главное — выбрать сайт, пользующийся данными, которые соответствуют действующему закону.

Онлайн-калькулятор процентов:

calculator.ru — позволяет выполнять разнообразные расчеты при работе с процентами;

mirurokov.ru — калькуляятор процентов;

Источник информации:

• nsovetnik.ru — статьяя о том, как высчитать процент от суммы;

«Нахождение числа по его дроби» — Учебник по математике 6 класс (Виленкин)

Краткое описание:

Вы уже умеете находить дробь от числа, а в этом разделе Вы выучите, как находить число по его дроби. Нужно быть очень внимательными, чтобы не запутаться, и все задачки решать быстро и правильно.
Давайте быстро вспомним, как мы находим дробь от числа: мы просто это число умножаем на дробь. Например, нужно найти 3/5 от числа 15. Решаем 3/5 * 15 = 3*15 / 5 =3*3=9. Зачем нам нужно знать, как это делать? Для того, чтобы уметь находить какую-то часть от чего-то целого. Например, зная какую часть книги Вы прочитали и сколько в ней всего страниц, Вы можете найти, сколько страниц осталось прочитать. Запомните, когда мы ищем дробь от числа, у нас есть что-то целое и его часть, и нам нужно это целое умножить на часть, таким образом, мы находим часть в количественном выражении и это число всегда будет меньше начального числа.
В задачах, когда мы ищем число по его дроби, это число всегда должно быть больше, ведь, по сути, мы ищем что-то целое, зная только его часть. Вот, например, Вы прочитали 100 страниц книги, но это только ее третья часть. А сколько всего страниц в книге? Как мы будем искать это число? Зная, что 100 страниц – это треть, нужно 100 * 3 и тогда мы узнаем, сколько страниц всего в книге – 100*3=300. А если попытаться решить через уравнение? Пусть х – общее число страниц в книге, как найти, сколько мы прочитали, нужно х умножить на 1/3 и это будет равно 100. Так – х * 1/3=100. Решаем уравнение дальше – х=100: 1/3, а мы уже выучили, чтобы поделить число на дробь, нужно его умножить на обратную дробь. Получается х=100: 1/3 = 100 * 3/1 = 300. Понятно? Значит, чтобы найти число, зная его дробную часть и ее значение, нам нужно значение (натуральное число) разделить на дробь, то есть умножить на перевернутую дробь и это число всегда будет больше, заданного нам в условии!
Если в задаче дана не дробь, а проценты, что нужно делать? Перевести проценты в десятичную дробь: 40%=0,40; 75%=0,75 и решать дальше по выученной схеме.

Одним из базовых понятий математики является процент. Для того чтобы понять, что такое процент, достаточно разделить заданную целую величину на сто. Одна сотая часть будет одним процентом (обозначается 1%). Как в точных и экономических науках, так и в других сферах жизни проценты используются для обозначения долей по отношению к целому. При этом само целое обозначается как 100%. В некоторых случаях используется при сравнении двух величин: например, иногда стоимость товаров не сравнивается в денежных единицах, а оценивается, на сколько % цена одного товара больше или меньше цены другого. Термин также получил широкое распространение в банковском деле и в большинстве случаев используется в качестве синонима словосочетания «процентная ставка».

Правило нахождения процентов от числа

Вычисление процентных долей от целого – одна из основных математических операций, к тому же часто используемая в повседневной жизни. Правило нахождения процентов от числа гласит о том, что для решения такой задачи его необходимо умножить на указанное в условиях количество %, после чего полученный результат разделить на 100. Также можно разделить число на 100, и полученный результат умножить на заданное количество %. Важно помнить ещё один тезис: если заданный условиями процент превышает 100%, то полученное числовое значение всегда больше исходного (заданного) – и наоборот.

Правило нахождения числа по его проценту

Существует обратное правило нахождения числа по его проценту. Для того чтобы получить результат по такой математической операции (второму из трёх базовых типов задач на процентные вычисления) необходимо указанное в условиях число разделить на заданную процентную величину, после чего полученный результат умножить на 100. При этом первым действием вычисляется количество единиц исходной величины в 1%, а вторым – в целом (то есть в 100%). Если количество % превышает 100, то полученный результат всегда будет меньше числового значения, заданного условиями задачи – и наоборот.

Правило нахождения процентного выражения числа от другого

Третьим базовым типом математических задач на процентные вычисления являются такие задания, в которых необходимо использовать правило нахождения процентного выражения числа от другого (или соотношения двух величин). Оно гласит о том, что для решения необходимо второе число разделить на первое, после чего полученный результат умножить на сто. Подобное соотношение показывает, сколько % одно числовое значение составляет от другого (то есть, фактически речь идёт об отношении между двумя числовыми значениями, выраженном в %).

мы видим достаточно часто в повседневной жизни. Возьмем плитку шоколада, пачку мороженого на которых написано «56 % какао», «пломбир 100 % ». А что такое процент?

Процентом
называется одна сотая часть. Кратко записывают 1 %
. Знак %
заменяет слово «процент».

Какое бы число или величину мы не взяли, его сотая часть — это один процент данного числа или величины. Например, для числа 400 (0,01 числа 400) — это число 4, поэтому 4 — это 1 % числа 400; 1 гривны (0,01 гривны) — это 1 копейка, поэтому 1 копейка — это 1 % гривны.

Например:

Пазл содержит 500 элементов. Сколько элементов приходится на 1 его процент? Пусть 500 элементов пазла — это 100 %. Тогда на 1 % приходится в 100 раз меньше его элементов. Отсюда 500: 100 = 5 (эл.). Итак, 1 % — это 5 элементов пазла.

Обратите внимание: чтобы найти 1 % от числа а
, нужно это число разделить на 100. Зная, какое число или величина составляет 1% , можно находить число или величину, приходящиеся на несколько процентов .

Например:

Марине надо пришить тесьму, 3 см которой составляет 1 % от её длины. Марина пришила 50 % тесьмы, Сколько сантиметров тесьмы она пришила? Поскольку 50 % больше 1 % в 50 раз, то Марина пришила тесьмы в 50 раз больше, чем 3 см. Отсюда 3.50 = 150 (см). Итак, Марина пришила 150 см тесьмы.

На практике часто случается так, что обе приведённые задачи надо решать вместе – сначала найти, какое число или величина приходится на 1 %, а затем – на несколько процентов. Такие задачи называют задачами на нахождение процента от числа
.

Например:

Груши сладких сортов содержат 15 % сахара. Сколько сахара содержится в 3 кг груш?

Составим краткую запись данных задачи.

Груши: З кг — 100%

Сахар: ? — 15%

1. Сколько килограммов соответствует 1 %?

Процентное отношение двух чисел
— это их отношение, выраженное в процентах. Процентное отношение показывает, сколько процентов одно число составляет от другого.