Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Найти многочлены по заданным корням…
|
|
30/08/07 |
|
|
|
|
|
Brukvalub |
|
||
01/03/06 |
Tarsik писал(а): С чего начинать? Использовать формулы Виета.
|
||
|
|
|||
|
Руст |
|
||
09/02/06 |
Brukvalub писал(а): Tarsik писал(а): С чего начинать? Использовать формулы Виета. Зачем, когда это ещё проще.
|
||
|
|
|||
|
Brukvalub |
|
||
01/03/06 |
Руст писал(а): Зачем, когда это ещё проще. Чтобы решить задачу.
|
||
|
|
|||
|
Руст |
|
||
09/02/06 |
Brukvalub писал(а): Руст писал(а): Зачем, когда это ещё проще. Чтобы решить задачу. Подставив вместо переменной Х величину Х-1 непосредственно получается решение первой, аналогично решается вторая.
|
||
|
|
|||
|
Brukvalub |
|
||
01/03/06 |
Согласен, Ваш вариант проще.
|
||
|
|
|||
|
Tarsik |
|
|
30/08/07 |
Спасибо. А нельзя ли как-то проверить?
|
|
|
|
|
Lion |
|
||
26/11/06 |
Tarsik писал(а): Спасибо. А нельзя ли как-то проверить? Что именно проверить?
|
||
|
|
|||
|
Tarsik |
|
|
30/08/07 |
|
|
|
|
|
Lion |
|
||
26/11/06 |
Если Вы хотите, чтобы корни увеличились на 1, нужно подставить не
|
||
|
|
|||
|
Tarsik |
|
|
30/08/07 |
Lion писал(а): Если Вы хотите, чтобы корни увеличились на 1, нужно подставить не
Спасибо.Прошу извинения за невнимательность.
|
|
|
|
|
Lion |
|
||
26/11/06 |
|||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен – это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена 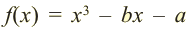
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной 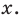
По определению одночлена числа и буквы (в нашем случае одна буква — 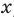 ) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида
) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида 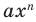 , где
, где 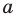 — некоторое число. Поэтому одночлен от одной переменной
— некоторое число. Поэтому одночлен от одной переменной 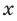 — это выражение вида
— это выражение вида 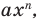 где
где 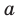 — некоторое число,
— некоторое число, 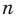 — целое неотрицательное число. Если
— целое неотрицательное число. Если 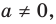 то показатель степени
то показатель степени 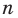 переменной
переменной 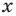 называется степенью одночлена. Например,
называется степенью одночлена. Например, 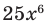 — одночлен шестой степени,
— одночлен шестой степени, 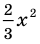 — одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку
— одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку 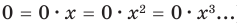 ).
).
По определению многочлен от одной переменной 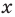 — это сумма одночленов от одной переменной
— это сумма одночленов от одной переменной 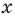 . Поэтому
. Поэтому
многочленом от одной переменной 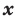 : называется выражение вида
: называется выражение вида
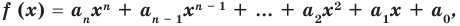 (1)
(1)
где коэффициенты 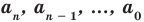 — некоторые числа.
— некоторые числа.
Если 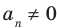 , то этот многочлен называют многочленом
, то этот многочлен называют многочленом 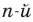 степени от переменной
степени от переменной 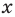 . При этом член
. При этом член 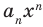 называют старшим членом многочлена
называют старшим членом многочлена 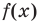 , число
, число 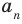 — коэффициентом при старшем члене, а член
— коэффициентом при старшем члене, а член 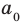 — свободным членом. Например,
— свободным членом. Например, 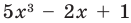 — многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
— многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 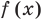 записывают так:
записывают так:
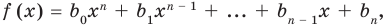
где 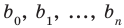 — некоторые числа.
— некоторые числа.
Теорема 1. Одночлены 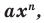 где
где 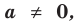 и
и 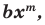 где
где 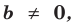 , тождественно равны тогда и только тогда, когда
, тождественно равны тогда и только тогда, когда 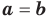 и
и 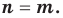 Одночлен
Одночлен 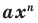 тождественно равен нулю тогда и только тогда, когда
тождественно равен нулю тогда и только тогда, когда 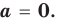
Поскольку равенство одночленов
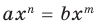 (2)
(2)
выполняется при всех значениях 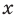 (по условию эти одночлены тождественно равны), то, подставляя в это равенство
(по условию эти одночлены тождественно равны), то, подставляя в это равенство 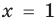 , получаем, что
, получаем, что 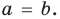 Сокращая обе части равенства (2) на
Сокращая обе части равенства (2) на 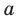 (где
(где 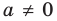 по условию), получаем
по условию), получаем 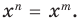 При
При 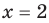 из этого равенства имеем:
из этого равенства имеем: 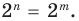 Поскольку 2
Поскольку 2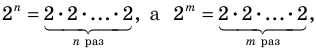 то равенство
то равенство 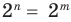 возможно только тогда, когда
возможно только тогда, когда 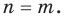 Таким образом, из тождественного равенства
Таким образом, из тождественного равенства 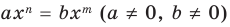 получаем, что
получаем, что 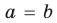 и
и 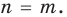 Если известно, что
Если известно, что 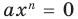 для всех
для всех 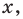 то при
то при 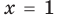 получаем
получаем 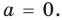 Поэтому одночлен
Поэтому одночлен 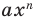 тождественно равен нулю при
тождественно равен нулю при 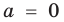 (тогда
(тогда 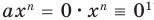 ).
).
Далее любой одночлен вида 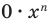 будем заменять на 0.
будем заменять на 0.
Теорема 2. Если многочлен 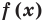 тождественно равен нулю (то есть принимает нулевые значения при всех значениях
тождественно равен нулю (то есть принимает нулевые значения при всех значениях 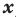 ), то все его коэффициенты равны нулю.
), то все его коэффициенты равны нулю.
 Значком
Значком  обозначено тождественное равенство многочленов.
обозначено тождественное равенство многочленов.
Для доказательства используем метод математической индукции. Пусть 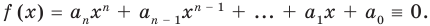
При 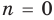 имеем
имеем 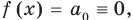 поэтому
поэтому 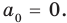 То есть в этом случае утверждение теоремы выполняется.
То есть в этом случае утверждение теоремы выполняется.
Предположим, что при 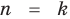 это утверждение также выполняется: если многочлен
это утверждение также выполняется: если многочлен 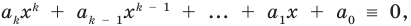 то
то 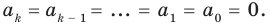
Докажем, что данное утверждение выполняется и при 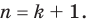 Пусть
Пусть 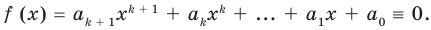 (3)
(3)
Поскольку равенство (3) выполняется при всех значениях  , то, подставляя в это равенство
, то, подставляя в это равенство 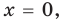 получаем, что
получаем, что 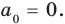 Тогда равенство (3) обращается в следующее равенство:
Тогда равенство (3) обращается в следующее равенство: 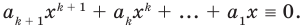 Вынесем
Вынесем  в левой части этого равенства за скобки и получим
в левой части этого равенства за скобки и получим
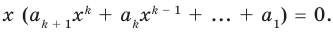 (4)
(4)
Равенство (4) должно выполняться при всех значениях  . Для того чтобы оно выполнялось при
. Для того чтобы оно выполнялось при 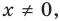 должно выполняться тождество
должно выполняться тождество
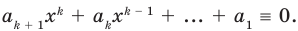 В левой части этого тождества стоит многочлен со степенями переменной от
В левой части этого тождества стоит многочлен со степенями переменной от 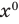 до
до 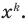 Тогда по предположению индукции все его коэффициенты равны нулю:
Тогда по предположению индукции все его коэффициенты равны нулю: 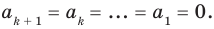 Но мы также доказали, что
Но мы также доказали, что 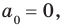 поэтому наше утверждение выполняется и при
поэтому наше утверждение выполняется и при 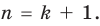 Таким образом, утверждение теоремы справедливо для любого целого неотрицательного
Таким образом, утверждение теоремы справедливо для любого целого неотрицательного 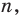 то есть для всех многочленов.
то есть для всех многочленов.
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 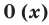 или просто
или просто 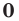 (поскольку
(поскольку 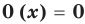 ).
).
Теорема 3. Если два многочлена 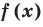 и
и 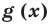 тождественно равны, то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
тождественно равны, то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
Пусть многочлен 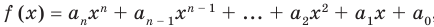 , а многочлен
, а многочлен 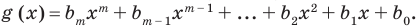 Рассмотрим многочлен
Рассмотрим многочлен 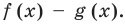 Поскольку многочлены
Поскольку многочлены 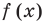 и
и 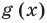 по условию тождественно равны, то многочлен
по условию тождественно равны, то многочлен 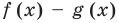 тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
Но 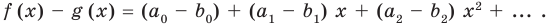 Тогда
Тогда 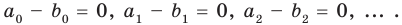 Отсюда
Отсюда 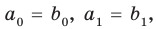
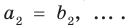 Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например,
Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например, 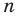 больше
больше 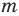 ), то коэффициенты разности будут равны нулю. Поэтому начиная с (
), то коэффициенты разности будут равны нулю. Поэтому начиная с (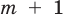 -го номера все коэффициенты
-го номера все коэффициенты 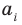 также будут равны нулю. То есть действительно многочлены
также будут равны нулю. То есть действительно многочлены 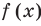 и
и 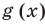
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение 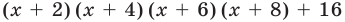
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 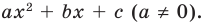 Получаем тождество:
Получаем тождество:
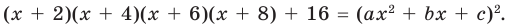 (5)
(5)
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 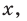 получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
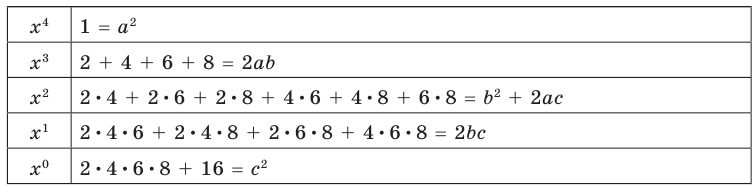
Из первого равенства получаем 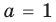 или
или 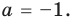
При 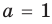 из второго равенства имеем а из третьего —
из второго равенства имеем а из третьего — 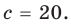 Как видим, при этих значениях
Как видим, при этих значениях 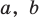 и
и 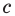 последние два равенства также выполняются. Следовательно, тождество (5) выполняется при
последние два равенства также выполняются. Следовательно, тождество (5) выполняется при 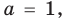
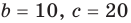 (аналогично можно также получить
(аналогично можно также получить 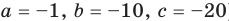 ). Таким образом,
). Таким образом, 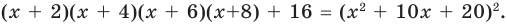
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 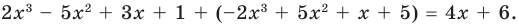 При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей степени слагаемого.
При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей степени слагаемого.
Например,  Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что целое число
Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что целое число  делится на целое число
делится на целое число  если существует такое целое число
если существует такое целое число  что
что 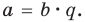
Определение: Многочлен  делится на многочлен
делится на многочлен 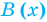 (где
(где 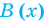 — не нулевой многочлен), если существует такой многочлен
— не нулевой многочлен), если существует такой многочлен  что
что 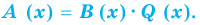
Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен  делится на многочлен
делится на многочлен  (где
(где  — не нулевой многочлен) с остатком, если существует такая пара многочленов
— не нулевой многочлен) с остатком, если существует такая пара многочленов  и
и  что
что  причем степень остатка
причем степень остатка  меньше степени делителя
меньше степени делителя  (в этом случае многочлен
(в этом случае многочлен  называют неполным частным.)
называют неполным частным.)
Например, поскольку 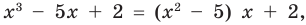 то при делении многочлена
то при делении многочлена 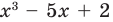 на многочлен
на многочлен 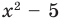 получаем неполное частное
получаем неполное частное 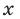 : и остаток 2.
: и остаток 2.
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 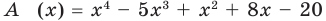 на многочлен
на многочлен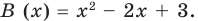
Решение:
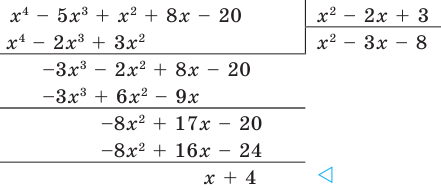 Докажем, что полученный результат действительно является результатом деления
Докажем, что полученный результат действительно является результатом деления 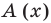 на
на 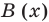 с остатком.
с остатком.
Если обозначить результат выполнения первого шага алгоритма через 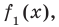 второго шага — через
второго шага — через 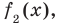 третьего — через
третьего — через 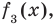 то операцию деления, выполненную выше, можно записать в виде системы равенств:
то операцию деления, выполненную выше, можно записать в виде системы равенств:
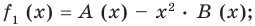 (1)
(1)
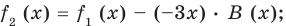 (2)
(2)
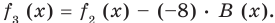 (3)
(3)
Сложим почленно равенства (1), (2), (3) и получим
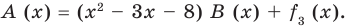 (4)
(4)
Учитывая, что степень многочлена 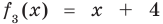 меньше степени делителя
меньше степени делителя 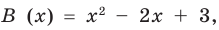 обозначим
обозначим 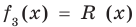 (остаток), а
(остаток), а 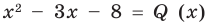 (неполное частное). Тогда из равенства (4) имеем:
(неполное частное). Тогда из равенства (4) имеем: 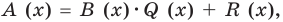 то есть
то есть 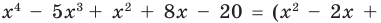
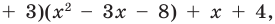 а это и означает, что мы разделили
а это и означает, что мы разделили 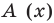 на
на 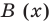 с остатком.
с остатком.
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 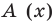 и
и 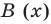 в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого
в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого 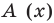 и делителя
и делителя 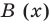 (где
(где 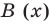 — не нулевой многочлен) найти неполное частное
— не нулевой многочлен) найти неполное частное 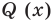 и остаток
и остаток 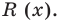
Отметим, что в случае, когда степень делимого 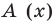 меньше степени делителя
меньше степени делителя 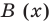 , считают, что неполное частное
, считают, что неполное частное 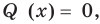 а остаток
а остаток 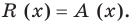
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 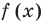 на двучлен
на двучлен 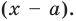 Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен
Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен 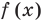 на двучлен
на двучлен 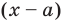 , то получим
, то получим
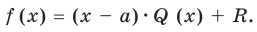
Это равенство выполняется тождественно, то есть при любом значении 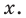 При
При 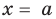 имеем
имеем 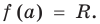 Полученный результат называют теоремой Безу
Полученный результат называют теоремой Безу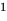 .
.
Теорема 1 (теорема Безу). Остаток от деления многочлена 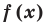 на двучлен
на двучлен 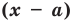 равен
равен 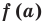 (то есть значению многочлена при
(то есть значению многочлена при 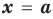 ).
).
Пример №2
Докажите, что 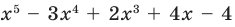 делится на
делится на 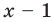 без остатка.
без остатка.
Решение:
► Подставив в 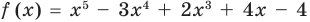 вместо
вместо 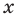 значение 1, получаем:
значение 1, получаем: 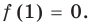 . Таким образом, остаток от деления
. Таким образом, остаток от деления 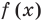 на
на  равен 0, то есть
равен 0, то есть 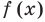 делится на
делится на  без остатка. <]
без остатка. <]
Определение: Число 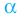 называют корнем многочлена
называют корнем многочлена 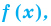 если
если
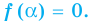
Если многочлен 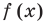 делится на
делится на  то
то 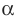 — корень этого многочлена.
— корень этого многочлена.
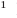 Безу Этьен (1730-1783) — французский математик, внесший значительный вклад в развитие теории алгебраических уравнений.
Безу Этьен (1730-1783) — французский математик, внесший значительный вклад в развитие теории алгебраических уравнений.
Действительно, если 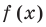 делится на
делится на 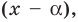 то
то  и поэтому
и поэтому 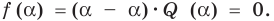 Таким образом,
Таким образом, 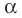 — корень многочлена
— корень многочлена 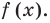
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 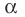 является корнем многочлена
является корнем многочлена 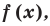 то этот многочлен делится на двучлен
то этот многочлен делится на двучлен 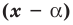 без остатка.
без остатка.
По теореме Безу остаток от деления 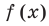 на
на  равен
равен 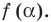 Но по условию
Но по условию 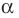 — корень
— корень 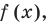 таким образом,
таким образом, 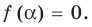
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 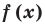 имеет попарно разные корни
имеет попарно разные корни 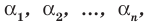 то он делится без остатка на произведение
то он делится без остатка на произведение 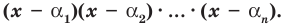
Для доказательства используем метод математической индукции.
При 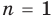 утверждение доказано в теореме 2.
утверждение доказано в теореме 2.
Допустим, что утверждение справедливо при 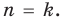 То есть если
То есть если 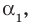
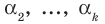 попарно разные корни многочлена
попарно разные корни многочлена 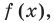 то он делится на произведение
то он делится на произведение 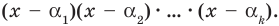 Тогда
Тогда
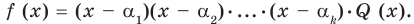 (1)
(1)
Докажем, что утверждение теоремы справедливо и при 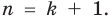 Пусть
Пусть 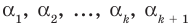 — попарно разные корни многочлена
— попарно разные корни многочлена 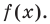 Поскольку
Поскольку 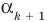 — корень
— корень 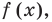 то
то 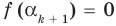 . Принимая во внимание равенство (1), которое выполняется согласно допущению индукции, получаем:
. Принимая во внимание равенство (1), которое выполняется согласно допущению индукции, получаем:
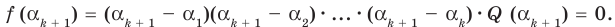
По условию все корни 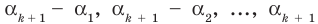 разные, поэтому ни одно из чисел
разные, поэтому ни одно из чисел 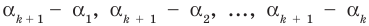 не равно нулю. Тогда
не равно нулю. Тогда 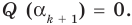 Таким образом,
Таким образом, 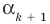 — корень многочлена
— корень многочлена 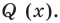 Тогда по теореме 2 многочлен
Тогда по теореме 2 многочлен 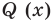 делится на
делится на 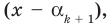 то есть
то есть 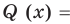
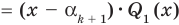 и из равенства (1) имеем
и из равенства (1) имеем

Это означает, что 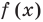 делится на произведение
делится на произведение
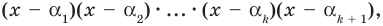 то есть теорема доказана и при
то есть теорема доказана и при 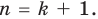
Таким образом, теорема справедлива для любого натурального 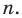
Следствие. Многочлен степени 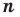 имеет не больше
имеет не больше 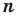 разных корней.
разных корней.
Допустим, что многочлен 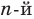 степени имеет
степени имеет 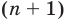 разных корней:
разных корней: 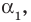
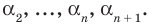 Тогда
Тогда 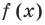 делится на произведение
делится на произведение 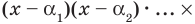
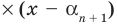 многочлен степени
многочлен степени 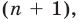 но это невозможно. Поэтому многочлен
но это невозможно. Поэтому многочлен 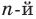 степени не может иметь больше чем
степени не может иметь больше чем 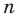 корней.
корней.
Пусть теперь многочлен 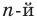 степени
степени 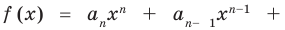
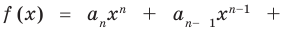 имеет
имеет 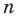 разных корней
разных корней 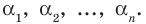 Тогда этот многочлен делится без остатка на произведение
Тогда этот многочлен делится без остатка на произведение 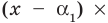
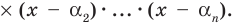 Это произведение является многочленом той же
Это произведение является многочленом той же
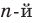 степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
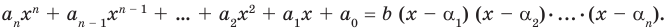 (2)
(2)
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 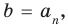 то есть
то есть
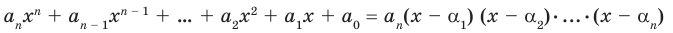 (3)
(3)
Сравнивая коэффициенты при одинаковых степенях 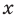 в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
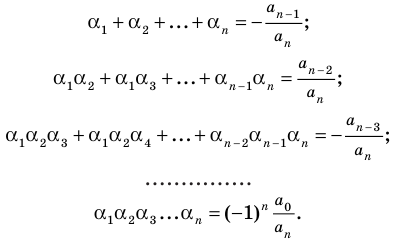 (4)
(4)
Например, при 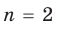 имеем:
имеем:
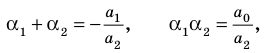
а при 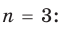
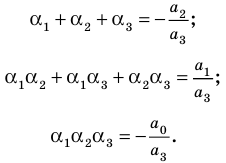 (5)
(5)
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 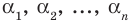 были корнями многочлена
были корнями многочлена
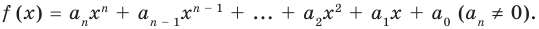
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 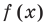 разные. Введем понятие кратного корня многочлена.
разные. Введем понятие кратного корня многочлена.
Если многочлен 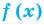 делится без остатка на
делится без остатка на 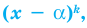 но не делится без остатка на
но не делится без остатка на 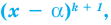 то говорят, что число
то говорят, что число  является корнем кратности
является корнем кратности  многочлена
многочлена 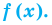
Например, если произведение  записать в виде многочлена, то для этого многочлена число
записать в виде многочлена, то для этого многочлена число 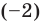 является корнем кратности 3, число 1 — корнем кратности 2, а число
является корнем кратности 3, число 1 — корнем кратности 2, а число 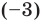 — корнем кратности 1.
— корнем кратности 1.
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена 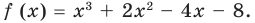
Решение:
► 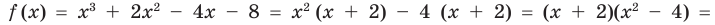
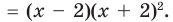
Поэтому 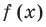 имеет корни:
имеет корни: 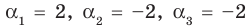 (поскольку
(поскольку 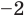 — корень кратности 2).
— корень кратности 2).
Проверим справедливость формулы (5). В нашем случае: 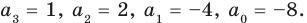 Тогда
Тогда
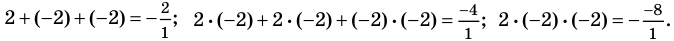
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения 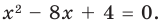
Решение:
► Обозначим корни уравнения 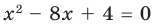 через
через 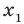 и
и 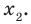 Тогда корнями искомого уравнения должны быть числа
Тогда корнями искомого уравнения должны быть числа 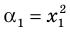 и
и 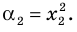 Поэтому искомое уравнение имеет вид
Поэтому искомое уравнение имеет вид 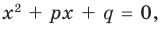 где
где
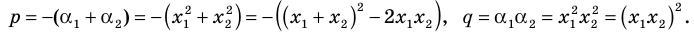
По формулам Виета имеем 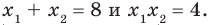 Отсюда находим, что
Отсюда находим, что 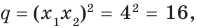 а
а 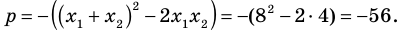 Таким образом, искомое уравнение имеет вид
Таким образом, искомое уравнение имеет вид 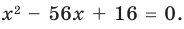
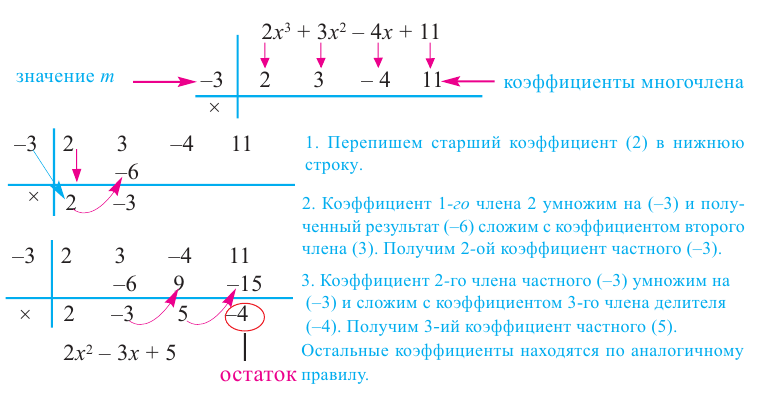
Схема Горнера
Делить многочлен 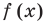 на двучлен
на двучлен 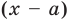 иногда удобно с помощью
иногда удобно с помощью
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 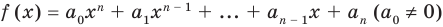 необходимо разделить на двучлен
необходимо разделить на двучлен 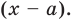 В результате деления многочлена
В результате деления многочлена 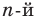 степени на многочлен первой степени получим некоторый многочлен
степени на многочлен первой степени получим некоторый многочлен 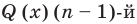 степени (то есть
степени (то есть 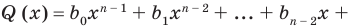
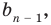 , где
, где 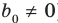 ) и остаток
) и остаток 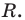 Тогда
Тогда 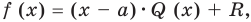 то есть
то есть
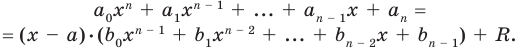
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях 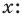
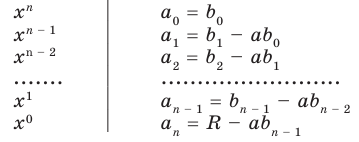
Найдем из этих равенств коэффициенты 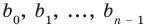 и остаток
и остаток 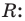

Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 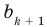 неполного частного, достаточно предыдущий найденный коэффициент
неполного частного, достаточно предыдущий найденный коэффициент 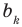 умножить на
умножить на 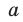 и добавить
и добавить 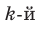 коэффициент делимого. Эту процедуру целесообразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.
коэффициент делимого. Эту процедуру целесообразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.

Пример №5
Разделите по схеме Горнера многочлен 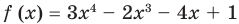 на двучлен
на двучлен 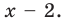
Решение:
► Запишем сначала все коэффициенты многочлена 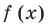 (если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:
(если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:

Таким образом, 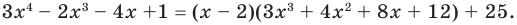
Пример №6
Проверьте, является ли 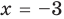 корнем многочлена
корнем многочлена 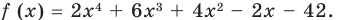
Решение:
► По теореме Безу остаток от деления многочлена 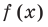 на
на 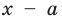 равен
равен 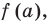 поэтому найдем с помощью схемы Горнера остаток от деления
поэтому найдем с помощью схемы Горнера остаток от деления 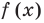 на
на 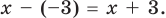

Поскольку 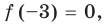 то
то 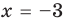 — корень многочлена
— корень многочлена 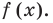
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 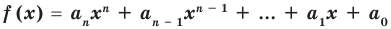 имеет рациональный корень
имеет рациональный корень 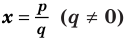 , то
, то 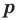 является делителем свободного члена
является делителем свободного члена 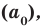 a
a 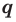 — делителем коэффициента при старшем члене
— делителем коэффициента при старшем члене 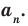
Если 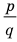 является корнем многочлена
является корнем многочлена 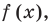 то
то 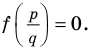 Подставляем
Подставляем
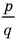 вместо
вместо 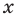 в
в 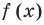 и из последнего равенства имеем
и из последнего равенства имеем
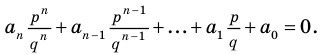 (1)
(1)
Умножим обе части равенства (1) на 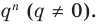 Получаем
Получаем
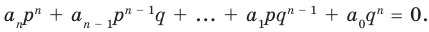 (2)
(2)
В равенстве (2) все слагаемые, кроме последнего, делятся на 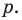 Поэтому
Поэтому 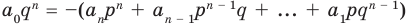 делится на
делится на 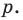
Но когда мы записываем рациональное число в виде 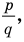 то эта дробь считается несократимой, то есть
то эта дробь считается несократимой, то есть 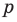 и
и 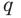 не имеют общих делителей. Произведение
не имеют общих делителей. Произведение 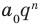 может делиться на
может делиться на 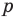 (если
(если 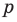 и
и 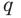 — взаимно простые числа) только тогда, когда
— взаимно простые числа) только тогда, когда 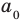 делится на
делится на 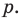 Таким образом,
Таким образом, 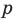 — делитель свободного члена
— делитель свободного члена 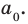
Аналогично все слагаемые равенства (2), кроме первого, делятся на 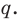 Тогда
Тогда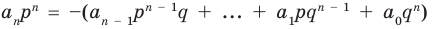 делится на
делится на 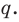 Поскольку
Поскольку 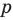 и
и 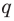 взаимно простые числа, то
взаимно простые числа, то 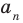 делится на
делится на 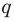 , следовательно,
, следовательно, 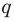 — делитель коэффициента при старшем члене.
— делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять 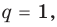 то корнем многочлена будет целое число
то корнем многочлена будет целое число 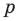 — делитель
— делитель 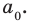 Таким образом, имеет место:
Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 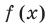 коэффициент
коэффициент 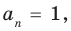 то делителями
то делителями 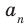 могут быть только числа
могут быть только числа 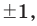 то есть
то есть 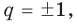 и имеет место:
и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена 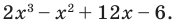
Решение:
► Пусть несократимая дробь 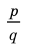 является корнем многочлена. Тогда
является корнем многочлена. Тогда 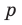 необходимо искать среди делителей свободного члена, то есть среди чисел
необходимо искать среди делителей свободного члена, то есть среди чисел 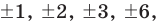 a
a 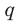 — среди делителей старшего коэффициента:
— среди делителей старшего коэффициента: 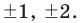
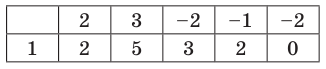
Таким образом, рациональные корни многочлена необходимо искать среди чисел 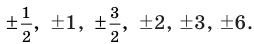 Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера.
Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера.
При 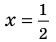 имеем следующую таблицу.
имеем следующую таблицу.
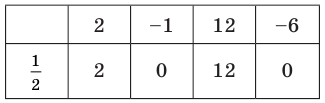
Кроме того, по схеме Горнера можно записать, что
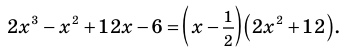
Многочлен 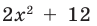 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень
не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень 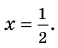
Пример №8
Разложите многочлен 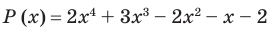 на множители.
на множители.
Решение:
► Ищем целые корни многочлена среди делителей свободного члена: 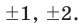
Подходит 1. Делим  на
на  с помощью схемы Горнера.
с помощью схемы Горнера.
Тогда 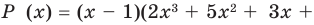
Ищем целые корни кубического многочлена 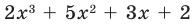 среди делителей его свободного члена:
среди делителей его свободного члена: 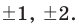 Подходит
Подходит 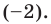 Делим на
Делим на 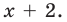

Имеем 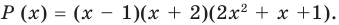
Квадратный трехчлен 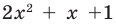 не имеет действительных корней и на линейные множители не раскладывается.
не имеет действительных корней и на линейные множители не раскладывается.
Ответ: 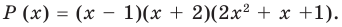
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 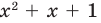 не имеет действительных корней). Таким образом, многочлен
не имеет действительных корней). Таким образом, многочлен 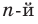 степени не всегда можно разложить на произведение линейных множителей. Но многочлен нечетной степени всегда можно разложить на произведение линейных и квадратных множителей, а многочлен четной степени — на произведение квадратных трехчленов.
степени не всегда можно разложить на произведение линейных множителей. Но многочлен нечетной степени всегда можно разложить на произведение линейных и квадратных множителей, а многочлен четной степени — на произведение квадратных трехчленов.
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен 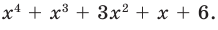
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
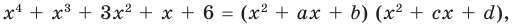 (3)
(3)
где 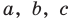 и
и 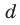 — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях
— неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях 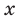 у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
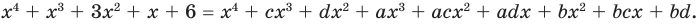
Получаем систему
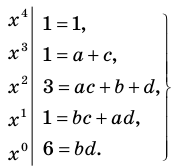 (4)
(4)
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 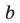 и
и 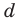 могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
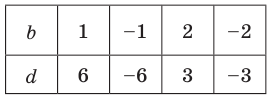
Коэффициенты 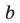 и
и 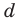 в равенстве (3) равноправны, поэтому мы не рассматриваем случаи
в равенстве (3) равноправны, поэтому мы не рассматриваем случаи 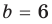 и
и 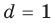 или
или 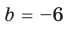 и
и  и т. д.
и т. д.
Для каждой пары значений  и
и  из третьего равенства системы (4) найдем
из третьего равенства системы (4) найдем 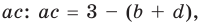 а из второго равенства имеем
а из второго равенства имеем 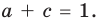 Зная
Зная 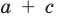 и
и 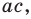 по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения
по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения 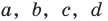 подставим в четвертое равенство системы (4)
подставим в четвертое равенство системы (4) 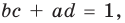 чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел 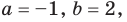
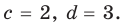 Тогда равенство (3) имеет вид
Тогда равенство (3) имеет вид
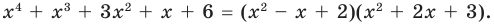 (5)
(5)
Поскольку квадратные трехчлены 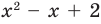 и
и 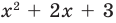 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 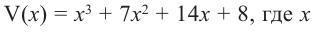 – положительное целое число и . Если высоты коробок можно определить при помощи линейной функции
– положительное целое число и . Если высоты коробок можно определить при помощи линейной функции 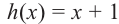 , то как можно выразить другие размеры коробки в виде многочлена? Вы сможете решить эту задачу, изучив правило деления многочлена на многочлен.
, то как можно выразить другие размеры коробки в виде многочлена? Вы сможете решить эту задачу, изучив правило деления многочлена на многочлен.
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
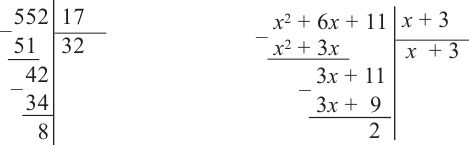
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 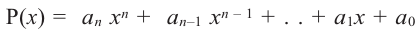 называется многочленом
называется многочленом 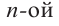 степени от одной переменной. Здесь
степени от одной переменной. Здесь 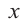 – переменная,
– переменная, 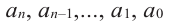 – определенные числа и
– определенные числа и  – старший член,
– старший член, 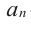 – коэффициент при старшем члене,
– коэффициент при старшем члене, 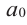 -свободный член. Многочлен можно разделить на многочлен аналогично правилу деления целых чисел столбиком.
-свободный член. Многочлен можно разделить на многочлен аналогично правилу деления целых чисел столбиком.
Деление целого числа па целое число можно проверить равенством
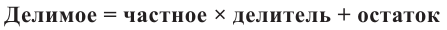
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 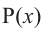 -делимое,
-делимое, 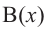 – делитель,
– делитель, 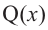 – неполное частное,
– неполное частное, 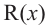 – остаток, то справедливо равенство
– остаток, то справедливо равенство
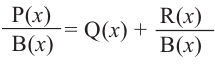 или
или 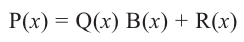 .
.
Здесь, степень многочлена 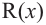 ниже степени многочлена
ниже степени многочлена 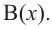 Если делителем является двучлен
Если делителем является двучлен 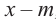 , то остатком может являться определенное число
, то остатком может являться определенное число 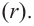
В этом случае: 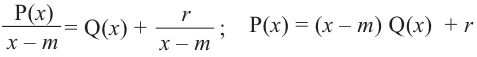
Пример №10
а) Разделите многочлен 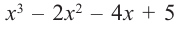 на двучлен
на двучлен 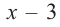 .
.
Ответ запишите в виде 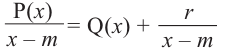
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
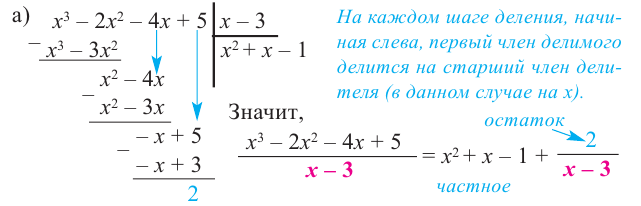
b) При этом 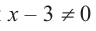 или
или 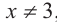 , иначе возникает деление на нуль.
, иначе возникает деление на нуль.
c) Должно выполняться тождество
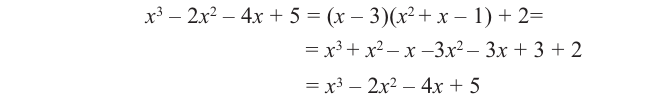
Пример №11
Разделите 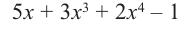 на многочлен
на многочлен 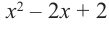 .
.
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0. 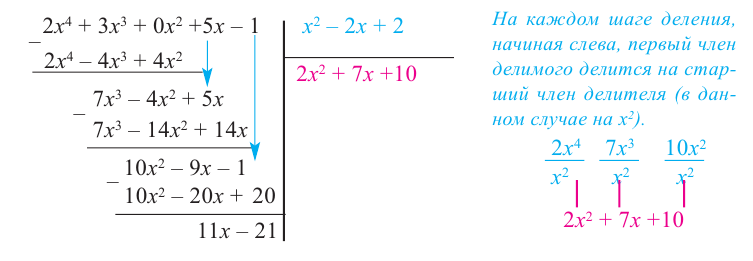
Пример №12
1) Исследуйте деление столбиком многочлена 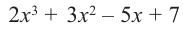 на двучлен
на двучлен 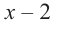 .
.
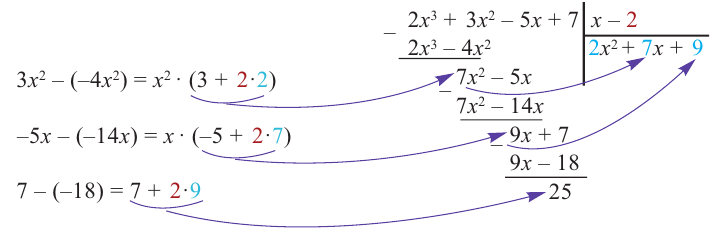
2) На каждом шаге деления делимое делится на старший член делителя, на 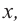 и результат записывается в частное. Установите, как можно найти первый член при делении на каждом из следующих шагов.
и результат записывается в частное. Установите, как можно найти первый член при делении на каждом из следующих шагов.
 Правило синтетического деления многочлена на двучлен
Правило синтетического деления многочлена на двучлен 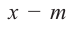 (схема Горнера)
(схема Горнера)
При делении многочлена на двучлен вида 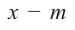 можно использовать метод, альтернативный делению столбиком – метод синтетического деления. При синтетическом делении, используя только коэффициенты, выполняется меньшее количество вычислений.
можно использовать метод, альтернативный делению столбиком – метод синтетического деления. При синтетическом делении, используя только коэффициенты, выполняется меньшее количество вычислений.
Пример №13
Разделите многочлен 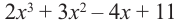 на двучлен
на двучлен 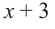 методом синтетического деления.
методом синтетического деления.
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 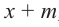 , то его записывают в виде
, то его записывают в виде 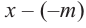 .
.
Запишем двучлен 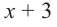 в виде
в виде 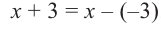 .
.
Таким образом, для делимого 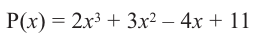 и делителя
и делителя 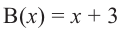 частным будет
частным будет 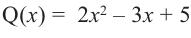 , а остатком
, а остатком 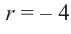 .
.
Деление можно записать в виде: 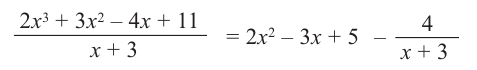 В общем случае, правило синтетического деления (или схема Горнера) многочлена и-ой степени на двучлен х -т приведено в таблице ниже.
В общем случае, правило синтетического деления (или схема Горнера) многочлена и-ой степени на двучлен х -т приведено в таблице ниже.
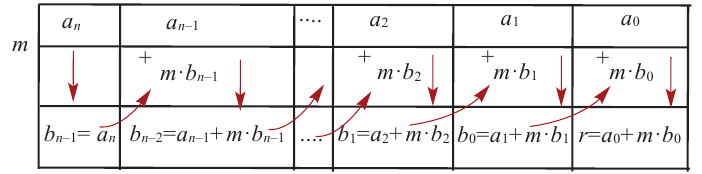
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 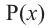 на двучлен
на двучлен 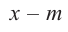 равен значению многочлена
равен значению многочлена 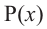 в точке
в точке 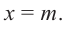
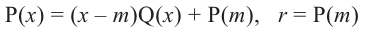
Доказательство: В равенстве 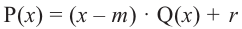 запишем
запишем 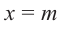 .
. 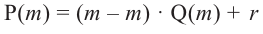 , тогда
, тогда 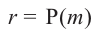 .
.
Пример №14
Найдите остаток от деления многочлена  на двучлен
на двучлен 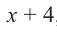 , применив теорему об остатке.
, применив теорему об остатке.
Решение: запишем делитель в виде 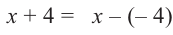 , тогда
, тогда 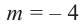 . По теореме об остатке получим, что остаток равен
. По теореме об остатке получим, что остаток равен 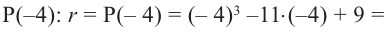
 .
.
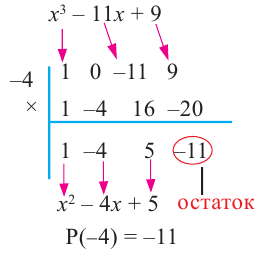
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 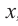 , которые обращают многочлен
, которые обращают многочлен 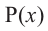 в нуль (т.е. корни уравнения
в нуль (т.е. корни уравнения 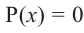 ), называются корнями (или нулями) многочлена.
), называются корнями (или нулями) многочлена.
Теорема. Если число 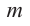 является корнем многочлена
является корнем многочлена 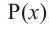 , то двучлен
, то двучлен 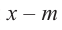 является множителем многочлена
является множителем многочлена 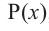 .
.
Действительно, если 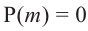 , то из равенства
, то из равенства 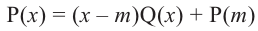 имеем
имеем 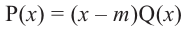 . Верно и обратное утверждение, т.е. если двучлен
. Верно и обратное утверждение, т.е. если двучлен 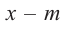 является множителем многочлена
является множителем многочлена 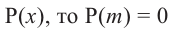 .
.
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 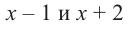 множителями многочлена
множителями многочлена 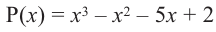 .
.
Решение: вычислим значение многочлена 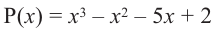 при
при 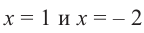 .
.
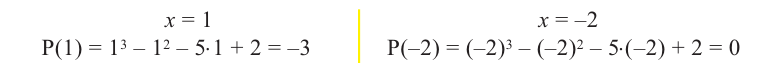
Значит, 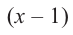 не является множителем, а
не является множителем, а 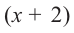 является одним из множителей данного многочлена.
является одним из множителей данного многочлена.
Пример №16
Зная, что 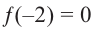 , разложите многочлен
, разложите многочлен 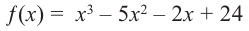 на множители.
на множители.
Решение: так как 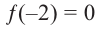 , то двучлен
, то двучлен 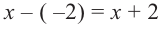 один из множителей многочлена
один из множителей многочлена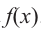 . Другой множитель найдем, используя метод синтетического деления.
. Другой множитель найдем, используя метод синтетического деления.
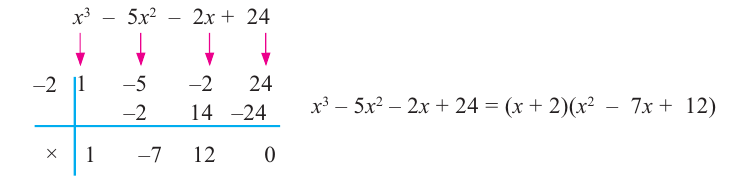
Учитывая, что 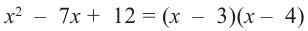 получим:
получим: 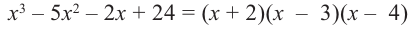 .
.
Отсюда получаем, что 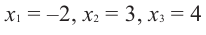 являются нулями многочлена.
являются нулями многочлена.
Примечание: Если многочлен задан в виде 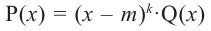 (здесь
(здесь 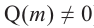 ), то число
), то число 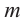 является
является 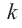 кратным корнем многочлена
кратным корнем многочлена 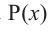 (повторяется
(повторяется 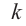 раз). Например, если разложение многочлена на множители имеет вид
раз). Например, если разложение многочлена на множители имеет вид 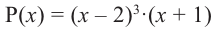 , то число
, то число 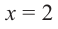 является корнем кратности 3.
является корнем кратности 3.
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 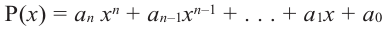 с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
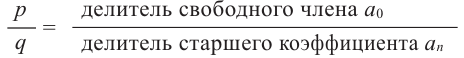
Доказательство. Пусть несократимая дробь 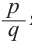 является корнем многочлена
является корнем многочлена 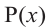 с целыми коэффициентами:
с целыми коэффициентами:
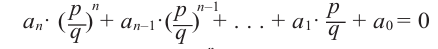
Умножим обе части равенства на 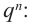
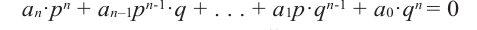
Так как в последнем равенстве каждый член, кроме члена 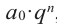 , содержит множитель
, содержит множитель 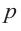 и каждый член, кроме члена
и каждый член, кроме члена 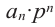 , содержит множитель
, содержит множитель 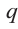 .то коэффициент
.то коэффициент 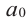 должен делится на
должен делится на 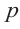 , а коэффициент
, а коэффициент 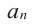 должен делится на
должен делится на 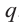 .
.
Пример №17
Найдите рациональные корни многочлена 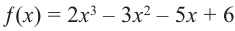 .
.
Решение: свободный член 6, старший коэффициент 2.
Для 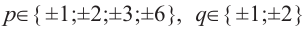 , запишем все возможные числа вида
, запишем все возможные числа вида 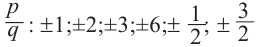
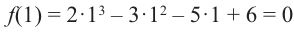 , т.е. одним из множителей является двучлен
, т.е. одним из множителей является двучлен 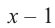 . Другие множители найдем, используя синтетическое деление:
. Другие множители найдем, используя синтетическое деление: 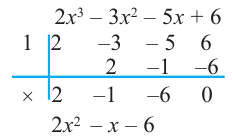
Так как, 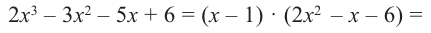
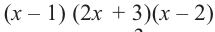 , получим, что
, получим, что 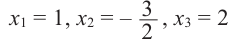 являются корнями многочлена.
являются корнями многочлена.
Следствие 1. Если старший коэффициент 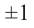 и многочлен имеет рациональный корень, то он является целым числом.
и многочлен имеет рациональный корень, то он является целым числом.
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена 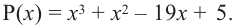
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
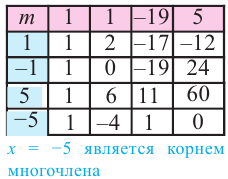
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 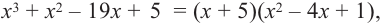 то, решив квадратное уравнение
то, решив квадратное уравнение 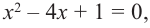 получим другие корни:
получим другие корни: 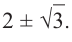 Значит данный многочлен третьей степени имеет три корня:
Значит данный многочлен третьей степени имеет три корня: 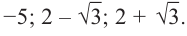
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 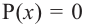 сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми. Например, для нахождения корней многочлена
сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми. Например, для нахождения корней многочлена
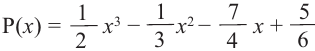 надо умножить все члены уравнения
надо умножить все члены уравнения 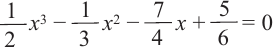 на 12, а затем решить полученное
на 12, а затем решить полученное
уравнение 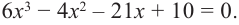
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 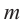 (обращающее значение многочлена в нуль), которое является корнем многочлена, т. е. определяется двучлен
(обращающее значение многочлена в нуль), которое является корнем многочлена, т. е. определяется двучлен 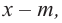 на который многочлен делится без остатка.
на который многочлен делится без остатка.
3. Для данного многочлена при помощи синтетического деления на двучлен 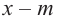 определяется другой множитель.
определяется другой множитель.
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 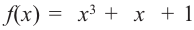 могут являться числа ±1.
могут являться числа ±1.
Проверим: 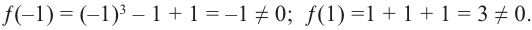 Значит, многочлен
Значит, многочлен 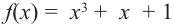 не имеет рациональных корней.
не имеет рациональных корней.
Основная теорема алгебры
Покажем на примере, что многочлен 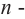 ой степени имеет
ой степени имеет 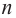 корней.
корней.
Пример №19
Найдите все корни многочлена 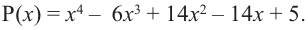
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
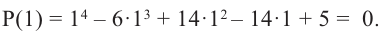
Значит, 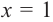 является корнем данного многочлена
является корнем данного многочлена 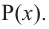 Другие корни найдем синтетическим делением.
Другие корни найдем синтетическим делением.
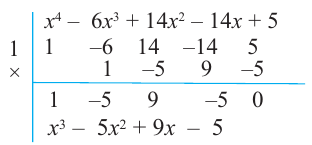
В выражении 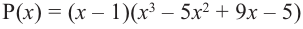 для множителя
для множителя 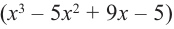 вновь применим теорему о рациональных корнях и синтетическое деление. Тогда
вновь применим теорему о рациональных корнях и синтетическое деление. Тогда 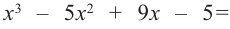
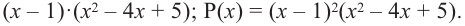 Решим уравнение
Решим уравнение 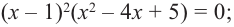
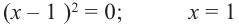 ( корень кратности 2);
( корень кратности 2);
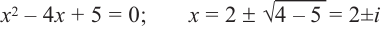
Корни: 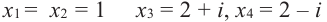
Во всех рассмотренных нами примерах уравнение 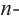 ой степени всегда имеет
ой степени всегда имеет 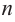 корней, включая кратные корни (действительных или комплексных).
корней, включая кратные корни (действительных или комплексных).
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 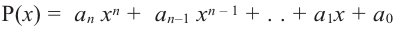 является многочленом ненулевой степени с комплексными коэффициентами, то согласно основной теореме алгебры, у него есть хотя бы один корень
является многочленом ненулевой степени с комплексными коэффициентами, то согласно основной теореме алгебры, у него есть хотя бы один корень 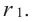 По теореме о разложении многочлена на множители получим
По теореме о разложении многочлена на множители получим 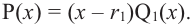 При этом многочлен
При этом многочлен 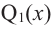 имеет степень
имеет степень 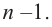 Если
Если 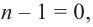 то
то 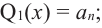 если
если 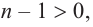 то согласно той же теореме, многочлен
то согласно той же теореме, многочлен 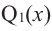 имеет хотя бы один корень. Обозначим его через
имеет хотя бы один корень. Обозначим его через 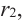 тогда справедливо разложение
тогда справедливо разложение 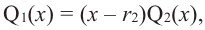 где
где 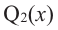 – многочлен степени
– многочлен степени 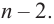 Значит, можно записать
Значит, можно записать 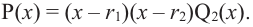 Аналогично, если
Аналогично, если 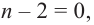 то
то 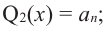 при
при 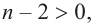 на основании той же теоремы, многочлен
на основании той же теоремы, многочлен 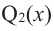 имеет хотя бы один корень. Обозначим его через
имеет хотя бы один корень. Обозначим его через 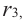 получим
получим 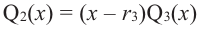 т. е. можно записать
т. е. можно записать 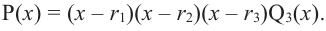
Продолжая процесс 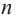 раз, получаем
раз, получаем 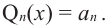 Тогда для многочлена
Тогда для многочлена 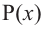 можно записать следующее разложение:
можно записать следующее разложение:
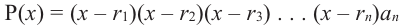
здесь числа  являются нулями многочлена
являются нулями многочлена 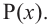 Эти нули могут и не быть различными.
Эти нули могут и не быть различными.
Следствие. Многочлен 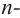 ой степени
ой степени 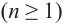 на множестве комплексных чисел имеет ровно
на множестве комплексных чисел имеет ровно 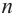 корней, включая кратные корни.
корней, включая кратные корни.
Отметим, что если комплексное число 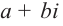 является корнем многочлена с действительными коэффициентами, то сопряженное комплексное число
является корнем многочлена с действительными коэффициентами, то сопряженное комплексное число 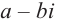 гак же является корнем данного многочлена.
гак же является корнем данного многочлена.
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 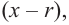 соответствующих действительным корням, и трехчленов вида
соответствующих действительным корням, и трехчленов вида 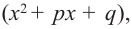 соответствующих сопряженным комплексным корням.
соответствующих сопряженным комплексным корням.
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и 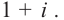
Решение: так как число 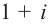 является корнем многочлена, то сопряженное комплексное число
является корнем многочлена, то сопряженное комплексное число 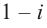 также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде
также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде
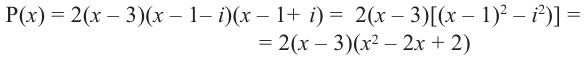
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 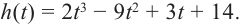 В какие моменты в течении 5 секунд после начала движения кабина карусели находилась на нулевом уровне?
В какие моменты в течении 5 секунд после начала движения кабина карусели находилась на нулевом уровне?
Решение: во всех случаях, кроме значений 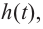 равных нулю, кабина карусели находится либо ниже, либо выше нулевого уровня. Значит, мы должны найти корни заданного многочлена. Применим правило нахождения рациональных корней.
равных нулю, кабина карусели находится либо ниже, либо выше нулевого уровня. Значит, мы должны найти корни заданного многочлена. Применим правило нахождения рациональных корней.
1. Проверим, является ли число 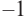 корнем.
корнем.
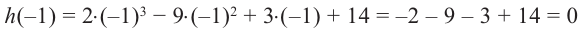
2. Число 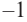 является корнем, значит одним из множителей данного многочлена является
является корнем, значит одним из множителей данного многочлена является  Другие корни найдем при помощи синтетического деления.
Другие корни найдем при помощи синтетического деления.
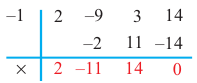
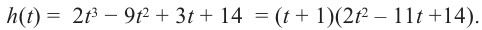
Учитывая, что 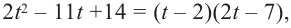 запишем многочлен в виде
запишем многочлен в виде 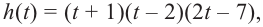 т. е.
т. е. 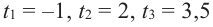 являются корнями уравнения. Значения
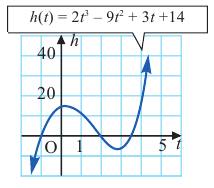
являются корнями уравнения. Значения 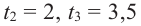 принадлежат временному интервалу в 5 секунд, и в этих моментах кабина карусели находилась на нулевом уровне. То, что корни найдены верно показывает график многочлена, построенный при помощи графкалькулягора.
принадлежат временному интервалу в 5 секунд, и в этих моментах кабина карусели находилась на нулевом уровне. То, что корни найдены верно показывает график многочлена, построенный при помощи графкалькулягора.
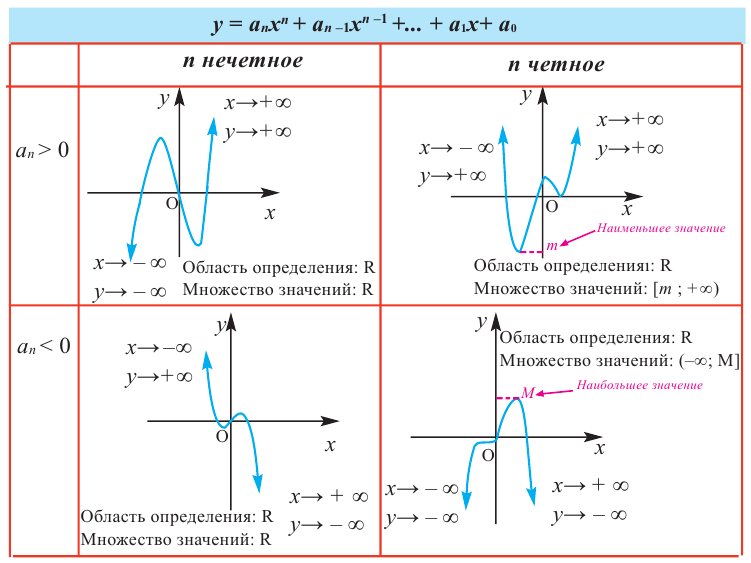
Функция-многочлен
График функции-многочлен
В стандартном виде функция – многочлен записывается как 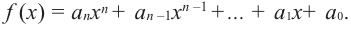 В частном случае, при
В частном случае, при 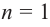 получаем линейную функцию (график – прямая линия), при
получаем линейную функцию (график – прямая линия), при 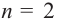 получаем квадратичную функцию (график- парабола). Любой многочлен определен на множестве действительных чисел и его графиком является непрерывная (сплошная) линия.
получаем квадратичную функцию (график- парабола). Любой многочлен определен на множестве действительных чисел и его графиком является непрерывная (сплошная) линия.
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 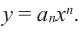 Ниже показаны примеры графиков функции – многочлен и их свойства.
Ниже показаны примеры графиков функции – многочлен и их свойства.
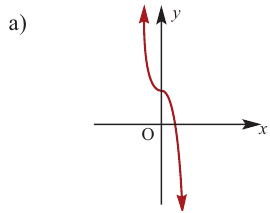
Пример №22
Определите характер поведения функции – многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 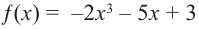 б)
б) 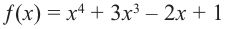
Решение: а) степень многочлена 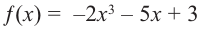 нечетная (равна 3). Коэффициент старшего члена равен
нечетная (равна 3). Коэффициент старшего члена равен 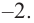 По таблице видно, что в данном случае при
По таблице видно, что в данном случае при 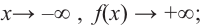 а при
а при 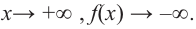
b) степень многочлена 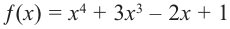 четная (равна 4). Коэффициент старшего члена равен 1. В данном случае при
четная (равна 4). Коэффициент старшего члена равен 1. В данном случае при  при
при 
Пример №23
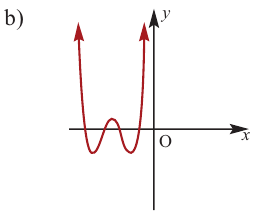
По графику определите как ведет себя функция – многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при 
при 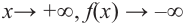
Многочлен нечетной степени
Решение:
при 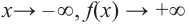
при 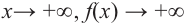
Многочлен четной степени
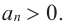
Отметим, что если 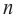 нечетно, то функция – многочлен имеет хотя бы один действительный нуль, если
нечетно, то функция – многочлен имеет хотя бы один действительный нуль, если 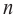 четно, то их вообще может и не быть.
четно, то их вообще может и не быть.
Алгоритм построения эскиза графика функции – многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
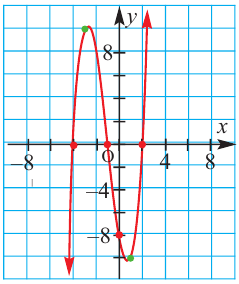
Пример №24
Постройте график функции 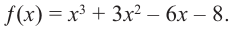
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа 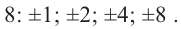
Проверим 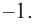
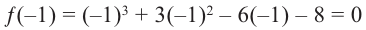
Значит, двучлен 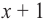 является одним из множителей. Остальные множители найдем синтетическим делением.
является одним из множителей. Остальные множители найдем синтетическим делением.
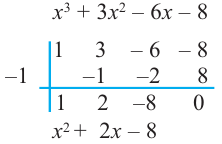
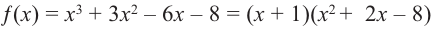
Зная, что 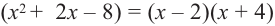 запишем все линейные множители многочлена:
запишем все линейные множители многочлена: 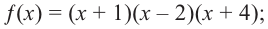
Отсюда находим нули 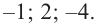 Т. е. график пересекает ось абсцисс в точках
Т. е. график пересекает ось абсцисс в точках 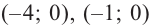 и
и 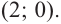 Так как
Так как 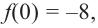 то точка
то точка 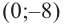 является точкой пересечения с осью
является точкой пересечения с осью 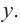 Отметим эти точки на координатной плоскости.
Отметим эти точки на координатной плоскости.
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 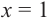 и
и 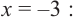
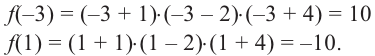
Отметим точки 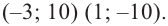
3. Определим, как меняется график при уменьшении или увеличении значений 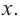 Степень при старшем члене равна 3, а коэффициент положителен, функция нечетная. Значит, при
Степень при старшем члене равна 3, а коэффициент положителен, функция нечетная. Значит, при  при
при 
4. Соединим отмеченные точки и получим схематический график функции 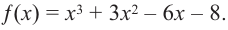
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
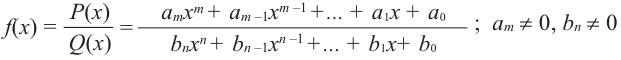
Самым простым примером рациональной функции является функция 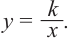
График функции 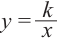 называется гиперболой.
называется гиперболой.
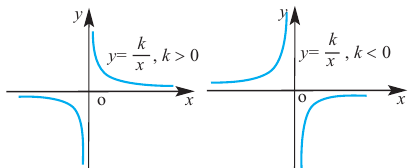
При стремлении значений 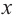 к нулю точки гиперболы стремятся к оси ординат, т е. к прямой
к нулю точки гиперболы стремятся к оси ординат, т е. к прямой 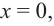 при неограниченном увеличении
при неограниченном увеличении 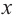 но абсолютному значению точки гиперболы неограниченно приближаются к оси абсцисс, т. е. к прямой
но абсолютному значению точки гиперболы неограниченно приближаются к оси абсцисс, т. е. к прямой 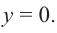 Прямая
Прямая 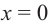 называется вертикальной асимптотой, а прямая
называется вертикальной асимптотой, а прямая 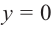 называется горизонтальной асимптотой гиперболы
называется горизонтальной асимптотой гиперболы 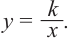 При параллельном переносе гиперболы
При параллельном переносе гиперболы 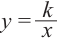 на вектор
на вектор 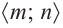 получается график функции
получается график функции 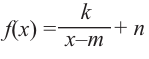 . В этом случае начало координат преобразуется в точку
. В этом случае начало координат преобразуется в точку 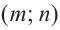 и вертикальной асимптотой становится прямая
и вертикальной асимптотой становится прямая 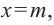 а горизонтальной- прямая
а горизонтальной- прямая 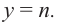
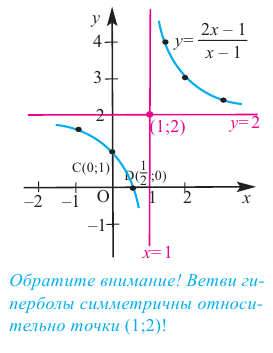
Пример №25
Постройте график функции 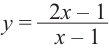
Решение: точки пересечения с осью 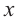 найдем из уравнения
найдем из уравнения 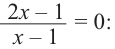
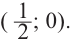
При 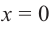 получим
получим 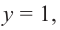 и график пересекает ось
и график пересекает ось 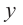 в точке
в точке 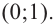 Разделим почленно числитель функции на знаменатель и запишем ее в виде
Разделим почленно числитель функции на знаменатель и запишем ее в виде 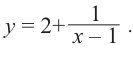 Прямая
Прямая 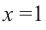 является вертикальной асимптотой, а прямая
является вертикальной асимптотой, а прямая 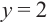 – горизонтальной асимптотой. Зададим таблицу значений для нескольких точек справа и слева от вертикальной асимптоты
– горизонтальной асимптотой. Зададим таблицу значений для нескольких точек справа и слева от вертикальной асимптоты
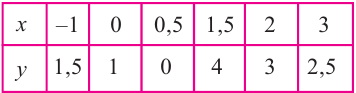
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 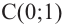 и
и 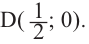
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 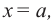 а числитель отличен от нуля, то данная функция имеет вертикальную асимптоту. Горизонтальные асимптоты для рациональной функции
а числитель отличен от нуля, то данная функция имеет вертикальную асимптоту. Горизонтальные асимптоты для рациональной функции  определяются в соответствии со степенью
определяются в соответствии со степенью  и
и 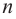 данных многочленов
данных многочленов 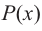 и
и 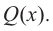
Для 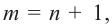 т. е. если степень многочлена в числителе на 1 единицу больше степени многочлена в знаменателе, частное, полученное при делении, имеет вид
т. е. если степень многочлена в числителе на 1 единицу больше степени многочлена в знаменателе, частное, полученное при делении, имеет вид 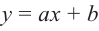 и является линейной функцией. При возрастании
и является линейной функцией. При возрастании 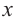 по абсолютному значению график функции приближается к данной прямой. В этом случае говорят, что прямая
по абсолютному значению график функции приближается к данной прямой. В этом случае говорят, что прямая 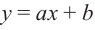 является наклонной асимптотой.
является наклонной асимптотой.
Пример №26
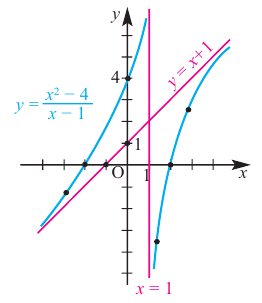
Найдите асимптоты и схематично изобразите график функции
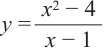
Решение: Точки пересечения с осью 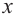 найдем из уравнения
найдем из уравнения 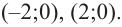 При
При 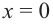 получим
получим 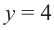 и график пересекает ось
и график пересекает ось 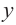 в точке
в точке 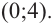 При
При 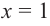 знаменатель обращается в нуль, а числитель отличен от нуля. Значит, прямая
знаменатель обращается в нуль, а числитель отличен от нуля. Значит, прямая 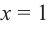 является вертикальной асимптотой. Горизонтальной асимптоты у данной функции нет
является вертикальной асимптотой. Горизонтальной асимптоты у данной функции нет 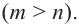 Разделив числитель на знаменатель, запишем функцию в виде:
Разделив числитель на знаменатель, запишем функцию в виде:
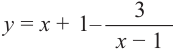
Для больших, но модулю, значений 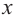 дробь
дробь 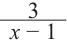 по абсолютному значению уменьшается и график заданной функции бесконечно приближается к прямой
по абсолютному значению уменьшается и график заданной функции бесконечно приближается к прямой 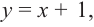 т. е. прямая
т. е. прямая 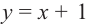 является наклонной асимптотой данной функции. Составим таблицу значений для некоторых точек слева и справа от вертикальной оси.
является наклонной асимптотой данной функции. Составим таблицу значений для некоторых точек слева и справа от вертикальной оси.
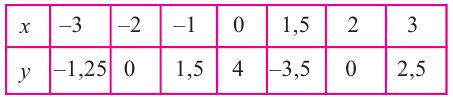
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
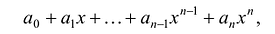 , где
, где 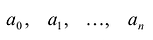 – действительные или комплексные числа, называемые коэффициентами, n – натуральное число, х – переменная величина, принимающая произвольные числовые значения.
– действительные или комплексные числа, называемые коэффициентами, n – натуральное число, х – переменная величина, принимающая произвольные числовые значения.
Если коэффициент 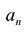 при
при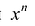 многочлена
многочлена 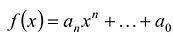 отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число n называется степенью многочлена,
отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число n называется степенью многочлена, 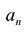 – старшим коэффициентом, а
– старшим коэффициентом, а 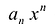 – старшим членом многочлена. Коэффициент
– старшим членом многочлена. Коэффициент 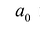 называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 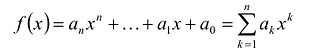 и
и 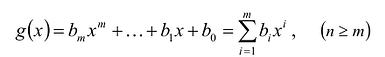 называется многочлен
называется многочлен
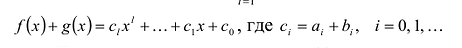
Произведением многочленов 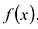 и
и 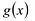 называется многочлен:
называется многочлен: 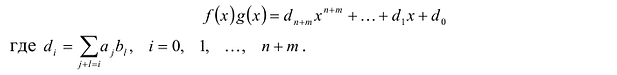
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 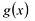 называется делителем многочлена
называется делителем многочлена 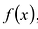 , если существует многочлен
, если существует многочлен 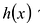 такой, что
такой, что 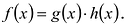
Теорема о делении с остатком
Для любых многочленов 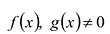 существуют многочлены
существуют многочлены 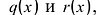 такие, что
такие, что 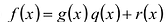 причем степень
причем степень 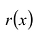 меньше степени g(x) или
меньше степени g(x) или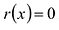 . Многочлены g(x) и r(x) определены однозначно.
. Многочлены g(x) и r(x) определены однозначно.
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит  , то остаток
, то остаток 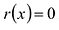 .
.
Число с называется корнем многочлена  , если
, если  .
.
Теорема Безу
Число с является корнем многочлена  тогда и только тогда, когда
тогда и только тогда, когда  делится на x – с.
делится на x – с.
Пусть с – корень многочлена  , т.е.
, т.е. . Разделим
. Разделим  на
на
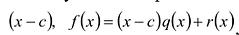 где степень r(х) меньше степени (x-с) которая равна 1. Значит, степень г(х) равна 0, т.е. r(х) = const. Значит,
где степень r(х) меньше степени (x-с) которая равна 1. Значит, степень г(х) равна 0, т.е. r(х) = const. Значит, 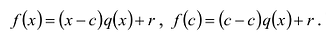 . Так как
. Так как  , то из последнего равенства следует, что r=0, т.е.
, то из последнего равенства следует, что r=0, т.е. 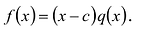
Обратно, пусть (х-с) делит  , т.е.
, т.е. 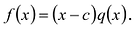 . Тогда
. Тогда 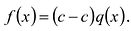
Следствие. Остаток от деления многочлена  на (x-с) равен
на (x-с) равен 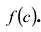 .
.
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена  равносильно разысканию его линейных делителей со старшим коэффициентом 1.
равносильно разысканию его линейных делителей со старшим коэффициентом 1.
Многочлен  можно разделить на линейный многочлен х-с с помощью алгоритма деления с остатком, но существует более удобный способ деления, известный под названием схемы Горнера.
можно разделить на линейный многочлен х-с с помощью алгоритма деления с остатком, но существует более удобный способ деления, известный под названием схемы Горнера.
Пусть 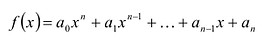 и пусть
и пусть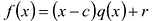 где
где 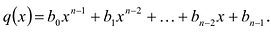 Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и правой частях последнего равенства, имеем:
Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и правой частях последнего равенства, имеем:
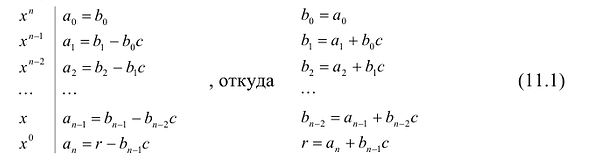
Число с-называется корнем кратности к многочлена  , если
, если 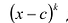 делит
делит  , но
, но 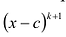 уже не делит
уже не делит  .
.
Чтобы поверить, будет ли число с корнем многочлена  и какой кратности, можно воспользоваться схемой Горнера. Сначала
и какой кратности, можно воспользоваться схемой Горнера. Сначала  делится на х-с, затем, если остаток равен нулю, полученное частное делится на х-с, и т.д. до получения не нулевого остатка.
делится на х-с, затем, если остаток равен нулю, полученное частное делится на х-с, и т.д. до получения не нулевого остатка.
Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 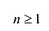 имеет в С (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.
имеет в С (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.

где 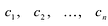 – корни
– корни  , т.е. во множестве С всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то:
, т.е. во множестве С всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то: 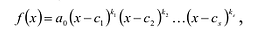 где
где 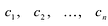 уже различные корни
уже различные корни  ,
, 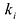 – кратность корня
– кратность корня 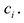
Если многочлен 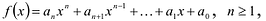 , с действительными коэффициентами имеет корень с, то число с также корень
, с действительными коэффициентами имеет корень с, то число с также корень 
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 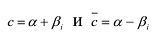 корни
корни  Тогда
Тогда  делится на х-с и
делится на х-с и 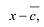 , но так как у
, но так как у 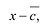 и х-с, нет общих делителей, то
и х-с, нет общих делителей, то  делится на произведение
делится на произведение 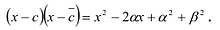
Утверждение 2. Многочлен с действительными коэффициентами степени 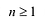 всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где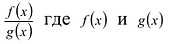 многочлены с действительными коэффициентами, причем многочлен
многочлены с действительными коэффициентами, причем многочлен 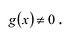 Рациональная дробь
Рациональная дробь  называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде
называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде 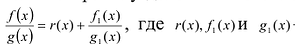 некоторые многочлены, а
некоторые многочлены, а 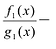 правильная рациональная дробь.
правильная рациональная дробь.
Лемма 1, Если  правильная рациональная дробь, а число
правильная рациональная дробь, а число 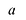 является вещественным корнем кратности
является вещественным корнем кратности 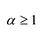 многочлена
многочлена 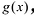 , т.е.
, т.е.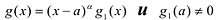 , то существует вещественное число A и многочлен
, то существует вещественное число A и многочлен 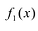 с вещественными коэффициентами, такие, что
с вещественными коэффициентами, такие, что 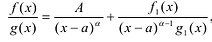 где дробь
где дробь 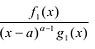 является правильной.
является правильной.
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если  правильная рациональная дробь, а число
правильная рациональная дробь, а число является корнем кратности
является корнем кратности 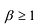 многочлена g(x), т.е.
многочлена g(x), т.е. 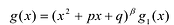 и если
и если 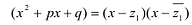 , то существуют вещественные числа M и N многочлен
, то существуют вещественные числа M и N многочлен 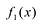 с вещественными коэффициентами, такие,
с вещественными коэффициентами, такие, 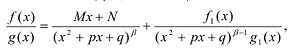 где дробь ,
где дробь , 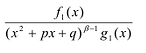 также является правильной.
также является правильной.
Рациональные дроби вида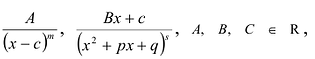
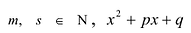 – трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
– трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 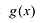 равна n, то в числителе после приведения к общему знаменателю получается многочлен степени n-1, т.е. многочлен
равна n, то в числителе после приведения к общему знаменателю получается многочлен степени n-1, т.е. многочлен 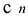 коэффициентами.
коэффициентами.
Число неизвестных 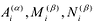 ‘ также равняется n:
‘ также равняется n: 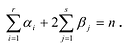
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
Разложение многочлена на множители. Часть 3. Теорема Безу и схема Горнера
Разложение многочлена на множители. Теорема Безу и схема Горнера
При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим, каким образом это сделать проще всего.
Как обычно, обратимся за помощью к теории.
Теорема Безу утверждает, что остаток от деления многочлена ![]() на двучлен
на двучлен ![]() равен
равен ![]() .
.
Но для нас важна не сама теорема, а следствие из нее:
Если число ![]() является корнем многочлена
является корнем многочлена ![]() , то многочлен
, то многочлен ![]() делится без остатка на двучлен
делится без остатка на двучлен ![]() .
.
Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на ![]() , где
, где ![]() – корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.
– корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.
Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.
Остановимся подробнее на этих моментах.
1. Как найти корень многочлена.
Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.
Здесь нам помогут такие факты:
Если сумма всех коэффициентов многочлена равна нулю, то число ![]() является корнем многочлена.
является корнем многочлена.
Например, в многочлене ![]() сумма коэффициентов равна нулю:
сумма коэффициентов равна нулю: ![]() . Легко проверить, что
. Легко проверить, что ![]() является корнем многочлена.
является корнем многочлена.
Если сумма коэффициентов многочлена при четных степенях ![]() равна сумме коэффициентов при нечетных степенях, то число
равна сумме коэффициентов при нечетных степенях, то число ![]() является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку
является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку ![]() , а
, а ![]() – четное число.
– четное число.
Например, в многочлене ![]() сумма коэффициентов при четных степенях
сумма коэффициентов при четных степенях ![]() :
: ![]() , и сумма коэффициентов при нечетных степенях
, и сумма коэффициентов при нечетных степенях ![]() :
: ![]() . Легко проверить, что
. Легко проверить, что ![]() является корнем многочлена.
является корнем многочлена.
Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.
Для приведенного многочлена степени ![]() (то есть многочлена, в котором старший коэффициент – коэффициент при
(то есть многочлена, в котором старший коэффициент – коэффициент при ![]() – равен единице) справедлива формула Виета:
– равен единице) справедлива формула Виета:
![]() , где
, где ![]() – корни многочлена
– корни многочлена ![]() .
.
Если многочлен не является приведенным, то его можно сделать таковым, разделив на старший коэффициент.
Есть ещё ![]() формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.
формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.
Из этой формулы Виета следует, что если корни приведенного многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.
Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.
Рассмотрим, например, многочлен ![]() .
.
Для этого многочлена произведение корней равно ![]()
Делители числа ![]() :
: ![]() ;
; ![]() ;
; ![]()
Сумма всех коэффициентов многочлена равна ![]() , следовательно, число 1 не является корнем многочлена.
, следовательно, число 1 не является корнем многочлена.
Сумма коэффициентов при четных степенях ![]() :
: ![]()
Сумма коэффициентов при нечетных степенях ![]() :
: ![]()
![]() , следовательно, число -1 также не является корнем многочлена.
, следовательно, число -1 также не является корнем многочлена.
Проверим, является ли число 2 корнем многочлена: ![]() , следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен
, следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен ![]() делится без остатка на двучлен
делится без остатка на двучлен ![]() .
.
2. Как разделить многочлен на двучлен.
Многочлен можно разделить на двучлен столбиком.
Разделим многочлен ![]() на двучлен
на двучлен ![]() столбиком:
столбиком:

Есть и другой способ деления многочлена на двучлен – схема Горнера.

Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.
Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 – так же, как при составлении таблицы для схемы Горнера.
Итак, если нам нужно разделить многочлен ![]() на двучлен
на двучлен ![]() и в результате деления мы получаем многочлен
и в результате деления мы получаем многочлен ![]() , то коэффициенты многочлена
, то коэффициенты многочлена ![]() мы можем найти по схеме Горнера:
мы можем найти по схеме Горнера:

Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число ![]() является корнем многочлена
является корнем многочлена ![]() , то остаток от деления многочлена на
, то остаток от деления многочлена на ![]() равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.
равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.
Используя схему Горнера, мы “убиваем двух зайцев”: одновременно проверяем, является ли число ![]() корнем многочлена
корнем многочлена ![]() и делим этот многочлен на двучлен
и делим этот многочлен на двучлен ![]() .
.
Пример. Решить уравнение:
![]()
1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.
Делители числа 24: ![]()
2. Проверим, является ли число 1 корнем многочлена.
Сумма коэффициентов многочлена ![]() , следовательно, число 1 является корнем многочлена.
, следовательно, число 1 является корнем многочлена.
3. Разделим исходный многочлен на двучлен ![]() с помощью схемы Горнера.
с помощью схемы Горнера.
А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.

Так как член, содержащий ![]() отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при
отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при ![]() пишем 0. Слева пишем найденный корень: число 1.
пишем 0. Слева пишем найденный корень: число 1.
Б) Заполняем первую строку таблицы.

В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен ![]() без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:
без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:
![]()
Будем делить дальше. Нам нужно найти корни многочлена ![]() . Корни также ищем среди делителей свободного члена, то есть теперь уже числа -24.
. Корни также ищем среди делителей свободного члена, то есть теперь уже числа -24.
Легко проверить, что числа 1 и -1 не являются корнями многочлена ![]()
В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена ![]() :
:

Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.
В последнем столбце мы получили -40 – число, не равное нулю, следовательно, многочлен ![]() делится на двучлен
делится на двучлен ![]() с остатком, и число 2 не является корнем многочлена.
с остатком, и число 2 не является корнем многочлена.
Идем дальше.
В) Проверим, является ли число -2 корнем многочлена ![]() . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:
. Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:

Отлично! В остатке мы получили ноль, следовательно, многочлен ![]() разделился на двучлен
разделился на двучлен ![]() без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена
без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена ![]() на двучлен
на двучлен ![]() в таблице изображены зеленым цветом.
в таблице изображены зеленым цветом.
![]()
В результате деления мы получили квадратный трехчлен ![]() , корни которого легко находятся по теореме Виета:
, корни которого легко находятся по теореме Виета: ![]()
Итак, корни исходного уравнения ![]() :
:
{![]() }
}
Ответ: {![]() }
}
И.В. Фельдман, репетитор по математике.
Итак,
мы
показали в п. 4, что достаточным условием
приводимости многочлена над полями С,
R,
Q
является наличие хотя бы одного корня
многочлена f(x)
в поле С, R
или Q.
Дня отыскания этих корней приходится
решать уравнения n
– ой степени в поле С, R
или Q.
Мы уже отмечали, что если
многочлен
f(x)
имеет рациональный корень, то он приводим
и над полем R,
и над С. Поэтому, обычно, решение задачи
о приводимости многочлена начинается
с поиска его рациональных корней.
Необходимые, но не достаточные условия
существования рациональных корней
многочлена с целыми коэффициентами
даёт следующая теорема.
Теорема
1.
Если
![]() –
–
рациональный корень многочленаf(x)
с целыми коэффициентами, причем (p,
q)
= l,
то числитель дроби (р) является делителем
свободного члена а0,
а знаменатель (q)
является делителем старшего коэффициента
аn.
Доказательство.
Пусть
![]() –
–
корень многочленаf(x)=anxn
+
an-1xn-1
+…+
a1x
+ a0,
где все аi
Î
Z.
Подставим
![]() ,
,
где (p,
q)
= l,
q
¹
1 в многочлен, получим:
![]() (1)
(1)
Умножим
обе части равенства (1) на qn,
тогда:
anpn
+
an-1qpn-1
+…+
a1
pqn-1
+
a0qn
= 0 (2)
Из равенства (2)
сначала можно выразить
anpn
= (-an-1pn-1
-…- a1pqn-2
–
a0qn-1)q
=> (аn
/q),
а
потом
-a0qn
=
p(anpn-1
+
an-1pn-2q+…
…+ а1qn-l)
=> (а0
/p) т.к.
(p, q) = 1
Замечание
1.
Так как
Z,
0 имеет лишь конечное число делителей,
то теорема позволяет, путем конечного
числа шагов, найти все рациональные
числа многочлена или проверить что их
нет.
Следствие
1.
Нормированный многочлен f
(x)
Z[x]
не имеет дробных корней;
Следствие
2.
Целый корень многочлена f(x)Z[x]
является
делителем свободного члена.
Задача
1.
Разложить многочлен
f(x)
= x6
– 2х5
+ х4
+ 6х3
– 10х2
– 4х + 8
над
полями Q,
R
и С.
Решение.
На
основании теоремы (1), рациональные корни
данного многочлена следует искать среди
делителей числа 8, т.к. аn
=
1
Делители:
+ 1, ±2,
±4,
±8.
Известно,
что число ()
является корнем многочлена f(x)
тогда и только тогда, когда f(x)
делится на (х
– )
(Смотри п. 4). Следовательно, для проверки,
какие из чисел ±1, ±2, ±4, ±8 являются
рациональными корнями, можно использовать
схему Горнера, а можно непосредственно
проверить, будет ли f(±1)
= 0, f(±2)
= 0,
f(±4)
= 0, f(±8)
= 0.
|
1 |
-2 |
1 |
6 |
-10 |
-4 |
8 |
|
|
1 |
1 |
-1 |
0 |
6 |
-4 |
-8 |
0 |
|
1 |
1 |
0 |
0 |
6 |
2 |
-6 |
|
|
-1 |
1 |
-2 |
2 |
4 |
-8 |
0 |
|
|
-1 |
1 |
-3 |
5 |
-1 |
-7 |
||
|
2 |
1 |
0 |
2 |
8 |
8 |
||
|
-2 |
1 |
-4 |
10 |
-16 |
24 |
||
|
4 |
1 |
2 |
10 |
44 |
166 |
||
|
-4 |
1 |
-6 |
26 |
… |
0 |
||
|
8 |
1 |
6 |
50 |
… |
0 |
||
|
-8 |
1 |
-10 |
42 |
… |
- |
Итак,
f(x)
= (x
– l)(x
+ l)(
x4
–
2x3
+
2x2
+
4x
– 8) над полем Q.
Чтобы
найти разложение над полями R
и С, нужно найти действительные и
комплексные корни этого многочлена,
для этого надо решить уравнение четвертой
степени х4
–
2х3
+
2х2
+
4х – 8 = 0.
Для
решения уравнений 4-ой степени разработан
частный метод
Феррари.
1-й шаг. Оставляем
в левой части равенства члены 4-ой и 3-ей
степени, остальные переносим в правую
часть, получим:
х4
–
2х3
=
-2х2
–
4х + 8
2-й
шаг. Дополняем левую часть равенства
до полного квадрата: х4
–
2х3
+
х2
=
х2
–
2х2
–
4х + 8
(х2
–
х)2
=
-х2
–
4х + 8
3-й шаг. Вводим
новую переменную (у) и дополняем левую
часть еще раз до полного квадрата,
получим:
(х2
–
х)2+2(х2–
x)у
+ у2
=
-х2
–
4х + 8 + 2(х2
–
х)у +
y2
[(x2-x)+y)]2
= (2y-1)x2+(-2y-4)x+(y2+8)
*
4-й
шаг. Потребуем, чтобы правая часть
также стала полным
квадратом,
для этого D
= В2
– 4АС = О
D=(-2y
– 4)2
–
4(2y
– l)(y2
+
8) = 0
у3
–
у2
+
6у – 6 = 0
Это
уравнение имеет рациональный корень
у0
=
1.
5-й
шаг. Подставим у0
в правую
и
левую части уравнения (*) вместо у.
Получим: (х2-х+1)2
= х2-6х+9
= (х-3)2
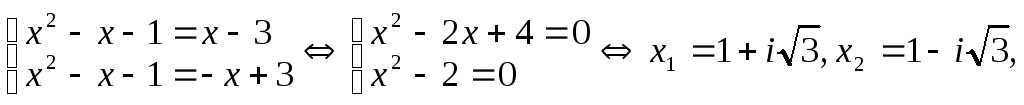
x3
=
-2,
x4
=
2
Итак,
многочлен f(x)
над полем С может быть представлен в
виде: f(х)
= (х – 1)(х + 1)(х + 2)(х
– 2)(x
– 1- i3)(x
– 1 + i3)
Для
того, чтобы найти разложение многочлена
над полем R,
нужно перемножить две последние скобки,
тогда:
f(х)
= (х – 1)(х + 1)(х + 2)(x
–
2)((х
– 1)2
+ 3).
Задача
2.
Разложить многочлен f(x)
= х4
– 2х3
– 6х2
– 4х – 1
Решение.
Так как многочлен
4-ой степени, то можно методом Феррари
сразу искать его действительные и
комплексные корни, а можно как и в первом
случае, найти сначала рациональные
корни (если они есть).
Так
как аn
= 1, то многочлен может иметь в качестве
рациональных корней целые числа, которые
являются делителями свободного члена
а0
= 1, т.е. ±1. Непосредственной подстановкой
убеждаемся, что (-1) является корнем, а
(1) нет, т.к. f(-l)
= 0, f(l)
¹
0.
Тогда,
f(x)
= (х + 1)( х3
– 3х2
– 3х – 1) над полем Q.
Теперь
найдем корни многочлена в поле С и R.
Для этого решим
уравнение:
х3
– 3х2
– 3х – 1 = 0.
Это
уравнение 3-ей степени, для таких уравнений
также существует частный метод решения
– метод
Кардано.
1-
й шаг. Приведем уравнение к виду, не
содержащему второй степени неизвестного.
Для этого введем подстановку
![]() где (а) коэффициент при х2
где (а) коэффициент при х2
.
Тогда,
(у + 1)3
– 3(у + 1)2
– 3(у + 1) – 1 = 0. Раскрыв скобки и приведя
подобные, получим: у3
– 6у – 6 = 0.
2-й
шаг. Полагаем, что у
=
+ ,
где
![]()
![]() ,
,
р – коэффициент при у,q
– свободный член.
В
нашем случае р = -6, q
= -6 Поэтому
 тогда
тогда![]() .
.
Тогда,
![]() ,
,
Наконец, находим
(х) из формулы х = у + 1
![]() ,
,
Тогда,
f(x)
= (x
+ l)(x
– x1)(x
– x2)(x
– x3)
– разложение многочлена над полем С.
Для
нахождения разложения многочлена f(x)
над полем действительных чисел R
достаточно в полученном выше разложении
перемножить скобки, соответствующие
сопряженным комплексным корням.
Тогда:
![]() над полемR.
над полемR.
Замечание
2.
Если дан многочлен f(х),
степень которого выше четвертой, причем
он не имеет рациональных корней, то
задача разложения многочлена f(x)
на неприводимые многочлены над полем
С и R
становится трудноразрешимой, т.к. общих
методов решения уравнений n-ой
степени, где n
> 4 не существует.
Существуют
различные методы приближенного вычисления
действительных корней многочлена f(x)
(метод хорд, метод касательных и т.п.)
Замечание
3.
В том случае, когда нужно найти сумму
корней многочлена f(x),
могут быть использованы формулы Виета,
которые устанавливают зависимость
между корнями и коэффициентами многочлена.
Выведем эти формулы:
Пусть
f(z)
= zn
+
c1zn-1
+
c2zn-2
+…+ cn-1z
+ cn
и 1,
2,…,
n
корни
этого многочлена в поле С, тогда
zn
+
c1zn-1
+
c2zn-2
+… + cn-1z
+ cn
= (z
– a1)(z
– a2)…(z
– an)
= = zn
– (a1
+ a2
+…+
an)zn-1
+ (a1a2
+ a1a3
+…+
an-1an)zn-2
+…+
+(-1)n
(a1a2
…an)
Приравняв
коэффициенты при соответствующих
степенях, получим формулы Виета:
с1
=
-(a1
+ a2
+…+ an)
с2
= (a1a2
+ a1a3
+…+
an-1an)
c3
= -(a1a2a3+
a1a2a4
+…+ an-2an-1an)
сn
=
(-1)n
(a1a2
…an)
Задача
3.
Найти сумму кубов корней многочлена
f(x)
= x4
+ 2х3
+ х2
+ 5х + 3, f(x)Q[x]
Решение.
Над
полем комплексных чисел С многочлен
f(x)
имеет четыре корня: х1,
х2,
х3,
х4.
Нам нужно найти X13+
X23+
X33+
X43
не находя самих корней.
По формулам Виета
х1+x2+
х3+
х4
= -2 =1
х1х2
+
х1х3
+
х1х4
+
x2x3+
х2х4
+
х3х4
=
1 = 2
х1х2х3
+ x1x2x4
+ х1х3х4
+
х2х3х4
= -5 = s3
х1х2х3х4
= 3 = s4
Тогда
X13+
X23+
X33+
X43
= 13
–
312
+ 33
=
=(-2)3
– 3(-2)l
+ 3(-5) = -17
Ответ: -17.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Схема Горнера
11 июля 2022
Схема Горнера — это алгоритм для быстрого (счёт идёт на секунды) вычисления значения многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
в точке $x=a$. Также схема Горнера позволяет быстро (быстрее, чем столбиком) делить многочлен $Pleft( x right)$ на линейные двучлены вида $x-a$, искать остатки от деления и многое другое.
Содержание
- Описание Схемы Горнера
- Вычисление значения многочлена
- Деление многочлена с остатком
- Перебор корней уравнения
- Разложение на множители
- Разложение по степеням
- Как всё это работает
1. Описание схемы Горнера
Итак, рассмотрим многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
Для наглядности коэффициенты выделены синим цветом. Распишем схему Горнера для многочлена $Pleft( x right)$ в точке $x=color{red}{a}$. Для этого заполним таблицу
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {} & {} & {} & {} & {} & {} \ end{array}]
В первой строке мы видим коэффициенты многочлена $Pleft( x right)$ в порядке убывания степеней. Таких коэффициентов всегда на один больше, чем степень многочлена: для квадратного многочлена всего 3 коэффициента, для кубического — уже 4, и т.д.
Во второй строке таблицы мы вписываем лишь число $color{red}{a}$ в самой левой клетке. Остальные клетки заполняются последовательно по следующему алгоритму.
В первую свободную клетку мы переносим элемент из верхней строки без изменений. Назовём этот элемент ${{b}_{n-1}}$ — дальше вы поймёте, зачем нужна такая нумерация:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}}={{a}_{n}} & {} & {} & {} & {} & {} \ end{array}]
Вторая клетка — элемент ${{b}_{n-2}}$ — считается по формуле ${{b}_{n-2}}={{b}_{n-1}}cdot color{red}{a}+color{blue}{{a}_{n-1}}$. Другими словами, берём элемент слева, умножаем на число $a$ и добавляем элемент сверху:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}}={{b}_{n-1}}cdot color{red}{a}+color{blue}{{a}_{n-1}} & {} & {} & {} & {} \ end{array}]
Далее находим элемент ${{b}_{n-3}}$ по аналогичной формуле: ${{b}_{n-3}}={{b}_{n-2}}cdot color{red}{a}+color{blue}{{a}_{n-2}}$. Заносим результат в третью клетку:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}a & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}}={{b}_{n-2}}cdot color{red}{a}+color{blue}{{a}_{n-2}} & {} & {} & {} \ end{array}]
Аналогично находим элементы ${{b}_{n-4}}$, ${{b}_{n-5}}$ и далее. Берём элемент слева, умножаем на исходное число $color{red}{a}$, добавляем элемент сверху, результат записываем в клетку:
[{{b}_{k-1}}={{b}_{k}}cdotcolor{red}{a}+color{blue}{{a}_{k}}]
В какой-то момент мы доберёмся до элемента ${{b}_{0}}$, который находится в клетке под коэффициентом $color{blue}{{a}_{1}}$:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}}={{b}_{1}}cdot color{red}{a}+color{blue}{{a}_{1}} & {} \ end{array}]
Элемент в последней клетке считается по той же схеме: ${{b}_{0}}cdot color{red}{a}+color{blue}{{a}_{0}}$. Обозначим его буквой $r$:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r={{b}_{0}}cdot color{red}{a}+color{blue}{{a}_{0}} \ end{array}]
Итак, мы заполнили все клетки и получили таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Схема заполнения этой таблицы как раз и называется схемой Горнера. Найденные элементы ${{b}_{n-1}}$, …, ${{b}_{0}}$ и $r$ позволяют переписать исходный многочлен $Pleft( x right)$ в виде
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
Такая запись оказывается грозным оружием для решения задач с многочленами, если знать её свойства. И сегодня мы изучим все эти свойства, но сначала немного практики.
Пример 1. Простой многочлен
Заполните таблицу по схеме Горнера для многочлена
[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]
в точке $x=3$.
Решение. Для начала аккуратно запишем коэффициенты исходного многочлена. Для наглядности они вновь помечены синим:
[Pleft( x right)= color{blue}{2}cdot {{x}^{4}}+left( color{blue}{-7} right)cdot {{x}^{3}}+color{blue}{1}cdot {{x}^{2}}+color{blue}{2} cdot x+left( color{blue}{-3} right)]
Составим таблицу. Поскольку степень многочлена $deg Pleft( x right)=4$, в таблице будет пять основных столбцов и один дополнительный столбец слева, в котором мы запишем число $x=color{red}{3}$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & {} & {} & {} & {} & {} \ end{array}]
Заполняем пустые клетки во второй строке. В первую клетку переносим без изменений элемент сверху:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & {} & {} & {} & {} \ end{array}]
Элемент во второй клетке считается по формуле $2cdot color{red}{3}+left( color{blue}{-7} right)=-1$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & {} & {} & {} \ end{array}]
Третью и четвёртую клетку заполняем аналогично: сначала $-1cdot color{red}{3}+color{blue}{1}=-2$, затем $-2cdot color{red}{3}+color{blue}{2}=-4$:
[begin{array}{c|c|r|r|r|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & {} \ end{array}]
Наконец, последняя клетка: $-4cdot color{red}{3}+left( color{blue}{-3} right)=-15$:
[begin{array}{c|c|r|r|r|r} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & -15 \ end{array}]
Готово! Мы заполнили таблицу по схеме Горнера.
Пример 2. Пропущенные коэффициенты
Заполните таблицу по схеме Горнера для многочлена
[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-4]
в точке $x=1$.
Решение. Обратите внимание: в записи многочлена отсутствуют одночлены ${{x}^{2}}$ и $x$. Другими словами, коэффициенты в этих двух одночленах равны нулю:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+color{blue}{0}cdot {{x}^{2}}+color{blue}{0} cdot x+left( color{blue}{-4} right)]
Для наглядности мы вновь отметили коэффициенты синим цветом — всего их снова пять, т.е. на один больше степени многочлена. И все они переносятся в таблицу. Пропуск нулевых коэффициентов будет грубой ошибкой:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & {} & {} & {} & {} & {} \ end{array}]
Заполняем таблицу по схеме Горнера. Первый элемент переносим сверху:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & {} & {} & {} & {} \ end{array}]
Второй, третий и четвёртый элемент считаем по формуле: $1cdot color{red}{1}+color{blue}{3}=4$; $4cdot color{red}{1}+color{blue}{0}=4$; $4cdot color{red}{1}+color{blue}{0}=4$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & {} \ end{array}]
Наконец, последний элемент таблицы: $4cdot color{red}{1}+left( color{blue}{-4} right)=0$:
[begin{array}{c|c|c|c|c|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & 0 \ end{array}]
Готово! Таблица заполнена, последний элемент оказался равен нулю. И это не случайно. Скоро узнаем почему.:)
2. Вычисление значения многочлена
Чтобы понять, зачем нужна схема Горнера, давайте вкратце повторим всю цепочку рассуждений. Берём произвольный многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
и произвольную точку $x=color{red}{a}$. Составляем таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Найденные коэффициенты ${{b}_{n-1}}$, …, ${{b}_{0}}$, $r$ позволяют переписать многочлен $Pleft( x right)$ в новом виде:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
Но чем так примечательна эта запись? В ближайших четырёх пунктах мы детально разберём все её свойства. И начнём с самого простого. Подставим в эту новую запись число $x=color{red}{a}$, т.е. вычислим $Pleft( color{red}{a} right)$:
[Pleft( color{red}{a} right)=left( {{b}_{n-1}}{color{red}{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]
Итак, последнее число $r$ в таблице — это значение многочлена $Pleft( x right)$ в точке $x=color{red}{a}$:
[Pleft( color{red}{a} right)=r]
А это значит, что благодаря схеме Горнера можно считать значения многочленов быстро (нет операции возведения в степень) и надёжно (в сложении мы ошибаемся реже, чем в умножении).
Так, из Примера 1 следует, что значение многочлена
[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]
в точке $x=3$ равно
[Pleft( 3 right)=r=-15]
Сравните это с прямой подстановкой $x=3$ в многочлен:
[begin{align} Pleft( 3 right) &=2cdot {{3}^{4}}-7cdot {{3}^{3}}+{{3}^{2}}+2cdot 3-3= \ &=2cdot 81-7cdot 27+left( 9+6-3 right)= \ &=162-189+12= \ &=-15 end{align}]
Результат один и тот же, но объём вычислений вырос на порядок.
Пример 3. «Некрасивые» значения
С помощью схемы Горнера найдите значение многочлена
[Pleft( x right)=8{{x}^{4}}-12{{x}^{3}}-24{{x}^{2}}+11x+7]
в точке $x=2,5$.
Решение. Выделим коэффициенты многочлена
[Pleft( x right)= color{blue}{8}cdot {{x}^{4}}+left( color{blue}{-12} right)cdot {{x}^{3}}+left( color{blue}{-24} right)cdot {{x}^{2}}+color{blue}{11} cdot x+color{blue}{7}]
и заполним таблицу для $x=color{red}{2,5}$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{8} & color{blue}{-12} & color{blue}{-24} & color{blue}{11} & color{blue}{7} \ hlinecolor{red}{2,5} & 8 & 8 & -4 & 1 & 9,5 \ end{array}]
Итого значение многочлена $Pleft( color{red}{2,5} right)=9,5$. Точно такое же значение можно получить прямой подстановкой, но вычисления будут настолько громоздкими, что мы не будем приводить их.
3. Деление многочлена с остатком
Напомню, что разделить многочлен $color{blue}{Pleft( x right)}$ на многочлен $color{red}{Aleft( x right)}$ с остатком — значит найти многочлены $Qleft( x right)$ и $Rleft( x right)$ такие, что
[color{blue}{Pleft( x right)}=Qleft( x right)cdot color{red}{Aleft( x right)}+Rleft( x right)]
причём степень многочлена $Rleft( x right)$ строго меньше степени делителя $color{red}{Aleft( x right)}$:
[deg Rleft( x right) lt deg color{red}{Aleft( x right)}]
Многочлен $Qleft( x right)$ называют неполным частным, $Rleft( x right)$ — остатком от деления. Можно показать, что $Qleft( x right)$ и $Rleft( x right)$ определены однозначно для исходных многочленов $color{blue}{Pleft( x right)}$ и $color{red}{Aleft( x right)}$.
3.1. Случай линейного делителя
Пусть $Aleft( x right)=x- color{red}{a}$ — линейный двучлен. Очевидно, его степень $deg Aleft( x right)=1$.
Рассмотрим произвольный многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
и составим таблицу для $x=color{red}{a}$ по схеме Горнера:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Получим новую запись многочлена $Pleft( x right)$:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
где $r$ — обычное число, т.е. $deg r=0 lt deg Aleft( x right)$. Но тогда многочлен
[Qleft( x right)={{b}_{n-1}}{{x}^{n-1}}+{{b}_{n-2}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}}]
является неполным частным при делении $Pleft( x right)$ на двучлен $x-color{red}{a}$, а число $r$ — остаток этого деления:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
Итак, схема Горнера позволяет быстро находить неполное частное и остаток от деления произвольного многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$.
Пример 4. Деление с остатком
Найдите частное и остаток при делении многочлена
[{{x}^{4}}-2{{x}^{3}}+4{{x}^{2}}-6x+10]
На многочлен $x-1$.
Решение. Выделим синим цветом коэффициенты исходного многочлена:
[color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-2} right)cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+left( color{blue}{-6} right)cdot x+color{blue}{10}]
Заполним таблицу по схеме Горнера для $x=color{red}{1}$:
[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & 1 & -1 & 3 & -3 & 7 \ end{array}]
Первые четыре числа — это коэффициенты многочлена-частного. Отметим их зелёным цветом:
[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & color{#green}{1} & color{#green}{-1} & color{#green}{3} & color{#green}{-3} & 7 \ end{array}]
Остаток от деления равен $r=7$. Составим многочлен-частное:
[Qleft( x right)= color{#green}{1}cdot {{x}^{3}}+left( color{#green}{-1} right)cdot {{x}^{2}}+color{#green}{3}cdot x+left( color{#green}{-3} right)]
Очевидно, при делении на линейный двучлен степень частного должна быть на единицу меньше степени исходного многочлена. Так и получилось:
[deg Qleft( x right)=4-1=3]
Пример 5. Проверка делимости
Убедитесь, что многочлен
[{{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28]
делится на двучлен ${{left( x-2 right)}^{2}}$.
Решение. Многочлен делится без остатка на ${{left( x-2 right)}^{2}}$, если сначала он делится на двучлен $x-2$, а затем частное вновь делится на $x-2$. Следовательно, решение состоит из двух шагов.
Первый шаг: выделим коэффициенты исходного многочлена
[color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right)]
[begin{align}color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right) \ end{align}]
Составим таблицу для $x=color{red}{2}$. В ней будет 6 основных столбцов:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & {} & {} & {} & {} & {} & {} \ end{array}]
Заполним все пустые клетки по схеме Горнера:
[begin{array}{c|c|c|c|r|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & color{green}{1} & color{green}{-4} & color{green}{8} & color{green}{-17} & color{green}{18} & 0 \ end{array}]
Получили остаток $r=0$, поэтому исходный многочлен действительно делится на $x-color{red}{2}$, а частное равно
[Qleft( x right)= color{green}{1}cdot {{x}^{4}}+left( color{green}{-4} right)cdot {{x}^{3}}+color{green}{8}cdot {{x}^{2}}+left( color{green}{-17} right) cdot x+color{green}{18}]
Следовательно, исходный многочлен можно представить так:
[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{4}}-4{{x}^{3}}+8{{x}^{2}}-17x+18 right)cdot left( x-color{red}{2} right) \ end{align}]
Второй шаг: выделяем коэффициенты и заполняем ту же самую таблицу, но уже для многочлена $Qleft( x right)$.
[Qleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-4} right)cdot {{x}^{3}}+color{blue}{8}cdot {{x}^{2}}+left( color{blue}{-17} right) cdot x+color{blue}{18}]
Но все коэффициенты в нужном количестве уже присутствуют в таблице, которую мы получили на предыдущем шаге. А потому достаточно приписать к этой таблице ещё одну строку и вновь заполнить её для $x=color{red}{2}$:
[begin{array}{c|c|c|c|r|c|c} {} & 1 & -6 & 16 & -33 & 52 & -36 \ hlinecolor{red}{2} & color{blue}{1} & color{blue}{-4} & color{blue}{8} & color{blue}{-17} & color{blue}{18} & 0 \ hlinecolor{red}{2} & color{green}{1} & color{green}{-2} & color{green}{4} & color{green}{-9} & 0 & {} \ end{array}]
Остаток от деления равен нулю, поэтому многочлен $Qleft( x right)$ делится на $x-color{red}{2}$, и его можно переписать так:
[Qleft( x right)=left( color{green}{1}cdot {{x}^{3}}+left( color{green}{-2} right){{x}^{2}}+color{green}{4} cdot x+left( color{green}{-9} right) right)cdot left( x-color{red}{2} right)]
Возвращаясь к исходному многочлену, получим
[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{3}}-2{{x}^{2}}+4x-9 right)cdot {{left( x-color{red}{2} right)}^{2}} \ end{align}]
Такая запись, как и приведённая выше таблица, доказывает, что исходный многочлен делится на ${{left( x-color{red}{2} right)}^{2}}$.
Обратите внимание: на каждом следующем шаге количество коэффициентов уменьшается на единицу:
- В первой строке мы выписали все 6 коэффициентов исходного многочлена.
- Во второй строке осталось лишь 5 коэффициентов, а последнее число — остаток.
- Третья срока — 4 коэффициента и вновь остаток.
Всё это пригодится нам в следующем пункте.
4. Перебор корней уравнения
До сих пор мы применяли схему Горнера для некоторой точки $x=color{red}{a}$, которая была прямо указана в условии задачи. Но что если найти такую точку — как раз и есть условие задачи?
Рассмотрим уравнение
[color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}=0]
Число $x=color{red}{a}$ будет корнем этого уравнения, если $Pleft( color{red}{a} right)=0$. Это значит, что последний элемент в схеме Горнера должен быть равен нулю:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & color{green}{0} \ end{array}]
Следовательно, мы можем быстро проверить, является ли число $x=color{red}{a}$ корнем уравнения. Достаточно просто подставить его в таблицу и найти последний элемент.
Кроме того, мы знаем, что последний элемент — это остаток $r$. При $r=color{green}{0}$ исходное уравнение примет вид
[left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)=0]
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Откуда либо $x-color{red}{a}=0$ (этот случай мы уже разобрали), либо
[color{blue}{{b}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{b}_{1}}x+color{blue}{{b}_{0}}=0]
Получили новое уравнение — меньшей степени, чем исходное. Коэффициенты этого уравнения уже занесены в таблицу, и к нему вновь применима схема Горнера для перебора кандидатов в корни.
Более того: этот перебор можно ускорить. Но об этом чуть позже. Сначала рассмотрим пару простых примеров.
Пример 6. Уравнение третьей степени
Решите уравнение:
[{{x}^{3}}+9{{x}^{2}}+23x+15=0]
Решение. Заметим, что все коэффициенты многочлена положительны, поэтому уравнение не имеет положительных корней. Иначе, если $x gt 0$, левая часть равенства представляет собой сумму положительных чисел, которая никогда не равна нулю.
Рассмотрим отрицательные числа. Начнём с $x=color{red}{-1}$:
[begin{array}{c|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ end{array}]
Получили $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ — корень, и всё уравнение можно переписать так:
[left( {{x}^{2}}+8x+15 right)left( x+1 right)=0]
Далее уравнение разделяется на линейное $x+1=0$, которое мы уже решили, и квадратное
[{{x}^{2}}+x+15=0]
Такое уравнение можно решить через дискриминант или по теореме Виета. Получим корни $x=-3$ и $x=-5$.
Окончательный ответ: $x=-1$, $x=-3$, $x=-5$.
Впрочем, с тем же успехом мы могли продолжить решение по схеме Горнера:
[begin{array}{r|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ hlinecolor{red}{-3} & 1 & 5 & color{green}{0} & {} \ hlinecolor{red}{-5} & 1 & color{green}{0} & {} & {} \ end{array}]
При этом уравнение примет вид
[left( x+3 right)left( x+5 right)left( x+1 right)=0]
По сути, мы получили разложение на множители. И чуть ниже об этом будет отдельный пункт.
Пример 7. Ещё одно уравнение
Решите уравнение:
[2{{x}^{3}}-{{x}^{2}}-5x-2=0]
Решение. В этот раз мы видим, что корни вполне могут быть положительными. Начнём с $x=color{red}{1}$:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ end{array}]
Получили $r=color{red}{-6}ne 0$. Следовательно, $x=color{red}{1}$ не является корнем. Проверим $x=color{red}{2}$:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]
Обратите внимание: при заполнении третьей строки таблицы мы игнорируем вторую строку, где нас постигла неудача. И если бы мы могли стирать строки, то схема Горнера выглядела бы так:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]
В любом случае мы получили $r=color{green}{0}$, поэтому $x=color{red}{2}$ — корень, и уравнение примет вид
[left( 2{{x}^{2}}+3x+1 right)left( x-2 right)=0]
Далее можно решить квадратное уравнение через дискриминант, а можно продолжить заполнять таблицу. Например, для $x=color{red}{-1}$:
[begin{array}{r|c|r|r|r} {} & 2 & -1 & -5 & -2 \ hline1 & 2 & 1 & -4 & -6 \ hline2 & color{blue}{2} & color{blue}{3} & color{blue}{1} & color{green}{0} \ hline-1 & 2 & 1 & color{green}{0} & {} \ end{array}]
Вновь получили ноль в последней клетке, поэтому $x=color{red}{-1}$ — тоже корень, а уравнение примет вид
[left( 2x+1 right)left( x+1 right)left( x-2 right)=0]
Теперь ответ очевиден: $x=2$, $x=-1$, $x=-0,5$.
Помните: «неудачные» строки — это нормально. Их бывает много. Главное при переборе корней — игнорировать такие строки и заполнять таблицу так, будто этих строк не существует.
4.1. Теорема Безу
Теорема Безу и следствия из неё позволяет значительно сузить круг потенциальных корней.
Теорема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x-a$ равен $Pleft( a right)$.
Несложно заметить, что схема Горнера и следующая из неё запись многочлена
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
является прямым доказательством этой теоремы. Действительно, если подставить в эту запись значение $x=color{red}{a}$, мы получим
[Pleft( color{red}{a} right)=left( {{b}_{n-1}}color{red}{{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]
У теоремы Безу огромное количество полезных приложений — см. урок «Теорема Безу». Сейчас же нас интересует не сама теорема, а следствие из неё, связанное с корнями многочлена.
Пусть $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. Распишем многочлен по схеме Горнера для $x=color{red}{a}$:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)]
Поскольку $x=color{red}{a}$ — корень, остаток $r=0$, и мы получили разложение многочлена $Pleft( x right)$ на множители. А теперь выполним обратную операцию — раскроем скобки и приведём подобные слагаемые:
[Pleft( x right)={{b}_{n-1}}{{x}^{n}}+ldots -color{red}{a}cdot {{b}_{0}}]
Получается, что корень $x=color{red}{a}$ является делителем свободного члена $Pleft( x right)$. Более того, можно показать, что в многочлене
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
с целыми коэффициентами $color{blue}{{a}_{n}}$, …, $color{blue}{{a}_{0}}$ все рациональные корни имеют вид
[x=frac{m}{n}]
где $min mathbb{Z}$ — делитель свободного члена $color{blue}{{a}_{0}}$, а $nin mathbb{N}$ — делитель старшего коэффициента $color{blue}{{a}_{n}}$.
И хоть при первом взгляде на все эти рассуждения они могут показаться сложными, на практике теорема Безу значительно упрощает поиск корней. Взгляните на примеры.:)
Пример 8. Сплошной перебор
Решите уравнение:
[{{x}^{5}}+8{{x}^{4}}+24{{x}^{3}}+35{{x}^{2}}+28x+12=0]
Решение. Слева от знака равенства стоит многочлен пятой степени. Старший коэффициент многочлена ${{a}_{5}}=color{blue}{1}$, свободный член ${{a}_{0}}=color{blue}{12}$. Если такой многочлен имеет рациональные корни вида
[x=frac{m}{n}]
то $n=1$ — это единственный натуральный делитель для ${{a}_{5}}=color{blue}{1}$. А вот число $m$ будем искать среди делителей числа ${{a}_{0}}=color{blue}{12}$:
[m=pm 1, pm 2, pm 3, pm 4, pm 6, pm 12.]
Итого 12 вариантов. Далее заметим, что все коэффициенты исходного многочлена положительны, поэтому достаточно проверить лишь отрицательные корни. Начнём с $x=color{red}{-1}$, затем $x=color{red}{-2}$, $x=color{red}{-3}$ и т.д.:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-1} & 1 & 7 & 17 & 18 & 10 & color{red}{2} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ end{array}]
Как видим, вариант $x=color{red}{-1}$ не подошёл, поэму строку с проверкой этого числа можно вычеркнуть. Зато $x=color{red}{-2}$ и $x=color{red}{-3}$ — корни. Более того: можно повторно проверить $x=color{red}{-2}$. Получим интересный результат:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ hline color{red}{-2} & 1 & 1 & 1 & color{green}{0} & {} & {} \ end{array}]
Другими словами, исходное уравнение можно переписать так:
[left( {{x}^{2}}+x+1 right){{left( x+2 right)}^{2}}left( x+1 right)=0]
Число $x=color{red}{-2}$ оказалось корнем второй кратности, а квадратное уравнение
[{{x}^{2}}+x+1=0]
не имеет корней. Поэтому окончательный ответ: $x=-2$, $x=-3$.
Пример 9. Дробные корни
Решите уравнение:
[3{{x}^{4}}+5{{x}^{3}}-{{x}^{2}}-5x-2=0]
Решение. По теореме Безу получаем, что рациональные корни вида
[x=frac{m}{n}]
должны быть составлены из чисел $min left{ pm 1, pm 2 right}$ и $nin left{ 1,3 right}$. Всего существует восемь таких комбинаций:
[xin left{ pm 1; pm 2; pm frac{1}{3}; pm frac{2}{3} right}]
Рассмотрим самые простые корни: $x=color{red}{1}$ и $x=color{red}{-1}$. Причём на каждом шаге будем проверять возможную кратность:
[begin{array}{r|c|c|c|c|c} {} & color{blue}{3} & color{blue}{5} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hline color{red}{1} & 3 & 8 & 7 & 2 & color{green}{0} \ hline color{red}{1} & 3 & 11 & 18 & color{red}{20} & {} \ hline color{red}{-1} & 3 & 5 & 2 & color{green}{0} & {} \ hline color{red}{-1} & 3 & 2 & color{green}{0} & {} & {} \ end{array}]
Получили корень $x=color{red}{1}$ (первой кратности) и $x=color{red}{-1}$ (как минимум второй кратности), а само уравнение можно переписать так:
[left( 3x+2 right){{left( x+1 right)}^{2}}left( x-1 right)=0]
Теперь очевидно, что всего уравнение имеет три корня: $x=1$, $x=-1$ и $x=-{2}/{3};$.
4.2. Учёт кратности корней
Как видим, схема Горнера позволяет не просто перебирать корни, но и определять их кратность. Это особенно важно при решении неравенств и задач с параметрами.
Чтобы определить кратность корня $x=color{red}{a}$, достаточно подставлять его в таблицу до тех пор, пока не появится остаток, отличный от нуля. Либо пока исходный многочлен не будет полностью разложен на множители.
Пример 10. Корень четвёртой кратности
Решите уравнение и определите кратность корней:
[{{x}^{5}}-10{{x}^{3}}-20{{x}^{2}}-15x-4=0]
Решение. Слева стоит многочлен с целыми коэффициентами. Выпишем потенциальные корни по теореме Безу:
[xin left{ pm 1; pm 2; pm 4 right}]
Начнём с самых простых чисел: $x=color{red}{1}$ и $x=color{red}{-1}$. Проверим их по схеме Горнера:
[begin{array}{r|c|r|r|r|r|r} {} & color{blue}{1} & color{blue}{0} & color{blue}{-10} & color{blue}{-20} & color{blue}{-15} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 1 & -9 & -29 & -44 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -1 & -9 & -11 & -4 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -2 & -7 & -4 & color{green}{0} & {} \ hlinecolor{red}{-1} & 1 & -3 & -4 & color{green}{0} & {} & {} \ hlinecolor{red}{-1} & 1 & -4 & color{green}{0} & {} & {} & {} \ end{array}]
Перепишем исходное уравнение:
[{{left( x+1 right)}^{4}}left( x-1 right)left( x-4 right)=0]
Итого уравнение имеет три различных корня: $x=-1$ (четвёртой кратности), $x=1$ (первой кратности) и $x=4$ (тоже первой кратности).
Ключевая мысль: с помощью схемы Горнера можно решать даже уравнения высших степеней. Поэтому если при решении текстовой задачи (и особенно задачи с параметром) возникло уравнение 3-й степени и выше, это вовсе не означает, что вы где-то ошиблись. Вполне возможно, что составители задачи хотят проверить, умеете ли вы решать уравнения высших степеней.
5. Разложение на множители
Схему Горнера часто применяют для разложения многочлена на множители. Мы знаем, что для всякого $x=color{red}{a}$ такого, что последний элемент таблицы $r=color{green}{0}$, можно переписать исходный многочлен $Pleft( x right)$ в виде
[Pleft( x right)=left( x-color{red}{a} right)cdot Qleft( x right)]
Коэффициенты многочлена $Qleft( x right)$ будут также даны в таблице, и к нему тоже применима схема Горнера.
Пример 11. Простой многочлен
Разложите на множители многочлен
[{{x}^{4}}+2{{x}^{3}}+4{{x}^{2}}+3x-10]
Решение. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+color{blue}{3}cdot x+left( color{blue}{-10} right)]
Будем выделять из него двучлены вида $left( x-color{red}{a} right)$, где $x=color{red}{a}$ — корни многочлена $Pleft( x right)$. Рассмотрим в качестве таких корней делители свободного члена ${{a}_{0}}=color{blue}{-10}$. Начнём с $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|c|c|c|c|c} {} & color{blue}{1} & color{blue}{2} & color{blue}{4} & color{blue}{3} & color{blue}{-10} \ hlinecolor{red}{1} & 1 & 3 & 7 & 10 & color{green}{0} \ hlinecolor{red}{-1} & 1 & 2 & 5 & color{red}{5} & {} \ hlinecolor{red}{-2} & 1 & 1 & 5 & color{green}{0} & {} \ end{array}]
Итого одна неудачная попытка и две удачных. Получили разложение многочлена
[Pleft( x right)=left( x-1 right)left( x+2 right)left( {{x}^{2}}+x+5 right)]
Квадратный трёхчлен в третьей скобке всегда положителен:
[{{x}^{2}}+x+5 gt 0]
Его нельзя разложить на множители, поэтому указанное разложение $Pleft( x right)$ — окончательное.
Пример 12. Сложный многочлен
Разложите на множители многочлен
[{{x}^{5}}-6{{x}^{4}}+2{{x}^{3}}+36{{x}^{2}}-27x-54]
Решение. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right)cdot x+left( color{blue}{-54} right)]
[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+ \ &+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right) cdot x+left( color{blue}{-54} right) \ end{align}]
Проверим делители свободного члена ${{a}_{0}}=color{blue}{-54}$. Таких делителей очень много, поэтому начнём с самых простых: $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{2} & color{blue}{36} & color{blue}{-27} & color{blue}{-54} \ hlinecolor{red}{1} & 1 & -5 & -3 & 33 & 6 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -7 & 9 & 27 & -54 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -8 & 17 & 10 & color{red}{-64} & {} \ hlinecolor{red}{2} & 1 & -5 & -1 & 25 & color{red}{-4} & {} \ hlinecolor{red}{-2} & 1 & -9 & 27 & -27 & color{green}{0} & {} \ hlinecolor{red}{3} & 1 & -6 & 9 & color{green}{0} & {} & {} \ hlinecolor{red}{3} & 1 & -3 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{3} & 1 & color{green}{0} & {} & {} & {} & {} \ end{array}]
Получили три неудачных попытки и пять удачных. В целом многочлен привет вид
[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]
Это и есть искомое разложение на множители.
Обратите внимание: после проверки корня $x=color{red}{-2}$ в таблице возникла формула сокращённого умножения — куб разности:
[{{x}^{3}}-9{{x}^{2}}+27x-27={{left( x-3 right)}^{3}}]
С этим замечанием дальше можно было вообще не заполнять таблицу, поскольку многочлен сразу примет вид
[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]
6. Разложение по степеням
Наконец, ещё одно применение схемы Горнера — это разложение многочлена по степеням двучлена $left( x-color{red}{a} right)$. Для этого достаточно составлять таблицу с указанным $x=color{red}{a}$ до тех пор, пока не закончатся столбцы с коэффициентами.
Полученные остатки будут коэффициентами искомого разложения. Взгляните на примеры.
Пример 13. Разложение многочлена
Разложите по степеням $left( x-1 right)$ многочлен
[{{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-17x-5]
Решение. Выделим коэффициенты многочлена:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-17} right)cdot x+left( color{blue}{-5} right)]
[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{4}} &+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-17} right) cdot x+left( color{blue}{-5} right) \ end{align}]
Занесём эти коэффициенты в таблицу и будем заполнять её по схеме Горнера для $x=color{red}{1}$ до тех пор, пока не вычеркнем все столбцы:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-17} & color{blue}{-5} \ hlinecolor{red}{1} & 1 & -5 & 11 & -6 & color{green}{-11} \ hlinecolor{red}{1} & 1 & -4 & 7 & color{green}{1} & {} \ hlinecolor{red}{1} & 1 & -3 & color{green}{4} & {} & {} \ hlinecolor{red}{1} & 1 & color{green}{-2} & {} & {} & {} \ hlinecolor{red}{1} & color{green}{1} & {} & {} & {} & {} \ end{array}]
Числа, выделенные зелёным — это остатки от деления в каждой новой строке. Они и будут коэффициентами разложения в порядке возрастания степеней. Внизу таблицы находится старший коэффициент, а в первой строке — свободный член:
[Pleft( x right)= color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right)]
[begin{align}Pleft( x right) &=color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+ \ &+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right) \ end{align}]
Представим эту запись более компактно:
[Pleft( x right)={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+4{{left( x-1 right)}^{2}}+left( x-1 right)-11]
[begin{align}Pleft( x right) &={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+ \ &+4{{left( x-1 right)}^{2}}+left( x-1 right)-11 \ end{align}]
Это и есть искомое разложение.
Пример 14. Финал
Разложите по степеням $left( x-2 right)$ многочлен
[{{x}^{4}}-8{{x}^{3}}+24{{x}^{2}}-50x+48]
Решение. В раз не будем переписывать многочлен с выделением коэффициентов, а сразу составим таблицу:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-8} & color{blue}{24} & color{blue}{-50} & color{blue}{48} \ hlinecolor{red}{2} & 1 & -6 & 12 & -26 & color{green}{-4} \ hlinecolor{red}{2} & 1 & -4 & 4 & color{green}{-18} & {} \ hlinecolor{red}{2} & 1 & -2 & color{green}{0} & {} & {} \ hlinecolor{red}{2} & 1 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{2} & color{green}{1} & {} & {} & {} & {} \ end{array}]
Запишем найденное разложение в порядке убывания степеней:
[color{green}{1}cdot {{left( x-2 right)}^{4}}+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right)]
[begin{align}color{green}{1}cdot {{left( x-2 right)}^{4}}&+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+ \ &+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right) \ end{align}]
То же самое разложение, но более компактно:
[{{left( x-2 right)}^{4}}-18left( x-2 right)-4]
Это окончательный ответ.
7. Как работает Схема Горнера
Очень просто. Вернёмся к исходному многочлену:
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
Вынесем за скобки множитель $x$ из всех слагаемых, кроме последнего:
[Pleft( x right)=left( color{blue}{{a}_{n}}{{x}^{n-1}}+color{blue}{{a}_{n-1}}{{x}^{n-2}}+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]
В скобках стоит новый многочлен. Вновь вынесем за скобки $x$. Сделаем так много раз и в какой-то момент получим запись вида
[Pleft( x right)=left( ldots left( left( color{blue}{{a}_{n}} right)cdot x+color{blue}{{a}_{n-1}} right)cdot x+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]
Мы видим множество скобок. Обозначим элемент в самой внутренней скобке через ${{b}_{n-1}}$:
[{{b}_{n-1}}=color{blue}{{a}_{n}}]
Элемент в предыдущей скобке обозначим ${{b}_{n-2}}$:
[{{b}_{n-2}}={{b}_{n-1}} cdot x+color{blue}{{a}_{k}}]
И так далее по уже известной формуле
[{{b}_{k-1}}={{b}_{k}} cdot x+color{blue}{{a}_{k}}]
В какой-то момент мы находим ${{b}_{0}}$ и $r$:
[begin{align} {{b}_{0}} &={{b}_{1}}cdot x+color{blue}{{a}_{1}} \ r &={{b}_{0}}cdot x+color{blue}{{a}_{0}} end{align}]
Собираем все найденные значения в таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hline x & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Легко показать, что $r=Pleft( x right)$. Кроме того, согласно теореме Безу, при подстановке $x=color{red}{a}$ найденное число $r=Pleft( color{red}{a} right)$ есть остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
В частности, при $r=0$ деление выполнено без остатка, поэтому многочлен $Pleft( x right)$ раскладывается на множители:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Далее по индукции или прямым вычислением можно показать, что коэффициенты $Qleft( x right)$ — это те самые числа ${{b}_{n-1}}$, …, ${{b}_{0}}$ из таблицы. Поскольку $deg Qleft( x right)=n-1$, на каждом шаге степень этого многочлена будет уменьшаться.
В какой-то момент окажется, что $Qleft( x right)= color{blue}{{a}_{n}}$ — константа, и дальнейшее заполнение таблицы по схеме Горнера невозможно. Вот и всё.:)
Смотрите также:
- Бином Ньютона

- Теорема Безу и корни многочленов

- Решение задач B12: №448—455

- Задача B3 — работа с графиками

- Пример решения задачи 15

- Задача B15: частный случай при работе с квадратичной функцией

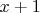 , а
, а 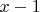 . Тогда все получится.
. Тогда все получится.