Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое диаметр круга?
Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.
Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.
Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).
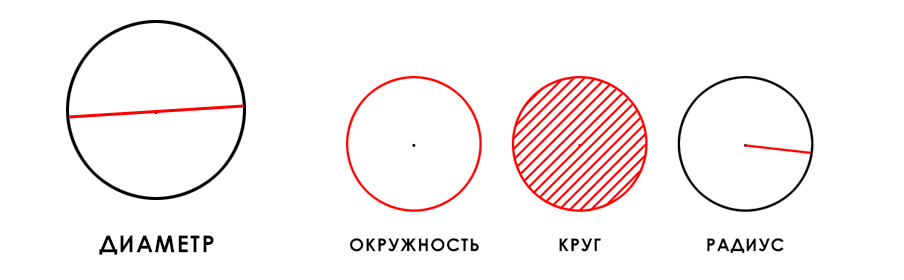
Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.
Формулы определения диаметра круга
Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.
По радиусу
Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.
d = r × 2
Где d – это диаметр, а r – радиус.
По длине окружности
Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.
d = L / π
Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.
Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).
Через площадь круга
Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр. Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:
d = 2 × (S/π)1/2
Где d – диаметр, S – площадь круга, а π – константа, которая примерно равна 3,14.
То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.
Примеры вычисления диаметра
Давайте для закрепления рассмотрим несколько примеров.
Пример 1. Диаметр по длине окружности трубы 🚿
Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).

А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:
d = 31,4 / 3,14 = 10 см.
Это и есть правильный ответ – 10 сантиметров.
Пример 2. Диаметр по колеса радиусу 🚲
Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?
Диаметру будет равен двум радиусам, то есть 20 дюймов.
Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.
❓Вопросы и ответы
И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.
Как работает ваш онлайн-калькулятор?
Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.
Достаточно ли у меня данных для расчёта?
Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Если у автомобильного колеса параметр R16, то какой у него диаметр?
16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру.
Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства,
которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой
ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения,
получила название центра шара.
Его поверхность, являющаяся своего рода оболочкой, ограничивающей
объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа
сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии
входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра,
одновременно выступающего и диаметром шара. Этот отрезок, называемый осью вращения, соединяет
противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через
центральную точку шара.
- Диаметр шара через плошадь поверхности шара
- Диаметр шара через обьём шара
Способ вычисления диаметра шара при известном значении объёма фигуры
Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной
формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:
D = √(S ⁄ π)
где S — площадь поверхности шара
Цифр после
запятой:
Результат в:
Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда,
принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.
Способ нахождения диаметра шара при заданном значении его объёма
Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину
диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя
преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄
3* πD³ ⁄ 8, отсюда
D = ³√(6V / π)
где V — объём шара
Цифр после
запятой:
Результат в:
Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу
π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14)
или, выполняя вычисление D=6.
В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и
параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых
инженерных, строительных задач также проводится с использованием геометрических вычислений,
связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть
выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и
представлено.
Как посчитать диаметр окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать диаметр окружности
Чтобы посчитать диаметр окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
 Для того чтобы вычислить диаметр окружности вам необходимо знать её радиус, либо длину окружности, либо её площадь. Если вы знаете хотя бы один из этих параметров, введите его в соответствующие поле и узнаете, чему равен диаметр окружности.
Для того чтобы вычислить диаметр окружности вам необходимо знать её радиус, либо длину окружности, либо её площадь. Если вы знаете хотя бы один из этих параметров, введите его в соответствующие поле и узнаете, чему равен диаметр окружности.
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Ответ:
0
Каков диаметр (d) если длина окружности C?
Формула
d = C/π, где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
её радиус ?
Ответ:
0
Каков диаметр окружности (d) если её радиус r?
Формула
d = 2⋅r
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
её площадь ?
Ответ:
0
Каков диаметр окружности (d) если её площадь S?
Формула
d = √4S/π, где π ≈ 3.14
Пример
Если площадь круга равна 5 см2, то его диаметр примерно равен 2.52 см.
См. также
Загрузить PDF
Загрузить PDF
Вычислить диаметр окружности не составит труда, если вы знаете какие-либо другие ее размеры: радиус, длину окружности или площадь ограничиваемого ею круга. Диаметр можно вычислить, даже не зная этих размеров – при наличии начерченной окружности. Если вы хотите узнать, как вычислить диаметр окружности, следуйте указанным ниже шагам.
-

1
Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его. Радиус – это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.
-

2
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
-

3
Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра. Данное вычисление вытекает из формулы площади круга, A = πr2, преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см2, разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.
Реклама
-

1
Внутри окружности начертите горизонтальную прямую, проходящую от одной точки окружности к другой. Для этого воспользуйтесь линейкой или угольником. Прямая может проходить в верхней части круга, в нижней, или где-нибудь посередине.
-

2
Пометьте точки, в которых прямая пересекает окружность, буквами “A” и “B.”
-

3
Начертите две пересекающиеся окружности, одну – с центром в точке A, а другую – с центром в точке B. Убедитесь, что две окружности пересекаются так, будто образуют диаграмму Венна.
-

4
Через две точки, в которых окружности пересеклись, проведите прямую. Отрезок этой прямой между двумя точками и будет равен диаметру окружности.
-

5
Измерьте диаметр. Измерьте его с помощью линейки, а если нужна большая точность – штангенциркулем с цифровой индикацией. Готово!
Реклама
Советы
- Научитесь пользоваться циркулем. Это очень полезный инструмент, который предназначен для многих целей, включая определение диаметра окружности описанным выше графическим способом. Для этого можно также использовать измерительный циркуль.
- Работа с геометрическими формулами и уравнениями станет легче при условии постоянной практики. Попросите кого-то, кто работал с окружностями или другими геометрическими фигурами, помочь вам. Когда вы наберетесь немного опыта, вы скорее всего почувствуете, что задачи по геометрии будут казаться легче.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Циркуль
- Линейка
- Штангенциркуль с цифровой индикацией (при необходимости)
Об этой статье
Эту страницу просматривали 1 261 507 раз.
Была ли эта статья полезной?
Чтобы найти диаметр шара при помощи этого калькулятора, достаточно заполнить любую одну ячейку, введя известное значение, и нажать на кнопку расчета. Программа автоматически вычислит все остальные значения, которые отобразятся в ответе вместе с удобными и понятными формулами.

Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Радиус (r)
Диаметр (d)
Площадь (S)
Объем (V)
Округление:
Знаков после запятой
* – обязательно заполнить

