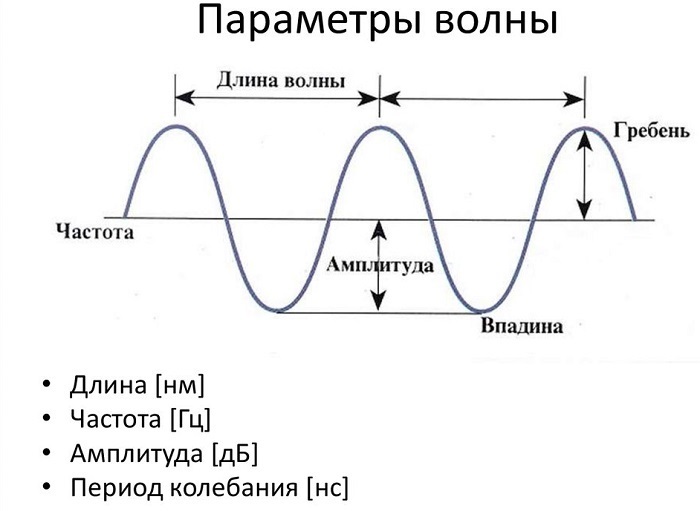
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
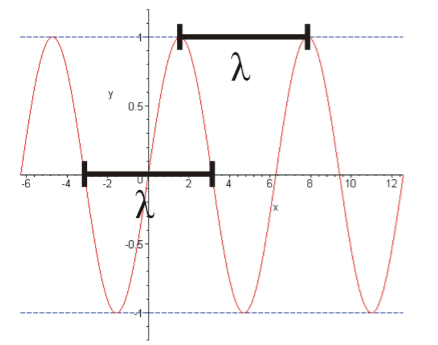
На рисунке показаны основные параметры волны, используемые в физике:
Определение и формула длины волн
Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.
Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.
У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
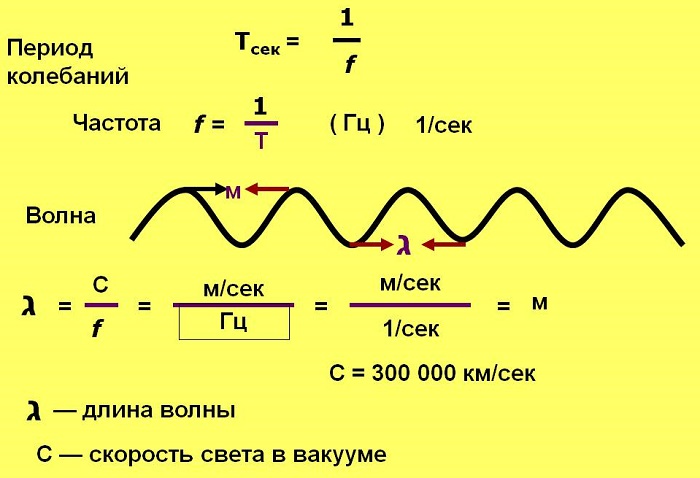
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
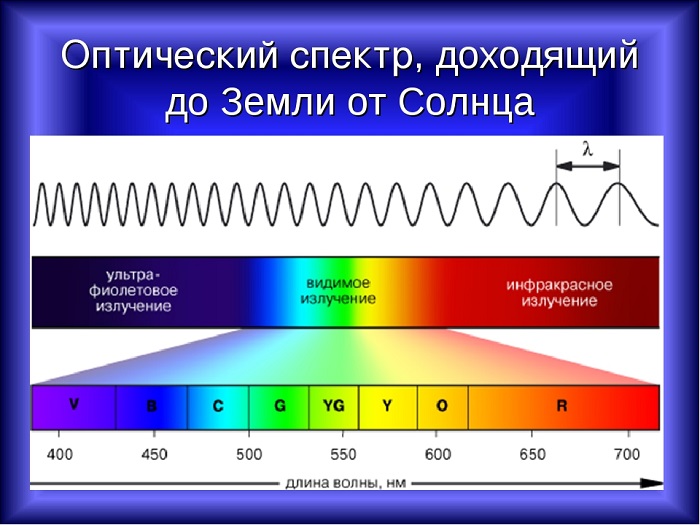
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
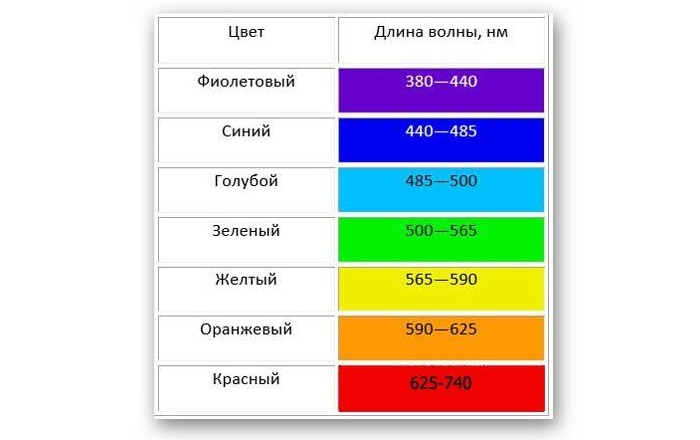
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
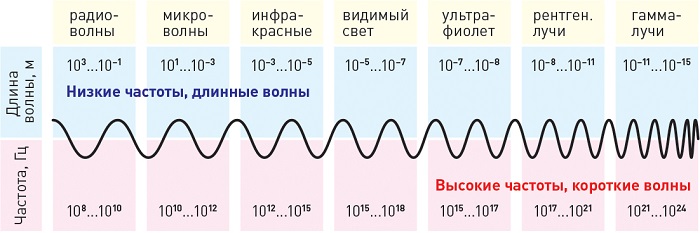
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Задания
Версия для печати и копирования в MS Word
Тип 6 № 13134 
i
На рисунке показан профиль волны.
Какова длина волны? Ответ запишите в сантиметрах.
Спрятать решение
Решение.
Для нахождения длины волны по профилю волны необходимо на рисунке выделить участки, где функция начинает «повторяться», то есть происходит полное повторение профиля волны. Из рисунка видно, что длина волны равна 18 см.
Ответ: 18.
Источник: ОГЭ по физике 2020. Досрочная волна. Вариант 2
Раздел кодификатора ФИПИ: 1.23 Механические колебания. Амплитуда, период и частота колебаний. Механические волны.
Спрятать решение
·
Помощь
Каждая волна имеет свои параметры движения.
Скорость волны — скорость распространения возмущения.
Пример:
воздействуя на стальной стержень с одного конца, можно вызвать волны сжатия и разрежения со скоростью (5000 frac{м}{с}).
Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.
Помимо скорости, важной характеристикой волны является длина волны.
Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.
Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. (1)).
Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.
Рис. (1). Модель упругой среды для демонстрации колебаний
Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.
Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. (2)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на (1/4) колебания.
Рис. (2). Изображение максимального смещения от положения равновесия первого шарика
В момент времени, когда смещение четвертого шарика будет наибольшим (рис. (3)), седьмой шарик будет отставать от него на (1/4) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет (1/2) колебания.
Рис. (3). Изображение максимального смещения от положения равновесия четвёртого шарика
Между седьмым и четвёртым шариком, а также седьмым и десятым (1/4) часть колебания (рис. (4)).
Рис. (4). Изображение максимального смещения от положения равновесия седьмого шарика
Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. (5)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.
Рис. (5). Изображение максимального смещения от положения равновесия десятого шарика
Начиная с тринадцатого шарика, мы можем отсчитывать новую волну (рис. (6)).
Рис. (6). Изображение модели новой волны
Длину волны измеряют расстоянием, на которое перемещается волновая поверхность за один период колебания источника волн;
Длиной волны является расстояние между двумя ближайшими точками бегущей волны на одном луче, который колеблется в одинаковой фазе:
, где (λ) («лямбда») — длина волны, (upsilon) — скорость волны, (T) — период колебания.
Период колебаний можно выразить как величину, обратную частоте колебаний:
T=1ν
.
Тогда выразим длину волны как отношение скорости и частоты:
λ=υν
.
Длина волны прямо пропорциональна скорости волны и обратно пропорциональна частоте колебаний (прямо пропорциональна периоду колебаний).
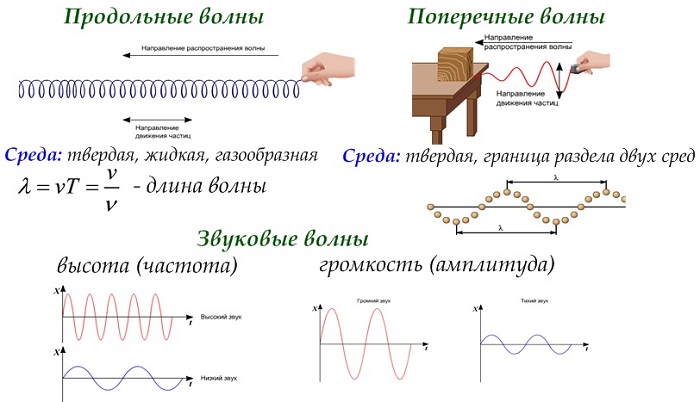
Поперечные и продольные волны описываются одними и теми же законами.
Выразим скорость волны:
как отношение длины волны к периоду колебаний:
υ=λT
;
как произведение длины волны на частоту колебаний:
υ=λν
.
За длину волны (λ) примем расстояние между шариками, колеблющимися в одинаковых фазах. Например (см. рис. (6)), между четвёртым и шестнадцатым, третьим и пятнадцатым.
Колебания проходят шарики, начиная с первого и заканчивая двенадцатым, проходят все фазы колебания. Новая волна начинается с тринадцатого шарика. Каждый шарик совершает одно полное колебание за время, которое называют периодом колебаний (T). За это время колебательный процесс проходит расстояние, называемое длиной волны (λ.)
Модель распространения продольных волн представлена на рисунке (7).
Длиной волны будет расстояние между соседними центрами сжатия пружины.
Рис. (7). Распространение продольных волн в упругой пружине
Источником колебаний генерируется волна той же частоты, поэтому вынужденные колебания совпадают по частоте с осциллятором и не зависит от плотности среды, в которой движется волна.
Если в ходе движения волна переходит в среду другой плотности, то скорость движения волны изменяется, а частота колебаний остаётся прежней.
Источники:
Рис. 1. Модель упругой среды для демонстрации колебаний. © ЯКласс.
Рис. 2. Изображение максимального смещения от положения равновесия первого шарика. © ЯКласс.
Рис. 3. Изображение максимального смещения от положения равновесия четвёртого шарика. © ЯКласс.
Рис. 4. Изображение максимального смещения от положения равновесия седьмого шарика. © ЯКласс.
Рис. 5. Изображение максимального смещения от положения равновесия десятого шарика. © ЯКласс.
Рис. 6. Изображение модели новой волны. © ЯКласс.
Рис. 7. Распространение продольных волн в упругой пружине. © ЯКласс.
График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе[1][2].
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π[3].
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на ;
- как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву 
, размерность длины волны — метр ([м]).
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
Длина волны — пространственный период волнового процесса[править | править код]
Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний 
[с] (интервалом времени, за который периодический колебательный процесс повторяется и размерность которого — секунда), длину волны [м] можно рассматривать как пространственный период волнового процесса. Следует заметить, что круговой частоте колебания 
[радиан/с], показывающей, на сколько радиан изменится фаза колебания за 1 с в фиксированной точке (в множестве точек если твердое тело), соответствует «пространственная круговая частота» 
[радиан/м], называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках пространства, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в [м], отличаются ровно на 
.
Связь с частотой[править | править код]
Получить соотношение, связывающее длину волны с фазовой скоростью 
и частотой 
можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду колебаний, поэтому
Для электромагнитных волн в вакууме скорость в этой формуле равна скорости света (299 792 458 м/с), и длина волны
. Если значение подставить в герцах, то будет выражена в метрах.
Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.
Длина волны в среде[править | править код]
В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.
Длина электромагнитной волны в среде короче, чем в вакууме:
- где — показатель преломления среды;
- — относительная диэлектрическая проницаемость среды;
- — относительная магнитная проницаемость среды.
Величины 
, 
и 
могут существенно зависеть от частоты 
(явление дисперсии). Поскольку для большинства сред в радиочастотном диапазоне 
(для диэлектриков 
, для ферромагнетиков с ростом частоты 
), то в инженерной практике используют величину 
, которую называют коэффициентом укорочения. Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) = 2,56, и коэффициент укорочения 
= 1/1,6 = 0,625.
Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением , но и больше, чем вакууме, поскольку фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же .
Волны де Бройля[править | править код]
Волнам де Бройля также соответствует определённая длина волны. Частице с энергией 
и импульсом 
, соответствуют:
- частота:
- длина волны:
- где — постоянная Планка.
Примеры[править | править код]
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару ↔ , например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м
Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм[4].
Примечания[править | править код]
- ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в , и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine
Литература[править | править код]
- Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Длина волны – минимальное расстояние между двумя точками одной и той же фазы колебаний.
Длина волны обычно обозначается греческой буквой лямбда $left(lambda right)$.
Рисунок 1. Определение длины волны
Длина волны зависит от среды, через которую она проходит (например, вакуум, воздух или вода).
Примерами волнообразных явлений могут служить звуковые волны, свет или ветровые волны.
Синусоидальные волны
В линейных средах, любая волновая картина может быть описана независимо от распространения синусоидальных компонентов. Длина волны $lambda $ синусоидального сигнала движения при постоянной скорости $v$ задается:
где $v-$ фазовая скорость волны.
В диспергирующей среде, сама фазовая скорость зависит от частоты волны.
В случае электромагнитного излучения, фазовая скорость является скоростью света, которая приблизительно равна ${rm 3cdot}{{rm 10}}^{{rm 8 }}{{rm м}}/{{rm с}}$. Для звуковых волн в воздухе, скорость звука составляет ${rm 343}{{rm м}}/{{rm с}}{rm }$(при комнатной температуре и атмосферном давлении).
Стоячие волны
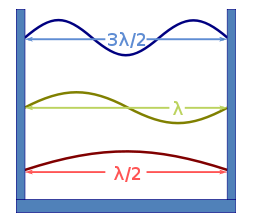
Стоячие волны – это волны в среде, в которой каждая точка на оси волны имеет связанную с ней постоянную амплитуду.
Рисунок 2. Синусоидальные стоячие волны
Стационарные волны можно рассматривать как сумму двух бегущих синусоидальных волн с противоположно направленными скоростями. Следовательно, длина волны, период, и скорость волны связаны так же, как и для бегущей волны. Например, скорость света может быть определена из наблюдения стоячих волн в металлическом корпусе, внутри которого находится идеальный вакуум.
«Длина волны» 👇
Математическое представление
Синусоидальные волны часто представляются математически:
где $y$ есть значение волны в любом положении $x$ и времени $t$, ${rm A}$ является амплитудой волны.
Или, используя волновые числа и угловую частоту:
Где длина волны и волновое число связаны со скоростью и частотой, как:
или
Для электромагнитных волн скорость в среде определяется ее показателем преломления в соответствии:
Пример 1
Чему равна длина волны, которая распространяется со скоростью $5$ м/с и в которой за $10$ с успевают произойти $4$ колебания?
Решение:
[lambda =vcdot T]
Где период
[T=frac{t}{n}=frac{10 c}{4}=2,5 c] [lambda =5frac{м}{с}cdot 2,5 с=12,5 м]
Ответ: $lambda =12,5 м$
Пример 2
Найти длину волны $lambda $ колебаний, если расстояние между первой и четвертой стоячей волны $l=15 см.$
Решение:
Длина стоячей волны
[{lambda }_{ст}=frac{lambda }{2} (1)]
где $lambda -$ длина волны колебаний.
С другой стороны
[{lambda }_{ст}=frac{l}{n_1-n_2} (2)]
Где $n_1и n_2-$ порядковые номера пучностей.
По условию
$n_1=1$ и $n_2=4$
Тогда приравнивая правые части уравнений (1) и (2), получаем
[frac{lambda }{2}=frac{l}{3}]
Откуда длина волны колебаний
[lambda =frac{2l}{3}=10 см=0,1 м]
Ответ:$ lambda =0,1 м$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
