Как по рисунку найти количество решений уравнения

Покажем, как задачи с параметрами можно решать графически.

Найдём количество решений уравнения

в зависимости от $$ a$$.

Искомое количество решений совпадает с числом точек пересечения графиков функций

График первой функции получается из графика функции, который был построен в предыдущем примере. Для этого нужно воспользоваться преобразованием вида ПР1 то есть график $$ y=_<1>left(xright)$$ имеет такой вид, как показано на рис. 43 $$ fleft(0right)=sqrt<5>$$.

Графиком функции $$ y=a$$ будет прямая, параллельная оси $$ Ox$$ (рис. 43). При этом она пересекает ось ординат в точке $$ (0,a)$$. Легко видеть, что при $$a 3$$ прямая $$ y=a$$ не имеет пересечений с графиком $$ y=_<1>left(xright)$$, при $$ a=3$$ и $$ ain [0;sqrt<5>)$$ есть две точки пересечения, а при $$ ain [sqrt<5>;3)$$ – четыре общие точки и при $$ a=sqrt<5>$$ – три общие точки. Остаётся лишь сформулировать ответ.

При $$ ain (-infty ;0)bigcup (3;+infty )$$ решений нет, при $$ ain [0;sqrt<5>)bigcup left<3right>$$ – два решения, при $$ ain left<sqrt<5>right>$$ – три решения, при $$ ain (sqrt<5>;3)$$ – четыре решения.

Найдём количество решений уравнения в зависимости от $$ a$$:

Методом интервалов нетрудно построить график функции

Количество решений уравнения совпадает с числом точек пересечения этого графика с прямой $$ fleft(xright)=a$$ (рис. 44).

Проанализировав график, несложно выписать ответ.

При $$ ain (8;+infty )$$ уравнение имеет 2 решения, при $$ a=8$$ уравнение имеет бесконечно много решений, при $$ ain (-infty ;8)$$ решений нет.

Рассмотрим ещё один пример задач с параметром, где используется построение множеств, задаваемых уравнениями с модулем. Напомним, что графиком уравнения называют линию на плоскости, на которой лежат те и только те точки, координаты которых удовлетворяют этому уравнению.

Найдём количество решений системы уравнений

в зависимости от $$ a$$.

Для решения необходимо построить график уравнения $$ left|xright|+left|yright|=4$$. Это можно сделать, последовательно выполнив построения таких графиков:

График второго уравнения – окружность с центром в точке $$ O(0;0)$$ и радиусом $$ left|aright|$$. Изобразим оба этих графика на координатной плоскости $$ xOy$$.

При $$ ain (-infty ;-4)cup (-2sqrt<2>;2sqrt<2>)cup (4;+infty )$$ система не имеет решений;

при $$ ain <-4;-2sqrt<2>;2sqrt<2>;4>$$ система имеет 4 решения;

при $$ ain (-4;-2sqrt<2>)cup (2sqrt<2>;4)$$ система имеет 8 решений.

В следующей задаче нам потребуется понятие локального экстремума функции. Говорят, что функция $$ y=fleft(xright)$$ имеет локальный максимум в точке $$ _<0>$$, если для некоторого числа $$ε > 0$$ при $$|x − x_0| 0$$ при $$|x − x_0| 0$$ график $$ y=at-3$$ касается линии $$ y=sqrt$$ (cм. рис. 46). Уравнение $$ D=0$$ имеет единственный положительный корень `a=1/4`. Следовательно, `a_2=1/4`. Если $$dfrac3<16>leq a 1/4` они не имеют общих точек.

Рассмотрим пример использования этого правила в задаче.

Найдём все значения параметра $$ a$$, при которых система

имеет хотя бы одно решение.

Неравенство системы после выделения полных квадратов можно записать в виде $$ ^<2>-8left|xright|+16+^<2>-8left|yright|+16le 1$$ или $$ left(right|x|-4<)>^<2>+(left|yright|-4<)>^<2>le 1$$. Множество $$ E$$ решений этого неравенства – объединение кругов $$ _<1>$$, $$ _<2>$$, $$ _<3>$$, $$ _<4>$$ (вместе с их границами) радиуса $$ 1$$ (см. рис. 47) с центрами $$ _<1>(4;4)$$, $$ _<2>(4;-4)$$, $$ _<3>(-4;-4)$$, $$ _<4>(-4;4)$$. Запишем уравнение системы в виде

Это уравнение задаёт окружность $$ L$$ радиуса $$ left|aright|$$ с центром в точке $$ M(0;1)$$, или точку $$ (0;1)$$ при $$ a=0$$. Исходная система имеет хотя бы одно решение при тех значениях $$ a$$, при которых окружность $$ L$$ имеет общие точки с множеством $$ E$$. При этом ввиду симметричного расположения соответствующих пар кругов относительно оси ординат достаточно выяснить, при каких значениях $$ a$$ окружность $$ L$$ имеет общие точки с кругами, центрами которых являются точки $$ _<1>$$ и $$ _<2>$$. Проведём из точки $$ M$$ лучи $$ _<1>$$ и $$ _<2>$$ в направлении точек $$ _<1>$$ и $$ _<2>$$. Пусть $$ _<1>$$ и $$ _<1>$$ – точки пересечения $$ _<1>$$ и окружности с центром $$ _<1>$$, $$ _<2>$$ и $$ _<2>$$ – точки пересечения $$ _<2>$$ и окружности с центром $$ _<2>$$. Тогда из геометрических соображений имеем:

При $$ 4le left|aright|le 6$$ окружность с центром $$ M$$ имеет общие точки с кругом $$ <omega >_<1>$$ , а при $$ sqrt<41>-1le left|aright|le sqrt<41>+1$$ – с кругом $$ <omega >_<2>$$.

а) Если $$b 0$$. Эта система не имеет решений при $$ a=0$$ и поэтому $$b 0$$. Теперь мы прибегнем к графическому методу. Рассмотрим два случая: $$0 1$$. Если $$b > 1$$, то $$sqrt Эта система не имеет решений, так как прямая $$ y=x-b$$ не пересекает график функции $$ y=|^<2>-b|$$ (см. рис. 48). Если $$0 0$$).

В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости.

Найдём все значения `a`, при каждом из которых уравнение

Рассмотрим функции `f(x)-a|x-3|` и `g(x)=5/(x+2)`.

Если построить график функции `f(x)` для разных `a` (рис. 50) и график функции `g(x)` (рис. 51), то можно без проблем исследовать на промежутке `[0;+oo)` уравнение `f(x)=g(x)`.

При `a При `a>0` функция `f(x)` возрастает на промежутке `(3;+oo)`. Функция `g(x)` убывает на этом промежутке, поэтому уравнение `f(x)=g(x)` всегда имеет ровно одно решение на промежутке `(3;+oo)`, поскольку `f(3) g(3+1/a)`. На промежутке `[0;3]` уравнение `f(x)=g(x)` принимает вид `3a-ax=5/(x+2)`. Это уравнение сводится к уравнению `ax^2-ax+(5-6a)=0`. Будем считать, что `a>0`, поскольку случай `a

Пусть уравнение имеет два корня, то есть `a>4/5`. Тогда оба корня меньше `3`, поскольку при `x>=3` значения функции `3a-ax` неположительны, а значения функции `5/(x+2)` положительны. По теореме Виета сумма корней равна `1`, а произведение равно `5/6-6`. Значит, больший корень всегда принадлежит промежутку `[0;3]`, а меньший принадлежит этому промежутку тогда и только тогда, когда `5/a-6>=0`, то есть `a 5/6`;

– три корня при `4/5

В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости. В следующем примере будем использовать известный подход к задачам, содержащим некоторые переменные в квадрате. Суть этого подхода – рассмотрение выражения как квадратичной функции относительно какой-нибудь переменной (остальные переменные при этом считаются параметрами) с последующим использованием известных свойств квадратичной функции.

Найдём все значения параметра $$ a$$, при каждом из которых система уравнений

имеет ровно три решения.

Первое уравнение данной системы равносильно совокупности двух уравнений $$ |y+9|+|x+2|=2$$ и $$ ^<2>+^<2>=3$$. Первое из них задаёт квадрат $$ G$$ с центром $$ (-2;-9)$$, диагонали которого равны $$ 4$$ и параллельны осям координат. Второе задаёт окружность $$ S$$ с центром $$ (0;0)$$ радиуса $$ sqrt<3>$$ (см. рис. 52).

Второе уравнение исходной системы при $$a > 0$$ задаёт окружность $$ Omega $$ с центром $$ (-2;-4)$$ радиуса $$ R=sqrt$$.

Отметим, что при $$a Рассмотрев случаи внешнего и внутреннего касания окружностей $$ Omega $$ и $$ S$$, можно заключить, что они имеют ровно `1` общую точку при $$ R=sqrt<20>pm sqrt<3>$$, ровно `2` общие точки при $$ Rin (sqrt<20>-sqrt<3>;sqrt<20>+sqrt<3>)$$ и ни одной общей точки при остальных $$ R$$. Поскольку центры окружности $$ Omega $$ и квадрата $$ G$$ лежат на прямой $$ x=-2$$, то $$ Omega $$ и $$ G$$ имеют ровно `1` общую точку при $$ R=3$$ или $$ R=7$$, ровно `2` общие точки при $$ Rin (3;7)$$ и ни одной общей точки при остальных значениях $$ R$$. Для того чтобы у системы было 3 решения, необходимо и достаточно, чтобы окружность $$ Omega $$ имела `2` общие точки с квадратом $$ G$$ и `1` общую точку с окружностью $$ S$$ или наоборот. Рассмотрим значения $$ R$$, при которых окружность $$ Omega $$ имеет с квадратом $$ G$$ или окружностью $$ S$$ ровно `1` общую точку.

1) $$ R=sqrt<20>+sqrt<3>$$. Тогда есть ровно `1` общая точка с окружностью $$ S$$, и ровно `2` общие точки с квадратом $$ G$$ (т. к. $$3 sqrt <20>+ sqrt<3>$$), т. е. у системы 1 решение.

Итак, подходят $$ R=3$$ и $$ R=sqrt<20>+sqrt<3>$$. Тогда искомые значения параметра $$ a=<3>^<2>=9$$ и $$ a=(sqrt<20>+sqrt<3><)>^<2>=23+4sqrt<15>$$.

Метод подсчёта количества решений

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.

В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.

Общая форма интересующего нас уравнения:

где n и m — положительные целые числа.

Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.

Нам нужен метод

Давайте начнём с частного случая общего уравнения:

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

Число решений в этом случае равно 10.

Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.

Значит, нужен эффективный метод.

Разрабатываем метод

Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:

Одним из решений было (5, 0). Давайте преобразуем его в:

Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.

В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.

Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

Это то же самое число, что мы получили методом прямого счёта!

Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.

Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

Простейшее решение этого уравнения:

Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:

На рис. изображён график функции y=F (x)

323077. На рисунке изображён график функции y=F (x) — одной из первообразных некоторой функции f (x), определённой на интервале (–3;5). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке [–2;4].

Необходимо определить сколько имеется точек на данном графике, в которых F′(x) = 0. Мы знаем, что производная равна нулю в тех точках, где касательная к графику функции параллельна оси ох. Покажем эти точки на интервале [–2;4]:

Это точки экстремума данной функции F (x). Их десять.

[spoiler title=”источники:”]

Метод подсчёта количества решений

http://matematikaege.ru/proizvodnaya/323077-na-risunke-izobrazhyon-grafik-funkcii-y-fx.html

[/spoiler]

Источник

Версия для печати и копирования в MS Word

На рисунке изображён график функции y = F(x)  — одной из первообразных функции f(x), определённой на интервале (−3; 4). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 3].

На рисунке изображён график функции y = F(x)  — одной из первообразных функции f(x), определённой на интервале (−4; 3). Найдите количество решений уравнения f(x) = 0 на отрезке [−3; 1].

На рисунке изображён график функции определённой на интервале (−3; 11). Найдите наименьшее значение функции f(x)на отрезке [2; 9,5].

На рисунке изображён график функции   — одной из первообразных некоторой функции определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

На рисунке изображён график функции y=F(x)   — одной из первообразных некоторой функции f(x) , определённой на интервале (-2;4) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3] .

На рисунке изображён график функции y=F(x)   — одной из первообразных некоторой функции f(x) , определённой на интервале (-2;6) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;5] .

На рисунке изображён график функции y=F(x)   — одной из первообразных некоторой функции f(x) , определённой на интервале (-3;5) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;4] .

На рисунке изображён график функции y=F(x)   — одной из первообразных некоторой функции f(x) , определённой на интервале (-3;4) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;3] .

На рисунке изображён график функции y=F(x)   — одной из первообразных некоторой функции f(x) , определённой на интервале (-2;5) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;4] .

На рисунке изображён график функции y=F(x)   — одной из первообразных некоторой функции f(x) , определённой на интервале (-3;6) . Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;5] .

На рисунке изображён график функции и одной из первообразных некоторой функции определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Источник

Лучшие онлайн-курсы для подготовки к ЕГЭ

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Первообразная функции»

Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №1164

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).

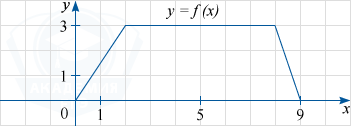
Показать решение

Решение

По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.

Её площадь равна frac{4+3}{2}cdot 3=10,5.

Ответ

10,5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1158

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].

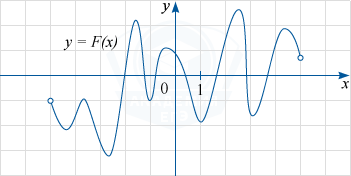
Показать решение

Решение

Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1155

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).

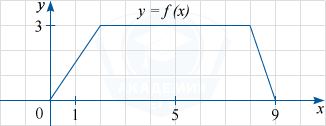
Показать решение

Решение

По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.

Её площадь равна frac{5+3}{2}cdot 3=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1149

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].

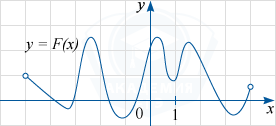
Показать решение

Решение

Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1146

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).

Найдите площадь заштрихованной фигуры.

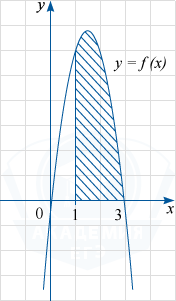
Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №907

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

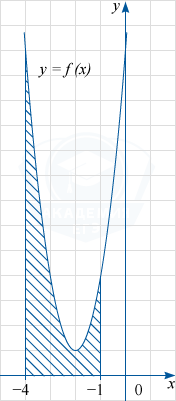
Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).

Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №307

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

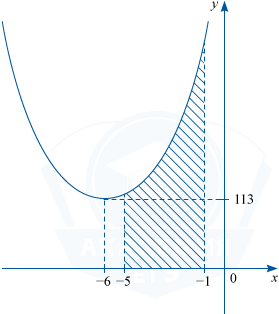
Показать решение

Решение

По формуле Ньютона-Лейбница S=F(-1)-F(-5).

F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.

F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.

F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.

Ответ

576

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №306

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).

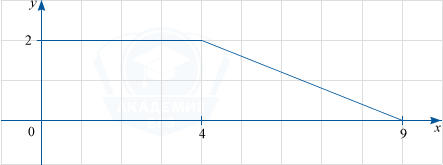
Показать решение

Решение

F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.

Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №104

Тип задания: 7
Тема:
Первообразная функции

Условие

На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.

Показать решение

Решение

На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:

intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)

Подставим значение первообразной из условия и получим площадь фигуры:

F(-1)-F(-4)=

=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=

=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5

Ответ

4,5

Задание №103

Тип задания: 7
Тема:
Первообразная функции

Условие

Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].

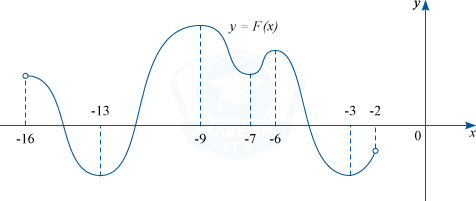
Показать решение

Решение

Формула первообразной имеет следующий вид:

f(x) = F'(x)

По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.

Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.

На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Источник

Главная › ЕГЭ. Производная и первообразная

Автор: Ирина Гайкова

Комментариев нет

713

На рисунке изображён график функции ?=?(?),— одной из первообразных некоторой функции ?(?), определённой на интервале (-3; 5). Пользуясь рисунком, определите количество решений уравнения ?(?)=0 на отрезке [−2;4] .

Интересная статья? Поделитесь ею пожалуйста с другими:

Facebook