Как по системе координат найти площадь фигуры - Сайт, где вы сможете решить свои вопросы

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми x=a и x=b и графиком функции y=f(x) . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция y=f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

${ S= intlimits_{a}^{b} f(x),dx,.}$

(4)

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции y=f(x) . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant Sleqslant sum_{k=0}^{n-1} M_kDelta x_k,,$

где $sum_{k=0}^{n-1}m_kDelta x_k$ — площадь внутренней ступенчатой фигуры, $sum_{k=0}^{n-1}M_kDelta x_k$ —площадь внешней ступенчатой фигуры, $m_k=min_{xin [x_k;x_{k+1}]}f(x)$ и $M_k=max_{xin[x_k;x_{k+1}]}f(x)$ . С другой стороны, по определению интеграла можно записать:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant intlimits_{a}^{b} f(x),dxleqslant sum_{k=0}^{n-1}M_kDelta x_k,.$

Таким образом, числа и $intlimits_{a}^{b} f(x),dx$ разделяют одни и те же числовые множества: $Biggl{,sum_{k=0}^{n-1}m_kDelta x_k,Biggr},$ $Biggl{,sum_{k=0}^{n-1}M_kDelta x_k,Biggr}$ . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому $S=intlimits_{a}^{b} f(x),dx$ . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции y=f_1(x) , сверху графиком функции y=f_2(x) , а слева и справа прямыми x=a,~x=b (рис. 30), то ее площадь выражается формулой

$S= intlimits_{a}^{b}bigl[f_2(x)-f_1(x)bigr]dx,.$

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами f(x) .

Площадь фигуры между двумя графиками функций

Пусть теперь функция y=f(x) непрерывна на отрезке [a;b] и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру Phi , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [a;b] функции y=f(x) , которая на [a;b] принимает только неотрицательные значения. По доказанному выше

Интегрирование знакопеременной функции

$S(Phi)= intlimits_{a}^{b} bigl(-f(x)bigr)dx$ . Но S(Phi)=S(F).

Значит,

$S(F)= intlimits_{a}^{b} bigl(-f(x)bigr)dx= -intlimits_{a}^{b} f(x),dx,.$

Как мы видим, в рассматриваемом случае интеграл $intlimits_{a}^{b} f(x),dx$ дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла $intlimits_{a}^{b} f(x),dx$ дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции y=f(x) , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой y=e^x , осью абсцисс и прямыми x=1,~x=2 (рис. 33).

Решение. Имеем: $S= intlimits_{1}^{2} e^x,dx= Bigl.{e^x}Bigr|_{1}^{2}= e^2-e= e(e-1)$ (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы y^2=4x и отрезком прямой x=2 (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

$S= 2int_{0}^{2}2sqrt{x},dx= left.{frac{4x^{3/2}}{3/2}}right|_{0}^{2}= frac{8}{3}cdot 2^{3/2}= frac{16}{3}sqrt{2},.$

Пример 3. Найти площадь фигуры, ограниченной графиками функций y^2=9x,~ y=3x (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника OAB и прямоугольного треугольника OAB:

$S= intlimits_{0}^{1} sqrt{9x},dx- intlimits_{0}^{1} 3x,dx= left.{3cdot frac{x^{3/2}}{3/2}}right|_{0}^{1}- left.{3cdot frac{x^2}{2} }right|_{0}^{1}= 2-frac{3}{2}= frac{1}{2},.$

Площадь фигуры, ограниченной кривой, осью абсцисс и двумя прямыми

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой a(y^2-x^2)+x^3=0 .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Площадь фигуры, ограниченной петлёй кривой

Записав уравнение кривой в виде $y^2=frac{x^2}{a}(a-x)$ , найдем точки пересечения ее с осью , положив y=0colon, x_1=0,~ x_2=a . Учитывая сказанное, найдем площадь половины петли:

$frac{1}{2}S= frac{1}{sqrt{a}} intlimits_{0}^{a} xsqrt{a-x},dx,.$

Воспользовавшись формулой из таблицы при a=-1,~ b=a , получим:

$intlimits_{0}^{a} xsqrt{a-x},dx= left.{frac{2(-3x-2a)sqrt{(a-x)^3}}{15}}right|_{0}^{a}= frac{4}{15},a^{5/2},.$

Значит, окончательно имеем:

$frac{1}{2}S= frac{1}{sqrt{a}}cdot frac{4}{15},a^{5/2}= frac{4}{15},a^2quad Leftrightarrowquad S=frac{8}{15},a^2,.$

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая y=f(x),~ f(x)geqslant0,~ aleqslant xleqslant b задана в параметрической форме

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} alpha leqslant tleqslant b,,$

где функция x=varphi(t) монотонна на отрезке [alpha;beta] , причем varphi(alpha)=a, varphi(beta)=b , и имеет на этом отрезке непрерывную производную. Так как y=f(x)= fbigl(varphi(t)bigr)= psi(t) , то по формуле замены переменной под знаком определенного интеграла получаем:

$S= intlimits_{a}^{b} f(x),dx= intlimits_{alpha}^{beta} fbigl(varphi(t)bigr) varphi'(t),dt= intlimits_{alpha}^{beta} psi(t) varphi'(t),dt,.$

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

$S= intlimits_{alpha}^{beta} psi(t)varphi'(t),dt,.$

(5)

Пример 5. Вычислить площадь эллипса, заданного параметрически $begin{cases} x=acos{t},,\ y=bsin{t},,end{cases} 0leqslant tleqslant 2pi,.$

Площадь фигуры, ограниченной эллипсом

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке A(a;0) соответствует значение t=0 , а точке B(0;b) — значение $t=frac{pi}{2}$ . Поэтому

$begin{aligned} S&= 4intlimits_{0}^{a}y,dx= -4intlimits_{0}^{pi/2}bsin{t}cdot(-asin{t}),dt= 4abintlimits_{0}^{pi/2} sin^2t,dt=\ &= 2abintlimits_{0}^{pi/2} bigl(1-cos2tbigr),dt= left.{2ab!left(t- frac{1}{2}sin2t right)}right|_{0}^{pi/2}= pi,ab,. end{aligned}$

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами ell и , выходящими из точки , и непрерывной кривой Gamma (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть rho=rho(varphi) — полярное уравнение кривой Gamma , а varphi_0 и Phi — углы между полярной осью и лучами ell и соответственно. При этом пусть функция непрерывна на [varphi_0;Phi] .

Разобьем данный сектор на частей лучами

$varphi_0< varphi_1< varphi_2< ldots< varphi_k< varphi_{k+1}< ldots< varphi_n= Phi$

и рассмотрим k-й частичный сектор $[varphi_k; varphi_{k+1}]$ (рис. 39). Пусть r_k — наименьшее значение функции rho(varphi) в $[varphi_k; varphi_{k+1}]$ , a R_k — наибольшее значение функции в этом отрезке.

Площадь в полярных координатах и разбиение сектора на n частей

Построим два круговых сектора с радиусами r_k и R_k . Обозначим через Deltavarphi_k величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

$frac{1}{2}cdot r_k^2cdot Deltavarphi_k leqslant S_kleqslant frac{1}{2}cdot R_k^2cdot Deltavarphi_k,.$

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна $frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_k$ , а площадь внешней фигуры равна — $frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k$ . Эти выражения являются нижней и верхней суммами Дарбу s_P и S_P для интеграла $frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi$ . Так как функция rho(varphi) непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого varepsilon найдется такое разбиение отрезка [varphi_0,Phi] , что S_P-s_P<varepsilon . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

Площадь, ограниченная одним лепестком полярной розы

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant Sleqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(6)

В то же время по определению определенного интеграла

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi leqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(7)

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

$S= frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi,.$

(8)

Пример 6. Вычислить площадь, ограниченную одним лепестком розы rho=asin2varphi (рис. 40).

Решение. Значениям varphi=0 и $varphi=frac{pi}{2}$ соответствует rho=0 Поэтому

$S= frac{1}{2} intlimits_{0}^{pi/2} a^2sin^22varphi,dvarphi= frac{a^2}{2} intlimits_{0}^{pi/2} frac{1-cos4varphi}{2},dvarphi= left.{frac{a^2}{4}! left(varphi- frac{1}{4}sin4varphiright)}right|_{0}^{pi/2}= frac{a^2}{4}cdot frac{pi}{2}= frac{pi}{2},a^2,.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

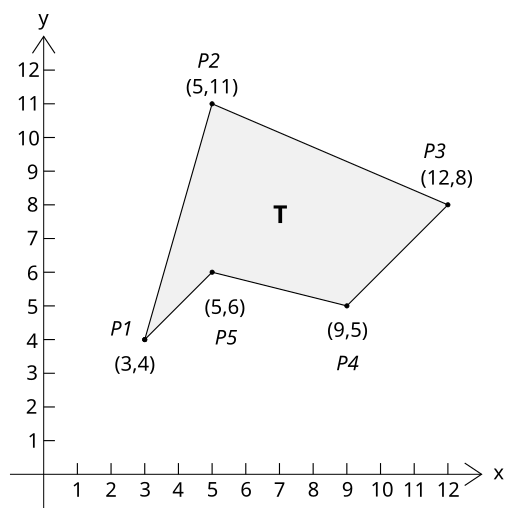
Площадь по заданным координатам.

Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам?

Какие есть формулы и методы, позволяющие находить площадь через координаты?

бонус за лучший ответ (выдан): 5 кредитов

Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая “формулой землемера”, “формулой геодезиста”, “формулой шнурования”, “алгоритмом шнурования”, а так же “методом треугольников”.

Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи.

Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки.

Фигура многоугольника может иметь произвольную геометрию. Например:

Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn).

Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна:

Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается.

Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG.

Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются:

S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG)

Площади трапеций рассчитываются по формуле;

Sтрапеции = 1/2 *((a+b))*h,

где a, b – основания трапеции,

h – высота трапеции.

Значения a, b и h вычисляются по координатам.

В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле:

автор вопроса выбрал этот ответ лучшим

Ксарфакс
[156K]

5 лет назад

Площадь фигуры по координатам вершин

Если известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам.

Эта формула выглядит следующим образом:

Здесь:

AB – отрезок,

точка A имеет координаты (x1, y1),

точка B имеет координаты (x2, y2).

Рассмотрим несколько примеров.

1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона:

Здесь:

S – площадь треугольника,

a, b, c – стороны,

p – полупериметр, который равен половине суммы сторон a, b и c.

Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам:

AB = √(4² + 4²) = √32 ≈ 5,66.

AC = √(3² + (-3)²) = √18 ≈ 4,24.

BC = √((-1)² + (-7)²) = √50 ≈ 7,07.

Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49.

Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04.

2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали:

Здесь:

S – площадь ромба,

d1 и d2 – диагонали.

Таким образом, нам нужно найти диагонали AC и BD.

AC = √(4² + 0) = √16 = 4.

BD = √(0 + (-4)²) = √16 = 4.

Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8.

3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая:

Здесь:

S – площадь трапеции,

a и b – основания,

h – высота.

Высота трапеции (пусть это будет BE) – это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD).

Определим координаты её отрезка:

координаты первой точки совпадают с точкой B, это (3,4).
координаты 2 точки (точка E) будут (3,1) – так как абсцисса совпадает с абсциссой точки B, а ордината совпадает с ординатой точек A и D.

Высота трапеции BE = √(0 + (-3)²) = √9 = 3.

Теперь посчитаем длину оснований:

BC = √(2² + 0) = √4 = 2.

AD = √(5² + 0) = √25 = 5.

Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5.

Степан-16
[34.5K]

5 лет назад

Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам.

Самый простой случай – для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат.

Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем – площадь по формуле: половина произведения основания на высоту.

И т.д.

Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны.

Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей.

Эления
[445K]

3 года назад

Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь.

Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры – это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь.

Пример 1. Ищем площадь треугольника.

Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC.

Даны значения: AC основание в промежутке от “-4” до “+4”, то есть длина основания равна восьми.

Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой “0” на графике.

Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 – 0 = 4 и y = 2 – 0 = 2 (BO).

Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле:

Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC.

И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств:

Пример 2.

Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл.

Бекки Шарп
[71.2K]

3 года назад

Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса.

У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту.

S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ – 10.

А теперь по теореме Гаусса.

Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число.

S= 0,5 х [3х6+6х6+9х2+5х2 – 2х6-6х9-6х5-2х3] = 10

Таким образом можно найти площадь любой сложной фигуры, зная ее координаты.

dydySacha
[10.8K]

5 лет назад

Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу.

Алиса в Стране
[363K]

3 года назад

Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит:

Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n – количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать.

Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник:

Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6).

Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится:

Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной.

duselldorf
[4.3K]

5 лет назад

Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании:

где

А – площадь многоугольника с заданными координатам его вершин,

n – количество сторон многоугольника,

(xi, yi) – координаты вершин многоугольника,

i = 1, 2,…, n — номер вершины многоугольника.

Бархатные лапки
[382K]

3 года назад

Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так:

S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 – 3х9 – 4х10 – 7х7 – 6х6] = 8 (квадратных единиц)

Как видим если применять при решении формулу Гаусса то решить такую задачку несложно.

Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса – квадрат, треугольник и т.п.

Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей.

Знаете ответ?

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 января 2022 года; проверки требуют 2 правки.

Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости. В формуле векторным произведением координат и сложением определяется площадь области, охватывающей многоугольник, а затем из нее вычитается площадь окружающего многоугольника, что дает площадь многоугольника внутри. Также она называется формулой шнурования, так как положительные и отрицательные слагаемые, состоящие из перемножаемых координат, располагаются крест-накрест, как при завязывании шнурков. Она находит применение в геодезии, лесном хозяйстве и других областях.

Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.

Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.

Формула площади верна для любого самопересекающегося многоугольника, который может быть выпуклым или вогнутым.

Определение[править | править код]

Формула может быть представлена следующим выражением:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}left|sum _{i=1}^{n-1}x_{i}y_{i+1}+x_{n}y_{1}-sum _{i=1}^{n-1}x_{i+1}y_{i}-x_{1}y_{n}right|=\&={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+dots +x_{n-1}y_{n}+x_{n}y_{1}-x_{2}y_{1}-x_{3}y_{2}-dots -x_{n}y_{n-1}-x_{1}y_{n}|,end{aligned}}}$

где

S — площадь многоугольника,

n — количество сторон многоугольника,

(x_i, y_i), i = 1, 2, …, n — координаты вершин многоугольника.

Другое представление этой же формулы^[1]^[2]:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}left|sum _{i=1}^{n}x_{i}(y_{i+1}-y_{i-1})right|=\&={frac {1}{2}}left|sum _{i=1}^{n}y_{i}(x_{i+1}-x_{i-1})right|=\&={frac {1}{2}}left|sum _{i=1}^{n}x_{i}y_{i+1}-x_{i+1}y_{i}right|=\&={frac {1}{2}}left|sum _{i=1}^{n}det {begin{pmatrix}x_{i}&y_{i}\x_{i+1}&y_{i+1}end{pmatrix}}right|,end{aligned}}}$

где

x_n+1 = x₁, x₀ = x_n,

y_n+1 = y₁, y₀ = y_n.

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.

Примеры[править | править код]

Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле^[3]:

${displaystyle mathbf {S} _{text{tri.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|,}$

где x_i и y_i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x₅ и y₅:

${displaystyle mathbf {S} _{text{pent.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|.}$

S для четырехугольника — переменные до x₄ и y₄:

${displaystyle mathbf {S} _{text{quad.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{1}y_{4}|.}$

Более сложный пример[править | править код]

Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}|3times 11+5times 8+12times 5+9times 6+5times 4-{}\&qquad -4times 5-11times 12-8times 9-5times 5-6times 3|=\&={frac {60}{2}}=30.end{aligned}}}$

Объяснение названия[править | править код]

Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу. В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:

${displaystyle {begin{bmatrix}2&4\3&-8\1&2\2&4end{bmatrix}}.}$

Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:

и перемножим пары чисел, соединённых чертой, а затем сложим все суммы:

(2 × −8) + (3 × 2) + (1 × 4) = −6.

Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:

(4 × 3) + (−8 × 1) + (2 × 2) = 8.

Затем вычтем сумму второй группы из первой и возьмём модуль:

|(−6) − (8)| = 14.

Деление результата на два даёт площадь.
Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы.
В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».

Хорошее описание “Шнуровки Гаусса” представлено в видео на канале Wild Mathing [1]

См. также[править | править код]

Планиметр
Теорема Грина

Примечания[править | править код]

↑ Shoelace Theorem Архивная копия от 23 сентября 2020 на Wayback Machine, Art of Problem Solving Wiki.
↑ Weisstein, Eric W. Polygon Area. Wolfram MathWorld. Дата обращения: 24 июля 2012. Архивировано 12 мая 2012 года.
↑ Richard Rhoad; George Milauskas; Robert Whipple. Geometry for Enjoyment and Challenge. — new. — McDougal Littell (англ.) (рус., 1991. — С. 717—718. — ISBN 0-86609-965-4.

Источник

В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y=f(x), x=g(y) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.

Краткий обзор статьи

Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.

Полярная система координат и криволинейный сектор

Определение 1

Точка, расположенная в полярной системе координат, имеет полярный угол φ0 и полярный радиус r0≥0. Полярный угол φ0 отсчитывается от полярной оси по часовой стрелке, а r0 – это расстояние от заданной точки до начала координат.

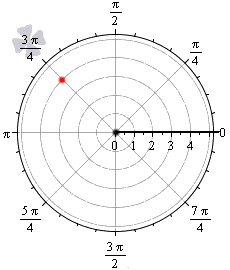
На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ0=3π4 и расстоянием до полюса r0=4.

Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.

Задать связь полярных и декартовых координат можно соотношениями r=x2+y2φ=arctgyx, x≠0 и обратно x=r·cosφy=r·sinφ.

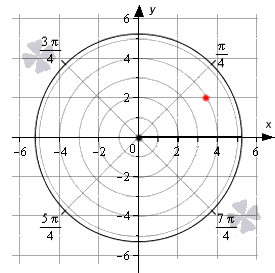
Координаты красной точки на чертеже 23; 2. Положение этой точки задается углом φ0=arctg223=π6 и расстоянием r0=232+22=4.

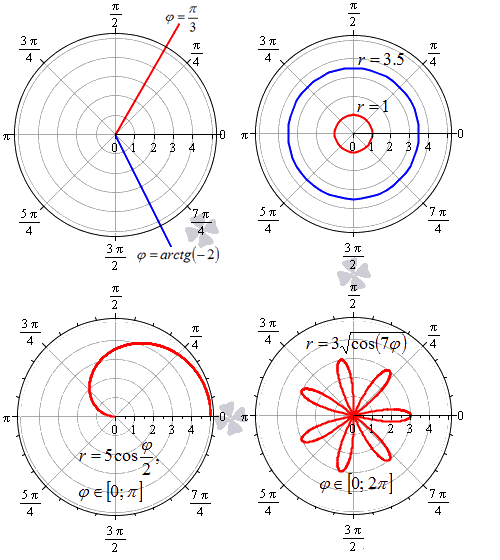
В полярной системе координат равенство φ=α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ=0. Равенство r=C>0 задает окружность с центром в начале координат, где – это радиус.

Функция r=p(φ), φ∈α; β определяет некоторую линию в полярных координатах.

Следует учитывать тот факт, что с позиции геометрии функция r=p(φ), φ∈α; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ=φ0∈α; β. Однако мы будем встречать и отрицательные значенияr=p(φ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.

На рисунке мы изобразили несколько примеров линий в полярной системе координат.

Дадим определение криволинейному сектору.

Определение 2

Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ=α, φ=β и некоторой линией r=p(φ)≥0, непрерывной на участке α; β.

На рисунке мы привели несколько примеров криволинейных секторов.

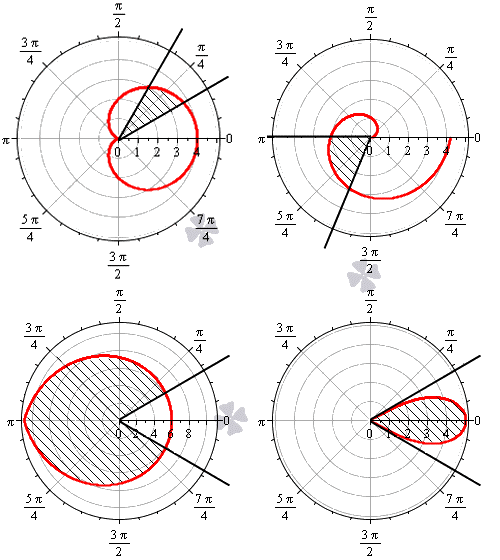
На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ=-π6, φ=π6, которые не являются ее границами.

Площадь криволинейного сектора – вывод формулы

Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: Sкругового сектора=γ·R22. Задаем внутренний угол γ в радианах.

Разобьем криволинейный сектор на n частей такими лучами

φ=φ1, φ=φ2,…, φ=φn-1, что α=φ0<φ1<φ2<…<φn-1<β и λ=maxi=1, 2,…, nφi-φi-1→0 при n→+∞.

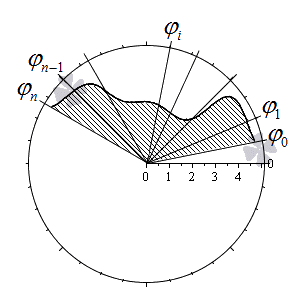
Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S(G) как сумму площадей секторов S(Gi) на каждом из участков разбиения:

S(G)=∑i=1nS(Gi)

Обозначим наибольшее и наименьшее значения функции r=p(φ) на i-ом отрезке φi-1; φi, i=1, 2,…, n как Rmini и Rmaxi . На каждом из отрезков построим по два круговых сектора Pi и Qi с максимальным и минимальным радиусами Rmini и Rmaxi соответственно.

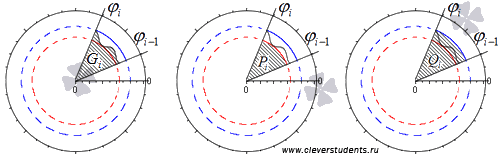
Фигуры, которые являются объединением круговых секторов Qi, i=1, 2,…, n; Pi, i=1, 2,…, n , обозначим как P и Q соответственно.

Их площади будут равны S(P)=∑i=1nS(Pi)=∑i=1n12(Rmini)2·φi-φi-1 и S(Q)=∑i=1nS(Qi)=∑i=1n12(Rmaxi)2·φi-φi-1, причем S(P)≤S(G)≤S(Q).

Так как функция r=pφ непрерывна на отрезке α; β, то функция 12p2φ будет непрерывна на этом отрезке. Если рассматривать S(P) и S(Q) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:

limλ→0S(P)=limλ→0S(Q)=S(G)⇒S(G)=limλ→0∑ i=1n12(Rmini)2·φi-φi-1==limλ→0∑ i=1n12(Rmaxi)·φi-φi-1=12∫βαp2φdφ

Определение 3

Формула для определения площади криволинейного сектора имеет вид:

S(G)=12∫βαp2φdφ

Примеры вычисления площади криволинейного сектора

Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.

Пример 1

Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r=2sin2φи лучами φ=π6, φ=π3.

Решение

Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r=2sin(2φ)положительна и непрерывна на отрезке φ∈π6, π3.

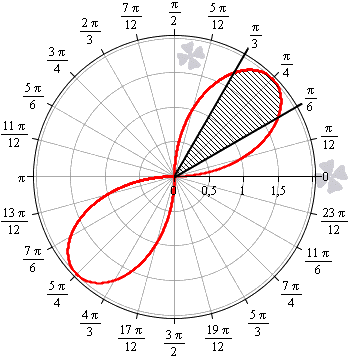
Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.

S(G)=12∫π6π3(2sin(2φ)2dφ=∫π6π32(sin(2φ)2dφ=∫π6π32·1-cos4φ2dφ=∫π6π3(1-cos(4φ))dφ=φ-14sin(4φ)π6π3==π3-14sin4π3-π6-14sin4π6=π6+34

Ответ: S(G)=π6+34

Задача упрощается в тех случаях, когда лучи φ=φ1, φ=φ2, ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.

Чаще встречаются задачи, где фигуру ограничивает лишь кривая r=p(φ). В этих случаях применить формулу S(G)=12∫αβp2(φ)dφ сразу не получится. Для начала придется решить неравенство p(φ)≥0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r=pφ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.

Пример 2

Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r=-3·cos3φ.

Решение

Функция определена для всех действительных значений аргумента. Решим неравенство -3·cos3φ≥0:

-3·cos3φ≥0⇔cos3φ≤0⇔cos φ≤0⇔⇔π2+2πk≤φ≤3π2+2πk, k∈Z

Построим функцию в полярных координатах на отрезке φ∈π2; 3π2 (при k=0). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.

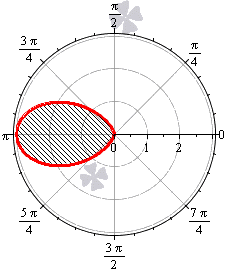
Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π2+2πk и 3π2+2πk соответственно для любого целого значения k.

S(G)=12∫π23π2(-3·cos3φ)dφ=92∫π23π2cos6φdφ

Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида Kn(x)=sin x·cosn-1(x)n+n-1nKn-2(x), где Kn(x)=∫cosn(x)dx.

∫cos6φdφ=sin φ·cos5φ6+56∫cos4φdφ==sin φ·cos5φ6+56sin φ·cos3φ4+34cos2φdφ==sin φ·cos5φ6+5sin φ·cos3φ24+1524sin φ·cos φ2+12∫cos0φdφ==∫π23π2cos6φdφ=sin φ·cos5φ6+5sin φ·cos3φ24+15sin φ·cos φ48+15φ48π23π2==1548·3π2-1548·π2=5π16

Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S(G)=92∫π23π2cos6φdφ=92·5π16=45π32.

Ответ: S(G)=45π32

В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.

Пример 3

Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r=3·cos(3φ).

Решение

Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.

cos(3φ)≥0⇔-π2+2πk≤3φ≤π2+2πk, k∈Z-π6+2π3k≤φ≤π6+2π3k, k∈Z

Таким образом, период функции r=3·cos3φ равен 2π3. Это значит, что фигура состоит из трех областей одинаковой площади.

Построим фигуру на графике.

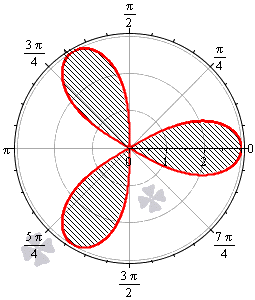
Вычислим площадь одного участка, расположенного на интервале φ∈π2; 5π6(при k=1):

12∫π25π69cos(3φ)dφ=12·3sin(3φ)π25π6=32sin3·5π6-sin3·π2=32(1-(-1)=3

Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.

Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.

Площадь фигуры, которую ограничивает лемниската Бернулли

Определение 4

Лемниската Бернулли задается уравнением r=α·cos2φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при -π4+π·k≤φ≤π4+π·k, k∈Z.

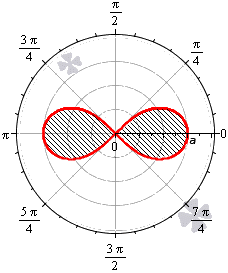
Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.

Для вычисления площади используем нужную формулу:

S(G)=2·12∫-π4π4a2cos(2φ)2φ=a22(sin(2φ))-π4π4==a22sin2·π4-sin2·-π4=a2

Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a.

Площадь фигуры, границей которой является кардиоида

В полярной системе координат кардиоида задается уравнением вида r=2a(1+cosφ). В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2π. Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2π больше нижнего.

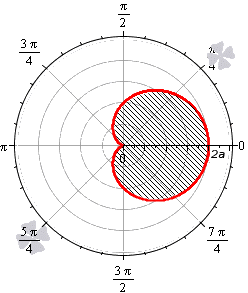
Вычислим площадь фигуры, ограниченной кардиоидой r=2a(1+cosφ), для φ∈0; 2π:

S(G)=12∫02π(2a(1+cosφ))2dφ=2a2∫02π(1+2cosφ+cos2φ)dφ==2a2∫02π1+2cosφ+1+cos2φ2dφ==2a2∫02π32+2cosφ+cos(2φ)2dφ==2a232φ+2sin φ+14sin2φ02π=6π·a2

Площадь фигуры, которую ограничивает улитка Паскаля

В полярной системе координат улитка Паскаля может быть задана уравнением r=b+2a·cosφ. В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b=2a.

Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.

При b<-2a функция r=b+2a·cosφ будет отрицательной для любого значения угла φ.

При b=-2a улитка Паскаля имеет вид точки, которая совпадает с полюсом.

При -2a< b< 0 функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z.

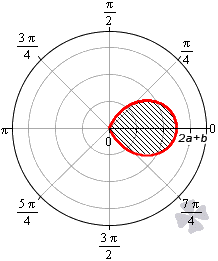
При 0<b<2a функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z. Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.

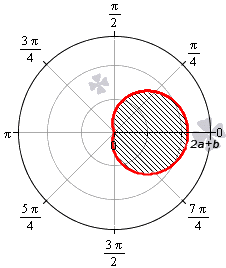
При b>2a функция r=b+2a·cosφ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже

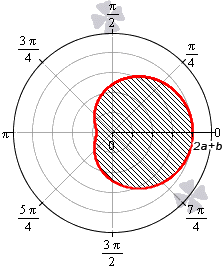
Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b.

Пример 4

Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r=-3+6cosφ и r=5+4cosφ в полярной системе координат.

Решение

Формула r=-3+6cosφ соответствует фигуре, известной как улитка Паскаля..

Функция r=-3+6cosφ определена для всех значений угла φ. Нам необходимо выяснить, при каких φ функция будет неотрицательной:

-3+6cosφ≥0⇔cosφ≥12⇔-π3+2πk≤φ≤π3+2πk, k∈Z

Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:

S(G)=12∫-π3π3(-3+6cosφ)2dφ=92∫-π3π3(1-4cosφ+4cos2φ)dφ==92∫-π3π31-4cosφ+4·1+cos2φ2dφ==92∫-π3π3(3-4cosφ+2cos(2φ))dφ=92·3φ-4sinφ+sin(2φ-π3π3==92·3·π3-4sinπ3+sin2π3-3·-π3-4sin-π3+sin-2π3==92·2π-33

Улитка Паскаля, определяемая формулой r=5+4cosφ, соответствует пятому пункту. Функция r=5+4cosφ определена и положительна для всех действительных значений φ. Поэтому, площадь фигуры в этом случае равна:

S(G)=12∫02π(5+4cosφ)2dφ=12∫02π(25+40cosφ+16cos2φ)dφ==12∫02π25+40cosφ+16·1+cos(2φ)2dφ==12∫02π(33+40cosφ+8cos(2φ))dφ=12·33φ+40sinφ+4sin(2φ02π==12·33·2π+40sin(2π+4sin(4π)-33·0+40sin 0+4sin 0=33π

Ответ: S(G)=33π

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль

Сразу обратимся к примеру.

Пример 5

Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r=αφ, α>0, а вторая первым витком логарифмической спирали r=αφ, α>1.

Решение

Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.

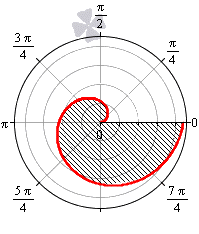
Исходя из этого, найдем площадь фигуры по формуле:

S(G)=12∫02π(αφ)2dϕ=α22∫02πφ2dφ=α22·φ3302π=4α3π33

Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:

S(G)=12∫02π(αϕ)2dϕ=12∫02πa2φdφ=14ln a·a2φ02π==14ln a·a4π-1

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов

Пусть фигура в полярной системе координат ограничена лучами φ=α, φ=β и непрерывными и неотрицательными на интервале φ∈α; β функциями r=p1(φ) и r=p2(φ), причем p1(φ)≤p2(φ) для любого угла φ=φ0∈α; β.

Находим площадь фигуры по формуле S(G)=12∫αβp22(φ)-p12(φ)dφ.

Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G2 и G1.

Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:

S(G)=S(G2)-S(G1)=12∫αβp22(φ)dφ-12∫αβp12(φ)dφ==12∫αβp22(φ)-p12(φ)dφ

Последний переход возможен в силу третьего свойства определенного интеграла.

Пример 6

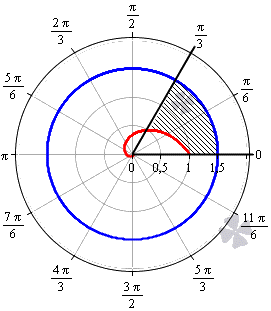
Необходимо вычислить площадь фигуры, которая ограничена линиями φ=0, φ=π3, r=32, r=12φв полярной системе координат.

Решение

Построим заданную фигуру на графике.

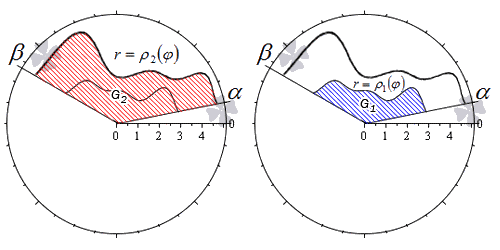
Очевидно, что r=32 больше r=12φ для любого φ∈0; π3. Применяем полученную формулу для вычисления площади фигуры:

S(G)=12∫0π3322-12φ2dφ=12∫0π394-2-2φdφ==12·94φ+12·2-2φln 20π3=12·94φ+1ln 2·122φ+10π3==12·94·π3+1ln 2·122·π3+1-94·0+1ln 2·122·0+1==12·3π4+2-2π3-12·ln 2

Ответ: S(G)=12·3π4+2-2π3-12·ln 2

А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.

Пример 7

Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y=13x, x=3x, окружностями (x-2)2+(y-3)2=13, (x-4)2+(y-3)2=25.

Решение

В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.

x=r·cosφy=r·sinφ⇒y=13x⇔r·sinφ=r·cosφ3⇔tgφ=13⇔φ=π6+πky=3x⇔r·sinφ=3·r·cosφ⇔tgφ=3⇔φ=π3+πk(x-2)2+(y-3)2=13⇔x2+y2=4x+6y⇔r=4cosφ+6sinφ(x-4)2+(y-3)2=25⇔x2+y2=8x+6y⇔r=8cosφ+6sinφ

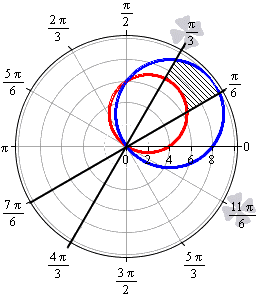
Функция r=8cosφ+6sinφ больше r=4cosφ+6sinφ для любого φ∈π6; π3. Вычисляем площадь фигуры в полярных координатах:

S(G)=12∫π6π38cosφ+6sinφ2-4cosφ+6sinφ2dφ==12∫π6π3(48cos2φ+48cosφ·sinφ)dφ==24∫π6π3cos2φdφ+24∫π6π3cosφ·sinφdφ==12∫π6π3(1+cos2φ)dφ+24∫π6π3sinφd(sinφ)==12·φ+12sin(2φ)π6π3+12·sin2φπ6π3==12·π3+12sin2π3-π6+12sin2π6+12·sin2π3-sin2π6==12·π6+12·322-122=2π+6

Ответ: S(G)=2π+6

Источник

Теория

Полярная система координат на плоскости — координаты объекта, выраженные через направление и расстояние. Эта система включает в себя точку отсчета — полюс и луч , начинающийся в этой точке, — полярную ось. Положительным направлением отсчета углов считается направление «против часовой стрелки». Полярная система координат используется в астрономии, военном деле, геодезии, медицине.

Выразим площадь S криволинейного сектора, то есть плоской фигуры, ограниченной непрерывной линией r = r(φ) и двумя лучами φ = α и φ = β , где r и φ – полярные координаты.

1. Будем считать часть искомой площади S как функцию угла φ, т.е. S = S(φ), где α < φ < β ( если φ = α, то S(α) = 0, если φ = β, то S(β) = S).

2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади ΔS равно площади “элементарного криволинейного сектора” OAB. Дифференциал dS представляет собой главную часть приращения ΔS при dφ → 0 и равен площади кругового сектора OAC (смотри рисунок) радиуса r с центральным углом dφ.
Поэтому dS = (1/2)⋅ r² ⋅ dφ.

3. Интегрируя полученное равенство в пределах от φ = α до φ = β, получим искомую площадь

О полярных координатах и нахождении площади в полярной системе координат

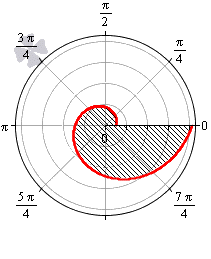
Задача 1. Найти площадь, ограниченную кривыми, заданными в полярной системе координат: r = 1 – cos(φ) ; r = 1; r ⩾ 1

Задача 2. Найти площадь фигуры, ограниченной “трехлепестковой розой” r = a ⋅ cos(3φ).

Задача 3. Если плоская фигура имеет “сложную” форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке ниже, имеем:

Задача 4. Вычислить площадь фигуры, ограниченной линией r = 2 cos²(φ)

Задача 5. Вычислить площадь фигуры, ограниченной линиями r = -2⋅sin(3φ) и r = 2⋅sin(φ) в полярной системе координат.

Задача 6. Вычислить площадь фигуры, ограниченной r = √3⋅cos(φ) и r = sin(φ) в полярной системе координат.

Важные заметки

1. Интегралы лучше всего считать раздельно. Когда площадь вы хотите сразу посчитать одним интегралом, то велика вероятность допустим ошибку из-за невнимательности. Да, здесь все интегралы оказываются положительными, поэтому один не сможет обнулить другой. Но вот большое количество упрощений, подстановок, коэффициентов в результате понижения степени могут вас запутать. Поэтому разбиваем фигуру на более простые части, затем ищем площади всех частей отдельно, потом складываем.

2. Некоторые сложные функции легче всего исследовать в полярной системе координат. Вы можете самостоятельно убедиться в этом, если попробуйте перейти в декартовую систему координат с помощью формул перехода: x = r⋅cos(φ) и y = r⋅sin(φ).

Переход от декартовой системы координат к полярной

r = √(x² + y²) ; cos(φ) = x / √(x² + y²) ; sin(φ) = y / √(x² + y²) ; φ = arctan(y/x)

Применение полярных координат

Полярные координаты оказываются удобнее декартовых, для задания кривых на плоскости, особенно для задания различных спиралей, например, спирали Архимеда, логарифмической спирали, трилистника.

В астрономических наблюдениях.
В фотографии используют фильтр, переводящий координаты точек из прямоугольной системы в полярную, создавая сферический эффект снимка.
Необычный формат биржевых графиков на основе полярных координат предложил в 1990-е годы российский математик Владимир Иванович Елисеев. Используя такую систему координат, относительно просто связать градусы и время (в году 365 дней, в окружности – 360 градусов)
В военном деле на радиолокационных станциях. Координаты цели могут выдаваться в полярной системе координат (азимут, дальность), прямоугольной (X, Y), геодезической (широта, долгота).
В медицине. Компьютерная томография сердца изображается в системе полярных координат.
В системах безопасности при идентификации по радужной оболочке глаза.
В геодезии в лазерном сканере получают координаты точек объекта с помощью измерения полярных углов и расстояний до объекта.
В приборах измерительных лабораторий на предприятиях точного приборостроения, машиностроения, микроэлектроники, в инструментальном производстве, в лабораториях институтов.
В компьютерных играх.

ARCHIMEDEAN SPIRAL ( Источник: https://mathcurve.com/courbes2d.gb/archimede/archimede.shtml )

Если Вам нужна помощь или репетитор по физике, математике или информатике/программированию, Вы можете написать в группу Репетитор IT mentor в VK

Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Источник

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Площадь фигуры, ограниченной кривой, заданной параметрически

Площадь фигуры, заданной в полярных координатах

Площадь фигуры по координатам вершин

Определение[править | править код]

Примеры[править | править код]

Более сложный пример[править | править код]

Объяснение названия[править | править код]

См. также[править | править код]

Примечания[править | править код]

Краткий обзор статьи

Полярная система координат и криволинейный сектор

Площадь криволинейного сектора – вывод формулы

Примеры вычисления площади криволинейного сектора

Площадь фигуры, которую ограничивает лемниската Бернулли

Площадь фигуры, границей которой является кардиоида

Площадь фигуры, которую ограничивает улитка Паскаля

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов

Вам также может понравиться

Как найти работу мечты в москве

Как найти файлы загрузки windows 10

Как найти коэффициент эластичности спроса на товар

Добавить комментарий Отменить ответ