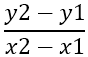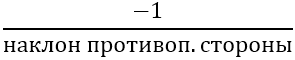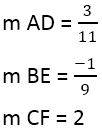Решение
Найдём уравнение прямой BC по двум точкам:

, или y = –
x – 6.
Тогда её угловой коэффициент k1 = – . Если k2 — угловой коэффициент прямой, содержащей высоту AP, то k1 . k2 = – 1. Поэтому
k2 = – = 2.
Уравнение прямой, содержащей высоту AP треугольника ABC, найдём по точке A(5; – 1) и угловому коэффициенту k2 = 2:
y + 1 = 2(x – 5), или y = 2x – 11.
Найдём уравнение прямой AC по двум точкам:

, или y =
x –
.
Тогда её угловой коэффициент k3 = . Если k4 — угловой коэффициент прямой, содержащей высоту BQ, то k4 . k3 = – 1. Поэтому
k4 = – = – 3.
Уравнение прямой, содержащей высоту BQ треугольника ABC, найдём по точке B(4; – 8) и угловому коэффициенту k4 = – 3:
y + 8 = – 3(x – 4), или y = – 3x + 4.
Координаты точки H пересечения высот треугольника ABC найдём, решив систему уравнений, задающих прямые AP и BQ:
Получим: x = 3, y = – 5.

Ответ
(3; – 5).
Точка пересечения высот треугольника

4.2
Средняя оценка: 4.2
Всего получено оценок: 412.
4.2
Средняя оценка: 4.2
Всего получено оценок: 412.
Точка пересечения высот треугольника относится к одной из трех замечательных точек треугольника. Замечательными эти точки зовутся не за красоту, а за отношение к золотому сечению треугольника, которое характеризует данную фигуру.
Опыт работы учителем математики – более 33 лет.
Высота
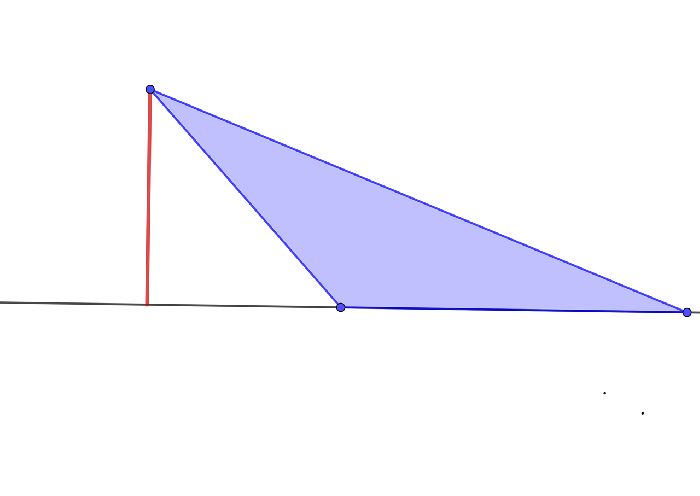
Что такое высота? Высота это перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону треугольника (может получиться, что высота будет падать на продолжение стороны, как это бывает с тупоугольными треугольниками).
Точка пересечения высот
У любого треугольника есть три высоты, и они всегда пересекаются в одной точке. Эта точка является одним из 3 центров треугольника и зовется ортоцентром.
Еще со времен Древней Греции приставкой «орто» обозначали перпендикуляр. Ортогоналями звались перпендикулярные прямые.
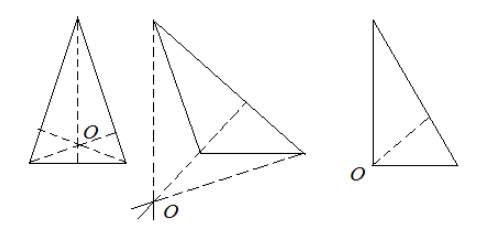
Ортоцентр имеет три варианта расположения в зависимости от вида треугольника:
- Внутри фигуры. В остроугольных треугольниках точка пересечения высот всегда находится внутри фигуры. Это обусловлено тем, что все высоты в таком треугольнике внутренние.
- Совпадает с вершиной. Этот случай характерен для прямоугольных треугольников. В таких треугольниках две из трех высот будут совпадать со сторонами. Если быть точнее, то совпадающие стороны это катеты. Остается одна высота, которая будет опускаться из вершины при остром угле. Именно эта вершина и будет ортоцентром треугольника.
- Вне фигуры. Внешнее расположение ортоцентра возможно только в тупоугольном треугольнике. Для того, чтобы получить ортоцентр такого треугольника, иногда потребуется продлить высоты до пересечения с внешней высотой. Почему? Потому что внешняя высота проходит за пределами треугольника и опускается на продолжение одной из сторон, а две внутренние стороны всегда ограничены треугольником. Поэтому без дополнительных построений ортоцентр тупоугольного треугольника не найти.
Золотое сечение треугольника
Золотое сечение треугольника это маленький треугольник внутри фигуры, который определяется как пересечение трех центров треугольника.
Три центра треугольника это:
- Точка пересечения биссектрис
- Точка пересечения высот
- Точка пересечения медиан.
Золотое сечение иногда может вырождаться в прямую или даже точку. В равнобедренном треугольнике точка пересечения высот и медиан совпадает, в результате для построения золотого сечения понадобится только 2 точки и золотое сечение выродится в отрезок.
О центрах треугольника существует целая онлайн энциклопедия. Список центров треугольника и свойств каждого из них был начат Карлом Кемберлингом в 1994 году. Онлайн ресурс пополняется все новыми и новыми данными по мере их открытия в высшей математике. В школьном курсе рассматривается только 3 центра треугольника.
В правильном треугольнике и вовсе каждая высота будет совпадать с соответствующей медианой, биссектрисой и высотой. Значит, все три центра треугольника совпадут, и золотым сечением треугольника будет – точка.
Обратите внимание, что нельзя составить уравнение точки пересечения высот треугольника. Можно составить только уравнение прямой. Например, составить два уравнения высот, затем приравнять их и найти координату точки пересечения.
Что мы узнали?
Мы узнали, в каких построениях участвует точка пересечения высот треугольника. Поговорили о случаях, когда эта точка совпадает с другими центрами треугольника, выяснили особенности расположения ортоцентра в разных видах треугольников.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 412.
А какая ваша оценка?
Чтобы найти ортоцентр треугольника, можно воспользоваться калькулятором, где следует внести координаты. В автоматическом режиме с помощью формул произведется расчет. Можно также все расчеты произвести самостоятельно.
Например, имеются следующие данные точек:
А – 4,3;
В – 0,5;
С – 3,-6.
Первое , что необходимо найти наклон сторон, который обозначается – m , используется формула :
Из этого следует:
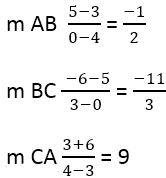
Далее необходимо найти наклон перпендикулярных сторон, для этого используется формула:
Имеем:
Когда найден наклон перпендикуляров, можно использовать уравнение линий, например, для линии AD, где точка 4,3, а наклон равен 3/11:
y-y1 = m(x-x1) y-3 = 3/11(x-4)
С помощью упрощения, имеем: 3х – 11у=-21
Для линии ВЕ, где точка 0,5, а наклон -1/9, имеем 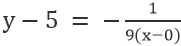
Упрощение дает: х+9у=45.
И последние линии CF, где точка 3, -6, а наклон 2, имеем уравнение y+6 = 2(x-3).
И упрощение, 2x — y = 12.
Если решить два из трех уравнений будут найдены значения х и у. Для данного примера:
Значение х = 8,05263;
Значение у = 4,10526.
Которые в данном случае являются координатами искомого Ортоцентра.
Для этого нужно найти уравнения прямых $%BH$% и $%CM$%.
$%CM:$%
Точка $%M$% имеет координаты
$$M(frac{x_a+x_b}{2};frac{y_a+y_b}{2})=M(frac{-7-2}{2};frac{5-3}{2})=M(-4,5;1)$$
Уравнение прямой, проходящей через точки $%M_1(x_1,y_1),M_2(x_2,y_2)$% можно найти как $$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$$
тогда уравнение прямой $%CM$% запишется как
$$frac{x+4,5}{6+4,5}=frac{y-1}{-5-1};frac{x+4,5}{10,5}=frac{y-1}{-6};frac{2x+9}{21}=frac{1-y}{6};$$
$$12x+54=21-21y; 21y+12x+33=0;7y+4x+11=0$$
$%BH:$% сначала найдем уравнение прямой $%AC:$%
$$frac{x+7}{6+7}=frac{y-5}{-5-5};frac{x+7}{13}=frac{y-5}{-10};-10x-70=13y-65;13y+10x+5=0$$
тогда уравнение нормали к этой прямой имеет вид: $%10y-13x+c=0$%, подставив в это уравнение координаты точки $%B$%, найдем уравнение $%BH.$% $%10times(-3)-13times(-2)+c=0;c=4;$% $%BH:10y-13x+4=0$%
Осталось определить точку пересечения. Для этого составляем систему $$7y+4x+11=0;$$ $$10y-13x+4=0$$
Домножим первое уравнение на 10, второе – на -7
$$70y+40x+110=0;$$ $$-70y+91x-28=0$$
Сложим уравнения:
$$131x+82=0, x=-frac{82}{131}$$
$$7y-4timesfrac{82}{131}+11=0;7y=frac{4times82-11times131}{131}; y=-frac{159}{131}$$
Таким образом, точка пересечения $%D(-frac{82}{131};-frac{159}{131})$%. Выглядит, конечно, не ахти, но все перепроверил и, по-моему, все правильно…
Даны уравнения сторон треугольника:
p = 4х – у – 7 = 0,
t = х + 3у – 31 = 0,
q = х + 5у – 7 = 0.
Находим вершины треугольника как точки пересечения прямых:
p + t = A. 4х – у – 7 = 0, 4х – у – 7 = 0,
х + 3у – 31 = 0|*-4 -4х – 12у + 124 = 0,
– 13y + 117 = 0
y = -117/-13 = 9, x = 31 – 3*y = 31 – 3*9 = 4.
Точка А(4; 9).
Аналогично находим:
Точка В = t + q = (67; -12).
Точка С = p + q = (2;1).
Векторы: АВ = (63; -21), ВС = (-65; 13), АС = (-2; -8).
Уравнения сторон:
АВ = (х – 4)/63 = (у – 9)/(-21),
ВС = (х – 67)/(-65) = (у + 12)/13,
АС = (х – 4)/(-2) = (у – 9)/(-8).
Находим угловые коэффициенты сторон:
Кав = Ув-Уа = -21 = -1/3.
Хв-Ха 63
Квс = Ус-Ув = -13 = -1/5.
Хс-Хв -65
Кас = Ус-Уа = -8 = 4.
Хс-Ха -2
Угловой коэффициент перпендикуляра равен -1/к(стороны).
к(АА1) = -1/к(ВС) = -1/(-1/5) = 5,
к(ВВ1) = -1/к(АС) = -1/4,
к(СС1) = -1/к(АВ) = -1/(-1/3) = 3.
Уравнение высоты равно: у = кх + в.
Подставив значения соответствующего к и координаты точек, получаем уравнения сторон:
АА1: у = 5х – 11.
ВВ1: у = (-1/4)х + 4,75
.
СС1: у = 3х – 5
.
Искомую точку пересечения высот находим как решение системы двух уравнений высот.
АА1: у = 5х – 11.
СС1: у = 3х – 5
.
Отсюда 5х – 11 = 3х – 5, 2х = 6, х = 6/2 = 3.
у = 3*3 – 5 = 9 – 5 = 4.
Ответ: точка пересечения (3; 4).