Как по уравнению касательной составить уравнение плоскости

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

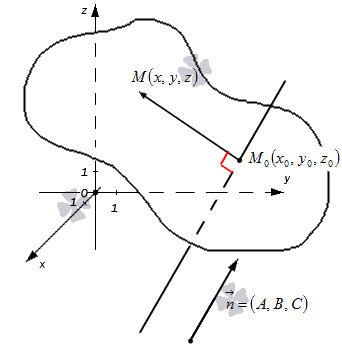
Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x”(t_0) & y”(t_0) & z”(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 – (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

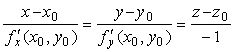
Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z – z₀ = f’_x(x₀,y₀,z₀)(x – x₀) + f’_y(x₀,y₀,z₀)(y – y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z – 5 = 0(x – 0) + 5(y – 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

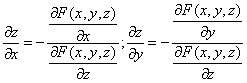
Для нашей функции:

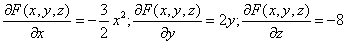
Тогда:

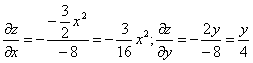
В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z – 1 = -3 /₁₆(x – 1) + 0(y – 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z – z₀ = f’_x(x₀,y₀,z₀)(x – x₀) + f’_y(x₀,y₀,z₀)(y – y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z – 25 = 26(x – 1) + 36(y – 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x – x 0 + B ( y – y 0 ) + C ( z – z 0 ) = A x + B y + C z – ( A x 0 + B y 0 + C z 0 )

Примем D = – ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x – x 0 , y – y 0 , z – z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x – 2 · y + 3 · z – 7 = 0 и – 2 · x + 4 · y – 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

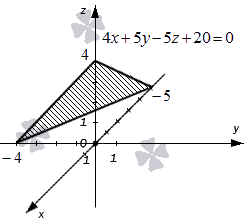
Укажем пример как иллюстрацию этих утверждений.

Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , – 1 , – 3 ) и N 0 ( 0 , 2 , – 8 ) и плоскость, определяемая уравнением 2 x + 3 y – z – 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( – 1 ) – ( – 3 ) – 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , – 1 , – 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 – ( – 8 ) – 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , – 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) – нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y – z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , – 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , – λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , – λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0

Задана точка М 0 ( – 1 , 2 , – 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , – 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = – 1 , y 0 = 2 , z 0 = – 3 , A = 3 , B = 7 , C = – 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0

3 ( x – ( – 1 ) ) + 7 ( y – 2 ) – 5 ( z – ( – 3 ) ) = 0 ⇔ 3 x + 7 y – 5 z – 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x – x 0 , y – y 0 , z – z 0 ) = ( x + 1 , y – 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y – 2 ) – 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y – 5 z – 26 = 0

Ответ: 3 x + 7 y – 5 z – 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

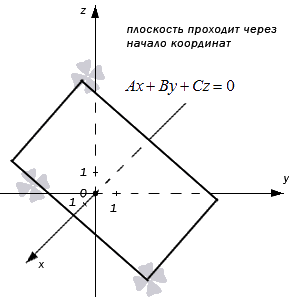
1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = – D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = – D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = – D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , – D C , 0 , – D B , 0 и – D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , – 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , – 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = – 7 , тогда требуемое уравнение имеет вид: x – 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x – x 0 ) + B ( y – y 0 ) + C ( z – z 0 ) = 0 ⇔ ⇔ 1 · ( x – 7 ) + 0 · ( y + 2 ) + 0 · ( z – 3 ) = 0 ⇔ ⇔ x – 7 = 0

Ответ: x – 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( – 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( – 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: – 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

[spoiler title=”источники:”]

http://math.semestr.ru/math/tangent-plane.php

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-ploskosti/

[/spoiler]

Пусть поверхность
задана уравнением

Тогда уравнение
касательной плоскостив точкеимеет вид:

(18.16)

где

Нормальюк поверхности в точкеназывается прямая, проходящая через
точкуперпендикулярно к касательной плоскости
в этой точке.

Уравнение
нормалик поверхности (18.16) в точкеимеет вид:

(18.17)

Если поверхность
задана уравнением

(18.18)

и в точке
этой поверхности существуют частные
производныене равные нулю одновременно, то уравнение
касательной плоскости к поверхности
(18.18) в точкеимеет вид:

(18.19)

Уравнение нормали
к поверхности (18.18) в точке
имеет вид:

(18.20)

Пример
1. Поверхность
задана уравнением
Составить уравнение касательной
плоскости и уравнение нормали к
поверхности в точке

Решение.
Найдем
частные производные:

Их
значения в точке
равны

Найдем
соответствующее значение
функции для

Тогда
уравнение касательной плоскости примет
вид:

или

Уравнение нормали:

Пример
2. Составить
уравнение касательной плоскости и
нормали к поверхности
в точке

Решение.
Частные
производные имеют вид:

Их
значения в точке N₀
равны:

Тогда
уравнение касательной плоскости в точке
N₀:
или

Уравнение
нормали:

Пример
3. Составить
уравнения касательных плоскостей к
поверхности
параллельных плоскости

Решение.
Найдем
частные производные:

Так
как касательная плоскость параллельна
плоскости
то справедливо условие параллельности
плоскостей:

т. е.

Координаты
точек касания найдем из системы уравнений

Решая
систему, получаем:

Точки касания
имеют координаты:

и

Тогда уравнения
касательных плоскостей имеют вид:

Пример
4. Составить
уравнение касательной плоскости к
поверхности, заданной уравнением
гдев точке

Решение.
Поверхность
задана сложной функцией. Найдем частные
производные, используя формулы (18.11)
(см. § 18.3):

Их
значения в точке
соответственно равны:

Найдем
соответствующее значение

Тогда уравнение
касательной плоскости:

или

Пример
5. Записать
уравнение нормали к поверхности, заданной
уравнением
в точке

Решение.
Найдем
частные производные и вычислим их в
точке N₀:

Уравнение
нормали в точке N₀:

или

Равенство
нулю
означает, что касательная плоскость
параллельна осиОх,
а нормаль к ней лежит в плоскости

Задания

I уровень

1.1.Найдите
уравнение касательной плоскости и
нормали к поверхности, заданной функциейв точке

1)
2)

3)
4)

5)
6)

1.2.Найдите
уравнение касательной плоскости и
нормали к поверхности, заданной уравнениемв точке

1)

2)

3)

II уровень

2.1.Найдите
уравнения касательных плоскостей к
поверхностиперпендикулярных координатным плоскостям.

2.2.Составьте
уравнения касательных плоскостей к
поверхностипараллельных:

1) координатным
плоскостям; 2) плоскости

2.3.Составьте
уравнение касательной плоскости и
нормали к поверхности, заданной уравнениемгдев точке

2.4.Найдите
точки на поверхности

в которых нормаль
к ее поверхности будет:

1) параллельна осям
координат;

2) перпендикулярна
осям координат.

III уровень

3.1.Определите,
в каких точках сферыкасательные плоскости к ней отсекают
на осях координат равные отрезки.

3.2.Найдите
точки эллипсоидав которых нормаль к его поверхности
образует равные углы с осями координат.

3.3. Выясните,
является ли плоскостьв точкекасательной:

1) к параболоиду
вращения

2) к конусу

3) к гиперболическому
параболоиду

3.4. Найдите
точки на поверхности

касательная
плоскость в которых к данной поверхности
будет:

1) параллельна
координатным плоскостям;

2) перпендикулярна
координатным плоскостям.

3.5.Докажите,
чтогде– направляющие косинусы нормали к
поверхности

Соседние файлы в папке Часть 3

• #
• #
• #
• #
• #
• #
• #
• #

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Касательная к кривой

Нормальная плоскость

Соприкасающаяся плоскость

Бинормаль и главная нормаль

Спрямляющая плоскость

Репер Френе

Решение задач

Задача 1

Решение задачи 1

Задача 2

Написать уравнение соприкасающейся плоскости к кривой
$$
x=t,,, y=frac{t^2}{2},,, z=frac{t^3}{3},
$$
проходящей через точку $N(0,0,9)$.

Решение задачи 2

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой:
$$
x=t^2,,, y=1+t,,, z=2t.
$$

Решение задачи 3

Касательная плоскость и нормаль к поверхности.

Пусть поверхность задана в неявном виде: $F(x,y,z)=0$ и пусть точка $M_0(x_0,y_0,z_0)$ принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке $M_0$ таково:

$$
begin{equation}
F_{x}^{‘}(M_0)cdot(x-x_0)+F_{y}^{‘}(M_0)cdot(y-y_0)+F_{z}^{‘}(M_0)cdot(z-z_0)=0
end{equation}
$$

Уравнение нормали имеет вид:

$$
begin{equation}
frac{x-x_0}{F_{x}^{‘}(M_0)}=frac{y-y_0}{F_{y}^{‘}(M_0)}=frac{z-z_0}{F_{z}^{‘}(M_0)}
end{equation}
$$

Если же уравнение поверхности задано в явном виде $z=f(x,y)$, то уравнение касательной плоскости имеет вид:

$$
begin{equation}
f_{x}^{‘}(x_0,y_0)cdot(x-x_0)+f_{y}^{‘}(x_0,y_0)cdot(y-y_0)-(z-z_0)=0
end{equation}
$$

Уравнение нормали в случае явного задания поверхности таково:

$$
begin{equation}
frac{x-x_0}{f_{x}^{‘}(x_0,y_0)}=frac{y-y_0}{f_{y}^{‘}(x_0,y_0)}=frac{z-z_0}{-1}
end{equation}
$$

Примечание (желательное для более полного понимания текста): показатьскрыть

Пример №1

Найти уравнение касательной плоскости и нормали к поверхности $z=3x^2y^4-6xy^3+5x-4y+10$ в точке $M_0(-2;1;20)$.

Решение

Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$, $y_0$, $z_0$ (координаты точки $M_0$) в нашем случае таковы: $x_0=-2$, $y_0=1$, $z_0=20$. Но перед тем, как переходить к решению, осуществим небольшую проверку. Убедимся, что точка $M_0$ действительно лежит на заданной поверхности. Эта проверка не является обязательной, но желательна, ибо ошибка в условиях подобных задач – дело вовсе не редкое. Подставим $x=x_0$, $y=y_0$ в уравнение нашей поверхности и убедимся, что $z_0$ действительно равно 20:

$$
z_0=3x_{0}^{2}y_{0}^{4}-6x_0y_{0}^{3}+5x_0-4y_0+10=3cdot (-2)^2cdot 1^4-6cdot (-2)cdot 1^3-4cdot 1+10=12+12-4=20.
$$

Проверка пройдена, точка $M_0$ действительно лежит на заданной поверхности. Теперь найдём частные производные, т.е. $z_{x}^{‘}$ и $z_{y}^{‘}$:

$$
z_{x}^{‘}=6xy^4-6y^3+5;\
z_{y}^{‘}=12x^2y^3-18xy^2-4.

$$

Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ в выражения частных производных:

$$
z_{x}^{‘} left(x_0, y_0right)=6x_0y_{0}^{4}-6y_{0}^{3}+5=-12-6+5=-13;\
z_{y}^{‘}left(x_0, y_0right)=12x_{0}^{2}y_{0}^{3}-18x_0y_{0}^{2}-4=48-(-36)-4=80.
$$

Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_{x}^{‘} left(x_0, y_0right)=-13$, $z_{y}^{‘} left(x_0, y_0right)=80$ в формулу (3) получим уравнение касательной плоскости:

$$

-13cdot(x-(-2))+80cdot(y-1)-(z-20)=0;\
-13x+80y-z-86=0.
$$

Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_{x}^{‘} left(x_0, y_0right)=-13$, $z_{y}^{‘} left(x_0, y_0right)=80$ в формулу (4) получим уравнение нормали:

$$
frac{x-(-2)}{-13}=frac{y-1}{80}=frac{z-20}{-1}; frac{x+2}{-13}=frac{y-1}{80}=frac{z-20}{-1}.
$$

Ответ: Касательная плоскость: $-13x+80y-z-86=0$; нормаль: $frac{x+2}{-13}=frac{y-1}{80}=frac{z-20}{-1}$.

Пример №2

Найти уравнение касательной плоскости и нормали к поверхности $z=5sqrt{x^2+y^2}-2xy-39$ в точке $M_0(3;-4;z_0)$.

Решение

Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=3$, $y_0=-4$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:

$$
z_0=5sqrt{x_{0}^{2}+y_{0}^{2}}-2x_0y_0-39=5sqrt{25}+24-39=10.
$$

Теперь, как и в предыдущем примере, перейдём к нахождению частных производных $z_{x}^{‘}$ и $z_{y}^{‘}$. После того, как мы найдём эти производные в общем виде, укажем их значения при $x=x_0$ и $y=y_0$:

$$
z_{x}^{‘}=frac{10x}{sqrt{x^2+y^2}}-2y; z_{x}^{‘} left(x_0, y_0right)=frac{10cdot 3}{sqrt{3^2+(-4)^2}}-2cdot(-4)=11;\
z_{y}^{‘}=frac{10y}{sqrt{x^2+y^2}}-2x; z_{y}^{‘} left(x_0, y_0right)=frac{10cdot (-4)}{sqrt{3^2+(-4)^2}}-2cdot 3=-10.\
$$

Подставляя $x_0=3$, $y_0=-4$, $z_0=10$, $z_{x}^{‘} left(x_0, y_0right)=11$, $z_{y}^{‘} left(x_0, y_0right)=-10$ в формулы (3) и (4) получим уравнения касательной плоскости и нормали:

$$
11cdot(x-3)+(-10)cdot(y-(-4))-(z-10)=0; 11x-10y-z-63=0; \
frac{x-3}{11}=frac{y-(-4)}{-10}=frac{z-10}{-1}; frac{x-3}{11}=frac{y+4}{-10}=frac{z-10}{-1}.
$$

Ответ: Касательная плоскость: $11x-10y-z-63=0$; нормаль: $frac{x-3}{11}=frac{y+4}{-10}=frac{z-10}{-1}$.

Пример №3

Найти уравнение касательной плоскости и нормали к поверхности $3xy^2z+5xy+z^2=10xz-2y+1$ в точке $M_0(1;-2;3)$.

Решение

Перенесём все слагаемые в левую часть равенства и обозначим полученное в левой части выражение как $F(x,y,z)$:

$$
3xy^2z+5xy+z^2-10xz+2y-1=0.
$$
$$F(x,y,z)=3xy^2z+5xy+z^2-10xz+2y-1$$

Используем формулы (1) и (2). Значения $x_0$, $y_0$ и $z_0$ как и ранее обозначают координаты точки $M_0$, т.е. $x_0=1$, $y_0=-2$, $z_0=3$.

Проверим, действительно ли точка $M_0$ лежит на данной поверхности. Для этого подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражение $3xy^2z+5xy+z^2-10xz+2y-1$ и выясним, равен ли нулю полученный результат:

$$
3x_0y_{0}^{2}z_0+5x_0y_0+z_{0}^{2}-10x_0z_0+2y_0-1=36-10+9-30-4-1=0.
$$

Итак, точка $M_0$ действительно лежит на данной поверхности. Естественно, что данная проверка не является обязательной, но она крайне желательна. Перейдём к дальнейшему решению. Нам нужно найти $F_{x}^{‘}$, $F_{y}^{‘}$ и $F_{z}^{‘}$:

begin{aligned}
& F_{x}^{‘}=3y^2z+5y-10z;\
& F_{y}^{‘}=6xyz+5x+2; \
& F_{z}^{‘}=3xy^2+2z-10x. end{aligned}

Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражения частных производных:

begin{aligned}
& F_{x}^{‘}(M_0)=3y_{0}^{2}z_0+5y_0-10z_0=-4;\
& F_{y}^{‘}(M_0)=6x_0y_0z_0+5x_0+2=-29; \
& F_{z}^{‘}(M_0)=3x_0y_{0}^{2}+2z_0-10x_0=8. end{aligned}

Подставляя $x_0=1$, $y_0=-2$, $z_0=3$, $F_{x}^{‘} left(M_0right)=-4$, $F_{y}^{‘} left(M_0right)=-29$ и $F_{z}^{‘} left(M_0right)=8$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:

$$
-4cdot(x-1)-29cdot(y-(-2))+8(z-3)=0; -4x-29y+8z-78=0.\
frac{x-1}{-4}=frac{y-(-2)}{-29}=frac{z-3}{8}; frac{x-1}{-4}=frac{y+2}{-29}=frac{z-3}{8}.
$$

Ответ: Касательная плоскость: $-4x-29y+8z-78=0$; нормаль: $frac{x-1}{-4}=frac{y+2}{-29}=frac{z-3}{8}$.

Пример №4

Найти уравнение касательной плоскости и нормали к поверхности $z^3+4xyz=-3x^2+5y+7$ в точке $M_0(0;-3;z_0)$.

Решение

Поверхность задана в неявном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (1) и (2). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=0$, $y_0=-3$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:

$$
z_{0}^{3}+4x_0y_0z_0=-3x_{0}^{2}+5y_0+7;\
z_{0}^{3}=-15+7; z_{0}^{3}=-8; z_0=-2.
$$

Перенесём все слагаемые в левую часть равенства:

$$
z^3+4xyz+3x^2-5y-7=0.
$$

Обозначим $F(x,y,z)=z^3+4xyz+3x^2-5y-7$ и применим формулы (1) и (2). Найдём частные производные первого порядка $F_{x}^{‘}$, $F_{y}^{‘}$ и $F_{z}^{‘}$. После того, как мы найдём эти производные в общем виде, укажем их значения в точке $M_0$:

begin{aligned}
& F_{x}^{‘}=4yz+6x; ; F_{x}^{‘}(M_0)=4y_0z_0+6x_0=-24;\
& F_{y}^{‘}=4xz-5; ; F_{y}^{‘}(M_0)=4x_0z_0-5=-5;\
& F_{z}^{‘}=3z^2+4xy; ; F_{z}^{‘}(M_0)=3z_{0}^{2}+4x_0y_0=12.
end{aligned}

Подставляя $x_0=0$, $y_0=-3$, $z_0=-2$, $F_{x}^{‘} left(M_0right)=-24$, $F_{y}^{‘} left(M_0right)=-5$ и $F_{z}^{‘} left(M_0right)=12$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:

$$
-24cdot(x-0)-5cdot(y-(-3))+12(z-(-2))=0; -24x-5y+12z+9=0.\
frac{x-0}{-24}=frac{y-(-3)}{-5}=frac{z-(-2)}{12}; frac{x}{-24}=frac{y+3}{-5}=frac{z+2}{12}.
$$

Ответ: Касательная плоскость: $-24x-5y+12z+9=0$; нормаль: $frac{x}{-24}=frac{y+3}{-5}=frac{z+2}{12}$.

Уравнение касательной плоскости и нормали к поверхности

Как найти?

Постановка задачи

Найти уравнение касательной плоскости и нормали к поверхности $ F(x,y,z) = 0 $ в точке $ M(x_0,y_0,z_0) $

План решения

Уравнение касательной плоскости к поверхности записывается следующем образом:

$$ F’_x bigg |_M (x-x_0) + F’_y bigg |_M (y-y_0) + F’_z bigg |_M (z-z_0) = 0 $$

Уравнение нормали к поверхности составляется по формуле:

$$ frac{x-x_0}{F’_x Big |_M} = frac{y-y_0}{F’_y Big |_M} = frac{z-z_0}{F’_z Big |_M} $$

1. Находим частные производные $ F’_x, F’_y, F’_z $ в точке $ M(x_0,y_0,z_0) $
2. Подставляем найденные значения производных в формулы для составления уравнений

ЗАМЕЧАНИЕ

Если в условии задачи задана точка $ M (x_0,y_0) $ с двумя координатами, то необходимо дополнительно вычислить координату $ z_0 $ из уравнения $ F(x_0,y_0,z_0) = 0 $, подставив в него известные координаты $ x_0 $ и $ y_0 $.

Примеры решений

Пример 1

Найти уравнение касательной плоскости и нормали к поверхности $ z = x^2 + y^2 $ в точке $ M(1,-2,5) $

Решение

Переносим $ z $ в правую часть и записываем поверхность в виде: $$ F(x,y,z) = x^2 + y^2 – z $$ Находим частные производные первого порядка функции $ F(x,y,z) $: $$ F’_x = 2x $$ $$ F’_y = 2y $$ $$ F’_z = -1 $$ Вычисляем значения полученных производных в точке $ M(1,-2,5) $: $$ F’_x Big |_M = F’_x(1,-2,5) = 2 cdot 1 = 2 $$ $$ F’_y Big |_M = F’_y (1,-2,5) = 2 cdot (-2) = -4 $$ $$ F’_z Big |_M = F’_z (1,-2,5) = -1 $$ Подставляем полученные данные в формулу касательной плоскости: $$ 2(x-1) + (-4)(y+2) + (-1)(z-5) = 0 $$ Раскрываем скобки и записываем окончательное уравнение плоскости: $$ 2x – 4y – z – 5 = 0 $$ Теперь запишем уравнение нормали к поверхности с помощью второй формулы: $$ frac{x-1}{2} = frac{y+2}{-4} = frac{z-5}{-1} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ 2x – 4y – z – 5 = 0 $$ $$ frac{x-1}{2} = frac{y+2}{-4} = frac{z-5}{-1} $$

Пример 2

Составить уравнение касательной плоскости и нормали к поверхности $ z = e^{xcos y} $ в точке $ M(1,pi, frac{1}{e}) $

Решение

Записываем поверхность в виде: $$ F = e^{xcos y} – z $$ Находим частные производные от функции $ F(x,y,z) $: $$ F’_x = e^{xcos y} cdot (xcos y)’_x = cos y e^{xcos y} $$ $$ F’_y = e^{xcos y} cdot (xcos y)’_y = -xsin y e^{xcos y} $$ $$ F’_z = -1 $$ Вычисляем значения производных в точке $ M(1,pi,frac{1}{e}) $: $$ F’_x Big |_M = F’_x (1,pi,frac{1}{e}) = cos pi cdot e^{1 cdot cos pi} = -1 cdot e^{(-1)} = -e^{-1} $$ $$ F’_y Big |_M = F’_y (1,pi, frac{1}{e}) = -1 cdot sin pi cdot e^{1 cdot cos pi} = -1 cdot 0 cdot e^1 = 0 $$ $$ F’_z Big |_M = -1 $$ Подставляем в первую формулу касательной плоскости полученные ранее неизвестные данные: $$ -e^{-1}(x-1) + 0 cdot (y-pi) + (-1) cdot (z-frac{1}{e}) = 0 $$ Раскрываем скобки: $$ -xfrac{1}{e} + frac{1}{e} – z + frac{1}{e} = 0 $$ Домножаем обе части уравнения на $ -e $ и получаем окончательное уравнение плоскости: $$ x + ez – 2 = 0 $$ Используя вторую формулу находим уравнение нормали к поверхности: $$ frac{x-1}{-e^{-1}} = frac{y-pi}{0} = frac{z-e^{-1}}{-1} $$ Умножим уравнение на дробь $ frac{1}{-e} $: $$ frac{x-1}{1} = frac{y-pi}{0} = frac{z-e^{-1}}{e} $$

Ответ

$$ x + ez – 2 = 0 $$ $$ frac{x-1}{1} = frac{y-pi}{0} = frac{z-e^{-1}}{e} $$