Примеры решений задач по дифференциальным уравнениям
Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.
Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать – это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.
В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам – изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям
Как решить дифференциальное уравнение онлайн?
Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?
У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.
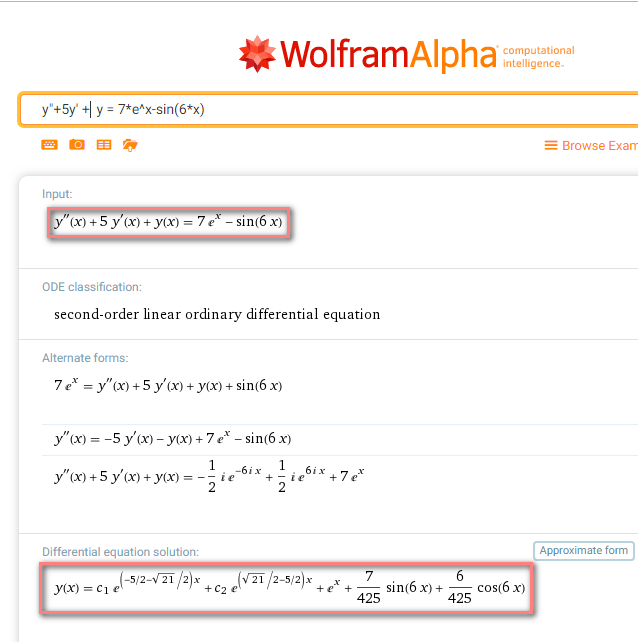
Если вы забьете в поисковик что-то вроде “решить дифференциальное уравнение онлайн”, то получите десятки ссылок на сайты, обещающие именно это.
Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.
Выводы? Бесплатно и полно и онлайн – не бывает. Хотите получать полные решения – используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы – там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!
Общий интеграл, семейство кривых
Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$
Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$
Решения дифференциальных уравнений 1 порядка
Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$
Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$
Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$
Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$
Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$
Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$
Решение задачи Коши для ДУ
Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.
Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y” +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.
Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac<2y-x><2x+y>, y(1)=1. $$
Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y”’=x+cos x, quad y(0)=0, y'(0)=0, y”(0)=0. $$
Решения дифференциальных уравнений 2 порядка
Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y”+4y’+4y=xe^<2x>.$
Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y”-3y’=frac<9e^<-3x>><3+e^<-3x>>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$
Cоставление дифференциальных уравнений
Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?
Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.
Решения нелинейных дифференциальных уравнений
Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$
Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$
III. Задачи на составление дифференциальных уравнений
Методика составления и решения прикладных задач теории обыкновенных дифференциальных уравнений
Составление дифференциального уравнения по условию задачи (механической, физической, химической или технической) состоит в определении математической зависимости между переменными величинами и их приращениями.
В ряде случаев дифференциальное уравнение получается без рассмотрения приращений – за счет их предварительного учета. Например, представляя скорость выражением 
, мы не привлекаем приращений ∆s и ∆t, хотя они фактически учтены в силу того, что
.
Ускорение в какой-нибудь момент времени t выражается зависимостью:
.
При составлении дифференциальных уравнений приращения сразу же заменяются соответствующими дифференциалами. Изучение любого процесса сводится:
1) к определению его отдельных моментов;
2) к установлению общего закона его хода.
Отдельный момент процесса (т. н. элементарный процесс) выражается уравнением, связывающим переменные величины процесса с их дифференциалами или производными — дифференциальным уравнением; закон общего хода процесса выражается уравнением, связывающим переменные величины процесса, но уже без дифференциалов этих величии.
Исчерпывающих правил для составления дифференциальных уравнений нет. В большинстве случаев методика решения технических задач с применением теории обыкновенных дифференциальных уравнений сводится к следующему:
1.Подробный разбор условий задачи и составление чертежа, поясняющего ее суть.
2.Составление дифференциального уравнения рассматриваемого процесса.
3.Интегрирование составленного дифференциального уравнения и определение общего решения этого уравнения.
4.Определение частного решения задачи на основании данных начальных условий.
5.Определение, по мере необходимости, вспомогательных пара
метров (например, коэффициента пропорциональности и др.),
используя для этой цели дополнительные условия задачи.
6. Вывод общего закона рассматриваемого процесса и число
вое определение искомых величии.
7. Анализ ответа и проверка исходного положения задачи.
Некоторые из этих рекомендаций в зависимости от характера
задачи могут отсутствовать.
Как и при составлении алгебраических уравнений, при решении прикладных задач по дифференциальным уравнениям многое зависит от навыков, приобретаемых упражнением. Однако здесь еще в большей степени требуется изобретательность и глубокое понимание сути изучаемых процессов.
Рассмотрим процесс решения следующих задач:
Температура вынутого из печи хлеба в течение 20 мин. падает от 100 0 до 60 0 (рис. 3.1). Температура воздуха равна 25 0 . Через сколько времени от момента начала охлаждения температура хлеба понизится до 30 0 ?
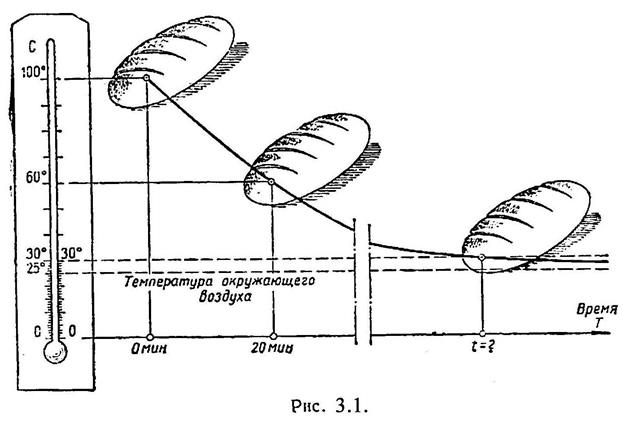
Решение:
В силу закона Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Это – процесс неравномерный. С изменением разности температур в течение процесса меняется также и скорость охлаждения тела. Дифференциальное уравнение охлаждения хлеба будет:
.
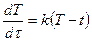где Т – температура хлеба;
t – температура окружающего воздуха ( в нашем случае 25 0 );
k – коэффициент пропорциональности;
– скорость охлаждения хлеба.
Пусть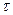 
– время охлаждения.
Тогда, разделяя переменные, получим:
,
или для условий данной задачи :
.
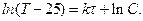
Потенцируя обе части последнего равенства, имеем:
,
. (1)
Произвольную постоянную С определяем, исходя из начального условия: при 
мин, Т=100 о .
или С=75.
Величину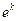 
определяем, исходя из данного дополнительного условия: при 
мин, Т=60 о .
и 
.
Таким образом, уравнение охлаждения хлеба при условиях нашей задачи примет вид:
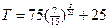. (2)
Из уравнения (2) легко определяем искомое время 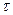при температуре хлеба Т=30 о :
, или
.
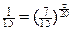мин.
Итак, после 1 часа 11 мин. Хлеб охлаждается до температуры 30 о С.
Задача 3.2. Трубопровод тепловой магистрали (диаметр 20 см) защищен изоляцией толщиной 10 см; величина коэффициента теплопроводности k=1,00017. Температура трубы 160о; температура внешнего покрова 30о (рис.8). Найти распределение температуры внутри изоляции, а также количество теплоты, отдаваемого одним погонным метром трубы.
Решение. Если тело находится в стационарном тепловом состоянии и температура Т в каждой его точке есть функция только одной координаты х, то согласно закону теплопроводности Фурье количество теплоты, испускаемое в секунду:
, (1)
где F(x)- площадь сечения тела на расстоянии х,
k – коэффициент теплопроводности.
Здесь 
(2)
где l – длина трубы в см,
х – радиус трубопровода в см.
Таким образом, после разделения переменных дифференциальное уравнение примет вид:
(3)
Интегрируя обе части равенства (3), находим:
или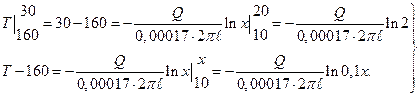 
(4)
Разделив почленно уравнения второе на первое, получим:
.
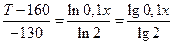Отсюда закон распределения температуры внутри изоляции:
.
Из первого уравнения системы(4) при 
=100 см имеем:
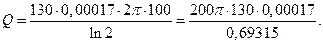
Количество теплоты, отдаваемое в течение суток, равно
кал.
Урок по теме “Составление дифференциальных уравнений”
Разделы: Математика
Цель урока:
- Научить составлять дифференциальное уравнение некоторого явления. Закрепить навык решения дифференциального уравнения.
- Развивать мышление и речь учащихся.
1. Повторить:
а) Какое уравнение называется дифференциальным?
б) Что значит решить дифференциальное уравнение?
в) Что называется решением дифференциального уравнения?
г) Какие способы решения дифференциального уравнения вам известны?
2. а) N 21. (Виленкин Н.Я. “Алгебра и математический анализ” )
y=f(x) – функция, (x;y) – координаты точки касания.
Точка пересечения касательной с осью Оx:
Абсцисса точки пересечения касательной с осью Оу равна 0.
Так как точка (х;у)- середина отрезка, абсциссы концов которого
В комнате, где температура 20 0 С , некоторое тело остыло за 20 мин. от 100 0 до 60 0 С. Найдите закон охлаждения тела; через сколько минут оно остынет до 30 0 С?
Повышением температуры в комнате пренебречь.
Решение: В силу закона Ньютона (скорость охлаждения пропорциональна разности температур тела и охлаждающей среды) можем записать:
в) Криминалисты, прибыв на место преступление, обнаружили труп человека, температура тела которого была 27 0 . Через один час температура трупа стала 25 0 . Температура окружающего воздуха 16 0 . Считая, что в момент убийства человек имел температуру тела 37 0 , определите промежуток времени между моментом убийства человека и моментом обнаружения его тела.
г) Напишите уравнение кривой, проходящей через точку В(3;1), для которой отрезок касательной между точкой касания и осью Ох делится пополам в точке пересечения с осью Оу.
[spoiler title=”источники:”]
http://lektsii.org/14-59762.html
http://urok.1sept.ru/articles/510639
[/spoiler]
Пусть известен общий интеграл некоторого дифференциального уравнения первого порядка
. (3.5)
Покажем, как найти это уравнение. Для этого продифференцируем равенство (1.14) по переменной 
. (3.6)
Составить дифференциальное уравнение первого порядка – значит найти соотношение между , 
и 
. Но для этого достаточно исключить произвольную постоянную 
из системы уравнений (3.5) и (3.6):
В результате получим новое уравнение, связывающее , и вида
.
Это и есть искомое дифференциальное уравнение. С геометрической точки зрения его называют дифференциальным уравнением семейства кривых (3.5).
Пример 3.8. Найти дифференциальное уравнение семейства окружностей
.
Решение. Имеем систему уравнений
Отсюда
, 
.
Итак, искомое уравнение
,
То есть
.
Окончательно
.
| < Предыдущая | Следующая > |
|---|
Для
составления и интегрирования
дифференциальных уравнений приводят
различные задачи физики, биологии,
химии и т.д.
Например,
при решении задач искомая кривая
представляется как график некоторой
функции, как y=y(x)
Все
связные (названные) в задачах величины,
выражаются через аргумент x,
функцию y
и её производную:
.
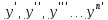Полученное
при таком условии соотношение и
представляет собой дифференциальное
уравнение.
Уравнение
(1) является искомым уравнением для
нахождения неизвестной функции у.
При
решении физических задач процесс
составления дифф. Уравнения разбивается
на 3 этапа:
1)одну
из величин выбираем в качестве независимой
переменной 2-го в качестве зависимой
переменной. Чаще всего в качестве
независимой переменной выбираются
время t,
а в качестве искомых функций
пространственные координаты x,y,z.
2)находим
на сколько измениться искомая функция
Х, если независимая переменная t
получит достаточно малое приращение
,
то есть пытаемся оценить разность ч/з
величины, данные в задачи.
3)делим
полученное неравенство на
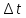и переходим кlim,
когда
в результате предельного перехода
получаем дифф. Уравнение из которого
можно найти искомую функцию.
1.Принципы составления дифференциальных уравнений.
Для
составления и интегрирования
дифференциальных уравнений приводят
различные задачи физики, биологии,
химии и т.д.
Например,
при решении задач искомая кривая
представляется как график некоторой
функции, как y=y(x)
Все
связные (названные) в задачах величины,
выражаются через аргумент x,
функцию y
и её производную:
.
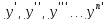Полученное
при таком условии соотношение и
представляет собой дифференциальное
уравнение.
Уравнение
(1) является искомым уравнением для
нахождения неизвестной функции у.
При
решении физических задач процесс
составления дифф. Уравнения разбивается
на 3 этапа:
1)одну
из величин выбираем в качестве независимой
переменной 2-го в качестве зависимой
переменной. Чаще всего в качестве
независимой переменной выбираются
время t,
а в качестве искомых функций
пространственные координаты x,y,z.
2)находим
на сколько измениться искомая функция
Х, если независимая переменная t
получит достаточно малое приращение
,
то есть пытаемся оценить разность ч/з
величины, данные в задачи.
3)делим
полученное неравенство на
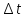и переходим кlim,
когда
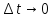в результате предельного перехода
получаем дифф. Уравнение из которого
можно найти искомую функцию.
3 Теорема существования решения задачи Коши дифф ур первого порядка.
Условие
(2) называется начальным
условием или условиями Коши.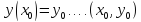
(2)
Под
задачей Коши будем понимать задачу об
отыскании решения уравнения (1)
удовлетв.данным (2)
Геометрически
это означает, что из всего множества
интегральных кривых нужно выделить ту
интегральную кривую, которая проходит
ч/з
.
Естественно
встаёт вопрос, есть ли вообще решение
у уравнение (1), а если и есть, то сколько
таких, удовл.условию (2).
Теорема
1.(теорема существования единственности
решения) – если функция f
и её частная производная
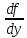непрерывна в областиD,
то решения дифф.уравнения (1),
удовлетв.начальным условиям (2) существенно
и единственно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
18.02.2016100.77 Кб1221.docx
- #
- #
- #
- #
- #
- #
- #
- #
- #
