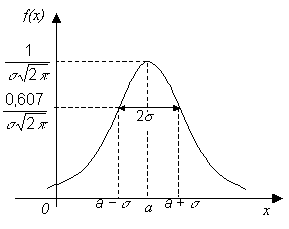
Закон распределения Пуассона
На этой странице мы собрали примеры решения учебных задач, где используется распределение Пуассона.
Краткая теория
Рассмотрим некоторый поток событий, в котором события наступают независимо друг от друга и с некоторой фиксированной средней интенсивностью $lambda$ (событий в единицу времени). Тогда случайная величина $X$, равная числу событий $k$, произошедших за фиксированное время, имеет распределение Пуассона. Вероятности вычисляются по следующей формуле:
$$
P(X=k)=frac{lambda^k}{k!}cdot e^{-lambda}, k=0,1,2,…
$$
Для пуассоновской случайной величины математическое ожидание и дисперсия совпадают с интенсивностью потока событий:
$$M(X)=lambda, quad D(X)=lambda.$$
Распределение Пуассона играет важную роль в теории массового обслуживания. При увеличении $lambda$ данное распределение стремится к нормальному распределению $N(lambda, sqrt{lambda})$. В свою очередь, оно само является “приближенной” моделью биномиального распределения при больших $n$ и крайне малых $p$ (см. теорию про формулу Пуассона).
Понравилось? Добавьте в закладки
Примеры решенных задач
Задача 1. Среднее число самолетов, взлетающих с полевого аэродрома за одни сутки, равно 10. Найти вероятность того, что за 6 часов взлетят:
А) три самолета,
Б) не менее двух самолетов.
Задача 2. На автовокзале время прибытия автобусов различных рейсов объявляет дежурный. Появление информации о различных рейсах происходит случайной и независимо друг от друга. В среднем на автовокзал прибывает 5 рейсов каждые полчаса.
А) Составьте ряд распределения числа сообщений о прибытии автобусов в течение получаса.
Б) Найдите числовые характеристики этого распределения.
В) Запишите функцию распределения вероятностей и постройте ее график.
Г) Чему равна вероятность того, что в течение получаса прибудут не менее трех автобусов?
Д) Чему равна вероятность того, что в течение четверти часа не прибудет ни один автобус?
Задача 3. АТС получает в среднем за час 480 вызовов. Определить вероятность того, что за данную минуту она получит: ровно 3 вызова; от 2 до 5 вызовов.
Задача 4. Случайная величина $X$ распределена по закону Пуассона с параметром $lambda=0,8$. Необходимо:
А) выписать формулу для вычисления вероятности $P(X=m)$;
Б) найти вероятность $P(1 le X lt 3)$;
В) найти математическое ожидание $M(2X+5)$ и дисперсию $D(5-2X)$.
Задача 5. Среднее число ошибочных соединений, приходящееся на одного телефонного абонента в единицу времени, равно 8. Какова вероятность того, что для данного абонента число ошибочных соединений будет больше 4?
Задача 6. В среднем в магазин заходят 3 человека в минуту. Найти вероятность того, что за 2 минуты в магазин зайдет не более 1 человека.
Задача 7. Автомобиль проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время техосмотра, распределяется по закону Пуассона с параметром 0,63. Если неисправностей не обнаружено, техническое обслуживание автомобиля продолжается в среднем 2 ч. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится в среднем еще полчаса. Если обнаружено больше двух неисправностей, то автомобиль становится на профилактический ремонт, где он находится в среднем 4 ч.
Определите закон распределения среднего времени $T$ обслуживания и ремонта автомобиля и его математическое ожидание $M(T)$.
Задача 8. В тексте учебника по психологии содержатся опечатки: в среднем, одна на
десять страниц. Пусть Х – число опечаток на одной странице. Определить закон распределения для Х. Найти вероятность, что на странице есть хотя бы одна опечатка.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по терверу
Если решения нужны срочно и почти даром? Ищите в решебнике по теории вероятностей:
Закон распределения Пуассона
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Дискретная случайная величина
имеет закон распределения Пуассона с
параметром
,
если она принимает значения 0,1,2,…,k,… (бесконечное, но счетное множество значений) с вероятностями
Ряд распределения закона Пуассона имеет вид:
Математическое ожидание и дисперсия случайной величины,
распределенной по закону Пуассона, совпадают и равны параметру этого закона,
т.е.
По закону Пуассона распределены, например, число рождений тройни,
число сбоев на автоматической линии, число отказов сложной системы в нормальном
режиме, число требований на обслуживания, поступивших в единицу времени в
системах массового обслуживания и тому подобное.
Если СВ представляет собой сумму двух независимых СВ,
распределенных каждая по закону Пуассона, то она также распределена по закону
Пуассона.
Распределение Пуассона также называют законом «редких» событий, так как оно всегда проявляется там, где производится большое
число испытаний, в каждом из которых с малой вероятностью происходит «редкое» событие.
Смежные темы решебника:
- Биномиальный закон распределения дискретной случайной величины
- Геометрический закон распределения дискретной случайной величины
- Гипергеометрический закон распределения дискретной случайной величины
- Простейший поток событий
Примеры решения задач
Пример 1
На
предприятии 1000 единиц оборудования определенного вида. Вероятность отказа
единицы оборудования в течение часа составляет 0,001. Составить закон
распределения числа отказов оборудования в течение часа. Найти числовые
характеристики.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Случайная
величина
– число отказов оборудования, может принимать
значения
Воспользуемся
законом Пуассона:
где
Найдем
эти вероятности:
Найдем
вероятность того, что откажет более 5 единиц оборудования:
Искомый
закон распределения числа отказов оборудования в течение часа:
Проверка гипотезы о распределении выборки по закону Пуассона.
Математическое
ожидание и дисперсия случайной величины, распределенной по закону Пуассона
равна параметру
этого распределения:
Среднее
квадратическое отклонение:
Пример 2
Станок-автомат штампует детали. Вероятность того, что изготовленная
деталь окажется бракованной, равна 0,001 Найти вероятность того, что среди 350
деталей окажется ровно 3 бракованных.
Определить закон распределения СВ X и её числовые характеристики.
Решение
Вероятность
события, состоящее в том, что деталь окажется бракованной мало, а число
велико. Поэтому воспользуемся распределением
Пуассона:
Искомая
вероятность:
Закон
распределения СВ
:
Математическое
ожидание:
Дисперсия:
Среднее
квадратическое отклонение:
Пример 3
Найти среднее число бракованных изделий в партии изделий, если
вероятность того, что в этой партии содержится хотя бы одно бракованное
изделие, равна 0,92. Предполагается, что число бракованных изделий в
рассматриваемой партии распределено по закону Пуассона.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Распределение
Пуассона:
Среднее
число бракованных изделий:
Пусть
событие
–в партии содержится хотя бы одно бракованное
изделие
Тогда
противоположное событие
– в партии нет ни одного бракованного изделия
Решая
уравнение, получаем:
Ответ:
Пример 4
Случайная величина ξ распределена по закону
Пуассона с параметром λ=0,2. Найти:
а)
;
б)
;
в)
Решение
Закон Пуассона:
Для закона Пуассона математическое ожидание:
Дисперсия:
а)
б)
в)
Ответ: а)
; б)
; в)
.
Пример 5
Случайные величины
распределены по закону Пуассона с одинаковым
математическим ожиданием, равным 6. Найдите математическое ожидание
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Поскольку случайные величины распределены по закону Пуассона и известны
их математические ожидания, соответствующие дисперсии равны:
Искомая величина:
Ответ: 504
Задачи контрольных и самостоятельных работ
Задача 1
Для пуассоновой случайной величины X
имеем
Найдите M(X)
Задача 2
Случайные величины X,Y распределены
по закону Пуассона. Найдите
, если M(X)=40 и M(Y)=70, а коэффициент корреляции X и
Y равен 0,8.
Задача 3
В
некоторой системе 810 приборов. Вероятность отказа каждого прибора в течение
заданного промежутка времени 0.001. Найти вероятность отказа не менее 3
приборов за данный промежуток времени. Найти характеристики данного
распределения случайной величины.
Задача 4
В партии
из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50
изделий, взятых наудачу из этой партии, ровно три окажутся дефектными.
Задача 5
Радиостанция
ведет передачу информации в течение 10 мкс. Работа ее происходит при наличии
хаотической импульсной помехи, среднее число импульсов которой в секунду
составляет
. Для срыва передачи
достаточно попадания одного импульса помехи в период работы станции. Считая,
что число импульсов помехи, попадающих в данный интервал времени, распределено
по закону Пуассона, найти вероятность срыва передачи информации.
Задача 6
Среди
семян пшеницы 0,6% семян сорняков. Какова вероятность при случайном отборе 1000
семян обнаружить не менее трех семян сорняков?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
На
телефонную станцию поступает в среднем 5 заявок на переговоры в минуту. Поток заявок
описывается распределением Пуассона. Рассчитать вероятность того, что за минуту
на станцию придут ровно две заявки.
Задача 8
Вероятность попадания в
цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель ровно
100 раз, если было произведено 2000 выстрелов.
Задача 9
Вероятность
изготовления нестандартной детали p=0.003. Найти
вероятность того, что среди 1000 деталей окажется 4 нестандартных.
Задача 10
Вероятность
сбоя в работе банкомата при каждом запросе равна 0,0016. Банкомат обслуживает
2000 клиентов в неделю. Определить вероятность того, что при этом число сбоев
не превзойдет 3.
Задача 11
Прядильщица
обслуживает 800 веретен. Вероятность обрыва нити на одном веретене в течение
одной минуты 0,003. Найти вероятность того, что в течение одной минуты обрыв
произойдет на трех веретенах.
Задача 12
Телефонный кабель состоит из 400 жил. С какой вероятностью этим
кабелем можно подключить к телефонной сети не менее 395 абонентов, если для
подключения каждого из них нужна одна жила, а вероятность того, что она
повреждена – 0,0125.
Задача 13
Вероятность «сбоя» в работе телефонной станции при каждом вызове
равна 0.05. Поступило 100 вызовов. Определить вероятность того, что произойдет
не более 3 сбоев.
Задача 14
На базе получено 10000 электроламп. Вероятность того, что в пути
лампа разобьется, равна 0,0003. Найдите вероятность того, что среди полученных
ламп будет пять ламп разбито.
Задача 15
Завод отправил в торговую сеть 500 изделий. Вероятность повреждения
в пути равна 0.002. Найти вероятность того, что при транспортировке будет
повреждено ровно три изделия.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
2.3.3. Распределение Пуассона
Случайная величина ![]() ,
,
распределённая по этому закону, принимает бесконечное и счётное количество значений ![]() , вероятности появления которых определяются формулой:
, вероятности появления которых определяются формулой:
![]()
Или, если расписать подробно:

Вспоминая разложение экспоненты в ряд,
легко убедиться, что:
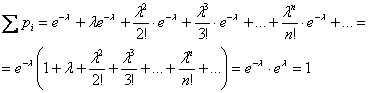
Математическое ожидание пуассоновской случайной величины равно ![]() и дисперсия – тому же самому значению:
и дисперсия – тому же самому значению: ![]() .
.
Во всех задачах параграфа Формула Пуассона мы лишь ПОЛЬЗОВАЛИСЬ распределением Пуассона для
приближенного расчёта вероятностей, в то время как ТОЧНЫЕ значения следовало находить по формуле Бернулли, т.е., там имело место биномиальное распределение. И
последующие задачи отличаются принципиально –
– отличие состоит в том, что сейчас речь идёт именно о РАСПРЕДЕЛЕНИИ Пуассона:
Задача 99
Случайная величина ![]() подчинена закону Пуассона с математическим ожиданием,
подчинена закону Пуассона с математическим ожиданием,
равным ![]() . Найти
. Найти
вероятность того, что данная случайная величина ![]() примет значение, меньшее, чем её математическое
примет значение, меньшее, чем её математическое
ожидание.
Решение: известно, что математическое ожидание распределения Пуассона в точности равно ![]() , таким образом, случайная величина
, таким образом, случайная величина ![]() принимает значения
принимает значения ![]() с вероятностями:
с вероятностями:
![]()
Интересующее нас событие ![]() состоит в трёх несовместных исходах: случайная величина
состоит в трёх несовместных исходах: случайная величина ![]() примет значение
примет значение ![]() или
или ![]() , или
, или ![]() . По теореме сложения вероятностей несовместных событий:
. По теореме сложения вероятностей несовместных событий:
![]() – вероятность
– вероятность
того, что случайная величина ![]() примет значение, меньшее, чем ее математическое
примет значение, меньшее, чем ее математическое
ожидание.
Ответ: ![]()
Аналогичная задача на понимание:
Задача 100
Случайная величина ![]() подчинена закону Пуассона с единичным математическим
подчинена закону Пуассона с единичным математическим
ожиданием. Найти вероятность того, что данная случайная величина примет положительное значение.
Решение и ответ в конце книги.
Помимо прочего, распределение Пуассона нашло широкое применение в теории массового обслуживания для вероятностной характеристики
простейшего потока событий. Постараюсь быть лаконичным:
Пусть в некоторую систему поступают заявки (телефонные звонки, приходящие клиенты и т.д.). Поток заявок называют
простейшим, если он удовлетворяет условиям стационарности, отсутствия последствий и ординарности.
Стационарность подразумевает то, что интенсивность заявок постоянна и не зависит от времени суток, дня недели или других
временнЫх рамок. Иными словами, не бывает «часа пик» и не бывает «мёртвых часов». Отсутствие последствий означает, что
вероятность появления новых заявок не зависит от «предыстории», т.е. нет такого, что «одна бабка рассказала» и другие «набежали» (или
наоборот, разбежались). И, наконец, свойство ординарности характеризуется тем, что за достаточно малый промежуток времени
практически невероятно появление двух или бОльшего количества заявок. «Две старушки в
дверь?» – нет уж, увольте, рубить удобнее по порядку.
Итак, пусть в некоторую систему поступает простейший поток заявок со средней интенсивностью ![]() заявок в некоторую единицу времени (минуту,
заявок в некоторую единицу времени (минуту,
час, день или в любой другой). Тогда вероятность того, что за данный промежуток времени, в систему поступит ровно ![]() заявок, равна:
заявок, равна:
![]()
Поразительно, с какой скоростью устаревают задачи:
Задача 101
Звонки в диспетчерскую такси представляет собой простейший пуассоновский поток со средней интенсивностью 30 вызовов в час. Найти
вероятность того, что: а) за 1 мин. поступит 2-3 вызова, б) в течение пяти минут будет хотя бы один звонок.
Решение: используем формулу Пуассона:
![]()
а) Учитывая стационарность потока, вычислим среднее количество вызовов за 1 минуту:
![]() вызова – в среднем
вызова – в среднем
за одну минуту.
По теореме сложения вероятностей несовместных событий:
![]() – вероятность
– вероятность
того, что за 1 минуту в диспетчерскую поступит 2-3 вызова.
б) Вычислим среднее количество вызов за пять минут:
![]()
По формуле Пуассона:
![]() – вероятность
– вероятность
того, что в течение 5 минут не будет ни одного звонка.
По теореме сложения вероятностей противоположных событий:
![]() –
–
вероятность того, что в течение 5 минут будет хотя бы один вызов.
Ответ: а) ![]() , б)
, б) ![]()
Обращаю внимание, что в отличие от задач параграфа Формула Пуассона, эту задачу уже нельзя
решить по формуле Бернулли. По той причине, что заранее не известно общее количество исходов ![]() (точное количество звонков в тот или иной
(точное количество звонков в тот или иной
час).
И предсказать это значение, разумеется, невозможно.
Для самостоятельного решения:
Задача 102
Среднее число автомобилей, проходящих таможенный досмотр в течение часа, равно 3. Найти вероятность того, что: а) за 2 часа пройдут
досмотр от 7 до 10 автомобилей; б) за пол часа успеет пройти досмотр только 1 автомобиль.
Таможня пройдена, достаём припрятанное:
 2.3.4. Гипергеометрическое распределение вероятностей
2.3.4. Гипергеометрическое распределение вероятностей
 2.3.2. Биномиальное распределение вероятностей
2.3.2. Биномиальное распределение вероятностей
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Распределение Пуассона — одно из самых популярных распределений в статистике.
Чтобы понять распределение Пуассона, сначала нужно понять эксперименты Пуассона.
Пуассоновые эксперименты
Эксперимент Пуассона — это эксперимент, обладающий следующими свойствами:
- Количество успехов в эксперименте можно подсчитать.
- Известно среднее количество успехов, которое происходит в течение определенного интервала времени (или пространства).
- Каждый результат является независимым.
- Вероятность того, что произойдет успех, пропорциональна размеру интервала.
Одним из примеров эксперимента Пуассона является количество рождений в час в данной больнице. Например, предположим, что в конкретной больнице происходит в среднем 10 родов в час. Это эксперимент Пуассона, поскольку он обладает следующими четырьмя свойствами:
- Количество успехов в эксперименте можно подсчитать – Мы можем подсчитать количество рождений.
- Известно среднее количество успехов, которое происходит в течение определенного интервала времени. Известно, что в среднем происходит 10 рождений в час.
- Каждый результат независим — вероятность того, что одна мать родит в течение данного часа, не зависит от вероятности того, что другая мать родит.
- Вероятность того, что произойдет успех, пропорциональна размеру интервала: чем длиннее интервал времени, тем выше вероятность того, что произойдет рождение.
Мы можем использовать распределение Пуассона, чтобы ответить на вопросы о вероятностях этого эксперимента Пуассона, такие как:
- Какова вероятность того, что в данный час произойдет более 12 родов?
- Какова вероятность того, что в данный час произойдет менее 5 родов?
- Какова вероятность того, что в данный час произойдет от 8 до 11 родов?
Распределение Пуассона
Распределение Пуассона описывает вероятность получения k успехов за заданный интервал времени.
Если случайная величина X подчиняется распределению Пуассона, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = λk * e – λ / k !
куда:
- λ: среднее количество успехов за определенный интервал
- k: количество успехов
- e: константа, равная приблизительно 2,71828.
Например, предположим, что в конкретной больнице в среднем рождается 2 человека в час. Мы можем использовать приведенную выше формулу, чтобы определить вероятность рождения 0, 1, 2, 3 и т. д. в данный час:
P(X=0) = 2 0 * e – 2 / 0! = 0,1353
P(X=1) = 2 1 * e – 2 / 1! = 0,2707
P(X=2) = 2 2 * e – 2 / 2! = 0,2707
P(X=3) = 2 3 * e – 2 / 3! = 0,1805
Мы можем рассчитать вероятность для любого числа рождений вплоть до бесконечности. Мы создаем, а затем создаем простую гистограмму для визуализации этого распределения вероятностей:
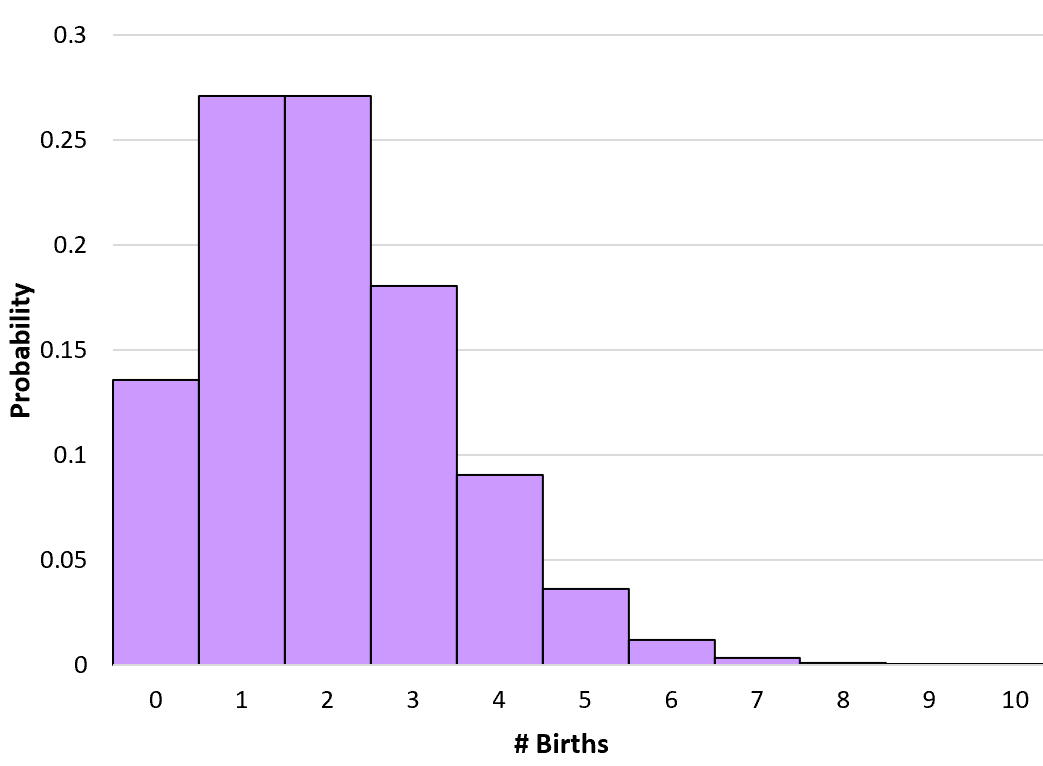
Вычисление кумулятивных вероятностей Пуассона
Несложно рассчитать одну вероятность Пуассона (например, вероятность того, что в больнице произойдет 3 рождения в течение заданного часа), используя приведенную выше формулу, но для расчета кумулятивной вероятности Пуассона нам нужно добавить индивидуальные вероятности.
Например, предположим, что мы хотим узнать вероятность того, что в больнице будет 1 или меньше родов в данный час. Мы будем использовать следующую формулу для расчета этой вероятности:
P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406
Это известно как кумулятивная вероятность , потому что она включает в себя добавление более одной вероятности. Мы можем рассчитать кумулятивную вероятность появления k или меньше рождений в данный час, используя аналогичную формулу:
Р(Х≤0) = Р(Х=0) = 0,1353
P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406
P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,1353 + 0,2707 + 0,2707 = 0,6767
Мы можем рассчитать эти кумулятивные вероятности для любого числа рождений вплоть до бесконечности. Затем мы можем создать гистограмму для визуализации этого кумулятивного распределения вероятностей:
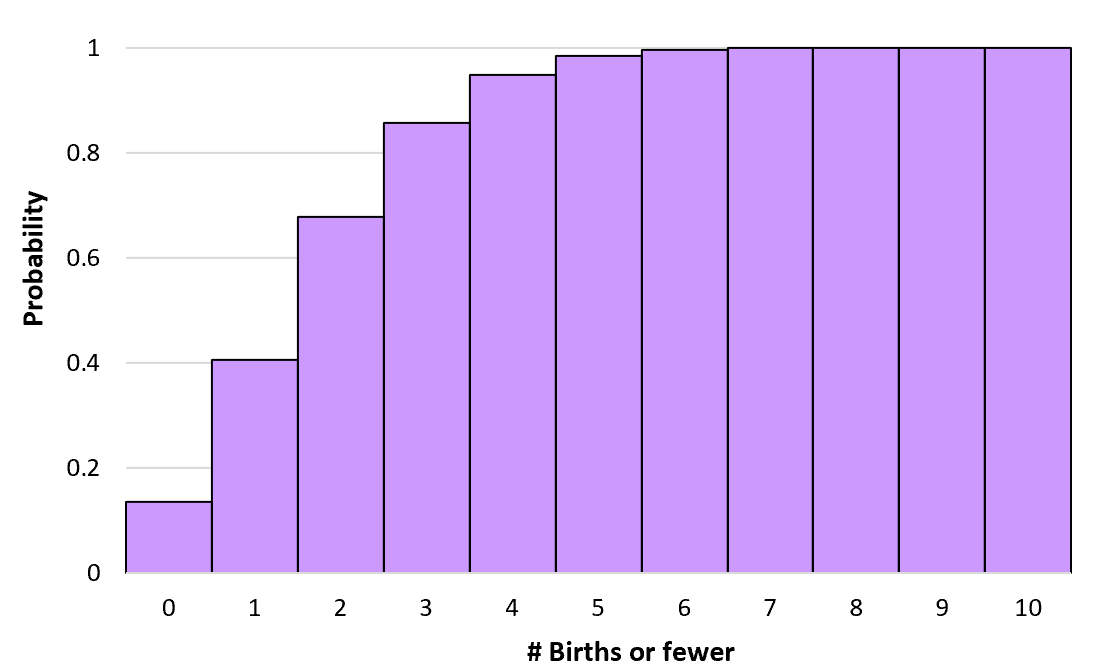
Свойства распределения Пуассона
Распределение Пуассона обладает следующими свойствами:
Среднее значение распределения равно λ .
Дисперсия распределения также равна λ .
Стандартное отклонение распределения равно √ λ .
Например, предположим, что в больнице в среднем рождается 2 ребенка в час.
Среднее число рождений, которое мы ожидаем в данный час, составляет λ = 2 рождения.
Ожидаемая дисперсия числа рождений составляет λ = 2 рождения.
Проблемы практики распределения Пуассона
Используйте следующие практические задачи, чтобы проверить свои знания о распределении Пуассона.
Примечание. Мы будем использоватькалькулятор распределения Пуассона для расчета ответов на эти вопросы.
Проблема 1
Вопрос: Известно, что некий сайт делает 10 продаж в час. Какова вероятность того, что за данный час сайт совершит ровно 8 продаж?
Ответ: Используя калькулятор распределения Пуассона с λ = 10 и x = 8, мы находим, что P(X=8) = 0,1126 .
Проблема 2
Вопрос: Известно, что некий риелтор делает в среднем 5 продаж в месяц. Какова вероятность того, что в данном месяце она совершит более 7 продаж?
Ответ: Используя калькулятор распределения Пуассона с λ = 5 и x = 7, мы находим, что P(X>7) = 0,13337 .
Проблема 3
Вопрос: Известно, что в одной больнице рождается 4 человека в час. Какова вероятность того, что в данный час произойдет 4 или менее родов?
Ответ: Используя калькулятор распределения Пуассона с λ = 4 и x = 4, мы находим, что P(X≤4) = 0,62884 .
Дополнительные ресурсы
В следующих статьях объясняется, как работать с распределением Пуассона в различных статистических программах:
Как использовать распределение Пуассона в R
Как использовать распределение Пуассона в Excel
Как рассчитать вероятности Пуассона на калькуляторе TI-84
Реальные примеры распределения Пуассона
Калькулятор распределения Пуассона
Дискретная
случайная величина распределена по
закону Пуассона, если она принимает
значения 0,1,2…m…n…,
бесконечное, но счетное число раз, с
вероятностями, определяемыми по формуле
Пуассона:

где ,p
,p .
.
Закон
распределения примет вид:
|
|
0 |
1 |
2 |
… |
m |
… |
|
|
|
|
|
… |
|
… |
 ,
,
 и
и
т.д.
Теорема.
Математическое
ожидание и дисперсия случайной величины,
распределенной по закону Пуассона,
равны параметру Пуассона.

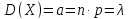
Пример
1.
Станок
изготавливает за смену 100000 деталей.
Вероятность изготовления бракованной
детали p
= 0,0001.
Найти
вероятность того, что за смену будет
изготовлено 5 бракованных деталей.
Решение:
Обозначим
n
= 100 000,
k
= 5, p
= 0,0001. События, состоящие в том, что
отдельная деталь бракована, независимы,
число испытаний n
велико, а вероятность p
мала, поэтому воспользуемся распределением
Пуассона:

где


Пример
2.
Устройство
состоит из 1000 элементов. Вероятность
отказа любого элемента в течение времени
t
равна 0,002.
Найти
математическое ожидание ,
,
дисперсию ,
,
среднее квадратическое отклонение и
и
моду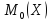 .
.
Решение:
X
‒ случайная величина ‒ число отказавших
за время t
элементов.
 ,
,
 .
.
Следовательно, случайная величина
распределена по закону Пуассона.
 элемента
элемента
Составим
закон распределения Пуассона:
|
|
0 |
1 |
2 |
3 |
… |
m |
… |
|
|
0,135335 |
0,270671 |
0,270671 |
0,180447 |
… |
|
… |
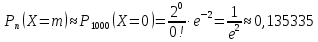


 и
и
т.д.
9. Непрерывная случайная величина. Функция распределения. Плотность вероятности. Вероятность попадания в заданный интервал.
Непрерывной
случайной величиной
называют случайную величину, значения
которой сплошь заполняют некоторый
интервал.
Например,
рост человека ‒ непрерывная случайная
величина.
Функцией
распределения случайной величины
называют вероятность того, что случайная
величина Х
принимает значения, меньшие х.
F
(x)
= P
(
X


Геометрически,
формула F(x)
= P
(X означает,
означает,
что все значения Х
будут находиться, левее х.
Функция F(x)
называется интегральной функцией.
Плотностью
вероятности непрерывной
случайной величины f
(x)
называется производная от функции
распределения этой случайной величины:

Следовательно,
F(x)
первообразная для f
(x).
Теорема.
Вероятность попадания непрерывной
случайной величины X
в интервал от a
до b
находится по формуле:

Доказательство.

Следствие.
Если все возможные значения случайной
величины

10. Математическое ожидание и дисперсия непрерывной случайной величины
1.
Математическое ожидание:

2.
Дисперсия:

Преобразуем
эту формулу:


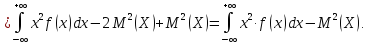

‒
формула
дисперсии для непрерывных случайных
величин.
Тогда
среднее квадратическое отклонение:


11. Основные законы распределения непрерывных случайных величин.
1.Нормальный закон распределения.
Из
всех законов распределения для непрерывных
случайных величин на практике чаще
всего встречается нормальный
закон
распределения. Этот закон распределения
является предельным, то есть все остальные
распределения стремятся к нормальному.
Теорема
1. Непрерывная
случайная величина распределена по
нормальному
закону с
параметрами а
и
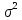 ,если
,если
плотность вероятности имеет вид:
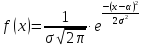
Математическое
ожидание случайной величины, распределённой
по нормальному закону распределения,
равно а,
то есть дисперсия
дисперсия
 .
.
Теорема
2. Вероятность
попадания непрерывной случайной
величины, распределенной по нормальному
закону распределения в интервал от α
до β,
находится по формуле:
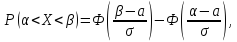

Пример.
Полагая,
что рост мужчин определенной возрастной
группы есть нормально распределенная
случайная величина X, c параметрами а =
173 и
 =
=
36.
Найти:
а)
выражение плотности вероятностей и
функции распределения случайной
величины X;
б)
долю костюмов 4-го роста (176 – 182 см) в
общем объеме производства.
Решение:
Плотность
вероятности нормально распределенной
случайной величины:

Доля
костюмов 4-го роста (176 – 182 см.) в общем
объеме производства определяется по
формуле как вероятность

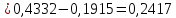
0,2417 100%
100% 24,2%
24,2%
‒ доля костюмов 4-го роста в общем объеме
производства.
Итак,
функция плотности вероятностей
нормального закона распределения имеет
вид:

Тогда
функция распределения:

|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #