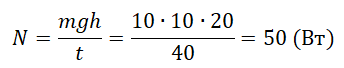Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505
 Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A

pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
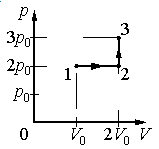 Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.8k
Содержание:
Работа в термодинамике:
В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1
Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).
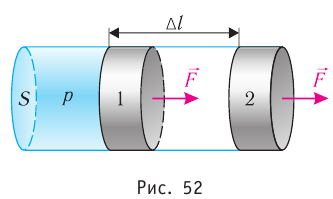
Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние 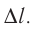
Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня
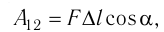 (10.1)
(10.1)
где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда
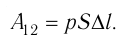
Произведение 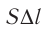 определяет приращение объёма
определяет приращение объёма 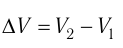 (см. рис. 52), поэтому работа газа при его изобарном расширении
(см. рис. 52), поэтому работа газа при его изобарном расширении
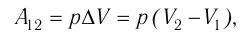 (10.2)
(10.2)
где 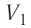 — начальный объём газа,
— начальный объём газа, 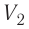 — объём газа в конечном состоянии.
— объём газа в конечном состоянии.
Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется 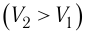 , работа, совершённая силой давления газа, положительная (
, работа, совершённая силой давления газа, положительная (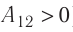 ), а в случае сжатия (
), а в случае сжатия (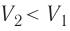 ) работа отрицательная (
) работа отрицательная (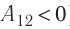 ).
).
Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом 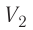 в состояние 1 с конечным объёмом
в состояние 1 с конечным объёмом 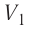 можно характеризовать работой
можно характеризовать работой 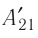 внешних сил над газом:
внешних сил над газом:
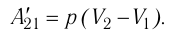 (10.З)
(10.З)
Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой 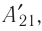 у совершённой внешними силами, и работой
у совершённой внешними силами, и работой 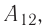 совершённой силой давления газа:
совершённой силой давления газа: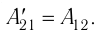 Это соотношение согласуется с третьим законом Ньютона (внешняя сила
Это соотношение согласуется с третьим законом Ньютона (внешняя сила 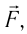 действующая на газ со стороны поршня, имеет
действующая на газ со стороны поршня, имеет
направление, противоположное силе давления 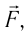 действующей на поршень со стороны газа). Из формулы (10.3) видно, что работа, совершённая внешними силами, положительная
действующей на поршень со стороны газа). Из формулы (10.3) видно, что работа, совершённая внешними силами, положительная 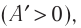 если происходит сжатие газа
если происходит сжатие газа 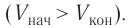
Если газ расширяется 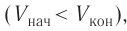 ), то работа, совершённая внешними силами отрицательная
), то работа, совершённая внешними силами отрицательная 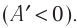
Геометрическое толкование работы
Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника 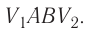
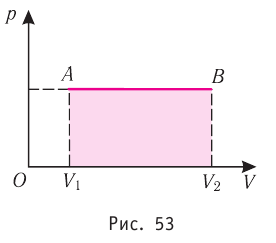
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от 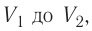 численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов
численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов 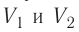 (рис. 54).
(рис. 54).
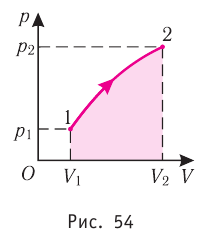
Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл: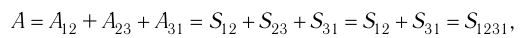
где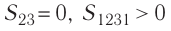 на рисунке 55, а и
на рисунке 55, а и 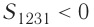 на рисунке 55, б.
на рисунке 55, б.
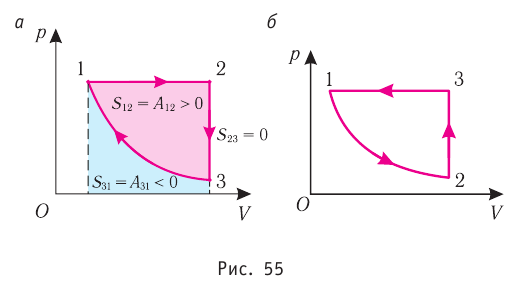
Если «кривая расширения» (изобара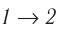 ) (см. рис. 55, а) расположена выше «кривой сжатия» (изотерма
) (см. рис. 55, а) расположена выше «кривой сжатия» (изотерма 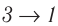 ), то полная работа, совершённая системой за цикл (работа цикла), положительная. Если же, как изображено на рисунке 55, б, «кривая сжатия» (изобара
), то полная работа, совершённая системой за цикл (работа цикла), положительная. Если же, как изображено на рисунке 55, б, «кривая сжатия» (изобара 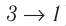 ) расположена выше «кривой расширения» (изотерма
) расположена выше «кривой расширения» (изотерма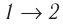 ), то работа цикла отрицательная.
), то работа цикла отрицательная.
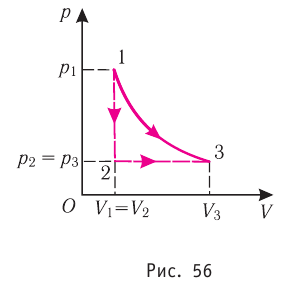
Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения 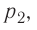 а затем изобарно увеличив его объём от значения
а затем изобарно увеличив его объём от значения 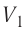 до значения
до значения 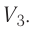
Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Количество теплоты и удельная теплоёмкость
Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.
Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.
Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).
Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
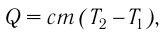 (10,4)
(10,4)
где m — масса тела, 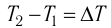 — разность температур в конце и в начале процесса теплопередачи, с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает или отдаёт вещество массой 1 кг при изменении его температуры на 1 К. Удельную
— разность температур в конце и в начале процесса теплопередачи, с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает или отдаёт вещество массой 1 кг при изменении его температуры на 1 К. Удельную
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин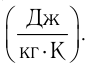
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин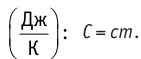 Теплоёмкость, в отличие от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
Теплоёмкость, в отличие от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
Удельная теплота плавления
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления 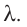 Для плавления тела массой m, предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты
Для плавления тела массой m, предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты 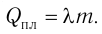 При кристаллизации тела выделяется количество теплоты
При кристаллизации тела выделяется количество теплоты 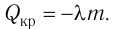
Удельная теплота парообразования
Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле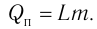 Конденсация пара сопровождается выделением количества теплоты
Конденсация пара сопровождается выделением количества теплоты 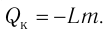
Удельная теплота сгорания топлива
Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле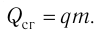 Оно передаётся телам, образующим термодинамическую систему, и по отношению к ним является положительной величиной.
Оно передаётся телам, образующим термодинамическую систему, и по отношению к ним является положительной величиной.
Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.
При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.
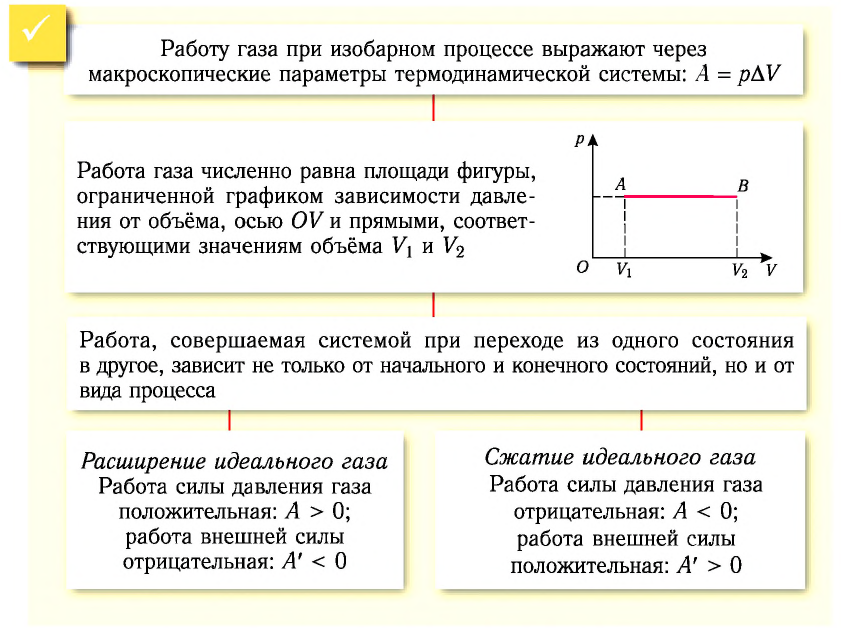
1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:
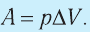
2. Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов 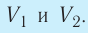
3. Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.
4. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.
Пример №1
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 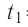 = 12 °С до
= 12 °С до 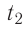 = 87 °С, если давление газа и его начальный объём соответственно p=190кПа и
= 87 °С, если давление газа и его начальный объём соответственно p=190кПа и 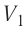 = 6,Одм’5.
= 6,Одм’5.
Дано:
Пример №2
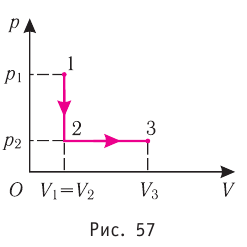
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре 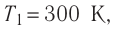 изменяется так, как показано на рисунке 57. Определите работу газа в ходе всего процесса, если на изохоре
изменяется так, как показано на рисунке 57. Определите работу газа в ходе всего процесса, если на изохоре 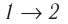 его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.
его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.
Дано:
v = 1,0 моль
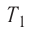 = 300 к
= 300 к
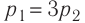
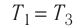
А — ?
Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках 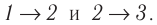 Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный
Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный 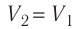 ), то работа газа
), то работа газа 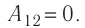 . Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (
. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (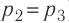 )следовательно, работа газа
)следовательно, работа газа 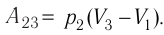 Тогда
Тогда 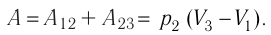
Так как по условию 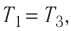 то воспользуемся уравнением Клапейрона (5.2):
то воспользуемся уравнением Клапейрона (5.2):
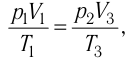 откуда
откуда 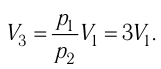 Следовательно,
Следовательно, 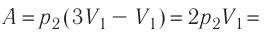
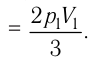 Согласно уравнению Клапейрона—Менделеева
Согласно уравнению Клапейрона—Менделеева 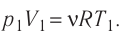
Тогда 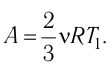
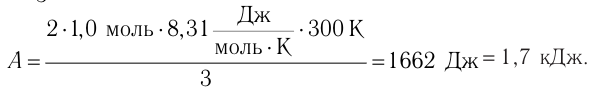
Ответ: А = 1,7 кДж.
Работа в термодинамике
В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.
Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.
Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.
Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.
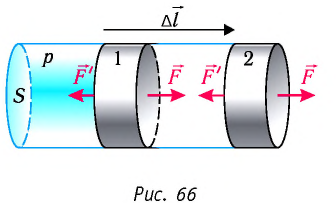
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре 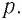 В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние
В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние 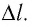 Модуль силы давления газа на поршень
Модуль силы давления газа на поршень 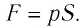 Эта сила совершила работу по перемещению поршня, равную
Эта сила совершила работу по перемещению поршня, равную
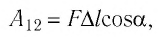
где 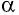 — угол между направлениями силы
— угол между направлениями силы 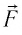 и перемещения поршня
и перемещения поршня 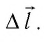 Поскольку в рассматриваемом примере
Поскольку в рассматриваемом примере 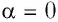 и
и 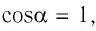 то
то
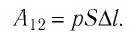
Произведение 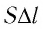 определяет изменение объёма
определяет изменение объёма 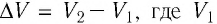 — начальный объём газа;
— начальный объём газа; 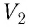 — объём газа в конечном состоянии (см. рис. 66).
— объём газа в конечном состоянии (см. рис. 66).
Таким образом, работа силы давления газа при его изобарном расширении:

Так как давление р газа — величина положительная, то из формулы (12.1) следует, что 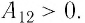
При изобарном расширении газа из состояния 1 в состояние 2 работа силы 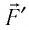 (см. рис. 66):
(см. рис. 66):
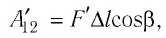
где 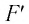 — модуль силы, действующей на газ со стороны поршня (внешняя сила);
— модуль силы, действующей на газ со стороны поршня (внешняя сила); 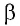 — угол между направлениями силы
— угол между направлениями силы 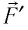 и перемещения
и перемещения 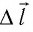 поршня.
поршня.
Перемещение 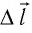 поршня одно и то же, а сила давления
поршня одно и то же, а сила давления 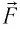 газа на поршень и сила давления
газа на поршень и сила давления 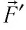 поршня на газ — силы, подчиняющиеся третьему закону Ньютона:
поршня на газ — силы, подчиняющиеся третьему закону Ньютона:
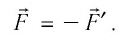
Следовательно, работы 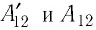 отличаются только знаком
отличаются только знаком 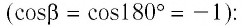
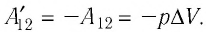
Таким образом, можно сделать следующие выводы.
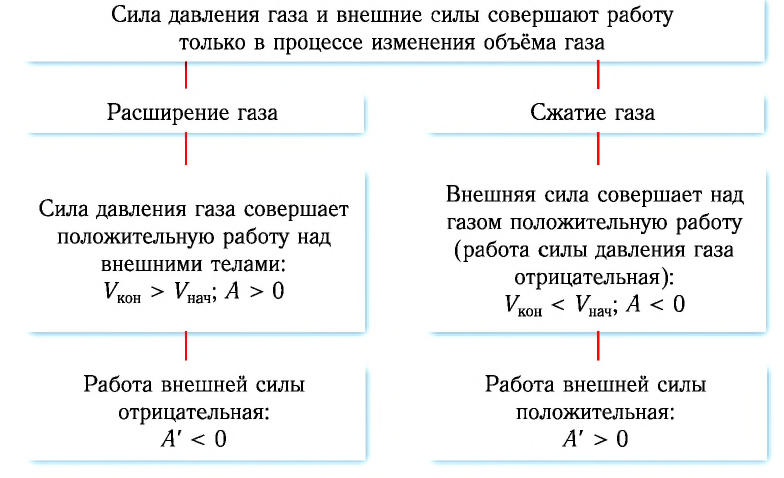
Геометрическое толкование работы:
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при 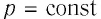 (рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника
(рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника 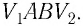
Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от 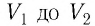 численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов
численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов 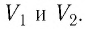
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения 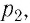 а затем изобарно увеличив его объём до значения
а затем изобарно увеличив его объём до значения 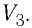 В первом случае работа газа больше, чем во втором.
В первом случае работа газа больше, чем во втором.
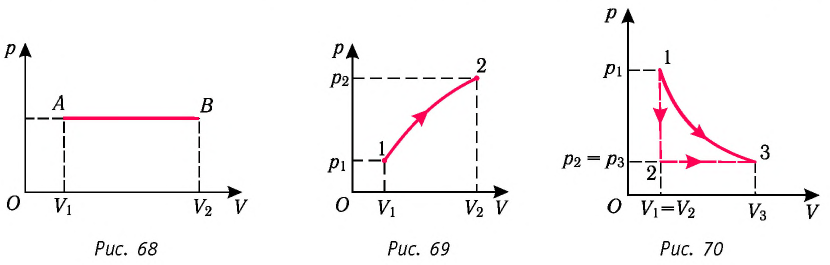
Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Пример №3
Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73). 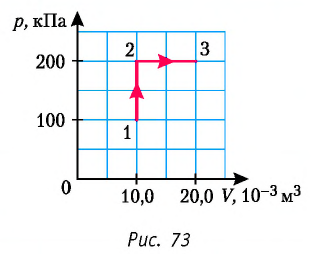
Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках 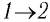 и
и 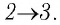 Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс
Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс 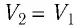 ), то работа, совершаемая силой давления газа,
), то работа, совершаемая силой давления газа, 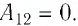 В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу
В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу
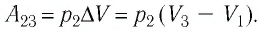
Тогда при переходе из состояния 1 в состояние 3 работа
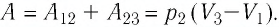
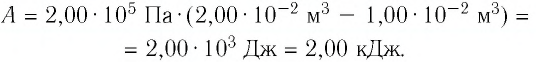
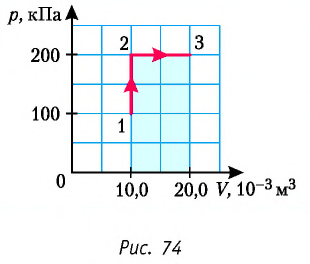
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма 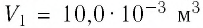 и
и 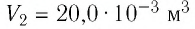 (закрашенная область на рисунке 74).
(закрашенная область на рисунке 74).
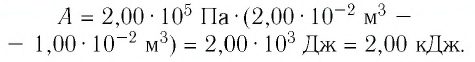
Ответ: 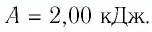
Пример №4
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 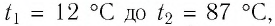 если давление газа
если давление газа 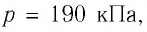 а его начальный объём
а его начальный объём 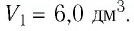

Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
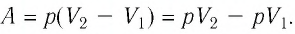
Согласно уравнению Клапейрона—Менделеева, 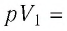
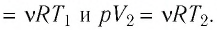 Следовательно,
Следовательно,
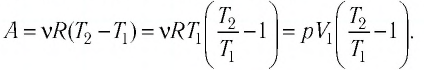
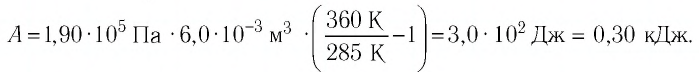
Ответ: 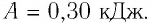
Как определить работу в термодинамике
В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?
Почему при изменении объема газа изменяется его внутренняя энергия
Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.
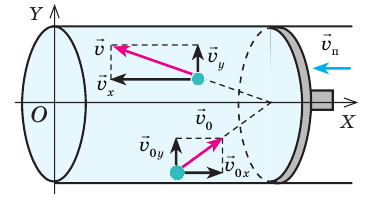
Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v > 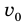 ) — газ нагревается. (Аналогично увеличивается скорость мяча после удара волейболиста, когда его рука движется навстречу мячу.)
) — газ нагревается. (Аналогично увеличивается скорость мяча после удара волейболиста, когда его рука движется навстречу мячу.)
Как вычислить работу газа
Вычислим работу, которую совершает сила давления газа при изменении его объема от 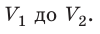 По определению работы: A=Fscosα. Если газ расширяется изобарно, то сила, действующая со стороны газа на поршень, постоянна: F=pS (p — давление газа; S — площадь поршня); модуль перемещения поршня
По определению работы: A=Fscosα. Если газ расширяется изобарно, то сила, действующая со стороны газа на поршень, постоянна: F=pS (p — давление газа; S — площадь поршня); модуль перемещения поршня 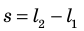 (рис. 37.2, а); α = 0.
(рис. 37.2, а); α = 0.
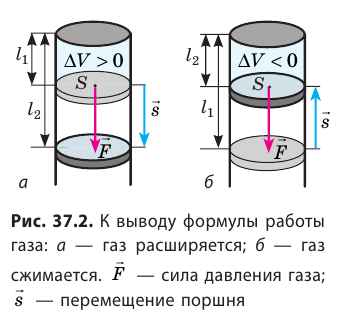
Таким образом, работа газа при его изобарном расширении равна:
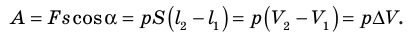
Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).
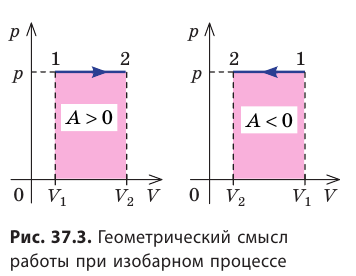
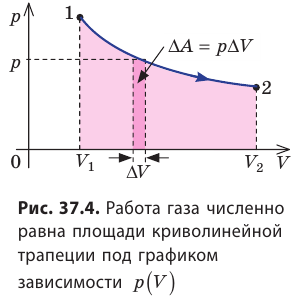
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от 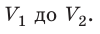 будет равна сумме площадей всех полос, то есть площади криволинейной трапеции под графиком зависимости p (V).
будет равна сумме площадей всех полос, то есть площади криволинейной трапеции под графиком зависимости p (V).
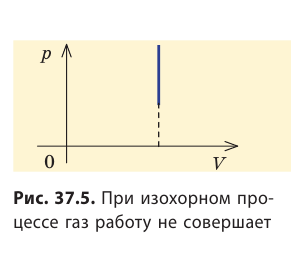
Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).
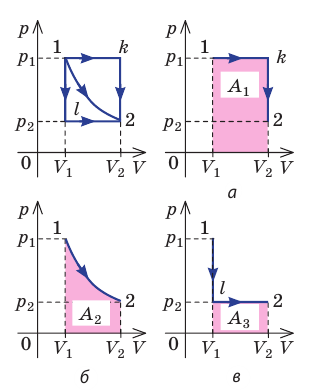
Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что: 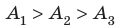
Пример №5
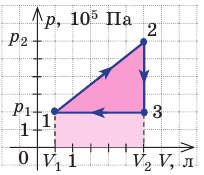
На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.
Решение:
Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны 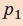 и
и 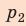 , а высота —
, а высота — 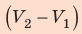 ; объем газа увеличивается, поэтому работа газа положительна. Работа газа в ходе процесса 2–3 равна нулю, поскольку этот процесс изохорный. Работа газа в ходе процесса 3–1 численно равна площади прямоугольника со сторонами
; объем газа увеличивается, поэтому работа газа положительна. Работа газа в ходе процесса 2–3 равна нулю, поскольку этот процесс изохорный. Работа газа в ходе процесса 3–1 численно равна площади прямоугольника со сторонами 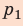 и
и 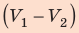 ; объем газа уменьшается, поэтому работа отрицательна. Следовательно, для определения работы за весь цикл нужно из площади трапеции вычесть площадь прямоугольника. То есть, как видно из рисунка, работа газа за цикл численно равна площади прямоугольного треугольника 1–2–3:
; объем газа уменьшается, поэтому работа отрицательна. Следовательно, для определения работы за весь цикл нужно из площади трапеции вычесть площадь прямоугольника. То есть, как видно из рисунка, работа газа за цикл численно равна площади прямоугольного треугольника 1–2–3:
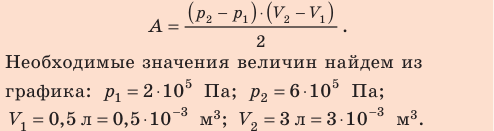

Выводы:
- При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
- Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
- Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.
- Первый закон термодинамики
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Термодинамика – основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Поэтому принято говорить о двух формах передачи энергии от одних тел к другим: о теплоте и работе.
Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p(V). На рис. 6.1 показана произвольная зависимость давления газа p от его объема V (объем газа в начальном состоянии V 1; объем газа в конечном состоянии V 2). Площадь заштрихованной фигуры совпадает с работой, совершенной газом.
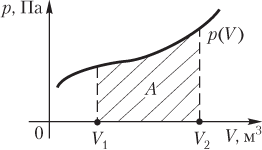
Если зависимость p(V) представляет собой прямую линию, то работа численно равна площади прямолинейной трапеции.
В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж).
Работа газа при изобарном процессе (p = const) может быть вычислена по одной из формул:
A = p∆V, или A = νR∆T,
где p — давление газа; ΔV — изменение объема газа при переходе из начального в конечное состояние, ΔV = V 2 − V 1; V 1 — объем газа в начальном состоянии; V 2 — объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); ΔT — соответствующее изменение температуры газа, ΔT = T 2 − T 1; T 1 — абсолютная температура начального состояния; T 2 — абсолютная температура конечного состояния.
Работа газа при изохорном процессе (V = const) не совершается:
Работа газа при круговом (циклическом) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p(V). На рис. 6.2 показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2, 3 — промежуточные состояния газа.
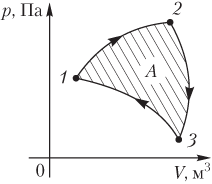
Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе.
Работа, совершаемая газом за цикл, может быть:
· положительной (прямой цикл);
· отрицательной (обратный цикл).
Пример 3. График циклического процесса, происходящего с некоторой массой идеального газа, в координатах p(V) имеет вид прямых, соединяющих точки (0,0250 м 3 ; 75,0 кПа), (0,0750 м 3 ; 125 кПа), (0,0750 м 3 ; 75,0 кПа). Определить абсолютную величину работы, совершаемой газом за цикл.
Решение. На рисунке изображен график циклического процесса в указанных термодинамических координатах p(V).
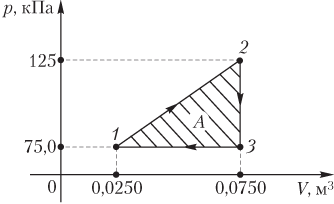
Величина искомой работы равна площади треугольника, ограниченного прямыми, соединяющими указанные точки:
A=12(125−75,0)⋅103⋅(0,0750−0,0250)=1,25⋅103 Дж=1,25 кДж.
Газ за цикл совершает работу 1,25 кДж.
Пример 4. Газ, состоящий из смеси 2,0 г водорода и 4,2 г гелия, при изобарном нагревании совершил работу 46 кДж. Во сколько раз увеличился объем газа, если его начальная температура была равна 300 К? Молярные массы водорода и гелия равны 2,0 и 4,0 г/моль соответственно.
Решение. Запишем формулу для расчета работы смеси газов при изобарном процессе:
где p — давление смеси газов (постоянная величина), p = const; V 1 — объем смеси газов в начальном состоянии; V 2 — объем смеси газов в конечном состоянии.
Давление смеси газов определяется законом Дальтона:
где p 1 — парциальное давление водорода; p 2 — парциальное давление гелия.
Давления указанных газов в смеси определяются следующими выражениями:
· парциальное давление водорода
где m 1 — масса водорода; M 1 — молярная масса водорода; T 1 — температура смеси газов в начальном состоянии; V 1 — объем смеси газов в начальном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);
· парциальное давление гелия
где m 2 — масса гелия; M 2 — молярная масса гелия.
Подстановка закона Дальтона и явного вида выражений для парциальных давлений водорода и гелия в формулу для работы, совершаемой смесью указанных газов, дает
Преобразование данного уравнения к виду
позволяет выразить искомое отношение объемов
Следовательно, при совершении указанной работы объем смеси увеличился в 10 раз.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 –  | 7304 –
| 7304 –  или читать все.
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Условие задачи:
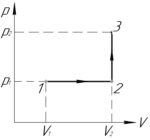 (V_1=2) л, (V_2=3) л, (p_1=400) кПа. Найти работу газа, совершенную в процессе 1-2-3 (схема к задаче приведена справа).
(V_1=2) л, (V_2=3) л, (p_1=400) кПа. Найти работу газа, совершенную в процессе 1-2-3 (схема к задаче приведена справа).
Задача №5.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(V_1=2) л, (V_2=3) л, (p_1=400) кПа, (p_2=600) кПа, (A-?)
Решение задачи:
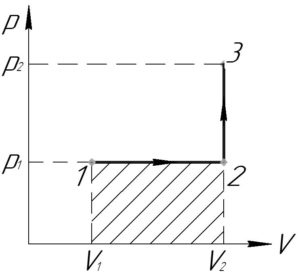 Работа газа (A), совершенная в процессе 1-2-3, равна сумме работ газа в процессах 1-2 и 2-3.
Работа газа (A), совершенная в процессе 1-2-3, равна сумме работ газа в процессах 1-2 и 2-3.
Процесс 1-2 — изобарный, поэтому работу газа (A_<1 — 2>) в этом процессе следует искать по такой формуле (численно работа равна площади фигуры под графиком процесса, на схеме к решению — заштриховано):
Процесс 2-3 — изохорный, работа газа (A_<2 — 3>) в этом процессе равна нулю, так как газ не изменяет своего объема (площадь фигуры под графиком этого процесса в координатах p-V также равна нулю).
В итоге формула (1) примет такой вид:
Переведём объемы газа (V_1) и (V_2) в систему СИ:
Ответ: 400 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода.
Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода. Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Поясните,почему умножение идет 2х10^5 ,когда газ совершает работу от 1 до 2, вроде должно быть 1х10^5,а по ответу получается от 0 до 2.
На участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется. Вся работа совершается на участке 2-3. Общее правило следующее, если процесс изображен на диаграмме , то работа равна площади под графиком со знаком плюс, если объем увеличивается, и со знаком минус, если уменьшается. Для тепловой машины, работающей по циклу, полезная работа равна площади ограниченной этим циклом, это укладывается в ранее озвученное правило. Когда мы идем по “верхней” части цикла, работа идет в +, потом возвращаемся по “нижней” в исходную точку, работа теперь идет в -, в результате остается только кусок внутри.
Алексей, вот Вы сказали, что “на участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется.”
а на участке 2-3 ведь не меняется давление.Так почему работа там совершается? Разве не A=pV ?
Не, не так. Давайте разбираться.
Будем выводить формулу, по которой можно посчитать работу совершенную газом. Когда газ работает? Когда он что-то перемешает. Для этого должен как-то меняться его объем. Например, газ расширяется и толкает поршень вверх, а с ним и какой-то груз, вот Вам и работа. То есть без изменения объема нет работы.
Чтобы вывести формулу, рассмотрим модельную задачу. Рассмотрим цилиндрический сосуд с газом. Пусть сосуд закрыт подвижным поршнем площади . Давление газа равно
. Определим, какую работу совершит газ, когда поршень сдвинется на малое расстояние
. Так как это работа на малом перемещении, то назовем ее элементарной работой и обозначим через
. Работа газа равна произведению силы, с которой он давит на поршень, на перемещение поршня (газ давит нормально, поэтому косинуса не возникает):
. Но сила, с которой газ давит на поршень связана с давлением газа соотношением:
. Если перемещение поршня мало, то можно считать, что давление газа не изменяется сильно и что оно остается постоянным. Тогда:
. Но
— это как раз изменение объема газа
. Окончательно имеем:
.
Получив эту формулу, можно забыть о том, как она выводилась (про сосуд и поршень), она оказывается верной для любого малого изменения объема.
Теперь, чтобы найти работу на конечном изменении объема нужно просуммировать работы по малым изменения, в математике это делается при помощи интеграла: Если внимательно приглядеться, то тут можно как раз увидеть площадь под линией процесса на диаграмме
. Вот почему говорят, что для поиска работы надо искать площадь под графиком на этой диаграмме.
Для частных случаев формула приобретает вид:
1) при изобарном процессе давление выносится за знак интеграла и получаем:
2) при изохорном объем не изменяется, поэтому пределы интегрирования совпадают, интеграл равен нулю, работа равна нулю.
3) при изотермическом процессе, давление уже изменяется с объемом, поэтому надо добавить в рассмотрение уравнение Клапейрона-Менделеева: . Следовательно,
. А значит работа при изотермическом процессе равна:
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).

Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).

Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Механическая работа

О чем эта статья:
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа
А = FScosα
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
α — угол между векторами силы и перемещения [°]
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия
Еп = mgh
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
h — высота [м]
На планете Земля g ≈ 9,8 м/с 2
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
За счет чего происходит процесс?
Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность
N = A/t
N — мощность [Вт]
A — механическая работа [Дж]
t — время [с]
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность
N = Fv
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность
N = Fvcosα
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
α — угол между векторами силы и скорости [°]
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
Сила вязкого трения.
Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Работа силы через векторы
4.1. Работа силы
Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).
Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.

Рис 4.1. Элементарная работа
Элементарная работа силы 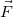 равна скалярному произведению вектора силы на вектор перемещения её точки приложения
равна скалярному произведению вектора силы на вектор перемещения её точки приложения 
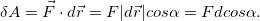
Работа — скалярная величина, ее знак зависит от знака  . Положительная работа совершается силой, если ее направление составляет острый угол
. Положительная работа совершается силой, если ее направление составляет острый угол 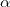 с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол
с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол 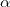 с направлением движения, при этом сила тормозит это движение. Величина
с направлением движения, при этом сила тормозит это движение. Величина
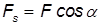
— это проекция силы F на направление перемещения. Следовательно,
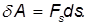
Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:
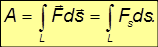
При перемещении вдоль оси x работу графически можно представить как площадь под кривой Fx(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.
Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = Fx(x)
Если перемещение ортогонально силе, то  = 0 и работа равна нулю:
= 0 и работа равна нулю:
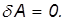
Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и  = 0. Здесь и ниже
= 0. Здесь и ниже  и
и 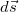 означают одно и то же — бесконечно малое перемещение, а |
означают одно и то же — бесконечно малое перемещение, а | |=|
|=|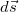 |=
|= 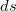 — соответствующий бесконечно малый путь.
— соответствующий бесконечно малый путь.
Если на тело действует несколько сил, то
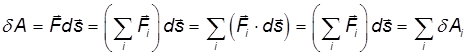
то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.
Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью 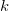 . Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука
. Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука
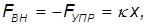
где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).
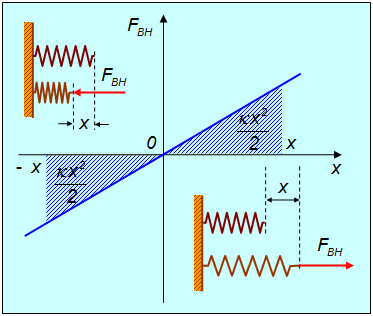
Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины
Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид
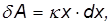
так что для полной работы упругой деформации пружины получаем
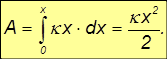
Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.
Механическая работа

О чем эта статья:
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа
А = FScosα
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
α — угол между векторами силы и перемещения []
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия
Еп = mgh
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
h — высота [м]
На планете Земля g ≈ 9,8 м/с 2
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
- За счет чего происходит процесс?
- Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность
N = A/t
N — мощность [Вт]
A — механическая работа [Дж]
t — время [с]
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность
N = Fv
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность
N = Fvcosα
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
α — угол между векторами силы и скорости []
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
- Выталкивающая сила.
- Сила вязкого трения.
- Сила тяжести.
- Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Механическая работа и мощность
теория по физике 🧲 законы сохранения
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
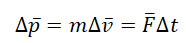
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
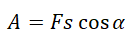
 Важно!
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
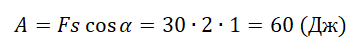
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
Модуль силы тяжести: Fтяж = mg
Работа силы тяжести: A = mgs cosα
Модуль силы трения скольжения: Fтр = μN = μmg
Работа силы трения скольжения: A = μmgs cosα
Модуль силы упругости: Fупр = kx
Работа силы упругости:

| Работа силы тяжести |
| Работа силы трения скольжения |
| Работа силы упругости |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0 о , то cosα = 1.
- Если 0 о o , то cosα > 0.
- Если α = 90 о , то cosα = 0.
- Если 90 о o , то cosα о , то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела
Работа при равномерном прямолинейном движении определяется формулой:
Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
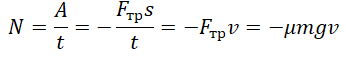
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия(КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство
Работа полезная и полная
Неподвижный блок, рычаг

Наклонная плоскость
l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Механическая работа и мощность
теория по физике 🧲 законы сохранения
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
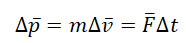
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
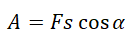
 Важно!
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
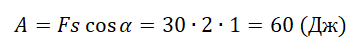
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
Модуль силы тяжести: Fтяж = mg
Работа силы тяжести: A = mgs cosα
Модуль силы трения скольжения: Fтр = μN = μmg
Работа силы трения скольжения: A = μmgs cosα
Модуль силы упругости: Fупр = kx
Работа силы упругости:

| Работа силы тяжести |
| Работа силы трения скольжения |
| Работа силы упругости |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0 о , то cosα = 1.
- Если 0 о o , то cosα > 0.
- Если α = 90 о , то cosα = 0.
- Если 90 о o , то cosα о , то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела
Работа при равномерном прямолинейном движении определяется формулой:
Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
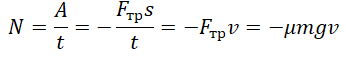
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия(КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство
Работа полезная и полная
Неподвижный блок, рычаг

Наклонная плоскость
l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/rabota-sily-cherez-vektory
[/spoiler]