Уверен, у каждого домашнего мастера был случай, когда ему нужно было сделать разметку какой-нибудь круглой заготовки и найти центр ее основания. Казалось бы, это очень просто сделать, но некоторые мастера долго не могут найти выход в данной ситуации. Сегодня я покажу вам два простых решения, с помощью которых можно быстро и точной найти центр любой окружности.
1. Первый способ подойдет для разметки небольших заготовок. В качестве примера я возьму заглушку от пластиковой трубы диаметром 50 мм.
Для того, чтобы найти центр окружности заглушки, не нужны будут какие-то математические вычисления и сложные манипуляции. Нам понадобятся всего лишь строительный угольник и обычная линейка (или второй угольник), которые есть в любой мастерской.
Складываем вместе угольник и линейку, так чтобы образовался угол в 45 градусов.
Затем, придерживая одной рукой угольник и линейку, прикладываем их к круглой заготовке (заглушке) так, чтобы она вплотную соприкасалась с двумя сторонами угольника.
Теперь берем карандаш и чертим на заглушке первую линию, потом немного ее поворачиваем и делаем вторую метку (достаточно провести две линии, но для уверенности можно поставить три метки).
Все задача решена! Точка пересечения этих двух линий и будет центром данной окружности. Данный способ один из самых быстрых и простых.
2. Второй способ подойдет, если окружность имеет большой диаметр или она расположена на плоскости. Для примера я обвел карандашом крышку от кастрюли. В этом случае тоже все очень просто. Для начала выбираем любую точку на окружности.
Потом от этой точки чертим две линии до пересечения с окружностью так, чтобы у нас получился прямой угол (90 градусов). Для построения данных линий проще всего воспользоваться угольником (если окружность очень большая, линии можно продлить с помощью линейки).
А теперь все очень просто, соединяем точки, в которых пересекаются линии с окружностью и измеряем длину получившегося отрезка. Его середина и будет центром окружности. Уверен, многие помнят это из уроков по геометрии. Середина гипотенузы прямого треугольника вписанного в окружность, является центром этой окружности.
Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».
Как найти центр окружности без циркуля монетой
Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».
Как найти центр окружности без циркуля
Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».
Как точно определить центр окружности
Как точно определить центр круга?
Как найти центр начерченной окружности?
Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр.
Как найти центр окружности без измерений?
Надо просто отложить внутри окружности две любых линии (хорды), не параллельных друг другу. Провести перпендикулярные линии через середины этих хорд к противоположной точке на окружности. И снова пересечение этих двух будет являться центром.
Как при помощи циркуля найти центр окружности?
При помощи циркуля начертите две пересекающиеся окружности.
Центром первой окружности сделайте точку А, а второй окружности – точку В. Чертите окружности так, чтобы они пересекались наподобие диаграммы Венна.
Как найти центр окружности из уравнения?
Уравнение окружности ω (A; R) имеет вид (x – a)2 + (y – b)2 = R2, где a и b – координаты центра A окружности ω (A; R) .
Как найти центр круга при помощи линейки?
Воспроизвести ее совсем нетрудно: необходимо лишь положить линейку на круг в любом месте так, чтобы она пересекала окружность в двух местах, и провести карандашом прямую линию. Отрезок внутри окружности и будет хордой.
Как вычислить длину окружности?
Формула Чтобы найти длину окружности, нужно либо диаметр окружности умножить на π ≈ 3 , 1415926535 … , либо найти удвоенное произведение радиуса и числа . Здесь — это радиус заданной окружности, а — диаметр, π ≈ 3 , 1415926535 … .
Как рассчитать диаметр круга по длине окружности?
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
Как разделить окружность на 6 равных частей?
Как разделить окружность на 6 частей с помощью циркуля
(окружность красного цвета). Не изменяя радиуса, переносим ножку циркуля на окружность (точка 1) и чертим еще одну окружность. Получаем две точки пересечения черной и красной окружностей 6 и 2.
Как определить радиус?
R = D : 2, где D — диаметр. Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Что такое центр круга?
Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности.
Как найти середину тарелки?
Для того, чтобы найти центр, необходимо повернуть наш треугольник таким образом, чтобы его углы касались края нашей тарелочки. Точка пересечения двух прямых будет являться центром окружности. Все эти работы надо делать очень аккуратно.
Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».
Как найти Как найти центр окружности?
Как найти центр отверстия?
Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.
Как найти центр окружности из уравнения?
Уравнение окружности ω (A; R) имеет вид (x – a) 2 + (y – b) 2 = R 2 , где a и b – координаты центра A окружности ω (A; R) .
Чем размечают отверстия?
Размечать центровые отверстия в деталях диаметром до 40 мм лучше при помощи специального приспособления, называемого колоколом. Оно состоит из корпуса, конического раструба и кернера, перемещаемого в корпусе.
Как найти центр окружности на плоской заготовки?
Есть и совсем простой способ нахождения центра плоской заготовки круглой формы. Всего-то нужно обвести её по периметру, положив на лист бумаги, затем вырезать по начерченной линии круг, согнуть его вчетверо и центр будет найден. Он находится точно на линии пересечения сгибов.
Как правильно разметить отверстия?
Разметка отверстий для сверления.
- Определить расположение отверстия по рабочему чертежу. Аккуратно отмерить расстояние отверстия от обоих краев доски. .
- Наколите центр отверстия шилом. .
- Если должны совпасть отверстия, просверленные в двух досках, зажмите обе доски в тисках.
Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
На данной ограниченной прямой построить равносторонний треугольник
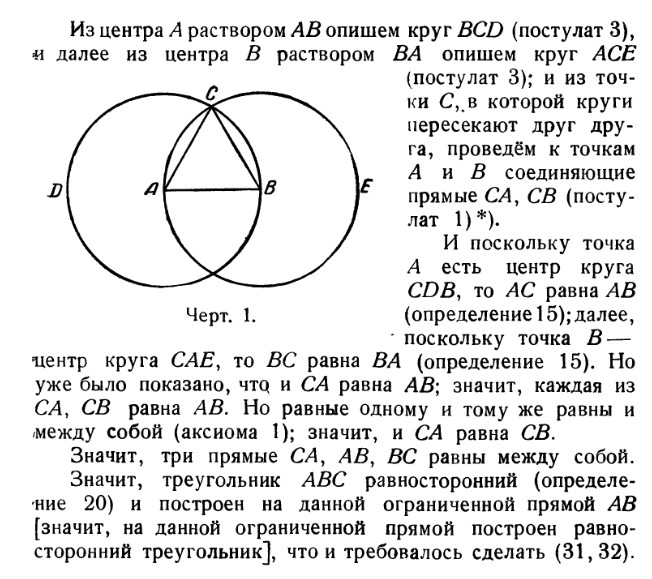
1.3 Середина отрезка
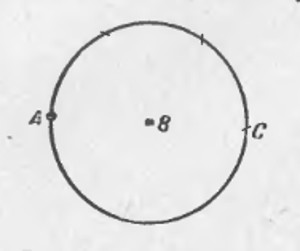
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
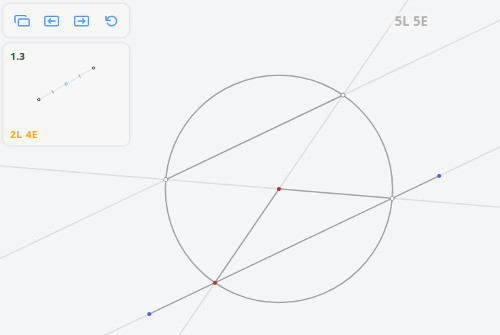
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
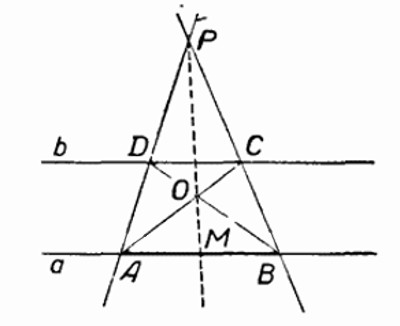
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
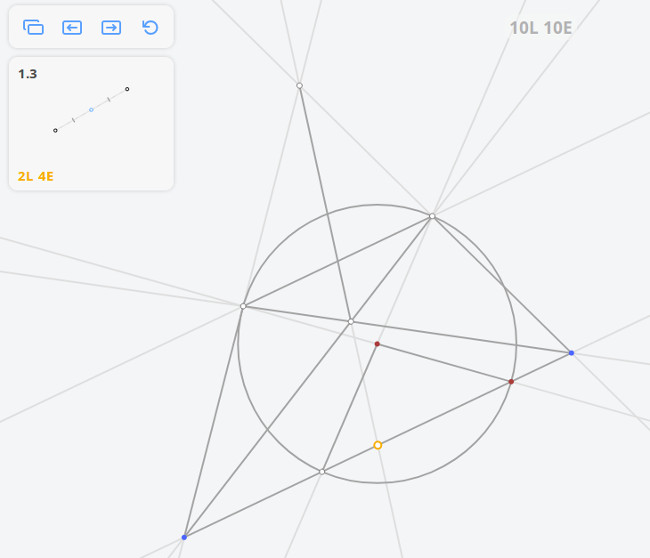
1.4 Окружность, вписанная в квадрат
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
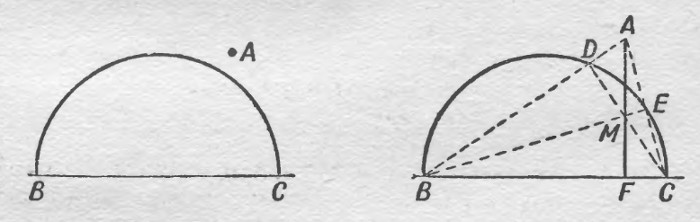
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
1.6 Найти центр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
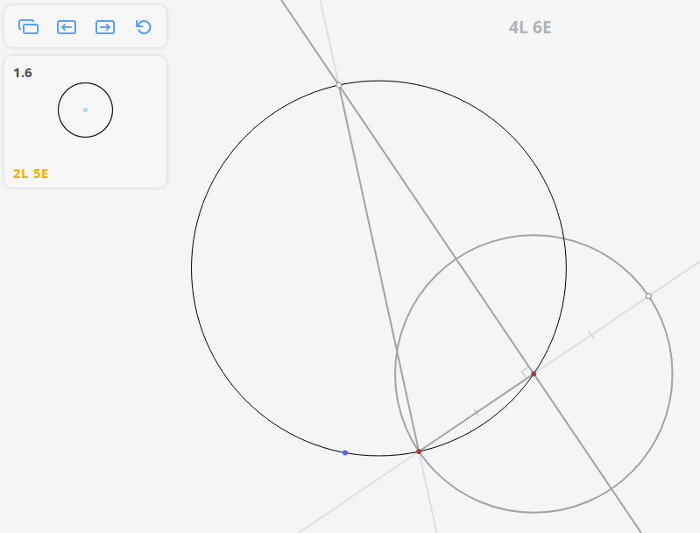
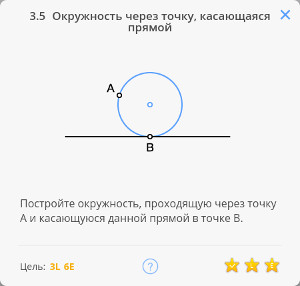
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
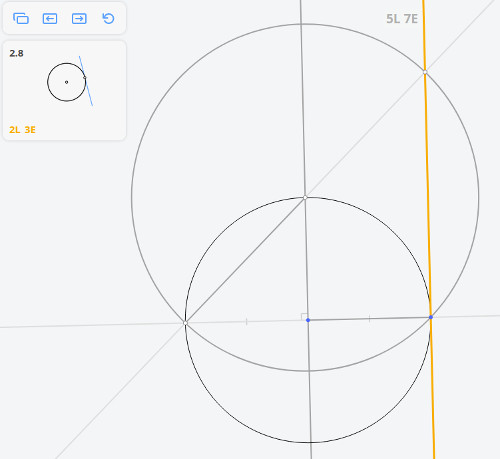
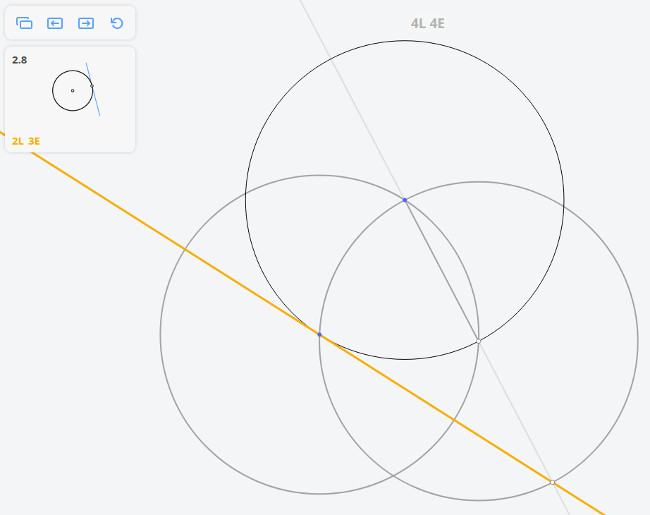
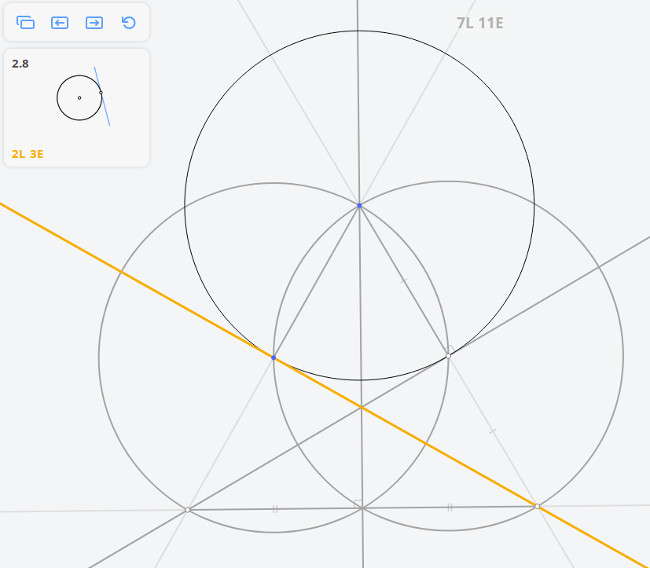
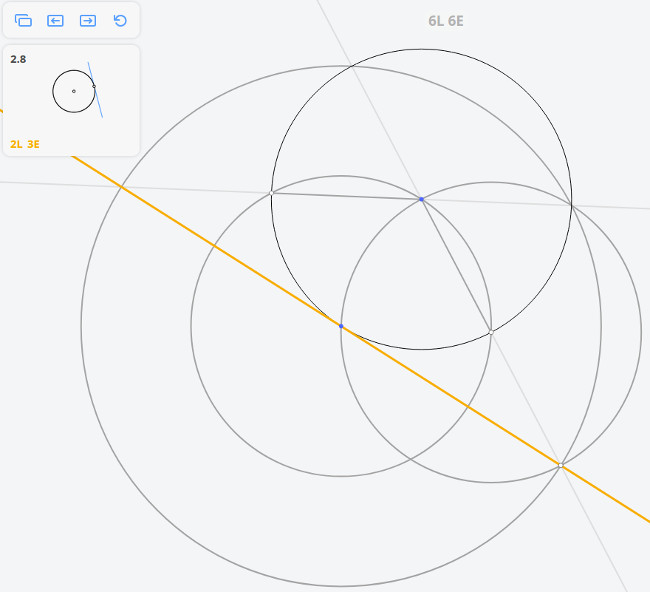
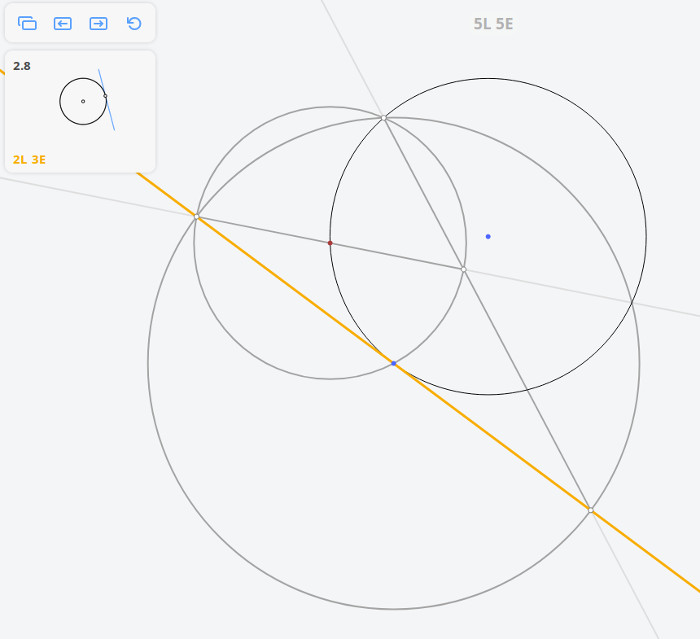
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
1.7 Квадрат, вписанный в окружность
Задача Наполеона

Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
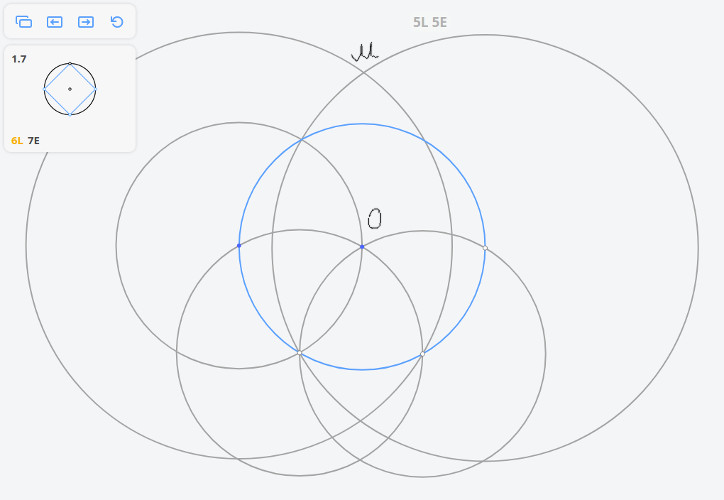
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом 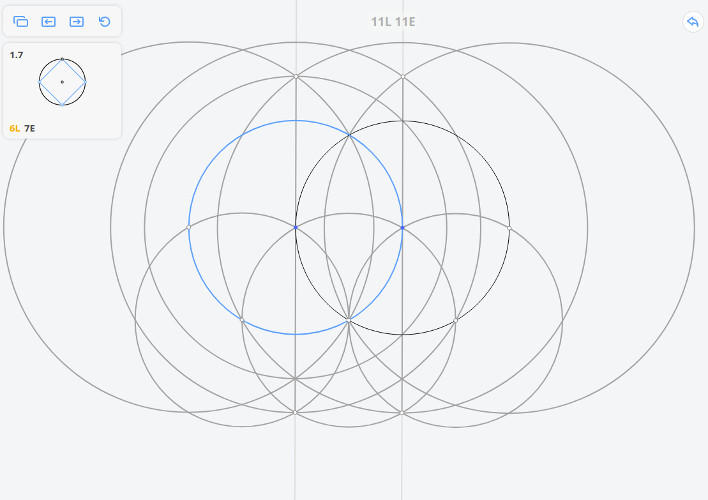
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО 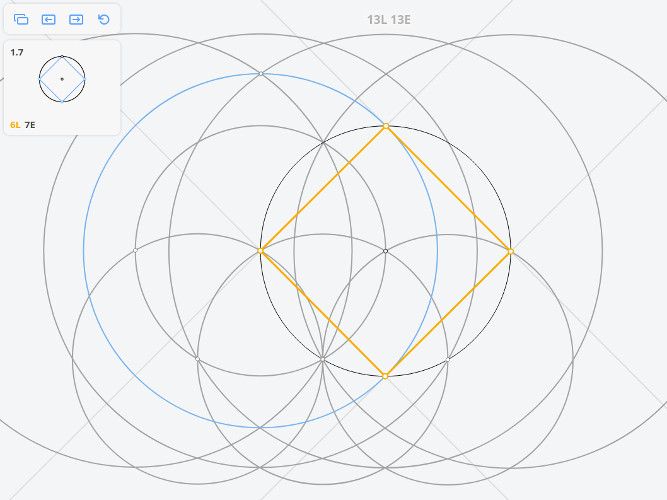
Как найти центр окружности без циркуля?
Как найти координаты центра окружности?
Уравнение окружности ω (A; R) имеет вид (x – a) 2 + (y – b) 2 = R 2 , где a и b – координаты центра A окружности ω (A; R) .
Как найти центр отверстия?
Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.
Как найти центр круглого стола?
- Нарисуйте два произвольных аккорда (линии поперек) в любом месте круга. .
- Найти точный центр каждой линии
- Используйте квадрат, чтобы спроецировать вторую линию к центру круга точно под углом 90 градусов к хорде.
- Где спроецированные линии перекрываются, это центр
Разметка окружностей, центров и отверстий. Деление окружности на равные части и построение многоугольников
При разметке все построения производятся с помощью двух линий — прямой и окружности (на рис. 3.42 с целью повторения представлены элементы окружности).
Рис. 3.42. Окружность и ее элементы
Нахождение центра окружности. На плоских деталях, где уже имеются готовые отверстия, центр которых неизвестен, его находят геометрическим способом. На торцах цилиндрических деталей нахождение центра производят при помощи циркуля, рейсмуса, угольника-цетроискателя и колокола.
Разметка центра по угольнику-центроискателю. Разметку выполняют в следующей последовательности.
- 1. Деталь устанавливают на разметочную плиту так, чтобы размечаемый торец был сверху.
- 2. На торец цилиндрической детали накладывают угольник-центроиска- тель так, чтобы две его стороны (планки) касались цилиндрической поверхности детали, рис. 3.43.
Рис. 3.43. Нахождение центра окружности с помощью угольника-центроискателя
- 3. Левой рукой плотно прижимают линейку угольника к поверхности торца, а правой проводят чертилкой первую диаметральную риску.
- 4. Угольник-центроискатель поворачивают по цилиндрической поверхности детали примерно на 90° и проводят вторую риску. Точка пересечения двух рисок будет центром размечаемой окружности.
Разметку центра детали с грубо обработанной цилиндрической поверхностью производят в такой же последовательности. В этом случае для более точного нахождения центра окружности необходимо нанести пять-семь рисок. Центром будет точка, в которой пересекается наибольшее число рисок.
Точность разметки центра окружности проверяют разметочным циркулем, рис. 3.44. Острие одной ножки циркуля устанавливают в размеченный центр, а другую ножку перемещают так, чтобы ее острие слегка касалось цилиндрической части детали. Если острие ножки циркуля касается по всей длине окружности, то центр размечен правильно.
Рис. 3.44. Способ проверки точности разметки центра окружности разметочным циркулем
Разметка центра рейсмусом (рис. 3.45). Деталь кладут на призмы или параллельные подкладки, уложенные на разметочную плиту. Устанавливают острый конец иглы рейсмуса несколько выше или ниже центра размечаемой
Рис. 3.45. Разметка центра рейсмусом
детали и, придерживая деталь левой рукой, правой рукой движением рейсмуса по плите прочерчивают его иглой на торце детали короткую рису. После этого поворачивают деталь на 1/4 окружности и таким же способом проводят вторую риску. То же повторяют через каждую четверть оборота для проведения третьей и четвертой рисок. Внутри рисок (на пересечении диагоналей) и будет находиться центр. Его набивают кернером.
Геометрический способ нахождения центра заключается в следующем. Пусть дана плоская металлическая плита с готовым отверстием, центр которого неизвестен. Перед тем как начать разметку, вставляют в отверстие широкий деревянный брусок и на него набивают пластинку из белой жести или из оцинкованного кровельного железа.
Затем на краю отверстия слегка намечают произвольно три точки Л, В и С и из каждой пары этих точек ЛВ и ВС описывают по обе стороны их пересекающиеся между собой дуги-засечки 1—2 и 3—4, рис. 3.46. Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.
Рис. 3.46. Нахождение центра геометрическим способом
Разметка центра циркулем (кронциркулем). Зажав деталь в тиски, растворяют ножки циркуля на величину, немного большую или немного меньшую радиуса размечаемой детали. После этого, приложив к боковой поверхности детали одну ножку циркуля и придерживая ее большим пальцем, другой ножкой циркуля очерчивают дугу. Далее переместив циркуль на 1/4 окружности (на глаз), таким же образом очерчиваю вторую дугу. Затем через каждую четверть окружности очерчивают третью и четвертую дуги. Затем соединить противоположные засечки диагоналями, рис. 3.47я. Центр окружности будет находиться внутри очерченных дуг на пересечении диагоналей.
Рис. 3.47. Разметка центра циркулем (кронциркулем)
Можно разметить центр и способом, показанным на рис. 3.476. Методика разметки аналогична разметке рейсмусом.
Разметка центра колоколом. Приспособление колокол устанавливается на торец цилиндрической детали. Придерживая колокол левой рукой в вертикальном положении, правой рукой наносят удар молотком по кернеру, находящемуся в колоколе, рис. 3.48. Кернер сделает углубление в центре торца.
Рис. 3.48. Разметка центра колоколом
Деление окружности на равные части. При разметке окружностей часто приходится их делить на несколько равных частей — 3, 4, 5, 6, и больше. Ниже приведены примеры деления окружности на равные части геометрическим способом и с помощью таблиц.
Деление окружности на три равные части с построением вписанного треугольника (рис. 3.49).
Рис. 3.49. Деление окружности на три части с построением вписанного треугольника
- 1. В центре размечаемой плоскости с помощью циркуля проводим окружность требуемого радиуса, например R = 26 мм.
- 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
- 3. Опорную ножку циркуля устанавливаем в точку А и при растворе циркуля, равном радиусу проведенной окружности, делаем на окружности две метки-засечки (точки С и D), где длина дуги между ними будет равна одной трети длины окружности.
- 4. Соединив точки прямыми рисками СД СВ и BD, получим вписанный равносторонний треугольник.
- 5. Правильность построения проверяем циркулем, устанавливая раствор циркуля равным одной из сторон треугольника и этим же размером определяя равенство остальных сторон треугольника.
Деление окружности на четыре равные части с построением вписанного квадрата, рис. 3.50.
Рис. 3.50. Деление окружности на четыре части с построением вписанного квадрата (а) и прием разметки квадрата (6)
- 1. В центре размечаемой плоскости циркулем проводим окружность требуемого радиуса, например R= 28 мм.
- 2. Через центр окружности по линейке проводим прямую риску что бы она пересекала окружности в двух точках А и В и разделяла ее на две равные части.
- 3. Опорную ножку циркуля устанавливаем в точку А и, раздвинув циркуль на расстояние несколько большее, чем половина отрезка АВ, проводим дугу в.
- 4. Опорную ножку циркуля переносим в точку В и, не изменяя раствора циркуля, проводим дугу б так, чтобы она пересекла первую выполненную дугу в точках 7 и 2.
- 5. Через точки 7 и 2 проводим риску, которая образует на окружности точки С и D.
- 6. Соединив точки AD, DB, ВС и СА прямыми рисками, получим квадрат, вписанный в окружность.
Деление окружности на пять равных частей (рис. 3.51). На данной окружности проводим два взаимно перпендикулярных диаметра, пересекающие окружность в точках А и В, С и D. Радиус ОА делим пополам и из полученной точки Е описываем дугу радиусом ЕС до пересечения в точке F на радиусе О В. После этого соединяем прямой точки D и F. Откладывая длину прямой DF по окружности, разделим ее на пять равных частей.
Деление окружности на шесть равных частей с построением вписанного шестиугольника, рис. 3.52.
Рис. 3.51. Деление окружности на пять равных частей
Рис. 3.52. Деление окружности на шесть частей с построением вписанного шестиугольника
- 1. В центре разметочной плоскости циркулем проводим окружность требуемого радиуса, например 7? = 27 мм.
- 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
- 3. Из точки А, как из центра, наносим дугу радиусом, равным радиусу проведенной окружности, и получаем точки 7 и 2
Аналогичное построение делаем из точки В, нанося точки 3 и 4. Полученные точки пересечения и концевые точки диаметра будут искомыми точками деления окружности на шесть частей.
4. Соединив точки прямыми рисками А — 1,2 — 4, 4 — В, В — 3, 3 — 1 и 1 — А, получим вписанный шестиугольник.
При разметке граней шестиугольника под размер h зева гаечного ключа (рис. 3.53) радиус описываемой окружности определяется по формуле R = 0,577/г.
Рис. 3.53. Пример разметки шестиугольника под размер зева гаечного ключа
Деление окружности на равные части с помощью таблицы. Эта таблица (табл. 3.5) имеет две графы: «Число делений окружности» и «Число, умножаемое на радиус окружности». Числа первой графы показывают, на сколько равных частей следует делить данную окружность. Во второй графе даны числа, на которые умножают радиус данной окружности. В результате умножения числа, взятого из второй графы, на радиус размечаемой окружности получаем величину хорды, т. е. расстояние по прямой между делениями окружности.
Таблица 3.5. Деление окружности на равные части
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/kak-nayti-tsentr-okruzhnosti-bez-tsirkulya-monetoy
http://studref.com/560649/tehnika/razmetka_okruzhnostey_tsentrov_otverstiy_delenie_okruzhnosti_ravnye_chasti_postroenie_mnogougolnikov
[/spoiler]
Как найти центр окружности – два простых способа, которые я использую в мастерской
01.03.2021
Покажу два простых способа, который могут вам пригодиться.
Если у вас под рукой есть угольник и линейка (или обычная рейка), можно использовать такой вариант.
В качестве примера найдем центр вот этой пластиковой заглушки диаметром 110 мм.
Совмещаем угольник и линейку так, чтобы линейка делила прямой угол пополам.
И чертим линию примерно по центру.
Затем чуть разворачиваем заглушку и чертим еще одну линию.
Центр окружности в месте пересечения. Весь процесс занял несколько секунд.
Усложним ситуацию и заодно вспомним школьную программу по геометрии. Допустим, у нас нет под рукой линейки. Воспользуемся одним угольником.
Отмечаем прямой угол.
А теперь осталось прочертить гипотенузу.
Находим середину гипотенузы.
Все, мы нашли центр. Тоже довольно простой способ.
Есть и другие способы, но это одни из самых простых и доступных. Всегда любил геометрию в школе, если нужно было выбирать экзамен на выбор (было и такое в девяностых), то я сдавал геометрию. Еще астрономия очень нравилась, помню несколько лет назад ее убирали из школьной программы (и совершенно зря – что станет с человечеством, если оно перестанет мечтать о звездах?!), а потом опять возвращали. Но это уже совсем другая история.
Если понравилась статья, ставьте лайк и подписывайтесь – чтобы не пропустить новые публикации.
Напишите, о какой теме стоит рассказать в ближайших выпусках на канале?
Вам может понравиться
Если необходимо просверлить отверстие в деревянной или металлической заготовке (круглой, квадратной или прямоугольной формы) строго по центру, то удобнее всего делать разметку не штангенциркулем, а специальным инструментом — центроискателем. Также можно найти центр окружности, используя обычные инструменты, которые всегда есть под рукой.
Быстрый способ, как найти центр окружности
В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Видео
Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала «ПОГРАНЕЦ 13».
 КАК БЫСТРО НАЙТИ ЦЕНТР КРУГА
КАК БЫСТРО НАЙТИ ЦЕНТР КРУГАКак сделать универсальный центроискатель
Для токарных станков сегодня продаются уже готовые заводские индикаторные и оптические центроискатели.
Но если станка под рукой нет, а центр найти надо, то можно воспользоваться самодельным центроискателем. Для его изготовления потребуется всего две детали: обычный металлический угольник и линейка.
Делаем центроискатель за 15 секунд
Изготовить самодельный инструмент для нахождения центра заготовки очень просто. Нужно всего лишь приложить линейку к угольнику под углом 45 градусов и зафиксировать ее, чтобы она была неподвижна.
Для фиксации можно использовать маленькую струбцинку или зажим. Также можно просверлить отверстия и закрепить линейку при помощи заклепок или болтов.

Вот так просто (и самое главное — быстро) в домашних условиях можно изготовить удобный и практичный в использовании центроискатель.
Принцип работы инструмент тоже очень прост. Прикладываем приспособление к заготовке, и линейка будет проходить как раз через центр.

Достаточно прочертить сначала первую линию, затем провернуть инструмент на 90 градусов и прочертить вторую. Потом можно будет сверлить отверстие.
Если заготовка «кривая», то линий желательно прочертить больше, чтобы максимально точно определить расположение центра. Пишите в комментариях под видео, что вы думаете по поводу данного метода.
Видео
 Как сделать центроискатель за 10 секунд.
Как сделать центроискатель за 10 секунд.Центровочный инструмент для круглых заготовок
Центровка круглых заготовок из металла доставляет массу неудобств, особенно для неподготовленного человека, далекого от слесарного дела.
Есть специальные инструменты для центровки, но их нужно еще купить. А почему бы не изготовить такой инструмент самостоятельно? В данном обзоре мы расскажем, как это сделать.
Для изготовления центровочного инструмента будут необходимы следующие материалы: небольшой кусок листового металла толщиной 2-3 мм, подшипники, три болта с гайками-барашками.
Рекомендуем также прочитать статью-обзор: как изготовить инструмент для быстрого снятия изоляции со старых проводов.
Если дома, на даче или в гараже часто приходится чистить провода от изоляции, то такая самоделка сэкономит вам время.
Основные этапы работ
Для начала определимся с будущим размером инструмента и вырежем квадратную заготовку из листа металла. Теперь размечаем центр диагональными линиями и кернером намечаем его.
Далее при помощи циркуля чертим по кругу контур и ещё два на небольшом расстоянии друг от друга. Размечаем три вершины треугольника. Обрисовываем контуры для вырезания заготовки инструмента.

По центрам вырезанных лучей на пересечении линий окружностей сверлим отверстия.
Соединяем центральное отверстие с тем, что ближе к центру, и вырезаем канавки. По ним будут двигаться ролики для регулировки.


Теперь шлифуем надфилем все края и снимаем фаски. Ролики можно сделать из подшипников, которые будут крепиться болтом и гайкой в канавках нашей заготовки.

По центру инструмента сверлим отверстие. При желании можно покрасить инструмент в понравившийся цвет. Циркулем намечаем шкалу размеров на верхней части инструмента, и закрепляем ролики.

Видео
Подробное изготовление самоделки можно увидеть на видео ниже. Этот обзор создан на основе видеоролика с YouTube канала Mistry MakeTool.
 How To Make Center Finder Tool || New Design Invention
How To Make Center Finder Tool || New Design InventionКак сделать универсальный центроискатель своими руками
Центроискатель в домашней мастерской — штука полезная и нужная. При помощи этого инструмента можно быстро найти центр заготовки и провести разметочную линию.

Причем центроискатель можно сделать своими руками.
В этом обзоре автор делится своей идеей. Конструкция универсальная — позволяет найти центр на заготовках из дерева и металла (это бруски, пластины, профильные трубы) разного размера.
Для изготовления центроискателя потребуется стальной квадрат, три болта и восемь маленьких подшипников (их можно извлечь из фиджет-спиннеров).

Основные этапы работ
В первую очередь автор делает разметку, после чего сверлит в квадрате семь отверстий на одинаковом расстоянии друг от друга. Еще одно сквозное отверстие надо будет просверлить на перпендикулярной стороне заготовки.

В просверленных отверстиях (во всех, кроме центрального) надо нарезать резьбу. Затем автор затачивает два болта под конус. Далее их нужно будет закалить.

Сборка центроискателя
На последнем этапе останется только собрать приспособление. Надеваем на болты по четыре подшипника и вставляем их в просверленные в квадратной заготовке отверстия.

В центральное отверстие вставляет чертилка по металлу или карандаш, и фиксируется третьим болтом.
Видео
Подробно о том, как сделать универсальный центроискатель для домашней мастерской своими руками, смотрите в видеоролике на нашем сайте.
 DIY AMAZING TOOL / Como Hacer la Mejor Herramienta Compas y Buscador de Centro METAL/MADERA
DIY AMAZING TOOL / Como Hacer la Mejor Herramienta Compas y Buscador de Centro METAL/MADERAУниверсальный центроискатель из квадратного прутка с возможностью регулировки
В интернете можно встретить разные варианты самодельных центроискателей, однако в данном случае автор предлагает изготовить своими руками не только простой, но еще и универсальный центроискатель.

При помощи этого приспособления можно быстро найти центр как на деревянных заготовках, так и на деталях из металла. Причем самодельный центроискатель имеет регулировку по ширине, что очень удобно.
Сначала необходимо отрезать болгаркой кусок квадратного прутка 10х10 мм длиной примерно 20-25 см.
Далее нужно будет разметить и просверлить семь отверстий с шагом 2,5-3 см. Во всех отверстиях, кроме центрального, надо нарезать резьбу.

Процесс изготовления универсального центроискателя
Перпендикулярно центральному отверстию (на другой стороне квадратного прутка) необходимо просверлить еще одно отверстие и нарезать в нем резьбу под фиксирующий болт.

В качестве 2-х боковых упоров мастер использует два длинных болта, предварительно срезав у них шляпки и часть резьбы. Собственно, на этом самоделка готова, и можно испытать ее в деле.

Чтобы найти центр на металлических заготовках, можно использовать чертилку по металлу или кернер. Да и автомобильный клапан тоже подойдет.
При работе с деревянными заготовками в центральном отверстии фиксируется обычный карандаш.

Видео
Подробнее о том, как сделать удобный и простой в использовании универсальный центроискатель с возможностью регулировки по ширине, смотрите в видеоролике на нашем сайте.
 Make A Center Finder Tool || DIY Centerline Tool
Make A Center Finder Tool || DIY Centerline ToolМебельный кернер-центроискатель для разметки отверстий под шканты
В данном обзоре расскажем, как своими руками изготовить комплект из двух мебельных центроискателей.
При помощи этих приспособлений (их еще называют наколками) удобно делать разметку для сверления отверстий под деревянные шканты.
Для изготовления самодельных мебельных центроискателей потребуются болты с гайками и круглый пруток (желательно, чтобы он был хорошего качества).
Этой полезной идеей с нами поделился автор YouTube канала DIYFixMan.
Кстати, своими руками можно изготовить также барашковые болты с гайками.
В магазинах не всегда можно найти требуемый размер. А так вы можете без проблем сделать себе болты и гайки-барашки любого диаметра.
Основные этапы работ
На болт накручиваем гайку.
Зажимаем болт с гайкой в тисках, и болгаркой срезаем часть шляпки. Обрабатываем место среза абразивным бруском.



После этого зажимаем болт с гайкой снова в слесарных тисках, и отрезаем шпильку болта заподлицо с гайкой.

Находим центр в шляпке болта, и с помощью дрели (а лучше — на сверлильном станке) сверлим глухое отверстие.

Далее нам потребуется стальной круглый пруток. Затачиваем один из его концов. Обрезаем до нужной длины.

В просверленное отверстие капаем каплю суперклея, и потом вставляем отрезок прутка с заостренным кончиком.


Как пользоваться «наколками»
В одной из заготовок сверлим два отверстия. Устанавливаем в них самодельные кернеры-центроискатели.

Прикладываем эту заготовку ко второй детали, и ударяем по ней молотком. Кернеры оставят углубления, в которых затем сверлим отверстия.

Когда все готово, останется только установить подготовленные деревянные шканты, и соединить вместе обе заготовки.

Видео
Подробно о том, как изготовить кернер-центроискатель для разметки отверстий под шканты, можно посмотреть ниже — в авторском видеоролике.
 How to make Dowel Centers and also how to use them
How to make Dowel Centers and also how to use themЦентроискатель для круглых и цилиндрических деталей
Чтобы быстро и точно разметить круглые или цилиндрические заготовки, советуем использовать специальное приспособление — центроискатель. Рассказываем, как изготовить его своими руками.
Данное приспособление не является предметом первой необходимости в домашней мастерской. Однако с ним работа по разметке заготовок занимает меньше времени.
Своим личным опытом изготовления самодельного центроискателя поделился с нами автор YouTube канала AX Creates.
Для изготовления самоделки понадобятся отрезки металлической полосы. Соединяться заготовки будут с помощью болтов с гайками.
Основные этапы работ
Первым делом отрезаем от металлической полосы заготовки требуемой длины. Высверливаем в них отверстия по краям и закругляем острые углы. Всего же потребуется изготовить четыре таких детали.


После этого необходимо будет изготовить направляющую.
Отрезаем четыре кусочка металлической полосы и свариваем их вместе, как показано ниже. С одной из сторон высверливаем отверстия, углы закругляем.


На следующем этапе останется только собрать все детали воедино. Для соединения деталей мы будем использовать болты с гайками.
Также потребуется одна барашковая гайка для быстрой фиксации подвижной части приспособления.


Как работать с инструментом
Самодельный центроискатель можно использовать для разметки круглых труб или круглых заготовок из дерева.
Варианты использования приспособления показаны на фото ниже.



Видео
Пошаговый процесс изготовления и сборки центроискателя для разметки деталей показан в авторском видеоролике ниже. Спасибо за внимание.
 DO NOT THINK TO BUY, BUILD IT YOURSELF!!! NEW DIY TOOL IDEA!!
DO NOT THINK TO BUY, BUILD IT YOURSELF!!! NEW DIY TOOL IDEA!!Как сделать центроискатель для разметки заготовок из фанеры
В данном обзоре мы поделимся с вами интересной идеей для домашней мастерской, а именно — расскажем, как своими руками изготовить удобный центроискатель. Это простое приспособление существенно облегчает разметку заготовок.
Для изготовления самоделки будем использовать обрезки фанеры и круглую деревянную палочку.
В качестве «чертилки» можно использовать обычную ручку, карандаш или маркер. В общем, любой предмет, который может рисовать.
Основные этапы работ
Первым делом отпиливаем кусок фанеры и делаем разметку — находим центр. После этого обрезаем все лишнее, придав заготовке форму ромба.

После этого высверливаем сквозное отверстие по центру заготовки. Затем с одной из сторон необходимо высверлить посадочное место под круглую деревянную палочку.

Обратите внимание: диаметр палочки должен быть больше диаметра ручки, карандаша или маркера (что вы будете использовать для разметки).
На следующем этапе отпиливаем круглую палочку подходящей длины и вклеиваем ее в посадочное место.

Далее в круглой палочке нужно будет просверлить отверстие для установки ручки (в данном случае будем использовать именно ручку).

По краям деревянной заготовки сверлим отверстия под шурупы. Затем к нижней части прикручиваем две пластиковых втулки, как показано на фото ниже. Самодельное приспособление готово.

Видео
Пошаговый процесс изготовления центроискателя для разметки заготовок можно посмотреть в авторском видеоролике. Идеей поделился автор YouTube канала Carpintero Del Desierto.
 MARCADOR de CENTROS Casero Herramienta de Carpinteria
MARCADOR de CENTROS Casero Herramienta de CarpinteriaСамодельный центроискатель для электрической дрели
Если нужно просверлить отверстие в деревянной планке или бруске точно по центру, то можно использовать центроискатель для электродрели. Его несложно изготовить своими руками.

Приспособление можно сделать из фанеры или дерева, и на это потребуется минимум времени.
Первым делом необходимо подготовить два металлических стержня и четыре пружинки.

Далее отпиливаем два деревянных бруска нужного размера и сверлим в них сквозные продольные отверстия.

С одной из сторон диаметр отверстия должен быть больше, чтобы можно было установить пружинки.

Основные этапы работ
На металлических стержнях с помощью ножовки по металлу нужно сделать пропилы.
Из проволоки делаем колечки и надеваем их на стержни — они будут служить упорами для пружинок.

Из куска доски автор вырезает крепление для дрели. Затем к нему нужно приклеить два бруска с отверстиями. В них надо вставить стержни с пружинками.

На последнем этапе надеваем насадку-центроискатель на дрель, и можно сверлить отверстия в заготовках. Полезная получилась самоделка.
Видео
Подробно о том, как своими руками сделать центроискатель для электродрели, вы можете посмотреть в видеоролике на нашем сайте.
 TRUCO PARA TU TALADRO FÁCIL — CENTRAR PERFORACIÓN SIN MARCAR
TRUCO PARA TU TALADRO FÁCIL — CENTRAR PERFORACIÓN SIN MARCAR
Задать вопрос
![]()
![]()
Очень просто – измеряем диаметр круга, строим вокруг нашей окружности равносторонний квадрат, со сторонами равными диаметру круга. Стороны квадрата пройдут по касательной к окружности. Далее делим этот квадрат по диагонали на четыре треугольника. В точке пересечения линий будет цент круга.

автор вопроса выбрал этот ответ лучшим
![]()
Galina7v7
[120K]
6 лет назад
Когда говорят о нахождении центра круга или окружности, то многие считают, что это просто, мол, проведи два диаметра.и всё.А как провести диаметр, если центра не видно.Но с помощью циркуля и простой линейки это сделать возможно.
Отмечаем на окружности(обрамляющей круг) четыре произвольных точки A,B,C,D,примерно располагающих на одном расстоянии друг от друга(это даже не важно).Из точек А и В произвольным радиусом провести засечки циркулем. Две точки А1 и В1-точки пересечения засечек, соединяем, и она точно лежит на диаметре круга.
Аналогично для точек С и Д получим точки С1 и Д1, соединяем их, и прямая С1Д1 тоже лежит на другом диаметре круга.Пересечение любых двух диаметров окружности даёт её центр, точку О.
И это один из верных способов построения центра круга и окружности.
![]()
Bokatashka
[22.4K]
8 лет назад
Чтобы найти середину круга нужно провести две хорды. У каждой из них найти середины и провести к ним перпендикулярные лучи. Точка пересечения этих лучей и будет центром круга.

Также центр круга можно найти при помощи циркуля. Для этого нужно провести горизонтальную линию от одной точки окружности до другой (отмечаем точки А и В):

При помощи циркуля начертить два одинаковых перекрывающихся круга с центрами в точках А и В.

Далее проводим вертикальную линию через точку, в которой круги пересекаются. Отмечаем на окружности точки C и D:

Для удобства стираем два вспомогательных круга и получаем такой рисунок:

Чертим ещё два одинаковых перекрывающихся круга с центрами в точках С и D:

Проводим горизонтальную линию через точки пересечения этих двух кругов. Отмечаем на окружности точки Е и F:

Стираем вспомогательные круги. Точка пересечения прямых СD и EF (назовём её точкой О) и будет искомой серединой круга.

Чтобы найти центр круга, достаточно провести диаметр и построить к нему перпендикуляр с помощью циркуля и линейки.
сначала проводим через круг линию (можно произвольно, но лично я для удобства провожу горизонтальную) и с помощью циркуля и линейки проводим перпендикулярную линию, которая делит нашу хорду и весь круг ровно пополам. Аналогично проводим перпендикуляр к уже полученному диаметру и находим центр круга. Ко всему прочему – мы еще разделили окружность на четыре ровные части.

Но бывает, что диаметр провести нельзя, так как есть только часть круга, тогда можно применить способ. который подходит практически везде:
в произвольном месте провести две хорды и через их центры провести перпендикуляры – в точке пересечения и будет центр

![]()
Грустный Роджер
[396K]
8 лет назад
Всех делов тут – вспомнить школьную геометрию. Два радиуса и хорда дают равнобедренный треугольник, в котором высота, опущенная на основание, делит его пополам.
Поэтому на окружности надо отметить три произвольные точки, и одну из них соединить с двумя другими. Это даст две хорды. Теперь делим эти хорды пополам и к каждой проводим перпендикуляр к середине – это стандартная школьная задачка на построение циркулем и линейкой. Точка пересечения перпендикуляров и будет центром круга.
![]()
Мне представляется достаточно простой способ нахождения центра окружности путем вписывания в нее прямоугольника. То есть проводим произвольную хорду и принимаем этот отрезок за одну сторону прямоугольника. Достраиваем сперва перпендикулярные стороны из точек пересечения хорды с окружностью, потом достраиваем противоположную параллельную сторону. Вся проблема – в проведении перпендикуляров, но и во всех остальных методах применяется тот же принцип построения. После получения такого прямоугольника проводим в нем диагонали и вуаля, точка их пересечения и будет центром окружности, ну а сами диагонали окажутся диаметрами.

![]()
Ксарфакс
[156K]
6 лет назад
Чтобы найти центр круга, можно отметить 2 любые точки на окружности и провести отрезок.
Затем нужно провести ещё один отрезок, имеющий такую же длину и параллельный первому отрезку.
Соединяем противоположные концы отрезков линиями, которые будут параллельными друг другу.
Таким образом, получится прямоугольник, который будет вписан в круг.
Центр пересечения его диагоналей и будет центром нашего круга.

![]()
Azamatik
[55.3K]
6 лет назад
Для этого берем треугольник (линейку) и проводим диаметр круга. Далее можно с помощью угольника провести такой же диаметр, перпендикулярный первой линии. Пересечение двух этих линий и будет центром (серединой) круга.
![]()
Ярослава Лещинская
[29.9K]
8 лет назад
Найти середину круга очень просто. Надо нарисовать круг и провести диаметр слева направо и сверху вниз, точка соединения линий и будет середина круга. Если круг уже вырезан, сложить его пополам и еще раз пополам, в точке соединений сгибов и будет середина круга.
Водяной
[7.5K]
8 лет назад
Проводим две не параллельные любые хорды. Каждую хорду делим пополам, известным всем способом, как делят отрезки при помощи циркуля и линейки. В точке пересечения разделивших хорды лучей получим центр окружности.
