Содержание:
- Определение суммы чисел
- Свойства суммы чисел
Определение суммы чисел
Суммой $s$ (лат. summa – итог, общее количество) чисел $a_{1}, a_{2}, dots, a_{n}$ называется результат
суммирования этих чисел: $s=a_{1}+a_{2}+ldots+a_{n}$ . В частности, если складывается два числа $a$ и $b$, то
Пример
Задание. Найти сумму чисел:
1) $12$ и $15$ 2) $1,1 ; 2,2 ; 3,3$ и $4,4$
Ответ.
$12+15=27$
$1,1+2,2+3,3+4,4=11$
Свойства суммы чисел
- Коммутативность: $n+m=m+n$
-
Ассоциативность: $(n+m)+k=n+(m+k)$
На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.
-
Дистрибутивность по отношению к умножению
$$(n+m) cdot k=n cdot k+m cdot k$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму чисел удобным способом:
1) $15+17+13$ ; 2) $34+22+16+18$
Решение. По свойствам сложения имеем
$$15+17+13 =15+(17+13)=15+30=45 $$
$$34+22+16+18 =(34+16)+(22+18)=50+40=90 $$
Ответ. 1) $15+17+13=45$
2) $34+22+16+18=90$
При сложении больших чисел или
десятичных дробей используется сложение в столбик.
Пример
Задание. Найти сумму чисел удобным способом:
1) $1562+13827$ ; 2) $34,71+356,161$
Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом.
В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем
числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном
столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:
Ответ. 1) $1562+13827=15389$
2) $34,71+356,161=390,871$
Сложение рациональных дробей производится по правилу
$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$
Пример
Задание. Найти сумму чисел:
1) $frac{1}{4}+frac{1}{6}$ ; 2) $frac{2}{3}+1 frac{1}{2}$
Решение. Вычислим первую сумму используя правило сложения рациональных чисел
$$frac{1}{4}+frac{1}{6}=frac{1 cdot 6+1 cdot 4}{4 cdot 6}=frac{6+4}{24}=frac{10}{24}$$
Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим
$$frac{1}{4}+frac{1}{6}=frac{5}{12}$$
Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого
умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим
правило сложение рациональных дробей
$$frac{2}{3}+1 frac{1}{2}=frac{2}{3}+frac{3}{2}=frac{2 cdot 2+3 cdot 3}{3 cdot 2}=frac{4+9}{6}=frac{13}{6}$$
Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком.
Полученное частное запишем в целую часть, а остаток от деления в числитель.
$$frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$$
Ответ. 1) $frac{1}{4}+frac{1}{6}=frac{5}{12}$ ;
2) $frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$
Читать дальше: что такое произведение чисел.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 декабря 2021 года; проверки требуют 9 правок.
У этого термина существуют и другие значения, см. сумма.
Су́мма (лат. summa — итог, общее количество) в математике — результат применения операции сложения величин (чисел, функций, векторов, матриц и т. д.), либо результат последовательного выполнения нескольких операций сложения (суммирования). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:
В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы объединяемых множеств, взятые без повторений.
Также сложение (нахождение суммы) может быть определено для более сложных алгебраических структур (сумма групп, сумма линейных пространств, сумма идеалов, и другие примеры). В теории категорий определяется понятие суммы объектов.
Сумма натуральных чисел[править | править код]
Пусть в множестве 









Алгебраическая сумма[править | править код]
Сумму математически обозначают заглавной греческой буквой Σ (сигма).
где: i — индекс суммирования; ai — переменная, обозначающая каждый член в серии; m — нижняя граница суммирования, n — верхняя граница суммирования. Обозначение «i = m» под символом суммирования означает, что начальное (стартовое) значение индекса i эквивалентно m. Из этой записи следует, что индекс i инкрементируется на 1 в каждом члене выражения и остановится, когда i = n.[1]
В программировании данной процедуре соответствует цикл for.
- Примеры записи
Границы могут опускаться из записи, если они ясны из контекста:
Итератор может быть выражением — тогда переменная оформляется со скобками как функция «


Сумма 


Сумма 


Под знаком итеративного суммирования может использоваться несколько индексов, например:
причём набор из нескольких индексов можно сократить в виде так называемого мультииндекса.
Бесконечная сумма[править | править код]
В математическом анализе определяется понятие ряда — суммы бесконечного числа слагаемых.
Примеры последовательных сумм[править | править код]
1. Сумма арифметической прогрессии:
2. Сумма геометрической прогрессии:
3.
4. 
Доказательство
5. 
6. 
-
-
- Например, при
получается
, а это последовательность равенств следующего вида:
- Например, при
-
Неопределённая сумма[править | править код]
Неопределённой суммой 



что 
«Дискретная» формула Ньютона — Лейбница[править | править код]
Если найдена «производная» 

Этимология[править | править код]
Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, а также появляется глагол «суммировать» (1489 год).
Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.
Специальный символ для обозначения суммы (Σ) первым ввёл Леонард Эйлер в 1755 году, его поддержал Лагранж, однако долгое время с этим символом конкурировал знак S. Окончательно обозначение Σ для суммы утвердили уже в XVIII веке Фурье и Якоби[2].
Кодировка[править | править код]
В Юникоде есть символ суммы U+2211 ∑ n-ary summation (HTML ∑ • ∑).
См. также[править | править код]
- Сложение
- Произведение
Примечания[править | править код]
- ↑ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren. Chapter 2: Sums // Concrete Mathematics: A Foundation for Computer Science (2nd Edition) (англ.). — Addison-Wesley Professional, 1994. — ISBN 978-0201558029. (недоступная ссылка)
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 175. — 248 с. — ISBN 978-5-382-00839-4.
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — 7-е. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
|
Как сложить целые числа от 1 до N? Целые числа – это числа, не содержащие дробную или десятичную часть. Если в задаче требуется сложить определенное количество целых чисел от 1 до заданного значения N, то их не нужно складывать вручную. Вместо этого воспользуйтесь формулой (N(N+1))/2, где N – наибольшее число ряда. Окончательный ответ есть сумма всех целых чисел от 1 до данного N. Пример: (100(100+1))/2 = 100(101)/2 = (10100)/2 = 5050 Сумма всех целых чисел от 1 до 100 равна 5050. автор вопроса выбрал этот ответ лучшим В Рокотов 2 месяца назад Этот вопрос один из самых популярных в школьном образовании, даже несмотря на то, что сейчас на любое действие имеется онлайн калькулятор или иной электронный ресурс с подстановкой данных. Однако, более пригодится все-таки иметь представление о счете в диапазоне самому. Самая удобная формула нахождения суммы последовательного ряда в диапазоне от 1 до какого-то еще числа, назовем его N, такая: S =(n+1)*n/2; где N – наибольшее число ряда. Математику на пальцах не объяснишь, нужны примеры. Возьмем скажем последовательный ряд от единицы до пятнадцати., где нужно найти сумму диапазона от 1 до 15: (1+15)*15/2=120. Теперь стало более понятно. Удачи в будущих свершениях! -Irinka- 2 месяца назад Для того, чтобы облегчить жизнь – сделать расчеты более быстрыми и легкими, необходимо знать и пользоваться формулами. Для того, чтобы быстро и легко рассчитать сумму чисел, не производить сложение чисел в ручную, стоит воспользоваться формулой. Данная формула проверена ниже в ответе. В данной формуле буквой n обозначено максимальное число в данном ряду. Для того, чтобы понять формулу, можно произвести наглядный рассчет. За n условно возьмём число 6. Теперь подставляем зга, гения в формулу. S = 6×(6+1)/2 = 42/2 = 21. Теперь произведём сложение чисел последовательно без использования формулы. S = 6 + 5 + 4 + 3 + 2 + 1 = 21. Данные расчёты доказывают, что формула рабочая и ч её помощью произвести расчёт быстрее. Extrimal 2 месяца назад В математике данный вопрос можно встретить довольно часто. Многие считают, что это проще сделать вручную, складывая числа друг с другом по очереди. Однако если речь идет о больших числах, например если N=100, то проще воспользоваться формулой. Формула следующая Сумма равна (n+1) умножаем на n и делим на 2. Пробуем вычислить сумму, если n равно 100. 101*100/2 получаем 5050. КорнетОболенский 2 года назад Имеем ряд натуральных чисел. Первое число в ряду – единица, последнее N. Их сумму можно вычислить по формуле Для примера рассмотри сумму первых 10 натуральных чисел. В формулу вместо N поставим 10. Получим 10*(10+1)/2 = 55. Проверить несложно, посчитав эту сумму вручную. Сергей11110 3 года назад На самом деле, можно заметить, что ряд натуральных чисел образует арифметическую прогрессию с шагом 1. Сумма первых n членов арифметической прогрессии определяется формулой: S = (a1+an)*n/2; a1 = 1, а значит S = (n+1)*n/2 Это и есть сумма первых n натуральных чисел. Есть еще много способов ее посчитать, к примеру, написать программу на языке программирования (примерный код прилагаю): program a; var sum, i, n:longint; begin sum = 0; read(n); for i:=1 to n do begin sum:=sum+i; end; writeln(sum); end. Это код на языке программирования “Паскаль”. Думаю, есть еще много способов посчитать сумму n первых натуральных чисел, но основные я перечислил. Просвет 7 лет назад Целые числа – это все числа, которые не дробные и не имеют десятично части, то есть 1, 2, 3, 10, 14, и так далее. Чтобы узнать их сумму, нужно ввести такой процесс с циклом: 1.. Задается N. A=0 S=0 2.. От 1 до N делать A=А+1 S=S+A В результате вы получите окончательный ответ S – сумма. (Вводить можно в паскале) MarkTolkien 6 лет назад Задача сложить ряд чисел от единицы до N не так сложна, но она требует слишком много времени. Упростить задачу призвана довольно простая формула: (N * (N + 1)) / 2 . Проверить формулу можем на простом примере вычисления суммы чисел от 1 до 5. 5 + 4 + 3 + 2 + 1 = 15. По формуле получаем 5 * (5 + 1) / 2 = 15. Чосик более года назад В данном примере мы обозначаем сумму чисел как S, а N – будет числом, до которого будет идти счет. То есть, N является самым большим числом среди всех. Рассчитываем сумму по формуле: Проверить правильность решения можно на малом числе. Допустим, N = 7. Можно просчитать сумму от 1 до 7. Выходит S = 1 +2 + 3 + 4 + 5 + 6 + 7 = 28. Теперь решим по формуле. S = 7 * (7+1)/ 2 = 7*8/2 = 56/2 = 28 владсандрович более года назад Если у нас идут натуральные числа вряд. При этом первым числом будет цифра 1, а последним N, то есть неизвестное. Тогда сумма их вычисляется вот такой вот формулой: (N * (N + 1)) / 2 . К примеру у вас в сумме идут 5 натуральных чисел. В формуле вместо N должна быть цифра 5. В итоге рассчитываем все так 5*(5+1)/2 =15. Степан БВ 2 месяца назад Сложить целые числа от 1 до N можно по формуле суммы арифметической прогрессии: S = (N * (N + 1)) / 2 где S – сумма чисел от 1 до N, N – последнее число в ряду. Например, если нужно сложить числа от 1 до 10, то S = (10 * (10 + 1)) / 2 = 55 Таким образом, сумма чисел от 1 до 10 равна 55. Natasha145 7 лет назад Это арифметическая прогрессия. Формула суммы N – первых членов такава: Знаете ответ? |
Если вы готовитесь к экзамену или хотите научиться быстро складывать числа, этот материал для вас.
Как найти сумму чисел 1 до N?
Для сложения определенного количества целых чисел в диапазоне от 1 до заданного значения N используется формула: N⋅(N+1)2frac{Ncdot(N+1)}{2}. Где NN — наибольшее число ряда.
Как работать с последовательностью чисел
- Определите арифметическую прогрессию, проверив последовательность чисел, которые вы собираетесь суммировать. Чтобы применить формулу для вычисления суммы целых чисел, убедитесь, что ряд чисел является арифметической прогрессией, то есть каждое последующее число увеличивается на одно и то же значение.
Пример
Последовательности чисел 5,6,7,8,95, 6, 7, 8, 9 и 17,19,21,23,257, 19, 21, 23, 25 являются арифметическими прогрессиями. Однако ряд чисел 5,6,9,11,145, 6, 9, 11, 14 не является арифметической прогрессией, так как числа увеличиваются на различные значения.
- Определите значение N в последовательности. Чтобы применить формулу для вычисления суммы целых чисел от 1 до N, определите наибольшее целое число, которое вы подставите вместо N.
Пример
Если вам нужно вычислить сумму всех целых чисел от 1 до 100, то N=100N = 100, поскольку это наибольшее целое число в последовательности. Помните, что вы работаете только с целыми числами, следовательно, NN не может быть дробным (обычным или десятичным) или отрицательным числом.
- Определите количество целых чисел, которые нужно сложить. Для того чтобы получить сумму целых чисел от начального числа до N, необходимо знать общее количество чисел, которые нужно сложить.
Пример
Если требуется сложить целые числа от 11 до 200200, то общее количество чисел равно 200−1+1=200200 – 1 + 1 = 200. Если нужно найти сумму целых чисел от 11 до 1212, то количество чисел равно 12−1+1=1212 – 1 + 1 = 12.
- Найдите сумму целых чисел между двумя заданными значениями, не включая сами эти значения. Для этого нужно вычесть единицу из разности между наибольшим и наименьшим числами.
Пример
Чтобы найти сумму целых чисел между 11 и 100100, нужно вычесть единицу из 100−1100 – 1, что даст 9999.
Как использовать формулу для сложения целых чисел
- Сформулируйте уравнение для вычисления суммы последовательных целых чисел. Чтобы вычислить сумму последовательных целых чисел до определенного значения n, используйте следующую формулу: Сумма =N⋅(N+1)2= Ncdotfrac{(N+1)}{2}.
Пример
Чтобы вычислить сумму целых чисел от 11 до 100100, замените NN на 100100 : 100⋅(100+1)2100cdotfrac{(100+1)}{2}.
- Запишите формулу для вычисления суммы четных целых чисел. Если вы хотите вычислить сумму четных целых чисел в последовательности, начинающейся с 1, воспользуйтесь формулой: Сумма =N⋅(N+2)4= frac{Ncdot(N+2)}{4} , где NN – наибольшее четное число в последовательности.
Пример
Чтобы вычислить сумму четных чисел от 1 до 20, замените N на 20⋅(20+2)4frac {20cdot(20+2)}{4}.
- Запишите уравнение для вычисления суммы нечетных целых чисел. Если вы хотите вычислить сумму нечетных целых чисел, то сначала найдите n, прибавив 1 к наибольшему числу в последовательности. Затем используйте следующую формулу: Сумма =(n+1)⋅(n+1)4= frac{(n+1)cdot(n+1)}{4}.
Пример
Чтобы вычислить сумму нечетных чисел от 1 до 9, замените NN на 99: (9+1)⋅(9+1)4frac{(9+1)cdot(9+1)}{4}.
- Примените соответствующую формулу, чтобы найти сумму. Когда вы подставили нужное число в формулу, умножьте его на себя, прибавьте 1,21, 2 или 44 (в зависимости от формулы), а затем разделите результат на 22 или 44.
Пример 1
Чтобы найти сумму целых чисел от 1 до 100, используйте формулу Сумма =100⋅(100+1)2= frac{100cdot(100+1)}{2}. Умножьте 100 на 101, затем поделите на 2, чтобы получить ответ: 50505050.
Пример 2
Чтобы найти сумму четных чисел от 1 до 20, используйте формулу Сумма =20⋅224= frac{20cdot22}{4}. Умножьте 20 на 22, затем поделите на 4, чтобы получить ответ: 110110.

Что такое сумма, и как ее найти
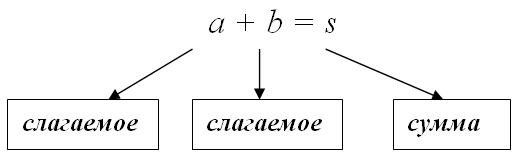
Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, – это одно из самых первых правил в математике, которое проходят в начальной школе.
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел

В общем виде вычитание можно записать так: a – b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.
А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.
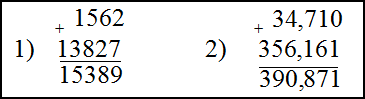














![sum limits _{{k=1}}^{n}k^{3}=left[{frac {n(n+1)}{2}}right]^{2}=left(sum limits _{{k=1}}^{n}kright)^{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c341ce59623204355f8577a50b0e02b49e30240d)









