Симметрия — соразмерность, соответствие, сходность, порядок в расположении частей. Это слово, как и многие другие математические понятия, произошли от греческих слов.
Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»
Рис. (1). Симметрия в архитектуре.
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
Рис. (2). Симметрия в природе.
Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
Симметрию относительно точки называют центральной симметрией.
Точки
M
и
M1
симметричны относительно некоторой точки (O), если точка (O) является серединой отрезка
MM1
.
Рис. (3). Центральная симметрия.
Точка (O) называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.
Рис. (4). Треугольники симметричны относительно точки (O).
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно центра (точки) (O).
1. Для этого соединим точки (A), (B), (C) с центром (O) и продолжим эти отрезки.
2. Измерим отрезки (AO), (BO), (CO) и отложим с другой стороны от точки (O) равные им отрезки
AO=OA1;BO=OB1;CO=OC1
;
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой точки этой фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки
M
и
M1
симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
Рис. (5). Осевая симметрия.
Алгоритм построения фигуры, симметричной относительно некоторой прямой.
Рис. (6). Треугольники симметричны относительно прямой.
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно красной прямой.
1. Для этого проведём из вершин треугольника (ABC) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
- для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
- Для равнобедренного треугольника есть единственная ось симметрии.
- Для равностороннего треугольника — три оси.
- Для прямоугольника и ромба существуют две оси симметрии.
- Для квадрата — целых четыре.
- Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
- Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
Источники:
Рис. 1 Симметрия в архитектуре. Указание авторства не требуется, 2021-06-02, Архитектура/Здания, бесплатно для коммерческого использования, https://clck.ru/VFC5B.
Рис. 2. Симметрия в природе. Указание авторства не требуется, 2021-06-02, бесплатно для коммерческого использования, https://clck.ru/VFECn.
Рис. 3. Центральная симметрия, © ЯКласс.
Рис. 4. Треугольники симметричны относительно точки O, © ЯКласс.
Рис. 5. Осевая симметрия, © ЯКласс.
Рис. 6. Треугольники симметричны относительно прямой, © ЯКласс.
Как найти центр симметрии
Одним из видов симметрии является центральная. Центр симметрии – некоторая точка O, относительно которой вращают плоскость, поворачивая ее на 180°. Каждая точка A переходит в такую точку A’, что O – середина отрезка AA’.
Инструкция
Если даны две точки, центром симметрии между ними, по определению, будет середина отрезка, соединяющего их. Сложнее обстоит дело с геометрической фигурой: здесь уже надо рассмотреть все точки, составляющие ее. Любая произвольная точка должна переходить в центрально симметричную ей, иначе принцип симметрии будет нарушен.
Если даны две фигуры, про которые сказано, что они являются симметричными относительно неизвестного центра, попробуйте мысленно вращать каждую из фигур. В итоге вы должны представить переход на 180° (пол-окружности). Найдите любые две симметричные точки, проведите между ними отрезок. В его центре будет располагаться центр симметрии и этих двух точек, и всей фигуры.
Пусть надо построить окружность, симметричную данной относительно точки O. Центр окружности пусть обозначен точкой C. Проведите прямую от точки C через точку O. Ножками циркуля отмерьте расстояние OC, отложите такое же расстояние на прямой от точки O в другую сторону. Зафиксируйте результат, это будет центр новой окружности. Измерьте циркулем радиус исходной окружности и достройте симметричную.
Чтобы построить многоугольник, симметричный данному относительно центра O, найдите образ каждой из его вершин. Исходная точка называется «прообразом», конечная – «образом». Последовательно соедините точки между собой. Мысленно повращайте фигуры, оцените, правильным ли получился результат.
Если дана пространственная фигура, и необходимо найти центр симметрии между какими-либо двумя точками, вспомните свойства этого объемного тела. Возможно, центр симметрии лежит на пересечении диагоналей, биссектрис, медиан, перпендикуляров. Докажите, что указанная вами точка является именной центром симметрии, используя свойства фигуры, другие данные в задаче условия и определение симметричности.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Осевая и центральная симметрии
Осевая симметрия
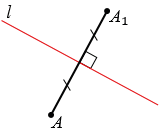
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой 
.
Пусть дана точка А и прямая .
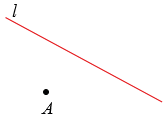
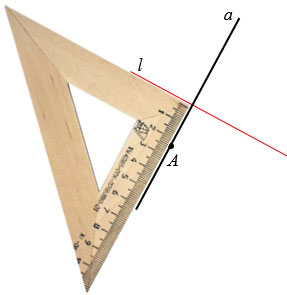
Точку симметричную точке А относительно прямой , можно построить так. Проведем через точку А прямую 
, перпендикулярную прямой . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую через точку А.
Пусть прямые и пересекаются в точке О. Отложим при помощи линейки на прямой отрезок ОА1, равный отрезку ОА.
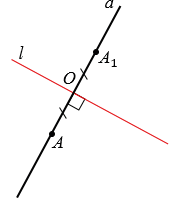
Получаем точки А и А1, которые симметричны относительно прямой .
Также можно построить фигуры, симметричные относительно прямой.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .
Пусть дан треугольник АВС и прямая .
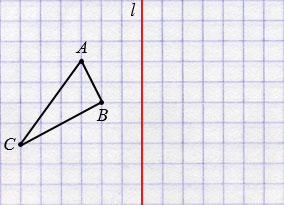
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .
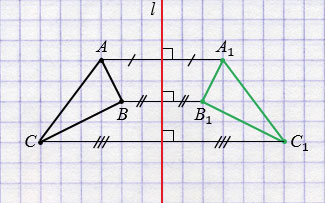
Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
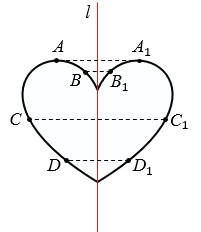
Если фигура имеет ось симметрии (прямая ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
Центральная симметрия
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).
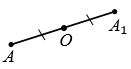
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
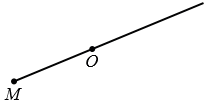
На луче МО отложим отрезок ОN , равный отрезку ОМ.
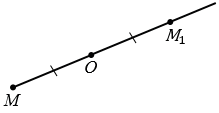
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
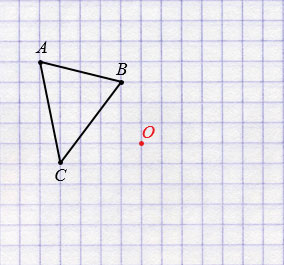
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
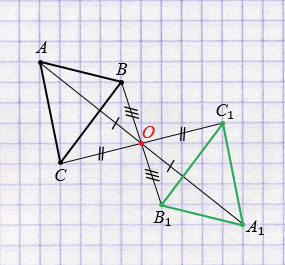
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
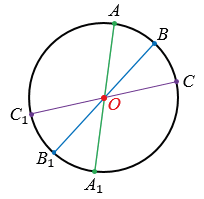
В таком случае говорят, что окружность имеет центр симметрии – точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Перпендикулярные прямые
Параллельные прямые
Координатная плоскость
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1246,
Мерзляк, Полонский, Якир, Учебник
Номер 1261,
Мерзляк, Полонский, Якир, Учебник
Номер 1264,
Мерзляк, Полонский, Якир, Учебник
Номер 1267,
Мерзляк, Полонский, Якир, Учебник
Номер 1271,
Мерзляк, Полонский, Якир, Учебник
Номер 1306,
Мерзляк, Полонский, Якир, Учебник
Номер 1307,
Мерзляк, Полонский, Якир, Учебник
Номер 1315,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Центральная симметрия — это симметрия относительно точки.
Пусть дана некоторая точка O. Чтобы построить точку, симметричную относительно точки O некоторой точке A, надо:
1) Провести луч AO.
2) С другой стороны от точки O на луче AO отложить отрезок OA1, равный отрезку AO.
Полученная точка A1 симметрична точке A относительно точки O.
Точка O называется центром симметрии.
Таким образом, точки A и A1симметричны относительно точки O, если O — середина отрезка AA1. Точка O считается симметричной самой себе.
Преобразование фигуры F в фигуру F1, при котором каждая точка A фигуры F переходит в точку A1, симметричную относительно данной точки O, называется преобразованием симметрии относительно точки O. Фигуры F и F1 называются фигурами, симметричными относительно точки O.
Чтобы построить треугольник, симметричный треугольнику ABC относительно точки O, достаточно построить точки A1, B1 и C1, симметричные точкам A, B и C относительно точки O, и соединить их отрезками.
Треугольники ABC и A1B1C1 симметричны относительно точки O.
Если преобразование симметрии относительно точки O переводит фигуру в себя, то такая фигура называется центрально-симметричной, а точка O называется центром симметрии этой фигуры.
Примеры центрально-симметричных фигур:
1) Параллелограмм.
Центр симметрии параллелограмма — точка пересечения его диагоналей.
2) Окружность.
Центр симметрии окружности — её центр.
3) Прямая.
Центром симметрии прямой является любая точка этой прямой ( то есть прямая имеет бесконечное множество центров симметрии).
Теорема.
Преобразование симметрии относительно точки является движением.
