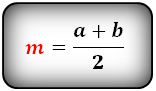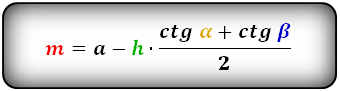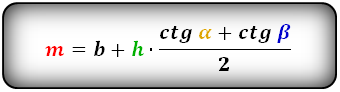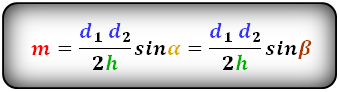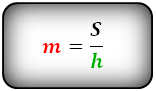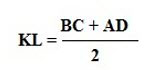Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
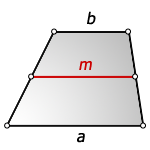
b – верхнее основание
a – нижнее основание
m– средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
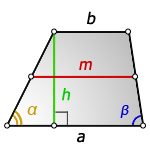
b – верхнее основание
a – нижнее основание
α, β – углы трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
α, β – углы между диагоналями
d1 , d2 – диагонали трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 24 сентября 2013
-
Обновлено: 13 августа 2021
Средняя линия трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Мы снова затронем тему трапеций (что это?).
И расскажем о том, что такое средняя линия этой геометрической фигуры.
Средняя линия – это…
Вообще, этот термин в геометрии весьма распространен.
Средняя линия – это отрезок, проходящий через противоположные стороны, и который делит их ровно на две одинаковых части.
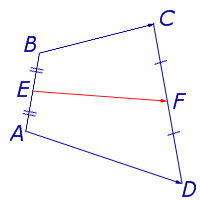
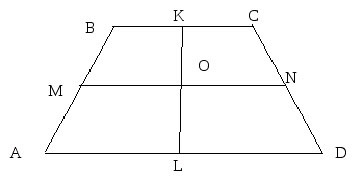
Средняя линия есть практически у каждой геометрической фигуры. Например, у четырехугольников она выглядит вот так:
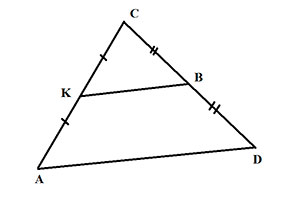
А вот так у треугольников:
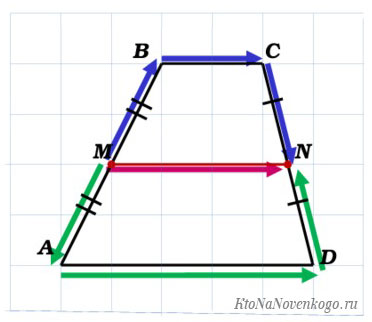
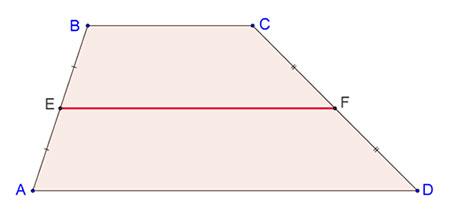
И наконец, в случае трапеции изображение средней линии будет вот таким:
На данном рисунке показана трапеция ABCD. Если кто забыл, то у такой фигуры две противоположные грани расположены на параллельных прямых.
Они называются основаниями. А оставшиеся стороны, которые соответственно не параллельны друг другу, это боковые.
Так вот в нашем случае мы имеем среднюю линию EF, которая делит боковые стороны АВ и СD на две половинки. То есть:
AE = EB и СF = FD
Как найти среднюю линию трапеции (формула)
Есть одна главная формула, позволяющая рассчитать значение нашего отрезка.
Так, длина средней линии будет равна сумме оснований фигуры, поделенной на два. Или, другими словами, половине суммы оснований.
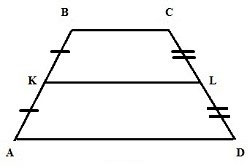
Возьмем для примера трапецию:
И тогда формула расчета будет выглядеть так:
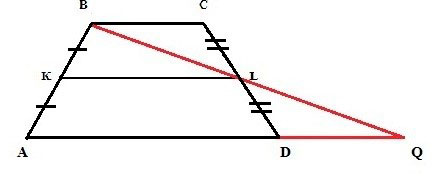
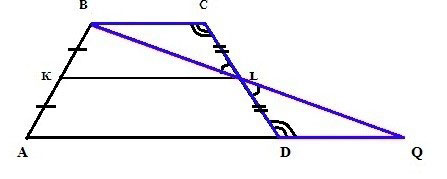
Если есть желание доказать правдивость этой формулы, нужно несколько дорисовать нашу изначальную фигуру. А именно провести линию через В и L, а также продлить сторону АD. И сделать так, чтобы эти две линии пересеклись.
В итоге получится вот что:
Далее нас будут интересовать оба треугольника, которые получились. Это BLC и DLQ. Необходимо доказать, что они имеют равные размеры.
И это просто, так как у них одинаковы углы:
- BLC и QLD – как вертикальные;
- BCL и QDL – как лежащие накрест при имеющихся параллельных прямых и секущей.
Соответственно, если равны в треугольниках углы и стороны между ними, то и сами фигуры одинаковы.
DLQ = BLC
А уже из этого следует, что ВL и LQ равны. А значит, КL является не только средней линией трапеции, но также и аналогичной линией для треугольника ABQ.
А дальше уже совсем просто, так как есть специальная формула для расчета средней линии треугольника. Она равна одной второй (половине) длины параллельной стороны:
KL = 1/2AQ
Длина стороны AQ у нас равна AD + DQ (или ВС). И таким образом мы и получаем ту самую формулу расчета средней линии трапеции:
KL = ½ AQ = ½ (AD + DQ) = ½ (AD + ВС)
Как принято говорить в таких случаях – что и требовалось доказать.
Свойства средней линии трапеции
У средней линии трапеции есть три главных свойства:
- Она параллельна основаниям трапеции;
- Она равна полусумме оснований (та самая формула, о которой мы только что рассказывали);
- Она разбивает исходную трапецию на две более маленькие по площади. Причем их площади имеют вполне конкретное соотношение друг к другу. А именно:
S1/S2 = (3BC + AD) / (BC + 3AD)
Эту формулу мы не будем доказывать. Просто поверьте, что так и есть на самом деле.
Вторая средняя линия
Внимательный читатель мог бы заметить, что мы рассказывали до этого только про одну среднюю линию. Ту, что лежит параллельно основаниям. Но ведь у этой геометрической фигуры, как и любого четырехугольника, таких отрезков должно быть два.
И действительно, у трапеции имеется вторая такая линия. И она уже делит на две равные части оба основания:
В нашем случае, это отрезок KL.
Интересно, что эту среднюю линию крайне мало изучают во время школьного обучения. И на экзаменах нет задач, с ней связанных. Хотя у нее есть несколько интересных свойств:
- Диагонали трапеции и эта средняя линия пересекаются в одной точке;
- Та прямая, частью которой эта линия является, пересекается в единой точке с теми прямыми, которые совпадают с боковыми сторонами;
- В равнобокой трапеции (у которой боковые стороны идут под одним углом) средняя линия пересекает основания под углом в 90 градусов;
- В точке, в которой пересекаются две средние линии, они делятся пополам…
Вот и все, что мы хотели рассказать о средних линиях в трапеции.
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD и BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD и MN=frac{AD+BC}{2}$.
Рассмотрим вектор $overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $overrightarrow{BC}$ и $overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15 см$ и $17 см$ соответственно. Периметр трапеции равен $52 см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52 см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ:
$10 см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9 см$ и $BC=5 см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $ADbot l$ и $BCbot l$ и так как $OH$ — радиус, то $OHbot l$, следовательно, $OH|left|ADright||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD и BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD и MN=frac{AD+BC}{2}$.
Рассмотрим вектор $overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $overrightarrow{BC}$ и $overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15 см$ и $17 см$ соответственно. Периметр трапеции равен $52 см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52 см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ:
$10 см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9 см$ и $BC=5 см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $ADbot l$ и $BCbot l$ и так как $OH$ — радиус, то $OHbot l$, следовательно, $OH|left|ADright||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Общие сведения
Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Виды трапеции
Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.
1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.
Главные принципы методики изучения свойств трапеции
К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Ее высота и средняя линия равны;
Центр окружности является точкой, в которой пересекаются ;
Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;
Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.
Подобные трапеции
Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Доказательство теоремы
Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Свойства подобия
Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).
2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.
Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Центр тяжести
Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.
Вписанные и описанные трапеции
Давайте перечислим особенности таких фигур:
1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.
2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Следствия вписанной окружности:
1. Высота описанной трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.
Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+Б)/2.
2. Через высоту, основание и углы:
М = А-Н*(ctgα+ctgβ)/2;
М = Б+Н*(ctgα+ctgβ)/2.
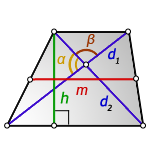
3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:
М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.
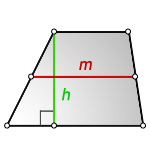
4. Через площадь и высоту: М = П/Н.
Четырёхугольник, у которого только две стороны параллельны называются трапецией
.
Параллельные стороны трапеции называются её основаниями
, а те стороны, которые не параллельны, называются боковыми сторонами
. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DC
AM = MD; BN = NC
MN
средняя линия, AB
и CD
— основания, AD
и BC
— боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача
: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема
: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания . На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD
, если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
Как вычислить длину средней линии трапеции?
Средняя линия трапеции А именно, имеет место такая формула: displaystyle m=frac{a+b}{2}, то есть: Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований.
Как найти длину средней линии?
Средняя линия равна половине длины основания и параллельна ему.
Как найти длину средней линии трапеции по клеткам?
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. Решение. Длина средней линии трапеции равна полусумме её оснований, т.
Как найти длину трапеции?
Формулы определения длин сторон трапеции:
- Формула длины оснований трапеции через среднюю линию и другую основу: a = 2m — b. b = 2m — a.
- Формулы длины основ через высоту и углы при нижнем основании: a = b + h · (ctg α + ctg β) …
- Формулы длины основ через боковые стороны и углы при нижнем основании: a = b + c·cos α + d·cos β
Чему равна средней линии трапеции?
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Как найти среднюю линию трапеции зная высоту и площадь?
Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два. Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Как найти среднюю линию равнобедренной трапеции?
Способы нахождения средней линии равнобедренной трапеции
- m = (a+b)/2, где:
- m — длина средней линии
- а и b — длины оснований
13 февр. 2020 г.
Как найти длину средней линии треугольника параллельной стороне?
Средняя линия треугольника равна половине той стороны, которой она параллельна. Длина стороны АВ равна 4, поэтому искомая длина средней линии равна 2.
Как найти среднюю линию трапеции если известна только высота?
В равнобокой трапеции средняя линия равна отрезку большего основания x, полученному при проведении высоты.
Как найти площадь трапеции?
Как найти площадь трапеции? Складываем основания трапеции, делим сумму на два и умножаем все это на высоту, проведенную к большему основанию.
Как найти сторону трапеции зная диагональ?
Если в трапеции провести диагонали, то они образуют серию подобных треугольников, и пропорциональные соотношения их сторон приводят к основному свойству трапеции, объединяющему диагонали трапеции и ее четыре стороны: d12+d22=c2+d2+2ab , где a и b – это основания трапеции, а c и d – ее боковые стороны.
Как доказать прямоугольную трапецию?
Основные свойства прямоугольной трапеции
- В трапеции есть два смежных прямых угла: ∠BAD = ∠ABC = 90°
- Одна боковая сторона перпендикулярна основам: AB ┴ BC ┴ AD.
- Высота равна меньшей боковой стороне:
Как найти длину средней линии трапеции в которую вписана окружность?
Пусть стороны трапеции равны a, b, c, d. В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны: a + c = b + d = 24. Длина средней линии равна полусумме длин оснований: 24/2 = 12.
Как найти высоту трапеции по основаниям и площади?
Зная площадь трапеции и ее среднюю линию (или два основания, среднее арифметическое которых дает среднюю линию), можно вычислить высоту трапеции, разделив одно на другое: Более изощренным является вычисление высоты трапеции через все ее стороны.
Как найти среднюю линию трапеции зная площадь?
Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два. Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Как найти среднюю линию треугольника параллельную АВ?
Средняя линия треугольника равна половине той стороны, которой она параллельна.
Как найти среднюю линию треугольника ABC?
По свойству средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна её половине. Значит, средняя линия MN будет параллельна стороне BC и равна BC/2. Следовательно, для определения длины средней линии треугольника достаточно знать длину стороны именно этой третьей стороны.
Средняя линия трапеции
Это отрезок, который соединяет середины 2 боковых сторон трапеции. Существует несколько способов (формул), позволяющих узнать, чему равна средняя линия.
Рассмотрим некоторые из них.
Как найти среднюю линию трапеции через основания
Если известно, чему равны основания трапеции, то среднюю линию найти совсем не сложно.
Она будет равна полусумме оснований.
EF = (AB + CD) / 2.
Например, если основание AB = 10 см, а основание CD = 6 см, то средняя линия равна (10 + 6) / 2 = 8 см.
Как найти среднюю линию трапеции через площадь и высоту
По классической формуле, площадь трапеции равна полусумме оснований умноженной на высоту. А полусумма оснований и есть средняя линия.
Поэтому, если площадь S = EF * DH, то средняя линия EF = S / DH.
Например, если площадь трапеции равна 30 кв. см, а высота – 6 см, то средняя линия = 30 / 6 = 5 см.
Как найти среднюю линию трапеции через высоту, диагонали и угол между ними
Если неизвестна площадь трапеции, но известны диагонали и угол между ними, то можно воспользоваться одной из формул нахождения площади.
А после этого подставить полученное значение в формулу, позволяющую найти среднюю линию через площадь и высоту.
Если даны диагонали d1 и d2, а также угол между ними (например, γ), то S = 0,5 * d1 *d2 * sinγ.
Подставим это в формулу нахождения средней линии: EF = S / DH = (0,5 * AC * BD * sinγ) / DH = AC * BD * sinγ / 2DH.
Например, высота = 6 см, диагонали – 8 и 10 см, угол между ними – 30 градусов.
EF = (8 * 10 * 0,5) / (2 * 6) = 40 / 12 = 3,33 см.