Содержание
- Построение горизонталей по отметкам
- 2. Горизонтали на топографических планах и картах.
- 1.4 Построение горизонталей методом графического интерполирования
- Горизонтали и их свойства. Способы построения горизонталей
- По отметкам точек
- Способы построения горизонталей по отметкам точек.
- Решение инженерных задач по планам и картам
- Определение площадей по картам и планам
Построение горизонталей по отметкам
Для построения топографического плана по отметкам точек выбирается высота сечения. Топографический план можно построить графическим или аналитическим способами.

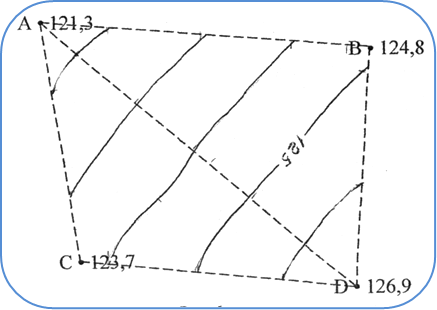
Для примера рассмотрим построение топографического плана с высотой сечения рельефа – 1м. Соединяем точки А и В тонкой линией. Между этими точками проходят горизонтали с отметками 122,0; 123,0. Делим линию АВ на 5 равных частей, каждая из которых будет соответствовать – 0,5м.
Отмечаем на линии АВ точки с отметками – 122,0 и 123,0. Аналогично делим все остальные линии. Точки с одинаковыми отметками соединяем плавными линиями (рис.12).
Аналитический способ. Измеряем расстояние линии АВ, LАВ = 7см. Между точками А и В пройдут горизонтали с отметками: 122,0; 123,0; 124,0. Для нахождения точки с отметкой 122,0 м, вычисляем превышения между точками А и В h = 124,8 – 121,3 = 3,5 м. Составим пропорцию:
3,5 м соответствует 7 см
Х = 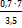 = 1,4 см
= 1,4 см
Откладываем полученное расстояние – 1,4 см от точки А и получаем точку с отметкой – 122,0 м. Находим точку с отметкой – 124,0 м.
Х = 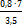 = 1,6 см
= 1,6 см
Откладываем полученное расстояние – 1,6 см от точки В. Аналогично рассчитываем расстояние до точки с отметкой – 123,0 м. Расчёты производим между всеми соседними точками. Находим точки с одинаковыми отметками и соединяем их плавными линиями (рис.13).
Уклон линии
Уклон линии i – отношение превышения h к её заложению d. Уклон i является мерой крутизны ската (рис.14).
i =  = tg γ
= tg γ
h = НВ – НА (превышение равно разнице отметок точек)
или d=h·сtg γ
Следовательно, уклон линии это тангенс угла наклона её к горизонту (рис.14). Уклоны линий выражают в процентах или промилях. Обычно крутизну ската и уклоны определяют графически с помощью специальных графиков, называемых масштабом заложений. Масштаб заложений для углов наклона строится следующим образом. На горизонтальной линии откладывают равные отрезки, подписанные значениями углов наклона. На концах этих отрезков восстанавливают перпендикуляры, на них откладывают в масштабе плана заложения ската – d, рассчитанного по формуле (рис.15).
В
h
γ
А d
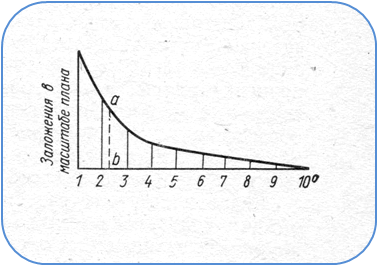
Рис. 14 Определение уклона линии
Для определения угла наклона берут циркулем расстояние авмежду двумя горизонталями и переносят его на график. На горизонтальной линии определяют угол наклона. Аналогичным образом можно построить масштаб заложений для определения уклонов.
Построение профиля. Для построения профиля, на карте отмечаются точки пересечения горизонталей с линией разреза (рис.16).
Выбирается масштаб для построения профиля и подписывается вверху листа. Горизонтальный – равен масштабу карты, вертикальный – в 10 раз крупнее. В нижней части листа проводится горизонтальная линия, на которой откладываются точки пересечения горизонталей с линией разреза. Слева проводится вертикальная линия, на которой ставятся деления через 1 см. Выбирается отметка условного горизонта. В соответствии с выбранным вертикальным масштабом ставится оцифровка у каждого деления. По отметкам наносятся точки, которые затем соединяются прямыми линиями.
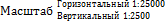
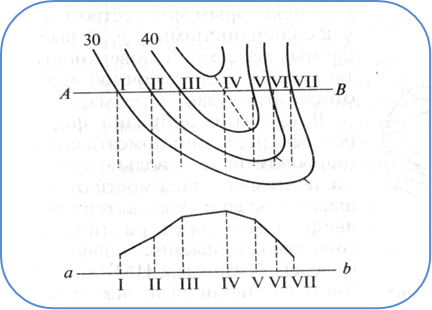
Рис.16 Построение профиля
Дата добавления: 2016-09-26 ; просмотров: 23455 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
2. Горизонтали на топографических планах и картах.
Рельефом местности называется совокупность неровностей земной поверхности. на планах рельеф изображается при помощи условных специальных знаков, от которых требуется:
— подробно и точно показать расположение всех форм неровностей местности, характеризующих ее расчлененность и доступность;
— обеспечить возможность определения высот точек местности и превышений (разность высот) одних точек над другими, направление склонов и их крутизну;
— наглядно изображать рельеф, позволяя, возможно яснее представить действительный ландшафт местности.
На современный топографических планах и картах рельеф изображается горизонталями, дополненными абсолютными отметками и Берг-штрихами.
Под горизонталью понимается след от пересечения земной физической поверхности секущей (уровенной) поверхностью. Горизонтали (изобаты) – это линии равных высот (отметки) или глубин. Отметкой называется высота точки местности над уровенной поверхностью.

Рис.3 Изображение горы горизонталями.
На рис.3 показано построение горизонталей для небольшого участка местности, где уровенные поверхности можно считать плоскостями. Секущие плоскости Р1, Р2, Р3 параллельны начальной (отсчетной) плоскости Р. Расстояние между ними hназывается высотой сечения рельефа. На топографических планах и картах высота сечения устанавливается в зависимости от масштаба и сложности рельефа. На равнинных участках высота сечения мала, а на горной местности велика. Обычно высота сечения принимается равной 1, 2, 5, 10, 20, 50, 100 метров. Отметки горизонталей подписываются либо для горизонталей кратных 5м, либо для каждой пятой горизонтали при большей высоте сечения рельефа. Надпись делается в разрыве. При этом верх цифр направляется в сторону повышения местности. Подписываемые горизонтали утолщаются.
Помимо направления верха цифр надписей горизонталей, о направлении склонов дают представление Берг-штрихи, которые вычерчиваются от горизонталей в сторону понижения местности. Так, на рис.3 берг-штрихи показывают направление склонов горы, если их расставить наоборот, не меняя горизонталей, то будет изображение котловины.
Расстояние между горизонталями на плане в любом направлении называется заложением и обозначается буквой а. Связь между высотой сечения рельефа и заложением определяется формулой: i=h/a, гдеi– уклон склона,h– высота сечения, а – заложение.
Задание для самостоятельной работы:
1. Построить сетку квадратов 3х4 квадрата со стороной 5 см (Рис.4), что на местности при численном масштабе плана 1:2000 соответствует 100 м.
2. Рассчитать отметки в вершинах квадратов. Расчет выполняется по формуле Hв=HRp+h(сложение алгебраическое, т.е. с учетом знакаh), гдеHв– отметка в вершине квадрата.HRp– отметка репера (закрепленное на местности точки), задаваемая преподавателем, индивидуально для каждого студента. Вычисляемые отметки выписываются у соответствующих вершин с округлением, до десятых долей метра. Далее методом интерполяции находят те места, где стороны квадратов будут пересекать горизонтали. После соединяют точки равных высот, кратные 1 метру, при этом учитываются все стороны квадратов и диагонали. Горизонтали, кратные 5 метрам утолщают и в разрывах подписывают их отметку. Отметка подписывается так, чтобы цифры верх был направлен вверх по склону. После прорисовываются Берг-штрихи вниз по склону. Все горизонтали и берг-штрихи вырисовываются коричневой тушью.
Если отметка (репер) не дана преподавателем, то значение отметки следует принять условно: количество целых метров в отметке должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра студента. В дробной части отметки (дм, см, мм) ставятся те же цифры, что и в целой части.
Источник
1.4 Построение горизонталей методом графического интерполирования
Для изображения рельефа горизонталями выполняют топографическую съемку участка местности. По результатам съемки определяют координаты (две плановые и высоту) для характерных точек рельефа и наносят их на план (рис. 1.13). В зависимости от характера рельефа, масштаба и назначения плана выбирают высоту сечения рельефа h.
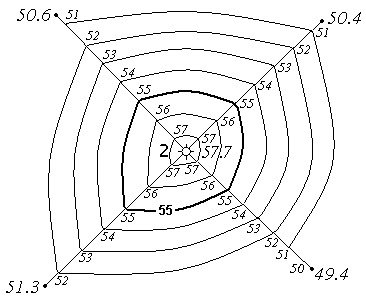
Рис. 1.13Изображение рельефа горизонталями
Положение горизонталей на плане или карте определяется с помощью интерполирования. На рис. 1.12 приведено построение горизонталей с отметками 51, 52, 53, 54, 55, 56, 57 м. Горизонтали кратные 5 или 10 м проводят на чертеже утолщенными и подписывают. Подписи наносят таким образом, чтобы верх цифр указывал сторону повышения рельефа. Там, где заложения больше, наносят штриховые линии (полугоризонтали). Иногда, чтобы сделать чертеж более наглядным, горизонтали сопровождают бергштрихами.
Приемы построения горизонталей методом интерполирования с помощью палетки
Метод интерполирования по отметкам высот состоит в следующем: между двумя соседними точками с известными отметками высот ищут след прохождения основных горизонталей с помощью специальной палетки (рис. 1.14). Такую палетку нужно вычертить в тетради с интервалом между линиями в 5 мм. Число линий соответствует числу горизонталей, проходящих по данному фрагменту рельефа; нижняя линия – по горизонтали, проходящей ниже самой нижней, а верхняя – выше самой верхней отметки горизонтали. На вспомогательном листке бумаги отмечают карандашом расстояние между двумя точками на карте, затем прикладывают край листка бумаги на палетку таким образом, чтобы карандашные отметки на нем совпали с уровнями высот на палетке. Точки пересечения линий палетки с краем бумаги нужно отметить карандашом – это и будут искомые следы горизонталей, проходящих между двумя соседними точками.
Интерполирование производится по линиям водораздела (1-2), тальвега (3-4) и вниз по склонам (1-3), (3-6), но нельзя интерполировать поперек этих линий (3-5) и (1-6). Не допускается также перекрестное интерполирование (1-7) и (2-3).

Рис. 1.14 Интерполирование по отметкам высот:
• — след пересечения горизонтали с линиями палетки
Последовательность выполнения задания
а) на чистом листе бумаги построить основу, состоящую из квадратов (приложение А), увеличенных в 2 раза по сравнению с исходным вариантом (размер квадратов 5 х 5 см);
б) нанести на основу все высотные отметки, аккуратно подписать их значения;
в) пунктирной линией отметить линии водоразделов, а сплошной – линии русел рек (в соответствии с исходной схемой);
г) перенести на составляемый фрагмент карты намеченные карандашом следы горизонталей, приложив вспомогательную бумагу к отметкам высот;
д) переходя от одной пары точек к другой, проводите линии горизонталей, используя полученные при интерполировании точки;
е) при прохождении только одной горизонтали допускается интерполирование на глаз.
Фрагмент карты оформить следующим образом:
1) выделить утолщенные горизонтали, кратные 5м;
2) для уплощенный участков рельефа, где линии горизонталей расположены далеко друг от друга, провести дополнительные горизонтали на половине основного сечения;
3) подписать некоторые горизонтали с основанием цифр в сторону понижения ската;
4) проставить бергштрихи на замкнутых горизонталях.
Источник
Горизонтали и их свойства. Способы построения горизонталей



По отметкам точек
Рельефом называют совокупность неровностей земной поверхности. Знание рельефа местности необходимо при проектировании и строительстве железных и автомобильных дорог, осушительных и оросительных систем, промышленных предприятий и т. д. Существует несколько способов изображения рельефа на топографических картах и планах. Наиболее старый способ – это изображение рельефа штрихами, наносимым на карту по особой шкале.
Рельеф местности может быть также изображен подписями отметок ряда точек или отмывкой красками различного тона. Однако наилучшим способом оказалось изображать рельеф горизонталями в сочетании с некоторыми условными знаками и подписями отметок характерных точек. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами.
Чтобы правильно изобразить рельеф, необходимо знать его основные формы.
Существует пять основных форм рельефа (рисунок 3.5):
— возвышенность (рисунок 3.5, а);
— котловина (рисунок 3.5, б);
— хребет (рисунок 3.5, в);
— лощина (рисунок 3.5, г);
— седловина (рисунок 3.5, д).
На рисунке 3.5 эти формы рельефа показаны в разрезе. Рассмотрим сущность изображения рельефа горизонталями. На рисунке 3.5, а показана возвышенность (холм, гора), наивысшую точку которой называют вершиной, низ – подошвой, а боковые поверхности – скатами. Для изображения возвышенности горизонталями представим себе, что эту возвышенность пересекают ряд равноотстоящих друг от друга плоскостей, параллельных основной уровенной поверхности. Линии пересечения этими плоскостями земной поверхности и будут являться горизонталями. Спроектировав их отвесными линиями на плоскость, получим на ней изображение возвышенности.
Для наглядности некоторые горизонтали подписывают, кроме того у них ставят черточки-бергштрихи, показывающие направление ската местности.
Расстояние между двумя соседними секущими плоскостями называют высотой сечения рельефа h. На картах и планах высота сечения рельефа характеризуется разностью высот двух смежных горизонталей. Например, на рисунке 3.5, а высота сечения рельефа h = 5 м.
Расстояние между горизонталями на плане или карте называется заложением. На рисунке 3.5, а заложение d = АС. Зависимость между высотой сечения рельефа h, заложением d, углом наклона υ, уклоном i и линии местности АВ можно получить из треугольника АВС (рисунок 3.5, а):
i = h / d = tg υ. (3.6)
Уклон и угол наклона линии местности являются основными характеристиками крутизны скатов. Чем больше угол наклона, тем круче скат местности. Из формулы (3.6) следует, что чем меньше заложение d или чем чаще горизонтали на плане, тем скат местности круче.
Изображение горизонталями котловины, лощины, хребта и седловины показано на рисунке 3.5. Котловина (впадина) – замкнутое углубление поверхности (см. рисунок 3.5, б). Самую низкую часть впадины называют дном, боковые поверхности – скатами, а линию слияния с окружающей местностью – бровкой.
Рисунок 3.5 – Основные формы рельефа
Хребет – вытянутая в одном направлении возвышенность с двумя скатами (см. рисунок 3.5, в). Линию встречи скатов в верхней части называют водоразделом (водораздельной линией).
Лощина – вытянутое в одном направлении понижение с двумя скатами (рисунок 3.5 г). Линию встречи скатов в нижней их части называют водосливом или тальвегом (водосливной линией).
Седловина – понижение между двумя возвышенностями (см. рисунок 3.5 д). Наиболее низкую точку между возвышенностями называют перевалом.
Бергштрихи на картах и планах обычно показывают по водораздельным и водосливным линиям. Подписи на горизонталях делают так, чтобы основание числа показывало направление ската. Горизонтали вычерчивают коричневым цветом. Каждую десятую или пятую из них вычерчивают утолщенной линией.
Из сущности горизонталей вытекают их свойства:
— горизонталь – это замкнутая кривая линия, все точки на которой имеют одинаковую высоту, кратную высоте сечения рельефа;
— горизонтали на плане не могут раздваиваться и обрываться; если горизонталь не замыкается в пределах плана, она замыкается за его пределом;
— горизонтали не должны пересекаться между собой, так как они получаются пересечением земной поверхности плоскостями, лежащими на разных высотах;
— чем чаще горизонтали на плане, тем уклон местности больше, или чем меньше заложение, тем скат круче;
— водораздельные и водосливные линии и направления максимального уклона горизонтали пересекают под прямым углом.
Высота сечения рельефа устанавливается в зависимости от масштаба плана и характера рельефа местности так, чтобы горизонтали не сливались между собой. В Республике Беларусь приняты следующие высоты сечения рельефа при масштабах съемки:
| 1:500 – h = 0,25; 0,5 м; 1:1000 – h = 0,25; 0,5; 1 м; 1:2000 – h = 0,5; 1; 2 м; | 1:5000 – h = 0,5; 1; 2; 5 м; 1:10000 – h = 1; 2,5; 5 м. |
Для более полного изображения и удобства чтения рельефа на картах и планах подписывают отметки характерных точек рельефа (вершин холмов, дна котловин, перевалов и т. д.). Например, на рисунке 3.5, б подписана отметка дна котловины 98,7 м.
Способы построения горизонталей по отметкам точек.
Для проведения горизонталей на плане нужно нанести характерные точки, снятые на местности, и выписать их высоты. Те точки, между которыми земная поверхность не имеет переломов, т. е. имеет постоянный уклон, соединить линиями. Далее на каждой линии интерполированием находят точки пересечения ее горизонталями и отмечают высоты этих горизонталей.
Соединив затем плавными кривыми линиями точки с одинаковыми высотами, получают изображение рельефа местности на плане. Таким образом, задача построения горизонталей на плане в основном сводится к умению находить проекции точек пересечения горизонталями линий, отметки концов которых известны, при этом высота сечения рельефа должна быть уже установлена. Эта задача называется интерполированием горизонталей, т. е. нахождением промежуточных значений высот горизонталей по отметкам точек. Интерполирование можно производить аналитическим или графическим способом.
Аналитический способ. По известным высотам точек А и В и расстоянию d между ними (рисунок 3.6, а) необходимо найти величины расстояний d1 и d2 от точки А до точек М0 и N0 c отметками Нм и HN, равными отметкам горизонталей. 
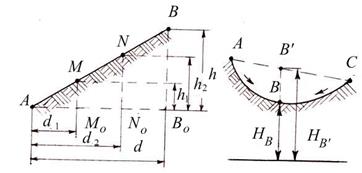
Рисунок 3.6 – Аналитический способ интерполирования
Из подобия треугольников АВВО, АММО и ANNO находим:
На плане откладывают отрезки d1 и d2 и получают точки MO и NO, у которых подписывают их отметки. Следует отметить, что интерполирование горизонталей проводят только по линиям с равномерным скатом. На рисунке 3.6, б показан случай неправильной интерполяции между точками А и С с неравномерным скатом местности. Как видно из рисунка, вместо действительного положения точки В будет получена точка В ‘ и соответственно вместо НВ будет получена неверная высота НВ ‘ .
Графический способ. Интерполирование этим способом выполняют с помощью миллиметровой или прозрачной бумаги. При наличии миллиметровой бумаги ее прикладывают к линии плана АВ. По отметкам концов АВ строят профиль этой линии. Проектируя затем на линию плана точки пересечения линии профиля с линиями миллиметровой бумаги, принятыми за секущие плоскости, получают искомые точки М и N.
При наличии прозрачной бумаги (восковки, кальки), на ней предварительно наносят ряд равноотстоящих друг от друга параллельных линий, которым придают отметки секущих плоскостей. Восковку накладывают на план так, чтобы конечные точки линии плана заняли положение, соответствующее их отметкам между линиями восковки (рисунок 3.7). Далее точки пересечения линии плана с линиями восковки перекалывают на план. Это и будут искомые точки на плане.
Решение инженерных задач по планам и картам
Современные топографические карты и планы дают богатый и разносторонний материал о той местности, которая на них изображена условными знаками. Зная условные знаки, при изучении карты можно получить необходимые данные о населенных пунктах, гидрографии, растительности, дорожной сети, рельефе и других объектах. Кроме того, при помощи карты можно решать ряд инженерных задач: определять географические и прямоугольные координаты точек, измерять дирекционные углы и азимуты направлений, определять высоты точек, уклоны заданных линий, водосборные площади бассейнов, строить профили земной поверхности, производить трассирование и т. д.
Рассмотрим решение этих задач более подробно .
1. Прямоугольные координаты точек на карте определяют от линии координатной (километровой) сетки, абсциссы и ординаты которых подписываются в общегосударственной системе координат.
2. На картах подписываются также широты и долготы точек пересечения параллелей и меридианов, ограничивающих данный лист. Кроме того, на обрамляющих карту рамках вычерчиваются одноминутные деления широты и долготы. Соединяя точки одноименных делений северной и южной сторон рамок, а также западной и восточной, получим на карте сетку меридианов и параллелей, пользуясь которой, можно определить широту и долготу любой точки карты.
3. Дирекционный угол или азимут линии можно измерить транспортиром непосредственно на карте, как угол между направлением линии километровой сетки или истинного меридиана и направлением заданной линии. Обычно на полях карты всегда дается для данного листа сближение меридианов и склонение магнитной стрелки, используя которые, по формулам (2.3) – (2.4) можно вычислить все углы ориентирования.
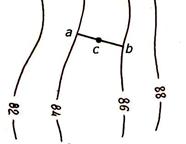
4. Высоту (отметку) любой точки, например С (рисунок 3.8, а), можно определить, если через нее провести линию ab по кратчайшему расстоянию между горизонталями.
Из подобия треугольников abb1 и acc1, учитывая, что h – высота сечения рельефа, d – заложение (рисунок 3.8, б), получим cc1 = ac bb1 / ab или Δh = Δd h /d. (3.7)
Отметка точки НС будет равна отметки точки a плюс величина Δh:
|
|
 б) б) |
Рисунок 3.8 – Определение отметки точки
В формуле (3.7) величины d и Δd измеряют на плане, а высота сечения рельефа известна на плане или карте.
5. Определяют уклон линии. Уклоном линии называется тангенс угла наклона этой линии или отношение высоты сечения рельефа к заложению (рисунок 3.8, б):
i = tg υ = h / d. (3.8)
Для определения уклона можно воспользоваться формулой (3.6) или (3.8). Из формул следует, что уклон – безразмерная величина. Его выражают в процентах (% – сотых долях) или в промилях (‰ – тысячных долях). Для определения угла наклона линии (крутизны ската) υ из формулы (3.8) можно получить:
υ = arctg i = arctg (h / d). (3.9)

Угол наклона можно также определить графически с помощью графика заложений, который обычно приведен под южной рамкой карты. При отсутствии графика заложений его можно построить. Для этого на горизонтальной прямой АВ от точки А откладывают равные отрезки произвольной величины (рисунок 3.9). Из точек отложения к прямой АВ восстанавливают перпендикуляры. Используя формулу (3.8), определяют заложение:
d = h / tg υ = h / i, (3.10)
где h – высота сечения рельефа
Подставляя в формулу (3.10) величины υ, равные 1, 2, 3 о и т. д., последовательно получают заложение для каждого из углов наклона υ и откладывают их на перпендикулярах в масштабе плана или карты. Полученные на перпендикулярах точки соединяют плавной кривой линией, а внизу подписывают углы наклона.
Для определения угла наклона по графику заложений с помощью циркуля-измерителя измеряют величину заложения на плане (ab) и прикладывают раствор измерителя к графику заложений так, чтобы одна игла измерителя находилась на основании графика, а вторая располагалась параллельно вертикальным линиям графика, и перемещают измеритель по горизонтальной линии основания вправо или влево до совпадения верхней иглы с кривой графика. По росписи графика заложений отсчитывают крутизну ската. Например, на рисунке 3.9 при заложении ab крутизна ската υ = 1,4 о . По графику заложений можно решать и обратную задачу, т. е. по заданной крутизне ската определять величину заложения на плане.
6. Для построения по заданному направлению АВ на плане профиля линии местности при помощи полоски бумаги линия с плана переносится на миллиметровую бумагу с отметками всех точек пересечения линии с горизонталями. Далее в заданном вертикальном масштабе по вертикальным линиям откладывают отметки точек, и все вершины перпендикуляров соединяют прямыми линиями. Получают профиль местности по заданному направлению (рисунок 3.10).
7. Для проведения на карте или плане линии заданного уклона по графику заложений или, исходя из формулы (3.10), определяют величину заложения соответствующего уклона. Затем циркулем-измерителем откладывают это заложение в масштабе плана и, начиная от первой горизонтали, пересекающей линию, последовательно засекают смежные горизонтали. Полученная ломаная линия будет иметь заданный уклон (рисунок 3.11).

Рисунок 3.10 – Продольный профиль
8. Водосборные площади по картам и планам определяют для вычисления расхода воды с бассейнов при строительстве плотин, мостов, труб и т. п. Водосборной площадью или бассейном водотока называют ту площадь, с которой поверхностные воды после дождя или таяния снега по условиям рельефа местности и его геологического строения стекают в данный водоток. Границами водосборной площади служат водораздельные линии и линии наибольшего ската. На карте или плане сначала намечают границы водосборной площади до створа строящегося сооружения, а затем при помощи планиметра или палетки определяют площадь в пределах установленной границы (рисунок 3.12).
Решение практических задач на планах и картах подробно изложено в учебно-методических пособиях по выполнению расчетно-графических и лабораторных работ по геодезии.
Определение площадей по картам и планам
При решении многих вопросов, связанных с использованием земельной территории, необходимо знать площади тех или иных участков. Площади участков могут быть определены или по результатам обмера участка в натуре или по планам и картам.
Существует три основных способа определения площадей:
— графический, когда площадь вычисляется по данным, взятым графически с плана или карты;
— аналитический, когда площадь вычисляют непосредственно по результатам полевых измерений или по их функциям – координатам вершин участка;
— механический, когда площадь определяется по плану при помощи специальных приборов, называемых планиметрами.
Часто эти способы применяются комбинированно. Например, общая площадь участка определяется аналитическим способом, а площадь внутренних контуров – графическим или механическим. Рассмотрим каждый из вышеуказанных способов более подробно.

Графический способ определения площадей. Сущность этого способа состоит в том, что данный участок на плане разбивают прямыми линиями на ряд простейших геометрических фигур (обычно треугольники, реже – прямоугольники, квадраты или трапеции) и с помощью циркуля-измерителя и масштабной линейки определяют в каждой фигуре размеры тех элементов, которые необходимы для вычисления площади фигуры.
Вычислив по известным формулам геометрии площади фигур и взяв их сумму, находят общую площадь участка. Ошибка определения площади графическим способом равна примерно 1:100 – 1:200 от величины вычисляемой площади. Для повышения точности определения площадей этим способом следует пользоваться планами наиболее крупного масштаба, а также использовать, где это возможно, данные измерений в натуре.
Площади криволинейных контуров удобно определять при помощи палеток. Палетка (рисунок 3.13) представляет собой сетку квадратов, нанесенную на восковке или прозрачной целлулоидной пластинке. Стороны квадратов могут быть от 2 до 10 мм. Пользование палеткой видно из рисунка 3.13. Для определения площади палетку накладывают на контур и считают число квадратов, поместившихся внутри контура.
Доли неполных квадратов при этом оценивают на глаз. Зная в масштабе плана площадь одного квадрата, умножением на число квадратов находят общую площадь контура. Точность определения площадей палеткой несколько ниже, описанного выше графического способа. Главная ошибка при этом происходит от оценки частей неполных квадратов на глаз. Более высокую точность дают палетки с меньшей стороной квадрата.
Аналитический способ определения площадей. Исходными данными для вычисления площадей данным способом служат координаты вершин многоугольника.
Пусть требуется вычислить площадь полигона 1-2-3-4 (рисунок 3.14), координаты вершин которого известны: 1 (X1, Y1); 2 (Х2, Y2); 3 (Х3, Y3); 4 (Х4, Y4). Из рисунка 3.14 видно, что площадь Р данного четырехугольника представляет собой алгебраическую сумму и разность площадей трапеции:
Раскрыв скобки, выполнив сокращение и приведение подобных членов, получим:
или в общем виде для n-угольника можно записать
Подобным образом из уравнения (3.11) после преобразований можно получить:
 или n
или n
Согласно формулам (3.12) и (3.13) двойная площадь многоугольника равна сумме произведений всех абсцисс на разность ординат последующей и предыдущей вершин, или сумме произведений всех ординат на разность абсцисс предыдущей и последующих вершин.
Следует иметь ввиду, что сумма всех разностей абсцисс (или ординат) от первой до последней точки должна равняться нулю. Это свойство используется для контроля вычисления разностей в формулах (3.12) и (3.13). Погрешность вычисления площадей аналитическим способом не превышает 1:1000 вычисляемой площади.
Механический способ определения площадей. Определение площадей механическим способом производится при помощи планиметров. Наибольшее распространение получил полярный планиметр (рисунок 3.15), состоящий из полюсного и обводного рычагов.
Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом – штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм (рисунок 3.15), состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета.
Червячная передача устроена так, что одному обороту колеса соответствует поворот циферблата на одно деление. Рядом с колесом находится верньер, по которому отсчитывают десятые доли делений колеса или тысячные доли его оборота.

Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья – по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру. Например, отсчет на рисунке 3.15 составит 3215.
При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Р при полюсе вне фигуры вычисляют по формуле
а при полюсе внутри фигуры –
где С – цена деления планиметра;
g – постоянное число планиметра.
Перед работой планиметр необходимо поверить и определить его цену деления и постоянное число.
При проверке планиметра должны быть проверено выполнение следующих условий:
— счетное колесо планиметра должно свободно вращаться на оси без трений и колебаний. Выполнение этого условия достигается регулировкой подшипников оси колеса при помощи исправительных винтов.
— плоскость ободка счетного колеса должна быть перпендикулярна к оси обводного рычага. Для проверки этого условия обводят одну и ту же фигуру при двух положениях планиметра, когда счетный механизм находится слева и справа от фигуры. Если расхождение между разностями отсчетов в обоих случаях не превышает 2-3 делений планиметра, то условие выполнено. В противном случае площадь следует определять при двух положениях планиметра и брать среднее из результатов.
Цену деления планиметра определяют многократными обводами двух-трех квадратов координатной сетки плана или карты при двух положениях планиметра, помещая полюс вне фигуры.
Тогда цена деления будет равна известной площади обводимой фигуры Р, деленной на среднюю разность отсчетов:
После определения цены деления планиметра находят его постоянное число. Для этого обводят планиметром большой квадрат координатной сетки с известной площадью при полюсе внутри фигуры.
Постоянное число планиметра:
При передвижении счетного механизма вдоль обводного рычага изменяется его длина и соответственно изменяется цена деления и постоянное число планиметра. Длина обводного рычага точно фиксируется по шкале с делениями, нанесенными на рычаге.
При определении площадей планиметром необходимо соблюдать следующие правила:
— план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;
— положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;
— обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;
— для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.
Точность определения площадей планиметром зависит от формы и размера обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10–30 см 2 ) ошибка определения площади планиметром не превышает 1:200 величины площади.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Источник
Отображение рельефа играет важную роль, так как он в значительной мере определяет характер всех остальных элементов содержания карт и планов. Кроме того, рельеф влияет на водный режим, на распределение растительности и на пространственное размещение большинства объектов местности. Без достаточно точного отображения рельефа и его детального изучения на карте или плане невозможно установить взаимосвязи между отдельными элементами ландшафта и, следовательно, рационально использовать природные ресурсы.
Традиционным представлением о рельефе местности на топографических картах и планах является его изображение горизонталями. Этот способ нагляден и дает однозначное представление о рельефе местности, позволяет быстро получать количественные характеристики рельефа и решать различные прикладные задачи.
Типы и формы рельефа местности
Рельеф — совокупность неровностей суши, дна океанов и морей, разнообразных по очертаниям, размерам, происхождению, возрасту и истории развития. Слагается из положительных (выпуклых) и отрицательных (вогнутых) форм. Основными формамирельефа являются: гора, котловина, хребет, лощина и седловина. 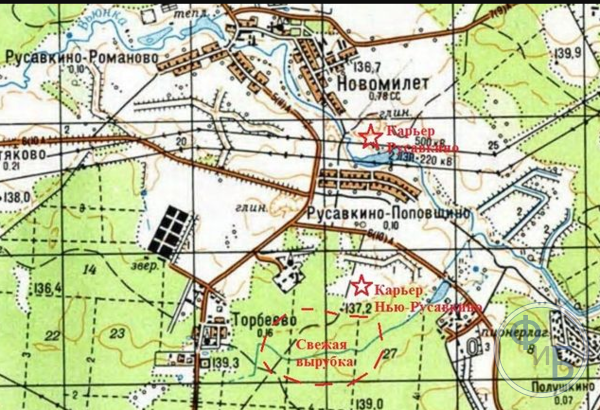
Кроме перечисленных форм рельеф имеет детали. К деталям рельефа относятся: овраги, промоины, курганы, насыпи, выемки, уступы, каменоломни и т. д. Все разновидности форм и деталей рельефа состоят из элементов. Основными элементами рельефа являются: основание (подошва), склон (скат), вершина (дно), высота (глубина), крутизна и направление ската, линии водораздела и водосбора (тальвег).
В военном деле под местностью понимают участок земной поверхности, на котором предстоит вести боевые действия. Неровности земной поверхности называются рельефом местности, а все расположенные на ней объекты, созданные природой или трудом человека (реки, населенные пункты, дороги и т. п.) — местными предметами.
Рельеф и местные предметы являются основными топографическими элементами местности, влияющими на организацию и ведение боя, применение боевой техники в бою, условия наблюдения, ведения огня, ориентирования, маскировки и проходимость, т. е. определяющими ее тактические свойства.
Топографическая карта является точным отображением всех наиболее важных в тактическом отношении элементов местности, нанесенных во взаимно точном расположении относительно друг друга. Она дает возможность изучить любую территорию в относительно короткий срок. Предварительное изучение местности и принятие решения для выполнения подразделением (частью, соединением) той или иной боевой задачи обычно производят по карте, а затем уже уточняют на местности.
Местность, оказывая влияние на боевые действия, в одном случае может способствовать успеху войск, а в другом оказывать отрицательное воздействие. Боевая практика убедительно показывает, что одна и та же местность может больше преимуществ дать тому, кто лучше ее изучит и более умело использует.
По характеру рельефа местность делится на равнинную, холмистую и горную.
Равнинная местность характеризуется небольшими (до 25 м) относительными превышениями и сравнительно малой (до 2°) крутизной скатов. Абсолютные высоты обычно небольшие (до 300 м).
Тактические свойства равнинной местности зависят главным образом от почвенно-растительного покрова и от степени пересеченности. Глинистые, суглинистые, супесчаные, торфяные грунты ее допускают беспрепятственное движение боевой техники в сухую погоду и значительно затрудняют движение в период дождей, весенней и осенней распутицы. Она может быть изрезана руслами рек, оврагами и балками, иметь много озер и болот, значительно ограничивающих возможности маневра войск и снижающих темпы наступления.
Холмистая местность характеризуется волнистым характером земной поверхности, образующей неровности (холмы) с абсолютными высотами до 500 м, относительными превышениями 25 — 200 м и преобладающей крутизной 2-3° (рис. 3, 4). Холмы обычно сложены твердыми породами, вершины и склоны их покрыты толстым слоем рыхлых пород. Понижения между холмами представляют собой широкие, ровные или замкнутые котловины.
Холмистая местность обеспечивает скрытое от наземного наблюдения противника передвижение и развертывание войск, облегчает выбор мест для огневых позиций ракетных войск и артиллерии, обеспечивает хорошие условия для сосредоточения войск и боевой техники. В целом она благоприятна как для наступления, так и для обороны.
Горная местность представляет собой участки земной поверхности, значительно приподнятые над окружающей местностью (имеющей абсолютные высоты 500 м и более). Она отличатся сложным и разнообразным рельефом, специфическими природными условиями. Основные формы рельефа — горы и горные хребты с крутыми скатами, часто переходящими в скалы и скалистые обрывы, а также лощины и ущелья, расположенные между горными хребтами. Горная местность характеризуется резкой пересеченностью рельефа, наличием труднодоступных участков, редкой сетью дорог, ограниченным количеством населенных пунктов, бурным течением рек с резкими колебаниями уровня воды, разнообразием климатических условий, преобладанием каменистых грунтов.
Боевые действия в горной местности рассматриваются, как действия в особых условиях. Войскам часто приходится использовать горные проходы, затрудняется наблюдение и ведение огня, ориентирование и целеуказание, в то же время она способствует скрытности расположения и передвижения войск, облегчает устройство засад и инженерных заграждений, организацию маскировки.
Сущность изображения рельефа на картах горизонталями
Рельеф является важнейшим элементом местности, определяющим ее тактические свойства.
Изображение рельефа на топографических картах дает полное и достаточно подробное представление о неровностях земной поверхности, форме и взаимном расположении, превышениях и абсолютных высотах точек местности, преобладающей крутизне и протяженности скатов.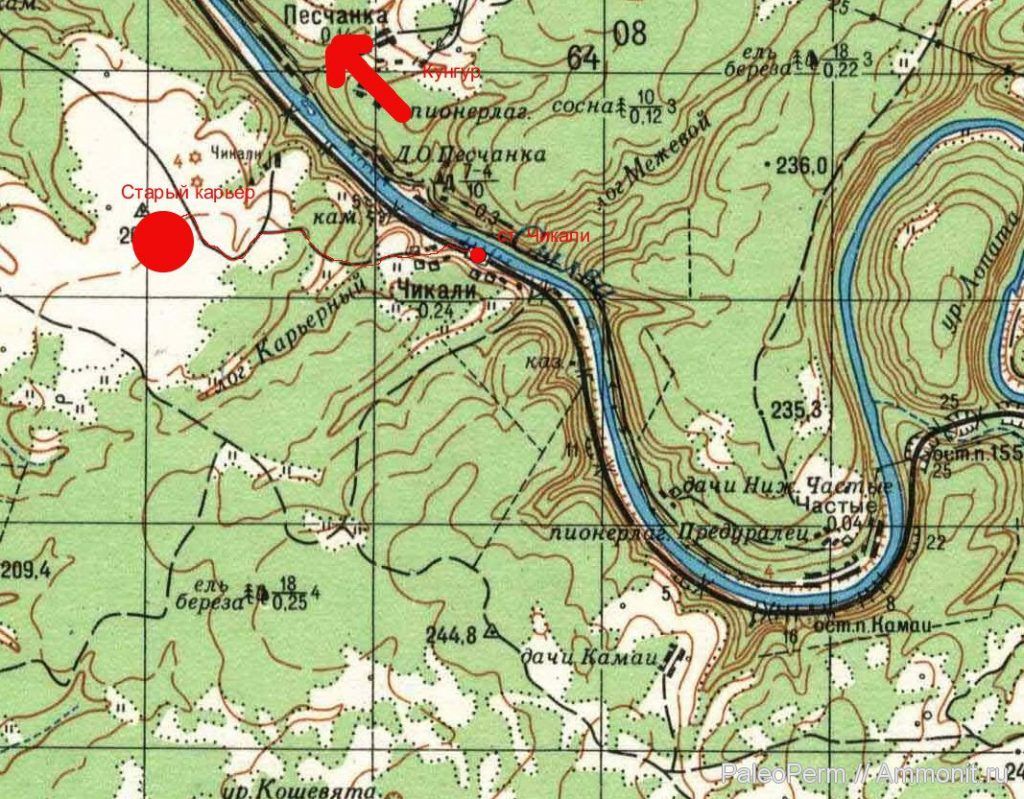
Рельеф на топографических картах изображается горизонталями в сочетании с условными знаками обрывов, скал, оврагов, промоин, каменных рек и т. п. Изображение рельефа дополняется отметками высот характерных точек местности, подписями горизонталей, относительных высот (глубин) и указателями направления скатов (бергштрихами). На всех топографических картах рельеф изображается в Балтийской системе высот, то есть в системе исчисления абсолютных высот от среднего уровня Балтийского моря.
Виды горизонталей
Горизонталь — замкнутая кривая линия на карте, которой соответствует на местности контур, все точки которого расположены на одной и той же высоте над уровнем моря.
Различают следующие горизонтали:
- основные (сплошные) — соответствующие высоте сечение рельефа;
- утолщенные — каждая пятая основная горизонталь; выделяется для удобства чтения рельефа;
- дополнительные горизонтали (полугоризонтали) — проводятся прерывистой линией при высоте сечения рельефа, равной половине основной;
- вспомогательные — изображаются короткими прерывистыми тонкими линиями, на произвольной высоте.
Расстояние между двумя смежными основными горизонталями по высоте называют высотой сечения рельефа. Высоту сечения рельефа подписывают на каждом листе карты под ее масштабом. Например: «Сплошные горизонтали проведены через 10 метров».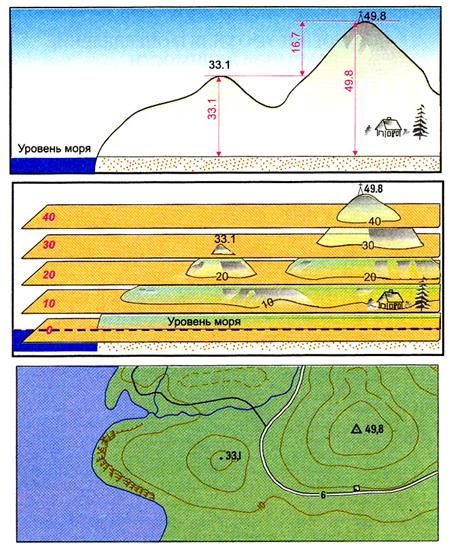
Для облегчения счета горизонталей при определении высот точек по карте все сплошные горизонтали, соответствующие пятой кратной высоте сечения, вычерчиваются утолщенно и на ней ставится цифра, указывающая высоту над уровнем моря.
Для того чтобы при чтении карты можно было быстро определить характер неровностей поверхности на картах, применяются специальные указатели направления скатов — бергштрихи — в виде коротких черточек, расставленных на горизонталях (перпендикулярно им) по направлению покатостей. Они помещаются на изгибах горизонталей в наиболее характерных местах, преимущественно у вершин седловин или на дне котловин.
Дополнительные горизонтали (полугоризонтали) применяются для отображения характерных форм и деталей рельефа (перегибов склонов, вершин, седловин и т. п.), если они не выражаются основными горизонталями. Кроме того, применяют для изображения равнинных участков, когда заложения между основными горизонталями очень велики (более 3 — 4 см на карте).
Вспомогательные горизонтали применяют для изображения отдельных деталей рельефа (блюдец в степных районах, западин, отдельных бугров на плоскоравнинной местности), которые не передаются основными или дополнительными горизонталями.
Изображение горизонталями типовых форм рельефа
Рельеф на топографических картах изображается кривыми замкнутыми линиями, соединяющими точки местности, имеющие одинаковую высоту над уровенной поверхностью, принятой за начало отсчета высот. Такие линии называются горизонталями. Изображение рельефа горизонталями дополняется подписями абсолютных высот, характерных точек местности, некоторых горизонталей, а также числовых характеристик деталей рельефа — высоты, глубины или ширины.
Определение на карте абсолютных высот и относительных превышений точек местности
Профиль — чертеж, изображающий разрез местности вертикальной плоскостью.
Для большей выразительности рельефа местности вертикальный масштаб профиля принимается в 10 или более раз крупнее горизонтального.
В связи с этим профиль, передавая взаимное превышение точек, искажает (увеличивает) крутизну скатов.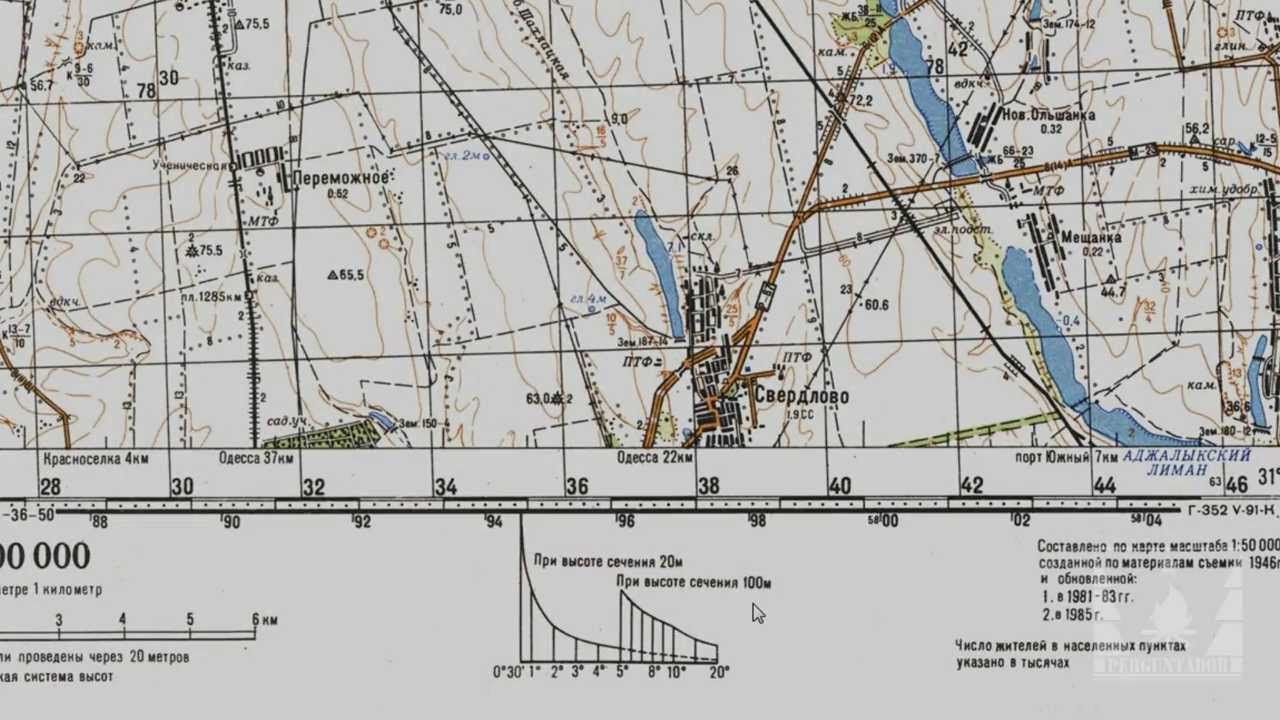
Для построения профиля нужно:
- прочертить на карте профильную линию (маршрут движения), приложить к ней лист разграфленной (миллиметровой) бумаги, перенести на ее край короткими черточками места горизонталей, точки перегиба скатов и местные предметы, которые сечет профильная линия, и подписать их высоты;
- подписать на листе разграфленной бумаги у горизонтальных линий высоты, соответствующие высотам горизонталей на карте, приняв условно промежутки между этими линиями за высоту сечения (установить вертикальный масштаб);
- от всех черточек, обозначающих места пересечения профильной линии с отметками высот горизонталей, точек перегиба скатов и местных предметов, опустить перпендикуляры до пересечения их с соответствующими по отметкам параллельными линиями и отметить полученные точки пересечения;
- соединить точки пересечения плавной кривой, которая и изобразит профиль местности (подъемы и спуски на маршруте движения).
Определение на карте крутизны скатов
Крутизна ската на карте определяется по заложению — расстоянию между двумя смежными основными или утолщенными горизонталями; чем меньше заложение, тем круче скат.
Для определения крутизны ската надо измерить расстояние между горизонталями циркулем, найти соответствующий отрезок на графике заложений и прочитать число градусов.
На крутых скатах это расстояние измеряется между утолщенными горизонталями, и крутизна ската определяется по графику, расположенному справа.
Рельефом местности называется совокупность
неровностей земной поверхности. на
планах рельеф изображается при помощи
условных специальных знаков, от которых
требуется:
– подробно и точно показать расположение
всех форм неровностей местности,
характеризующих ее расчлененность и
доступность;
– обеспечить возможность определения
высот точек местности и превышений
(разность высот) одних точек над другими,
направление склонов и их крутизну;
– наглядно изображать рельеф, позволяя,
возможно яснее представить действительный
ландшафт местности.
На современный топографических планах
и картах рельеф изображается горизонталями,
дополненными абсолютными отметками и
Берг-штрихами.
Под горизонталью понимается след от
пересечения земной физической поверхности
секущей (уровенной) поверхностью.
Горизонтали (изобаты) – это линии равных
высот (отметки) или глубин. Отметкой
называется высота точки местности над
уровенной поверхностью.

Рис.3 Изображение горы горизонталями.
На рис.3 показано построение горизонталей
для небольшого участка местности, где
уровенные поверхности можно считать
плоскостями. Секущие плоскости Р1, Р2,
Р3 параллельны начальной (отсчетной)
плоскости Р. Расстояние между ними hназывается высотой сечения рельефа. На
топографических планах и картах высота
сечения устанавливается в зависимости
от масштаба и сложности рельефа. На
равнинных участках высота сечения мала,
а на горной местности велика. Обычно
высота сечения принимается равной 1, 2,
5, 10, 20, 50, 100 метров. Отметки горизонталей
подписываются либо для горизонталей
кратных 5м, либо для каждой пятой
горизонтали при большей высоте сечения
рельефа. Надпись делается в разрыве.
При этом верх цифр направляется в сторону
повышения местности. Подписываемые
горизонтали утолщаются.
Помимо направления верха цифр надписей
горизонталей, о направлении склонов
дают представление Берг-штрихи, которые
вычерчиваются от горизонталей в сторону
понижения местности. Так, на рис.3
берг-штрихи показывают направление
склонов горы, если их расставить наоборот,
не меняя горизонталей, то будет изображение
котловины.
Расстояние между горизонталями на плане
в любом направлении называется заложением
и обозначается буквой а. Связь между
высотой сечения рельефа и заложением
определяется формулой: i=h/a,
гдеi– уклон склона,h– высота сечения, а – заложение.
Задание для самостоятельной работы:
1. Построить сетку квадратов 3х4 квадрата
со стороной 5 см (Рис.4), что на местности
при численном масштабе плана 1:2000
соответствует 100 м.
2. Рассчитать отметки в вершинах квадратов.
Расчет выполняется по формуле Hв=HRp+h(сложение алгебраическое, т.е. с учетом
знакаh), гдеHв– отметка в вершине квадрата.HRp– отметка репера (закрепленное на
местности точки), задаваемая преподавателем,
индивидуально для каждого студента.
Вычисляемые отметки выписываются у
соответствующих вершин с округлением,
до десятых долей метра. Далее методом
интерполяции находят те места, где
стороны квадратов будут пересекать
горизонтали. После соединяют точки
равных высот, кратные 1 метру, при этом
учитываются все стороны квадратов и
диагонали. Горизонтали, кратные 5 метрам
утолщают и в разрывах подписывают их
отметку. Отметка подписывается так,
чтобы цифры верх был направлен вверх
по склону. После прорисовываются
Берг-штрихи вниз по склону. Все горизонтали
и берг-штрихи вырисовываются коричневой
тушью.
Если отметка (репер) не дана преподавателем,
то значение отметки следует принять
условно: количество
целых метров в отметке должно быть
трехзначным
числом, в котором количество сотен
метров равно единице, а количество
десятков и единиц метров составляют
две последние цифры шифра студента.
В дробной части отметки (дм, см, мм)
ставятся те же цифры, что и в целой
части.
Пример:
|
Зуев |
АД — 66229 |
129,129 |
|
Иванова |
МТ — 67020 |
120,120 |
|
Соколов-Осадчий |
АД — 68002 |
102,102 |
|
Руднев |
МТ — 65100 |
100,100 |
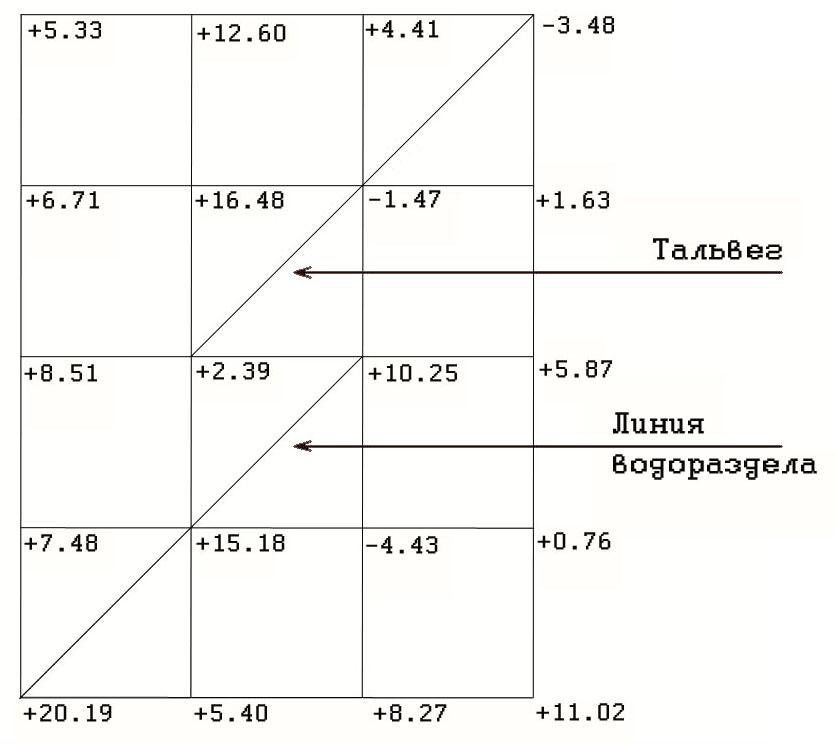
Рис. 4 Превышение точек над репером.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как провести горизонталь
Горизонталью называют кривую линию, проведенную через точки местности, имеющие одинаковые отметки. Для того, чтобы передать на карте особенности рельефа, необходимо провести не одну, а несколько таких линий. Они получаются в результате сечения рельефа параллельными плоскостями, находящимися на равных по высоте расстояниях друг от друга.
Вам понадобится
- – GPS-навигатор;
- – нивелир;
- – компас;
- – карта с координатной сеткой;
- – реперы или деревянные колышки;
- – географический объект.
Инструкция
Определите вид объекта, рельеф которого вам надо обозначить. К основным формам рельефа относятся горы, хребты, седловины, лощины и котловины. Найдите опорные точки и определите их координаты. У горы это будет вершина, у хребта – самая высокая из вершин и верхняя точка линии водораздела. Для седловины важно найти вершины и самую низкую точку находящегося между ними углубления. Для котловины важно дно, а для лощины – начало линии водослива. С помощью навигатора определите их координаты. Нанесите точки на карту.
Определите высоту над уровнем моря самой высокой и самой низкой точек рельефа. Это также можно сделать с помощью навигатора. Нанесите результаты на карту. Вычислите общую высоту или глубину объекта H, отняв от показателя самой высокой точки результат для самой низкой.
Вычислите высоту сечения рельефа h. Она представляет собой частное от деления высоты H на равное количество частей. Оно зависит от масштаба карты и сложности рельефа. Для крупномасштабной карты высота сечения должна быть меньше, то есть разделить общую высоту необходимо на большее количество частей. На 1 кв. дм карты должно находиться 5 отметок или даже больше.
Начните выносить отметки с самой длинной линии. У горы это будет подножие, у котловины – ее верхняя часть. Обойдите с навигатором и картой объект по периметру. Ищите точки, имеющие одну и ту же высоту над уровнем моря. Обнаружив такую точку, нанесите ее на карту, записав координаты. Количество измерений тоже зависит от сложности рельефа.
Вернувшись к исходной точке, соедините все обозначения замкнутой кривой линией. Это и есть горизонталь. На картах она обычно обозначается линией коричневого цвета. Подпишите отметку. Верхняя часть цифр должна быть направлена в сторону повышения рельефа. Точно таким же образом нанесите на карту и остальные горизонтали.
Видео по теме
Обратите внимание
Если вам предстоит не просто нанести линию на карту, а, допустим, что-то построить на склоне – пометьте точки и на местности. Обычно в геодезии это делается с помощью реперов, но можно использовать обычные деревянные колья, на которые наносится отметка.
Полезный совет
В некоторых случаях приходится пользоваться дедовскими методами. Например, если объект слишком мал. Это может быть холм или овраг. Сначала определите и обозначьте на плане стороны света. Затем вынесите отметки, используя деревянные нивелиры. Это 2 рейки длиной ровно 1 м. К каждой из них крепится поперечина, к которой для обеспечения вертикальности крепится отвес. Такое нивелирование проводится вдвоем. Один участник устанавливает свой нивелир, например, на вершине холма. Второй спускается вниз по склону, ставит свой нивелир и целится визиром в нижнюю точку первого нивелира.Затем то же проделывает первый участник. Таким образом измерьте высоту всего холма. Определите высоту сечения. В данном случае она может составлять всего 1 м. Остальные работы проводятся точно так же, как и с навигатором или другими современными приборами.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Горизонталь плоскости
Горизонталь плоскости – одна из главных линий плоскости.

Горизонталь плоскости
На рисунке показаны:
горизонталь плоскости α – h,
фронталь υ плоскости α,
профильная прямая ω плоскости α,
задание линий уровня на эпюре.
Главными линиями плоскости называют:
1. Прямые, принадлежащие плоскости и параллельные какой-либо плоскости проекции.
2. Прямые принадлежащие плоскости и перпендикулярные к какой-либо линии, отмеченной в пункте 1.
Прямые, параллельные плоскости проекции (1), принадлежат плоскости уровня, поэтому их называют также, прямыми (или линиями) уровня.
Линии уровня подразделяют на три вида:
а) Если h⊂α ^ h║H, то прямая h представляет собой горизонталь плоскости α;
б) В случае когда υ⊂α ^ υ║V, то прямую υ называют фронталь плоскости α;
в) В случае когда ω⊂α ^ ω║W, то прямую ω называют профильная прямая плоскости α.
| Наименование линии | Горизонтальная проекция | Фронтальная проекция | Профильная проекция |
| Горизонталь | ║αH | ║оси x | ║оси y |
| Фронталь | ║оси x | ║αV | ║оси z |
| Профильная прямая | ║оси y | ║оси z | ║αW |
В плоскости можно провести множество горизонталей
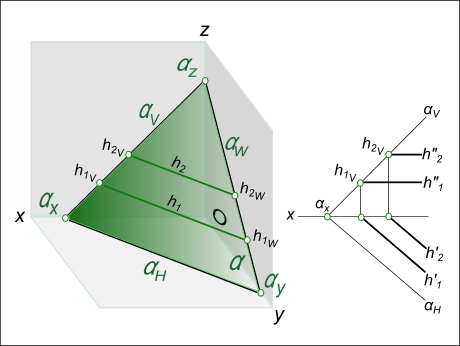
Горизонталь плоскости
и по горизонталям плоскости построить следы плоскости, то есть перейти от какого то способа задания плоскости к заданию следами.
И наоборот, от задания плоскости следами, по горизонталям плоскости можно перейти к другим способам задания той же самой плоскости.
построить горизонталь треугольника ABC
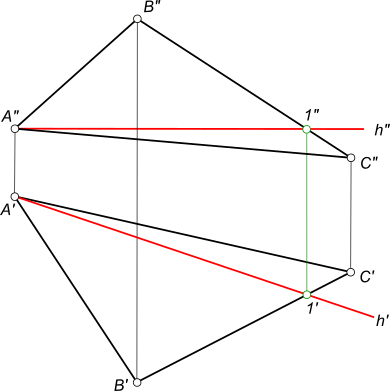
Горизонталь плоскости
чтобы построить горизонталь плоскости выраженной треугольником ABC необходимо:
– построить фронтальную проекцию h” искомой горизонтали, причем h” ‖ x, проводим из вершины A треугольника, достигая этим цели наименьшим количеством построений;
– в пересечении h” с B”C” противолежащей стороной треугольника отмечаем точку 1″;
– находим 1` в пересечении ее линии проекционной связи со стороной B`C`;
– находим h` искомой горизонтали, соединив прямой линией точки A` и 1`.
+