Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
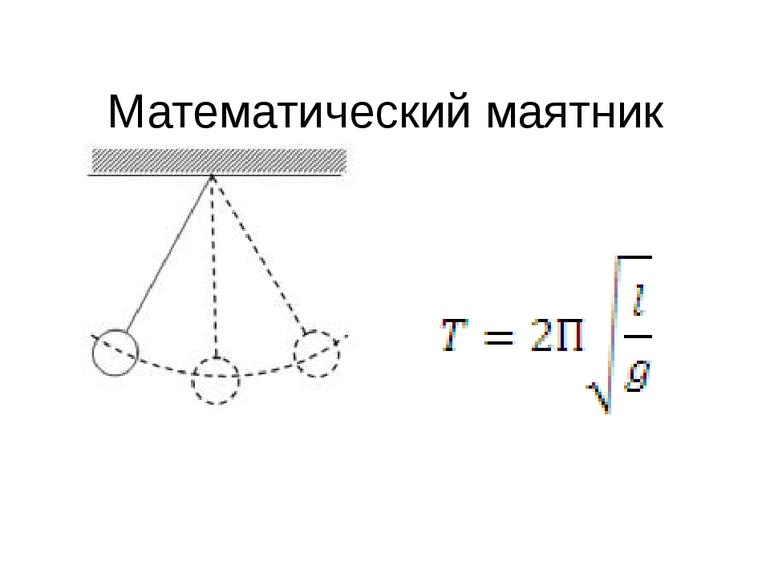
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание:
Пружинные и математические маятники:
Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.
Система, состоящая из груза массой
Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:
Если учесть, что ускорение тела, совершающего гармонические колебания 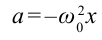
Из этого уравнения мы имеем:
Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника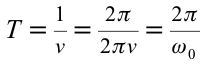
Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, 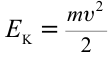
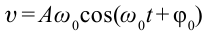
Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:
В большинстве случаев важно знать полную энергию системы:
Если учесть, что 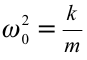
Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
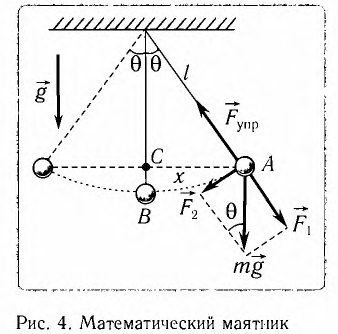
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.
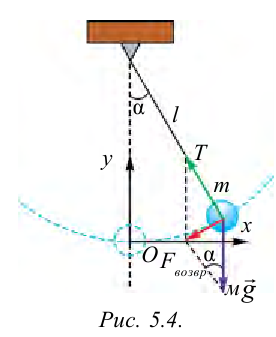
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки 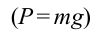

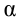
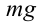

Из рис. 5.4. видим, что:
Согласно второму закону Ньютона, сила 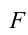
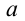
Из-за того, что угол наклона очень маленький 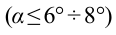
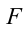
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой 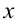
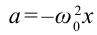
Следовательно
Исходя из смысла периода колебания и учитывая, что 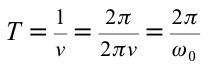
Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:
- при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
- период колебания математического маятника также не зависит от массы подвешенного на него груза;
- период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.
Отсюда колебание математического маятника записывается следующим выражением:
Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 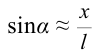
Пример:
Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.
Дано:
Найти:
Формула:
Решение:
Ответ: 5 cек.
Пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
Закон Гука: модуль силы упругости 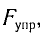
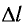
где k — жесткость тела, 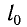
Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.
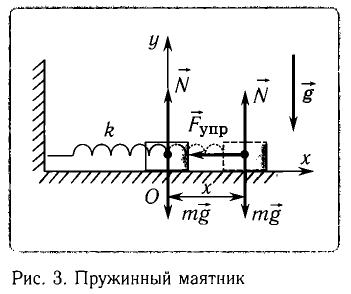
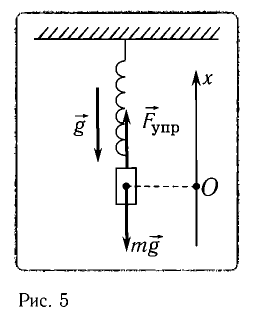
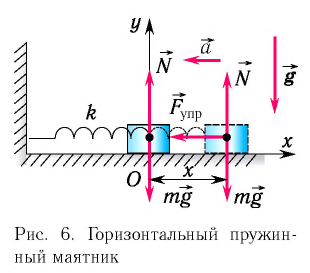
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).
Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 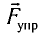
Запишем второй закон Ньютона для движения груза:
В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем
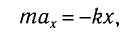
Следовательно,
Это уравнение аналогично уравнению гармонических колебаний
Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:
Тогда период колебаний пружинного маятника можно найти по формуле
Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов 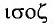
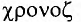
Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).
Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.
Галилео Галилей экспериментально определил, что период малых колебаний (9 < 10°) математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения 
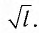
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
При углах отклонения математического маятника 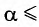
Отклонение маятника от положения равновесия будем характеризовать углом 
Согласно второму закону Ньютона для движения шарика можем записать:
Смещение маятника вдоль дуги х = l

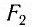
Заметим, что при малых углах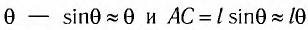
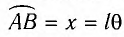
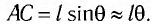


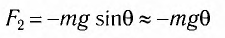
является очень хорошим приближением.
Подставляя в выражение (1) значение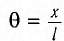
Таким образом, уравнение движения маятника запишется в виде
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 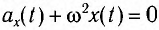
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 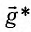
Пример:
Определите амплитуду А, циклическую частоту 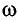
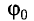
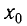
Решение
Циклическая частота колебаний «вертикального» пружинного маятника также определяется по формуле
Найдем жесткость k пружины. Из условия равновесия тела следует
По закону Гука
В проекции на ось Ох условие равновесия запишется в виде:
Отсюда для циклической частоты 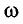
Так как по условию задачи тело сместили на расстояние х = 30 мм от положения равновесия, то амплитуда его колебаний
Период колебаний находим из соотношения
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний
Ответ:
Пример:
Металлический шарик, подвешенный на длинной легкой нерастяжимой нити, поднимают по вертикали до точки подвеса и отпускают. Затем нить маятника отклоняют на небольшой угол от вертикали и также отпускают. В каком из этих случаев шарик быстрее возвратится в начальное положение?
Решение
В первом случае шарик свободно падает без начальной скорости с высоты h = l, следовательно,
Отсюда находим промежуток времени 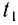
Во втором случае промежуток времени 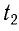
Поскольку в начальный момент времени t = 0 маятник имеет максимальное
отклонение от положения равновесия, то начальная фаза колебаний 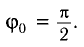
Используя формулу для периода колебаний математического маятника
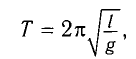
Разделив почленно уравнения для промежутков времени 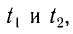
Ответ: шарик быстрее возвратится в начальное положение в случае, когда он движется вертикально вниз.
Пример:
Найдите периоды колебаний математического маятника длиной l= 1,0 м при перемещении его точки подвеса с ускорением, модуль которого а = 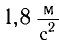
Решение
Период колебаний математического маятника в поле силы тяжести Земли
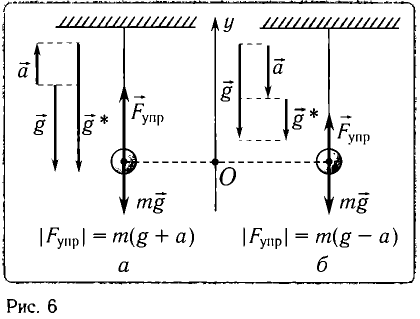
а) При движении маятника с ускорением 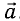
где Fy — проекция силы упругости нити.
Откуда находим
где g* = g + а — «эффективное ускорение».
Период колебаний определяется по формуле
б) При движении точки подвеса маятника с ускорением 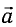
где Fy — проекция силы упругости нити. Откуда находим
где g*=g-a — «эффективное ускорение». Период колебаний
Ответ:
Что такое пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение тела прямо пропорционально результирующей силе и обратно пропорционально массе тела:
Закон Гука: при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален модулю изменения длины тела:
где 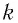
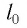
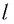
Колебательная система, состоящая из тела с прикрепленной к нему пружиной, называется пружинным маятником. Пружина может располагаться как вертикально (вертикальный пружинный маятник), так и горизонтально (горизонтальный пружинный маятник).
Рассмотрим колебания горизонтального пружинного маятника. Пусть груз массой 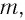
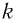
Выведем груз из положения равновесия, сместив его на расстояние 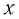
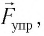
Согласно второму закону Ньютона для движения груза
В проекции на ось 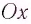
или
Перепишем полученное соотношение в виде:
которое является уравнением гармонических колебаний пружинного маятника.
Сравнивая (1) с уравнением гармонических колебаний 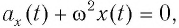
которая определяется массой 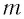
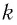
Для нахождения периода колебаний пружинного маятника воспользуемся формулой 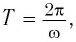
Как следует из формул (2) и (3), период и частота колебаний пружинного маятника не зависят от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греч. 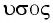
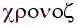
Изохронность колебаний маятника была открыта Гали-лео Галилеем в 1583 г. при изучении движения груза, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
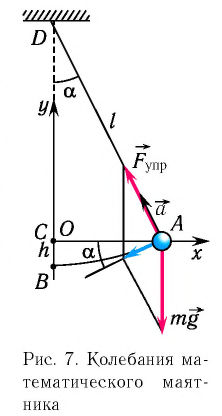
Колебательная система, состоящая из находящегося в поле силы тяжести тела, подвешенного на легкой нерастяжимой нити, размеры которого малы по сравнению с длиной нити, а его масса значительно больше массы нити, называется математическим маятником. При таких условиях тело можно считать материальной точкой, а нить — легкой нерастяжимой (рис. 7).
Рассмотрим колебания математического маятника.
Отклонение маятника от положения равновесия будем характеризовать углом 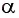
После отклонения маятника на него действуют две силы: направленная вертикально вниз сила тяжести 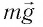
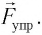
Согласно второму закону Ньютона для движения маятника можем записать:
В проекциях на выбранные оси координат 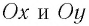
Для углов отклонения 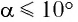
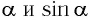
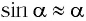
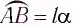
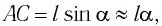
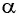
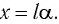
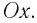
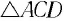
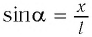
Таким образом, силой, возвращающей маятник к устойчивому положению равновесия, является сила упругости его нити.
При малых углах отклонения маятника проекция вектора ускорения 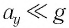
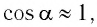
Следовательно, уравнение движения маятника вдоль оси 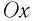
где 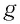
Отсюда получаем уравнение гармонических колебаний математического маятника:
При сравнении уравнения (8) с уравнением гармонических колебаний 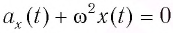
Тогда период малых колебаний математического маятника в поле тяжести Земли определяется по формуле Гюйгенса:
которую впервые получил ученик И. Ньютона Христиан Гюйгенс.
При углах отклонения математического маятника 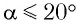
Как видно из формул (9) и (10), циклическая частота и период математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной 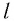
Галилео Галилей первый экспериментально определил, что период малых колебаний 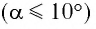
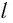
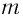
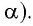
Если маятник приобретает дополнительное ускорение 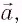
где 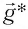
- Заказать решение задач по физике
Пример:
Выведите формулу для периода колебаний вертикального пружинного маятника, если масса груза 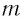
Решение
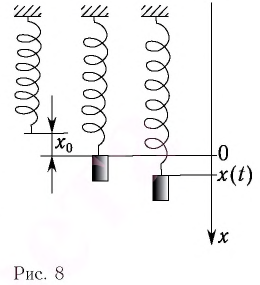
Рассмотрим вертикальное движение груза, происходящее под действием силы упругости пружины и силы тяжести груза после толчка. Начало координат поместим в точку, соответствующую равновесному положению тела (рис. 8). В этом положении пружина растянута на величину 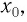
При смещении груза на величину 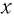
Тогда по второму закону Ньютона
С учетом соотношения (1) это уравнение перепишем в виде:
Если ввести обозначение 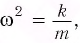
Оно описывает гармонические колебания вертикального пружинного маятника с частотой такой же, как у горизонтального пружинного маятника. Следовательно, период колебаний вертикального пружинного маятника такой же, как и горизонтального:
Ответ:
Таким образом, действующая в колебательной системе постоянная сила только смещает положения равновесия, но не изменяет частоту колебаний.
Пример:
Определите амплитуду 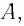
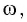
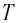
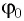
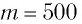
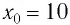
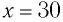
Дано:
Решение
Циклическая частота колебаний вертикального пружинного маятника так же, как и горизонтального, определяется по формуле (см. пример 1):
Для нахождения жесткости к пружины запишем условие равновесия тела:
По закону Гука
В проекции на ось 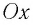
Отсюда для циклической частоты 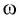
Амплитуда колебаний маятника определяется начальным смешением:
Период колебаний находим из соотношения:
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний
Ответ:
Подробное объяснение пружинного и математического маятника
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
Закон Гука: модуль силы упругости 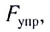
где k — жесткость тела, 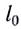
Простейшая колебательная система может быть получена с использованием груза и пружины.
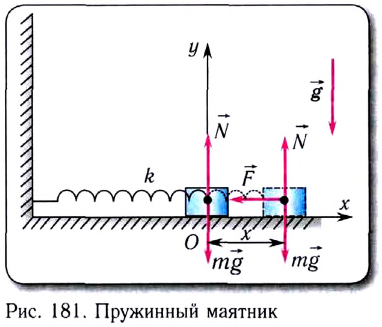
Прикрепим груз массой m, лежащий на гладкой горизонтальной поверхности, к невесомой упругой пружине жесткостью k, второй конец которой зафиксирован (рис. 181). Такая система называется пружинным маятником.
Запишем второй закон Ньютона для этой системы
В проекции на ось Ох с учетом закона Гука получаем
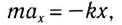
Запишем это уравнение в форме, аналогичной уравнению движения гармонического осциллятора:
Сравнивая полученное выражение с уравнением гармонических колебаний
находим циклическую частоту колебаний пружинного маятника
Тогда период колебаний пружинного маятника можно найти по формуле
Свойство независимости периода колебаний маятника от амплитуды, открытое Галилеем, называется изохронностью (от греческих слов 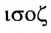
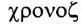
Как видим, пружинный маятник обладает свойством изохронности, поскольку период его колебаний не зависит от амплитуды.
Одной из наиболее распространенных колебательных систем является математический маятник.
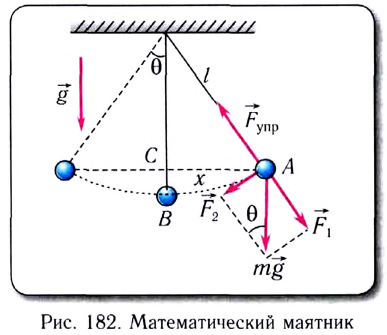
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 182).
Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
При углах отклонения математического маятника 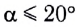
Отклонение маятника от положения равновесия будем характеризовать углом 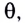
Из второго закона Ньютона следует (см. рис. 182):
Смещение маятника вдоль дуги 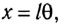
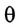
Возвращающей силой в данном случае является проекция на касательную к дуге силы тяжести 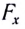
Заметим, что при малых углах 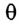
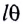
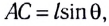
Для небольших углов (до 10°) значения 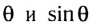
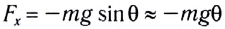
Используя полученное соотношение между координатой х и углом 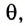
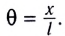
Таким образом, уравнение движения маятника запишется в виде
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 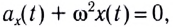
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 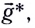
Математический и пружинный маятники и энергия колебаний
Колебательные движения очень разнообразны. При этом существует «классика» колебательных движений — они описаны сотни лет назад, их изучением занимались Галилео Галилей (1564– 1642) и Христиан Гюйгенс (1629–1695). Это колебания пружинного и математического маятников.
Колебания пружинного маятника
Пружинный маятник — это колебательная система, представляющая собой закрепленное на пружине тело.
Рассмотрим колебания горизонтального пружинного маятника — тележки массой m, закрепленной на пружине жесткостью k. Будем считать, что силы трения, действующие в системе, пренебрежимо малы, а значит, колебания маятника незатухающие (их амплитуда с течением времени не изменяется, а полная механическая энергия системы сохраняется). При этом потенциальная энергия деформированной пружины будет превращаться в кинетическую энергию движения тележки, и наоборот.
Колебания пружинного маятника:
Обратите внимание! В течение всего времени колебания сила упругости направлена в сторону, противоположную смещению тележки, — сила упругости все время «толкает» тележку к положению равновесия.
Итак, причины свободных колебаний пружинного маятника: 1) действующая на тело сила всегда направлена к положению равновесия; 2) колеблющееся тело инертно, поэтому оно не останавливается в положении равновесия (когда равнодействующая сил становится равной нулю), а продолжает движение в том же направлении.
Как вычислить период колебаний пружинного маятника
Рассмотрим колебания тележки, закрепленной на горизонтальной пружине, с точки зрения второго закона Ньютона (рис. 20.1). Запишем уравнение второго закона Ньютона в векторном виде:
Сила тяжести и сила нормальной реакции опоры уравновешивают друг друга, поэтому 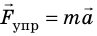
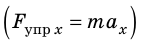
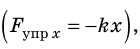
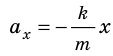
Последнее уравнение можно записать в виде 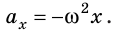
Приняв во внимание, что 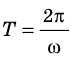
Обратите внимание! Период колебаний пружинного маятника не зависит ни от амплитуды колебаний, ни от места расположения маятника (на поверхности Земли или Луны, в космическом корабле и т. д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость k пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
Что называют математическим маятником
Любое твердое тело, которое совершает или может совершать колебания относительно оси, проходящей через точку подвеса, называют физическим маятником. Примером может быть игрушка, подвешенная на нити в салоне автомобиля. Если игрушку вывести из положения равновесия, она начнет колебаться. Однако изучать такие колебания сложно: их характер определяется размерами и формой игрушки, свойствами нити и другими факторами.
Чтобы размеры тела не влияли на характер его колебаний, следует взять нить, длина которой намного больше размеров тела, а масса незначительна по сравнению с его массой. В таком случае тело можно считать материальной точкой. А чтобы во время колебаний тело все время находилось на одинаковом расстоянии от точки подвеса, нить должна быть нерастяжимой. Таким образом будет получена физическая модель — математический маятник.
Математический маятник — это физическая модель колебательной системы, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити, и гравитационного поля.
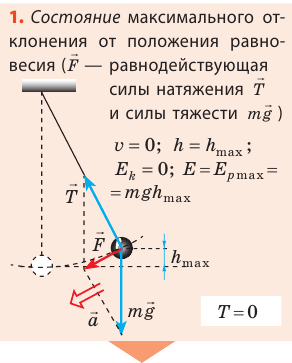
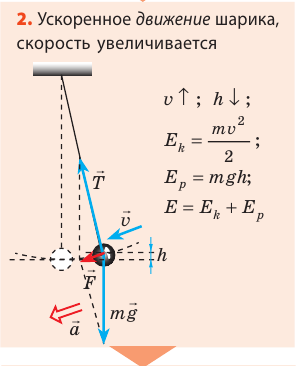
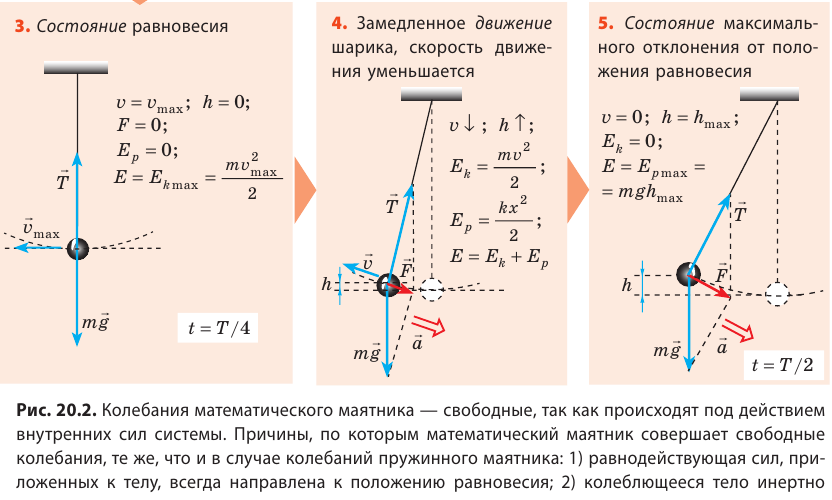
Колебания математического маятника
Возьмем небольшой, но достаточно тяжелый шарик и подвесим его на длинной нерастяжимой нити — такой маятник можно считать математическим. Если отклонить шарик от положения равновесия и отпустить, то в результате действия гравитационного поля Земли (силы тяжести) и силы натяжения нити шарик начнет колебаться около положения равновесия. Поскольку сопротивление воздуха пренебрежимо мало, а силы, действующие в системе, являются консервативными, полная механическая энергия шарика будет сохраняться: потенциальная энергия шарика будет превращаться в его кинетическую энергию, и наоборот.
Рассмотрите колебательное движение шарика (рис. 20.2). Объясните причины его движения. Какие происходят превращения энергии?
Как вычислить период колебаний математического маятника
Математический маятник, отклоненный от положения равновесия на небольшой угол (3–5°), будет совершать гармонические колебания, то есть ускорение его движения все время будет прямо пропорционально смещению и направлено в сторону, противоположную смещению:
Для математического маятника: 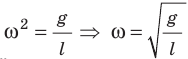
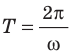
где l — длина маятника; g — ускорение свободного падения.
Данную формулу впервые получил в XVII в. голландский ученый Христиан Гюйгенс, поэтому ее называют формулой Гюйгенса.
Период колебаний математического маятника не зависит от массы маятника, а определяется только длиной нити и ускорением свободного падения в том месте, где расположен маятник. Поэтому, измерив длину нити и период колебаний маятника, можно определить ускорение свободного падения в данной местности.
Пример:
Уравнение колебаний груза массой 1 кг на пружине имеет вид: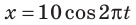
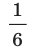
Решение:
Трение отсутствует, поэтому полная механическая энергия сохраняется:
Сравним уравнение колебаний в общем виде с уравнением, приведенным в задаче:
Поскольку
Определив удлинение пружины через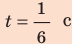
Выводы:
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июля 2022 года; проверки требует 1 правка.
Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Дифференциальное уравнение движения физического маятника[править | править код]
Момент инерции относительно оси, проходящей через точку подвеса, по теореме Штейнера:
,
где 

Динамическое уравнение произвольного вращения твёрдого тела:
,
где 
,
где 

Момент, вызванный силой тяжести, зависит от угла отклонения тела от положения равновесия:
.
Если пренебречь сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести:
.
Если разделить обе части уравнения на 
,
получим:
.
Такое уравнение аналогично уравнению колебаний математического маятника длиной 

Центр качания физического маятника. Теорема Гюйгенса[править | править код]
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести, точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром тяжести. Тогда момент инерции относительно оси подвеса будет равен 

Согласно теореме Гюйгенса,
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Вычислим приведённую длину для нового маятника:
.
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
Период колебаний физического маятника[править | править код]
Наиболее общий случай[править | править код]
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.
Для этого умножим левую 

.
Интегрируя это уравнение, получаем:
,
где 



Подставляем и преобразовываем получившееся уравнение:
Отделяем переменные и интегрируем это уравнение:
.
Удобно сделать замену переменной полагая 
Здесь 
Здесь 
Период малых колебаний физического маятника[править | править код]
Если 



Период колебания маятника в этом случае:
В иной формулировке: если амплитуда колебаний 
Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.
Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах отклонения до 1 радиана (≈57°):
См. также[править | править код]
- Математический маятник
- Маятник Дубошинского
Ссылки[править | править код]
- маятник — статья из Большой советской энциклопедии.
Простая гравитация
Так называемый простой маятник — это всего лишь идеализированная математическая модель. Это груз на конце безмассового шнура, подвешенного на оси без трения. Если его толкнуть, он будет раскачиваться с постоянной амплитудой, но с некоторыми условиями:
- Стержень или нить, на котором качается отвес, не имеет массы и не может растягиваться.
- Груз — это точечная масса.
- Движение происходит только в двух измерениях, то есть отвес не может очертить эллипс, а только дугу.
- Энергия движения не расходуется на трение или сопротивление воздуха.
- Гравитационное поле однородно.
- Поддержка всей конструкции не двигается.
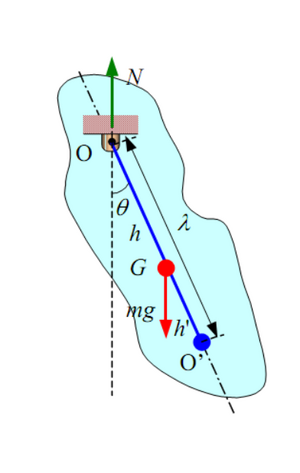
Дифференциальное уравнение, которое представляет движение простого маятника, выглядит следующим образом (где g – ускорение силы тяжести, ℓ – длина маятника, θ – угловое смещение): d² / dt² + g / ℓ sin θ = 0.
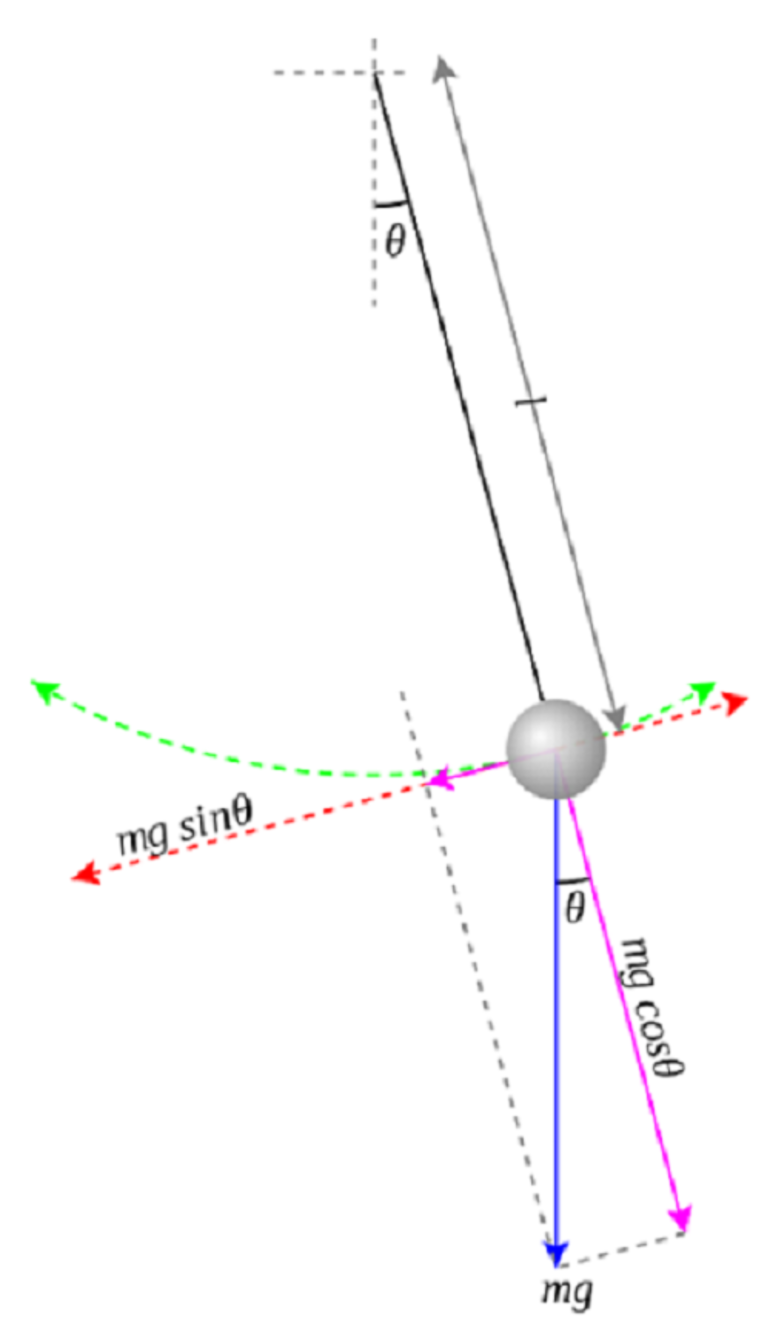
На графике 1 показаны силы, действующие на отвес. Стоит обратить внимание, что груз описывает дугу. Угол θ измеряется в радианах, и это имеет решающее значение для этой формулы. Синяя стрелка — гравитационная сила, которая действует на маятник, а фиолетовые векторы — это та же самая сила, только разложенная на компоненты, параллельные и перпендикулярные мгновенному движению груза.
График 1.
Направление мгновенной скорости всегда указывается вдоль красной оси, которая считается тангенциальной, поскольку её направление всегда касается окружности. И прежде чем вывести уравнение силы деривации, стоит вспомнить второй закон Ньютона: F = ma. За F принимают сумму сил, действующих на объект, m – масса, a — ускорение.
Поскольку интерес составляет только измерение скорости, а груз вынужден оставаться на круговой траектории, уравнение Ньютона применяется только к тангенциальной оси. Короткая фиолетовая стрелка представляет компонент гравитационной силы, используя тригонометрию можно определить её величину. Таким образом, получается (g – ускорение силы тяжести вблизи поверхности земли): F = – mg sin θ = ma; a = – g sin θ.
Отрицательный знак на правой стороне означает, что θ и отвес всегда указываются в противоположных направлениях. Это вполне логично, поскольку когда маятник качается сильнее влево, ожидается, что он ускорится при движении назад — вправо. Это линейное ускорение, a вдоль красной оси может быть связано с изменением угла θ по формулам длины дуги (s): s = ℓθ; v = ds / dt = ℓdθ / dt; a = d²s / dt² = ℓd²θ / dt². Из этого следует: ℓd²θ/dt² = – gsin θ, d²θ / dt² + d / ℓ sin θ = 0.
Крутящий момент
Для начала нужно определить этот показатель на маятниковом шарнире, используя силу, вызванную гравитацией (Fg): T = ℓ x Fg, где ℓ – векторы длины маятника.
Здесь самое время рассмотреть величину крутящего момента на маятнике: |T| = – mgℓ sinθ, где m – масса, g – ускорение силы тяжести, ℓ – длина, а θ – угол между вектором длины и гравитацией. Далее, самое время переписать момент импульса: L = r x p = mr x (ꞷ x r).
Просто величина углового момента и его производная по времени: |L| = mr² w = mℓ² d²θ / dt². Формула крутящего момента после всех вычислений будет выглядеть следующим образом: T = r x F = dL / dt.
Сохранение механической энергии
Такое уравнение можно получить с помощью одноимённого принципа. Формулируется он так: любой объект, падающий на вертикальное расстояние h, получит кинетическую энергию, равную той, которую потерял при падении. Изменение потенциальной энергии выражается: Δ U = mgh, тогда как кинетическая (отвес начал движение с покоя) представлена формулой: Δ K = 1/2 mu².
Поскольку, как известно, никакая энергия не теряется, выигрыш в одном должен быть равен потере в другом: 1/2 mu² = mgh.
Колебательные движения
Период колебаний математического маятника (простого гравитационного) зависит от его длины, локальной силы тяжести и в небольшой степени от максимального угла, от которого отвес отклоняется от вертикали θ 0, называемого амплитудой.
Он не зависит от массы груза. Если амплитуда ограничена малыми колебаниями, то на период T, время, необходимое для полного цикла является: T≈ 2 π √ L/g. При этом L – длина маятника, а g – местное ускорение гравитации.
Нужно сказать, что для небольших колебаний период не зависит от амплитуды. Такое свойство называется изохронизмом, именно оно стало причиной того, что маятники используются для хронометража. Последовательные колебания маятника, даже если они меняются по амплитуде, занимают одинаковое количество времени. Для большого размаха свойственно увеличение периода с каждым раскачиванием, поэтому он длиннее, чем задано уравнением, отражающим частоту колебаний математического маятника.
Период возрастает до бесконечности как только θ 0 приближается к 180°, так как это значение является нестабильной точкой равновесия для маятника. Истинный период может быть записан в нескольких различных формах, например, бесконечный ряд: T = 2 π √ L/g )1+ 1/16 θ²/º + 11/3072 θ ⁴/º + …). Разница между истинным и периодом небольших колебаний называется круговой ошибкой. В случае с типичными напольными часами, у которых маятник имеет размах 6° и, следовательно, амплитуду 3° (0,05 радиана), разница составит около 15 секунд в день.
Формула математического маятника, при малых колебаниях, когда он приближается к гармоническому осциллятору, и его движение, как функция времени t, находит выражение следующим образом: θ(t) = θₒ cos (2 π / T * t + ⱷ). Где фи (ⱷ) — постоянная величина, зависящая от начальных условий. Для маятников этот период незначительно меняется в зависимости от некоторых факторов, например:
- плавучесть и вязкостное сопротивление воздуха;
- масса нити или стержня;
- размер и форма отвеса и способы его прикрепления к шнуру;
- гибкость и растяжение нити.
Если необходимы точные расчёты, конечно, все эти поправки должны учитываться.
Составной маятник
Другое название — физический, представляет собой любое качающееся твёрдое тело, свободно вращающееся вокруг фиксированной горизонтальной оси. Соответствующая эквивалентная длина – L, а для расчёта времени используется расстояние от оси до центра колебаний. Эта точка расположена над центром массы на расстоянии от оси, традиционно называемым радиусом колебаний, который зависит от распределения веса груза.
Христиан Гюйгенс в 1673 году доказал, что точка вращения и центр колебаний взаимозаменяемы. Это означает, если какой-либо маятник перевёрнут и ротирован от оси, расположенной в его предыдущем центре колебаний, он будет иметь тот же период, что и раньше, и новый центр будет находиться в старой точке вращения.
В 1817 году Генри Кэтер использовал эту идею для создания обратимого маятника, теперь известного под именем создателя, для улучшения измерений ускорения под действием силы тяжести.
Историческая хроника
Одним из самых ранних известных применений маятника было устройство сейсмометра (I века) китайского учёного династии Хань Чжан Хэна. Его функция состояла в том, чтобы раскачивать и активировать один из серии рычагов после того, как он был нарушен тремором землетрясения, которое происходило далеко от места измерения. Освобождённый рычагом, маленький шарик выпадал из устройства в форме урны в одну из восьми горловин металлической жабы внизу, в восьми точках компаса, что указывало направление землетрясения.
Многие источники утверждают, что египетский астроном X века Ибн Юнус использовал маятник для измерения времени, но это была ошибка, возникшая в 1684 году с британским историком Эдвардом Бернардом.
В эпоху Возрождения большие маятники с ручной накачкой использовались в качестве источников энергии для ручных поршневых машин, таких как пилы, сильфоны и насосы. Леонардо Давинчи сделал много рисунков движения маятников, хотя и не осознавал его значения для хронометража.
Исследования Галилея
Итальянский учёный Галилео Галилей был первым, кто начал изучать свойства маятников, начиная примерно с 1602 года. Самый ранний существующий отчёт о его исследованиях содержится в письме Гвидо Убальдо дель Монте из Падуи от 29 ноября 1602 года. Его биограф и ученик, Винченцо Вивиани, утверждал, что его интерес был вызван около 1582 года, когда физик раскачивал люстры в соборе Пизы.
Галилей обнаружил важнейшее свойство, которое делает маятники полезными в качестве хронометриста, называемое изохронизмом; период маятника приблизительно не зависит от амплитуды или ширины качания. Он также обнаружил, что период не зависит от массы отвеса и пропорционален квадратному корню из длины всей конструкции. Сначала он использовал маятники свободного вращения в простых приложениях синхронизации.
Его друг — врач Санторио Санторий, используя наработки Галилея, изобрёл прибор, который измерял пульс пациента. В 1641 году Галилео задумал и продиктовал своему сыну Винченцо конструкцию маятниковых часов. Тот начал строительство, но не завершил его, поскольку умер в 1649 году. Так, появился первый гармонический осциллятор, использованный человеком.
Маятниковые часы
Первый образец построил в 1656 году голландский учёный Христиан Гюйгенс. Это было значительное улучшение по сравнению с существующими механическими часами. Их точность была улучшена с отклонений от 15 минут до 15 секунд в день. Маятники распространились по Европе, так как все существующие часы стали модифицироваться.
Английский учёный Роберт Гук изучил конический маятник (около 1666), который мог свободно колебаться в двух измерениях, а груз вращаться по кругу или эллипсу. Он использовал движение этого устройства в качестве модели для анализа орбитального движения планет. Гук предложил Исааку Ньютону в 1679 году свои наработки.
Он утверждал, что составляющие орбитального движения состояли из инерционного движения по касательному направлению и привлекательного движения в радиальном направлении. Это сыграло свою роль в формулировке Ньютоном закона всемирного тяготения. Роберт Гук также был ответственным за то, что ещё в 1666 году предположил, что маятник можно использовать для измерения силы тяжести.
Во время своей экспедиции в Кайенна (Французская Гвиана) в 1671, Жан Рише обнаружил, что там часы с маятником шли на 2,5 минуты медленнее, чем в Париже. Из этого он сделал вывод, что сила гравитации была ниже в Кайенне. В 1687 году Исаак Ньютон в Principia Mathematica показал, что это произошло потому, что Земля была не настоящей сферой, а слегка сплюснутой (сплющенной на полюсах) от действия центробежной силы из-за её вращения, это и вызывает увеличение силы гравитации.
Портативные маятники стали совершать рейсы в дальние страны, в качестве прецизионных гравиметров для измерения ускорения свободного падения в разных точках Земли, что в итоге привело к определению точной модели формы планеты. Затем последовало превращение исследований и выводов учёных в новые классы приборов, с дополнительными параметрами. Например:
- 1721 г. — маятник с температурной компенсацией;
- 1851 г. — маятник Фуко.
В 1930 году решение задачи по точному хронометражу было найдено, в 1921 был изобретён кварцевый генератор.
Текущая страница: 5 (всего у книги 15 страниц) [доступный отрывок для чтения: 3 страниц]
Биолокационный маятник
Что такое биолокационный маятник
Применяемый в биолокации маятник представляет собой очень простое приспособление и состоит из отвеса (груза) на нитке или цепочке, который приводится в движение рукой человека и служит для решения многих бытовых проблем. С его помощью также ведут поиск полезных ископаемых, подземных вод, геопатогенных зон и т. д. В настоящее время маятник является наиболее часто используемым инструментом в биолокации. С помощью маятника можно получить информацию, которую невозможно получить иным путем. Маятник считывает сведения с энергетических структур, что позволяет добывать информацию из глубин подсознания человека.
Из истории маятника
Маятник применяют уже несколько тысяч лет. В давние времена священники, мудрецы, оракулы, врачи, предсказатели и астрологи всегда носили с собой подвешенные на нитях или на тонких цепочках предметы из металла или других веществ, которые назывались не маятниками, а отвесами. Служили отвесы для получения неизвестных сведений из настоящего, прошлого и будущего. Их удерживали за подвеску между указательным и большим пальцами, и отвесы делали прямолинейные, эллиптические или кругообразные движения, значения которых предварительно устанавливалось владельцем отвеса.
В Древнем Китае отвесами пользовались только аристократы и властители. Императоры всегда носили свой отвес с собой и использовали его при принятии решений. С помощью отвеса изгоняли злых духов и выясняли, откуда они пришли. Применяли отвесы и в Индии, откуда эта тайна переместилась в Египет. В Древнем Египте с его помощью определяли лучшие места для выращивания урожая. В школах Древней Греции, которые одновременно являлись медицинскими школами, тоже применяли отвесы-маятники.
Один из историков Древнего Рима Маркселлинус, рассказавший об устройстве маятника, писал о треножнике, украшенном змеями и изображениями других животных, символизирующими прорицания и гадания. Из центра треножника свисало кольцо, которое должно было отвечать на задаваемые вопросы. Тех, кто использовал маятник, в Древнем Риме приговаривали к смерти. Основной причиной сурового наказания являлось его использование в заговорах против императора. Из Рима применения маятника достигли Западной Европы, где он на протяжении столетий использовался для предсказаний.
Старинные маятники (отвесы)
Рекомендуемые индикаторы. Настольного типа (А – латунный, Б – спиральный) и для работы на местности (В).
В начале XIV века Папой Римским была издана булла, которая осуждала применение кольца для гаданий. Со временем практика использования маятника была забыта. Наука работой маятника не интересовалась почти до конца XVIII – начала XIX века, пока итальянец Кампетти не стал применять его для обнаружения полезных ископаемых и подземных вод, что вызвало большой интерес в научных кругах и привело к возникновению множества теорий, в которых делались попытки объяснить работу маятника. Через некоторое время маятником воспользовались медики и применили его в целях диагностики.
В 1834 году в Париже директор Национального исторического музея в результате тщательного изучения и наблюдения за работой маятника пришел к выводу, что движения маятника являются результатом неосознанной реакции человека, который его применяет. В начале XX века сельский священник Мерме, не выходя из дверей своей конторы, при помощи маятника отыскал воду в Колумбии и нефть в Африке. Кроме того, он по всему миру успешно занимался розыском пропавших людей. Вскоре талант священника был замечен, и он в качестве специалиста был приглашен на археологические раскопки в Рим. Через некоторое время аббат Мерме обобщил свой опыт работы с маятником в книге «Принципы и практика радиэстезии», которая до нашего времени считается основной работой в области биолокации.
В XX веке маятник, кроме всего прочего, стали применять для определения пола еще не родившихся детей. В инструкции к одному из маятников говорилось, что маятник в виде шара нужно подвесить над ладонью беременной. Если он будет двигаться кругами – родится девочка, если будет двигаться по прямой – родится мальчик. В 1930 году во Франции аббат Ламбер применил маятник для поиска подземных вод. С помощью маятника он мог обнаружить под землей как неподвижную воду, так и текущую. Кроме этого, он определял глубину, на которой находилась вода, направление течения и ее объем.
Во время войн специалисты по биолокации с помощью маятника определяли продвижение военных кораблей, а вьетнамские солдаты использовали его для поиска подземных туннелей и мин.
Многие специалисты утверждают, что возможности маятника безграничны. Его помощь реальна во всех сферах жизни.
Внешние характеристики маятника
Маятник представляет собой небольшой груз, прикрепленный к нити, шнуру или цепочке. В качестве маятника можно использовать привязанное к нити обручальное кольцо или даже скрепку.
Как выбрать маятник
Правильнее всего применять в работе тот маятник, который удобен в пользовании и нравится внешне. Форма маятника может быть различной, например круглой, вес – от 2 до 20 г и более. В качестве привязанного к нити маятника можно использовать свинцовый грузик, пуговицу или полудрагоценный камень на цепочке. В качестве камня лучше всего использовать кварц, так как он хорошо сохраняет природную энергию. Кристаллические маятники применяют для оздоровления и исцеления.
Внутри маятник может быть полым. Полое пространство необходимо для того, чтобы перед началом работы положить внутрь образец того, что нужно отыскать. Если идет поиск воды, можно внутрь капнуть несколько капель. Если идет поиск нефти, можно в полость капнуть нефть. Если идет поиск золота, можно положить крупинку золота и т. д. В принципе для маятника полость необязательна, но может и пригодиться.
Для биолокационных работ в качестве маятника можно применять и особые инструменты: ключ от машины, ювелирные украшения, другую вещь, которую можно подвесить на цепочке или на нити. Если маятник продается в магазине, то перед тем, как его приобрести, следует спросить: «Находится ли этот маятник в гармонии со мной?» Если ответ положительный, прибор можно купить.
Как изготовить маятник
Маятник с успехом можно изготовить самому. Работая над его изготовлением, человек вкладывает в него свою энергию. В этом случае важную роль играет правильный выбор материала, из которого он будет изготовлен. В качестве материала можно выбрать дерево, кристалл, стекло, ракушку, поплавок, катушку из-под ниток, воск и др. Некоторые специалисты рекомендуют применять кристалл (полудрагоценный камень), который подходит к человеку по гороскопу.
При изготовлении маятника из прополиса или воска берут нить длиной 3 – 5 см. В отличие от металлов и других твердых материалов, обладающих способностью запоминать и накапливать информацию, маятники из воска и прополиса имеют аморфное строение, что позволяет им отсекать информацию, не закрепляя ее в себе. Кроме того, при длительной работе с маятником из воска или прополиса эти вещества накапливают не информацию, а энергию, которая поступает в общее поле энергетики человека, создавая ему дополнительную защиту.
Маятник можно также вырезать из любого мягкого материала или приспособить для него любую вещь, подходящую по весу и форме. Маятником может быть необычная вещь, имеющая особое значение или привлекающая внешне.
Выбирая металлический маятник, следует помнить, что металл, как правило, служит проводником, что может отрицательно повлиять на результат исследований и экспериментов. Хорошие маятники изготавливают из бронзы, латуни, серебра, алюминия и меди. Однако лучшим является материал, который не является проводником, – стекло, пластмасса, дерево и др.
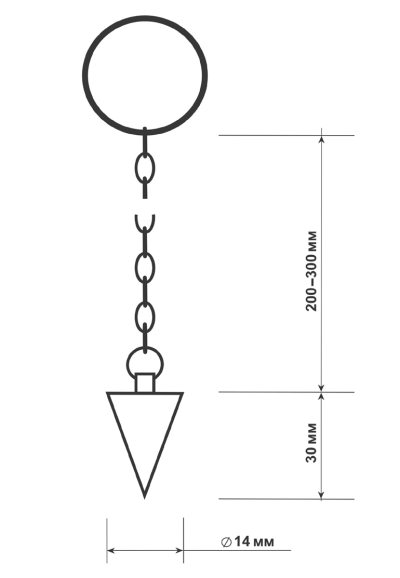
Форма маятника может быть круглой, напоминать каплю, сферической, цилиндрической с закругленными концами, спиральной, конусообразной с заостренным концом. Величина его может быть 2,5 – 3 см. Чем длиннее маятник, тем медленнее он колеблется. Подвешивать маятник можно на цепочке, шелковой или хлопчатобумажной нити, тонком шнурке, которые не должны мешать движениям маятника. Длина нити или цепочки обычно составляет 20 – 30 см. Маятник на короткой нити (10 см) колеблется в три раза чаще, чем маятник с нитью длиной в 100 см, вправо-влево или по кругу. Изменяя длину маятника, можно регулировать время срабатывания и одновременно чувствительность. Как правило, длина нити зависит от чувствительности оператора. Некоторые специалисты наилучшие результаты получают с короткими нитями, длина которых не превышает 5-10 см. Обычно длина наиболее удобной нити определяется экспериментально.
Маятник с нитью можно поместить в футляр или мешочек, чтобы он не запутывался и меньше воспринимал негативную энергию. Как упоминалось, масса маятника может быть от 2 до 20 г и более. Чтобы заставить колебаться маятник весом 100 г, нужно приложить силу в четыре раза большую, чем для маятника в 25 граммов. Но зато он накапливает в себе больше энергии движения, чем легкий маятник, и колеблется дольше, когда прекращается подача энергии. Кроме этого, он меньше отклоняется от направления своего движения, на него меньше влияют помехи, например ходьба при работе на местности и др. Поэтому, применяя более тяжелый маятник, в значительной мере можно исключить помехи его колебанию или круговому вращению, однако это произойдет за счет чувствительности и времени срабатывания.
Если маятник будет применяться для работ над столом в сидячем положении, вес его может быть 10 – 30 г, длина нити или цепочки – 10–30 см. Если маятник будет в основном применяться для замеров на местности во время ходьбы, вес его может составлять 80-120 г, длина нити – 80-120 см.
Как работать с маятником. Движения маятника
В действие маятник приводят неосознанные движения руки. Подсознание воздействует на мышцы руки, заставляя их реагировать на полученные импульсы, вызывая идеомоторную реакцию (идео – мысль, идея, мотор – движение). Роль маятника состоит в том, что он усиливает эту реакцию, которая без его движений была бы незаметной. Между мыслями человека, в руках которого находится маятник, и движениями маятника существует определенная связь. Ученые говорят, что маятник, открывая доступ к подсознанию, является продолжением центральной нервной системы. Маятник не снабжает информацией. Информация извлекается из подсознания человека и поступает в сознание через центральную нервную систему. Маятник лишь усиливает, проявляет послания подсознания. Вступить в контакте подсознанием маятник позволяет по желанию человека.
Подсознание человека связано с космическим сознанием, которому доступна любая информация. Поэтому в некоторых случаях происходит так, что человек лег спать с нерешенной проблемой, а утром проснулся с готовым решением. Таких примеров довольно много. Во время сна подсознание человека обратилось за помощью к космическому сознанию, а утром передало ему правильный ответ. Следовательно, можно задать маятнику любой вопрос и получить ответ от космического сознания. Лучший результат получается, если эти вопросы важные и человек действительно нуждается в ответе. С большей готовностью, как правило, маятник предоставляет информацию в более серьезных случаях.
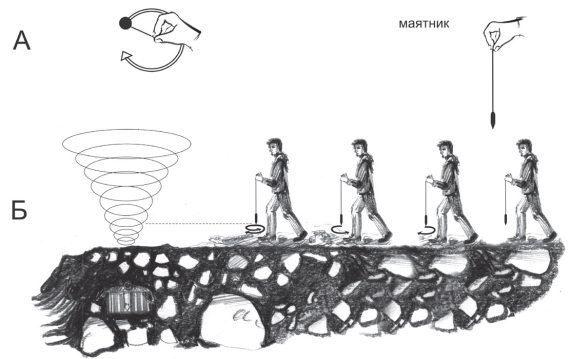
Схема работы с маятником на местности: А – правильное удержание маятника; Б – отыскание на местности подземного захоронения
Работать с маятником может любой человек. Приступать к работе с маятником лучше всего тогда, когда никто не мешает. Таким образом, можно быстрее достичь успехов. Работе с маятником можно обучиться примерно в течение месяца и приобрести неплохой навык в обращении с прибором, но совершенства достигают в течение долгих лет. Как правило, тренируются правой рукой или рукой, которой пишут.
В начале занятия необходимо сесть за стол, не прикасаясь к нему животом или другой рукой, опустить на стол локоть и слегка зажать нить или цепочку маятника между большим и указательным пальцами так, чтобы цепочка могла свободно раскачиваться. Ладонь руки, в которой держат маятник, должна быть обращена вниз, маятник должен находиться на высоте 5 – 10 мм над столом и в 30 см от тренирующегося. Руку необходимо удерживать в определенном положении по возможности более спокойно, желательно неподвижно, чтобы она не двигалась в такт маятнику и не влияла на его колебания. Ноги и руки не должны перекрещиваться. При перекрещивании оказывается определенное воздействие на маятник, искажающее результаты работы. Для тех, кто желает в этом убедиться, достаточно, держа маятник перед собой, сдвинуть или скрестить ступни, и маятник перестанет двигаться.
Далее необходимо достаточно интенсивно представить себе, что маятник начинает двигаться. И действительно, почти сразу же он начинает двигаться туда-сюда. Сначала колебания будут робкими, затем все более размашистыми. Основными видами движений маятника являются:
• колебания (маятник движется вперед и назад или в стороны по прямой линии);
• обороты (маятник не колышется, но выполняет вращательные движения как бы по окружности);
• обороты вправо (маятник вращается по ходу часовой стрелки);
• обороты влево (маятник вращается против хода часовой стрелки);
• эллиптические движения (маятник совершает среднее движение, без практического применения). Движение сигнализирует о том, что маятник изменит свое движение, так как перейдет из одного движения в другое, начнет двигаться или остановится.
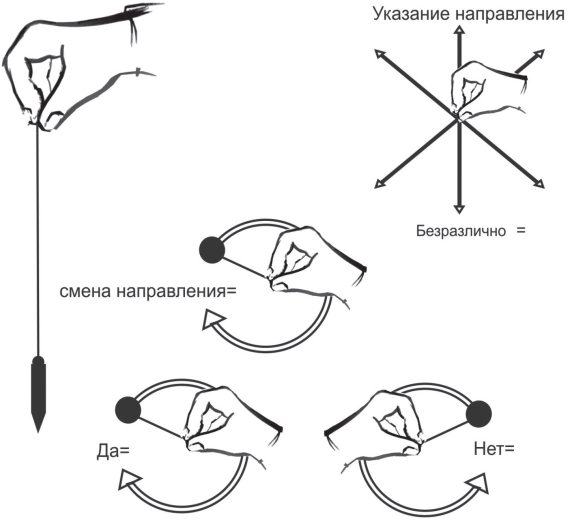
Схема правильного удержание маятников и основные виды движения
Для того чтобы остановить маятник, достаточно представить себе, что он опять должен занять свое вертикальное положение. Упражняясь в положении стоя, локоть нужно согнуть под углом в 90 градусов. В этом случае предплечье должно находиться параллельно земле.
Перед началом занятий следует легко и свободно покачать маятник в разных направлениях, чтобы с ним освоиться. Затем продольные движения переводят в круговые. Нить можно отпускать на разную длину, чтобы определить, в каком положении движение маятника будет наиболее свободным. Наилучший вариант – 12 – 14 см. Чтобы отметить лучшее положение маятника для работы, в этом месте на нити можно завязать узелок.
Освоившись с движениями маятника, его останавливают мысленно или свободной рукой. Чтобы объяснить движения маятника, необходимо определить, что они означают, усвоить все значения каждого движения и придерживаться этого, для того чтобы в работе избежать ошибок. В качестве примера предлагается следующий метод, который каждый может модифицировать, так как он не является обязательным или совершенным.
После того как маятник остановился, с самим собой нужно заключить мысленный договор, по которому оборот вправо означает: «да», «много», «очень много», «очень близко», «в добром здравии», «живет», «кислый», «позитивный» и т. д. (мужской род); оборот влево означает: «нет», «очень мало», «очень далеко», «болен», «умер», «щелочной», «негативный» и т. д. (женский род); колебание означает «безразлично». Эти соответствия нужно выучить наизусть и во избежание ошибок придерживаться их всегда. Однако, если это необходимо и обоснованно, время от времени их можно изменять.
Некоторые специалисты рекомендуют после остановки маятника попросить его указать, какое движение обозначает ответ «нет». Этот вопрос можно произнести про себя или вслух. Ответить маятник может не сразу, нужно подождать. Поначалу он может двигаться незаметно, однако если сосредоточиться на положительном ответе некоторое время, амплитуда его движений будет постепенно возрастать.
Чтобы приобрести определенный навык, данными упражнениями можно заниматься всего час или несколько дней – у кого как получится. После того как работа станет привычной, маятник будет приходить в движение сразу после того, как окажется над столом. При некоторых затруднениях можно сконцентрироваться на грузе и представить, как он движется из стороны в сторону, и маятник действительно начнет качаться. Если маятник не работает, необходимо отложить его, отдохнуть и приступить к упражнению через пару минут.
При затруднениях помочь своему ученику может оператор-наставник. Для этого он должен положить свою правую руку на правое плечо ученика, если маятник находится у ученика в правой руке. Обычно после этого маятник начинает раскачиваться. Замечено, что маятник начинает быстрее работать у того, кто обладает более сильным воображением и быстрым умом.
Задание:
работать с маятником ежедневно по 7 минут, пока он не начнет раскачиваться вперед и назад, из стороны в сторону и кругами. Если маятник на каждом занятии начинает регулярно двигаться этими способами – значит, занятия были успешными.
Определение формы
Упражнение
Необходимо вырезать 7–9 геометрических фигур и вложить каждую фигуру в конверт. Конверты перемешать и разложить перед собой. Затем нужно поместить маятник по очереди над каждым конвертом и задать себе вопрос: «Находится ли круг в этом конверте?» Когда маятник окажется над конвертом с кругом, он будет вращаться в правую сторону, что будет означать «да». Вращение должно быть четким. Над оставшимися конвертами маятник будет вращаться в другом направлении, подергиваться или остановится.
Определение цвета
Упражнение
Необходимо вырезать несколько фигур (7 – 9), раскрасить их в разные цвета и повторить предыдущее упражнение. Следует искать, какого цвета фигуры находятся в каждом конверте.
Как концентрировать внимание
Упражнение
При работе с маятником крайне важно научиться умению концентрировать внимание. Чтобы проверить свое умение концентрироваться, следует выполнить следующее упражнение. Для выполнения упражнения необходим круг диаметром 15 см, разделенный на четыре части двумя перекрещивающимися линиями. Над центром круга необходимо подвесить маятник и проследить за тем, как он начнет двигаться по одной из двух линий. Движения маятника будут все более и более интенсивными.
Далее следует представить, что эти движения замедляются и, наконец, прекращаются вовсе. Маятник останавливается, а затем начинает двигаться по другой прямой линии круга. Это же упражнение можно выполнять с закрытыми глазами. Открыв глаза, можно заметить, что маятник двигается именно в том направлении, которое было представлено в воображении. Данное упражнение проверяет концентрацию внимания и демонстрирует власть над маятником, который можно заставить раскачиваться в любом направлении, которое представит ум оператора.
Использование маятника с закрытыми глазами
Упражнение
Закройте глаза и мысленно прикажите маятнику двигаться по часовой стрелке. Через 20 секунд глаза откройте. Открыв глаза, вы заметите, что маятник действительно движется по часовой стрелке. Затем остановите маятник, снова закройте глаза и мысленно попросите маятник двигаться против часовой стрелки. Через 20 секунд откройте глаза. Вы увидите, что маятник выполнил вашу просьбу, несмотря на то что вы специально не раскачивали его.
Как маятнику задавать вопросы
Прежде чем начать учиться задавать маятнику вопросы, нужно твердо усвоить, что с легкомысленными вопросами обращаться к нему не следует. Если вопрос задан серьезно, ответ будет правдивым. Если маятник почувствует, что с ним играют, он ответит то, что желают от него услышать.
Работа с маятником за столом
Упражнение
Целью упражнения является ответ на мысленно поставленные вопросы при помощи заданных колебаний маятника.
Воздействиями являются вопросы любого рода, которые человек задает своему подсознанию, где они сравниваются с космоэнергетической информацией окружающего мира. Если ответ найден, то автоматически вырабатывается соответствующая информация, которая как нейронная программа движения иннервирует мышцы кисти, держащей индикатор.
Для выполнения упражнения необходимы настольный индикатор из латуни или любой другой весом от 10 до 30 г.
Ход упражнения
Удобно сидя за столом, необходимо переместиться в состояние высшей внимательности и концентрации. Затем взять маятник за нить или цепочку между большим и указательным пальцами. В случае если маятник полностью остановился, следует мысленно сформулировать вопрос как можно более ярко и интенсивно, при постоянном представлении того, что он должен поступить в область подсознания, где ответ будет найден автономно.
Сначала нужно задавать лишь такие вопросы, чтобы правильность ответов, полученных с помощью маятника, можно быстро и однозначно проверить. Например: «Завтра будет солнечная погода?», «Придут ли гости ко мне сегодня?», «Позвонят ли гости ко мне по телефону сегодня?».
Задавать следует только те вопросы, на которые можно ответить «да» или «нет». Упражняясь с маятником, необходимо запомнить, какое его движение обозначает ответ «да». Затем у маятника нужно спросить, какие его движения будут соответствовать ответам «нет», «не хочу отвечать», «не знаю». Время от времени эти ответы нужно перепроверять, так как они могут изменяться, особенно если с маятником не работали в течение долгого времени (20 – 25 дней).
Сразу после постановки вопроса или спустя несколько секунд маятник может начать вращаться либо по часовой стрелке, чтобы выразить утвердительный ответ, либо в противоположном направлении, если ответ на поставленный вопрос отрицательный.
Продолжительность упражнения
• опрос подсознания с помощью маятника должен продолжаться не более двух минут.
Частота выполнения упражнения
выполнять упражнение необходимо в течение недели раз в день в любое время до тех пор, пока оно не будет выполняться безупречно.
Если в работе был перерыв, у маятника следует спросить, не изменились ли его движения, соответствующие тому или иному вопросу. Задайте ему вопросы, на которые можно ответить однозначно одним из четырех указанных способов.
Лучше всего начинать с вопросов, ответы на которые уже известны. Можно, например, спросить: «Я женщина?», и если это так, маятник должен дать утвердительный ответ. Если вы мужчина, ответ будет «нет». Можно задавать вопросы о своем возрасте, количестве детей, имени, семейном положении и др. Основная цель вопросов:
• изучение движений маятника;
• убеждение в обоснованности ответов маятника.
Через некоторое время эти вопросы можно задавать мысленно и вслух. И можно будет убедиться, что разницы никакой нет. Если маятник отвечает на подобные вопросы, можно начинать его спрашивать о том, что интересует.
Маятник способен отвечать на достаточно сложные вопросы, так как может считывать необходимую информацию из подсознания, передавая ее сознанию. Сознание может вместить в себя лишь ограниченное количество информации, в то время как ресурсы подсознания несравнимо больше.
Выбирать вопросы следует осторожно, так как движения маятника зависят от воздействия собственной воли. Например, если есть желание узнать, кто родится – мальчик или девочка, и есть желание, чтобы родился мальчик, маятник может отразить это желание и сказать, что родится мальчик, несмотря на то что на самом деле это будет не так. При работе с маятником необходимо иметь в виду, что он может сказать то, что человек, задающий вопрос, желает услышать.
При желании получить от маятника ответ на важный вопрос, чтобы соблюдать нейтралитет, можно попросить задать этот вопрос другого человека.
Некоторые начинающие работать с маятником задают ему вопросы, на которые он не может ответить в силу определенных ограничений. Например, маятник не может дать ответ на вопрос: «Провести ли мне отпуск в Сочи или в Петербурге?» В этом случае вопрос следует разбить на две части и спросить о каждом городе по очереди. Нужно спросить: «Получу ли я удовольствие от отдыха, если проведу его в Сочи?» Затем то же самое спросить о Санкт-Петербурге. Возможно, он ответит положительно и в том, и в другом случае. Тогда следует спросить его более конкретно: «Будет ли мой отпуск более интересным, если я проведу его в Сочи, а не в Санкт-Петербурге?»
При работе с маятником следует сосредоточиться на вопросе, повторяя его про себя несколько раз. При посторонних мыслях необходимо вновь возвращаться к вопросу, так как маятник может ответить на случайную мысль, а не на заданный вопрос.



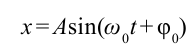
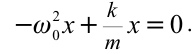

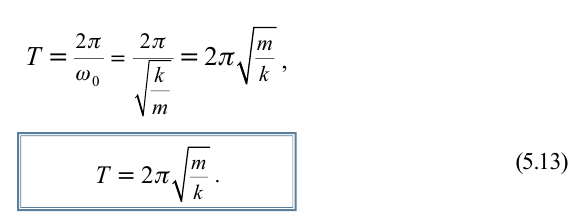
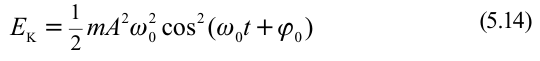
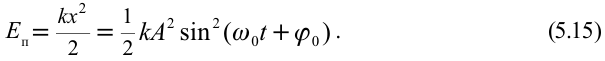
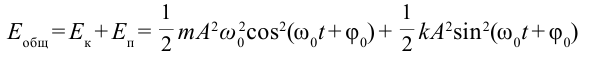
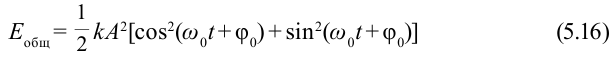

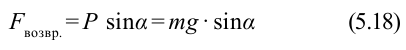
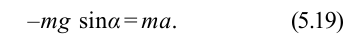

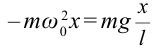


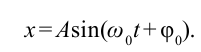
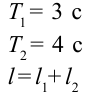
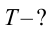
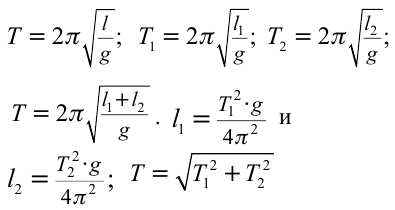
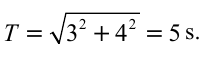
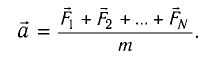
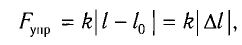
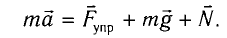
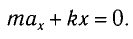
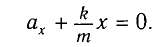
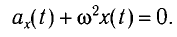
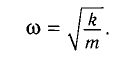
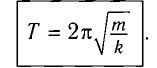
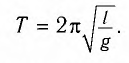
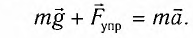
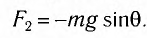
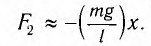
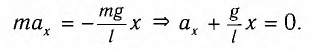
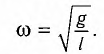
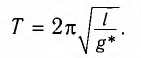
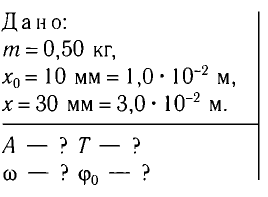
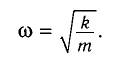
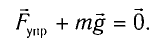
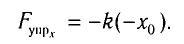
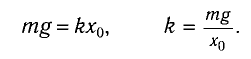
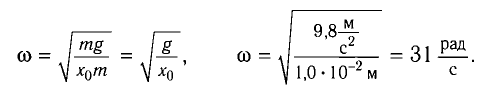
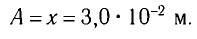
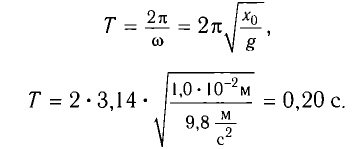
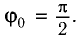
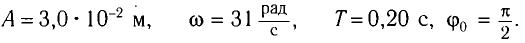
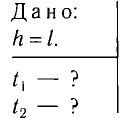
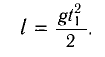
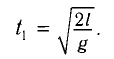
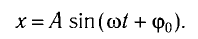
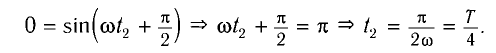
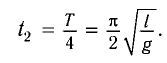
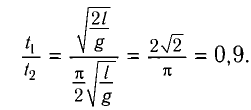
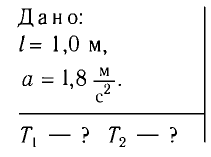
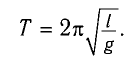
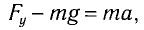
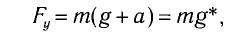
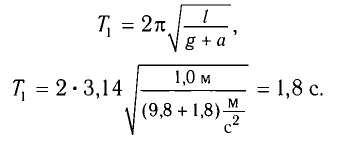
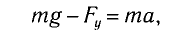
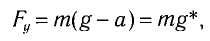
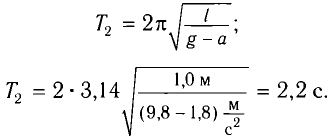
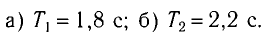
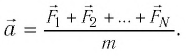
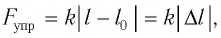
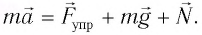
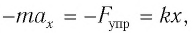
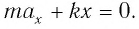
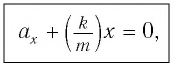
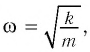
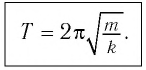
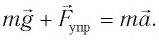
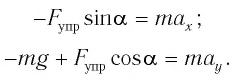
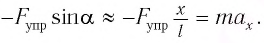
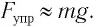
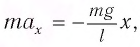
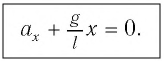
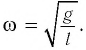
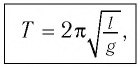
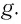
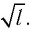
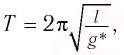
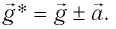
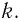
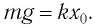
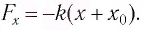
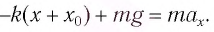
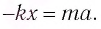
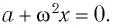
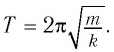
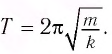
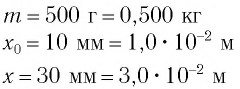
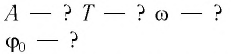
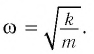
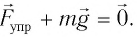
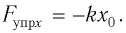
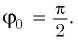
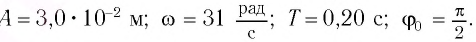
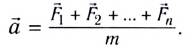
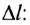
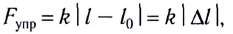
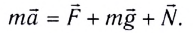
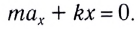
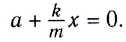
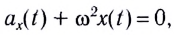
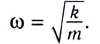
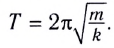
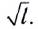
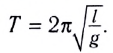
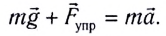
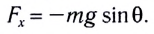
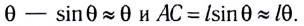
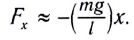
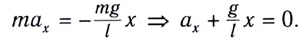
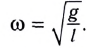
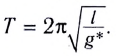


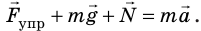
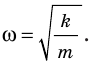
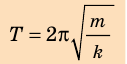
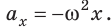
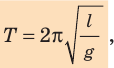
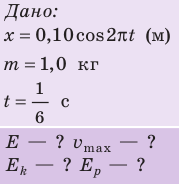
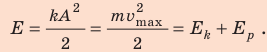















![{displaystyle T=2pi {sqrt {frac {lambda }{g}}}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {alpha }{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {alpha }{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {alpha }{2}}right)+dots right}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aae1c69041f6957ab485b97bcbe5025dc688c47a)