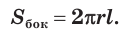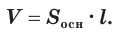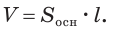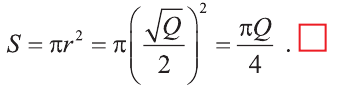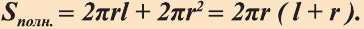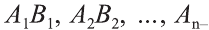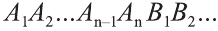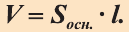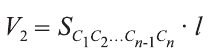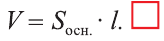В предыдущей части этой серии статей о субъективной рефрактометрии было рассмотрено определение наилучшей сферы*. Следующий шаг – проведение силовой и осевой пробы (определение силы и направления оси линзы для коррекции астигматизма). Это мы обычно делаем либо с помощью кросс-цилиндра Джексона либо используя фигуру «блок и веер» (fan-and-block).
________________
* См.: Патель Т. Субъективная рефрактометрия: определение наилучшей силы сферы // Современная оптометрия. 2020. № 6. С. 38–45.
Кросс-цилиндр
Кросс-цилиндр можно определить как «фиксированную комбинацию линз с положительным и отрицательным цилиндром с взаимно перпендикулярными осями, закрепленных на ручке, которая расположена между двумя осями» (рис. 1).

В зависимости от остроты зрения используют разные силы кросс-цилиндра. Обычно положительный и отрицательный цилиндры обозначаются метками разного цвета. Пользуясь ручкой, можно задавать различные ориентации кросс-цилиндру в целях определения силы и положения оси. В этой статье мы предположим, что отрицательный цилиндр обозначен красным цветом*, а положительный – черным (это типично для кросс-цилиндров, но бывают и другие цветовые вариации).
__________________
* В данной статье на рисунках красный цвет будет отображаться как серый. – Примеч. ред.
Использование кросс-цилиндра (с установленной в пробную оправу цилиндрической линзой после ретиноскопии)
Нахождение оси цилиндра (осевая проба):
- Выберите подходящую мишень и силу кросс-цилиндра до начала проверки (см. вставку «Заметки о проведении теста с кросс-цилиндром»).
- Перед началом теста убедитесь, что круг наименьшего рассеяния расположен правильно*.
- Определение оси цилиндра: сориентируйте ручку кросс-цилиндра параллельно оси цилиндрической линзы, установленной в пробной оправе, как показано на рис. 2 (ось цилиндра в пробной оправе – 180°).
- Попросите пациента смотреть на расположенную вдали мишень; объясните, что будете менять две линзы и нужно будет сравнить качество зрения при их использовании (рис. 3).
- Поверните ручку кросс-цилиндра на 180° и спросите пациента, как лучше видно мишень, где она резче, с первой линзой или со второй, или же разницы нет. В зависимости от того, какую линзу предпочел пациент, поверните ось отрицательного цилиндра в пробной оправе в направлении отрицательной оси кросс-цилиндра примерно на 10° (рис. 4).
- Расположите ручку кросс-цилиндра теперь таким образом, что ее направление совпадало с осью, повернутой на 10° линзы в пробной оправе (например, 170°). Повторите описанную выше процедуру с поворотом ручки кросс-цилиндра и последовательно изменяйте ось цилиндра в пробной оправе до тех пор, пока пациент не скажет, что между обеими линзами кросс-цилиндра нет разницы относительно четкости мишени.
- Если пациент изначально не видит разницы между двумя положениям кросс-цилиндра, это говорит о том, что при ретиноскопии вы верно установили положение оси астигматизма и поэтому линзу в пробной оправе поворачивать не нужно. Некоторые пациенты в таком случае выражают недоумение, поэтому будьте готовы пояснить им суть дела.
________________
* См.: Патель Т. Субъективная рефрактометрия: определение наилучшей силы сферы.
Заметки о проведении теста с кросс-цилиндром
- Чтобы убедиться, что круг наименьшего рассеяния находится на сетчатке, на каждые 0,50 дптр изменения силы цилиндра сила сферы корректируется на 0,25 дптр в обратном направлении. Так, при увеличении отрицательной силы цилиндра на –0,50 дптр необходимо добавить +0,25 дптр к силе сферы; при уменьшении силы цилиндра на +0,50 дптр необходимо добавить –0,25 дптр к силе корригирующей сферы в пробной оправе.
- Используйте линзы с большим шагом у пациентов с низкой остротой зрения.
- Значительнее изменяйте положение оси (например, на 15° вместо 10°) у пациентов с низкой остротой зрения. По мере приближения пациента к конечной точке меньше меняйте положение оси (например, на 5°) вместо 10°.
- Перепроверьте еще раз ось цилиндра, если сила цилиндра была сильно изменена.
- В таблице Снеллена (Snellen) используются круги или кольца Верхоеффа (Verhoeff) (рис. 3, слева), эквивалентные остроте зрения 6/9 и 6/12. Если острота зрения пациента ниже 6/12, использование кругов Верхоеффа невозможно. В таком случае пациента просят смотреть на букву, которая эквивалентна его лучшей остроте зрения с коррекцией и имеют форму, аналогичную форме кругов Верхоеффа, например на букву O.
- Выбор соответствующего кросс-цилиндра будет зависеть от остроты зрения пациента на момент определения цилиндрического компонента. Если острота зрения пациента равна или выше 6/7,5, используются кросс-цилиндры ±0,25 дптр, а если ниже 6/9, то кросс-цилиндры ±0,50 дптр. Кросс-цилиндры ±1,00 дптр применяются в работе с пациентами с низкой остротой зрения.
Определение силы цилиндра (силовая проба):
- На этом этапе сориентируйте ручку кросс-цилиндра под углом 45° к направлению оси цилиндрической линзы, установленной в пробную оправу. Благодаря этому ось кросс-цилиндра совпадет с осью линзы в пробной оправе (рис. 5).
- Поверните кросс-цилиндр на 180° и спросите пациента, в каком положении мишень выглядит четче или же разницы нет.
- Если он отвечает, что лучше видно тогда, когда отрицательная ось кросс-цилиндра накладывается на ось цилиндра в пробной оправе, увеличьте отрицательную силу линзы. В противоположном случае, когда лучше видно, если положительная ось кросс-цилиндра накладывается на ось цилиндра в пробной оправе, уменьшите отрицательную силу пробной линзы.
- Повторяйте процедуру до тех пор, пока пациент не скажет, что он не видит разницы между двумя положениями кросс-цилиндра в отношении четкости мишени.
Использование кросс-цилиндра без пробной цилиндрической линзы
Алгоритм следующий:
- Поместите подходящий по силе кросс-цилиндр (см. вставку «Заметки о проведении теста с кросс-цилиндром») перед правым глазом таким образом, чтобы ручка находилась под углом 45° к вертикальной и горизонтальной воображаемым линиям, то есть отрицательная ось кросс-цилиндра (обозначена красной меткой) совпадает с горизонтальным меридианом (180°), а затем – с вертикальным меридианом (90°).
- Спросите пациента, в каком положении кросс-цилиндра лучше видно мишень – с первой линзой (отрицательная ось на 180°) или со второй линзой (отрицательная ось на 90°). Если пациент отдаст предпочтение первой линзе, то, вероятно, присутствует астигматизм, и его ось ближе скорее к 180°, нежели к 90°.
- В таком случае держите ручку кросс-цилиндра вдоль меридиана 180°, так чтобы отрицательная ось кросс-цилиндра (у нас обозначена серой меткой) была ориентирована при поворотах вдоль меридианов 45 и 135°.
- Спросите пациента, в каком положении кросс-цилиндра лучше видно мишень – с первой линзой (отрицательная ось на 45°) или со второй (отрицательная ось на 135°). Если лучше видно с первой линзой, то ось цилиндра ближе к 45°, а не к 180°. Учитывая предыдущую информацию, можно утверждать, что ось цилиндра расположена между 180 и 45°.
- Теперь поместите цилиндрическую линзу силой –0,25 дптр (или более высокой оптической силы: –0,50 или –0,75 дптр, в зависимости от остроты зрения на данном этапе) в любом направлении между 180 и 45° и проведите процедуру, описанную в разделе «Использование кросс-цилиндра (с установленной в пробную оправу цилиндрической линзой после ретиноскопии)».)
Эту фигуру (рис. 6) для определения оси и силы корригирующей цилиндрической линзы сегодня используют реже, поскольку считается, что она не очень чувствительна к небольшим цилиндрам, также ее результаты ненадежны при астигматизме выше 2,50 дптр, а человек с наклоненной головой будет давать неверные ответы. Кроме того, в некоторых современных проекторах знаков и компьютеризированных таблицах этой фигуры просто нет. Она, тем не менее, полезна для определения неправильного астигматизма, а еще может быть альтернативой в тех случаях, когда при применении кросс-цилиндра пациент дает невнятные или неожиданные ответы.
Применение фигуры «веер и блок» после ретиноскопии:
- Измерьте межзрачковое расстояние и наденьте пробную оправу так, чтобы пациенту в ней было комфортно.
- Проведите ретиноскопию обоих глаз, учтите рабочее расстояние, если этого еще не было сделано, с линзой с допуском рабочего расстояния. Запишите результаты.
- Измерьте остроту зрения обоих глаз после ретиноскопии.
- Начиная с правого глаза (левый глаз закрыт окклюдером), извлеките из пробной оправы цилиндрическую линзу, сила и ось которой установлены при ретиноскопии.
- Определите наилучшую силу сферы (НСС), как это описано в предыдущей статье в разделе «Использование линз 0,25 дптр (флиппер)»*:
- если острота зрения 6/18, стоит воспользоваться большим шагом в оптической силе, чтобы пациент смог заметить различие в остроте зрения;
- ожидаемая наилучшая сила сферы составит половину силы цилиндра; например, при цилиндре силой –3,00 дптр можно ожидать НСС = –1,50 дптр.
- Проведите дуохромный тест и убедитесь, что мишени на обоих фонах равноценны.
- Переключите внимание пациента на фигуру «веер и блок». Спросите его, есть ли какие-то линии на ней, которые видны лучше и четче.
- Пока пациент смотрит на фигуру веера, предъявляйте поочередно затуманивающие сферические линзы (их сила должно быть примерно равна половине силы цилиндра), пока он не скажет, что все линии веера нерезкие и размытые. Теперь уменьшите силу сферической затуманивающей линзы на –0,25 дптр.
- Чтобы определить главные меридианы, поворачивайте стрелку, расположенную под веером, к той линии (или группе линий), которую пациент видит лучше. Продолжайте это делать до тех пор, пока оба ее края не станут одинаково четкими. Направление стрелки укажет на расположение отрицательной оси цилиндра.
- После этого установите в пробную оправу цилиндрическую линзу в два раза меньшей оптической силы относительно той, что выяснили при ретиноскопии, а ее ось сориентируйте в соответствии с осью, выясненной на предыдущем этапе. Попросите пациента смотреть на два блока линий, расположенных под стрелкой.
- Спросите пациента, какой из двух блоков линий выглядит четче/темнее. Если четче выглядит тот, в котором линии ориентированы в одном направлении с осью цилиндрической линзы, увеличьте ее силу на –0,25 дптр. А если четче виден блок, в котором линии расположены в перпендикулярном к оси цилиндра направлении, уменьшите силу цилиндра на +0,25 дптр. Таким образом, добавляя или отнимая доли цилиндра, добейтесь ситуации, когда оба блока выглядят одинаково четко. При каждом изменении силы цилиндра на 0,50 дптр следует изменять на 0,25 дптр силу сферу.
- Еще раз проверьте, верно ли выставлен цилиндр. Для этого спросите пациента, все ли линии веера и обе стороны стрелки выглядят одинаково четко. Если нет, значит, ось цилиндра определена неправильно и линзу в пробной оправе нужно повернуть.
________________
* См.: Патель Т. Субъективная рефрактометрия: определение наилучшей силы сферы.
Теперь можно проводить финальную проверку силы сферы.
Финальная проверка силы сферы
После проверки правильности определения астигматического компонента коррекции зрения необходимо перепроверить, верно ли определена НСС, с тем чтобы при необходимости внести изменения, которые могут возникнуть из-за подбора цилиндрической составляющей.
Проверка наилучшей силы сферы после теста с использованием кросс-цилиндра:
- Попросите пациента смотреть на самую нижнюю строку, которую он видит и может прочесть. Добавьте к сферической линзе +0,25 дптр и спросите, стали ли буквы четче, размытее или ничего не изменилось.
- Если пациент говорит, что стало лучше или без изменений, добавьте к сферической линзе еще +0,25 дптр. Так продолжайте делать до тех пор, пока пациент не перестанет сообщать об улучшении остроты зрения. Предложите максимальную положительную или минимальную отрицательную сферическую составляющую.
- Если при первоначальном предъявлении добавочной силы сферы +0,25 дптр оптотипы размываются, предъявите вместо нее линзы с силой сферы –0,25 дптр. Отрицательные добавки делайте исключительно в тех случаях, когда на самом деле наблюдается улучшение остроты зрения, то есть человек действительно может прочесть больше букв, чем до этого.
Затуманивание линзой с силой +1,00 дптр
Этот тест проводится с целью убедиться, что сферический компонент коррекции выбран правильно, нет гипер- или гипокоррекции. Он также предваряет оценку бинокулярного баланса, который проводится после процедуры монокулярной рефрактометрии (описана далее в этой статье)
Традиционно для затуманивания зрения используют линзы с силой +0,75 или +1,00 дптр; они дают возможность расслабить аккомодацию и провести супрессию центрального зрения ради задействования зрения периферического. При предъявлении линзы с силой +1,00 дптр острота зрения должна снижаться до 6/12–6/18, а если этого не происходит, значит, наилучшая сила сферы еще окончательно не определена и нужно снова ее выставлять.
Алгоритм затуманивания с линзой силой +1,00 дптр:
- После выяснения НСС, использования кросс-цилиндра и проверки остроты зрения скажите пациенту, что разместите перед его правым глазом линзу, которая «размоет» изображения букв на таблице.
- При закрытом левом глазе предъявите линзу +1,00 дптр перед правым глазом.
- Спросите пациента, какую самую низкую строку таблицы он сейчас способен прочесть.
- На этом этапе острота зрения должна составить примерно 6/12–6/18 (то есть ухудшится примерно на три строки), и это искомый уровень.
- Если же такого не произошло, уберите линзу +1,00 дптр и снова выясняйте НСС, добиваясь максимального «плюса» или «минуса» в коррекции.
- Закройте правый глаз и повторите процедуру для левого.
- Запишите в карточку остроту зрения каждого глаза.
Комментарии к тесту с затуманиванием сферической линзой +1,00
- При проведении теста с затуманиванием с помощью линзы +1,00 дптр острота зрения обоих глаз должна ухудшаться одинаково.
- Разная острота зрения глаз и маленький размер зрачков могут повлиять на степень ухудшения зрения при проведении теста.
- Тест с успехом используется для маленьких детей, так как он помогает расслабить аккомодацию.
Создание бинокулярного баланса при помощи быстрого контраста Хамфрисса
Создание бинокулярного баланса – это этап, который позволяет оптометристу уравновесить аккомодацию обоих глаз в ситуации, когда пациент смотрит на удаленную мишень бинокулярно.
Обычно для этого применяют метод быстрого контраста Хамфрисса (БКХ), поскольку при его использовании глаза сохраняют свой нормальный бинокулярный статус при небольшой диссоциации и добавлении затуманивающей линзы в целях расслабления аккомодации.
Конечно, нет необходимости проводить такую процедуру пациентам с монокулярным зрением, слабой аккомодацией или если вы проводили бинокулярную рефрактометрию.
Алгоритм создания бинокулярного баланса:
- Проведите тест с затуманиванием линзой +1,00 дптр на обоих глазах, как описано выше, и убедитесь, что достигается равноценное снижение их остроты зрения
- Оставьте линзу +1,00 дптр перед левым глазом, удостоверьтесь, что ни перед каким глазом нет окклюдера. Сообщите пациенту, что специально провели затуманивание зрения и что ему не нужно закрывать глаза на время теста. Если из-за наличия разницы в остроте зрения между глазами одинакового размытия изображения линзой +1,00 дптр достичь не удалось, оставьте ее перед тем глазом, на котором ситуация хуже.
- Начав с правого глаза, попросите пациента прочесть самую нижнюю строку букв, которую они видят четко. Добавьте к силе сферической линзы +0,25 дптр и спросите, стали ли видны буквы лучше, хуже или все без изменений. Если пациент сообщит, что видно лучше или так же, как было, добавьте еще +0,25 дптр. Так делайте до тех пор, пока пациент не перестанет видеть улучшение или пока строка не расплывется.
- Если размытие букв появляется при предъявлении первой добавочной силы сферы +0,25 дптр, меняйте ее на –0,25 дптр. Добавляете отрицательную силу сферы только тогда, когда заметно улучшение в чтении букв, то есть пациент может прочесть больше букв, чем до этого.
- Уберите линзу +1,00 дптр от левого глаза и разместите ее перед правым. Повторите процедуру.
Бинокулярная добавка
Это процедура установления максимальной положительной силы сферической линзы, которую можно добавить пациенту бинокулярно.
Алгоритм определения бинокулярной добавки:
- После завершения тестов с затуманиванием линзой силой +1,00 дптр и с использованием БКХ попросите пациента прочесть самую низкую строку, которую он четко видит, обоими глазами.
- Добавьте к силе сферической линзы +0,25 дптр для обоих глаз и спросите пациента, стало ли лучше видно буквы, или хуже, или без изменений.
- Если пациент сообщит, что лучше или без изменений, добавьте еще +0,25 дптр к силе линз для обоих глаз. Делайте это до тех пор, пока пациент не перестанет видеть улучшение или строка просто расплывется.
- Если уже при первоначальном предъявлении сферы +0,25 дптр строка расплывается, вышеописанная процедура не проводится.
Бинокулярная острота зрения
По возможности регистрируйте бинокулярную остроту зрения. Прежде всего это важно делать в особых ситуациях, например при нистагме, когда бинокулярная острота зрения лучше, чем при монокулярном измерении, а также для того чтобы заниматься деятельностью или управлять транспортным средством, где требуется знать бинокулярную остроту зрения.
Проверка бинокулярной остроты зрения: после монокулярной проверки остроты зрения попросите пациента обоими глазами прочесть самую нижнюю четко видимую им строку таблицы.
Запись результатов обследования
Данные обследования нужно записывать как можно детальнее. Как минимум следует указать финальные сферу, цилиндр и ось, монокулярную и бинокулярную остроту зрения. Помимо этого, запись может содержать результаты теста с затуманиванием линзой +1,00 дптр, бинокулярную добавку и результаты определения бинокулярного баланса. Например:
OD: Sph –2,00; Cyl –0,50; ax 180; Vis 6/5; тест с затуманиванием линзой +1,00 дптр; Vis 6/12 (бинокулярный баланс: +0,25 дптр).
OS: Sph –2,50; Cyl –0,50; ax 10. Vis 6/5; тест с затуманиванием линзой +1,00 дптр; Vis 6/12 (бинокулярная добавка?)
OU: Vis 6/4.
Выписаны очки:
OD: Sph –1,75; Cyl –0,50; ax 180.
OS: Sph –2,25; Cyl –0,50; ax 10.
Заключение
На рис. 7 изображен полный алгоритм монокулярной субъективной рефрактометрии. Ее цель – оценить и улучшить зрительные функции пациента посредством взаимодействия между оптометристом и пациентом. Здесь много зависит от хорошей коммуникации и уровня комфорта, испытываемого пациентом. Алгоритм должен быть плавным и следовать определенной логике. Всегда объясняйте тесты пациенту, в частности, чего он должен ожидать. Умейте менять алгоритм, если человек плохо отвечает или ответы недостоверные.
Автор: Т. Патель, практикующий оптометрист, экзаменатор Колледжа оптометристов (Лондон, Великобритания)
Перевод: И. В. Ластовская
© РА «Веко»
Печатная версия статьи опубликована в журнале «Современная оптометрия» [2020. № 8 (137)].
По вопросам приобретения журналов и оформления подписки обращайтесь в отдел продаж РА «Веко»:
- Тел.: (812) 603-40-02.
- E-mail: magazine@veko.ru
- www.veko.ru
Наши страницы в соцсетях:
- vk.com/vekomagazine
- fb.com/vekomagazine
Содержание:
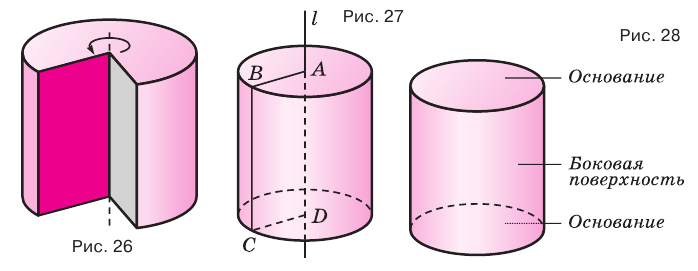
Цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через его сторону (рис. 26). На рисунке 27 показано образование цилиндра при вращении прямоугольника
Образующая цилиндра является его высотой.
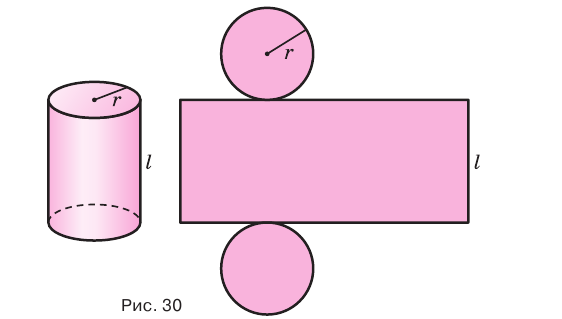
Поверхность цилиндра можно развернуть на плоскость, в результате получится прямоугольник, представляющий боковую поверхность цилиндра, и два круга, представляющих его основания. На рисунке 30 показан цилиндр и его развертка.
Теорема 4.
Боковая поверхность цилиндра равна произведению длины окружности основания и образующей:
На плоскости важной конфигурацией, которая часто встречается в задачах, является сочетание окружности с прямой. Подобной пространственной конфигурацией является сочетание цилиндра с плоскостью.
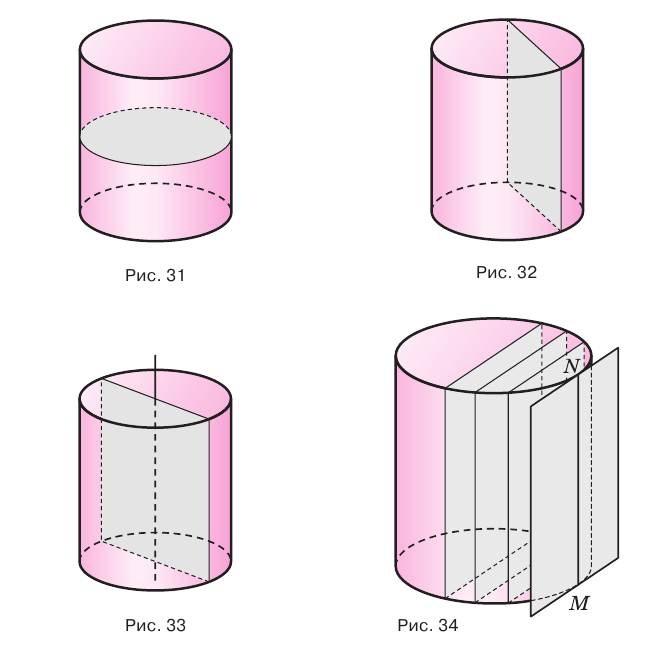
Если цилиндр пересечь плоскостью, параллельной основанию, то получится круг, равный основанию (рис. 31), а если плоскостью, перпендикулярной основанию, то — прямоугольник, одна сторона которого равна высоте цилиндра (рис. 32). Осевое сечение цилиндра, т. е. сечение плоскостью, проходящей через ось цилиндра, является прямоугольником, стороны которого равны высоте цилиндра и диаметру его основания (рис. 33).
Будем двигать плоскость, проходящую через ось цилиндра, параллельно самой себе (рис. 34). При этом две противолежащие стороны прямоугольника-сечения цилиндра, являющиеся хордами оснований, будут уменьшаться, а две другие стороны, которые являются образующими цилиндра, — сближаться до того момента, пока не совпадут. Получим плоскость, содержащую образующую 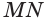
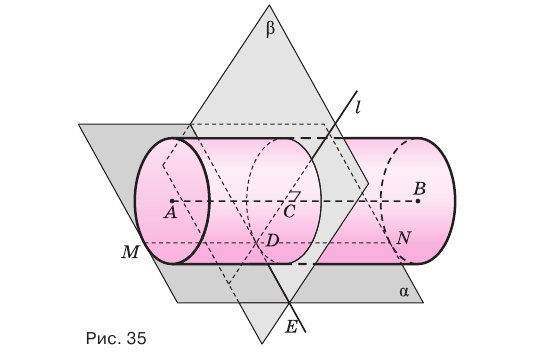
Теорема 5.
Если плоскость касается цилиндра по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 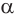
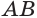
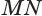
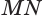
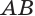
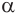
Проведем прямую 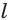
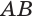
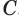
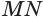
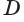
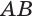
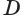
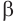
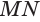
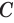
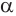
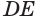
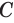
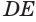
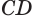
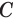
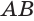
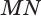
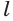
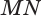
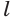
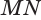
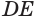
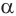
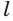
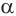
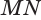
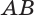
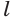
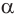
Теорема 5 выражает свойство касательной плоскости цилиндра.
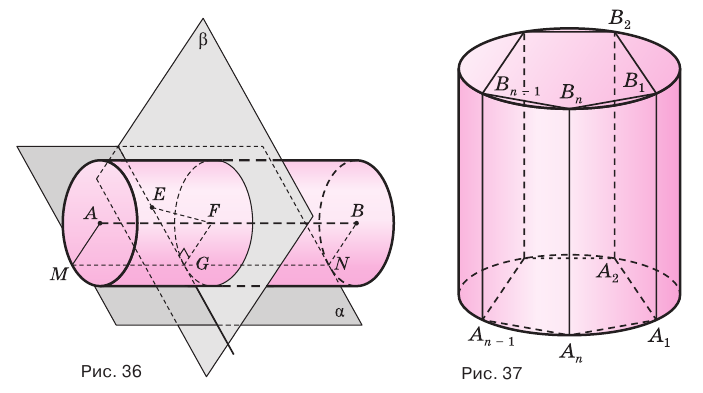
Теорема 6.
Плоскость касается цилиндра, если она проходит через его образующую и перпендикулярна плоскости, содержащей эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 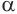
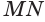
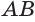
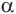
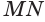
Пусть 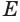
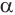
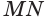
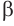
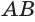
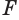
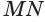
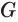
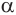
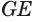
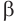
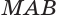
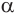
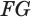
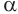
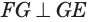
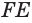
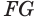
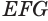
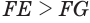
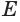
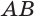
Теорема 6 выражает признак касательной плоскости цилиндра.
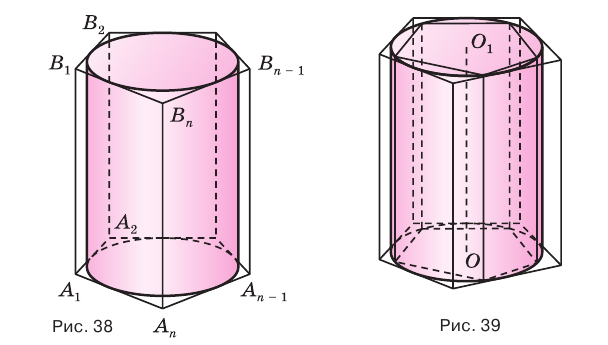
Пусть имеется цилиндр (рис. 37). Впишем в одно из оснований цилиндра многоугольник 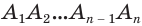
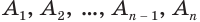
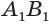
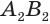
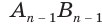
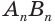
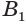
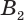
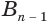
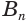
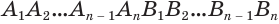
Если цилиндр описан около призмы, то основания цилиндра описаны около оснований призмы, а боковая поверхность цилиндра содержит боковые ребра призмы.
Подобным образом вводится понятие призмы, описанной около цилиндра, и цилиндра, вписанного в призму (рис. 38). Если призма описана около цилиндра, то ее основания описаны около оснований цилиндра, а боковые грани касаются боковой поверхности цилиндра.
Теорема 7.
Объем цилиндра равен произведению площади его основания и образующей:
Доказательство:
Пусть имеется цилиндр с осью 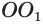
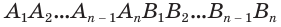
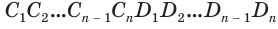
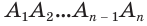
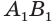
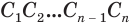
Будем количество 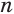
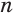
В описанном процессе высота 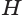
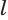
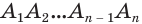
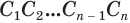
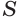
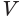
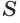
Поверхность цилиндра
Ещё один важный класс пространственных фигур – тела вращения. Цилиндр является одним из них, мы познакомимся с ним глубже. Свойства цилиндра похожи на свойства призм, мы последовательно изучим их.
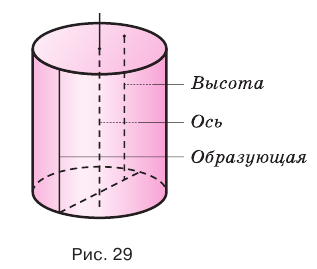
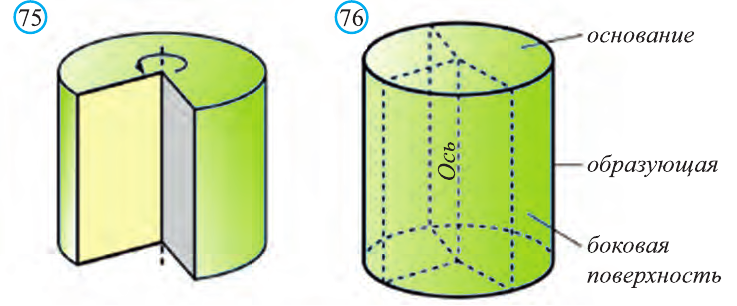
Тело, полученное вращением прямоугольника вокруг одной из его сторон называют цилиндром (точнее, прямой круговой цилиндр) (рис. 75). При вращении прямоугольника одна его сторона остаётся неподвижной. Её называют осью цилиндра. Поверхность, образованную при вращении противоположной стороны прямоугольника называют цилиндрической поверхностью, а саму сторону образующей цилиндра. Две другие стороны прямоугольника при этом вращении образуют два равных круга, которые называют основаниями цилиндра (рис. 76).
Замечание. Тело, полученное вращением прямоугольника вокруг одной из его сторон называют прямым круговым цилиндром. Более широкое понятие цилиндра вводят следующим образом.
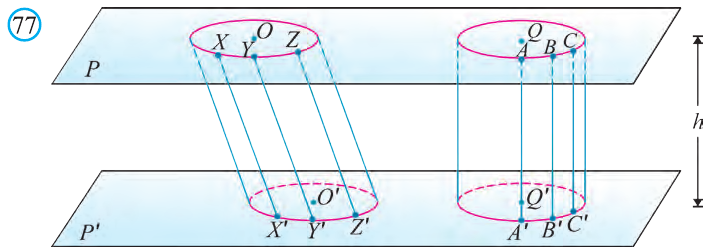
Пусть в пространстве параллельный перенос переводит плоскую фигуру F1, в фигуру F2. Тело, состоящее из этих фигур и отрезков, соединяющих их соответствующие точки, называют цилиндром (рис. 77).
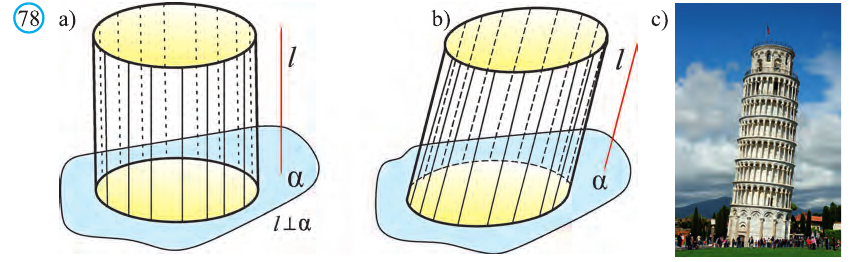
Если при параллельном переносе образующая перпендикулярна плоскости фигуры F1 , цилиндр называют прямым (рис. 78.а), в противном случае наклонным цилиндром (рис. 78.b). На рисунке 78.с изображена Пизанская башня, имеющая вид наклонного цилиндра.
Если фигура F1 является кругом, то цилиндр называют круговым цилиндром.
Только прямой круговой цилиндр является телом вращения. В дальнейшем мы будем рассматривать прямые круговые цилиндры, которые для краткости будем называть цилиндрами.
Основания цилиндра являясь равными кругами, лежат на параллельных плоскостях. Перпендикуляр, опущенный из некоторой точки одного основания на другое, называют его высотой.
Расстояние между параллельными плоскостями равно высоте цилиндра. Ось цилиндра также является его высотой.
Образующие цилиндра параллельны и равны. Точно также, длины высоты, оси и образующих цилиндра будут равны между собой.
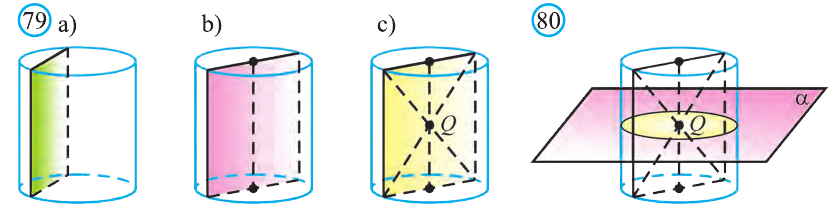
Сечением цилиндра плоскостью параллельной его оси является прямоугольник (рис.79.а). Две противоположные его стороны – это образующие цилиндра, а две другие стороны – соответствующие параллельные хорды оснований цилиндра.
В частности, осевое сечение также прямоугольник, образованный сечением цилиндра плоскостью, проходящей через его ось (рис. 79.b).
Диагонали осевого сечения цилиндра проходят через точку являющуюся серединой отрезка, соединяющего центры оснований цилиндра. Следовательно, эта точка Q есть центр симметрии цилиндра (рис. 79.с).
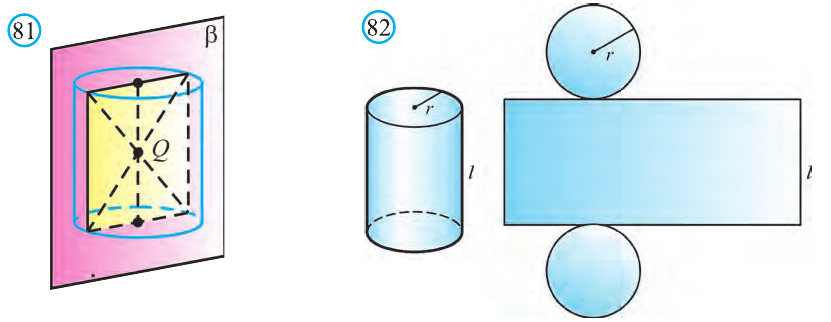
Плоскость, проходящая через точку Q перпендикулярно оси цилиндра является его плоскостью симметрии (рис. 80). Любая плоскость, проходящая через ось цилиндра также будет ось симметрии цилиндра (рис. 81).
Пример:
Осевое сечение цилиндра – квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Решение:
Сторона квадрата равна 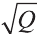
основания. Поэтому его площадь равна
Докажите самостоятельно эту теорему пользуясь рисунком 82.
Следствие. Полная поверхность цилиндра равна сумме его боковой поверхности и площадей двух его оснований:
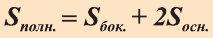
Пусть дан произвольный цилиндр. Впишем в одно из его оснований многоугольник 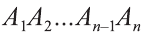
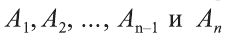
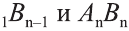
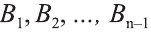
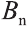
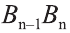
Ясно, что если вокруг основания призмы можно описать окружность, то вокруг призмы можно описать цилиндр.
Аналогично вводятся понятия призмы, описанной вокруг цилиндра и цилиндра, вписанного в призму (рис. 84). Если призма описана вокруг цилиндра, то основание призмы будет описано вокруг основания цилиндра и боковые грани призмы будут касаться боковой поверхности цилиндра.
Ясно, что если в основание призмы можно вписать окружность, то вокруг цилиндра можно описать призму.
Объём цилиндра
Теорема. Объём цилиндра равен произведению площади его основания и образующей цилиндра:
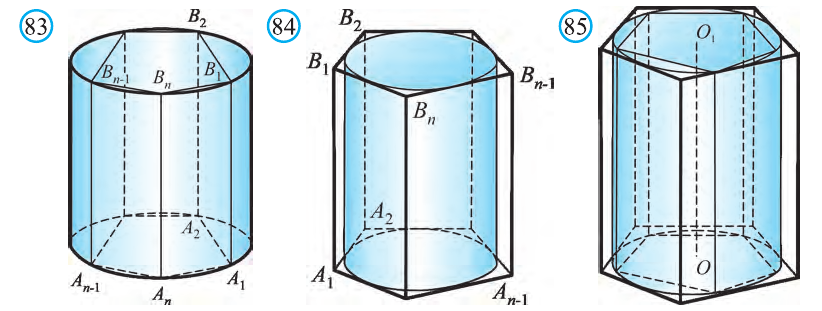
Доказательство. Пусть дан цилиндр с осью ОО1 (рис. 85). Впишем в него призму 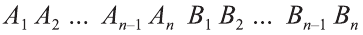
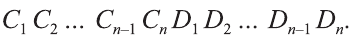
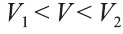
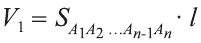
Будем всё больше и больше увеличивать число n сторон оснований призм. Тогда объём вписанной призмы будет увеличиваться, а объём описанной призмы уменьшаться. Если число n сторон увеличивать неограниченно, то разность между объёмами будет стремится к нулю. Число, к которому приближаются объёмы вписанной и описанной призм, принимают за объём данной призмы. При этом площади многогранников 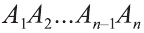
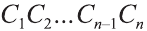
Исторические сведения:
В произведении Абу Райхна Беруни «Книга о началах искусства астрономии» («Астрономия») как введение в стереометрию в разделе о геометрии приводятся следующие определения фигур:
Куб – физическая фигура, похожая на кубик для игры в нарды, ограниченная с шести сторон квадратами.
Призма – представляет собой фигуру, ограниченную по бокам плоскостями в форме квадрата или прямоугольника, а сверху и снизу -двумя треугольниками. В этом определении Беруни приведено описание частного вида призмы, а именно треугольной призмы.
Книга Беруни «Канон Масьуда» написана в 1037 году. В ней приведены правила нахождения объёмов параллелепипеда и призмы: «Если тело не четырёхугольное или другого вида, то его расчёт таков: найди площадь, умножь его на глубину, в итоге получишь объём». В произведении Абу Али ибн Сино «Книга знания» в разделе «Основы изучения геометрических тел» дано описание тела и треугольной призмы. А также описаны условия взаимного равенства двух призм. Ибн Сино даёт следующее определение призмы: «Призма – тело, ограниченное двумя плоскими треугольными сторонами.»
В произведении Аль Каши «Книга счёта» приведёт много примеров расчета площадей поверхностей и объёмов тел. Благодаря своим глубоким знаниям в математике, геометрии, тригонометрии, механике и астрономии он пользовался вниманием и уважением Улугбека. Аль Каши наряду с многоугольниками изучачл призмы, пирамиды, цилиндры, конусы, усечённые конусы.
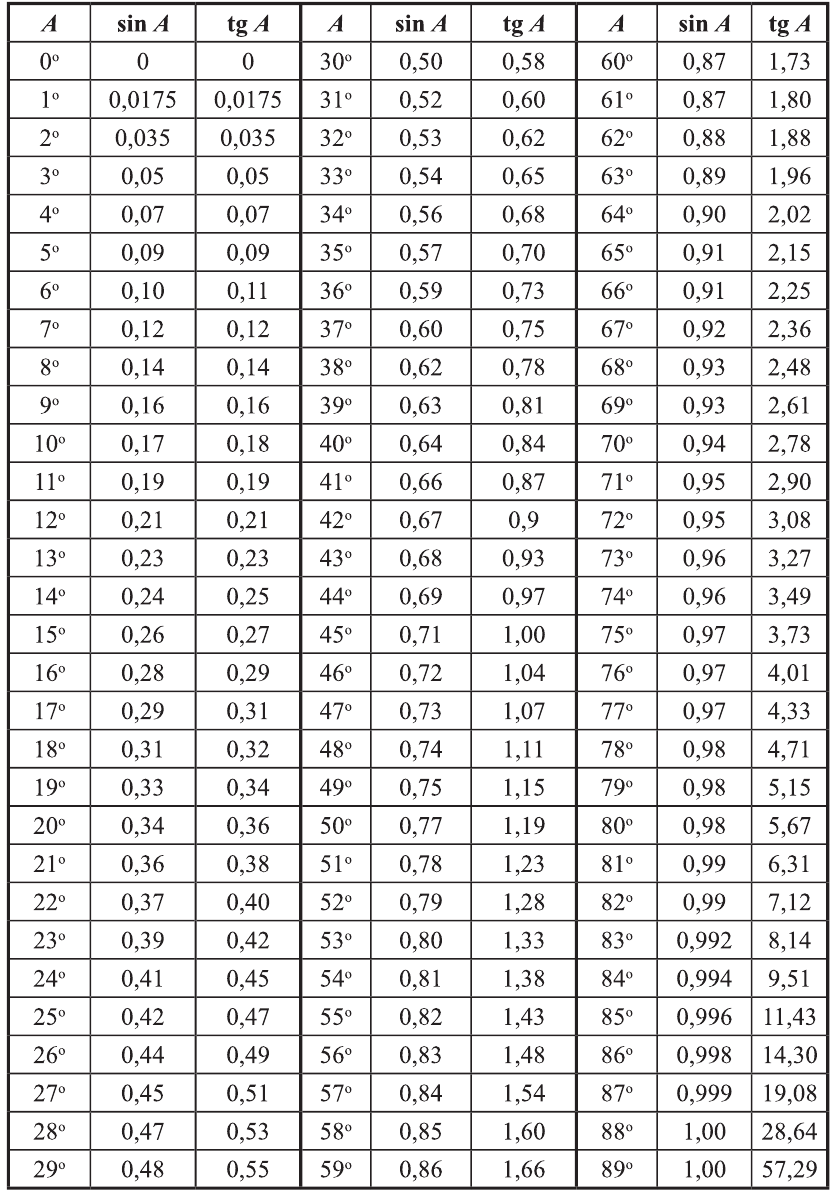
Таблица приближенных значений тригонометрических функций:
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Возникновение геометрии
- Призма в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
Как рисовать цилиндр? Подробная инструкция рисования цилиндра.
December 21, 2020
Цилиндр – геометрическое тело, форма которого состоит из трех поверхностей: двух одинаковых по форме плоских кругов и одной, образующей форму, цилиндрической поверхности. Для того чтобы лучше разобраться и понять конструктивную основу строения формы цилиндра, в качестве наглядного пособия рассмотрим его каркасную модель. Изготовить такую модель-каркас не составляет труда. Для этого можно использовать проволоку – алюминиевую, медную, стальную или из мягкого сплава. Длина большой стороны каркаса может быть в пределах 7-10 см.
Изучение в рисунке каркасных моделей позволяет студентам лучше освоить конструктивную сущность предмета, его взаимосвязь и пространственность формы.
Рис.49. Перспективное построение окружностей оснований цилиндра: а – с одной точкой схода; б – с двумя точками схода
Изображение геометрического тела, расположенного на горизонтальной плоскости в обычном вертикальном положении, следует начинать с построения его основания. Как видно, на основаниях цилиндра имеются круглые по форме поверхности, ограниченные окружностью. С окружностью мы уже ознакомились и знаем методы и способы ее построения на плоскости. Основываясь на методе линейно-конструктивного построения изображения каркасных моделей, следует перейти к рассмотрению изображения цилиндра.
Изображение цилиндра следует начинать с определения основных пропорциональных величин – диаметра оснований и высоты.
Построение плоскостей кругов оснований производят тем же способом, что и при изображении окружностей – вписыванием в квадрат (рис.48).
Рис.50
Ось вращения тела (ось цилиндра) всегда перпендикулярна к плоскостям кругов основания. При прорисовывании окружности в квадратах их вертикальные и горизонтальные оси попадают своими концами в середины сторон квадрата, т.е. в точки касания окружности со сторонами поверхности цилиндра (рис.48,49).
Рассматривая форму каркаса цилиндра, видим, что нижнее основание шире верхнего, следовательно, ближняя высота поверхности цилиндра больше, чем дальняя. Их различия обусловлены перспективной закономерностью. При этом необходимо заметить, что чрезмерно широкое нижнее основание цилиндра не способствует правильному и убедительному построению рисунка цилиндра. Поэтому ширина нижнего эллипса относительно верхнего должна быть чуть больше, равно как при наблюдении цилиндра с дальней точки зрения, а не с ближней.
При изображении окружностей оснований эллипса на гипсовом цилиндре его нижнее основание следует прорисовывать насквозь, т.е. видимым, с последующим его удалением для продолжения работы с помощью светотеней. Это даст возможность проследить за различиями в размерах оснований.
Завершив перспективное построение окружностей оснований цилиндра, приступайте к прорисовке краев формы образующей поверхности, соединяющей оба круга. При этом линии не должны быть чрезмерно контрастными, так как они находятся дальше, чем ближние поверхности цилиндра – ближние края эллипса и его изображающая поверхность. Однако без усиления линий ближних краев оснований получить в рисунке достаточное впечатление объемно-пространственной формы невозможно.
По окончании работы над построением рисунка цилиндра необходимо приступить к его проверке. Проверять следует, отходя от своего места на расстояние не менее 2-4 м, в зависимости от размера рисунка. Чем больше его размер, тем с большего расстояния его следует рассматривать.
Внимательно проверив допущенные в процессе работы ошибки, их следует, не откладывая, исправить.
Изображение цилиндра в горизонтальном положении имеет свои особенности в отличие от построения цилиндра в вертикальном положении. Это обусловлено его цилиндрической образующей поверхностью, связывающей между собой оба круглых основания цилиндра. Для примера рассмотрим каркас цилиндра (рис.52).
Цилиндр в горизонтальном положении можно строить на основе прямоугольной призмы. Это облегчает объемно-пространственное и конструктивное построение цилиндра, позволяет правильно определить ось вращения по отношению к оси эллипса и, следовательно, правильно строить окружности оснований (эллипсы). Определив линию горизонта и положение предмета в пространстве относительно угла зрения (в этом случае цилиндр находится несколько сбоку, а точка зрения выше цилиндра), нужно наметить его местоположение. При построении очень важно правильно определить углы горизонтальных направлений предмета на плоскости, поэтому изображение призмы начинают с построения ее основания, у которого все стороны попарно равны высоте цилиндра и диаметру оснований окружностей. В последующем эта призма будет служить каркасом для построения цилиндра в горизонтальном положении.
Построение призмы производят с ближайших к нам точек на пересечении сторон параллелепипеда. В соответствии с положением предмета нужно наметить горизонтальную, уходящую по направлению к точкам схода линию основания сторон призмы. Направления этих двух основных линий, идущих к точкам схода, должны определять основу для правильного построения призмы, а затем – цилиндра. После чего производят построение с учетом перспективы. Для определения точек осевой линии призмы следует провести диагонали противоположных углов ее передней грани. Точка пересечения диагоналей будет центром оси призмы и цилиндра. Чтобы правильно вписать окружность основания цилиндра (эллипс) в переднюю грань призмы, необходимо точно определить прямой угол между осью призмы и отрезком линии, которая и будет большой осью эллипса. Эта важная деталь, о ней следует всегда помнить студентам, является причиной грубых ошибок при изображении цилиндра в горизонтальном положении. При этом, независимо от ракурсов и углов поворота, прямой угол между большой осью эллипса и осью вращения тела является основой для правильного построения окружностей оснований в его горизонтальном положении.
Итак, определив прямой угол, приступайте к вписыванию окружностей оснований цилиндра. Здесь большая ось будет определять наибольший диаметр основания, а малая, которая располагается по оси цилиндра, – наименьший.
Рис.52
Следует обратить внимание, что дальнее основание цилиндра по мере удаления от рисующего всегда несколько шире (по малой оси), чем переднее. Это обусловлено закономерностью перспективы.
Построив таким образом основания и дополнительно уточнив окружности (эллипсы), соединяют их образующими. В завершающей стадии построения изображения следует придать рисунку большую пространственность за счет усиления линий близлежащих и ослабления линий дальних форм.
Завершив построение, следует непременно его проверить. Внимательно проверив возможные ошибки, допущенные в процессе построения, и исправив их (если таковые имеются), следует перейти к длительному рисунку с помощью света, тени, полутени и рефлекса.
Для продолжения работы над длительным рисунком студентам необходимо дополнительное изучение закономерностей распределения светотеней. Без этого невозможно переходить к практическому выполнению учебных задач в академическом учебном рисунке. Вопросы, касающиеся законов света и теней, изложены в конце этого раздела.
Хотите начать обучение?
На самом деле, всё не так сложно.
Во-первых, цилиндр есть поверхность второго порядка. Очевидно? Значит, он задаётся уравнением вида
a_11 x^2 + a_12 xy + a_13 xz + ... + a_33 z^2 + a_0 = 0
Подставляя имеющиеся точки, получаете систему линейных уравнений на коэффициенты a_i. Заметьте, что коэффициенты определены с точностью до постоянного множителя, поэтому система будет иметь серию решений, вам подходит любое ненулевое.
Первая часть есть. Теперь, вам нужно найти ось, исходя из уравнения. Для этого можно воспользоваться классификацией поверхностей второго порядка (например, здесь), это уже чисто математическая задача.
P.S.: если ваша система координат ориентирована по отношению к трубе известным образом, то конечно задача сильно упрощается.
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
- Определение цилиндра
- Основные элементы цилиндра
- Виды сечений цилиндра
- Виды цилиндров
Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
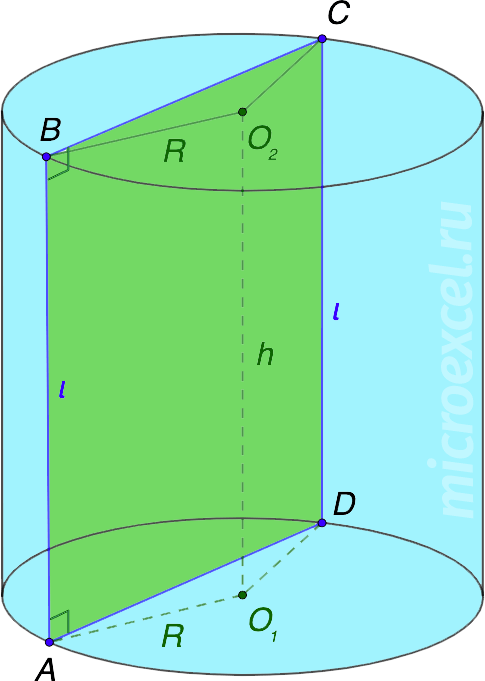
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
- длина данного прямоугольника равна длине окружности основания цилиндра (2πR);
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Виды сечений цилиндра
- Осевое сечение цилиндра – прямоугольник, образованный в результате пересечения фигуры плоскостью, проходящей через ее ось. В нашем случае – это ABCD (см. первый рисунок публикации). Площадь такого сечения равна произведению высоты цилиндра на диаметр его основания.
- Если секущая плоскость проходит не по оси цилиндра, но при этом перпендикулярна его основаниям, то сечением, также, является прямоугольник.
- Если секущая плоскость параллельна основаниям фигуры, то сечение – это идентичный основаниям круг.
- Если цилиндр пересекается плоскостью, не параллельной его основаниям и, при этом, не касающейся ни одной из них, то сечением является эллипс.
- Если секущая плоскость пересекает одно из оснований цилиндра, сечением будет парабола/гипербола.
Виды цилиндров
- Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
- Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
- Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
- Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
- Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.