Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 декабря 2021 года; проверки требуют 7 правок.
У этого термина существуют и другие значения, см. сумма.
Су́мма (лат. summa — итог, общее количество) в математике — результат применения операции сложения величин (чисел, функций, векторов, матриц и т. д.), либо результат последовательного выполнения нескольких операций сложения (суммирования). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:
В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы объединяемых множеств, взятые без повторений.
Также сложение (нахождение суммы) может быть определено для более сложных алгебраических структур (сумма групп, сумма линейных пространств, сумма идеалов, и другие примеры). В теории категорий определяется понятие суммы объектов.
Сумма натуральных чисел[править | править код]
Пусть в множестве 
находится 
элементов, образующих подмножество 
, и 
элементов, образующих подмножество 
(
, a и b — натуральные числа). Тогда арифметической суммой 
будет количество элементов 
, образующих подмножество 
, полученное при дизъюнктном объединении двух исходных подмножеств 
Алгебраическая сумма[править | править код]
Сумму математически обозначают заглавной греческой буквой Σ (сигма).
где: i — индекс суммирования; ai — переменная, обозначающая каждый член в серии; m — нижняя граница суммирования, n — верхняя граница суммирования. Обозначение «i = m» под символом суммирования означает, что начальное (стартовое) значение индекса i эквивалентно m. Из этой записи следует, что индекс i инкрементируется на 1 в каждом члене выражения и остановится, когда i = n.[1]
В программировании данной процедуре соответствует цикл for.
- Примеры записи
Границы могут опускаться из записи, если они ясны из контекста:
Итератор может быть выражением — тогда переменная оформляется со скобками как функция «
». Например, сумма всех 
при натуральных числах 
в определённом диапазоне:
Сумма 
элементов 
множества 
:
Сумма 
всех положительных чисел 
, являющихся делителями числа 
:
Под знаком итеративного суммирования может использоваться несколько индексов, например:
причём набор из нескольких индексов можно сократить в виде так называемого мультииндекса.
Бесконечная сумма[править | править код]
В математическом анализе определяется понятие ряда — суммы бесконечного числа слагаемых.
Примеры последовательных сумм[править | править код]
1. Сумма первых элементов арифметической прогрессии:
2. Сумма первых элементов геометрической прогрессии:
3.![sum limits _{{k=1}}^{n}k^{3}=left[{frac {n(n+1)}{2}}right]^{2}=left(sum limits _{{k=1}}^{n}kright)^{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c341ce59623204355f8577a50b0e02b49e30240d)
4. 
Доказательство
5. 
6. 
-
-
- Например, при
получается , а это последовательность равенств следующего вида:
- Например, при
-
Неопределённая сумма[править | править код]
Неопределённой суммой 
по 
называется такая функция 
, обозначаемая
,
что 
.
«Дискретная» формула Ньютона — Лейбница[править | править код]
Если найдена «производная» 
, то 
.
Этимология[править | править код]
Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, а также появляется глагол «суммировать» (1489 год).
Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.
Специальный символ для обозначения суммы (Σ) первым ввёл Леонард Эйлер в 1755 году, его поддержал Лагранж, однако долгое время с этим символом конкурировал знак S. Окончательно обозначение Σ для суммы утвердили уже в XVIII веке Фурье и Якоби[2].
Кодировка[править | править код]
В Юникоде есть символ суммы U+2211 ∑ n-ary summation (HTML ∑ • ∑).
См. также[править | править код]
- Сложение
- Произведение
Примечания[править | править код]
- ↑ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren. Chapter 2: Sums // Concrete Mathematics: A Foundation for Computer Science (2nd Edition) (англ.). — Addison-Wesley Professional, 1994. — ISBN 978-0201558029. (недоступная ссылка)
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 175. — 248 с. — ISBN 978-5-382-00839-4.
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — 7-е. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
Содержание:
- Определение суммы чисел
- Свойства суммы чисел
Определение суммы чисел
Суммой $s$ (лат. summa – итог, общее количество) чисел $a_{1}, a_{2}, dots, a_{n}$ называется результат
суммирования этих чисел: $s=a_{1}+a_{2}+ldots+a_{n}$ . В частности, если складывается два числа $a$ и $b$, то
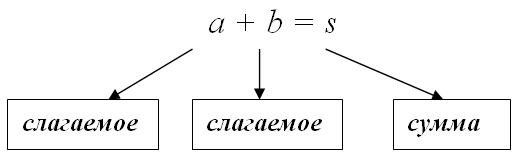
Пример
Задание. Найти сумму чисел:
1) $12$ и $15$ 2) $1,1 ; 2,2 ; 3,3$ и $4,4$
Ответ.
$12+15=27$
$1,1+2,2+3,3+4,4=11$
Свойства суммы чисел
- Коммутативность: $n+m=m+n$
-
Ассоциативность: $(n+m)+k=n+(m+k)$
На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.
-
Дистрибутивность по отношению к умножению
$$(n+m) cdot k=n cdot k+m cdot k$$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму чисел удобным способом:
1) $15+17+13$ ; 2) $34+22+16+18$
Решение. По свойствам сложения имеем
$$15+17+13 =15+(17+13)=15+30=45 $$
$$34+22+16+18 =(34+16)+(22+18)=50+40=90 $$
Ответ. 1) $15+17+13=45$
2) $34+22+16+18=90$
При сложении больших чисел или
десятичных дробей используется сложение в столбик.
Пример
Задание. Найти сумму чисел удобным способом:
1) $1562+13827$ ; 2) $34,71+356,161$
Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом.
В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем
числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном
столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:
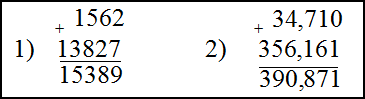
Ответ. 1) $1562+13827=15389$
2) $34,71+356,161=390,871$
Сложение рациональных дробей производится по правилу
$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$
Пример
Задание. Найти сумму чисел:
1) $frac{1}{4}+frac{1}{6}$ ; 2) $frac{2}{3}+1 frac{1}{2}$
Решение. Вычислим первую сумму используя правило сложения рациональных чисел
$$frac{1}{4}+frac{1}{6}=frac{1 cdot 6+1 cdot 4}{4 cdot 6}=frac{6+4}{24}=frac{10}{24}$$
Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим
$$frac{1}{4}+frac{1}{6}=frac{5}{12}$$
Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого
умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим
правило сложение рациональных дробей
$$frac{2}{3}+1 frac{1}{2}=frac{2}{3}+frac{3}{2}=frac{2 cdot 2+3 cdot 3}{3 cdot 2}=frac{4+9}{6}=frac{13}{6}$$
Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком.
Полученное частное запишем в целую часть, а остаток от деления в числитель.
$$frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$$
Ответ. 1) $frac{1}{4}+frac{1}{6}=frac{5}{12}$ ;
2) $frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$
Читать дальше: что такое произведение чисел.
Содержание
Определение действия сложение и компоненты сложения
Переместительный и сочетательный законы сложения
Правило прибавления слагаемого к сумме или суммы к слагаемому
Изменение суммы чисел с изменением слагаемых
Сложение однозначных чисел
Сложение многозначного и однозначного чисел
Сложение двух многозначных чисел в столбик
Сложение в столбик нескольких многозначных чисел
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Как вы уже знаете, любое натуральное число представляет собой единицу или собрание нескольких единиц. Так вот, мы можем взять несколько чисел и объединить все единицы, которые их составляют, в одно большое собрание. Число, которое получилось в результате этого объединения, называется суммой.
Сумма чисел – это такое число, которое получается после объединения всех единиц других данных натуральных чисел.
Слагаемые – это числа, над которыми мы выполняем действие сложения. Иными словами, это те числа, количество единиц которых мы объединяем в новом числе.
Арифметическое действие – это нахождение нового числа при помощи двух или нескольких других данных чисел.
В курсе математики 5 класса изучаются основные арифметические действия – сложение, вычитание, умножение и деление.
Определение
Сложение – это арифметическое действие, которое выполняется для получения суммы нескольких чисел.
Или другими словами:
Сложение – это действие увеличения числа на количество единиц, содержащихся в другом числе.
Сумма – это результат действия сложения.
На записи действие сложения обозначается знаком + (плюс). То есть, если записано 3+2+5, то это означает, что нам нужно найти сумму этих трех чисел: 3, 2 и 5. Сумма записывается обычно справа от слагаемых после знака = (равно): 3+2+5 = 10.
Сумма чисел состоит (слагается, складывается, – можно говорить по-разному) из двух или более слагаемых. Понятно, что сумма всегда больше любого ее слагаемого.
Слагаемые – это не что иное, как состав числа, обозначающего сумму этих слагаемых.
Компоненты действия сложения для двух слагаемых:
Компоненты сложения для трех слагаемых:
Действие сложения можно выполнить всегда. Действительно, так как натуральный ряд бесконечен, то мы всегда можем любые числа этого ряда объединить в другое, какое угодно большое число.
Действие сложения всегда имеет единственный результат. Действительно, если мы, к примеру, отметим на координатном луче с началом в точке O и единичным отрезком 1 см отрезок OA длиной 5 см, а потом построим еще один отрезок AB длиной 7 см, то у нас получится только единственный отрезок OB длиной 12 см.
Рисунок 1. Сумма двух чисел на координатном луче.
Основные свойства суммы натуральных чисел
Есть два основных закона суммы, из которых следуют остальные ее свойства:
- переместительный закон сложения,
- сочетательный закон сложения.
Переместительный закон сложения
Сумма двух или нескольких чисел от изменения порядка сложения слагаемых не меняется.
Это значит, что значение суммы не зависит от порядка выполнения действия сложение.
Например, в каком бы порядке мы ни складывали числа 2, 3 и 5, результат неизменно будет 10:
Сочетательный закон сложения
Сумма нескольких чисел не поменяется, если некоторые слагаемые заменить их суммой.
Это значит, что мы можем группировать слагаемые как угодно, а также выполнять действия сложения в любом порядке.
Например, если в нашем примере мы заменим слагаемые 2 и 3 их суммой, то результат останется такой же, как и при обычном сложении слагаемых:
То же самое будет, если мы заменим слагаемые 3 и 5, или 2 и 5 их суммами:
или
или
Из этих законов вытекает правило прибавления слагаемого к сумме или суммы к слагаемому.
Правило
Для прибавления суммы некоторых чисел к числу или некоторого числа к сумме чисел, нужно сложить это число с одним из слагаемых суммы, а получившийся результат сложить последовательно с остальными слагаемыми.
Пример 1. Прибавление числа к сумме чисел:
Можно сразу вычислить сумму чисел в скобках и сложить ее с первым слагаемым:
325+(12+64+5) = 325+81 = 406
Также можно использовать правило прибавления слагаемого и суммы. Результат при этом не поменяется
325+12 = 337;
337+64 = 401;
401+5 = 406
или
325+64 = 389;
389+12 = 401;
401+5 = 406.
Пример 2. Прибавление суммы чисел к другому числу:
Можно сразу вычислить сумму чисел в скобках и сложить ее со вторым слагаемым
(54+240+189)+37 = 483+37 = 520
Или можно использовать правило прибавления суммы чисел к числу. Результат останется тот же.
54+37 = 91;
91+240 = 331;
331+189 = 520
или
240+37 = 277;
277+54 = 331;
331+189 = 520.
Изменение суммы чисел с изменением слагаемых
Чтобы понять, как изменится сумма чисел, если изменить одно или несколько ее слагаемых, нужно вспомнить, что сумма представляет собой собрание всех единиц, из которых состоят слагающие ее числа. Поэтому, легко можно понять, что:
При увеличении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже увеличится на это же число (на это же количество единиц).
При уменьшении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже уменьшится на это же число (на это же количество единиц).
Эти два свойства справедливы и в обратную сторону. То есть, если увеличить или уменьшить сумму на какое-то число, тогда для сохранения равенства нужно соответственно увеличить или уменьшить одно из слагаемых.
Если увеличить одно из слагаемых на какое-то число (на какое-то количество единиц), а другое уменьшить на это же число (на это же количество единиц), то в результате сумма не поменяется.
Простой пример увеличения суммы при увеличении слагаемого: у вас есть 700 рублей; 200 рублей лежит в левом кармане, а 500 – в правом. Вы нашли на улице 300 рублей и положили их в левый карман, после чего там стало 200+300=500 рублей. Таким образом, всего у вас оказалось 500+500=1000 рублей, то есть, сумма всех ваших денег увеличилась на 300 рублей.
Попробуйте самостоятельно придумать примеры для всех трех правил.
Сложение однозначных чисел
Сложение двух однозначных чисел выполняется так: одно число увеличивается на количество единиц другого числа. То есть, единицы одного числа присоединяются к единицам другого числа.
Например, для нахождения суммы 5+2 нужно к числу 5 присоединить 2 единицы. Тогда получим 5+2=7. А если нужно к числу 7 прибавить число 8, или другими словами, найти сумму 7+8, то после присоединения к 7 единиц числа 8 получим 1 десяток единиц и еще 5 единиц, то есть, число 15.
Сложение однозначных чисел – это первый и очень важный шаг в освоении этого арифметического действия. Если хорошо выучить все результаты сложения однозначных чисел между собой, тогда вы сможете намного быстрее складывать в уме любые числа.
Сложение многозначного числа с однозначным
Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.
Допустим, нам нужно найти сумму чисел 88 и 5.
Способ 1.
Представим число 88 в виде суммы 80+8 и прибавим к ней число 5. После этого, найдем сумму однозначных чисел 8 и 5, получится 13. Прибавим этот результат к числу 80. Число 13 – это 10+3, поэтому мы к 8 десяткам прибавляем 1 десяток, получаем 9 десятков, или число 90, а к нему прибавляем еще 3 (оставшиеся от числа 13), и получим 93.
То есть, мы проделываем такие действия:
88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.
Способ 2.
Замечаем, что если к 88 прибавить 2, то получим полный десяток, то есть, число 90. Тогда представляем число 5 в виде суммы 2+3; число 2 складываем с 88, получаем замеченное нами ранее число 90. Добавляем к нему оставшееся число 3, и получаем результат 93.
То есть, ход вычисления был такой:
88+5 = 88+2+3 = 90+3 = 93.
Сложение в столбик многозначных чисел
Сумма многозначных чисел удобно вычисляется, если использовать так называемое сложение в столбик.
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Этот способ простой, и он помогает не запутаться во время вычисления, не допустить ошибки. Но, чтобы складывать быстро, как я и говорил раньше, вам нужно очень хорошо знать все попарные суммы однозначных чисел.
Итак, допустим, что нам нужно найти сумму : 5728+803
Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел, т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. плюс. У нас получилась такая запись:
Теперь нам нужно сложить между собой единицы каждого разряда, начиная с первого: сперва простые единицы, потом десятки единиц, потом сотни единиц и т.д. Результаты этих сложений записываем под чертой в том разряде, единицы которого мы складывали.
Начинаем с простых единиц: 8+3=11. У нас получилось число 11, то есть, 1 десяток и 1 единица. 1 единицу мы записываем под чертой в разряде единиц, а 1 получившийся десяток нужно будет дополнительно прибавить к сумме единиц разряда десятков. Чтобы не забыть совершить это действие, мы пишем над цифрами разряда десятков маленькую цифру 1 или ставим там точку.
Про подобное действие обычно говорят: «один пишем, один в уме» , то есть, оставляем в памяти, чтобы не забыть добавить при следующем действии.
Далее переходим к десяткам. У первого слагаемого 2 единицы разряда десятков, а у второго 0, поэтому: 2+0=2. Мы помним, что после сложения простых единиц у нас образовался дополнительно 1 десяток, поэтому к этому результату добавляем еще единицу: 2+1=3. У нас получилось 3 десятка, поэтому записываем цифру 3 под чертой в разряде десятков.
Следующими идут сотни: 7+8=15. Первым делом проверяем, не нужно ли нам дополнительно добавлять единицу? В нашем случае нет, потому что на предыдущем шаге при сложении десятков мы получили однозначное число. Поэтому, пишем под чертой в разряде сотен цифру 5. И у нас получилось дополнительно 10 сотен, то есть, 1 тысяча единиц. Значит, нам нужно отметить эту получившуюся 1 тысячу как дополнительную, поставив маленькую цифру 1 над цифрами разряда тысяч.
В разряде тысяч у первого слагаемого стоит цифра 5, а у второго ничего не стоит. Но мы помним, что при отсутствии разрядов в начале числа (слева) нули не пишутся, но подразумевается, что в этих разрядах по 0 единиц. Поэтому мы находим сумму 5+0=5, т.е. 5 единиц разряда тысяч и добавляем к ней дополнительную 1 единицу тысяч, полученную после сложения разрядов сотен. 5+1=6. Записываем эту цифру под чертой в разряде тысяч.
После нахождения суммы чисел методом сложения столбиком, записываем результат решения в исходном строчном примере:
5728+803 = 6531
Сложение в столбик нескольких многозначных чисел
Этим способом так же легко можно найти сумму нескольких многозначных чисел.
Рассмотрим пример: 12044+28609+1358
Сложив простые единицы, мы получим 21, то есть, 2 десятка и 1 единицу. Записываем под чертой в разряде единиц цифру 1, а 2 отмечаем «в уме».
Сложив десятки этих трех чисел, мы получим 4+0+5=9 единиц разряда десятков. Добавив 2 десятка единиц, которые у нас были «в уме», получаем 11, то есть, 10 десятков и ещё 1 десяток. Под чертой мы записываем цифру 1 в разряде десятков, а так как 10 десятков – это не что иное как 1 сотня, то мы отмечаем «единицу в уме», то есть, ставим над всеми тремя числами в разряде сотен маленькую цифру 1.
Теперь складываем 0 сотен первого числа, 6 сотен второго и 3 сотни третьего. Получается 9 сотен. Добавляем 1 сотню, которая была «в уме» после сложения всех десятков, и у нас выходит 10 сотен, то есть, 1 тысяча единиц. Значит, под чертой в разряде сотен мы пишем 0 (так как у нас не получилось ни одной единицы сотен, только десяток сотен), а над всеми числами в разряде тысяч отмечаем дополнительную 1 тысячу.
В разряде тысяч мы находим сумму 2+8+1, это будет 11 тысяч единиц, добавляем 1 тысячу, которая получилась после сложения сотен. Получаем 12 тысяч единиц, то есть, 10 тысяч и 2 тысячи. Цифру 2 пишем в разряде тысяч единиц под чертой, а единицу десятка тысяч (наши 10 тысяч единиц) отмечаем сверху в соответствующем разряде.
Нам осталось сложить десятки тысяч единиц: 1+2+0=3 десятка тысяч, и прибавить к результату 1 десяток тысяч, получившийся после прошлого шага. У нас вышло 4 десятка тысяч, поэтому в этом разряде под чертой мы пишем цифру 4.
Нам остается только записать результат в начальном примере:
12044+28609+1358
Хочу обратить внимание, что при сложении в столбик все шаги (сложение единиц каждого разряда) совершаются последовательно в одной записи. Я расписывал их отдельными только для лучшего понимания сути процесса сложения. И конечно же, не нужно выделять каждый разряд отдельным цветом. В случае рассмотренных выше примеров все решение выглядит так:
- Главная
- Справочники
- Справочник по математике для начальной школы
- Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
Подскажи ему.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
Рассмотрите рисунок.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Рассмотри рисунок.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
8 + 4 = 12
12 – 4 = 8
12 – 8 = 4
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 – 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 – первое слагаемое
2 – второе слагаемое
5 сумма
2 + 3 = 5
2 – первое слагаемое
3 – второе слагаемое
5 – сумма
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = …. (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
29 + 1 = 30
37 + 30 = 67, значит,
(37 + 29) + 1 = 67
Вывод: два соседних слагаемых можно заменить их суммой.
Советуем посмотреть:
Табличное сложение
Письменное сложение в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 26. Тест 1,
Волкова, Проверочные работы
Страница 17. Урок 10,
Петерсон, Учебник, часть 1
Страница 31. Урок 20,
Петерсон, Учебник, часть 1
Страница 34. Урок 23,
Петерсон, Учебник, часть 1
Страница 45. Урок 28,
Петерсон, Учебник, часть 1
Страница 22. Урок 12,
Петерсон, Учебник, часть 2
Страница 23. Урок 12,
Петерсон, Учебник, часть 2
Страница 26. Урок 14,
Петерсон, Учебник, часть 2
Страница 46. Урок 24,
Петерсон, Учебник, часть 3
Страница 96. Повторение,
Петерсон, Учебник, часть 3
2 класс
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 25. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 64. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 33,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 74,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 80. Дополнительные задачи,
Петерсон, Учебник, часть 1
3 класс
Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 107,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 8. Урок 2,
Петерсон, Учебник, часть 1
Страница 73. Урок 25,
Петерсон, Учебник, часть 1
4 класс
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 43,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 82. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 88. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16. Урок 6,
Петерсон, Учебник, часть 1
5 класс
Задание 219,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Загрузить PDF
Загрузить PDF
Сложение – один из немногих навыков, которые мы изучали в школе, и он действительно пригодился нам в жизни. К счастью, научиться сложению не так уж и трудно. Есть несколько правил сложения, в зависимости от видов чисел, которые вы прибавляете, но wikiHow сделает все за вас. Просто перейдите к первому пункту!
-
1
Для начала усвойте принцип сложения. Возьмите пригоршню бобов (или других мелких предметов). Сложите бобы в кучку, одновременно ведя счет (1, 2, 3 и др.) После того, как кучка вырастет, остановитесь. Сколько штук вы туда положили? Запишите это число. Теперь проделайте тоже самое, но складывайте бобы уже в другую кучку. Затем смешайте обе кучки друг с другом. Сколько у вас теперь? Вы можете подсчитать бобы один за другим и узнать! Это и есть сложение!
- Например, представим, что в первой кучке было 5 бобов. Во второй – 3 боба. Когда вы смешали кучки и подсчитали все бобы, у вас оказалось 8! Так получилось, потому что 5 + 3 равно 8.
-
2
Учите числовые пары. Так как большинство людей считает с помощью десятичных множеств и чисел, делящихся на десять, вы можете использовать более легкий метод – выучить числовые пары, дающие в сумме десять. К примеру: 1+9, 2+8, 3+7, 4+6 и 5+5.
-
3
Составьте числовые пары самостоятельно. Составьте как можно больше числовых пар для того, чтобы получить десятичные множества.
- Предположим, что вам нужно сложить ряд таких чисел, как 2, 16, 9, 3, 5, 18. Вы можете сложить 18 и 2 и получить 20. 4 подходит к 6, так что отнимите 4 от 5, прибавьте к 16, и у вас получится 20. У вас останется единица от 5, которую вы можете прибавить к 9 для того, чтобы получить 10.
-
4
Сложите остальные числа. Подсчитайте оставшиеся числа с помощью пальцев или в уме, начиная с десятичных множеств, которые вы уже знаете.
- В предыдущем примере после подсчитанных 50 у вас осталось всего 3. Это очень легко подсчитать в уме!
-
5
Вторично проверьте результат на пальцах! По возможности вы всегда можете перепроверить ответ с помощью пальцев или другого метода.
Реклама
-
1
Выучите расположение чисел. Когда вы пишите числа, то каждое число в цепочке имеет свои вид или название. Если вы поймете, как правильно выстраивать числа в ряд, то вам будет легче их складывать. Например:
- 2, если она сама по себе, должна находиться на месте «единиц».
- В 20 двойка должна находиться на месте «десятых».
- В 200 двойка – на месте «сотых».
- Следовательно, в номере 365 пятерка будет находиться на месте единиц, шестерка – на месте десятых, а 3 – сотых.
-
2
Расположите числа по цепочке. Расположите числа в ряд так, чтобы каждое целое число, которое вы прибавляете, находилось сверху следующего. С помощью «разрядов после десятичной» вы сможете расположить числа по цепочке так, чтобы каждое последующее число располагалось над предыдущим. Оставьте место слева, если какое-то из чисел меньше остальных. Например, при сложении 16, 4 и 342 они должны располагаться так:
- 342
- _16
- __4
-
3
Сложите числа в первом столбике. Начните складывать числа, расположенные в крайнем столбце справа. Как только вы вычислите сумму (сколько у вас получилось после сложения чисел), запишите это число под цифрами, которые вы прибавляли, внизу столбика, где стоят единичные простые числа.
- В нашем примере, приведенном выше, сложив 2, 6 и 4, мы получим 12. Запишите последнюю цифру 12 – 2 снизу крайнего правого столбца.
-
4
Держите в уме десятки. Если у вас осталось число, которое следует вписать в столбец десятых, запишите его сверху следующего столбца (слева).
- В этом примере у нас есть число, которое следует вписать в столбец десятых, так что запишите 1 из 12 сверху столбца, расположенного посередине, т.е. над 4 из 342.
-
5
Подсчитайте числа в следующем столбце. Переходите к следующему столбцу и сложите все числа, включая также те, которые вы держали в уме после предыдущего шага. Запишите полученное число внизу столбца, держа в уме десятки, как в предыдущем действии.
- В этом примере мы имеем 1 из 12, плюс 4 от 342 и 1 от 16. В сумме будет 6.
-
6
Подсчитайте, сколько у вас получится в ответе. Повторяйте эти действия, двигаясь справа налево от столбца к столбцу, пока не подсчитаете числа в каждой цепочке. Число, которое появится внизу и будет ответом.
- В данном примере в ответе получилось 362.
Реклама
-
1
Расположите по цепочке числа с десятичными дробями. Если перед вами стоит число с десятичной дробью (к примеру, 24.5), вам следует быть немного осторожными при сложении подобных чисел столбиком. Тонкость заключается в том, что нужно расположить по цепочке все числа, содержащие десятичные дроби. Десятичные дроби должны стоять в своем собственном столбике[1]
.Например:- 107.8
- _24.5
- __3.2
- _15.0
-
2
Добавьте десятичную дробь, если она не содержится в числе. Если в числе нет десятичной запятой, поставьте ее и впишите нули справа от нее для того, чтобы сохранить столбцы.
- В вышеприведенном примере после 15 не стоял ноль, он был добавлен для того, чтобы было легче различить столбцы.
-
3
Сложите остальные числа в обычном порядке. Как только вы расположили цифры по цепочке, начните прибавлять их как обычно.
- Ответ в этом примере будет равен 150.5.
Реклама
-
1
Найдите общий знаменатель. Знаменатель – это число, стоящее под знаком обыкновенной дроби. Вам нужно найти общий знаменатель для того, чтобы сложить дроби. Это делается с помощью умножения (или деления) обеих чисел дробей – верхнего и нижнего до тех пор, пока нижние числа обеих дробей не будут равны. К примеру, представим, что вы решили сложить 1/8 и 3/4:
- Вам необходимо уравнять 8 и 4. Как можно превратить 4 в 8, спросите вы? Умножив на 2!
- Умножите на два 3 и 4 из дроби 3/4. Тогда у вас получится 6/8.
-
2
Сложите числители. Числитель – это число, стоящее над знаком обыкновенной дроби. Теперь, когда у вас есть 1/8 и 6/8, сложите 1 и 6 для того, чтобы получить 7.
-
3
Узнайте ответ. Возьмите полученные числители и запишите их над знаменателем. Знаменатель оставьте без изменений. Это значит, что сумма дробей равна 7/8.
-
4
Упростите дробь. Если вы хотите, чтобы дробь читалась проще, вам придется поделить или умножить ее числитель и знаменатель на одно и то же число. В нашем примере нам не нужно ее упрощать. Это число итак достаточно небольшое. Но если ваша дробь, предположим, равна 3/6, вы можете сократить ее.
- Для этого вам нужно найти наименьшее число, на которое делятся и числитель, и знаменатель. В данном примере это 3. Разделяем каждое число на 3 для того, чтобы получить сокращенную дробь, в данном случае это 1/2.
Реклама
-
1
Старайтесь оперировать более легкими числами. Если вам пришлось работать всего с несколькими числами, которые не очень увязываются с 10-ми, вы можете прибавить к ним или вычесть определенные числа для того, чтобы вам было легче подсчитать их в уме. К примеру, представим, что вам нужно провести следующее действие: 19 + 30. Было бы гораздо легче прибавить 20 + 30, не так ли? Поэтому прибавьте 1 к 19! И тогда все, что вам будет нужно сделать, – это вычесть ту цифру, которую вы прибавили для того чтобы получить окончательную сумму. Следовательно, 19 + 1 + 30 = 50 и 50 – 1 = 49.
-
2
Разбейте числа на множества или круглые цифры. Подобно составлению числовых пар, которое обсуждалось в первом пункте, постарайтесь найти группы чисел, в результате сложения которых можно получить 5 или 10 (или 50, 100, 500, 1000 и т.д.) Сложите эти группы для облегчения вашей задачи.
- К примеру, если 7+1+2=10 и 2+3=5, то при сложении 1+2+2+3+7 в сумме вы получите 15.
-
3
Прибавляйте их по частям. Разделите на части единицы и десятки для того, чтобы вам было легче работать с цифрами, сложив сначала десятки, а уже затем единицы. Некоторым легче сложить, например, 40+30+10, а затем 2+5+7 вместо 42+35+17.
-
4
Используйте формы цифр. Если вы хотите быстро сложить цифры в уме, не прибегая к столбцам и группам чисел, то можете использовать формы цифр для подсчета, вместо того, чтобы полагаться на свои пальцы. Лучше всего это работает, если у вас уже есть несколько чисел, которые нужно сложить. Например:
- В цифре 2 есть две концевые вершины. Этим она схожа с цифрой 3.
- Числа 4 и 5 содержат соответствующие числа на конце своих вершин и соединений, а кривую дугу цифры 5 можно рассматривать, как соединение.
- В некоторых числах, таких как 6, 7, 8 и 9, это не так заметно. Кривую чисел 6 и 9 можно разложить на три точки (верхнюю, среднюю и нижнюю), т.е. в 6 их будет две, а в 9 – три. Каждая сторона окружности дуги в цифре 8 может считаться за 1 (4 в сумме), данную цифру следует умножить на два, чтобы получить 8. 7 можно разложить на 3 точки с верхней короткой стороны и на 4 – с длинной стороны.
Реклама
Советы
- Если все настолько плохо, что вам становится сложно безошибочно посчитать числа на бумаге (к примеру, 22 + 47),тогда вам придется научиться более сложным способам сложения.
- Если пример не сложный, и вы уверены, что ответ будет в пределах 10 (как в случае с примером 2 + 5), вы сможете обойтись без карандаша и бумаги, сделав расчеты на пальцах.
- Как только ребенок освоится с данной методикой, вы можете объяснить ему, что необязательно считать с единицы, достаточно начать с числа, данного в примере. Например, 8 + 2. Просто возьмите два числа и начните отсчет с последующей цифры… 8… 9, 10. Этот метод также позволит вам проводить операции с двумя числами больше 10 с помощью пальцев, до тех пор, пока число, которое следует прибавить, не станет меньше или равным 10.
Реклама
Предупреждения
- Не пользуйтесь калькулятором во время учебы. Его можно использовать для того, чтобы проверить ответы, но не стоит поддаваться соблазну воспользоваться калькулятором – решайте примеры самостоятельно. Если вы будете зависимы от калькулятора, то вы рискуете попасть в такую неудобную ситуацию, где вам будет нужно прибавить числа, а под рукой не окажется калькулятора (к примеру, во время похода по магазинам вы хотите узнать, хватит ли у вас денег на какие-нибудь вещи…или туфли…или инструменты).
Реклама
Об этой статье
Эту страницу просматривали 13 301 раз.
