Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.
Синус, косинус, тангенс и котангенс. Определения
Зачем разделять понятия синуса, косинуса, тангенса и котангенса?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Что такое синус?
Синус угла (sin α) – это отношение противолежащего этому углу катета к гипотенузе.
Что такое косинус?
Косинус угла (cosα) – это отношение прилежащего катета к гипотенузе.
Что такое тангенс?
Тангенс угла (tg α) – это отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Синус и косинус можно представить через экспоненту (экспоненциальная функция).
Приведем иллюстрацию.

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.
Что и почему важно и принято помнить в ходе такого нахождения?
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг – вся числовая прямая, то есть эти функции могут принимать любые значения.
Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором – теорему косинусов.
Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.
Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус угла поворота α – это ордината точки A1(x , y). sin α=y
Косинус угла поворота α – это абсцисса точки A1(x , y). cos α=икс
Тангенс угла поворота α – это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котанг угла поворота α – это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Простое правило: синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят “синус угла поворота α”. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
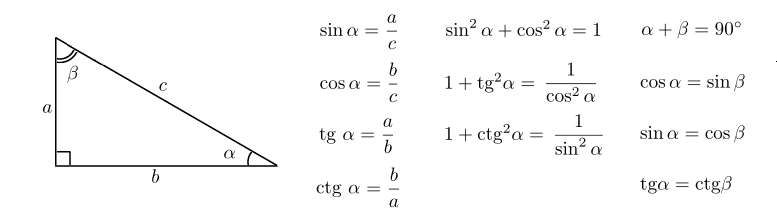
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .

Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:

Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.

Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.

Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.

Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB – BH = 18 – 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.

Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.

Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:

Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:

Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:

В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:

A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:

1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:

Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:

Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:

Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 – = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
У многих учеников возникают проблемы с этой темой, в основном, из-за непонимания общего смысла тригонометрии. В этой статье я постараюсь помочь вам разобраться зачем нужна тригонометрия и расскажу про лайфхак, чтобы не учить значения синуса и косинуса.
К моменту начала изучения тригонометрии Вы, скорее всего, уже знаете: определение прямоугольного треугольника и окружности — этого вполне достаточно для понимания темы.
*прошу заметить, что некоторые формулировки могут не соответствовать действительности – это сделано для того, чтобы вы лучше запомнили основы. Точные понятия и определения расскажет ваш учитель математики.
Что такое синус и косинус?
Изначально не было никакой окружности. Изучая треугольники, древние ученые выражали углы через соотношение сторон. То-есть синусы и косинусы появились раньше градусной меры углов.
Поскольку угол может быть найден через разные соотношения сторон, решили дать им названия: синус и косинус.
Синус – это отношение стороны треугольника, лежащей напротив данного угла, к гипотенузе (большей стороне).
Косинус – это отношение прилежащей стороны к гипотенузе.
Думаю не ошибусь, если скажу, что теорема Пифагора – самая полезная теорема в геометрии. Давайте применим её для данного треугольника:
Пояснение: делим обе части уравнения на квадрат гипотенузы и делаем замену.
Тригонометрическая окружность
Большие числа тяжело было показывать на координатной прямой, поэтому математики придумали также поделить окружность на равные части:
При переходе через равное расстояние одни и те же точки могут менять свою координату. Например, точка 0 (начало отсчёта) может являться 16, точка 1 может принимать значение 17 и так далее.
Идея с бесконечной прямой хороша, но как переводить эти величины в известную нам координатную плоскость?
На помощь приходит определение круга:
Проведём два перпендикулярных диаметра круга (это будет условная координатная плоскость), а радиус будет равен 1.
Центр круга будет точкой отсчёта (0) для новых осей.
Далее всё предельно просто:
- Выберем любую точку на окружности
- Опустим из этой точки перпендикуляр вниз и соединим её с центром окружности
Где-то мы это уже видели.
Но почему катеты прямоугольного треугольника подписаны как синус и косинус?
Обратимся к определению синуса и косинуса – это отношения к гипотенузе. В данном случае наша гипотенуза всегда будет равна 1, а значит, что синусом и косинусом угла будет являться сама сторона треугольника.
Измерения окружности
Буквой «П» принято отмечать Полуокружности.
Если из точки П пройти ещё одну Полуокружность, Вы снова попадете в точку 0, но уже с другим значением – 2П (2 полуокружности).
Мы можем разбить всю окружность на несколько частей:
Эти значение НЕ НУЖНО учить. Просто нужно понять, что мы делим Полуокружности на определенное количество частей.
Как найти синус и косинус?
Для синуса и косинуса достаточно запомнить всего 5 значений:
Всё на одной схеме:
Не судите строго, это моя первая статья на Дзене;)
Буду рад Вашей обратной связи!
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Тригонометрия в прямоугольном треугольнике
- Тригонометрический круг
- Основное тригонометрическое тождество
- Таблица значений тригонометрических функций
- Градусы и радианы
- Формулы приведения
- Теорема синусов
- Расширенная теорема синусов
- Теорема косинусов
- Тригонометрические уравнения (10-11 класс)
- Примеры решений заданий из ОГЭ
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.


Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:

sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).

Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.

Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos 150 ° = − 3 2
sin 150 ° = 1 2
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β:

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Запросы «sin» и «синус» перенаправляются сюда; у терминов sin и синус есть также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.

Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
Тригонометри́ческие фу́нкции — элементарные функции[1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям традиционно причисляют:
- прямые тригонометрические функции:
- синус (
);
- косинус (
);
- производные тригонометрические функции:
- тангенс
;
- котангенс
;
- секанс
;
- косеканс
;
- обратные тригонометрические функции:
- арксинус, арккосинус и т. д.
В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются 


Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках 

Графики тригонометрических функций показаны на рис. 1.
Способы определения[править | править код]
Определение для любых углов[править | править код]

Рис. 2.
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически[3]. В декартовой системе координат на плоскости построим окружность единичного радиуса (






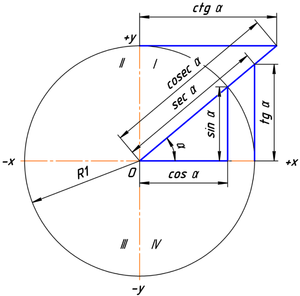
Синусом угла 






Косинусом угла 






Тангенсом угла 


Котангенсом угла 


Таким образом, определения тригонометрических функций выглядят следующим образом:
Нетрудно видеть, что такое определение также основывается на отношениях прямоугольного треугольника, с тем отличием, что учитывается знак (

В тригонометрии удобным оказывается вести счёт углов не в градусной мере, а в радианной. Так, угол в 






Наконец, определим тригонометрические функции вещественного числа 

Определение для острых углов[править | править код]

Рис. 4.
Тригонометрические функции острого угла

Определение тангенса. Марка СССР 1961 года
В геометрии тригонометрические функции острого угла определяются отношениями сторон прямоугольного треугольника[5]. Пусть 



Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).
Определение как решений дифференциальных уравнений[править | править код]
Синус и косинус можно определить как единственные функции, вторые производные которых равны самим функциям, взятым со знаком минус:
То есть задать их как чётное (косинус) и нечётное (синус) решения дифференциального уравнения
с дополнительными условиями:


Определение как решений функциональных уравнений[править | править код]
Функции косинус и синус можно определить[7]
как решения (


при дополнительных условиях:




Определение через ряды[править | править код]
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также равенствами 



где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов[править | править код]
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («
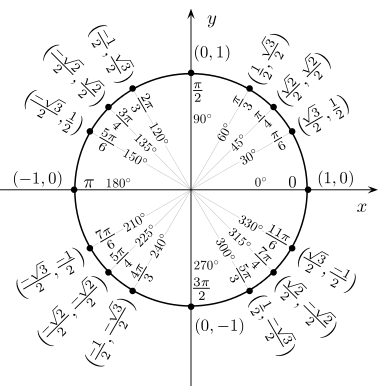
Значения косинуса и синуса на окружности
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций нестандартных углов[править | править код]
| Радианы | 
|

|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
| Радианы | 
|

|

|

|

|

|

|

|
|---|---|---|---|---|---|---|---|---|
| Градусы | 
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Значения тригонометрических функций для некоторых других углов
Свойства тригонометрических функций[править | править код]
Простейшие тождества[править | править код]
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности (
Это соотношение называется основным тригонометрическим тождеством.
Разделив это уравнение на квадрат косинуса и синуса соответственно, получим:
Из определения тангенса и котангенса следует, что
Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом (с точностью до знака из-за неоднозначности раскрытия квадратного корня). Нижеприведённые формулы верны для 
| sin | cos | tg | ctg | sec | cosec | |
|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Непрерывность[править | править код]
Чётность[править | править код]
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность[править | править код]
Функции 




Формулы приведения[править | править код]
Формулами приведения называются формулы следующего вида:
Здесь 



или что то же самое:
Некоторые формулы приведения:

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Интересующие формулы приведения так же могут легко быть получены рассмотрением функций на единичной окружности.
Формулы сложения и вычитания[править | править код]
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов[править | править код]
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для гамма-функции.
Из формулы Муавра можно получить следующие общие выражения для кратных углов:
где ![[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)


Формулы половинного угла:
Произведения[править | править код]
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени[править | править код]

Иллюстрация равенства
Суммы[править | править код]
Существует представление:
где угол 
Универсальная тригонометрическая подстановка[править | править код]
Все тригонометрические функции можно выразить через тангенс половинного угла:






Исследование функций в математическом анализе[править | править код]
Разложение в бесконечные произведения[править | править код]
Тригонометрические функции могут быть представлены в виде бесконечного произведения многочленов:
Эти соотношения выполняются при любом значении 
Непрерывные дроби[править | править код]
Разложение тангенса в непрерывную дробь:
Производные и первообразные[править | править код]
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:






Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом[8]:






Тригонометрические функции комплексного аргумента[править | править код]
Определение[править | править код]
Формула Эйлера:
Формула Эйлера позволяет определить тригонометрические функции от комплексных аргументов через экспоненту по аналогии с гиперболическими функциями, или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x:
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики[править | править код]
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
Тригонометрические функции в комплексной плоскости|
|
|
|
|
|
|

|

|

|

|

|

|
История названий[править | править код]
Линия синуса (линия 
Современные краткие обозначения 

Термины «тангенс» (лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
Позднее были введены и термины для обратных тригонометрических функций — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — с помощью добавления приставки «арк» (от лат. arcus — дуга), — Ж. Лагранжем и др.
См. также[править | править код]
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Интегральный секанс
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Тригонометрические тождества
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература[править | править код]
- Бермант А. Ф., Люстерник Л. А. Тригонометрия. — М.: Наука, 1967.
- Тригонометрические функции — статья из Большой советской энциклопедии. — М.: Советская энциклопедия, 1977. — Т. 26. — С. 204—206.
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6 www.alleng.ru/d/math/math42.htm
- Двайт Г. Б. Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
- Кожеуров П. А. Тригонометрия. — М.: Физматгиз, 1963.
- Маркушевич А. И. Замечательные синусы. — М.: Наука, 1974.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1984. — И. М. Виноградов. Тригонометрические функции // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
- Тригонометрические функции // Энциклопедический словарь юного математика / Ред. коллегия, Гнеденко Б. В. (гл. ред.), Савин А. П. и др. — М.: Педагогика, 1985 (1989). — С. 299—301—305. — 352 с., ил. — ISBN 5-7155-0218-7 (С. 342, 343 — таблицы тригонометрических функций 0°-90°, в том числе в радианах)
- Тригонометрические функции // Справочник по математике (для ср. уч. заведений) / Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 240—258. — 480 с.
Ссылки[править | править код]
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Trigonometric Functions (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций (в том числе нахождение углов треугольника по сторонам)
- Интерактивная карта значений тригонометрических функций
- Тригонометрические таблицы (0° — 360°)
- «Синус и косинус — это проценты» — перевод статьи How To Learn Trigonometry Intuitively | BetterExplained (англ.)
Примечания[править | править код]
- ↑ Справочник: Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с. Архивная копия от 19 января 2015 на Wayback Machine относит их к специальным функциям.
- ↑ Знак математический. // Большая советская энциклопедия. 1-е изд. Т. 27. — М., 1933.
- ↑ Справочник по элементарной математике, 1978, с. 282—284.
- ↑ Шахмейстер А. Х. Определение основных тригонометрических функций // Тригонометрия : [рус.] : книга / А. Х. Шахмейстер; под ред. Б. Г. Зива. — 3-е изд., стереотипное. — М. : Издательство МЦНМО ; СПб. : «Петроглиф» : «Виктория плюс», 2013. — С. 11, 14, 18, 20. — 752 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-4439-0050-6. — ISBN 978-5-98712-042-2. — ISBN 978-5-91673-097-5.
- ↑ Справочник по элементарной математике, 1978, с. 271—272.
- ↑ Латинско-русский словарь. Дата обращения: 9 апреля 2023.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. 1. — М.: Наука, 1998. — ISBN 5-02-015231-5.
- ↑ В формулах, содержащих логарифм в правой части равенств, константы интегрирования
, вообще говоря, различны для различных интервалов непрерывности.















































![sin(nalpha)=sum_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}cos^{n-2k-1}alpha,sin^{2k+1}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb020e5dfc3b2d5dfe1d1a0c571487ce387a8153)
![cos(nalpha)=sum_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}cos^{n-2k}alpha,sin^{2k}alpha,](https://wikimedia.org/api/rest_v1/media/math/render/svg/84f285d7cb530e87d8a9e33cff84fd4a4c9a8205)
![mathrm{tg}(nalpha)=frac{sin(nalpha)}{cos(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{tg}^{2k+1}alpha}}{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{tg}^{2k}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/8800a20a70495802fc2de287bb98d155e14720b1)
![mathrm{ctg}(nalpha)=frac{cos(nalpha)}{sin(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{ctg}^{n-2k}alpha}}{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{ctg}^{n-2k-1}alpha}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/90744f04ee2a1e34b1f0763e310c1c1d071f240d)