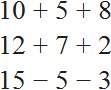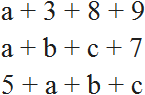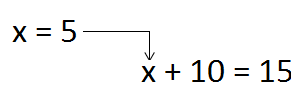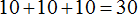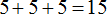Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[
3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=?
]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[
(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}
]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[
21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21
]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[
2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6}
]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[
6 frac{2}{13}+4 frac{1}{13}=?
]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[
frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}
]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[
frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13}
]
Ответ. [10 frac{3}{13}]
Примеры(2):
Задача. Решить:
[
frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=?
]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[
frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4}
]
Теперь можем придать нашему первоначальному выражению следующий вид:
[
frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4}
]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
Это позволит нам решить пример следующим образом:
Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[
frac{24}{sin ^{2} 127+1+sin ^{2} 217}
]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[
frac{24}{sin ^{2} 127+cos ^{2} 127+1}
]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[
frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2
]
Ответ. 2
Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[
sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=?
]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:
Теперь по формуле приведения решаем наш пример:
[
sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6
]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[
-frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=?
]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:
Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[
sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right.
]
Со знаменателем дела обстоят куда проще:
[
ln e^{2}=2
]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:
Теперь остается решить следующее выражение:
Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
Здравствуйте, уважаемые читатели. В этот раз рассмотрим решение задания, которое некоторые делают его очень сложно. Во само задание:
Найти значение выражения:
Для того чтобы найти значение выражения, будем работать с дробью. Воспользуемся основным свойством пропорции: произведение крайних членов пропорции равно произведению ее средних.
Выражение принимает вид:
Раскроем справой стороны скобку:
Перенесем все слагаемые из правой части равенства в левую, приравняв к нулю:
Красным, синим и черным выделены подобные слагаемые. Выполним вычисления и умножим на (-1)
Сравним выражения, которое нужно было найти и которое у нас получилось:
Как видим, выражения отличаются только последним числом. Дальше, как вариант, можно выразить из получившегося выражения 41а-11b=-12, и подставить в исходное: 41а-11b+15=-12+15=3. Или к получившемуся выражению можно добавить 3, но что бы ничего не изменилось, то и вычтем тоже 3.
Выполним сложение чисел 12 и 3, получаем 15, а число -3 перенесем вправо с противоположным знаком.
Обязательно в конце решения пишем ответ:
Некоторые решают такое задание через систему и выражают переменные a или b, что приводит к усложнению. Если знаете, как это задание решить еще легче, пишите в комментариях.
Критерии оценивания задания:
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
a + 5
Это буквенное выражение. Здесь одна переменная a. Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5
a = 5
Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Вспомним второй урок «Основные операции». Чтобы понять сложение, мы привели пример 5 + 2 = 7 и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но можно было понять эту тему и без примера, если бы мы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с.
Тогда у нас получилось бы выражение с тремя переменными a + b = c, и можно было сказать, что a и b — это слагаемые, c — сумма.
И далее имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того какие числа будут подставлены вместо a и b
В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.
Решение:
a + b = c
10 + 6 = 16
Ответ: при a = 10 и b = 6, переменная c равна 16.
Значение выражения
Фраза «выполнить действие» означает выполнить одну из операций действия.
В учебниках младших классов часто можно встретить задания такого содержания: выполнить действия, и далее приводятся примеры, которые нужно решить. Когда перед нами подобное задание, мы сразу должны понимать, что от нас требуют решить пример. В народе это звучит как «решить пример«, но более правильно надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Например, если дано выражение 10 + 6, и от нас требуют найти значение этого выражения, это означает что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:
10 + 6 = 16
Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
- 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
- 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
- 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5
Задания для самостоятельного решения
Задание 1. Найдите значение выражения 5 + x при x = 4
Задание 2. Найдите значение выражения a + 3 при a = 7
Задание 3. Найдите значение выражения a + a + a при a = 10
Задание 4. Найдите значение выражения a + b при a = 10 и b = 20
Задание 5. Найдите значение выражения b + b + b при b = 5
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

- Главная
- Справочники
- Справочник по математике для начальной школы
- Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
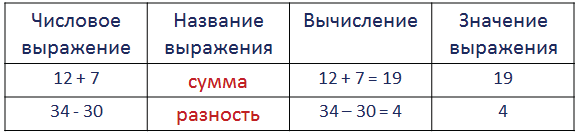
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения – это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения – это 76.
Чтение числовых выражений
12 + 9 – сумма
49 – 20 – разность
34 – (8 + 21) – из 34 вычесть сумму чисел 8 и 21
13 + (26 – 8) – к 13 прибавить разность чисел 26 и 8
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 – 6 и 18 – 9.
Для этого найдем значения каждого из них:
14 – 6 = 8
18 – 9 = 9
8 < 9, значит,
14 – 6 < 18 – 9
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.
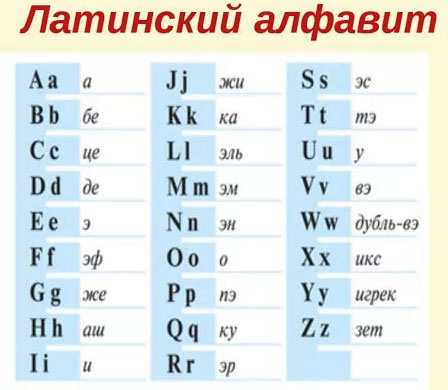
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм – значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Вычисляем результат:
28 – 4 = 24
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
c = 2, x = 3
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2 + 3 + 2
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Советуем посмотреть:
Уравнения
Правило встречается в следующих упражнениях:
1 класс
Страница 57. Урок 29,
Петерсон, Учебник, часть 2
Страница 9. Урок 5,
Петерсон, Учебник, часть 3
Страница 15. Урок 8,
Петерсон, Учебник, часть 3
Страница 19. Урок 10,
Петерсон, Учебник, часть 3
Страница 22. Урок 12,
Петерсон, Учебник, часть 3
Страница 31. Урок 16,
Петерсон, Учебник, часть 3
Страница 35. Урок 18,
Петерсон, Учебник, часть 3
Страница 37. Урок 19,
Петерсон, Учебник, часть 3
Страница 43. Урок 22,
Петерсон, Учебник, часть 3
Страница 88. Урок 35,
Петерсон, Учебник, часть 3
2 класс
Страница 76,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 32. ПР 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 44. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6. Урок 2,
Петерсон, Учебник, часть 2
Страница 6. Урок 2,
Петерсон, Учебник, часть 3
Страница 37. Урок 13,
Петерсон, Учебник, часть 3
Страница 70. Урок 26,
Петерсон, Учебник, часть 3
Страница 82. Урок 31,
Петерсон, Учебник, часть 3
3 класс
Страница 6,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 61,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 75. Урок 26,
Петерсон, Учебник, часть 1
Страница 42. Урок 16,
Петерсон, Учебник, часть 2
Страница 78. Урок 33,
Петерсон, Учебник, часть 2
4 класс
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 50,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 14. Урок 5,
Петерсон, Учебник, часть 1
5 класс
Задание 566,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 973,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1291,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1372,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1440,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 260,
Мерзляк, Полонский, Якир, Учебник
Номер 434,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 329,
Мерзляк, Полонский, Якир, Учебник
Номер 400,
Мерзляк, Полонский, Якир, Учебник
Номер 1036,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 583,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 597,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1118,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1122,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1127,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 4,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 259,
Мерзляк, Полонский, Якир, Учебник
Номер 316,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 481,
Мерзляк, Полонский, Якир, Учебник
Номер 906,
Мерзляк, Полонский, Якир, Учебник
Номер 1040,
Мерзляк, Полонский, Якир, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 392,
Мерзляк, Полонский, Якир, Учебник