История
Археологи нашли свидетельства того, что волшебные таблицы были известны еще древним грекам и китайцам. «Магическими» эти фигуры назвали арабы, которые наделяли их сверхъестественными защитными свойствами.
В середине XVI в. европейские математики занялись исследованиями загадочных таблиц, положив начало их новой жизни. Они искали общий метод построения магических квадратов и пытались описать все возможные их варианты.
На уроках математики в школе
Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Дети учатся планировать и контролировать свою работу. В клетки магических квадратов можно записывать не только числа, но и выражения. Все зависит от изучаемой темы. Задания с магическими квадратами часто дают как дополнительные или олимпиадные уже в начальной школе.
Один из способов решения магического квадрата
Нетрудно решить магический квадрат третьего порядка (у которого по три столбца и строки). Можно воспользоваться тем фактом, что число (выражение), стоящее на пересечении его диагоналей, всегда равно ⅓ волшебной суммы. Отсюда следует алгоритм построения:
- Вписываем в первую строку или столбец 3 любых числа.
- Вычисляем магическую сумму (0 + 2 + 4 = 6).
- Ищем ее третью часть (6/3 = 2).
- Полученное число записываем на пересечении диагоналей.
- Подбираем остальные числа и заполняем ими пустые клеточки квадрата.
 Смотрите также:
Смотрите также:
- Презентация “Магические квадраты”; 2 класс
- Презентация “Магические квадрат”; 2-3 класс
- Сценарий мероприятия “Магические квадраты и фокусы”; 5 класс
- Серия “Гимнастика для ума”. Магические квадраты; 3-4 класс
Как рассчитать магический квадрат Пифагора самому?
Пифагор — математик, заложивший основы нумерологии. Ученый верил, что миром правят числа. Даже человеческая сущность зависит от них, ведь дата рождения не что иное, как число.
Магический квадрат Пифагора — фигура третьего порядка, клетки которой заполнены числами от 1 до 9. Он делится на 3 уровня: материальный, души и разума.
Цифры даты рождения вписываются в определенном порядке. Полученная комбинация рассказывает о заложенных природой способностях человека.
Материал может быть использован на занятии математического кружка, на внеклассном мероприятии. Цель — развить и расширить познавательный кругозор и логическое мышление.
Решаем магический квадрат Пифагора: пример
Дата рождения: 17.09.2005 г. Складываем эти цифры, не учитывая нули: 1 + 7 + 9 + 2 + 5 = 24. Аналогично поступаем с цифрами результата: 2 + 4 = 6.
Из первой суммы вычитаем удвоенную первую цифру дня рождения: 24 -2 = 22. Снова складываем: 2 + 2 = 4. Полученные числа: 17; 9; 25; 24; 6; 22; 4.
Цифры вписываем в магический квадрат так, чтобы все единицы оказались в первой клеточке, двойки — во второй и так далее. Нули не учитываем.
Результат:
Значение:
|
Клетка 1 – волевые качества, эгоизм. |
|
|
1 |
Очень эгоистичные люди. |
|
11 |
Эгоизм — яркая, но не преобладающая черта характера. |
|
111 |
Спокойные, покладистые люди. |
|
1111 |
Сильный, волевой человек. |
|
11111 |
Люди с замашками диктатора. |
|
111111 |
Жестокость. |
|
Клетка 2 — биоэнергетика. |
|
|
— |
Воспитанность, природное благородство. |
|
2 |
Люди с повышенной чувствительностью к атмосферным изменениям. |
|
22 |
Человек с хорошим запасом биоэнергетики. |
|
222 |
Экстрасенсы. |
|
Клетка 3 — организованность, любовь к точности, конкретности, скрупулезность, скупость. |
|
|
Чем больше троек, тем сильнее выражены вышеперечисленные качества. |
|
|
Клетка 4 — здоровье. |
|
|
4 |
Среднее, требуется закаливание. |
|
44 |
Все в норме. |
|
444 и более |
Очень крепкое здоровье. |
|
Клетка 5 — интуиция, экстрасенсорные способности |
|
|
Чем больше пятерок, тем более выражена связь с космосом. |
|
|
Клетка 6 — материализм. |
|
|
— |
Люди с неординарным воображением, которым необходим физический труд. |
|
6 |
Могут посвятить время и творчеству, и точным наукам. Физические нагрузки обязательны. |
|
66 |
Заземленные личности, тянущиеся к физическому труду. |
|
666 |
Повышенная темпераментность. |
|
6666 |
Очень много заземленности. |
|
Клетка 7 — талант. |
|
|
Чем больше семерок, тем талантливее человек. |
|
|
Клетка 8 — судьба, отношение к обязанностям. |
|
|
— |
Чувства долга нет. |
|
8 |
Добросовестные личности. |
|
88 |
Люди, которые всегда спешат помочь другим. |
|
888 |
Признак служения народу. |
|
8888 |
Парапсихологические способности. |
|
Клетка 9 — умственные способности |
|
|
Полное отсутствие девяток означает очень низкий уровень умственной деятельности. Чем больше количество девяток, тем умнее человек. |
Задачи на составление магических квадратов часто включаются в сборники нестандартных заданий. Они встречаются на олимпиадах. Увлеченным математикой школьникам будет полезно узнать об этом классе задач.
Об авторе: Филиппова Оксана, учитель математики, физики и информатики.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Маги́ческий, или волше́бный квадра́т — квадратная таблица 




Нормальные магические квадраты существуют для всех порядков 


Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
Первые значения магических констант приведены в следующей таблице (последовательность A006003 в OEIS):
Порядок 
|
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|

|
15 | 34 | 65 | 111 | 175 | 260 | 369 | 505 | 671 | 870 | 1105 |





Исторически значимые магические квадраты[править | править код]
Квадрат Ло Шу[править | править код]

Изображение Ло Шу в книге эпохи Мин
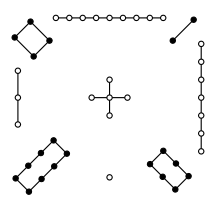
Ло Шу (кит. трад. 洛書, упр. 洛书, пиньинь luò shū) Единственный нормальный магический квадрат 3×3. Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 г. до н. э.
В Западноевропейской традиции этот квадрат называется «Печать Сатурна» (Sigillum Saturni). Параметры квадрата: 3, 9, 15, 45 (3х3, 9 ячеек, сумма по всем направлениям 15, сумма всех чисел в квадрате — 45).[1]
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
45 : 3 = 15
Квадрат, найденный в Кхаджурахо (Индия)[править | править код]
Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо:
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Это первый магический квадрат, относящийся к разновидности так называемых «дьявольских» квадратов[2].
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 136
136 : 4 = 34
Магический квадрат Ян Хуэя (Китай)[править | править код]
В XIII в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37)[3]:
| 27 | 29 | 2 | 4 | 13 | 36 |
| 9 | 11 | 20 | 22 | 31 | 18 |
| 32 | 25 | 7 | 3 | 21 | 23 |
| 14 | 16 | 34 | 30 | 12 | 5 |
| 28 | 6 | 15 | 17 | 26 | 19 |
| 1 | 24 | 33 | 35 | 8 | 10 |
Сумма всех 36 чисел равна 666
666 : 6 = 111
Квадрат Альбрехта Дюрера[править | править код]

Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I», считается самым ранним в европейском искусстве[4]. Два средних числа в нижнем ряду указывают дату создания гравюры (1514).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+12+15+5 и 3+8+14+9), в вершинах прямоугольников, параллельных диагоналям (2+8+15+9 и 3+12+14+5), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.
Данный квадрат является «Печатью Юпитера» (Sigillum Iouis), имеет параметры: 4, 16, 34, 136 (размер 4х4, 16 ячеек, сумма по направлениям — 34, сумма всех чисел равна 136).[1]
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 136
136 : 4 = 34
Магические квадраты Афанасия Кирхера[1][править | править код]
Квадрат Марса[править | править код]
Квадрат или печать Марса (Sigillum Martis) имеет параметры: 5, 25, 65, 325 (размер 5х5, 25 ячеек, сумма по направлениям — 65, сумма всех чисел равна 325).
| 12 | 25 | 8 | 21 | 4 |
| 5 | 13 | 26 | 9 | 17 |
| 18 | 6 | 14 | 22 | 10 |
| 11 | 19 | 2 | 15 | 23 |
| 24 | 7 | 20 | 3 | 16 |
325 : 5 = 65
Квадрат Солнца[править | править код]
Печать Солнца (Sigillum Solis) имеет параметры: 6, 36, 111, 666 (размер 6х6, 36 ячеек, сумма по направлениям — 111, сумма всех чисел равна 666).
| 6 | 32 | 3 | 34 | 35 | 1 |
| 7 | 11 | 27 | 28 | 8 | 30 |
| 19 | 14 | 16 | 15 | 23 | 24 |
| 18 | 20 | 22 | 21 | 17 | 13 |
| 25 | 29 | 10 | 9 | 26 | 12 |
| 36 | 5 | 33 | 4 | 2 | 31 |
666 : 6 = 111
Квадрат Венеры[править | править код]
Печать Венеры (Sigillum Veneris) имеет параметры: 7, 49, 175, 1225 (размер 7х7, 49 ячеек, сумма по направлениям — 175, сумма всех чисел — 1225).
| 22 | 47 | 16 | 41 | 10 | 35 | 4 |
| 5 | 23 | 48 | 17 | 42 | 11 | 29 |
| 30 | 6 | 24 | 49 | 18 | 36 | 12 |
| 13 | 31 | 7 | 25 | 43 | 19 | 37 |
| 38 | 14 | 32 | 1 | 26 | 44 | 20 |
| 21 | 39 | 8 | 33 | 2 | 27 | 45 |
| 46 | 15 | 40 | 9 | 34 | 3 | 28 |
1225 : 7 = 175
Квадрат Меркурия[править | править код]
Печать Меркурия (Sigillum Mercurio) имеет параметры: 8, 64, 260, 2080 (размер 8х8, 64 ячейки, сумма по направлениям — 260, сумма всех чисел — 2080).
| 8 | 58 | 59 | 5 | 4 | 62 | 63 | 1 |
| 49 | 15 | 14 | 52 | 53 | 11 | 10 | 56 |
| 41 | 23 | 22 | 44 | 45 | 19 | 18 | 48 |
| 32 | 34 | 35 | 29 | 28 | 38 | 39 | 25 |
| 40 | 26 | 27 | 37 | 36 | 30 | 31 | 33 |
| 17 | 47 | 46 | 20 | 21 | 43 | 42 | 24 |
| 9 | 55 | 54 | 12 | 13 | 51 | 50 | 16 |
| 64 | 2 | 3 | 61 | 60 | 6 | 7 | 57 |
2080 : 8 = 260
Квадрат Луны[править | править код]
Печать Луны (Sigillum Lune) имеет параметры: 9, 81, 369, 3321 (размер 9х9, 81 ячейка, сумма по направлениям — 369, сумма всех чисел — 3321).
| 37 | 78 | 29 | 70 | 21 | 62 | 13 | 54 | 5 |
| 6 | 38 | 79 | 30 | 71 | 22 | 63 | 14 | 46 |
| 47 | 7 | 39 | 80 | 31 | 72 | 23 | 55 | 15 |
| 16 | 48 | 8 | 40 | 81 | 32 | 64 | 24 | 56 |
| 57 | 17 | 49 | 9 | 41 | 73 | 33 | 65 | 25 |
| 26 | 58 | 18 | 50 | 1 | 42 | 74 | 34 | 66 |
| 67 | 27 | 59 | 10 | 51 | 2 | 43 | 75 | 35 |
| 36 | 68 | 19 | 60 | 11 | 52 | 3 | 44 | 76 |
| 77 | 28 | 69 | 20 | 61 | 12 | 53 | 4 | 45 |
3321 : 9 = 369
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.[править | править код]
Если в квадратную матрицу n × n заносится не строго натуральный ряд чисел, то данный магический квадрат — нетрадиционный. Ниже представлены два таких магических квадрата, заполненные простыми числами (хотя 1 в современной теории чисел не считается простым числом). Первый имеет порядок n=3 (квадрат Дьюдени); второй (размером 4×4) — квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия[5]:
|
Есть еще несколько подобных примеров:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
| 1 | 823 | 821 | 809 | 811 | 797 | 19 | 29 | 313 | 31 | 23 | 37 |
| 89 | 83 | 211 | 79 | 641 | 631 | 619 | 709 | 617 | 53 | 43 | 739 |
| 97 | 227 | 103 | 107 | 193 | 557 | 719 | 727 | 607 | 139 | 757 | 281 |
| 223 | 653 | 499 | 197 | 109 | 113 | 563 | 479 | 173 | 761 | 587 | 157 |
| 367 | 379 | 521 | 383 | 241 | 467 | 257 | 263 | 269 | 167 | 601 | 599 |
| 349 | 359 | 353 | 647 | 389 | 331 | 317 | 311 | 409 | 307 | 293 | 449 |
| 503 | 523 | 233 | 337 | 547 | 397 | 421 | 17 | 401 | 271 | 431 | 433 |
| 229 | 491 | 373 | 487 | 461 | 251 | 443 | 463 | 137 | 439 | 457 | 283 |
| 509 | 199 | 73 | 541 | 347 | 191 | 181 | 569 | 577 | 571 | 163 | 593 |
| 661 | 101 | 643 | 239 | 691 | 701 | 127 | 131 | 179 | 613 | 277 | 151 |
| 659 | 673 | 677 | 683 | 71 | 67 | 61 | 47 | 59 | 743 | 733 | 41 |
| 827 | 3 | 7 | 5 | 13 | 11 | 787 | 769 | 773 | 419 | 149 | 751 |
Последний квадрат, построенный в 1913 г. Дж. Н. Манси, примечателен тем, что он составлен из 143 последовательных простых чисел за исключением двух моментов: привлечена единица, которая не является простым числом, и не использовано единственное чётное простое число 2.
Квадраты с дополнительными свойствами[править | править код]
Пандиагональный магический квадрат[править | править код]
Пандиагональный или дьявольский квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям[en] (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.
Существует 48 дьявольских квадратов 4×4 в стандартной форме Френикля[fr] — с точностью до поворотов и отражений. Пандиагональный квадрат сохраняет свойства при параллельном переносе строк или столбцов. Поэтому единицу можно переместить в левый верхний угол. Таких пандиагональных квадратов на плоскости 12. Они приведены ниже:
|
|
|
|
|
|
|
|
|
|
|
|
На торе каждой четвёрке таких квадратов соответствует один квадрат. Это происходит потому, что если разрезать тор, начиная с единичной клетки как угловой, то это можно сделать четырьмя способами, сопоставляя каждому из четырёх углов единичной клетки угол плоского квадрата. Поэтому пандиагональных квадратов на торе всего 3. Для изображения торического квадрата на плоскости можно использовать любой из соответствующей ему четвёрки.
Пандиагональные квадраты существуют для нечётного порядка n>3, для любого порядка двойной чётности n=4k (k=1,2,3…) и не существуют для порядка одинарной чётности 

Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными. Совершенных квадратов нечётного порядка не существует. Среди пандиагональных квадратов двойной чётности выше 4 имеются совершенные[6].
С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов. Один из них показан ниже.
| 1 | 15 | 24 | 8 | 17 |
| 9 | 18 | 2 | 11 | 25 |
| 12 | 21 | 10 | 19 | 3 |
| 20 | 4 | 13 | 22 | 6 |
| 23 | 7 | 16 | 5 | 14 |
Разломанные диагонали пандиагонального квадрата
Если пандиагональный квадрат ещё и ассоциативный, то он носит название идеальный[7]. Пример идеального магического квадрата:
| 21 | 32 | 70 | 26 | 28 | 69 | 22 | 36 | 65 |
| 40 | 81 | 2 | 39 | 77 | 7 | 44 | 73 | 6 |
| 62 | 10 | 51 | 58 | 18 | 47 | 57 | 14 | 52 |
| 66 | 23 | 34 | 71 | 19 | 33 | 67 | 27 | 29 |
| 4 | 45 | 74 | 3 | 41 | 79 | 8 | 37 | 78 |
| 53 | 55 | 15 | 49 | 63 | 11 | 48 | 59 | 16 |
| 30 | 68 | 25 | 35 | 64 | 24 | 31 | 72 | 20 |
| 76 | 9 | 38 | 75 | 5 | 43 | 80 | 1 | 42 |
| 17 | 46 | 60 | 13 | 54 | 56 | 12 | 50 | 61 |
Известно, что не существует идеальных магических квадратов порядка n = 4k+2 и квадрата порядка n = 4. В то же время существуют идеальные квадраты порядка n = 8.
Методом построения составных квадратов можно построить на базе данного квадрата восьмого порядка идеальные квадраты порядка n = 8k, k=5,7,9…и порядка n = 8^p, p=2,3,4… В 2008 г. разработан комбинаторный метод построения идеальных квадратов порядка n = 4k, k = 2, 3, 4,…
Построение магических квадратов[править | править код]
Метод террас[править | править код]
Описан Ю. В. Чебраковым в «Теории магических матриц».
Для заданного нечетного n начертим квадратную таблицу размером n на n. Пристроим к этой таблице со
всех четырех сторон террасы (пирамидки). В результате получим ступенчатую симметричную фигуру.
Начиная с левой вершины ступенчатой фигуры, заполним её диагональные ряды последовательными натуральными числами от 1 до 
После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером NxN, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.
| 3 | 16 | 9 | 22 | 15 |
| 20 | 8 | 21 | 14 | 2 |
| 7 | 25 | 13 | 1 | 19 |
| 24 | 12 | 5 | 18 | 6 |
| 11 | 4 | 17 | 10 | 23 |
Кроме того, данный способ является верным и в том случае, если магический квадрат нужно составить не из чисел от 1 до N, но и от K до N, где 1 <= K< N.
Прочие способы[править | править код]
Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы.[8][9]
Найти все магические квадраты порядка 







Ещё проще построение выполнить следующим образом. Берётся матрица n x n . Внутри её строится ступенчатый ромб. В нём ячейки слева вверх по диагоналям заполняются последовательным рядом нечётных чисел. Определяется значение центральной ячейки C. Тогда в углах магического квадрата значения будут такими: верхняя правая ячейка C-1 ; нижняя левая ячейка C+1 ; нижняя правая ячейка C-n; верхняя левая ячейка C+n. Заполнение пустых ячеек в ступенчатых угловых треугольниках ведётся с соблюдением простых правил: 1)по строкам числа слева направо увеличиваются с шагом n + 1; 2) по столбцам сверху вниз числа увеличиваются с шагом n-1.
Также разработаны алгоритмы построения пандиагональных квадратов[10][11]
и идеальных магических квадратов 9×9.[12]
[13] Эти результаты позволяют строить идеальные магические квадраты порядков 


[16]
Разработаны методы построения идеальных магических квадратов порядка n=8k, k=1,2,3…[17] и совершенных магических квадратов.[18]
Пандиагональные и идеальные квадраты четно-нечётного порядка удаётся скомпоновать лишь в том случае, если они нетрадиционные.[19][20]
[21] Тем не менее, можно находить почти пандиагональные квадраты[22] Найдена особая группа идеально-совершенных магических квадратов (традиционных и нетрадиционных)[23].
Примеры более сложных квадратов[править | править код]
Методически строго отработаны магические квадраты нечётного порядка и порядка двойной чётности.[24] Формализация квадратов порядка одинарной чётности намного труднее, что иллюстрируют следующие схемы:
|
|
|
Существуют несколько десятков других методов построения магических квадратов
Шахматный подход[править | править код]
Известно, что шахматы, как и магические квадраты, появились десятки веков назад в Индии. Поэтому не случайно возникла идея шахматного подхода к построению магических квадратов. Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы. Тем не менее шахматная разбивка позволяет создавать любой магический квадрат. Цифры заполняются регулярно и построчно с учётом цвета ячеек.

Изображение схем построения магических квадратов
См. также[править | править код]
- Математическая магия
- Латинский квадрат
- Магический граф
- Магический куб
- Магический шестиугольник
- Чисугвимундо
- Палиндром
- Рамочный магический квадрат
- Судоку
- Супермагический квадрат
- Супермагический куб
Примечания[править | править код]
Литература[править | править код]
- Я. В. Успенский. Избранные математические развлечения. — Сеятель, 1924.
- Б. А. Кордемский. Математическая смекалка. — М.: ГИФМЛ, 1958. — 576 с.
- М. М. Постников. Магические квадраты. — М.: Наука, 1964.
- Н. М. Рудин. От магического квадрата к шахматам. — М.: Физкультура и спорт, 1969.
- Е. Я. Гуревич. Тайна древнего талисмана. — М.: Наука, 1969.
- М. Гарднер. Математические досуги. — М.: Мир, 1972.
- Энциклопедический словарь юного математика / Сост. А. П. Савин. — М. : Педагогика, 1989. — 352 с. — ISBN 5-7155-0218-7.
- Ю. В. Чебраков. Магические квадраты. Теория чисел, алгебра, комбинаторный анализ. — СПб.: СПб гос. техн. ун-т, 1995.
- Ю. В. Чебраков. Теория магических матриц. — СПб., 2008.
- М. Гарднер. Глава 17. Магические квадраты и кубы // Путешествие во времени. — М.: Мир, 1990. (недоступная ссылка)
- Чирказов Д. Буквенные магические квадраты как симметричные текстовые массивы. // Современные научные исследования и инновации. — № 11 Ноябрь 2012
Ссылки[править | править код]
- Магические квадраты (недоступная ссылка) (англ.)
- последовательность A164843 в OEIS
- М. Гарднер »Рецензия на книгу Кэтлин Оллереншоу и Дэвида Бри”
- H. Heinz Magic Squares, Magic Stars & Other Patterns (англ.)
- Н. Скрябина, В.Дубовской Магические квадраты
- Шахматный подход
- Нетрадиционные магические квадраты из простых чисел
- Наименьшие магические квадраты из простых чисел
- «Общие формулы магических квадратов.»
- Магические квадраты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
16
Существует несколько различных классификаций магических квадратов
пятого порядка, призванных хоть как-то их систематизировать. В книге
Мартина Гарднера [ГМ90, сс. 244-345] описан один из таких способов –
по числу в центральном квадрате. Способ любопытный, но не более того.
Сколько существует квадратов шестого порядка, до сих пор неизвестно, но их примерно 1.77 х 1019. Число огромное, поэтому нет никаких надежд пересчитать их с помощью полного перебора, а вот формулы для подсчёта магических квадратов никто придумать не смог.
Как составить магический квадрат?
Придумано очень много способов построения магических квадратов. Проще всего составлять магические квадраты нечётного порядка. Мы воспользуемся методом, который предложил французский учёный XVII века А. де ла Лубер (De La Loubère). Он основан на пяти правилах, действие которых мы рассмотрим на самом простом магическом квадрате 3 х 3 клетки.
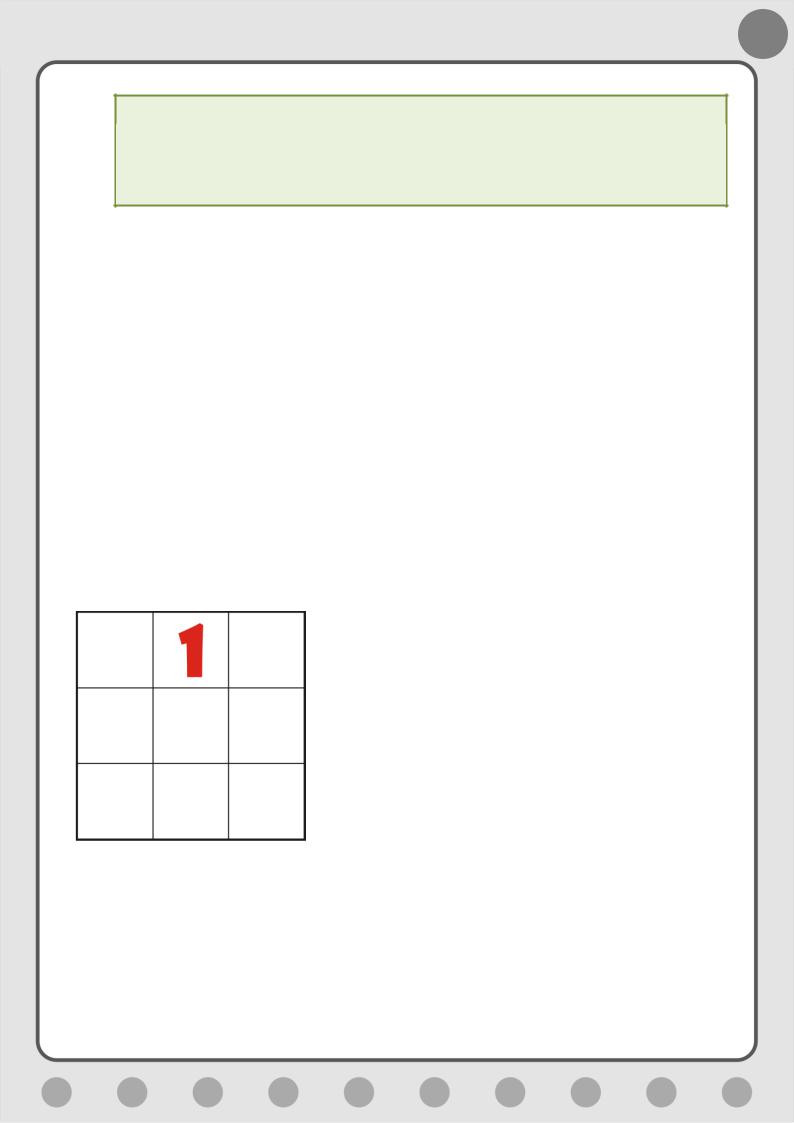
Правило 1. Поставьте 1 в среднюю колонку первой строки (Рис. 5.7).
Рис. 5.7. Первое число
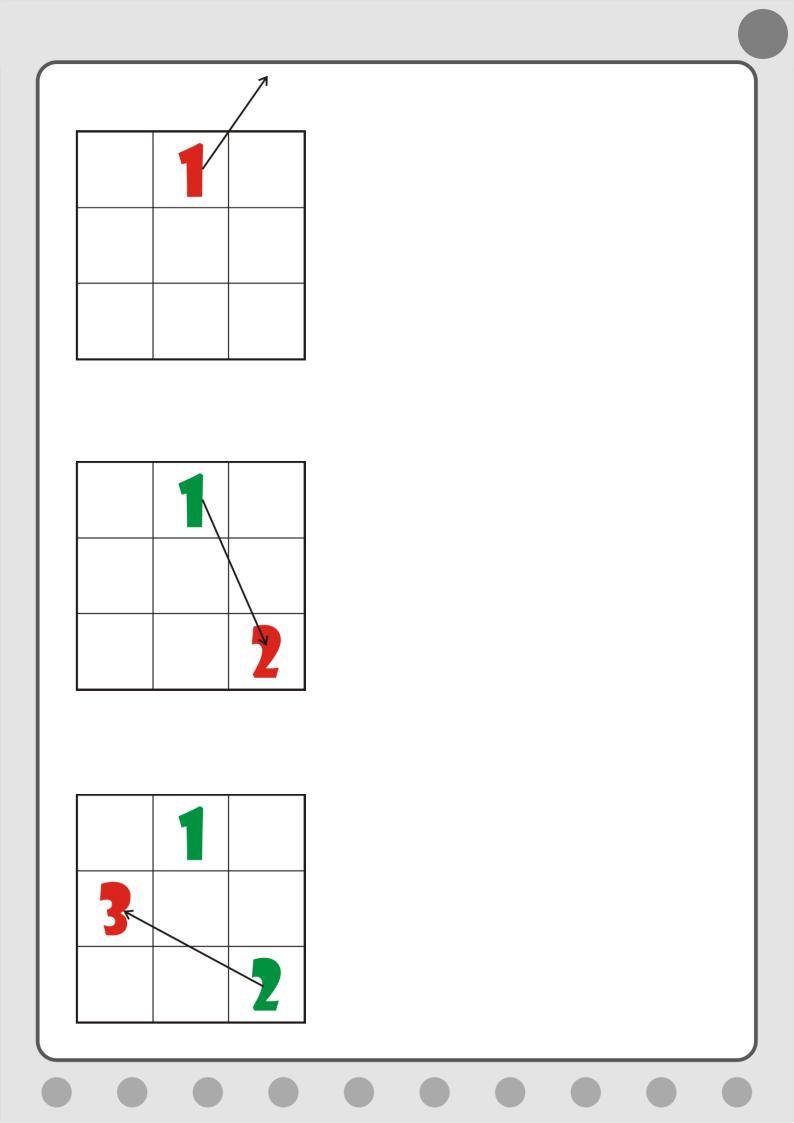
Правило 2. Следующее число поставьте, если возможно в клетку, соседнюю с текущей по диагонали правее и выше (Рис. 5.8).
17
Рис. 5.8. Пытаемся поставить второе число
Правило 3. Если новая клетка выходит за пределы квадрата сверху, то запишите число в самую нижнюю строку и в следующую колонку (Рис. 5.9).
Рис. 5.9. Ставим второе число
Правило 4. Если клетка выходит за пределы квадрата справа, то запишите число в самую первую колонку и в предыдущую строку (Рис. 5.10).
Рис. 5.10. Ставим третье число
18
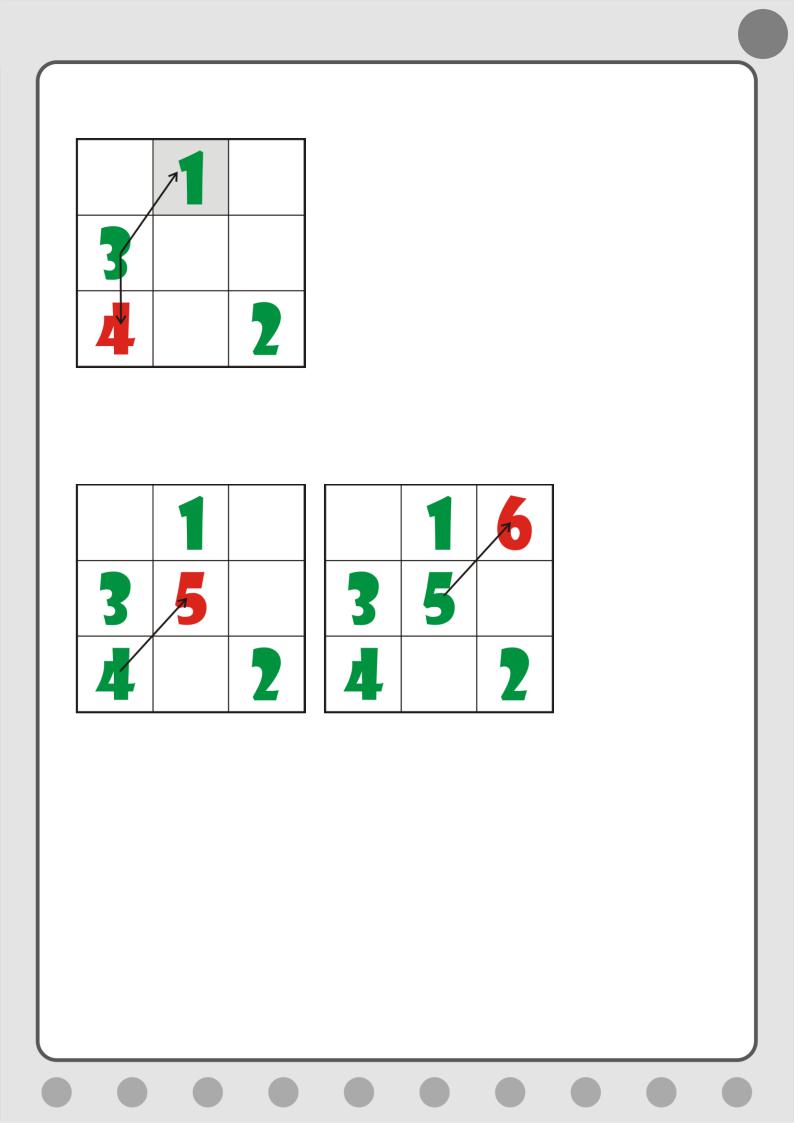
Правило 5. Если в клетке уже занята, то очередное число запишите под текущей клеткой (Рис. 5.11).
Рис. 5.11. Ставим четвёртое число
Далее переходите к Правилу 2 (Рис. 5.12).
Рис. 5.12. Ставим пятое и шестое число
Снова выполняйте Правила 3, 4, 5, пока не составите весь квадрат (Рис.
5.13).
Не правда ли, правила очень простые и понятные, но всё равно довольно утомительно расставлять даже 9 чисел. Однако, зная алгоритм построения магических квадратов, мы сможем легко перепоручить компьютеру всю рутинную работу, оставив себе только творческую, то есть написание программы.
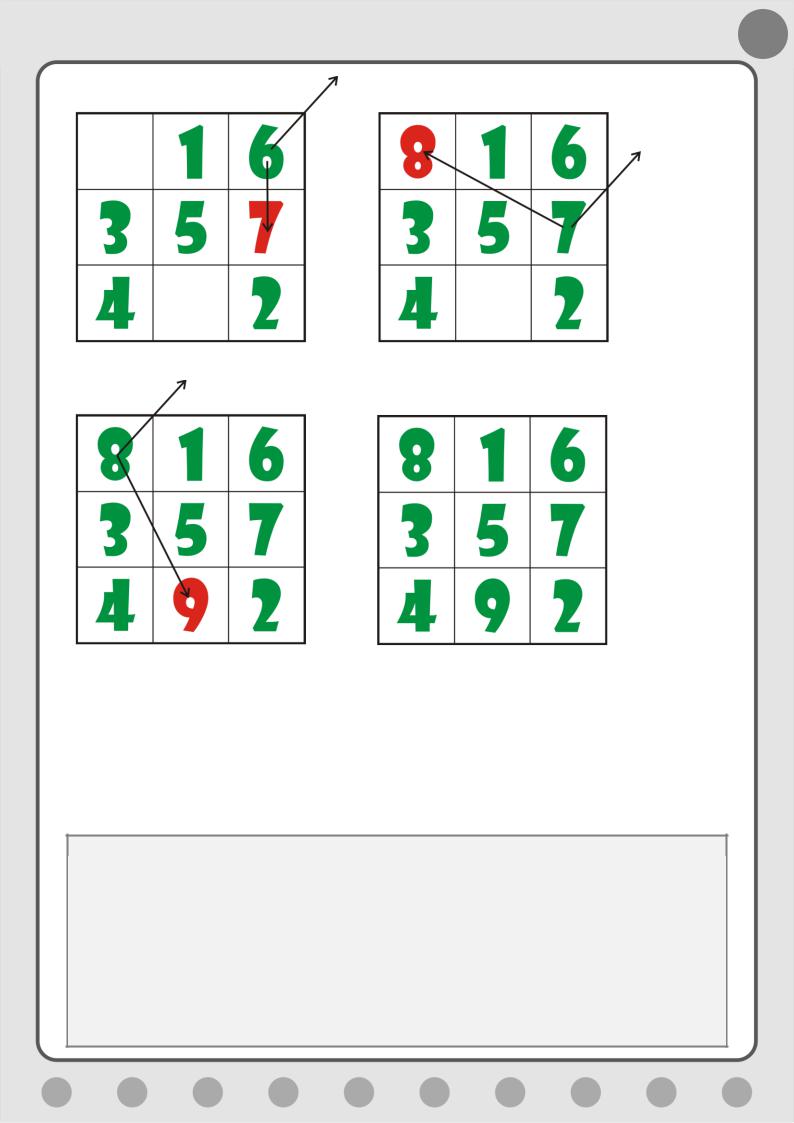
19
Рис. 5.13. Заполняем квадрат следующими числами
Проект Магические квадраты (Magic)
Набор полей для программы Магические квадраты совершенно очевиден:
//ПРОГРАММА ДЛЯ ГЕНЕРИРОВАНИЯ
//НЕЧЕТНЫХ МАГИЧЕСКИХ КВАДРАТОВ
//ПО МЕТОДУ ДЕ ЛА ЛУБЕРА
public partial class Form1 : Form
{
//макс. размеры квадрата: const int MAX_SIZE = 27; //var
int n=0; // порядок квадрата int [,] mq; // магический квадрат
int number=0;// текущее число для записи в квадрат

20
int col=0; // текущая колонка int row=0; // текущая строка
Метод де ла Лубера годится для составления нечётных квадратов любого размера, поэтому мы можем предоставить пользователю возможность самостоятельно выбирать порядок квадрата, разумно ограничив при этом свободу выбора 27-ью клетками.
После того как пользователь нажмёт заветную кнопку btnGen Генерировать!, метод btnGen_Click создаёт массив для хранения чисел и переходит в метод generate:
//НАЖИМАЕМ КНОПКУ “ГЕНЕРИРОВАТЬ”
private void btnGen_Click(object sender, EventArgs e)
{
//порядок квадрата:
n = (int)udNum.Value;
//создаем массив:
mq = new int[n+1, n+1];
//генерируем магический квадрат: generate();
lstRes.TopIndex = lstRes.Items.Count-27;
}
Здесь мы начинаем действовать по правилам де ла Лубера и записываем первое число – единицу – в среднюю клетку первой строки квадрата (или массива, если угодно):
//Генерируем магический квадрат void generate(){
//первое число: number=1;
rule1:
//колонка для первого числа – средняя: col = n / 2 + 1;
//строка для первого числа – первая: row=1;
//заносим его в квадрат: mq[row,col]= number;
Теперь мы последовательно пристраиваем по клеткам остальные числа – от двойки до n * n:
//переходим к следующему числу:
21
nextNumber:
number++;
Запоминаем на всякий случай координаты актуальной клетки
int tc=col; int tr = row;
и переходим в следующую клетку по диагонали:
col++; row–;
Проверяем выполнение третьего правила:
rule3:
if (row < 1) row= n;
А затем четвёртого:
rule4:
if (col > n) { col=1;
goto rule3;
}
И пятого:
rule5:
if (mq[row,col] != 0) { col=tc;
row=tr+1; goto rule3;
}
Как мы узнаем, что в клетке квадрата уже находится число? – Очень просто: мы предусмотрительно записали во все клетки нули, а числа в готовом квадрате больше нуля. Значит, по значению элемента массива мы сразу же определим, пустая клетка или уже с числом! Обратите внимание, что здесь нам понадобятся те координаты клетки, которые мы запомнили перед поиском клетки для следующего числа.
Рано или поздно мы найдём подходящую клетку для числа и запишем его в соответствующую ячейку массива:

22
//заносим его в квадрат: mq[row, col] = number;
Попробуйте иначе организовать проверку допустимости перехода в но-
вую клетку!
Если это число было последним, то программа свои обязанности выполнила, иначе она добровольно переходит к обеспечению клеткой следующего числа:
//если выставлены не все числа, то if (number < n*n)
//переходим к следующему числу: goto nextNumber;
И вот квадрат готов! Вычисляем его магическую сумму и распечатываем на экране:
//построение квадрата закончено: writeMQ();
} //generate()
Напечатать элементы массива очень просто, но важно учесть выравнивание чисел разной «длины», ведь в квадрате могут быть одно-, дву- и трёхзначные числа:
//Печатаем магический квадрат void writeMQ()
{
lstRes.ForeColor = Color.Black;
string s = “Магическая сумма = ” + (n*n*n +n)/2; lstRes.Items.Add(s);
lstRes.Items.Add(“”);
// печатаем магический квадрат: for (int i= 1; i<= n; ++i){
s=“”;
for (int j= 1; j <= n; ++j){
if (n*n > 10 && mq[i,j] < 10) s += ” “; if (n*n > 100 && mq[i,j] < 100) s += ” “; s= s + mq[i,j] + ” “;
}
lstRes.Items.Add(s);
}
lstRes.Items.Add(“”); }//writeMQ()
23
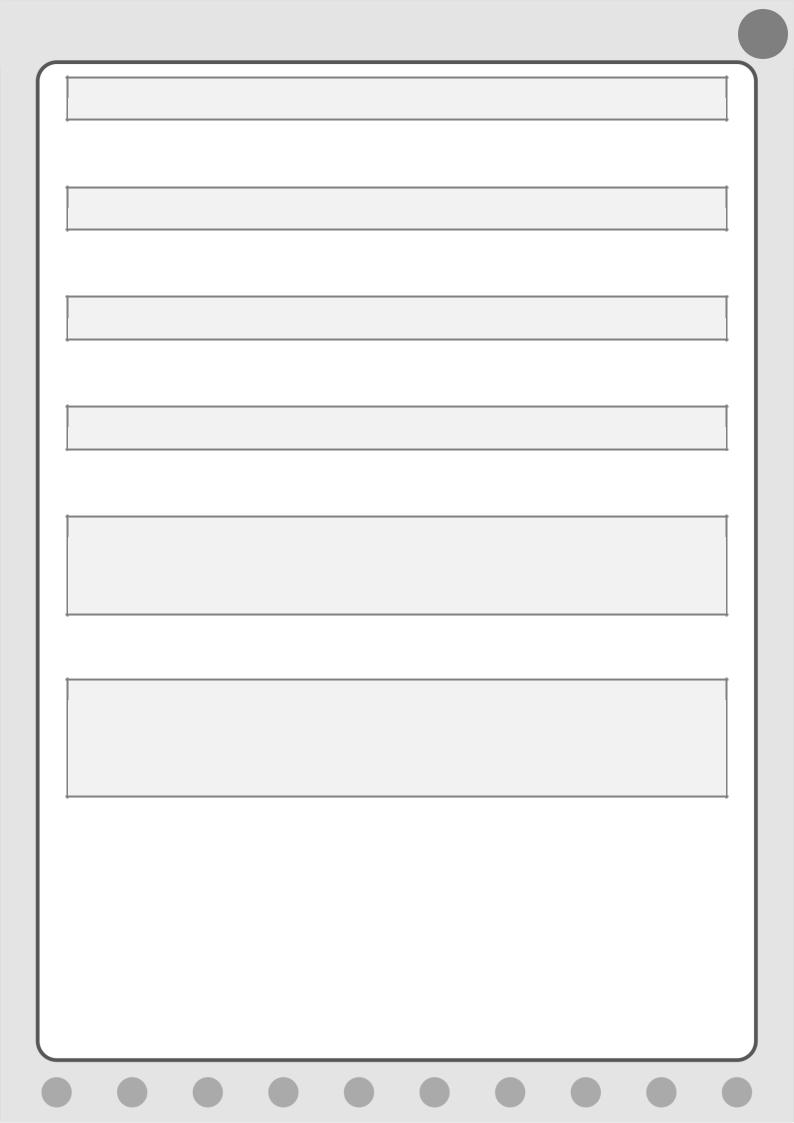
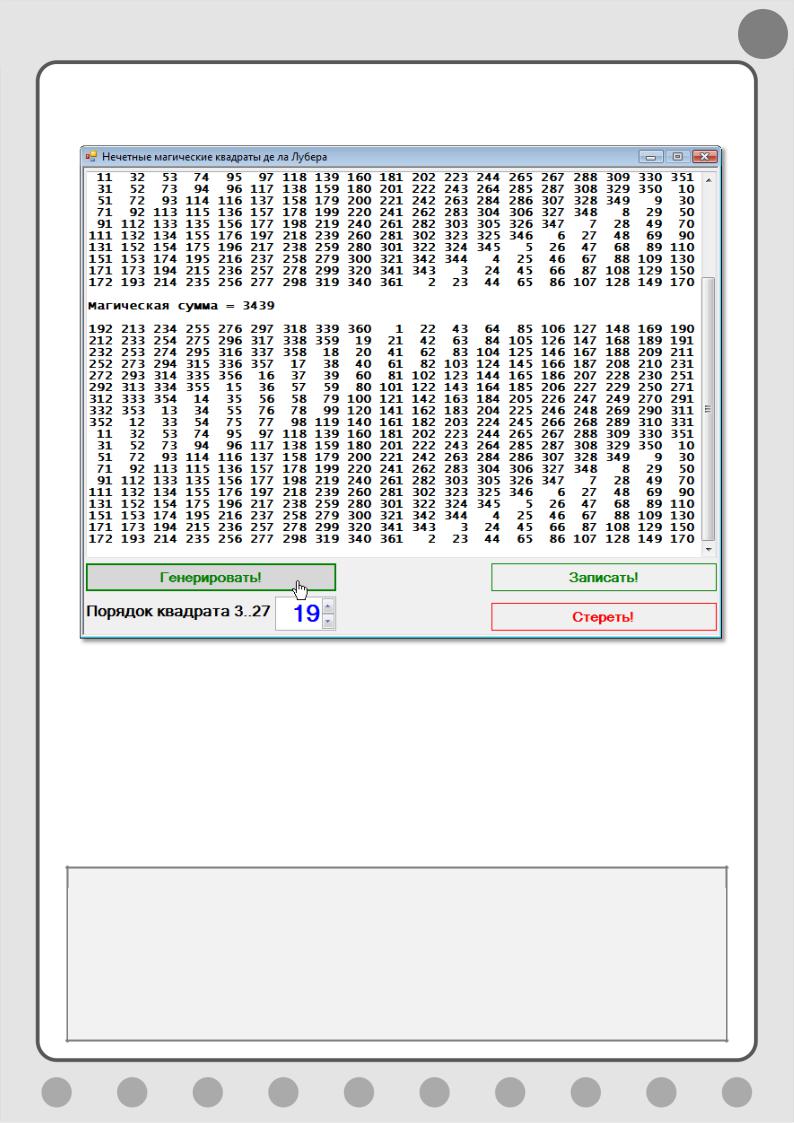
Запускаем программу – квадраты получаются быстро и на загляденье (Рис.
5.14).
Рис. 5.14. Изрядный квадратище!
В книге С.Гудман, С.Хидетниеми Введение в разработку и анализ алгорит-
мов, на страницах 297-299 мы отыщем тот же самый алгоритм, но в «сокращённом» изложении. Он не столь «прозрачен», как наша версия, но работает верно.
Добавим кнопку btnGen2 Генерировать 2! и запишем алгоритм на языке
Си-шарп в метод btnGen2_Click:
//Algorithm ODDMS
private void btnGen2_Click(object sender, EventArgs e)
{
//порядок квадрата: n = (int)udNum.Value;
//создаем массив:
mq = new int[n + 1, n + 1];
//генерируем магический квадрат: int row = 1;
24
int col = (n+1)/2;
for (int i = 1; i <= n * n; ++i)
{
mq[row, col] = i; if (i % n == 0)
{
++row;
}
else
{
if (row == 1) row = n;
else
–row;
if (col == n) col = 1;
else
++col;
}
}
//построение квадрата закончено: writeMQ();
lstRes.TopIndex = lstRes.Items.Count – 27;
}
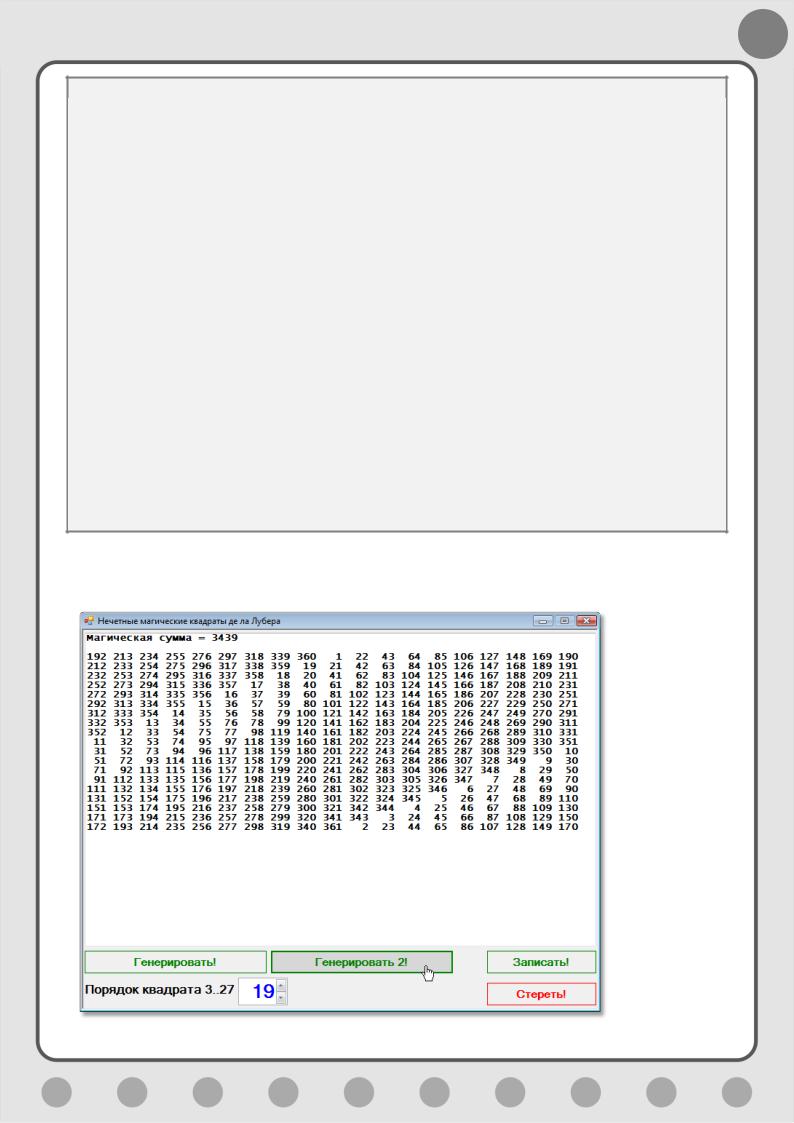
Кликаем кнопку и убеждаемся, что генерируются «наши» квадраты (Рис.
5.15).
Рис. 5.15. Старый алгоритм в новом обличии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приветствую Вас, уважаемые Читатели! Близятся долгожданные праздники, поэтому вопрос развлечений во время длительных посиделок становится всё более актуальным. Сегодня покажу, как создать магический квадрат из чисел, который будет обладать интересными свойствами. Запомнить, как его делать, очень легко, впрочем, как и достигнуть вау-эффекта после его заполнения. Поехали!
Магический квадрат проще всего привязать к конкретному человеку, “бросившему Вам вызов”. Попросите его назвать свой возраст, а затем расчертите после 4 на 4. Если Возраст Вашего собеседника – 31, то мы получим вот такой магический квадрат:
Обратите внимание, суммы все вертикальных, горизонтальных линий и диагоналей равны 31. Кроме того, все квадраты 2х2 также в сумме дают искомое число. Сейчас покажу, как составить такой квадрат на память (листайте галерею):
Данный математический фокус работает для людей с возрастом до 65 лет. В случае, если собеседнику менее 21 года, квадрат содержит отрицательные числа. Спасибо за внимание!
ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.
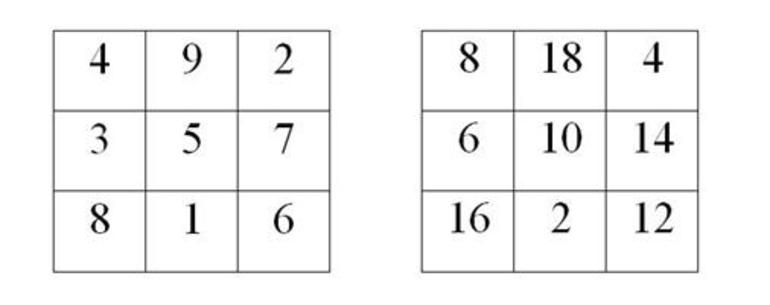
История и современное применение
Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.
В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.
С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.
Квадрат нечётного порядка
Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

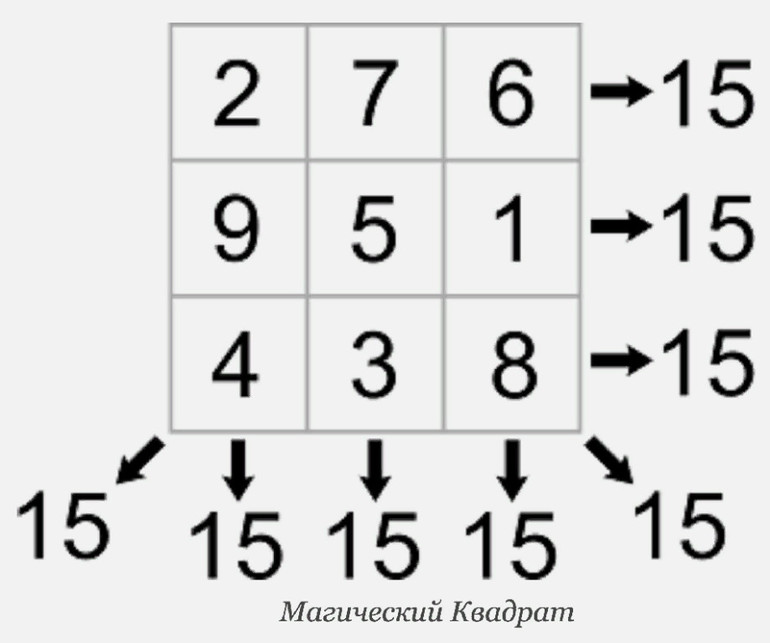
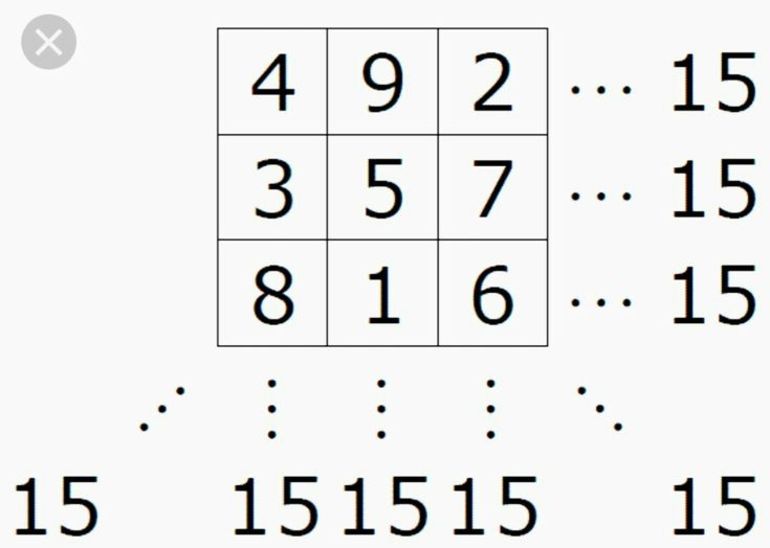
- Подсчитывается сумма, которая должна получиться в каждой строке. Для этого используется формула: 3 * (32 +1) / 2 = 3 * 10 / 2. Ответом будет число 15.
- Числа в ячейках расставляются так, чтобы сумма их была равна 15 в каждой строчке. Это требует смекалки и воображения.
- В средней клетке верхней строки вписывается 1.
- Каждое следующее число ставится справа по диагонали вверх. Поставить цифру 2 нельзя, так как выше нет строк. Если мысленно добавить сверху ещё один квадрат, цифра 2 окажется в его нижнем правом углу. Значит, цифра 2 вписывается в нижнюю правую клетку.
- По тому же принципу вписывается цифра 3. Она попадает в среднюю ячейку слева.
- Если нужная клетка уже занята, очередной символ вписывается ниже предыдущего. Таким образом, 4 ставится под 3.
- Записывается цифра 5 по диагонали вправо и вверх, а 6 в верхний угол справа.
- Поскольку место цифры 7 уже занято, она вписывается ниже 6.
- Восьмёрка занимает место в левом нижнем углу.
- Оставшуюся клетку занимает девятка.
Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.
Одинарная чётность
Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.
Вычисление магической константы
Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.
Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.
Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.
Дальнейшие действия
Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.
Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:
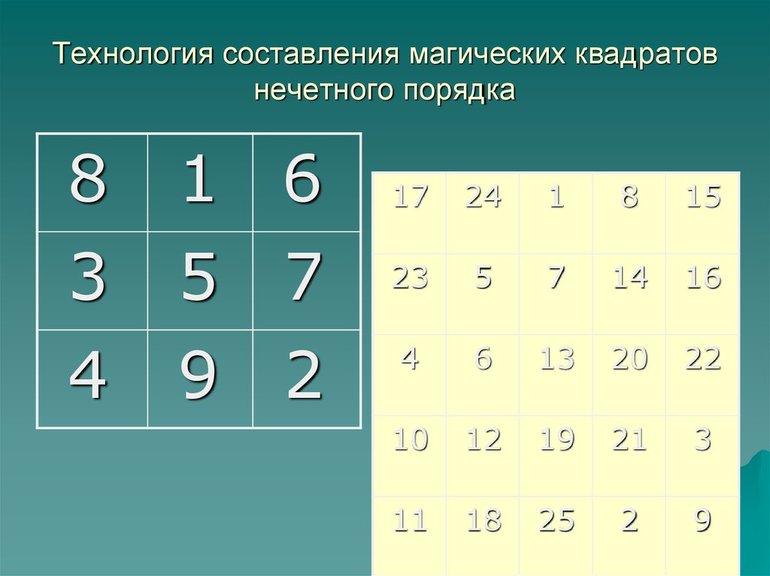
- Минимальное число, которым начинается заполнение ячеек, всегда ставится в верхнем ряду посередине. У каждой части эта ячейка находится отдельно.
- Каждая часть заполняется как новый математический объект. Даже если есть пустое место в другом квадрате, его в этих случаях игнорируют.
В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.
Алгоритм действий:

- Начинать нужно с крайней левой клетки в верхней строке. Если фигура имеет размеры 6х6, выделяется только первая верхняя строка части А. В ней должно быть вписано число 8. Если величина таблицы составляет 10х10, выделяют 2 первые клетки в верхнем ряду. В них стоят 17 и 24.
- Из выделенных клеток формируется промежуточный квадрат. В таблице с количеством строк и столбцов 6х6 он будет состоять из 1 клетки. Его условно обозначают А1.
- Если размер 10х10, в верхней строке выделяется 2 первые ячейки. Вместе с ними выделяется ещё 2 клетки, во второй строке получается поле из 4 прилежащих друг к другу ячеек.
- В следующей строке первая ячейка пропускается, затем выделяется столько клеток, сколько было в промежуточной таблице А1. Полученную фигуру можно обозначить А2.
- Таким же способом строят промежуточный квадрат А3.
- Эти 3 промежуточных фигуры формируют выделенную область А.
- Далее переходят в квадрант D и формируют обособленную область D.
Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.
Двойной порядок
Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.
Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.
В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:
- Если длина стороны составляет 4 ячейки, промежуточные зоны будут иметь по 1 клетке.
- В таблице 8х8 эти области включают 4 элемента (2х2).
- В квадрате 12х12 выделяются промежуточные фигуры размером 3х3.
Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.
Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:
- В первой сверху строке и первом слева столбце пишется 1. В верхней клетке четвертого столбика — 4.
- В центр второй горизонтальной строчки ставятся цифры 6 и 7.
- В четвёртой строке слева пишется 13, а справа — 16.
По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.


