План исследовательской работы
1. Титульный лист исследовательской работы
Оформляется титульный лист исследовательской работы или проекта на листе формата А4 и является первой страницей проектной работы школьника.
Поля:
- левое поле листа – 20 мм
- правое – 10 мм
- верхнее и нижнее – по 15 мм
Междустрочный интервал – 1,5 (полтора).
Титульный лист не нумеруется!
В верхнем поле титульного листа исследовательской работы пишется полное название учебного заведения (размер шрифта – 16 пт.).
Посередине листа пишется без кавычек «Исследовательская работа» (шрифт – 24 пт.)
На следующей строке – заглавными буквами указывается название исследовательской работы без слова “тема”, без кавычек и без точки в конце (шрифт – 28 пт.).
Название не должно быть длинным, “стандартным или избитым”, а по возможности кратким, интригующим. Название на титульном листе должно соответствовать общему содержанию проекта и заинтересовать ознакомиться с работой.
Название, если необходимо, может содержать подзаголовок для более конкретного представления темы проекта, но он должен быть очень кратким и не превратиться во второе заглавие работы.
В правом нижнем углу титульного листа указываются сведенья об авторе исследовательской работы (фамилия, имя, класс), ниже – о руководителе исследовательской работы (пишут «Руководитель» и указывают его фамилию, инициалы и должность.
Если руководителей исследовательского проекта несколько, указываются все через запятую. Если в вашей работе помогал консультант, то его инициалы и фамилия помещается ниже руководителя с указанием «Консультант».
В самом низу титульного листа по центру указывается место выполнения исследовательской работы школьника: Киев, на следующей строчке – год выполнения работы – 2013 – без точки, кавычек, слова “год” или “г” (шрифт – 14 пт.).
2. Содержание исследовательской работы
Оформление содержания исследовательской работы
При оформлении работы содержание исследовательского проекта помещается на втором листе и оформляется согласно приведенному нами примеру и образцу ниже.
Все главы в «Содержании» начинаются с заглавной буквы.
В Содержании исследовательской работы пишутся названия глав и параграфов с указанием номеров страниц, с которых они начинаются. Последнее слово главы или параграфа соединяется с соответствующим ему номером страницы многоточием.
При оформлении заголовки ступеней одинакового уровня необходимо располагать друг под другом. Заголовки каждой последующей ступени смещаются на пять знаков вправо. Все они начинаются с заглавной буквы без точки в конце.
Главы и параграфы в содержании проекта нумеруются по многоуровневой системе, то есть обозначаются цифровыми номерами, содержащими во всех ступенях номер своей рубрики и рубрики которой они подчинены (напр. 1.1, 1.2, и т.д.).
Разделы “Введение“, “Заключение“, “Список литературы” и “Приложения” не нумеруются!
Образец содержания исследовательской работы (проекта)
Простыми словами содержание оформляется строго по правилам, нумеруются и отмечаются разделы исследовательской работы, расположенные в тексте проекта, указываются страницы.
Содержание
Введение………………………………………………………..3
(Во введении обычно описывают: обоснование выбора темы работы, объект и предмет исследования, цель и задачи исследования, гипотезу, методы исследования, новизну исследовательской работы(при наличии), теоретическую и практическую(при наличии) значимость работы)
1. Подготовка к исследованию (например)……….5
1.1 Исторические сведения……………………….5
1.2 Сбор информации……………………………….7
1.3 Проведение анкетирования…………………8
1.4 Техника безопасности…………………………9
(Правила техники безопасности описываются при необходимости)
2. Проведение исследования(например)………….10
2.1 Первый этап исследования………………..10
2.2 Второй этап исследования…………………11
2.3 Заключительный этап исследования…..12
Заключение……………………………………………………13
(Итоги исследовательской работы)
Список литературы………………………………………..14
Приложения…………………………………………………..15
Обращаем внимание, что Содержание исследовательского проекта оформляется очень аккуратно, со всеми выравниваниями текста и нумерации.
3. Введение исследовательской работы
Во Введении исследовательской работы обосновывается актуальность выбранной темы, определяются объект, предмет исследования и основные проблемы, формулируется цель и содержание поставленных задач, сообщается, в чем состоит новизна исследования (если имеется).
Также во введении определяются методы исследования, обосновывается теоретическая и практическая значимость (если есть практическая часть) исследовательской работы (проекта).
Что отражается в разделе Введение?
В главе “Введение” необходимо сжато представить основные идеи исследовательской работы!
– первый раздел исследовательского проекта, располагается на третьем листе после Содержания исследовательской работы.
В нем раскрывается актуальность темы, цель и задачи проекта, объект исследования и гипотеза, которая формулируется при наличии практической части в исследовательской работе, наличии экспериментов, опытов, наблюдений.
О доказывает значимость, современность, нужность результатов проводимого исследования.
Формулируется также – модель желаемого конечного результата исследования ребенка.
акже важно указать конкретные , которые предстоит решить в процессе всего хода работы. Во Введении исследовательской работы можно также указать степень разработанности данной темы в литературе, сформулировать .
Структура введения исследовательской работы
Приведем пример плана введения исследовательской работы (проекта) школьника:
- Актуальность темы исследования
- Проблема, на решение которой направлено исследование
- Объект и предмет исследования
- Цель исследовательской работы
- Задачи исследовательской работы
- Гипотеза (предположение)
- Основные этапы работы, организация
- Методы исследования
- Научная новизна исследования
- Теоретическая значимость работы
- Практическая значимость работы
- Характеристика основных источников получения информации
Каждый из перечисленных выше пунктов Введения в исследовательский проект описывается с нового абзаца без нумерации и без оформления в виде заголовка.
Ж
актуальность работы, предмет исследования, объект исследования, цель исследования, задачи исследования и т.п.
Объем раздела Введение – обычно 1-1,5 страницы.
Раздел Введение оформляется согласно правил оформления исследовательской работы.
Введению исследовательской работы рекомендуется уделить особое внимание, это как это визитная карточка вашего проекта, в которой кратко отражается суть вашего исследования или поисковой работы.
4. Историческая справка по проблеме проекта
Историческая справка по проблеме исследовательской работы или проекта обычно берется из сети Интернет (Википедия или др. ресурсы) или из литературы библиотек и архивов.
5. Основная часть исследовательской работы, проекта
П
- Поиск необходимой информации, знаний для проведения исследования.
- Выбор идей и вариантов, их обоснование и анализ.
- Выбор материала, методов для проведения исследования.
- Подбор оборудования и организация рабочего места для исследования (если это опыт).
- Описание этапов проведения исследования.
- Техника безопасности при выполнении работ (если это опыт).
6. Заключение
Заключение исследовательской работы – это краткие выводы по результатам исследовательской работы или проекта школьника, оценка полноты решения поставленных задач.
В Заключении исследовательской работы последовательно излагаются полученные результаты, определяется их соотношение с общей целью и конкретными задачами, сформулированными во введении, а также дается самооценка о проделанной работе.
В некоторых случаях можно указать пути продолжения исследования темы, а также конкретные задачи, которые предстоит при этом решать.
При планировании и составлении плана исследовательской работы (проекта) школьника очень важным и значимым является заключение работы, на него необходимо обратить особое внимание.
7. Используемая литература
Согласно плану, после заключения принято помещать в текст индивидуальной исследовательской работы список литературы, использованной при изучении материала теоретической части исследования, проведения поисковой работы в сети Интернет или архивах.
Каждый включенный в список литературы источник должен иметь отражение в пояснительной записке. Не следует включать в данный список работы, которые фактически не были использованы в исследовательском проекте.
Оформление Списка использованной литературы
Использованная литература
Государственные стандарты и сборники документов
1. ГОСТ 7.1.-84 – Введ. 01.01.86 – М, 1984 – 75с.
2. О правительственной комиссии по проведению административной реформы: Постановление Правительства РФ от 1 июля 2004 N 458 // Собрание законодательства РФ. – 2004. – N 34. – Ст. 3158
Учебники и учебные пособия
3. Экономика предприятия: учеб. пособие / Е. А. Соломенникова, В. В. Гурин, Е. А. Прищепко, И. Б. Дзюбенко, Н. Н. Кулабахова – Киев: НАУ, 2003. – 245 с.
Книги с одним автором
4. Атаманчук, Г. В. Сущность государственной службы: История, теория, закон, практика / Г. В. Атаманчук. – М.: РАГС, 2003. – 268 с.
Книги одного, двух, трех и более авторов
5. В.С., Семенюк Э.П., Урсул А.Д. Категории современной науки: Становление и развитие – М.: Мысль, 1984.-268с.
Статья из газеты или журнала
6. Егорова П.Д., Минтусов И.Л. Портрет делового человека // проблемы теории и практики управления. – 1992 – №6. – С.3-17.
Статья из энциклопедии или словаря
7. Бирюков Б.В. Моделирование // БСЭ – 3е изд. – М., 1974. – Т. 16. – С.393-395
8. Ожегов, С. И. Толковый словарь русского языка / С. И. Ожегов, Н. Ю. Шведова. – М.: Азбуковник, 2000. – 940 с.
Электронные ресурсы
9. Tvorcheskie proekty, Inc.(2013). План оформления творческого проекта. Симферополь, Tvorcheskie proekty. Web: http://tvorcheskie-proekty.ru/plan
Книги с одним автором
10. Игнатов, В. Г. Государственная служба субъектов РФ: Опыт сравнительно-правового анализа: науч.-практ. пособие/ В. Г. Игнатов. – Ростов-на-Дону: СЗАГС, 2000. – 319 с.
Также могут использоваться и другие виды информационных источников.
8. Приложения
В приложении исследовательской работы и проекта размещаются диаграммы, графики, схемы, фотографии, таблицы, карты. Согласно плану раздел приложения размещается последним в работе.
Вспомогательные или дополнительные материалы, которые загромождают основную часть работы, помещают в приложениях. Каждое приложение должно начинаться с нового листа (страницы) с указанием в правом верхнем углу слова «Приложение» и иметь тематический заголовок.
При наличии в работе более одного приложения они нумеруются арабскими цифрами (без знака №) и т. д. нумерация страниц, на которых даются приложения, должна быть сквозной и продолжать общую нумерацию основного текста. Связь его с приложениями осуществляется через ссылки, которые употребляются со словом «смотри» (см.), заключаемым вместе с шифром в круглые скобки.
Если четко придерживаться плана исследовательской работы, ваш индивидуальный или групповой проект будет соответствовать всем нормам и требованиям, а конечно получит высокую оценку.
Более подробно, вы можете ознакомиться на сайте http://obuchonok.ru/plan
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К САМОСТОЯТЕЛЬНОЙ РАБОТЕ
ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНОГО ПРОЕКТА
ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»
Учебный предмет ОУД.10 Математика
специальность
среднего профессионального образования
43.02.14 Гостиничное дело
Разработчик:
Чернова Т.В., преподаватель математики
« ___ » _______________ 2021 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
СТРУКТУРА И СОДЕРЖАНИЕ ИНДИВИДУАЛЬНОГО ПРОЕКТА 3
ОФОРМЛЕНИЕ ИНДИВИДУАЛЬНОГО ПРОЕКТА. 6
ОФОРМЛЕНИЕ ЗАГОЛОВКОВ 6
OРГАНИЗАЦИЯ КОНТРОЛЯ ЗА ВЫПОЛНЕНИЕМ ИНДИВИДУАЛЬНОГО ПРОЕКТА ОБУЧАЮЩИМИСЯ 7
ФОРМЫ КОНТРОЛЯ ЗА ВЫПОЛНЕНИЕМ ИНДИВИДУАЛЬНОГО ПРОЕКТА ОБУЧАЮЩИМИСЯ 7
ТРЕБОВАНИЯ К ЗАЩИТЕ ИНДИВИДУАЛЬНОГО ПРОЕКТА 7
КРИТЕРИИ ОЦЕНКИ ИНДИВИДУАЛЬНОГО ПРОЕКТА 7
ТЕМЫ ИНДИВИДУАЛЬНЫХ ПРОЕКТОВ 8
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ 9
ВВЕДЕНИЕ
Методические рекомендации определяют самостоятельную работу студентов, ее назначение, планирование, формы организации и виды контроля. Проектная и исследовательская деятельность студентов является неотъемлемой частью образования, в соответствии с требованиями ФГОС среднего общего образования, предъявляемых к структуре, содержанию и результатам освоения учебных дисциплин общеобразовательного цикла и одним из приорететных направлений модернизации и практико-ориентированного обучения для подготовки конкурентоспособного специалиста.
Проектно-исследовательская деятельность — деятельность по проектированию собственного исследования, предполагающая выделение целей и задач, принципов отбора методик, планирование хода исследования, определение необходимых ресурсов и ожидаемых результатов, оценка результата исследования. Главной целью исследования является развитие личности, приобретение студентами функционального навыка исследования как универсального способа освоения действительности, развитии способности к исследовательскому типу мышления, активизации личностной позиции в образовательном процессе.
Результатом исследовательской деятельности является интеллектуальный продукт, представленный в форме:
– письменной работы (эссе, реферат, аналитические и обзорные материалы, мультимедийный продукт и т.д.);
– творческой работы (графический объект, презентация, аудио- и видео файлы и т.д.);
– демонстрации практической работы с программным обеспечением;
-макета или иного конструкторского изделия;
– отчета в рамках проведенного социального исследования.
СТРУКТУРА И СОДЕРЖАНИЕ ИНДИВИДУАЛЬНОГО ПРОЕКТА
Индивидуальный проект по предмету «Математика» является одним из методов формирования информационной компетентности студентов, направленной на достижение следующих целей:
-
формирование у студентов представлений о роли математики и информационно-коммуникационных технологий (ИКТ) в современном обществе;
-
формирование у студентов умений осуществлять поиск и использование информации;
-
формирование у студентов умений применять, анализировать, преобразовывать информационные модели реальных объектов и процессов, используя при этом ИКТ;
-
развитие у студентов познавательных интересов, интеллектуальных и творческих способностей;
-
приобретение студентами опыта использования информационных технологий в индивидуальной и коллективной, учебной и познавательной, в том числе проектной деятельности;
-
владение информационной культурой, способностью анализировать и оценивать информацию с использованием информационно-коммуникационных технологий, средств образовательных и социальных коммуникаций.
Индивидуальный проект включает в себя подготовительный, основной и заключительный этапы.
Подготовительный этап – выбор темы.
Основной этап – разработка и утверждение плана проекта, подбор и изучение литературы, анализ полученной информации, выбор способа представления полученных результатов, оформление и предварительная проверка работы руководителем проекта.
Заключительный этап – предзащита и защита индивидуального проекта.
В процессе выполнения индивидуального проекта по учебной дисциплине «Математика» студенты должны иметь возможность доступа:
-
к электронным учебным материалам по математике в сети Интернет (электронным книгам, практикумам, тестам);
-
к электронным периодическим изданиям, посвященным информационным технологиям;
-
к программному обеспечению, необходимому для подготовки проекта;
-
к прочим энциклопедическим, специализированным ресурсам, необходимым для подготовки индивидуального проекта.
Структура индивидуального проекта:
-
титульный лист работы;
-
содержание;
-
введение;
-
основная часть;
-
заключение;
-
список использованной литературы и интернет ресурсов;
-
приложения.
Введение раскрывает значение и актуальность выбранной темы, состояние изучаемых вопросов и необходимость проведения исследования. В нём формулируются цель работы, её основные задачи, указывается объект и методы исследования, теоретическая и методологическая основа.
Под актуальностью темы понимается её теоретическая и практическая значимость, важность для формирования информационной грамотности лиц, практического применения знаний основ информатики в профессиональной деятельности.
При формулировании цели и задач исследования необходимо исходить из того, что в них описываются как теоретические, так и практические результаты работы. Главная цель характеризует итог индивидуального проекта в целом, вклад, вносимый в разработку теоретического и практического аспектов обозначенной проблемы. Задачи конкретизируют содержание цели исследования, характеризуя промежуточные итоги работы.
В соответствии с поставленной целью в индивидуальном проекте выделяют задачи, которые перечисляются в повелительной форме: систематизировать…, изучить…, описать…, установить…, выяснить…, обосновать…, проанализировать…, разработать…, предложить… и т.д.
Формулировки содержащихся во введении актуальности, цели и задач работы, научной новизны и практической значимости должны быть чёткими и не иметь двояких толкований.
Описанию решений, указанных во введении целей и задач посвящается всё содержание индивидуального проекта, поэтому в каждой части проекта должна решаться та или иная задача исследования.
Объект исследования представляет собой часть основ информатики в дальнейшей профессиональной деятельности.
Во введении должны быть указаны использованные в работе над проектом методы исследования.
Теоретической и методологической основой при работе над проектом могут послужить научные труды отечественных и зарубежных учёных в области исследуемой проблемы.
В конце введения можно раскрыть структуру работы, т.е. кратко описать перечень её структурных элементов и обосновать последовательность их расположения. Объём введения не должен превышать 1-1,5 страниц.
Основная часть должна состоять из одного или двух разделов.
Первый раздел носит теоретический характер. В ней автор определяет методологические и теоретические основы исследуемой проблемы. Для этого: изучает и делает обзор по изучаемой теме; рассматривает представленные в литературе точки зрения учёных по изучаемому вопросу, выявляет противоречия, критически оценивает представленные взгляды на освещаемый вопрос. В ходе такого размышления формируется собственная точка зрения на предмет и объект исследования, приобретаются навыки подбора аргументов для доказательства своих позиций по тем или иным вопросам.
Первый раздел исследования может содержать 2-3 теоретических вопроса, в которых:
– раскрываются сущность и значимость поставленной проблемы;
– даётся обзор литературных источников, касающихся темы исследования, обобщается отечественный и зарубежный опыт по исследуемой тематике, обосновывается возможность его применения для решения поставленной проблемы.
Объём первого раздела 3-4 страницы машинописного текста.
Второй раздел содержит 3–5 страниц машинописного текста и носит экспериментальный характер.
При изложении материала делаются ссылки на литературные источники путём указания в квадратных скобках их номера в списке литературы и страниц, с которых заимствованы цитаты или цифровой материал, например: [5, с. 77]. При произвольном изложении принципиальных вопросов достаточно указать номер источника, например: [5].
При работе над индивидуальным проектом допускаются промежуточные выводы, которые формируются по итогам написания разделов работы. Вывод по разделу не подлежит обособлению и представляет собой его заключительный абзац, в котором в тезисной форме излагаются полученные автором результаты.
При формулировке выводов по разделу проекта целесообразно использовать речевые конструкции: в работе систематизировано…; установлено…, предложено…, исследовано…, выявлено…, сформулировано…, разработано…, сформировано…
Заключение (1-1,5 страницы) содержит краткие выводы по результатам проведенного исследования. В выводах кратко, но чётко отражаются ключевые положения каждого раздела индивидуального проекта, уделяется внимание решению поставленных задач и целей исследования.
Список литературы и интернет ресурсов включает источники информации, которые студент прямо или косвенно использовал при подготовке и выполнении индивидуального проекта. Литературные источники указываются в алфавитном порядке.
Общее количество источников должно быть не менее 7, при этом на 50% из них должны быть ссылки в тексте работы.
Приложения могут включать графики, схемы, рисунки, таблицы, копии документов и другие необходимые данные. Они располагаются в порядке их упоминания в тексте и служат для иллюстрации отдельных положений исследуемой проблемы или являются результатом предлагаемых автором рекомендаций. Приложений может быть не более 10 страниц.
Текст индивидуального проекта необходимо излагать от первого лица множественного лица: нами, по нашему мнению, на наш взгляд и т.д. Изложение материала должно быть последовательным, логичным и творческим. Пересказывать учебники, учебные пособия, другую специальную литературу не следует. Особое внимание следует обращать на «переходы» от одного раздела к другому, а внутри них – от вопроса к вопросу.
Изложение вопросов, при необходимости, должно иллюстрироваться таблицами, графиками, диаграммами, схемами. Наличие иллюстраций свидетельствует о высоком качестве проработки автором изучаемой проблемы и помогает лучше воспринять материал. Содержание иллюстрированного материала должно быть понятно без обращения к тексту работы.
Общий объём работы должен быть не менее 12 и не более 15 страниц. В нормируемый объём не входят титульный лист, содержание, список использованной литературы и интернет ресурсов, приложения. Объём ниже нормы предполагает, что студент не владеет достаточным количеством информации для обоснованных выводов по исследуемой тематике, а превышение объёма говорит о неумении сортировать и обобщать информацию.
ОФОРМЛЕНИЕ ИНДИВИДУАЛЬНОГО ПРОЕКТА.
Готовый проект брошюруется в папку, предназначенную для такого оформления. В сброшюрованной работе не должно быть пустых страниц.
Титульный лист оформляется строго в соответствии с образцом. Не допускается оформление титульного листа с применением рамок, цветного изображения, изменения шрифта, межстрочных расстояний, применение разрежённости, теней, контуров и других спецэффектов.
Содержание включает введение, наименование разделов, вопросов, заключение, список использованных источников и приложений с указанием номеров страниц, с которых начинаются эти элементы работы.
Текст печатается на одной стороне листа белой бумаги формата А4 через полтора интервала. Цвет шрифта – чёрный. Размер шрифта (кегль) – 14,тип шрифта, но обычно – шрифт «Times New Roman», строчные буквы, без разреженности, теней, контуров и др. спецэффектов, по тексту не допускается курсив, полужирные, подчёркивание в т.ч. при оформлении рисунков и таблиц. Не применяется перенос слов и их разрыв.
Не допускается располагать на странице менее пяти строк, а также заканчивать параграф работы таблицей, рисунком или формулой.
Интервал полуторный, без отступов перед и после абзаца, отключить опции «автоматический перенос слов». Выравнивание текста – «по – ширине».
В тексте работы не допускается сокращение, исключения составляют общепринятые описанные соответствующим стандартом или правилом русской орфографии или пунктуации. Например, и так далее – и т. д.; год (годы) – г (гг.); рубли, тысячи рублей, миллионы рублей – руб., тыс. руб., млн. руб., открытое акционерное общество – ОАО и т.д.
При выполнении индивидуального проекта следует использовать однотипные знаки препинания, например « » или ” ” , при перечислении однородных членов предложения следует использовать маркировку в виде точек, тире, арабских цифр и русских букв, недопустимо использовать знаки не указанные в приложении.
Размеры полей: правое – 1,5 см, верхнее и нижнее – 2,0 см, левое – 3,0 см.
Страницы проекта нумеруются арабскими цифрами (нумерация сквозная по всему тексту). Номер страницы ставится в правой нижней части листа без точки. Титульный лист включается в общую нумерацию, номер на нём не ставится.
По всей работе не допускается обрамление текста с применением рамок, уголков и т.п. объектов.
ОФОРМЛЕНИЕ ЗАГОЛОВКОВ
Вопросы основной части работы не являются структурными элементами – таким элементом является только вся основная часть в целом. Заголовки структурных элементов работы располагают в середине строки без точки в конце и печатают заглавными буквами без подчеркивания. Каждый структурный элемент следует начинать с новой страницы.
Расстояние между заголовком и текстом должно быть равно 3 или 4 интервалам (15мм). Если проект напечатан интервалом 1,5, то это значит, что расстояние между заголовком и текстом равно одной пустой строке. Расстояние между заголовками раздела и вопросов – 2 интервала (8мм).
Для установки необходимых отступов необходимо использовать стандартное меню редактора MS WORD: «формат – абзац – интервал».
Вопрос раздела начинается на той же странице, на которой закончился предыдущий, исключение составляют случаи, когда после названия структурного элемента помещается менее 4-х строк, в этой ситуации структурный элемент и его вопросы переносятся на следующую страницу.
OРГАНИЗАЦИЯ КОНТРОЛЯ ЗА ВЫПОЛНЕНИЕМ ИНДИВИДУАЛЬНОГО ПРОЕКТА ОБУЧАЮЩИМИСЯ
Выполнение индивидуального проекта осуществляется в соответствии с утвержденным графиком консультаций под контролем руководителя проекта.
Студент 1 раз в месяц представляет итоги реализации плана выполнения индивидуального проекта.
ФОРМЫ КОНТРОЛЯ ЗА ВЫПОЛНЕНИЕМ ИНДИВИДУАЛЬНОГО ПРОЕКТА ОБУЧАЮЩИМИСЯ
-
Просмотр и проверка этапов выполнения индивидуального проекта.
-
Обсуждение результатов выполненной работы на конкретном этапе индивидуального проекта.
ТРЕБОВАНИЯ К ЗАЩИТЕ ИНДИВИДУАЛЬНОГО ПРОЕКТА
Защита проектной работы проводится на открытом заседании предмено-цикловой комиссии. Студент публично представляет результаты проведенного исследования. Процедура защиты включает доклад (не более 5 -7 минут) с использованием мультимедийной презентации, в которой он отражает актуальность темы проекта; цель и задачи проекта; результаты проведенного теоретического и практического исследования, выявляет проблемы и выдвигает предполагаемые пути решения; а также делает общий вывод по теме исследования.
Если индивидуальный проект предусматривает демонстрацию практической работы студента, то кроме демонстрации студент предоставляет к индивидуальному проекту файл с выполненной работой.
Студент отвечает на вопросы теоретического и практического характера по теме проекта. Ему предоставляется возможность в кратком выступлении разъяснить положения, которые вызвали дискуссию, интерес к проблеме, дать необходимые пояснения, привести дополнительные материалы.
По итогам защиты руководитель проекта составляет отзыв и выставляет оценку.
Работа не допускается к защите по следующим основаниям:
-
представлен отрицательный отзыв научного руководителя;
-
по мнению председателя ПЦК не соответствует требованиям по структуре и содержанию, или не соответствует теме исследования;
-
работа выполнена с грубым нарушением правил оформления или на её титульном листе указана тема отличная от заявленной студентом и закреплённой в приказе;
-
работа представлена на проверку и рецензирование с нарушением сроков.
КРИТЕРИИ ОЦЕНКИ ИНДИВИДУАЛЬНОГО ПРОЕКТА
Результаты защиты индивидуального проекта оцениваются по пятибалльной шкале и фиксируются в виде оценок «отлично», «хорошо», «удовлетворительно», «неудовлетворительно» при этом необходимо учитывать:
-
качество представленной работы и степень самостоятельности в выполнении различных этапов работы над проектом;
-
аргументацию актуальности и значимости изучаемой проблемы;
-
количество новой информации, использованной для выполнения проекта, степень ее осмысления;
-
полноту раскрытия содержания выбранной темы индивидуального проекта;
-
логичность, четкость и связность выступления;
-
качество ответов на вопросы комиссии;
-
оригинальность идеи, способа решения проблемы;
-
использование презентации и творческий подход в подготовке наглядного и раздаточного материалов;
-
социальное и прикладное значение полученных результатов.
Результаты защиты индивидуального проекта объявляются в тот же день после оформления в установленном порядке протоколов заседания предметно-цикловой комиссии.
ТЕМЫ ИНДИВИДУАЛЬНЫХ ПРОЕКТОВ
-
Непрерывные дроби.
-
Применение сложных процентов в экономических расчетах.
-
Параллельное проектирование.
-
Средние значения и их применение в статистике.
-
Векторное задание прямых и плоскостей в пространстве.
-
Сложение гармонических колебаний.
-
Графическое решение уравнений и неравенств.
-
Правильные и полуправильные многогранники.
-
Конические сечения и их применение в технике.
-
Понятие дифференциала и его приложения.
-
Схемы повторных испытаний Бернулли.
-
Исследование уравнений и неравенств с параметром.
-
Теория чисел и Пьер Ферма.
-
Треугольники с целочисленными сторонами.
-
Прикладное значение процентных задач в современной жизни.
-
Владение методом математической индукции.
-
Математика и литература – два крыла одной культуры.
-
Изопиранное неравенство.
-
Применение функции Эйлера при построении уникурсальных звёзд.
-
Квадратное уравнение с целыми коэффициентами. Критерии качества корней.
-
Исследование одной задачи на минимум.
-
Цепные дроби: скрытая красота.
-
Симметрия в природе.
-
Сечение многогранников.
-
Стереометрия вокруг нас.
-
Задачи на движение.
-
В мире функций.
-
Производная и её приложение.
-
Загадки пирамиды.
-
Геометрия Лобачевского.
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ
-
Андреева Е.В. и др. Математические основы информатики. Элективный курс. – М.: 2005.
-
Григорьев С.Г., Иволгина С.В. Математика. – М.: Образовательно-издательский центр «Академия», 2011.
-
Богомолов Н.В. Практические занятия по математике. – М.: Высшая школа. 2009.
-
Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике. – Издательский центр «Академия», 2011.
-
Дадаян А.А. Математика: учеб. – М.: ФОРУМ: ИНФРА-М, 20133.
-
Математика и информатика: учебник для студ. учреждений сред. проф. образования/ Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В./ – М.: Издательский центр «Академия», 2009.
-
Математика для профессий и специальностей социально-экономического профиля: учебник для образовательных учреждений нач. и сред. образования / В.А. Гусев, С.Г. Григорьев, С.В. Иволгина – М.: Издательский центр «Академия», 2011.
-
Высшая математика для экономистов. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2007.
-
Спирина М.С. дискретная математика: учеб. – М.: Издательский центр «Академия», 2006.
-
Омельченко В.П. Математика. – Ростов-на-Дону.: Феникс, 2006.
Дополнительные источники:
-
Запорожец Г.И. Руководство к решению задач по математическому анализу. М.: Высшая школа, 1966.
-
Смирнов В.И. Курс высшей математики. Т.1. – М.: Наука, 1974.
-
Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1. – М.: Наука, 1989.
Интернет-ресурсы
-
www.fcior.edu.ru/ Информационные, тренировочные и контрольные материалы.
-
www.school-collection.ru/ Единая коллекция цифровых образовательных ресурсов.
-
http://www.razumdom.ru/ – интернет ресурс «Разумный дом».
-
http://school-collection.edu.ru/ Единая Национальная Коллекция цифровых образовательных ресурсов (ЦОР). Каталог ИУМК, ИИСС, ЦОР.
-
http://www.fcior.edu.ru/ ФЦИОР – Федеральный центр информационно-образовательных ресурсов. Каталог учебных модулей по дисциплинам.
-
http://window.edu.ru/window Единое окно доступа к образовательным ресурсам. Каталог учебных продуктов.
-
http://eor-np.ru/ Электронные образовательные ресурсы.
-
www.osw.mit.edu/OcnWeb/Global/all-courses.htm/ обучающий сайт – Информационно-коммуникационные технологии в образовании. http://emag/ils/ru/infosoc/emag.nsf
Во все времена школа, помимо обучения детей
основам наук, выполняла и важнейшую задачу
подготовки подрастающего пфоколения к
самостоятельной жизни в обществе.
А для современного общества характерна
сложность социальных, культурных, экономических
условий, поэтому оно остро нуждается в людях,
которые умеют самостоятельно думать и решать
разнообразные проблемы, обладают критическим и
творческим мышлением, умеют работать в
коллективе, обладают коммуникационными
навыками, то есть являются конкурентоспособными.
Таким образом, сегодня школа должна решить
непростые вопросы: какой должна быть новая
модель образования и как наиболее безболезненно
для всех участников педагогического процесса
изменить свою работу с целью выполнения
социального заказа, и что очень важно, сделать
привлекательной эту модель для самих учащихся.
Одним из решений этой проблемы может быть
организация учебного процесса, направленного на
развитие творческих способностей учащихся и
навыков исследовательской, проектной
деятельности, что способствовало бы
формированию выше указанных качеств будущих
выпускников.
Осмысление и применение этого метода в новой
учебной, социально-культурной ситуации, в свете
требований к образованию на современной ступени
общественного развития позволяет говорить о
школьном проекте как о новой технологии в
педагогике, которая позволит эффективно решать
задачи личностно-ориентированного подхода в
обучении подрастающего поколения. Проект ценен
тем, что в ходе его выполнения школьники учатся
самостоятельно добывать знания, получают опыт
познавательной и учебной деятельности. Если
ученик получит в школе исследовательские навыки
ориентирования в потоке информации, научится
анализировать ее, обобщать, сопоставлять факты,
делать выводы и заключения, то он в силу более
высокого образовательного уровня легче будет
адаптироваться в современном обществе, к
меняющимся условиям жизни, правильно будет
ориентироваться в выборе профессии и будет жить
творческой жизнью.
Главные цели введения метода проектов на
уроках математики:
- показать умения отдельного ученика или группы
обучающихся использовать приобретенный на
уроках математики в школе исследовательский
опыт; - реализовать свой интерес к предмету математики;
приумножить знания по математике и донести
приобретенные знания своим одноклассникам; - продемонстрировать уровень обученности по
математике; совершенствовать свое умение
участвовать в коллективных формах общения; - подняться на более высокую ступень обученности,
образованности, развития, социальной зрелости.
Организуя работу над проектом на уроках
математики важно соблюсти несколько условий:
- Тематика проектов должна быть известна
заранее. Учащиеся должны быть ориентированы на
сопоставление и сравнение некоторых фактов,
фактов из истории математики и жизни ученых
математиков, подходов и решений тех или иных
проблем. Желательно чтобы ученик или группа
выбрала тему самостоятельно. - Проблема, предлагаемая ученикам,
формулируется так, чтобы ориентировать учеников
на привлечение фактов из смежных областей знаний
и разнообразных источников информации. - Необходимо вовлечь в работу над проектом как
можно больше учеников класса, предложив каждому
задание с учетом уровня его математической
подготовки.
Ученик (или группа учащихся) подчеркивает
актуальность темы проекта для общественной
жизни, для расширения познавательного и
образовательного уровня тех, кто будет
знакомиться с результатами исследования,
желание и возможность раскрыть и развить тему
интересно для своих одноклассников, для
коллектива учителей своей школы или за ее
пределами. Следующий этап предполагает
формулировку проблемы, которые ученик выбрал для
исследования. К этому моменту он уже продумал и
осмыслил тему, прежде чем самостоятельно
определить вопросы, ориентирующие на примерное
содержание его работы. Может и быть такое, что
ученик полностью не справится с такой работой, но
тут и должен прийти на помощь учитель (или более
сильные одноклассники).
Следующая ступень в организации проектной
деятельности на уроках математики предполагает,
что участники разных проектов обсудят
конкретные проблемы исследования, уточнят или
даже изменят формулировку своей темы, наметят
сроки выполнения. В процессе обсуждения
выявляется эрудиция участника проекта, их
математический кругозор, знание ими других
источников кроме учебника. Также важно на этом
этапе и участие тех детей, которые не выбрали
проект. На данном этапе они чувствуют свою
причастность к исследовательской деятельности,
расширяют круг своих знаний по математике.
Полезны также промежуточные отчеты учащихся по
проектам. В дискуссии по коллективному проекту
обязательно выслушивается мнение каждого
участника. Это покажет учителю одинаковый ли
уровень подготовки обучающихся, не возникнут ли
в процессе исследовательской деятельности
разногласия, которые будут тормозить ее
выполнение. Далее идет полностью работа с
информативным материалом.
Проекты могут оформляться в письменном виде и
путем публичной защиты. Объем письменно
оформленных проектов по математике может быть
различным, в зависимости от типа проекта и
времени его выполнения, в зависимости от
количества графического материала, рисунков,
таблиц исследования и т.д. Меньшим, как правило,
бывает объем краткосрочного проекта. Он
охватывает небольшой круг вопросов.
В любом случае проектная методика предполагает
самостоятельную работу ученика с источниками
информации. Как же работать с источниками? В
начале учащийся должен при беглом просмотре
источника определить – имеет ил отношение
информация к проблематике проекта. С этой целью
читается название книги, просматриваются схемы,
формулы, таблицы и т.д. Если источник
заинтересовал ученика, он должен переходить к
чтению с полным пониманием. Таким образом, путем
разных стратегий, отбирается важный
исследовательский материал по выбранной теме.
Вообще не нужно бояться данного этапа. Именно на
данном этапе снимаются все трудности: они
сопоставляют план изложения материала, в котором
отражен прогноз результатов исследования,
излагают свои знания, соображения, идеи по
проблеме. Далее на каком-то уроке можно провести
предварительную апробацию написанного проекта.
Итак, мы видим ведущую линию в осуществлении
проектной деятельности на уроках математики. Она
состоит в том, чтобы выбрать тему проекта,
выделить в ней проблемы, наметить направление и
ход ее разработки, наполнить ее интересным
материалом и содержанием, логически ее
завершить, продемонстрировать свою эрудицию в
предмете исследования. В процессе проектной
деятельности по предмету математика расширяется
образовательный кругозор учащихся, возрастает
стойкий познавательный интерес к предмету,
формируется исследовательский навык. Ученик
способный к такой исследовательской
деятельности способен занять определенную
жизненную позицию при оценке любой социальной
ситуации. Опыт изучения проектной деятельности
показывает высокий уровень обученности по
математике, богатый словарный запас по предмету.
У учащихся к выпуску наблюдается формирование
всех компонентов исследовательской культуры:
мыслительных умений и навыков (анализ и
выделение главного, сравнение, обобщение и
систематизация); умения и навыки работы с
дополнительными источниками информации; умения
и навыки, связанные с культурой устной и
письменной речи.
Работа с обучающимися
Занятие 1.
Учитель знакомит ребят с необходимым
теоретическим материалом, основываясь на
брошюре “Проектное портфолио”, которая
предлагается ученикам в конце занятия. Метод,
преобладающий на занятии – беседа.
Вопросы, которые были заданы ученикам:
- Что такое проекты? Принимали ли вы когда-нибудь
в них участие? Приведите примеры. - Как вы думаете, как организовывается работа над
проектом? - Какие виды проектов бывают?
ПРОЕКТНОЕ ПОРТФОЛИО
I. Что такое проектная работа?
Проект – самостоятельная творческая работа
учащегося, выполненная от идеи до ее воплощения в
жизнь с помощью консультаций учителя.
Хотелось бы, чтобы в результате работы над
проектом вы получили удовольствие, смогли
проявить самостоятельность, фантазию,
творческий подход. Кроме того, подобная работа
поможет вам укрепить дружеские и товарищеские
отношения. Вы, надеемся, будете в работе
поддерживать друг друга, подсказывать пути
решения возникающих проблем, сумеете
распределить обязанности, взаимодействовать
друг с другом.
Очень хотелось бы, чтобы в процессе работы вы
научились планировать свою работу, заранее
просчитывать возможные результаты; использовать
различные источники информации, а также
самостоятельно отбирать и накапливать материал;
анализировать отобранный материал, сопоставлять
факты; аргументировать свою точку зрения,
отстаивать её; распределять обязанности внутри
группы; представлять созданный проект перед
аудиторией; оценивать себя и других; лучше
овладеть умениями и навыками работы с
современными информационно-техническими
средствами
II. Как ты будешь работать над проектом? (краткий
экскурс)
Работа будет включать в себя
последовательность этапов.
Первый этап – этап планирования. Это этап
подготовки проекта. Прежде всего необходимо
определиться с темой проекта. Причем тему надо
выбрать такую, чтобы она была интересна каждому
участнику проекта. После необходимо определить
цель проекта, и то, как мы эту цель будем
достигать, т.е. задачи нашего проекта. Здесь
необходимо точно представлять себе объем и
конечный результат проекта. После этого
составляется план выполнения проекта. Далее, с
опорой на имеющийся план, формируются группы и
распределяются роли (обязанности) внутри каждой
из групп. Здесь же определяются материалы и
средства, необходимые для реализации проекта,
обсуждаются сроки выполнения каждого из этапов
деятельности, форма представления готового
результата.
Второй этап – этап выполнения проекта.
Обычно этот этап разбивается на два:
аналитический этап и этап обобщения информации.
На аналитическом этапе происходит
самостоятельное исследование, поиск и обработка
информации. Как правило, для выполнения проекта
необходимо довольно много различного материала,
поэтому можно распределить обязанности внутри
группы. Распределить между участниками фронт
работы. Когда вся необходимая информация для
выполнения проекта получена, ее необходимо
обработать. То есть наступает этап обобщения
информации. Здесь необходимо привести
полученные данные в систему, обобщить их.
На последнем этапе работы над проектом
необходимо поработать над тем, как представить
результат всей работы остальным участникам.
Здесь надо описать все этапы работы, методы и
приемы, которые использовались. Выявить
трудности, с которыми столкнулись, как они были
преодолены.
III. Проекты бывают:
а) краткосрочные проекты (это могут быть
проекты, предусмотренные для проведения на уроке
или во внеурочное время для решения небольшой
проблемы);
б) долгосрочные, предусматривающие решение
достаточно сложной проблемы, требующей
длительного наблюдения, постановки
экспериментов, опытов, сбор данных, их обработка.
Такие проекты могут предусматривать серию
подпроектов, которые могут образовывать целую
программу. Длительность таких проектов может
быть от месяца до года и даже более.
Какие бывают типы проектов? (если тебе трудно
понимать смысл текста читай только жирный шрифт
и примеры).
а) исследовательские. Такие проекты требуют
хорошо продуманной структуры, обозначенных
целей, актуальности проекта для всех участников,
продуманных методов, в том числе
экспериментальных и опытных работ, методов
обработки результатов. Пример: проекты для
старшеклассников: эссе, исследовательские
рефераты.
б) творческие. Такие проекты, как правило, не
имеют детально проработанной структуры, она
только намечается и далее развивается,
подчиняясь логике и интересам участников
проекта. Пример: газета, видеофильм, спортивная
игра, подготовка выставки.
в) игровые. В таких проектах структура также
только намечается и остается открытой до
окончания проекта. Участники принимают на себя
определенные роли, обусловленные характером и
содержанием проекта. Это могут быть литературные
персонажи или выдуманные герои, имитирующие
социальные или деловые отношения, осложняемые
придуманными участниками ситуациями. Результаты
таких проектов могут намечаться в начале
проекта, а могут вырисовываться лишь к его концу.
Степень творчества здесь очень высокая, но
доминирующим видом деятельности все-таки
является ролево-игровая, приключенческая.
Пример: сценарий праздника эпохи, фрагмент урока,
кроссворды.
г) информационные проекты. этот тип проектов
изначально направлен на сбор информации о
каком-то объекте, ознакомление участников
проекта с этой информацией, ее анализ и обобщение
фактов, предназначенных для широкой аудитории.
Пример: различные сообщения, доклады.
д) практико-ориентированные. Эти проекты
отличает четко обозначенный с самого начала
предметный результат деятельности участников
проекта. Причем этот результат обязательно
ориентирован на интересы самих участников. Такой
проект требует хорошо продуманной структуры,
даже сценария всей деятельности его участников с
определением функций каждого из них, четкие
выводы и участие каждого в оформлении конечного
продукта. Здесь особенно важна хорошая
организация координационной работы. Пример:
проект закона, справочный материал, программа
действий, совместная экспедиция, наглядное
пособие.
2 занятие.
IV. Как лучше организовать работу над проектом?
Предлагается следующая последовательность
работы:
1. Уточнение и формулировка задач.
Правильная формулировка задачи проекта (т.е.
проблемы, которую предстоит решить)
предопределяет результативность работы группы.
Здесь необходима помощь учителя. Сначала члены
каждой группы обмениваются уже имеющимися
знаниями по выбранному ими направления работы, а
также соображениями о том, что ещё, на их взгляд,
необходимо узнать, исследовать, понять. Затем
учитель при помощи проблемных вопросов подводит
учащихся к формулировке задачи. Если учащиеся
априорно знают решение поставленной проблемы и
легко отвечают на вопросы учителя, задачи для
группы поставлены не правильно, так как не
отвечают основной цели проекта – обучению
навыкам самостоятельной работы и
исследовательской деятельности.
Во время работы над проектом учителю
необходимо следить, чтобы каждая группа и каждый
её член чётко понимали свою собственную задачу,
поэтому рекомендуется оформить стенд, на котором
были бы вывешены: общие темы проекта, задачи
каждой группы, списки членов групп,
консультантов, ответственных и т.д. Такой стенд
способствует также осознанию каждым учащимся
ответственности за выполняемую работу перед
остальными участниками проекта.
2. Поиск и сбор информации.
Здесь учащиеся определяют, где и какие данные
им предстоит найти. Затем начинается
непосредственно сбор данных и отбор необходимой
информации. Этот процесс может осуществляться
различными способами, выбор которых зависит от
времени, отведённого на данный этап,
материальной базы и наличия консультантов.
Учащиеся (с помощью учителя) выбирают способ
сбора информации: наблюдение, анкетирование,
социологический опрос, интервьюирование,
проведение экспериментов, работ со средствами
массовой информации, с литературой. Задача
учителя – обеспечить, по мере необходимости,
консультации по методике проведения такого вида
работы. Здесь необходимо уделить особое внимание
обучению учащихся навыкам конспектирования. На
данном этапе учащиеся получают навыки поиска
информации её сравнения, классификации;
установления связей и проведения аналогий;
анализа и синтеза; работы в группе, координации
разных точек зрения посредством:
– личных наблюдений и экспериментирования;
– общения с другими людьми (встречи,
интервьюирование, опросы);
– работы с литературой и средствами массовой
информации.
Учитель играет роль активного наблюдателя:
следит за ходом исследований, соответствием цели
и задачам проекта; оказывает группам необходимую
помощь, не допуская пассивности отдельных
участников; обобщает промежуточные результаты
исследования для подведения итогов на конечном
этапе.
3. Обработка полученной информации.
Необходимое условие успешной работы с
информацией – ясное понимание каждым учеником
цели работы и критериев отбора информации.
Задача учителя – помочь группе определить эти
критерии. Обработка полученной информации – ее
понимание, сравнение, отбор наиболее значимой
для выполнения поставленной задачи. Учащимся
потребуются умение интерпретировать факты,
делать выводы, формировать собственные суждения.
Именно этот этап наиболее труден для учащихся,
особенно если они привыкли находить в книгах
готовые ответы на все вопросы учителя. Учителю
могут помочь в работе вопросы, приведенные ниже.
Вопросы, которые может задать учитель на
аналитическом этапе
| Определение задач: |
|
|
| Поиск и сбор информации: |
|
|
| Интерпретация полученных данных: |
|
|
3 занятие.
III. Этап обобщения информации.
На этом этапе осуществляются структурирование
полученной информации и интеграции полученных
знаний, умений, навыков. При этом учащиеся:
систематизируют полученные данные; объединяют в
единое целое полученную каждой группой
информацию; выстраивают общую логическую схему
выводов для подведения итогов. (Это могут быть:
рефераты, доклады, проведение конференций, показ
видеофильмов, спектаклей; выпуск стенгазет,
школьных журналов, презентация в интернете и
т.д.).
Учителю необходимо проследить, чтобы учащиеся
обменивались знаниями и умениями, полученными в
процессе различных видов работ с информацией
(анкетирование и обработка полученных знаний,
проведение социологического опроса,
интервьюирование, экспериментальная работа и
т.д.). Все необходимые мероприятия данного этапа
должны быть направлены на обобщение информации,
выводов и идей каждой группы. Учащиеся должны
знать порядок, формы и общепринятые нормы
представления полученной информации (правильное
составление конспекта, резюме, реферата, порядок
выступления на конференции и т.д.). И на этом этапе
учителю необходимо предоставить учащимся
максимальную самостоятельность выбора форм
представления результатов проекта, поддерживать
такие, которые дадут возможность каждому ученику
раскрыть свой творческий потенциал. Если
случиться так, что ребята испытывают затруднения
в процессе решения какой-либо проблемы, учитель
должен прийти им на помощь, но только с личного
приглашения ребят. Не следует вмешиваться в их
творческий исследовательский процесс без их
согласия. В то же время следует помнить, что
пускать все на самотек, допускать стихийную
самостоятельность нельзя.
Процесс обобщения информации важен потому, что
каждый из участников проекта как бы “пропускает
через себя” полученные всей группой знания,
умения, навыки, так как в любом случае он должен
будет участвовать в презентации результатов
проекта.
Варианты вопросов:
- Какие данные и выводы целесообразно обобщить и
вынести на презентацию? - Кому, по – вашему, будет интересна проблема над
которой вы работали? - В какой форме вы хотели бы представить итоги
вашей работы? Составьте план. - В чем вы могли бы помочь (исходя из личных
склонностей, интересов, способностей) при
подготовке презентации итогов проекта? - В чем будет состоять “изюминка” вашей
презентации? - Какие формы презентации вы считаете наиболее
приемлемыми, и учитывая содержание, цель проекта,
возраст и уровень знаний предполагаемой
аудитории, а также ваши способности и интересы? - Какие затраты предполагает выбранная форма
презентации? - Сколько времени потребуется на подготовку
выбранной вами формы презентации? - Чем необходимо заняться в первую очередь? В
каком порядке будет выполняться работа? Как она
будет распределяться между участниками
мероприятия? Кто и за что будет отвечать?
4 занятие.
IV. Представление полученных результатов
работы (презентация).
На этом этапе учащиеся осмысливают полученные
данные и способы достижения результата;
обсуждают и готовят итоговое представление
результатов работы над проектом (в школе, округе,
селе и т.д.). Учащиеся представляют не только
полученные результаты и выводы, но и описывают
приемы, при помощи которых была получена и
проанализирована информация; демонстрирует
приобретенные знания и умения; рассказывают о
проблемах, с которыми пришлось столкнуться в
работе над проектом.
Любая форма презентации также является учебным
процессом, в ходе которого учащиеся приобретают
навыки представления итогов своей деятельности.
Основные требования к презентации каждой группы
и к общей презентации: выбранная форма должна
соответствовать целям проекта, возрасту и уровню
аудитории, для которой она проводится. В процессе
работы по обобщению материала и подготовки к
презентации у учащихся, как правило, появляются
новые вопросы, при обсуждении которых может быть
даже пересмотрен ход исследований. Задача
учителя – объяснить учащимся основные правила
ведения дискуссий и делового общения; научить их
конструктивно относиться к критике своих
суждений; признавать право на существование
различных точек зрения решения одной проблемы.
Работая над проектом, учителю не следует
забывать, что основными критериями успешности
являются радость и чувство удовлетворения у всех
его участников от осознания собственных
достижений и приобретенных навыков. Как видно из
вышесказанного степень активности учеников и
учителя на разных этапах разная. В учебном
проекте ученики должны работать самостоятельно.
Степень активности и самостоятельности учащихся
можно представить в виде схемы
Из практики
Отличительная черта проектной методики –
особая форма организации. Организуя работу над
проектом, стараюсь соблюсти основные этапы
проектной деятельности.
Каждый проект соотносится с определенной темой и
разрабатывается в течение определенного
времени.
Я использую следующую классификацию проектов.
По продолжительности подготовки:
– краткосрочный
– средней продолжительности
– долгосрочный
2. По количеству участников:
– индивидуальный
– работа в парах
– групповой (4-6 человек)
По методу:
– творческий
– исследовательский
– информационный
(ознакомительно-ориентированный).
Необходимо отметить, что при выполнении
учащимися мультимедийной презентации в
программе Microsoft Publisher, проекты оцениваются по
100-бальной шкале. Оцениваются содержание,
оформление, устное выступление. Бланк оценки
вывешивается в кабинете
для ознакомления.
Небольшие проекты на несколько уроков, где
проводится совместная работа над подготовкой
проекта – прекрасная возможность дать каждому
участнику шанс проявить свою творческую
индивидуальность.
Вот как, например, проходила защита групповых
проектов по теме: “ Теорема Виета”. Учащимся
предлагаю разделиться на группы по 3-4 человека.
Каждая группа получает домашнее задание: найти
различные способы доказательства теоремы Виета
.Оформить доказательство в виде презентации (это
может быть компьютерная, стендовая, альбомная и
др.) и подготовить защиту одного понравившегося
доказательства , указав его преимущества и
недостатки.
Каждая группа выдвигает своего представителя и
консультанта, которые делают презентацию своей
работы на уроке. Другие группы принимают
активное участие в обсуждении и доказательстве,
делая записи в тетрадях, задавая дополнительные
вопросы.
Учитель направляет учебную дискуссию в нужном
направлении.
Техническая группа (2-3 учащихся) в ходе урока
собирает весь проект полностью и готовит
презентацию всего проекта в целом.
Также предлагаю учащимся творческие мини–
проекты для домашнего задания. Планируемыми
результатами и формами их представления могут
быть: кроссворд, чайнворд, ребусы, газета, журнал
и др.
Эти проекты предполагают активизацию учащихся,
т. к. они должны знакомиться с учебной
литературой, справочниками, подбирать рисунки и
рисовать. Учащиеся с разным уровнем подготовки
могут участвовать в проектной работе в
соответствии со своими возможностями. Ведь
составить и красочно оформить кроссворд, ребус
может ученик, у которого трудности с математикой,
но отличные способности к рисованию. А возникший
интерес и чувство радости от выполненного
задания у школьника – и есть критерий успешной
работы.
Однако, в последнее время, учащиеся
заинтересованы использовать компьютерные
технологии, так как они позволяют сделать
процесс создания проекта более увлекательным.
Информационные проекты
В 5-м классе “Старинные меры”, в 6-м классе
“Пропорции вокруг нас”, в 7-м классе “Как
функция может связать воедино окружающий нас
мир”, в 8-м классе проект “В мире симметрии”.
Исследовательские проекты
В 7-м классе “Взаимное расположение графиков
линейных функций”, “Формулы сокращенного
умножения”, проект в 8-м классе “Теорема Виета”,
“Золотое сечение”.
|
Как сделать проект: “Математика вокруг нас. Числа в загадках пословицах”? Проект “Числа в загадках, пословицах и поговорках”. План выполнения проекта:
Пример загадок, в которых участвуют цифры: Примеры пословиц и поговорок в тексте которых использованы различные цифры: автор вопроса выбрал этот ответ лучшим Сначала не лишним будет набросать порядок действий по реализации Проекта Математика вокруг нас. Числа в загадках и пословицах. Он может выглядеть вот так:
Придется изучить немало материала, что бы выбрать из всего многообразия загадок и пословиц, те в которых фигурируют числа. Ответившие в этом вопросе авторы уже любезно помогли вам в этом деле, и привели в пример много таких загадок и пословиц с числами. Можете взять и из этого вопроса. Структурирование Проекта можно конечно и упростить, по сравнению с моим порядком действий и ограничится просто приведением примеров загадок и пословиц с числами, но если вы выразите свое мнение например на то какую роль играют числа в пословицах и поговорках, какие числа чаще всего встречаются и почему, это будет дополнительным баллом при оценке Проекта. Не обязательно делать электронную презентацию, Проект может быть и на обычном листе А4. Viridi 3 года назад Для того чтобы сделать проект на заданную тему нужно хорошо поработать с дополнительной литературой или поискать информацию на интернет сайтах. Обычно проекты начинаются с титульного листа. Выглядеть он может например так: Далее можно обозначить цели и задачи, которые вы ставили при выполнении данной работы. Пословиц и поговорок, которые тем или иным образом связанных с математикой, числами и цифрами существует очень много. Вот некоторые из них: Теперь что касается загадок. Обычно автор описывает в них основные черты и признаки цифры, по которым её легко узнать. Вот пара примеров про самую первую цифру под названием единица: В конце работы можно подвести небольшой итог, обозначив важность математики как науки в нашей жизни. -Irinka- 3 года назад Проект на тему “Математика вокруг нас. Числа в загадках, пословицах и поговорках” выполнить не сложно. Для того, чтобы сделать соответствующий проект необходимо собрать, найти пословицы, поговорки, загадки в которых фигурируют цифры. Проект можно выполнить на плакатах, можно использовать бумагу формата А4 и представить проект в виде слайдов. Каждый из листов проекта для наглядности снабдить картинкой, цифрой. Для удобства в одном углу размещаем цифру, а в другом пишем пословицы, загадки в которых имеется соответствующая цифра.
Пример оформления проекта на данную тему на примере двух цифр 1 и 2 приведён ниже. Таким образом делаем весь проект, собирая информацию о всех цифрах с 1 до 9 и не забываем про 0. Бархатные лапки 3 года назад Для начала оформим титульный лист. Когда люди еще не знали цифр они все равно пользовались разными обозначениями, это были зарубки на деревьях, узелки и так далее. Сначала идет цифра один (или единичка). Цифра один встречается во многих загадках. Также эту цифру мы видим в большом количестве разных пословиц. А теперь напишем разные загадки, в которых встречаются цифры. Вот в этих пословицах идет речь о такой цифре как двойка. В таких пословицах встречается тройка. Напишем загадки про цифры шесть и девять. Также вспомним и запишем и другие пословицы, в которых встречаются цифры. В конце сделаем выводы и придем к тому, что везде нас окружают цифры, они встречаются в загадках, пословицах, поговорках, крылатых выражениях. Светланочка100 5 лет назад Для того, чтобы нам сделать такой проект, нам понадобиться собрать соответствующий материал. Первое что нам нужно, это составить план проекта, чтобы поэтапно ему следовать, это облегчит вам задачу. Второе найти пословицы, поговорки и загадки о числах. И третье, нам нужно иллюстрировать ваш проект. Читаем и вдумываемся в суть пословиц и загадок и ищем подходящие картинки. Четвёртое, это вывод, что вы узнали при выполнении данного проекта. Дальше идёт выступление перед классом. Я предлагаю использовать такие пословицы и загадки про числа, а также картинки, которые завершат проект по данной теме. На каждую цифру своя загадка или пословица. Образец. Евгений трохов 6 лет назад 1) Где на улице, дороге есть числа (ответы, например, номера домов) 2) Почему мы считаем десятками (10 пальцев на руках и ногах) 3) Собственно пословицы и поговорки: один в поле не воин, два братца в воду глядятся…и т.д. 4) Книги: “Два капитана”, “Три мушкетёра”, “Али-Баба и 40 разбойников”, “1000 и одна ночь”. Миром правят числа. 1-3 классы. 88SkyWalker88 3 года назад Проект про числа начинаем с титульного листа. На нем указываем название проекта, кто его выполнил. укажем числа от 0 до 10. Далее приведем пословицы с цифрами: Теперь приведем загадки с цифрами: Следующий этап проекта – загадки про каждую цифру: ![]11 ![][16] Nelli4ka 4 года назад Проект должен состоять из:
Соответственно, нужно провести серьезную работу, найти достаточное количество необходимых пословиц и загадок. Также к найденному материалу нужно подобрать подходящие картинки. Но с картинками получится долго и увесисто, а потому слайды можно оформлять таким образом. Один угол занимает изображение цифры. Над (или под) ним пишем коротенькое стихотворение. В другой половине слайда пишем пословицы и загадки. Причем необязательно писать ответ на загадку, ведь он и так очевиден. А теперь приведу примеры пословиц, содержащих в себе числа от 1 до 10. YurahaU 3 года назад Вот тоже сыну первокласснику задали дома сделать проект на тему “Математика вокруг нас. Числа в загадках пословицах”. Очередное задание “для родителей”! А что, родителям то нечем заниматься, так пусть проекты делают для школы, которые потом “никому не нужны”… Не долго думаю “состряпал” в Word’e таблицу, вставил рисунки в виде цифр и написал к каждой загадки, пословицы и поговорки: Если вам понравилось моё “творение”, то вот вам ссылка, по которой можно скачать Word’овский документ, изменить по собственному усмотрению и проект готов! Дени эль 4 года назад Можно сделать проект на тему “Математика вокруг нас. Числа в загадках пословицах” в виде презентации: всего 9 слайдов цифра 9 фото кошки цифра 7 рисунок ребенка или рисунок ножницы цифра 5 рисунок телеги цифра 4 цифра 3 рисунок плаксы цифра 2 цифра 1 Знаете ответ? |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ПЕРМСКОГО КРАЯ
Государственное бюджетное профессиональное образовательное учреждение
«Горнозаводский политехнический техникум»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
по математике
О, Великие математики!
Обучающийся: Агафонов Данил Константинович
Специальность: 15.02.08
Технология машиностроения
Группа: ТМ – 108
Руководитель: Малкова Венера Александровна
Горнозаводск 2018
Содержание
Введение 3
Глава 1 Великие математики 5
1.1Биография математиков 5
1.2 Математические открытия 18
Глава 2 Создание стенда «О, Великие математики!» 22
2.1 Викторина «Великие математики и математические открытия» 22
2.2 Обработка результатов викторины 24
2.3.Создание стенда 26
Заключение 28
Приложение 1 30
Введение
Актуальность исследования
Математика появилась одновременно со стремлением человека изучить мир вокруг себя. Изначально она входила в состав философии – матери наук – и не была выделена как отдельная дисциплина наравне с той же астрономией, физикой. Однако с течением времени ситуация изменилась.
Знаний у людей накапливалось все больше, в итоге произошло разделение точных и естественных наук. После официального “рождения” каждая из них пошла своим путем, развиваясь, укрепляя фундамент теорией, подкрепленной практикой. Казалось бы, какая практика может быть у математики, самой абстрактной из наук? Этот предмет способен описать абсолютно все процессы, происходящие на нашей планете и за ее пределами, а знание природы явления позволяет делать выводы и строить прогнозы. Отсюда можно сделать вывод, что все науки связаны между собой, наиболее очевидна эта зависимость между математикой и физикой. Поэтому в большинстве случаев великие математики и физики составляют одну группу ученых.
Проблема: Изучая математику, мы очень часто сталкиваемся с именами великих ученых, но в учебнике очень мало конкретной информации о них
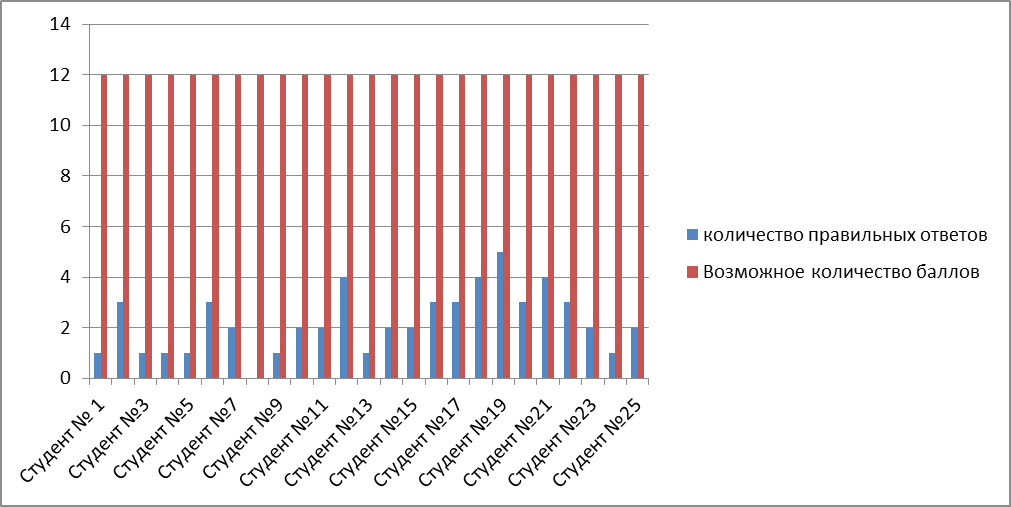
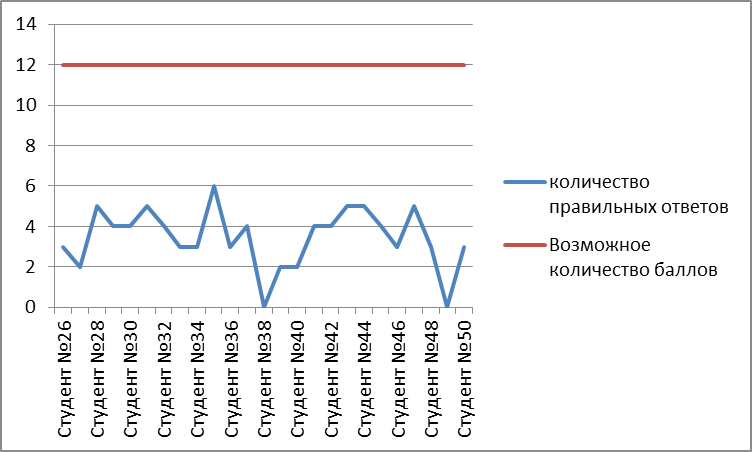
Цель исследования: изучение биографии некоторых великих математиков и знакомство с самыми важными их открытиями.
Гипотеза: студенты техникума мало знают о великих математиках и их открытиях.
Задачи исследования:
1. Ознакомиться с информацией о великих математиках, их биографии и открытиях в науке.
2. Составить презентацию, содержащую портреты математиков и некоторые факты из жизни и деятельности.
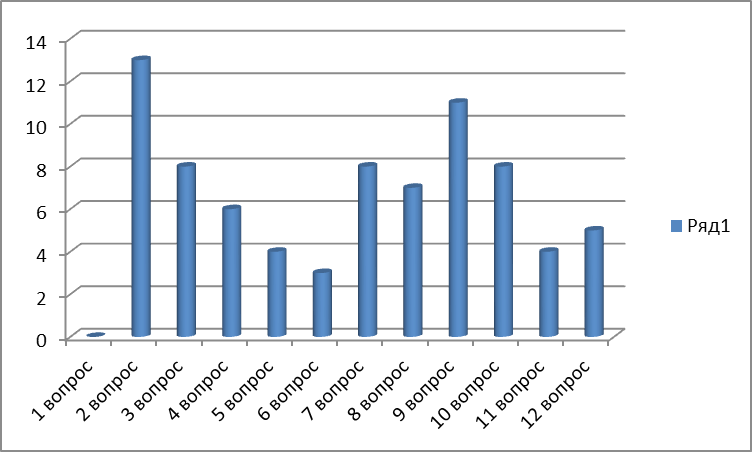
3. Провести анкетирование студентов (викторину) с целью выявления знаний о великих математиках, сделавших открытия в математике.
4. Сделать выводы о результатах анкетирования
5. Создать информационный стенд о великих математиках, их биографии и открытиях в науке.
Глава 1 Великие математики 1.1Биография математиков Эварист Галуа (1811-1832) Французский математик.

В возрасте 12 лет Эварист поступил в Королевский коллеж Луи-ле-Гран. В годы учёбы Галуа стал свидетелем попытки заговора учеников, придерживающихся республиканских взглядов, против руководства коллежа из-за слухов о возможном преобразовании коллежа в иезуитское училище (коим он был до революции). Заговор был раскрыт, и более ста учащихся коллежа были с позором исключен.
В 15 лет он открыл для себя математику и с тех пор, по словам одного изпреподавателей, «был одержим демоном математики». Ему было неполных 18 лет, когда была опубликована его первая работа.
Несмотря на свою молодость, успел сделать много открытий в математике, но, к сожалению, был убит на дуэли в 20 лет.
Открытия в математике:
Теория Галуа — раздел алгебры, изучающий симметрии корней многочленов. Симметрии описываются в терминах группы перестановок корней многочлена.
В 17 лет опубликовал свою первую работу в журнале «Annales de Gergonne».
Высказывание:
Математика! Только она принесла в мою жизнь минуты счастья, которое достается очень немногим.
Э. Галуа

Пьер Ферма(1601-1665)
Французский математик.
Биография: Пьер Ферма родился 17 августа 1601 года в гасконском городке Бомон-де-Ломань (Beaumont-de-Lomagne, Франция). Его отец, Доминик Ферма, был зажиточным торговцем-кожевником, вторым городским консулом. В семье, кроме Пьера, были ещё один сын и две дочери. Ферма получил юридическое образование — сначала в Тулузе (1620—1625), а затем в Бордо и Орлеане (1625—1631).
В колледже Пьер приобрел хорошее знание языков: латинского, греческого, испанского, итальянского. Ферма славился как тонкий знаток античности. Крупную заслугу Ферма перед наукой видят, обыкновенно, во введении им бесконечно малой величины в аналитическую геометрию.
Пьер де Ферма умер 12 января 1665 года в городе Кастр, во время выездной сессии суда
Открытия в математике
Создание теории чисел.
Сформулировал теорему о возможности представления произвольного числа суммой не более четырёх квадратов
Великая теорема – Для любого натурального числа n 2 уравнение не имеет натуральных решений a, b и c.
Высказывание: Природа всегда действует наиболее короткими путями.
П. Ферма
И
Британский физик
Биография: Исаак Ньютон родился в деревне Вулсторп (англ. Woolsthorpe, графство Линкольншир) в канун гражданской войны.
1661 году Ньютон успешно окончил школу и отправился продолжать образование в Кембриджский университет. В конце 1664 года Ньютон стал бакалавром, а в 1668 году стал магистром. Ньютон стал знаменит и в январе 1672 года был избран членом Королевского общества. 28 апреля 1686 года первый том «Математических начал» был представлен Королевскому обществу. Все три тома вышли в 1687 году. С 1699 года он стал управляющим («мастером») Монетного двора. В декабре 1701 года он официально ушёл в отставку со всех своих постов в Кембридже.
Исаак Ньютон умер в 1727 году во время эпидемии чумы.
Открытия в математике:
Универсальная арифметика
Теории бесконечных рядов
Анализа бесконечно малых
Высказывание: Опыт – это не то, что происходит с вами; это то, что вы делаете с тем, что происходит с вами.
И. Ньютон.
Н
Русский математик(1792-1856)
Биография: Н. И. Лобачевский родился в Нижнем Новгороде. Его родителями были Иван Максимович Лобачевский (чиновник в геодезическом департаменте) и Прасковья Александровна Лобачевская
Большое влияние во время обучения в университете на Лобачевского оказал Мартин Фёдорович Бартельс — друг и учитель великого немецкого математика Карла Фридриха Гаусса. По окончании университета Лобачевский получил степень магистра по физике и математике с отличием (1811) и был оставлен при университете. В 1814 году стал адъюнктом, спустя 2 года — экстраординарным, и в 1822 году — ординарным профессором.
Открытия в математике:
Лобачевский пришел к выводу о возможности создания новой, непротиворечивой геометрии, которую назвал «воображаемой геометрией».
Николай Иванович изменил существующую аксиому на другую. Она звучит так: “через точку, не лежащую на прямой, может проходить множество прямых параллельных с первой”.
Он разработал метод приближенного решения уравнений.
Также Лобачевский дал понятие о признаке сходимости рядов и о непрерывной функции.
Высказывание: Ученый должен идти по непроторенным путям, несмотря на препятствия.
Н. И. Лобачевский.
К
Немецкий математик
Биография: Гаусс Карл Фридрих – Иоганн Фридрих Карл Гаусс родился 30 апреля 1777г. Едва трех лет от роду он уже умел считать и выполнять элементарные вычисления. Однажды, при расчетах своего отца, который был водопроводным мастером, его трехлетний сын заметил ошибку в вычислениях. Расчет был проверен, и число, указанное мальчиком было верно. В 1784г. Карл пошел в школу. Учитель очень заинтересовался маленьким Гауссом и в 1786г. он получил из Гамбурга специальный арифметический текст. Карл покинул родительский дом в 1788г., когда поступил в школу следующей ступени. Гаусс не терял в новой школе времени даром: он хорошо выучил латынь, необходимую для дальнейшей учебы и карьеры. В 1791г. Гаусс, в качестве одаренного молодого горожанина, был представлен государю.
Открытия в математике:
Ему не было еще девятнадцати – доказательство того, что можно построить правильный 17 – угольник циркулем и линейкой.
Метод Гаусса — классический метод решения системы линейных алгебраических.
Он открыл характеристику поверхности (гауссову кривизну), которая не изменяется при изгибаниях, тем самым заложив основы римановой геометрии.
Гаусс доказал, основную теорему теории поверхностей.
П
Немецкий математик
Биография: Биография Дирихле родился в вестфальском городе Дюрене в семье почтмейстера. Его предки были выходцами из бельгийского городка Ришле, этим обусловлено происхождение необычной для немецкого языка фамилии. Часть фамилии «Лежён» имеет аналогичное происхождение — деда называли «молодым человеком из Ришле ». В 12 лет Дирихле начал учиться в гимназии в Бонне, спустя два года — в иезуитской гимназии в Кёльне, где в числе прочих преподавателей его учил Георг Ом. С 1822 по 1827 г. жил в качестве домашнего учителя в Париже, где вращался в кругу Фурье.
Он умер в Гёттингене, через несколько месяцев после смерти своей жены Ребекки.
Открытия в математике:
Он ввёл такое понятие, как «условная сходимость» и определил её признак.
Доказал теорему о прогрессии.
Значительно развил теорию потенциала.
Внёсший существенный вклад в математический анализ, теорию функций и теорию чисел.
Доказал теорему о существовании бесконечно большого числа простых чисел во всякой арифметической прогрессии из целых чисел, первый член и разность которой числа взаимно простые.
Е
Греческий математик
Биография: О жизни этого ученого почти ничего не известно. До нас дошли только отдельные легенды о нем.
Первый комментатор «Начал» Прокл (V век нашей эры) не мог указать, где и когда родился и умер Евклид. По Проклу, «этот ученый муж» жил в эпоху царствования Птолемея I. Некоторые биографические данные сохранились на страницах арабской рукописи XII века: «Евклид, сын Наукрата, известный под именем «Геометра», ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира».
Его называли ”Отец Геометрии”
Открытия в математике:
Алгоритм Евклида
Главный труд Евклида – “Начала” (по-другому “Элементы”). Все книги Евклида основываются на аксиомах – утверждениях, не требующих доказательств.
Одиннадцатая аксиома – Если дана прямая и точка не лежащая на ней, то можно провести только одну прямую, проходящую через точку и не пересекающуюся с данной прямой
Евклид первый начал изучать свойства простых чисел – и доказал, что их множество бесконечно.
Евклид сформулировал закон прямолинейного распространения света и закон отражения, а также теорему о делении с остатком.
Высказывание: Если теорему так и не смогли доказать, она становится аксиомой.
Евклид.
Н
Норвежский математик
Биография: Рождение и учёба родился в семье пастора. Детство Абеля было омрачено слабым здоровьем, а также пьянством и постоянными раздорами его родителей. В школе, благодаря учителю Берту Михаэлю Хольмбоэ, увлёкся математикой. В 1821 году Абель поступил в университет Христиании (ныне Осло), где преподаватели, ознакомившись с его ранними работами, решили установить ему стипендию из личных средств, «дабы сохранить для науки это редкое дарование». Чтобы облегчить жизнь матери, Нильс Хенрик взял одного из братьев к себе и стал подрабатывать репетиторством.
Две болезни на ложились друг на друга, и в 1829 году Нильс Хенрик Абель умер
Открытия в математике:
Абель закончил блестящее исследование древней проблемы: доказал невозможность решить в общем виде (в радикалах) уравнение 5-й степени.
В алгебре Абель нашёл необходимое условие для того, чтобы корень уравнения выражался «в радикалах» через коэффициенты этого уравнения.
Он первый определил эллиптические функции как функции, обратные эллиптическим интегралам, распространил их определения на общий комплексный случай и глубоко исследовал их свойства.
Высказывание: Несомненно, ты считаешь, что плохо растрачивать столько времени на путешествие, но я не думаю, что это можно назвать словом “растрачивать”
Н. Х. Абель

Готфрид Вильгельм Лейбниц(1646-1716)
Немецкий философ
Биография: Отфрид Вильгельм родился в семье профессора лейпцигского университета Фридриха Лейбница и Катерины Шмюк. Когда мальчику было 8 лет, его отец умер, оставив после себя большую личную библиотеку. Свободный до со теки — это сокровищницы всех богатств человеческого духа туп к книгам и врождённый талант позволили молодому Лейбницу уже к 12 годам самостоятельно изучить латынь и взяться за изучение греческого языка. В 15-летнем возрасте Готфрид сам поступил в тот же Лейпцигский университет, где когда-то работал его отец. Спустя 2 года переходит в Йенский университет, где изучает математику.
4ноября 1716 г., вследствие ухудшения здоровья, Готфрид В. Лейбниц умирает.
Открытия в математики:
Анализ — дифференциальное и интегральное исчисление.
Он обосновал необходимость регулярно мерить у больных температуру тела.
Новый метод максимумов и минимумов
Используя геометрическое истолкование отношения dy/dx, он кратко разъясняет признаки возрастания и убывания, максимума и минимума, выпуклости и вогнутости, а также точки перегиба.
П
Греческий философ
Биография: Его отцом был некий Мнесарх из Самоса, человек благородного происхождения и образования. Родился на острове Самос около 580 года до н. э. (по другим источникам, в 586 до н. э.). Пифагор объездил весь свет и собрал свою философию из различных систем, к которым имел доступ. Так, он изучал эзотерические науки у брахманов Индии, астрономию и астрологию в Халдее и Египте. Основал общество в Кротоне, италийском городе, находившемся в тесных сношениях с Самосом. Он был ученее всех своих современников Биография Пифагора Пифагор жил в Кротоне, но несомненно, что умер он в Метапонте, куда переселился вследствие враждебного отношения кротонцев к его союзу.
Открытия в математики:
В геометрии: знаменитая и любимая всеми теорема Пифагора, а также построение отдельных многогранников и многоугольников.
Высказывание: Лесть подобна оружию, нарисованному на картине: она доставляет приятность, а пользы никакой. Пифагор
С
Русский математик
Биография: Родилась 15 января 1850 года в Москве в имение Палибино Отец: Василий Васильевич Корвин-Круковский, генерал Мать: Елизавета Федоровна Корвина-Круковская, человек искусства.
В течении двух с половиной лет она усвоила всю арифметику, затем был изучен обширный курс алгебры и на шестом году обучения была освоена геометрия Софья хотела поступить в университет, но доступ женщинам во все российские университеты был закрыт. Высшее образование она могла получить только за границей.
Открытия в математике:
Она открыла третий классический случай разрешимости задачи о вращении твёрдого тела вокруг неподвижной точки, которую начали Леонард Эйлер и Ж. Л. Лагранж.
Она доказала существование аналитического (голоморфного) решения задачи Коши для систем дифференциальных уравнений с частными производными, исследовала задачу Лапласа о равновесии кольца Сатурна, получила второе приближение.
Решила задачу о приведении некоторого класса абелевых интегралов третьего ранга к эллиптическим интегралам.
Высказывание: Стоит мне только коснуться математики, как я опять забуду всё на свете. С. Ковалевская
Ф
Греческий философ
Биография: Сообщается, что Фалес был торговцем и много путешествовал. Некоторое время жил в Египте, в Фивах и Мемфисе, где учился у жрецов, изучал причины наводнений, продемонстрировал способ измерения высоты пирамид. Считается, что именно он «привез» геометрию из Египта и познакомил с ней греков. Его деятельность привлекла последователей и учеников, которые образовали милетскую (ионийскую) школу. Предание рисует Фалеса не только собственно философом и учёным, но также «тонким дипломатом и мудрым политиком»;. Сообщается, что Фалес был торговцем и много путешествовал. Некоторое время жил в Египте, в Фивах и Мемфисе, где учился у жрецов, изучал причины наводнений, продемонстрировал способ измерения высоты пирамид. Считается, что именно он «привез» геометрию из Египта и познакомил с ней греков. Его деятельность привлекла последователей и учеников, которые образовали милетскую (ионийскую) школу.
Открытия в математике:
Ему принадлежит открытие следующих теорем:
Вертикальные углы равны.
В равнобедренном треугольнике углы, лежащие при основании, равны.
Теорема о равенстве двух треугольников по стороне и двум прилежащим к ней углам.
Высказывание: Блаженство тела состоит в здоровье, блаженство ума — в знании.
Ф. Милетский
К
(1903-1987)
Советский математик
Биография: Биография Ранние годы Андрей Николаевич Колмогоров родился 12 апреля (25 апреля по новому стилю) 1903 года в Тамбове, где его мать задержалась по пути из Крыма домой в Ярославль. Андрей Николаевич Колмогоров воспитывался в Ярославле 3 сёстрами матери, одна из них, Вера Яковлевна Колмогорова, официально усыновила Андрея и в 1910 году переехала с ним в Москву для определения в гимназию. Тётушки Андрея в своём доме организовали школу для детей разного возраста, которые жили поблизости, занимались с ними, для ребят издавался рукописный журнал «Весенние ласточки». В нём публиковались творческие работы учеников — рисунки, стихи, рассказы. В нём же появлялись и «научные работы» Андрея — придуманные им арифметические задачи. Здесь же мальчик опубликовал в пять лет свою первую работу по математике.
Открытия в математике:
Исследования и открытия в области:
Метрическая теория функций.
Дескриптивная теория множеств.
Математическая логика.
Функциональный анализ
Дифференциальные уравнения.
Теория приближений.
Высказывание: Я всегда считал, что истина — главное.
А.Н.Колмогоров
1.2 Математические открытия
В отличие от других наук, математика, как представительница чистого разума, развивается поступательно, вне зависимости от увлечений человечества на том или ином историческом промежутке времени, от революций и катаклизмов общества. Иногда математики любят ставить проблемные вопросы, на решение которых уходят столетия.
Теорема есть некое математическое утверждение, правильность которого требует построения логической цепочки доказательств, основанной на использовании законов формальной логики с привлечением аксиом – истин, принимаемых как само собой разумеющееся, очевидное и доказательств не требующее. Особого интереса заслуживают теоремы, доказательства которых вызывают сомнение или отсутствуют. Такое бывает у непререкаемых авторитетов. Ландау, например, на лекции по теоретической физике в спешке мог пропустить звено логической цепочки «как очевидное», тогда как другим теоретикам «очевидное» могло не даваться многие годы, вызывая в голове ступор.
Юрист по профессии и математик по увлечению (в наше время у юристов подобные увлечения – нонсенс) Пьер Ферма (1601-1665) в письме другу, написанном в 1636 году, выдвинул любопытное утверждение из теории чисел, впоследствии получившее название Великой теоремы Ферма. На полях он оставил следующее сопровождение: «Я располагаю изумительным доказательством, но оно слишком велико для размещения на полях». То есть великий ученый прямо заявил, что доказал свою теорему.
Потомкам пришлось 360 лет разбираться с тем, действительно ли Ферма доказал, или просто соврал. Благо еще удалось бы показать, что теорема неверна, найти один единственный опровергающий пример, но, несмотря на все усилия, сделать этого не удавалось. И формулировка то проще некуда: уравнение Xn+Yn=Zn не имеет целочисленных решений при n2. При n=2 эта теорема (так называемая теорема Пифагора, предложенная ненавистником бобов более двух тысячелетий тому назад) имеет бесконечное множество решений.
История доказательств Великой теоремы трагична и полна драматизма. Складывается впечатление, будто ехидный Ферма бросил вызов потомкам (открыл ящик Пандоры), а когда речь идет о деле чести, можно представить, как болезненно переживали математики-профессионалы подобную «легкомысленность» в последующие столетия. Можно без преувеличения сказать, что у математиков начался массовый психоз: «почему я не могу доказать то, что доказал Ферма черт знает в какие примитивные времена?» Увлечение превращалось в цель и смысл жизни. Некоторые в буквальном смысле свихнулись на этом.
Перед теоремой пасовали даже такие гиганты мысли, как Гаусс, Леонард Эйлер, доказавший теорему для n=3 и 4, Лежандр (n=5), Дирихле (n=6)…
После того, как в 1907 году состоятельный немецкий любитель математики, наподобие Нобеля, завещал 100 тысяч марок тому, кто докажет Великую теорему, и вовсе начался массовый ажиотаж. Выскочек без образования презрительно называли ферматистами, а говорить о теореме Ферма в высшем математическом свете стало признаком дурного тона, вроде как нецензурно выругаться. Однако в тиши кабинетов и великие прикладывались к «запретному зелью». Мало-помалу появились доказательства для степени nВ эти смутные времена в Японии жил математик Ютака Танияма. Когда ему исполнилось 28 лет, он выдвинул гипотезу (впоследствии получившую название гипотезы Танияма-Шимура-Вейла), что каждой эллиптической кривой соответствует определенная модулярная форма. Гипотеза, казалось, не имеет отношения к теории чисел, она соединяла понятия двумерных и четырехмерных форм: уравнения двух абсолютно разных математических объектов можно разложить в одинаковые математические ряды.
После выступления Танияма на международном математическом конгрессе, состоявшемся в Токио в1955 году, и демонстрации соответствия нескольких эллиптических кривых модулярным формам, многие увидели в этом не более чем забавное совпадение. Через три года Танияма покончил жизнь самоубийством, и о гипотезе забыли.
А в 1985 году произошла революция – немец Герхард Фрей опубликовал следующее заявление: «Если доказать гипотезу Танияма, тем самым будет доказана и Великая теорема Ферма». Заявление Фрея через год удалось строго доказать профессору калифорнийского университета Риббету. Поскольку, однако, у математиков уже сложилась аллергия на теорему Ферма, возиться с доказательством гипотезы Танияма, из которой следует верность теоремы Ферма, из соображений сложности не хотелось. Чем гипотеза Танияма должна быть проще теоремы Ферма?
Поток гениев, однако, не остановить. Как настоящий ученый, английский профессор математики Эндрю Уайлс, зная историю, не обольщался результативностью своих изысканий в области доказательства гипотезы Танияма. Позже он признавался, что работу над Великой теоремой скрывал даже от жены. И все-таки 23 июня 1993 года он набрался храбрости, надел на голову петлю и на математической конференции по теории чисел в Кембридже громогласно объявил о достижении цели.
Такой наглости никто из присутствующих не ожидал от не очень известного математика. Тотчас подключилась пресса. Состоялась публичное доказательство теоремы Танияма, а следовательно и теоремы Ферма. Ошибок никто не обнаружил. Следовательно, масштабное событие произошло: Великая теорема доказана. Но, по закону подлости, за два дня до публикации, хитрый коллега Уайлса Кац, заметил, что «один фрагмент рассуждений опирается на систему Эйлера, на самом деле таковой не являясь». Это была катастрофа.
Бедный Уайлс понял, что проиграл, и ему оставалось либо повеситься, чтобы не остаться навсегда осмеянным потомками, либо бросить занятия математикой, сменить имя, сделать пластическую операцию и уехать на край земли, где математические проблемы людям, как говорится, по барабану. Уайлс впал в депрессию: как смотреть коллегам в глаза? Он отказывался от пищи и здоровье его ухудшалось.
Но в сентябре 1994 года, размышляя над узким местом доказательства Уайлса, его коллега Тейлор из Оксфорда неожиданно обнаружил, что если заменить систему Эйлера на теорию Ивасава, то все сойдется. Около года математики изучали непротиворечивость доказательства Уайлса с замечанием Тейлора, и летом 1995 года в ведущем математическом журнале «Анналы математики» было опубликовано доказательство гипотезы Танияма, занявшее целый номер.
Итак, в 1995 году мир признал, что Эндрю Уайлс доказал Великую теорему Ферма. Уайлс оказался тем счастливчиком, которому удалось нанести последний нокаутирующий удар по проблеме. Но не следует забывать, что за ним стоят все великие математики предыдущих столетий. Если кому-то покажется незначительность этого события, достаточно вспомнить, что математика стоит в авангарде всех научных достижений, а решение казалось бы «легкомысленной задачи» порождает целые направления в развитии математики. Леонардо да Винчи однажды заметил, что «наукой можно назвать только математически подтвержденное учение».
Так все-таки доказал Ферма свою теорему, или это была гипотеза? Возможно, ему показалось, что доказал, но на самом деле ошибся. Сознательно соврал, упоенный красотой открытия? И этого исключить нельзя. Все же большинство математиков склоняются к мысли, что во времена Ферма нельзя было придумать альтернативное доказательство, как нельзя в эпоху дилижансов и рыцарских турниров изобрести атомную бомбу.
Ферма не доказал, но гениально угадал!
С точки зрения морали, из этой очень поучительной истории следует хотя бы тот маленький вывод, что, внимая пламенной риторике ведущих авторитетов в своей области, каждый имеет право усомниться в справедливости сладкоречивых слов говорящего.
Глава 2 Создание стенда «О, Великие математики!» 2.1 Викторина «Великие математики и математические открытия»
Я изучил биографии Великих математиков и историю математических открытий. После этого я составил вопросы викторины по этой теме.
Викторина для студентов ГБПОУ «ГПТ»
Автор-составитель: Студент группы ТМ-108 Агафонов Д.К.
Вопросы:
-
Главный труд этого математика «Математические начала натуральной философии»
a) Пифагор
б)Архимед
в)Ньютон
г)Гаусс -
По основной профессии он был юристом, а математикой занимался на досуге
а)Евклид
б)Ньютон
в)Вейерштрасс
г) Ферма -
Впервые вычислил число и доказал, что оно одинаково для любого круга
а) Пифагор
б) Архимед
в) Евклид
г) Гаусс -
Его считали математиком-универсалом, так как он сделал множество открытий в самых разных областях математики
а) Архимед
б) Евклид
в) Пифагор
г) Чебышев -
Кому принадлежат слова « Для того, чтобы быть настоящим математиком, нужно быть поэтом в душе» ?
а) Колмогоров
б) Ковалевская
в) Чебышев
г) Гаусс
-
Ввёл многие понятия и символы, употребляемые в математике и сейчас
а) Лейбниц
б) Лобачевский
в) Гаусс
г) Колмогоров -
Имел титул одного из семи мудрецов Греции
а) Фалес
б) Архимед
в) Пифагор
г) Гаусс -
Основатель научных школ по теории вероятностей и теории функций
а) Лобачевский
б) Фалес
в) Колмогоров
г) Чебышев -
Один из создателей математического анализа, проективной геометрии
а) Чебышев
б) Паскаль
в) Колмогоров
г) Гаусс -
Его «великая теорема» – одна из самых популярных теорем математики
а) Гаусс
б) Ферма
в) Ньютон
г) Декарт -
Написал большой труд по геометрии « Начала» (13 книг)
а) Архимед
б) Евклид
в) Чебышев
г) Гаусс -
Создал новую геометрическую систему, известную под названием геометрии … Его называли «Коперником геометрии»
а) Вейерштрасс
б) Лобачевский
в) Евклид
г) Ньютон.
2.2 Обработка результатов викторины
Собрав ответы студентов на вопросы викторины, я обработал данные и получил следующий результат: количество набранных баллов и точность ответа на поставленный вопрос.
Количество набранных баллов
За каждый правильный ответ можно получить 1 балл. Максимальное количество баллов – 12. В исследовании принимали участие все группы 2 курса и группа ТМ – 108 (1 курс).
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
1 |
3 |
1 |
1 |
1 |
3 |
2 |
0 |
1 |
2 |
2 |
4 |
1 |
2 |
2 |
3 |
3 |
4 |
5 |
3 |
4 |
3 |
2 |
1 |
2 |
|
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
3 |
2 |
5 |
4 |
4 |
5 |
4 |
3 |
3 |
6 |
3 |
4 |
0 |
2 |
2 |
4 |
4 |
5 |
5 |
4 |
3 |
5 |
3 |
0 |
Самое большое количество баллов набрали студенты групп ТМ – 108 и ТП – 210 (6 баллов)
Правильные ответы на вопросы
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
0 |
13 |
8 |
6 |
4 |
3 |
8 |
7 |
11 |
8 |
4 |
5 |
Как показал результат викторины, самый сложный вопрос для студентов нашего техникума – 1 вопрос: Главный труд этого математика «Математические начала натуральной философии». На него никто не ответил правильно. На вопрос №2: По основной профессии он был юристом, а математикой занимался на досуге. –
ответили правильно 13 студентов.
2.3.Создание стенда
Проанализировав результаты викторины, мы решили создать стенд в кабинет математики.
Для начала мы определились с количеством и Именами математиков, которые будут на нашем стенде. Выбор наш пал на ученых, которые внесли наибольший вклад в создание алгебры и геометрии школьного курса (10-11 класс). У нас получилось 19 математиков.
Теперь я изучил и поработал с информацией об этих ученых. Я оставил краткую биографию, портрет, открытие и высказывание математика.
Следующим этапом стало создание самого стенда, подходящего по размерам, дизайну. На стенде нужно разместить 19 файлов формата А4. Я измерил длину и ширину этого файла. Я решил расположить их в форме прямоугольника 4 х 5.
Недостающий файл на стенде, я компенсирую эпиграфом и актуальностью моей темы.
Для стенда я взял термоплиту, оклеил ее клейкой пленкой, края спрятал под пластиковые уголки. Наклеил кармашки и вставил в них информацию о выбранных Великих математиках. Также прикрутил уголки для того, чтобы стенд можно было повесить на стену.
Заключение
Жизнь великих учёных так тесно переплелась с наукой, что уже невозможно представить математику без Пифагора, а Лобачевского – без математики. Но всё же мы надеемся, что факты из их биографий составят более полные образы учёных, которым ничто человеческое не чуждо.
Математика – уникальная наука. Она способствует выработке адекватного представления и понимания знания. “Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства” – писал Леонардо да Винчи.
В ходе своего исследования, я достиг поставленной цели. Все поставленные задачи я выполнил, а именно:
1. Ознакомился с информацией о великих математиках, их биографии и открытиях в науке
3. Провел анкетирование студентов (викторину) с целью выявления знаний о великих ученых, сделавших открытия в математике
4. Сделал выводы о результатах анкетирования, построил таблицы и графики
5. Создал информационный стенд о великих математиках, их биографии и открытиях в науке.
Список использованных источников
-
http://www.fizmatolimp.ru/biografii.html
-
http://obrazovaka.ru/category/matematiki
-
http://fb.ru/article/170806/velikie-matematiki-i-ih-otkryitiya
-
https://math-city.nethouse.ru/articles
Приложение 1
Ответы к викторине
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
в |
г |
б |
г |
б |
а |
а |
в |
б |
б |
б |
б |
30