Как правильно составить пропорцию по числам. Составить пропорцию
Для решения большинства задач в математике средней школы необходимо знание по составлению пропорций. Это несложное умение поможет не только выполнять сложные упражнения из учебника, но и углубиться в саму суть математической науки. Как составить пропорцию? Сейчас разберем.
Самым простым примером является задача, где известны три параметра, а четвертый необходимо найти. Пропорции бывают, конечно, разные, но часто требуется найти по процентам какое-нибудь число. Например, всего у мальчика было десять яблок. Четвертую часть он подарил своей маме. Сколько осталось яблок у мальчика? Это самый простой пример, который позволит составить пропорцию. Главное это сделать. Изначально было десять яблок. Пусть это 100%. Это мы обозначили все его яблоки. Он отдал одну четвертую часть. 1/4=25/100. Значит, у него осталось: 100% (было изначально) – 25% (он отдал) = 75%. Эта цифра показывает процентное отношение количества оставшихся фруктов к количеству имевшихся сначала. Теперь у нас есть три числа, по которым уже можно решить пропорцию. 10 яблок – 100%, х
яблок – 75%, где х – искомое количество фруктов. Как составить пропорцию? Необходимо понимать, что это такое. Математически это выглядит так. Знак равно поставлен для вашего понимания.

10 яблок = 100%;
x яблок = 75%.
Оказывается, что 10/x = 100%/75. Это и есть основное свойство пропорций. Ведь чем больше x, тем больше процентов составляет это число от исходного. Решаем эту пропорцию и получаем, что x=7,5 яблок. Почему мальчик решил отдать нецелое количество, нам неизвестно. Теперь вы знаете, как составить пропорцию. Главное, найти два соотношения, в одном из которых есть искомое неизвестное.
Решение пропорции часто сводится к простому умножению, а потом к делению. В школах детям не объясняют, почему это именно так. Хотя важно понимать, что пропорциональные отношения есть математическая классика, сама суть науки. Для решения пропорций необходимо уметь обращаться с дробями. Например, часто приходится переводить проценты в обыкновенные дроби. То есть запись 95% не подойдет. А если сразу написать 95/100, то можно провести солидные сокращения, не начиная основного подсчета. Сразу стоит сказать, что если ваша пропорция получилась с двумя неизвестными, то ее не решить. Никакой профессор вам здесь не поможет. А ваша задача, скорее всего, имеет более сложный алгоритм правильных действий.

Рассмотрим еще один пример, где нет процентов. Автомобилист купил 5 литров бензина за 150 рублей. Он подумал о том, сколько он бы заплатил за 30 литров топлива. Для решения этой задачи обозначим за x искомое количество денег. Можете самостоятельно решить эту задачу и потом проверить ответ. Если вы еще не поняли, как составить пропорцию, то смотрите. 5 литров бензина – это 150 рублей. Как и в первом примере, запишем 5л – 150р. Теперь найдем третье число. Конечно, это 30 литров. Согласитесь, что пара 30 л – х рублей уместна в данной ситуации. Перейдем на математический язык.
5 литров – 150 рублей;
30 литров – х рублей;
Решаем эту пропорцию:
x = 900 рублей.
Вот и решили. В своей задаче не забудьте проверить на адекватность ответ. Бывает, что при неправильном решении автомобили достигают нереальных скоростей в 5000 километров в час и так далее. Теперь вы знаете, как составить пропорцию. Также вы сможете ее решить. Как видите, в этом нет ничего сложного.
§ 125. Понятие о пропорции.
Пропорцией называется равенство двух отношений. Вот примеры равенств, называемых пропорциями:
Примечание. Наименования величин в пропорциях не указаны.
Пропорции принято читать следующим образом: 2 так относится к 1 (единице), как 10 относится к 5 (первая пропорция). Можно читать иначе, например: 2 во столько раз больше 1, во сколько раз 10 больше 5. Третью пропорцию можно прочесть так: – 0,5 во столько раз меньше 2, во сколько раз 0,75 меньше 3.
Числа, входящие в пропорцию, называются членами пропорции
. Значит, пропорция состоит из четырёх членов. Первый и последний члены, т. е. члены, стоящие по краям, называются крайними
, а члены пропорции, находящиеся в середине, называются средними
членами. Значит, в первой пропорции числа 2 и 5 будут крайними членами, а числа 1 и 10 – средними членами пропорции.
§ 126. Основное свойство пропорции.
Рассмотрим пропорцию:
Перемножим отдельно её крайние и средние члены. Произведение крайних 6 4 = 24, произведение средних 3 8 = 24.
Рассмотрим другую пропорцию: 10: 5 = 12: 6. Перемножим и здесь отдельно крайние и средние члены.
Произведение крайних 10 6 = 60, произведение средних 5 12 = 60.
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних её членов.
В общем виде основное свойство пропорции записывается так: ad = bc
.
Проверим его на нескольких пропорциях:
1) 12: 4 = 30: 10.
Пропорция эта верна, так как равны отношения, из которых она составлена. Вместе с тем, взяв произведение крайних членов пропорции (12 10) и произведение средних её членов (4 30), мы увидим, что они равны между собой, т. е.
12 10 = 4 30.
2) 1 / 2: 1 / 48 = 20: 5 / 6
Пропорция верна, в чём легко убедиться, упростив первое и второе отношения. Основное свойство пропорции примет вид:
1 / 2 5 / 6 = 1 / 48 20
Нетрудно убедиться в том, что если мы напишем такое равенство, у которого в левой части стоит произведение двух каких-нибудь чисел, а в правой части произведение двух других чисел, то из этих четырёх чисел можно составить пропорцию.
Пусть у нас имеется равенство, в которое входят четыре числа, попарно перемноженные:
эти четыре числа могут быть членами пропорции, которую нетрудно написать, если принять первое произведение за произведение крайних членов, а второе – за произведение средних. Изданного равенства можно составить, например, такую пропорцию:
Вообще, из равенства ad = bc
можно получить следующие пропорции:
Проделайте самостоятельно следующее упражнение. Имея произведение двух пар чисел, напишите пропорцию, соответствующую каждому равенству:
а) 1 6 = 2 3;
б) 2 15 = б 5.
§ 127. Вычисление неизвестных членов пропорции.
Основное свойство пропорции позволяет вычислить любой из членов пропорции, если он неизвестен. Возьмём пропорцию:
х
: 4 = 15: 3.
В этой пропорции неизвестен один крайний член. Мы знаем, что во всякой пропорции произведение крайних членов равно произведению средних членов. На этом основании мы можем написать:
x
3 = 4 15.
После умножения 4 на 15 мы можем переписать это равенство так:
х
3 = 60.
Рассмотрим это равенство. В нём первый сомножитель неизвестен, второй сомножитель известен и произведение известно. Мы знаем, что для нахождения неизвестного сомножителя достаточно произведение разделить на другой (известный) сомножитель. Тогда получится:
х
= 60: 3, или х
= 20.
Проверим найденный результат подстановкой числа 20 вместо х
в данную пропорцию:
Пропорция верна.
Подумаем, какие действия нам пришлось выполнить для вычисления неизвестного крайнего члена пропорции. Из четырёх членов пропорции нам был неизвестен только один крайний; два средних и второй крайний были известны. Для нахождения крайнего члена пропорции мы сначала перемножили средние члены (4 и 15), а затем найденное произведение разделили на известный крайний член. Сейчас мы покажем, что действия не изменились бы, если бы искомый крайний член пропорции стоял не на первом месте, а на последнем. Возьмём пропорцию:
70: 10 = 21: х
.
Запишем основное свойство пропорции: 70 х
= 10 21.
Перемножив числа 10 и 21, перепишем равенство в таком виде:
70 х
= 210.
Здесь неизвестен один сомножитель, для его вычисления достаточно произведение (210) разделить на другой сомножитель (70),
х
= 210: 70; х
= 3.
Таким образом, мы можем сказать, что каждый крайний член пропорции равен произведению средних, делённому на другой крайний.
Перейдём теперь к вычислению неизвестного среднего члена. Возьмём пропорцию:
30: х
= 27: 9.
Напишем основное свойство пропорции:
30 9 = х
27.
Вычислим произведение 30 на 9 и переставим части последнего равенства:
х
27 = 270.
Найдём неизвестный сомножитель:
х
= 270: 27, или х
= 10.
Проверим подстановкой:
30: 10 = 27: 9. Пропорция верна.
Возьмём ещё одну пропорцию:
12: б = х
: 8. Напишем основное свойство пропорции:
12 . 8 = 6 х
. Перемножая 12 и 8 и переставляя части равенства, получим:
6 х
= 96. Находим неизвестный сомножитель:
х
= 96: 6, или х
= 16.
Таким образом, каждый средний член пропорции равен произведению крайних, делённому на другой средний.
Найдите неизвестные члены следующих пропорций:
1) а
: 3= 10:5; 3) 2: 1 / 2 = x
: 5;
2) 8: b
= 16: 4; 4) 4: 1 / 3 = 24: х
.
Два последних правила в общем виде можно записать так:
1) Если пропорция имеет вид:
х: а = b: с
, то
2) Если пропорция имеет вид:
а: х = b: с
, то
§ 128. Упрощение пропорции и перестановка её членов.
В настоящем параграфе мы выведем правила, позволяющие упрощать пропорцию в том случае, когда в неё входят большие числа или дробные члены. K числу преобразований, не нарушающих пропорцию, относятся следующие:
1. Одновременное увеличение или уменьшение обоих членов любого отношения в одинаковое число раз.
П р и м е р. 40: 10 = 60: 15.
Увеличив в 3 раза оба члена первого отношения, получим:
120:30 = 60: 15.
Пропорция не нарушилась.
Уменьшив в 5 раз оба члена второго отношения, получим:
Получили опять правильную пропорцию.
2. Одновременное увеличение или уменьшение обоих предыдущих или обоих последующих членов в одинаковое число раз.
Пример. 16:8 = 40:20.
Увеличим в 2 раза предыдущие члены обоих отношений:
Получили правильную пропорцию.
Уменьшим в 4 раза последующие члены обоих отношений:
Пропорция не нарушилась.
Два полученных вывода можно кратко высказать так: Пропорция не нарушится, если мы одновременно увеличим или уменьшим в одинаковое число раз любой крайний член пропорции и любой средний.
Например, уменьшив в 4 раза 1-й крайний и 2-й средний члены пропорции 16:8 = 40:20, получим:
3. Одновременное увеличение или уменьшение всех членов пропорции в одинаковое число раз. Пример. 36:12 = 60:20. Увеличим все четыре числа в 2 раза:
Пропорция не нарушилась. Уменьшим все четыре числа в 4 раза:
Пропорция верна.
Перечисленные преобразования дают возможность, во-первых, упрощать пропорции, а во-вторых, освобождать их от дробных членов. Приведём примеры.
1) Пусть имеется пропорция:
200: 25 = 56: x
.
В ней членами первого отношения являются сравнительно большие числа, и если бы мы пожелали найти значение х
, то нам пришлось бы выполнять вычисления над этими числами; но мы знаем, что пропорция не нарушится, если оба члена отношения разделить на одно и то же число. Разделим каждый из них на 25. Пропорция примет вид:
8:1 = 56: x
.
Мы получили, таким образом, более удобную пропорцию, из которой х
можно найти в уме:
![]()
2) Возьмём пропорцию:
2: 1 / 2 = 20: 5.
В этой пропорции есть дробный член (1 / 2), от которого можно освободиться. Для этого придётся умножить этот член, например, на 2. Но о д и н средний член пропорции мы не имеем права увеличивать; нужно вместе с ним увеличить какой-нибудь из крайних членов; тогда пропорция не нарушится (на основании первых двух пунктов). Увеличим первый из крайних членов
(2 2) : (2 1 / 2) = 20: 5, или 4: 1 = 20:5.
Увеличим второй крайний член:
2: (2 1 / 2) = 20: (2 5), или 2: 1 = 20: 10.
Рассмотрим ещё три примера на освобождение пропорции от дробных членов.
Пример 1. 1 / 4: 3 / 8 = 20:30.
Приведём дроби к общему знаменателю:
2 / 8: 3 / 8 = 20: 30.
Умножив на 8 оба члена первого отношения, получим:
Пример 2. 12: 15 / 14 = 16: 10 / 7 . Приведём дроби к общему знаменателю:
12: 15 / 14 = 16: 20 / 14
Умножим оба последующих члена на 14, получим: 12:15 = 16:20.
Пример 3. 1 / 2: 1 / 48 = 20: 5 / 6 .
Умножим все члены пропорции на 48:
24: 1 = 960: 40.
При решении задач, в которых встречаются какие-нибудь пропорции, часто приходится для разных целей переставлять члены пропорции. Рассмотрим, какие перестановки являются законными, т. е. не нарушающими пропорции. Возьмём пропорцию:
3: 5 = 12: 20. (1)
Переставив в ней крайние члены, получим:
20: 5 = 12:3. (2)
Переставим теперь средние члены:
3:12 = 5: 20. (3)
Переставим одновременно и крайние, и средние члены:
20: 12 = 5: 3. (4)
Все эти пропорции верны. Теперь поставим первое отношение на место второго, а второе – на место первого. Получится пропорция:
12: 20 = 3: 5. (5)
В этой пропорции мы сделаем те же перестановки, какие делали раньше, т. е. переставим сначала крайние члены, затем средние и, наконец, одновременно и крайние, и средние. Получатся ещё три пропорции, которые тоже будут справедливыми:
5: 20 = 3: 12. (6)
12: 3 = 20: 5. (7)
5: 3 = 20: 12. (8)
Итак, из одной данной пропорции путём перестановки можно получить ещё 7 пропорций, что вместе с данной составляет 8 пропорций.
Особенно легко обнаруживается справедливость всех этих пропорций при буквенной записи. Полученные выше 8 пропорций принимают вид:
а: b = с: d; c: d = a: b ;
d: b = с: a; b: d = a: c;
a: c = b: d; c: a = d: b;
d: c = b: a; b: a = d: c.
Легко видеть, что в каждой из этих пропорций основное свойство принимает вид:
ad = bc.
Таким образом, указанные перестановки не нарушают справедливости пропорции и ими можно пользоваться в случае надобности.
Но не все так сложо и непонятно, как кажется на первый взгляд. Для чего вообще все это нужно? Вот самый распространенный пример.
Допустим, у нас на сайте есть загрузка изображений, и мы хотим, чтобы после загрузки у нас создавалась миниатюрная копия, превьюшка какртинки. Часто это надо для анонса новостей, например. А скрипт требует, чтобы вы задали хотя бы примерные размеры миниатюрного изображения – его ширину и высоту.
Допустим также, что вы уже наметили его ширину, но как быть с высотой? Как высчитать ее та, чтобы картинка казалась более-менее пропорциональной по отношению к исходной.
Формула расчета
Все делается в два этапа:
- 1 – Делим исходную ширину на требуемую ширину;
- 2 – Получаем требуемую высоту, поделив исходную высоту на результат деления двух ширин (п.1).
Пример. Возьмем уже всем известные размеры изображений: 1024×768 и 800×600
. Представим, что мы не знаем высоту второй картинки. По формуле получается следующее: 768/(1024/800) = 600
. Это и есть требуемая нам высота.
Если же мы знаем высоту, а нам нужно получить ширину, то необходимо проделать все, как в первой формуле, только наоборот.
Чтобы получить требуемую ширину, нужно:
- 1 – Делим исходную высоту на требуемую высоту;
- 2 – Получаем требуемую ширину, поделив исходную ширину на результат деления двух высот (п.1).
То есть, 1024/(768/600) = 800
.
Задача 1
. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?
Решение.
Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:
3,3:
300 или х:
500.
Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание:
пропорция — это равенство двух отношений
):
х=(3,3·
500):
300;
х=5,5.
Ответ:
пачка 500
листов бумаги имеет толщину 5,5 см
.
Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:
или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.
Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6
классе.
Задача 2.
Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?
Решение.
Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.
5:
100 или х:
98. Получаем пропорцию:
5:
100 = х:
98.
х=(5·
98):
100;
х=4,9
Ответ: в 5кг
арбуза содержится 4,9 кг воды
.
Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?
Решение.
Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:
16,8:
21 или х:
35. Получаем пропорцию:
16,8:
21=х:
35.
Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8
и 35
) и делим на известный средний член (21
). Сократим дробь на 7
.
Умножаем числитель и знаменатель дроби на 10
, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5
(5 и 10) и на 3
(168 и 3).
Ответ:
35
литров нефти имеют массу 28 кг.
После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?
Решение.
Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:
х:
100 или 9:
18. Составляем пропорцию:
х:
100 = 9:
18.
 Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100
Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100
и 9
) и делим на известный крайний член (18
). Сокращаем дробь.
Ответ
: площадь всего поля 50 га.
Страница 1 из 1
1
Пропорция в переводе с латинского языка (proportio) обозначает соотношение, выравненность частей, то есть равенство 2-х отношений. Знание вычислять пропорции зачастую бывает нужным в бытовых обстановках.
Инструкция
1.
Легкой пример, когда нужно применить познания о решении пропорций: как вычислить 13% от вашей заработной платы – те самые проценты, которые уходят в Пенсионный фонд.
2.
Напишите две строчки пропорции. В первой укажите всеобщую сумму зарплаты, которая представляет собой 100%, то есть, скажем, 15 000 (рублей) = 100%.
3.
Строчкой ниже обозначьте ту сумму, которую надобно вычислить, знаком «Х», тот, что равен 13%, то есть Х = 13%.
4.
Основное качество пропорции звучит так: произведение крайних членов пропорции равно произведению её средних членов. Это значит, что если вы помножите 15 000 на 13, то полученное число будет равняться значению Х, помноженному на 100. То есть перемножая члены пропорции крест накрест, вы получите идентичное значение.
5.
Дабы вычислить, чему равен в финальном результате Х, умножьте 15 000 на 13 и поделите на 100. У вас получится, что 13 процентов от вашей зарплаты составляет 1950 рублей, таким образом, на руки вы получаете 15 000 – 1950 = 13 050 рублей чистой зарплаты.
6.
Если вам надобно взять для пирога 100 граммов сахарной пудры, а вы знаете, что в одном граненом стакане помещается 140 граммов, составьте следующую пропорцию:100 = Х140 = 1
7.
Подсчитайте, чему равен Х.Х = 100 х 1 / 140 = 0,7То есть вам потребуется 0,7 стакана сахарной пудры.
8.
Бывает, что надобно вычислить целое, зная только процентную часть. Скажем, вы знаете, что 21 человек на предприятии, а это 5% от всеобщего числа работников, имеют среднее особое образование. Составьте пропорцию, дабы вычислить всеобщее число работников: Х (человек) = 100%, 21 = 5%. 21 х 100 / 5 = 420 человек.
9.
Таким образом, записав в две строки имеющиеся данные, значение неведомого члена надобно находить так: помножьте между собой те члены пропорции, которые оказываются рядом и сверху незнакомого и поделите полученное число на значение, которое находится по диагонали от неведомого.А=БС=ДА = Б х С / Д; Б = А х Д / С; С = А х Д / Б; Д = С х Б / А
В геометрии существует несколько видов диагоналей. Диагональю
именуется отрезок, тот, что соединяет две не соседние (не принадлежащие одной стороне либо одному ребру) вершины многоугольника либо многогранника. Различают так же диагонали граней, рассматриваемых как многоугольники и пространственные диагонали, соединяющие вершины различных граней многогранника. Существуют фигуры, у которых все диагонали равны между собой. На плоскости это верный пятиугольник и квадрат, в пространстве – положительный октаэдр.Зная длины сторон положительного многоугольника либо длины рёбер положительного многогранника дозволено вычислить длину всякий диагонали.

Инструкция
1.
В любом верном многоугольнике углы равны между собой и вычисляются по формуле?? = (N — 2) * 180?/N, где?? – всякий из углов положительного многоугольника, N – число вершин.Зная углы при вершинах многоугольника, его диагонали дозволено вычислить, применяя теорему косинусовBE = v(AB? + AE? – 2 * AB * AE * cos??)

2.
Если число вершин огромнее пяти, то для вычисления диагоналей, которые соединяют вершины, лежащие на различных сторонах дозволено воспользоваться той же теоремой косинусов для вычисления углов образующихся треугольников. Скажем, в шестиугольнике ABCDEF, для нахождения диагонали BE, нужно вычислить диагональ CE, после этого по той же теореме косинусов вычислить угол??, тогда?? = ?? — ??. Таким образом,BE = v(BC? + CE? – 2 * BC * CE * cos??).

Видео по теме
Обратите внимание!
Для вычисления пространственной диагонали многогранника, нужно возвести сечение, содержащее эту диагональ, вычислить углы при вершинах этого сечения, рассматривая сечение как плоский многоугольник. Тогда диагональ дозволено рассчитать по приведённой выше схеме.
Что представляет собой пропорция? С математической точки зрения, пропорция – это равенство 2-х отношений. Все части пропорции являются взаимозависимыми, а их итог непоколебим.

Вам понадобится
- — Учебник алгебры за 7 класс.
Инструкция
1.
Числа, которые находятся по краям равенства, именуются крайними. Соответственно, те, что находятся в середине – средними. Основным свойством пропорции является то, что крайние и средние части равенства дозволено перемножать между собой. Возьмите пропорцию 6:3=8:4. Перемножьте между собой крайние части, получится 6*4=24, произведение средних частей тоже будет равным 24. Отсель итог: произведение одних частей пропорции должно быть равно произведению других частей (крайние = средние).
2.
Возьмите это качество пропорции на вооружение, вычислите незнакомый член уравнения x:4=15:3. Для того, дабы обнаружить неведомую часть пропорции, воспользуйтесь правилом равнозначности крайних и средних частей. Запишите это уравнение так: x*3=4*15. Решив это уравнение, вы получите правильную пропорцию.
3.
Если пропорция состоит из огромных либо дробных чисел, ее дозволено упростить. Уменьшите оба члена отношения на идентичное число раз. Дабы не случилось нарушения пропорции, сделайте так: 40:10=60:15. Увеличьте оба члена отношения в три раза (120:30=60:15) либо уменьшите части второго отношения (40:10=12:3). Обе пропорции будут положительными.
4.
Увеличивайте либо сокращайте пропорции только в идентичное число раз. Получив упрощенные реформирование, вы освобождаете пропорцию от дробных членов и упрощаете уравнение. Возьмите пример: 200:25=56:х. Дабы не исполнять вычисление с огромными числами, поделите их на одно и то же число. Если за это число взять 25, уравнение примет дальнейший вид: 8:1=56:х. Неведомую часть этой пропорции дозволено определить в уме, не прибегая к трудным вычислениям.
5.
Части пропорций дозволено переставлять. Возьмите пропорцию 3:5=12:20. Переставьте крайние части (20:5=12:3), допустима и одновременная перегруппировка всех частей (20:12=5:3). Все пропорции будут правильными. Так из одной пропорции вы получите несколько, и все они будут положительными.
Обратите внимание!
Перегруппировка частей пропорций местами комфортна при решении задач.
Полезный совет
Основное качество всех пропорций: ab = bc.
В математике пропорцией называют равенство 2-х отношений. Для всех ее частей характерна взаимозависимость и постоянный итог. Довольно разглядеть один пример, дабы осознать тезис решения пропорций.

Инструкция
1.
Изучите свойства пропорций. Числа по краям равенства называют крайними, а находящиеся посередине – средними. Основное качество пропорции заключается в том, что средние и крайние части равенства могут быть перемножены между собой. Довольно взять пропорцию 8:4=6:3. Если перемножить крайние части между собой, получится 8*3=24, как и при умножении средних чисел. Это обозначает, что произведение крайних частей пропорции неизменно равно произведению ее средних частей.
2.
Возьмите на вооружение основное качество пропорции, дабы вычислить неведомый член в уравнении x:4=8:2. Для нахождения незнакомой части пропорции следует воспользоваться правилом равнозначности средних и крайних частей. Запишите уравнение в виде x*2=4*8, то есть x*2=32. Решите это уравнение (32/2), вы получите недостающий член пропорции (16).
3.
Упростите пропорцию, если она состоит из дробных либо крупных чисел. Для этого поделите либо умножьте оба ее члена на идентичное число. Скажем, комбинированные части пропорции 80:20=120:30 дозволено упростить, поделив ее члены на 10 (8:2=12:3). Вы получите эквивалентное равенство. То же самое будет, если вы увеличите все члены пропорции, скажем, на 2, таким образом 160:40=240:60.
4.
Испробуйте переставить части пропорций. К примеру, 6:10=24:40. Поменяйте местами крайние части (40:10=24:6) либо же единовременно сделайте перегруппировку всех частей (40:24=10:6). Все полученные пропорции будут эквивалентными. Так вы сумеете получить несколько равенств из одного.
5.
Решите пропорцию с процентами. Запишите ее, скажем, в виде: 25=100%, 5=x. Сейчас необходимо перемножить средние члены (5*100) и поделить на знаменитый крайний (25). В результате получается, что x=20%. Таким же образом дозволено перемножать знаменитые крайние члены и разделять их на имеющийся средний, получая желанный итог.
Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 |
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
![]()
Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной. Для начала напомню, что такое пропорция. Это равенство вида:

что тоже самое (это разная форма записи).
Пример:

Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).
Основное правило пропорции:
a:b=c:d
произведение крайних членов равно произведению средних
то есть
a∙d=b∙c
*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.
Если рассматривать форму записи вида:

то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали
a∙d=b∙c
Как видите результат тот же.
Если три элемента пропорции известны, то мы всегда можем найти четвёртый.
Именно в этом суть пользы и необходимость пропорции при решении задач.
Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:

![]()
Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.
Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:
1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях “Задачи на проценты. Часть 1!“ и “Задачи на проценты. Часть 2!“.
2. Многие формулы заданы в виде пропорций:
> теорема синусов
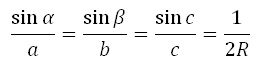
> отношение элементов в треугольнике

> теорема тангенсов

> теорема Фалеса и другие.
3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.
4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:
— часы в минуты (и наоборот).
— единицы объёма, площади.
— длины, например мили в километры (и наоборот).
— градусы в радианы (и наоборот).
здесь без составления пропорции не обойтись.
Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:

Необходимо определить число, которое составляет 35% от 700.
В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:
Можно сказать, что семисот тридцати пяти соответствует 100 процентов.
Иксу соответствует 35 процентов. Значит,
700 – 100%
х – 35 %
Решаем

Ответ: 245

Переведём 50 минут в часы.
Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие – x часов это 50 минут. Значит
1 – 60
х – 50
Решаем:
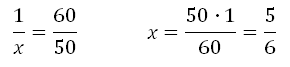
То есть 50 минут это пять шестых часа.
Ответ: 5/6

Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?
Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:
Одной миле соответствует 1,6 километра.
Икс миль это три километра.
1 – 1,6
х – 3

Ответ: 1,875 миль
Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.
Переведём 65 градусов в радианную меру.
Главное это запомнить, что 180 градусов это Пи радиан.
Обозначим искомую величину как х. Устанавливаем соответствие.
Ста восьмидесяти градусам соответствует Пи радиан.
Шестидесяти пяти градусам соответствует х радиан.

Если записать отношение в общем виде, то получится

То есть, если необходимо перевести градусы в радианы, то подставляете в эту пропорцию градусы и вычисляете радианы; если необходимо перевести радианы в градусы, то подставляете радианы и вычисляете градусы.
Можете изучить статью по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!
Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ — здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!
Всего доброго!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Определение пропорции:
Связь между четырьмя алгебраическими выражениями А, В, С и D, имеющая вид
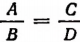
называется пропорцией.
(Равенство 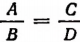 теряет смысл и перестает быть пропорцией как при В = О, так и при D = 0. Оно теряет смысл и перестает быть пропорцией и тогда, когда В и D равны нулю одновременно.)
теряет смысл и перестает быть пропорцией как при В = О, так и при D = 0. Оно теряет смысл и перестает быть пропорцией и тогда, когда В и D равны нулю одновременно.)
Примеры пропорции:
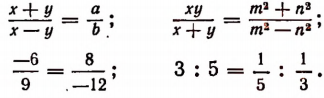
В пропорции 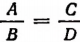 величины А и D называются крайними, а В и С средними членами. Далее выражение
величины А и D называются крайними, а В и С средними членами. Далее выражение 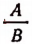 называется первым отношением, а
называется первым отношением, а 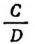 вторым; А и С называются предыдущими членами этих отношений, а В и D —последующими.
вторым; А и С называются предыдущими членами этих отношений, а В и D —последующими.

Главное свойство пропорции
Умножив левую и правую части пропорции
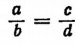
на произведение bd, получим ad = be, т. е. во всякой пропорции произведение крайних членов равно произведению средних.
Составление пропорции по данному равенству двух произведений
Пусть pq = ху. Разделив левую и правую части этого равенства на qx, получим
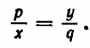
Этот результат можно сформулировать следующим образом.
Если произведение двух чисел равно произведению двух других, то из этих четырех чисел можно составить пропорцию, беря множители одного произведения за крайние, а множители другого произведения за средние члены пропорции. (При этом дополнительно требуется, чтобы оба последующих члена пропорции не оказались равными нулю.)
Перестановка членов пропорции
Пусть ad = be и числа а, b, с, d — все отличны от нуля. Разделив левую и правую части равенства ad = bc первый раз на bd, второй на ab, третий на ас и четвертый на cd, получим соответственно четыре пропорции:
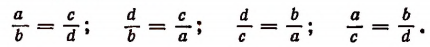
Поменяв местами отношения в этих равенствах, получим еще четыре пропорции:
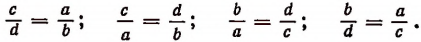
Этот результат показывает, что в пропорции можно менять местами средние и крайние члены и ставить оба крайних члена на места средних, а оба средних на места крайних.
Производные пропорции
1. Прибавив к левой и правой частям пропорции  по единице, получим
по единице, получим
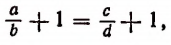
или
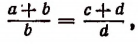
т. е. во всякой пропорции сумма членов первого отношения так относится к своему последующему, как сумма членов второго отношения — к своему последующему.
2. Вычтя из левой и правой частей пропорции  по единице, получим:
по единице, получим:
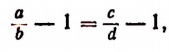
или
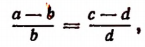
т. е. во всякой пропорции разность членов первого отношения так относится к своему последующему, как разность членов второго отношения — к своему последующему.
3. Разделив левую часть равенства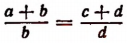 на левую часть равенства
на левую часть равенства 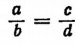 и правую на правую, получим:
и правую на правую, получим:
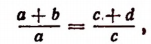
т. е. во всякой пропорции сумма членов первого отношения так относится к своему предыдущему, как сумма членов второго отношения — к своему предыдущему.
4. Разделив левую часть равенства 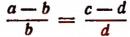 на левую часть равенства
на левую часть равенства  и правую на правую, получим:
и правую на правую, получим:
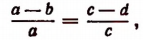
т. е. во всякой пропорции разность членов первого отношения так относится к своему предыдущему, как разность членов второго отношения —к своему предыдущему.
5. Разделив левую часть равенства 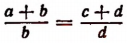 на левую часть равенства
на левую часть равенства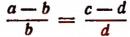 и правую на правую, получим:
и правую на правую, получим:
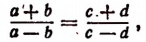
т. е. во всякой пропорции сумма членов первого отношения так относится к их разности, как сумма членов второго отношения — к их разности.
Из пропорции  мы вывели пять производных пропорций. Однако надо иметь в виду, что из пропорции
мы вывели пять производных пропорций. Однако надо иметь в виду, что из пропорции  можно было бы получить сколько угодно производных пропорций.
можно было бы получить сколько угодно производных пропорций.
Например, умножив обе части пропорции 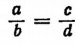 на число а, получим
на число а, получим 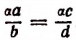 . Прибавив к левой и правой частям последнего равенства число
. Прибавив к левой и правой частям последнего равенства число 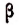 , будем иметь, что
, будем иметь, что
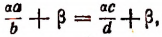
или
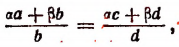
т. е. получим новую производную пропорцию.
Определение неизвестного члена пропорции
Пусть в пропорции 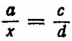 числа а, с, d известны, a х изображает число неизвестное. Тогда по свойству пропорции cx = ad, откуда
числа а, с, d известны, a х изображает число неизвестное. Тогда по свойству пропорции cx = ad, откуда 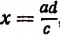 , т. е. неизвестный средний член пропорции равен произведению крайних членов, деленному на известный средний. Аналогично определяется и неизвестный крайний член.
, т. е. неизвестный средний член пропорции равен произведению крайних членов, деленному на известный средний. Аналогично определяется и неизвестный крайний член.
Примеры:
1. Найти неизвестное число х из пропорции 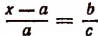 , где а, b и с числа известные.
, где а, b и с числа известные.
Составим производную пропорцию по правилу: сумма членов первого отношения так относится к своему последующему члену, как сумма членов второго отношения к своему последующему:
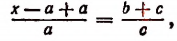
т. е.
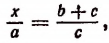
откуда
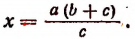
2. Найти неизвестное х из пропорции 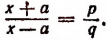 Составим производную пропорцию по правилу: сумма членов первого отношения так относится к их разности, как сумма членов второго отношения к их разности, т. е.
Составим производную пропорцию по правилу: сумма членов первого отношения так относится к их разности, как сумма членов второго отношения к их разности, т. е.
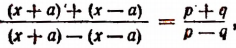
или
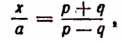
отсюда
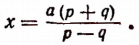
Ряд равных отношений
Иногда бывает удобно вместо различных букв употреблять для обозначения чисел одну и ту же букву, снабженную дополнительными значками — индексами. Например 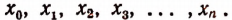 Эти обозначения читаются так: икс нулевое, икс первое, икс второе, икс третье, … , икс энное.
Эти обозначения читаются так: икс нулевое, икс первое, икс второе, икс третье, … , икс энное.
Основное свойство ряда равных отношений
Пусть имеется ряд равных отношений:
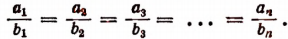
Обозначим общее значение всех этих отношений буквой k. Тогда
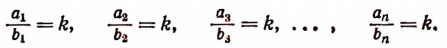
Отсюда
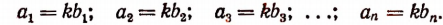
Складывая левые и правые части этих равенств, получим:
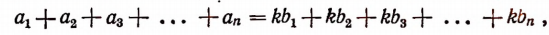
или
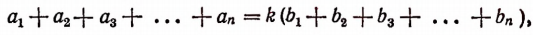
или
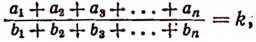
т.е.
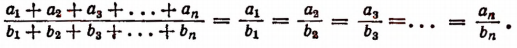
Итак, доказано следующее:
если несколько отношений равны друг другу, то отношение суммы их предыдущих членов к сумме последующих равно каждому из этих отношений.
Пример:
Пусть длины 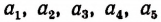 сторон одного многоугольника (рис. 53) пропорциональны длинам
сторон одного многоугольника (рис. 53) пропорциональны длинам 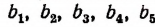 сторон другого многоугольника, т. е.
сторон другого многоугольника, т. е.
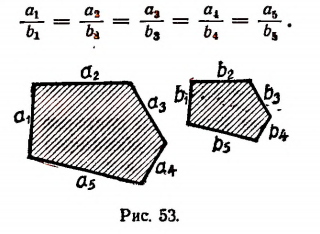
По свойству ряда равных отношений получим:
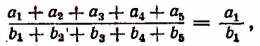
или
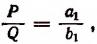
где Р и Q периметры многоугольников.
Прямая пропорциональность
Сначала рассмотрим несколько примеров.
Пример:
Пусть буква х обозначает в годах возраст сына, а буква у — возраст отца и пусть в данный момент сыну один год, а отцу 25 лет.
Составим таблицу значений х и соответствующих им значений буквы у. В третьей строке этой таблицы выпишем значения отношения  :
:
В этом примере отношение  (отношение возраста отца к возрасту сына) не остается неизменным. Оно с течением времени убывает.
(отношение возраста отца к возрасту сына) не остается неизменным. Оно с течением времени убывает.
Пример:
Пусть буква х обозначает в сантиметрах длину стороны квадрата, а буква у — площадь квадрата в квадратных сантиметрах.
Составим таблицу, подобную предыдущей.
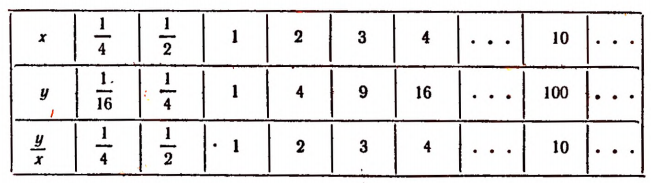
Отношение  и здесь не остается неизменным. Оно возрастает при возрастании х.
и здесь не остается неизменным. Оно возрастает при возрастании х.
Пример:
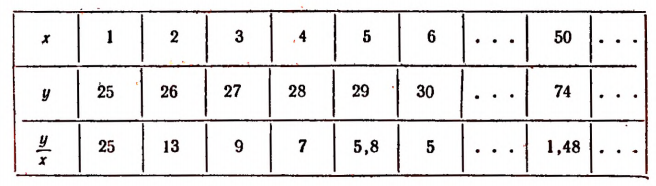
Пусть буква х обозначает в кубических сантиметрах объем ртути при температуре 0°, а буква у — вес этой ртути в граммах. Известно, что 1 куб. см ртути при температуре 0° весит 13,6 г.
Опять составим таблицу значений х, у и  .
.

Этот третий пример существенно отличается от двух предыдущих. Здесь отношение  сохраняет неизменное значение.
сохраняет неизменное значение.
Определение:
Две величины у и х называются прямо пропорциональными (или просто пропорциональными), если при всех их возможных изменениях отношение  остается равным одному и тому же числу и если при х = 0 значение у также равно нулю.
остается равным одному и тому же числу и если при х = 0 значение у также равно нулю.
Значит, вес ртути и объем ртути при постоянной температура являются величинами пропорциональными.
Возраст отца и возраст сына не пропорциональны.
Также не пропорциональны сторона квадрата и его площадь.
Пусть изменяющиеся величины у и х пропорциональны. Тогда отношение  будет равно некоторому постоянному числу.
будет равно некоторому постоянному числу.
Обозначая это постоянное число буквой k, получим:
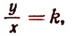
или
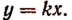
Следовательно, если величины у и х пропорциональны и отношение  равно k, то у выражается в зависимости от х формулой
равно k, то у выражается в зависимости от х формулой
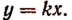
Число k называется коэффициентом пропорциональности (величины у по отношению к величине х).
Теперь докажем обратное положение. Пусть
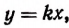
где k — постоянное число.
Отсюда следует, что при х = 0 и у = 0 и что 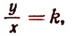 А это и означает, что величины у и х пропорциональны.
А это и означает, что величины у и х пропорциональны.
Из того что 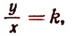 следует, что
следует, что 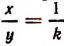 , или что
, или что 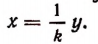 Отсюда можно сделать следующий вывод:
Отсюда можно сделать следующий вывод:
Если коэффициентом пропорциональности величины у по отношению к величине х служит постоянное число k, то коэффициентом пропорциональности величины х по отношению к величине у будет служить число 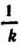 .
.
Приведем еще один пример пропорциональных величин. Путь s, пройденный при равномерном движении, пропорционален. времени t, т. е.
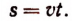
Здесь постоянное число v есть коэффициент пропорциональности величины s по отношению к величине t (v есть скорость равномерного движения).
Сделаем еще два замечания.
Замечание:
Если имеется два ряда чисел:

и

и если
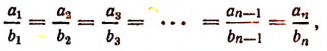
то числа одного из этих рядов называются пропорциональными числам другого ряда.
Замечание:
Если имеются только два постоянных числа а и b, то бессмысленно говорить о них, что они пропорциональны или не пропорциональны.
В этом случае можно интересоваться либо характером этих чисел, либо их разностью, либо их отношением и т. д.
В заключение решим две простые задачи на пропорциональные величины.
Задача:
На карте в масштабе 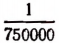 расстояние между двумя пунктами равно 42,5 см. Определить, чему равно это расстояние на карте в масштабе
расстояние между двумя пунктами равно 42,5 см. Определить, чему равно это расстояние на карте в масштабе 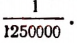
Решение:
Длина на карте прямо пропорциональна масштабу. Поэтому.

Задача:
С помощью непосредственного измерения установили, что при повышении температуры рельса на 24°С его длина увеличивается на 1,5 мм. Требуется вычислениями определить изменение длины рельса при понижении его температуры на 40°С. (Считать изменение длины рельса величиной, прямо пропорциональной изменению температуры.)
Решение:
Обозначив искомое изменение (в мм) буквой х, получим:
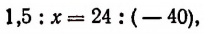
откуда
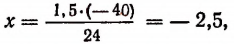
т. е. при понижении температуры рельса на 40°С его длина сократится на 2,5 мм.
Обратная пропорциональность
Сначала приведем примеры.
1. Рассмотрим изменяющийся прямоугольный параллелепипед с квадратным основанием, имеющий неизменный объем, равный 3600 куб. см (рис. 54).
Пусть буква х обозначает в сантиметрах изменяющуюся сторону основания, а буква у — изменяющуюся высоту параллелепипеда.
Рассматривая таблицу:
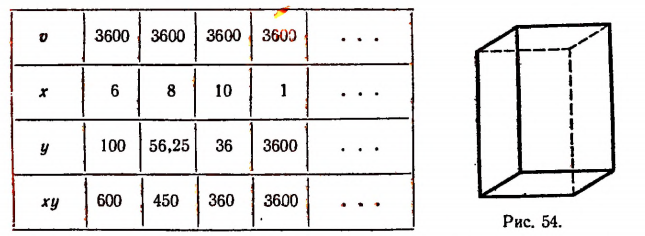
легко видеть, что произведение ху не остается неизменным при постоянстве объема.
2. Рассмотрим изменяющийся прямоугольник, имеющий неизменную площадь, равную 100 кв. см.
Пусть буква х обозначает одно изменяющееся измерение (например, длину прямоугольника), а буква у — другое изменяющееся измерение (ширину). Пусть х и у выражены в сантиметрах.
Так как произведение измерений прямоугольника равно его площади, то величины х и у при всех своих возможных изменениях будут давать в своем произведении число 100, т. е. произведение изменяющихся величин х и у будет оставаться неизменным.
Существенное отличие второго примера от первого заключается в том, что в нем произведение ху остается неизменным, в то время как в первом оно изменяется.
Определение:
Две величины х и у называются обратно пропорциональными, если при всех их возможных изменениях произведение ху остается равным одному и тому же числу.
Обозначая это число буквой k, получим
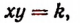
или
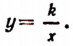
Следовательно, если величины х и у обратно пропорциональны, то величина у выражается через величину х по формуле следующего вида:
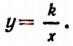
Число k называется коэффициентом обратной пропорциональности.
Длина прямоугольника и ширина прямоугольника при заранее заданной площади прямоугольника являются величинами обратно пропорциональными. Коэффициентом обратной пропорциональности служит как раз эта площадь.
Сторона основания прямоугольного параллелепипеда с квадратным основанием и высота параллелепипеда при заранее заданном объеме не являются величинами обратно пропорциональными.
Задача:
Зал освещается m лампами по а свечей каждая. Сколькими лампами в b свечей можно получить ту же освещенность зала?
Число ламп и число свечей каждой лампы при данной освещенности зала являются величинами обратно пропорциональными. Поэтому, обозначая число ламп в b свечей буквой x, получим

откуда
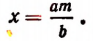
Пропорциональное деление
Задача:
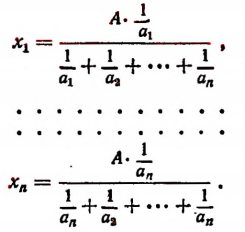
Число А разделить на n слагаемых прямо пропорционально числам 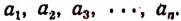
Обозначим искомые слагаемые буквами 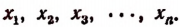 Тогда по условию задачи
Тогда по условию задачи
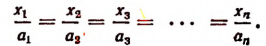
Пользуясь свойством ряда равных отношений, получим
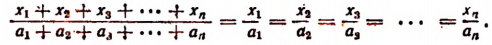
Но
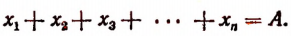
Поэтому
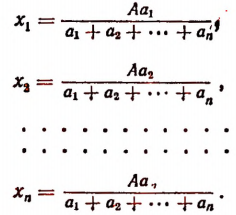
Задача:
Число А разделить на n слагаемых обратно пропорционально числам 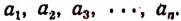
Обозначим искомые слагаемые буквами 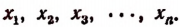 Тогда согласно условию задачи
Тогда согласно условию задачи
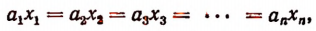
или
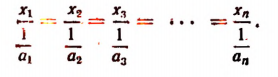
По свойству ряда равных отношений получим
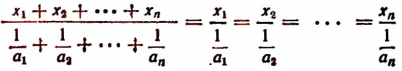
Но

Поэтому
Пропорции и пропорциональная зависимость
- Отношением числа а к числу b называется частное
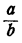 , а называется предыдущим, b — последующим членом отношения.
, а называется предыдущим, b — последующим членом отношения. - Пропорцией называется равенство, каждая часть которого является отношением двух чисел. В пропорции
члены а и d называются крайними, а b и с средними.
При изложении свойств пропорции будем считать, что ни один из членов пропорции не равен нулю.
Пример:
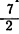 отношение числа 7 к числу 2. Предыдущий член здесь 7, последующей 2.
отношение числа 7 к числу 2. Предыдущий член здесь 7, последующей 2.
Пример:
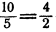 пропорция. Крайние члены здесь 10 и 2, средние— 4 и 5.
пропорция. Крайние члены здесь 10 и 2, средние— 4 и 5.
Главное свойство пропорции
Теорема:
Во всякой пропорции произведение крайних
членов равно произведению средних.
Доказательство:
Дана пропорция

Умножим обе части равенства (1) на bd, получим
Теорема доказана.
Теорема:
Если произведение двух чисел
равно произведению двух других чисел, то из этих четырех чисел можно составить пропорцию^ крайними членами которой являются сомножители одного из двух произведений, а средними—сомножители другого.
При этом предполагается, что ни один из сомножителей не равен нулю.
Доказательство:
Пусть
a, b, с, d все отличны от нуля. Разделим обе части равенства на bd, получим
Теорема доказана.
Пример:
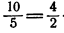 — пропорция. Произведение крайних ее членов равно 20, произведение средних ее членов также равно 20.
— пропорция. Произведение крайних ее членов равно 20, произведение средних ее членов также равно 20.
Пример:
8 • 9 = 3 • 24 — равенство двух произведений.
Разделим обе части этого равенства на 9 • 24, получим пропорцию
Определение неизвестного члена пропорции
Теорема:
Средний член пропорции равен произведению крайних, деленному на другой средний. Крайний член пропорции равен произведению средних, деленному на другой крайний.
Пусть

Покажем, что

На основании теоремы 1 имеем

Разделим обе части равенства (4) на с, получим равенство (2). Разделим обе части равенства (4) на d, получим равенство (3). Теорема доказана.
Пример:
Найти х, если 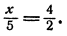
Решение:
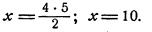
Пример:
Найти х, если 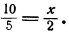
Решение:
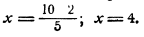
Перестановка членов пропорции
Теорема:
Во всякой пропорции можно переставить
средние члени, переставить крайние члени, переставить и средние члени и крайние, средние поставить на место крайних, а крайние на место средних.
Иными словами, если

то

(переставлены средние члены),

(в (1) переставлены крайние члены),

(в (1) переставлены и средние и крайние члены),

(средние поставлены на место крайних, крайние — на место средних).
Доказательство:
В пропорций (1)

Разделим обе части равенства (6) на cd, получим равенство (2). Точно так же, разделив обе части равенства (6) на аb, а затем на ас, получим равенства (3) и (4). Равенство (5) получается из равенства (4) посредством перестановки отношений. Теорема доказана.
Следствие:
Переставим отношения в равенствах (I), (2), (3), получим еще три пропорции
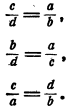
Таким образом, всякую пропорцию посредством перестановки ее членов можно представить в восьми различных видах.
Производные пропорции
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к последующему члену этого отношения, как сумма членов второго отношения относится к своему последующему.
2) Во всякой пропорции разность членов первого отношения так относится к последующему члену этого отношения, как разность членов второго отношения относится к своему последующему.
Иными словами, если

то

Доказательство:
Прибавим к каждой части равенства (1)
по 1, получим равенство (2). Вычтем из каждой части равенства (1) по 1, получим равенство (3). Теорема доказана.
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к предыдущему члену этого отношения, как сумма членов второго отношения относится к своему предыдущему.
2) Во всякой пропорции разность членов первого отношения так относится к предыдущему члену этого отношения, как разность членов второго отношения относится к своему предыдущему.
Иными словами, если
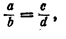
то

Доказательство:
Разделим равенство (2) почленно на
равенство (1), т. е., левую часть равенства (2) разделим на левую часть равенства (1), а правую часть равенства (2) на правую часть равенства (1). Получим равенство (4). Разделив равенство (3) почленно на равенство (1), получим равенство 5). Теорема доказана.
Теорема:
Во всякой пропорции сумма членов первого
отношения так относится к их разности, как сумма членов второго отношения относится к их разности, если только эти разности отличны от нуля.
Иными словами, если
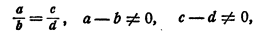
то

Доказательство:
Разделив почленно равенство (4) на
равенство (5), получим равенство (6).
Ряд равных отношений
Теорема:
Если даны несколько равных отношений* то
сумма всех предыдущих членов отношений относится к сумме всех последующих как любой из предыдущих к своему последующему.
Доказательство:
Пусть имеется несколько равных отношений
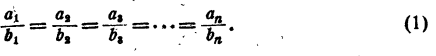
Обозначим результат деления 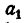 на
на 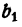 буквой q. Так как все отношения ряда (1) равны между собой, каждое из них также равно q. Таким образом,
буквой q. Так как все отношения ряда (1) равны между собой, каждое из них также равно q. Таким образом,
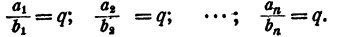
Отсюда
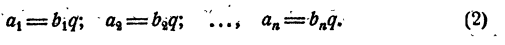
Сложив почленно все равенства (2), имеем
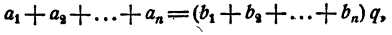
откуда
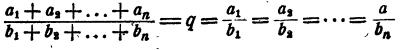
Теорема доказана.
Задача:
Дано, что
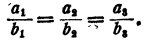
Доказать, что при любых 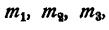 отличных от нуля,
отличных от нуля,
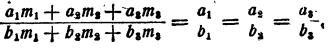
Решение:
Умножим каждый, член первого отношения на 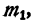 получим пропорцию
получим пропорцию
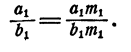
Точно так же
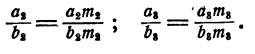
Значит,
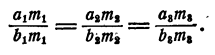
На основании теоремы 8 имеем
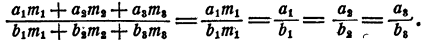
Задача:
Решить уравнение 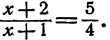
Решение:
Пользуясь теоремой 7 § 5, имеем
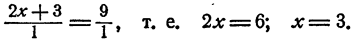
Пропорциональная зависимость
Мы много раз составляли уравнения, выражающие зависимость между величинами, и могли наблюдать, что. зависимости эти бывают весьма разнообразны.
При решении многих задач мы встречаемся с двумя величинами, зависимость между которыми такова, что при изменении этих величин их отношение остается неизменным. Такие величины называются прямо пропорциональными, а зависимость между ними — пропорциональной зависимостью.
Для примера приведем несколько задач, в которых мы встретимся с величинами, находящимися в пропорциональной зависимости.
Задача:
Скорость течения реки 3 км в час. Плот за t часов прошел вниз по реке S км. Составить уравнение, выражающее зависимость между S и t.
Ответ. S = 3t.
Задача:
С каждого гектара собрано 30 ц ржи и, таким образом, с k га собрано А ц. Составить уравнение, выражающее зависимость между А и k.
Ответ. А = 30k
Задача:
Основание прямоугольника 2 см, высота h см, площадь Q 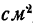 . Составить уравнение, выражающее зависимость между Q и h.
. Составить уравнение, выражающее зависимость между Q и h.
Ответ. Q = 2h.
Задача:
1 м материи стоит 20 руб. За m м этой материи
уплатили N pyб. Составить уравнение, выражающее зависимость между N и m.
Ответ. N=20m.
Мы рассмотрели четыре задачи, которые по своему содержанию относятся к различным областям практической деятельности. Нетрудно убедиться, что в каждой из этих задач мы действительно имеем дело с прямо пропорциональными величинами.
Так, в первой задаче отношение расстояния (в kм), пройденного плотом, к времени (в часах), в течение которого плот находился в пути, всегда одно и то же и равно 3. Поэтому расстояние, которое проходит плот вниз по реке, пропорционально времени, в течение которого плот находится в пути, при условии, что скорость течения реки повсюду одна и та же.
Точно так же во второй задаче количество ржи, собранной с нескольких гектаров, пропорционально количеству ржи, собранной с одного гектара, при условии, что с каждого гектара собрано по одному и тому же количеству ржи и т. д.
Заметим, что уравнения, к которым мы пришли в рассмотренных задачах, имеют один и тот же вид. В этих уравнениях одна, из величин равна произведению некоторого числового множителя на другую величину. Этот множитель называется коэффициентом пропорциональности. В первой задаче коэффициент
пропорциональности равен 3, во второй задаче он равен 30, в третьей задаче он равен 2, в четвертой задаче он равен 20.
Таким образом, пропорциональная зависимость между величинами всегда выражается уравнением y = kx, где k — коэффициент пропорциональности. Известно, что зависимость между двумя величинами может быть наглядно представлена таблицей, а затем и графиком.
Для примера представим таблицей зависимость, выражаемую уравнением S = 3/ (первая задача):
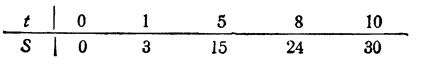
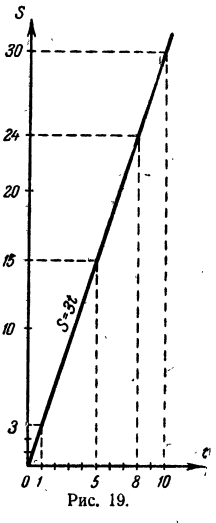
Построим график зависимости S = 3t (рис. 19). Обратим внимание на следующие обстоятельства:
- Отношение чисел, находящихся в одном столбце таблицы, повсюду одно и то же и равно коэффициенту пропорциональности:
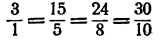
и т. д. (для первого столбца это отношение не имеет смысла; так как на нуль делить нельзя).
2, График представляет собой луч, выходящий из начала координат (при t= 0, S = 0). (Доказательство этого утверждения здесь провести нельзя, так как для этого требуются некоторые сведения из геометрии.)
То же самое можно наблюдать и при графическом представлении любой другой пропорциональной зависимости между двумя величинами.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Для решения большинства задач в математике средней школы необходимо знание по составлению пропорций. Это несложное умение поможет не только выполнять сложные упражнения из учебника, но и углубиться в саму суть математической науки. Как составить пропорцию? Сейчас разберем.

Самым простым примером является задача, где известны три параметра, а четвертый необходимо найти. Пропорции бывают, конечно, разные, но часто требуется найти по процентам какое-нибудь число. Например, всего у мальчика было десять яблок. Четвертую часть он подарил своей маме. Сколько осталось яблок у мальчика? Это самый простой пример, который позволит составить пропорцию. Главное это сделать. Изначально было десять яблок. Пусть это 100%. Это мы обозначили все его яблоки. Он отдал одну четвертую часть. 1/4=25/100. Значит, у него осталось: 100% (было изначально) – 25% (он отдал) = 75%. Эта цифра показывает процентное отношение количества оставшихся фруктов к количеству имевшихся сначала. Теперь у нас есть три числа, по которым уже можно решить пропорцию. 10 яблок – 100%, х яблок – 75%, где х – искомое количество фруктов. Как составить пропорцию? Необходимо понимать, что это такое. Математически это выглядит так. Знак равно поставлен для вашего понимания.

10 яблок = 100%;
x яблок = 75%.
Оказывается, что 10/x = 100%/75. Это и есть основное свойство пропорций. Ведь чем больше x, тем больше процентов составляет это число от исходного. Решаем эту пропорцию и получаем, что x=7,5 яблок. Почему мальчик решил отдать нецелое количество, нам неизвестно. Теперь вы знаете, как составить пропорцию. Главное, найти два соотношения, в одном из которых есть искомое неизвестное.
Решение пропорции часто сводится к простому умножению, а потом к делению. В школах детям не объясняют, почему это именно так. Хотя важно понимать, что пропорциональные отношения есть математическая классика, сама суть науки. Для решения пропорций необходимо уметь обращаться с дробями. Например, часто приходится переводить проценты в обыкновенные дроби. То есть запись 95% не подойдет. А если сразу написать 95/100, то можно провести солидные сокращения, не начиная основного подсчета. Сразу стоит сказать, что если ваша пропорция получилась с двумя неизвестными, то ее не решить. Никакой профессор вам здесь не поможет. А ваша задача, скорее всего, имеет более сложный алгоритм правильных действий.

Рассмотрим еще один пример, где нет процентов. Автомобилист купил 5 литров бензина за 150 рублей. Он подумал о том, сколько он бы заплатил за 30 литров топлива. Для решения этой задачи обозначим за x искомое количество денег. Можете самостоятельно решить эту задачу и потом проверить ответ. Если вы еще не поняли, как составить пропорцию, то смотрите. 5 литров бензина – это 150 рублей. Как и в первом примере, запишем 5л – 150р. Теперь найдем третье число. Конечно, это 30 литров. Согласитесь, что пара 30 л – х рублей уместна в данной ситуации. Перейдем на математический язык.
5 литров – 150 рублей;
30 литров – х рублей;
5/30 = 150 / x.
Решаем эту пропорцию:
5x = 30*150;
x = 900 рублей.
Вот и решили. В своей задаче не забудьте проверить на адекватность ответ. Бывает, что при неправильном решении автомобили достигают нереальных скоростей в 5000 километров в час и так далее. Теперь вы знаете, как составить пропорцию. Также вы сможете ее решить. Как видите, в этом нет ничего сложного.
