Как правильно составить таблицу по математике

---

Использование таблиц для решения текстовых задач по математике в основной школе

© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Инфоурок

›

Математика

›Другие методич. материалы›Памятки – алгоритмы по созданию таблиц и диаграмм на уроках математики в начальной школе

Памятки – алгоритмы по созданию таблиц и диаграмм на уроках математики в начальной школе

Дисперсией ряда чисел называется среднее арифметическое
Какой удобный способ хранения информации использовался человечеством с давних времён?

Дисперсией ряда чисел называется среднее арифметическое
Человечество с давних времён для хранения информации использовало таблицы.

Дисперсией ряда чисел называется среднее арифметическое
Как представить информацию в виде таблиц?

Дисперсией ряда чисел называется среднее арифметическое
Как читать и составлять таблицы?

Дисперсией ряда чисел называется среднее арифметическое
Чтение и составление
таблиц

Дисперсией
Как устроены таблицы

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
В любой таблице есть столбцы.

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Кроме столбцов есть строки.

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
А это ячейки.

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Рассмотрим страницу классного журнала. Перед вами часть таблицы с отметками по математике за две недели октября.

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Рассмотрим таблицу по вертикали. Первый столбец −
номера ребят по списку, второй столбец −список фамилий.

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Дальше идут столбцы оценок по дням.
Например, 14 и 22 октября оценки стоят у всех.

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Однако чаще ученика интересует не вся таблица, а только одна её строка. Например, Олега Баталина интересует 2 строка.

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Кто из учащихся учился лучше всех за эти две недели?

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Кто из учащихся учился лучше всех за эти две недели?

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Какую отметку получил Олег Баталин 20 октября?

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Как устроены таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Какую отметку получил Олег Баталин 20 октября?

№

Список учащихся

Октябрь

13

14

15

16

17

20

21

22

23

24

1

Аржанов Иван

4

4

5

5

2

Баталин Олег

3

2

5

4

3

Бибичев Андрей

5

4

4

4

4

Дунаева Ольга

4

4

4

4

5

Захарова Елена

3

4

н

н

2

3

6

Иванов Денис

5

5

5

Дисперсией ряда чисел называется среднее арифметическое
Как составлять и читать таблицы

Как составлять таблицы
Дисперсией ряда чисел называется среднее арифметическое
Пример 1. В школе проводилась олимпиада по математике. При правильном решении задач можно было получить 40 баллов. Работы оценивались так:
от 1 до 10 баллов − слабо,
от 10 до 20 баллов − удовлетворительно,
от 20 до 30 баллов − хорошо,
от 30 до 40 баллов − отлично.
Было решено за отличные результаты
давать приз, а за хорошие − грамоты.

Как составлять таблицы
Дисперсией ряда чисел называется среднее арифметическое
Результаты олимпиады занесли в таблицу.

Число баллов

Число учащихся

1 − 10

3

10 − 20

7

20 − 30

6

30 − 40

4

Всего

20

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Сколько человек получили низкие результаты?

Число баллов

Число учащихся

1 − 10

3

10 − 20

7

20 − 30

6

30 − 40

4

Всего

20

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Сколько человек получили низкие результаты?

Число баллов

Число учащихся

1 − 10

3

10 − 20

7

20 − 30

6

30 − 40

4

Всего

20

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Сколько человек получили грамоты?

Число баллов

Число учащихся

1 − 10

3

10 − 20

7

20 − 30

6

30 − 40

4

Всего

20

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Сколько человек получили грамоты?

Число баллов

Число учащихся

1 − 10

3

10 − 20

7

20 − 30

6

30 − 40

4

Всего

20

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Сколько человек получили призы?

Число баллов

Число учащихся

1 − 10

3

10 − 20

7

20 − 30

6

30 − 40

4

Всего

20

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Ответьте на вопрос:
Сколько человек получили призы?

Число баллов

Число учащихся

1 − 10

3

10 − 20

7

20 − 30

6

30 − 40

4

Всего

20

Дисперсией ряда чисел называется среднее арифметическое
Как составлять и читать таблицы

Как составлять таблицы
Дисперсией ряда чисел называется среднее арифметическое
Пример 2. Таблица по итогам шахматного турнира.

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как составлять таблицы
Дисперсией ряда чисел называется среднее арифметическое
1очко − победа, 0 очков − проигрыш, очка − ничья.

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как составлять таблицы
Дисперсией ряда чисел называется среднее арифметическое
Почему есть закрашенные клетки?

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как составлять таблицы
Дисперсией ряда чисел называется среднее арифметическое
Шахматист не может играть сам с собой.

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Как сыграли между собой Виноградов и Антипов?

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Виноградов выиграл, а Антипов проиграл.

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Сколько партий сыграно вничью?

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Сколько партий сыграно вничью?

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Назовите победителя турнира и его набранные очки.

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Как читать таблицы
Дисперсией ряда чисел называется среднее арифметическое
Назовите победителя турнира и его набранные очки.

№

Фамилия, имя

1

2

3

4

Очки

Место

1

Виноградов Олег

0

0

1

1

3 – 4

2

Галкин Михаил

1

1

1

3

Поликарпов Сергей

1

0

2

4

Антипов Евгений

0

0

1

1

3 – 4

Дисперсией ряда чисел называется среднее арифметическое
Приведите примеры разных таблиц

Активные приёмы работы с текстом на уроке математики.

     Главная особенность работы с текстом на уроке  математики в том, что  ученикам  приходится работать с нехудожественными  текстами, которые характеризуются установкой на однозначность восприятия.

     На уроках математики встречаются и сплошные тексты (статья в учебнике) и, чаще всего, несплошные. К несплошным текстам относятся таблицы, графики, схемы, диаграммы.

    Одной из самых эффективных форм подачи, систематизации и  моделирования информации являются таблицы.

Умение использовать различные способы кодирования информации в знаково-символической или графической форме – это метапредметное (познавательное) умение. Однако в курсе изучения математики в 1- 4 классах умение работать с таблицами является и предметным результатом. Данные планируемые результаты формируются при работе с информацией и решении задач (слайд )

Виды таблиц на уроках математики в начальной школе (слайды):

Информационные таблицы содержат данные, которые ученику нужно использовать при выполнении задания. Могут быть указаны площади стран, количество попаданий… и другие показатели. Дети получают задания: «найди информацию», «классифицируй», «расположи по уменьшению» (и возрастанию), «сделай вычисления», «составь вопросы по таблице» и т.д.

К информационным таблицам можно отнести таблицы, заполняемые  по результатам выполнения практической работы;
Справочные таблицы в первом классе показывают числа в пределах 20 с разных точек зрения. И далее, они помогают познакомить учеников с названиями чисел, видами вычислений, разрядами чисел и т.д.

Логические таблицы ставят перед учениками логические задачи: проанализировать данные, найти закономерности. Например: «дополни таблицу нужными элементами» (фигурами/числами), «продолжи запись», «сопоставь числа и формулы», «вставь подходящее число из предложенных и сделай вычисление» и т.д.
Вычислительные таблицы являются формой вычислительного задания, то есть ученики производят вычисления непосредственно в таблице. Так школьники повторяют компоненты действий и составы чисел, работают с множителями, делимыми, разностями, остатками и т.д.
Таблицы для решения задач подобны вычислительным таблицам, однако используются в заданиях с текстовыми задачами, сопровождаются иллюстрациями, схемами. Такие таблицы часто предусматривают работу с формулами и с пропорциями.

Традиционно в начальной школе таблицы составляют при решении задач:

-) на расчёт стоимости (цена, количество, стоимость);

-) задач, в которых рассматриваются процессы движения (скорость, время, расстояние);

-) на нахождение работы (производительность труда, время, объём работы);

-) на нахождение массы (масса 1 предмета, количество, общая масса / масса всех предметов);

-) логических задач.

Система заданий, направленных на формирование умений работы с таблицами, должна включать задания, развивающие умения извлекать и анализировать информацию, представленную в таблице (умение читать), а также умение представлять необходимую информацию в виде таблицы.

Использование табличной формы позволяет расположить данные компактно, наглядно и рационально. За счёт чего облегчается их анализ, вскрываются те или иные характерные особенности изучаемых явлений: сходство и различие, взаимосвязь признаков и т. п. Это достигается тем, что внутри таблицы сведения располагаются рядами и столбцами, что дает возможность охватить их взглядом и сравнить между собой.

Традиционно выделяют три этапа, по которым следует проводить работу учащихся с текстом на уроках математики:

1 этап – работа до чтения; 

2 этап – работа с текстом задачи непосредственно и решение;

3 этап-  работа после чтения и решения. 

Этапы обучения работе с таблицами при решении задач:

1.Начальный этап: понимание элементов таблицы и чертёж (слайд).

При работе с таблицами в начальной школе следует объяснить ученикам, что в самом простом случае таблица делится на строки и столбцы. Обычно каждый столбец имеет название, которое указывается в первой строке таблицы. До выполнения заданий, в которых информация представлена в таблице, необходимо отработать умение ее читать.

Это можно сделать при помощи вопросов:

–  какую информацию из нее можно извлечь;

– зачем таблица в задании;

– какая информация представлена в столбцах, в строках;

-назовите, сколько строк в таблице; сколько столбцов;

– что представлено в столбцах, в строка;

какое значение у ячейки…; какие данные в ней представлены и др.

2. Методика работы с текстом задачи на уроке.

1) Поиск информации и понимание прочитанного- подготовительная работа к решению задачи. 

Стратегии работы с текстом во время чтения:

–  чтение с остановками (беседа),

 – чтение про себя с пометками – выделение ключевых/опорных  слов (ставим перед учениками задачу: представьте себя авторами учебника, какие слова вы бы выделили для облегчения понимания задачи) или выделение цветом (например, зеленой ручкой подчёркиваем, что дано; красной – что надо найти).

2) Преобразование и интерпретация информации.

Стратегия моделирования — преобразование объекта в модель, где выделены существенные характеристики объекта.    

Построение  модели задачи, с последующим анализом, активизирует познавательную деятельность учащихся. Правильно составленные таблицы являются математическими моделями.

Таблица удовлетворяет главному требованию модели: она отражает как количественные отношения, так и структуру связей между данными величинами и искомыми.

Работа над любым видом задач начинается с простых задач ( в 1 действие). (слайд)

Большое внимание обычно уделяется задачам на нахождение цены/ количества/ стоимости и задачам на движение. Поэтому я буду использовать фрагменты уроков при решении задач на нахождение массы.

– Читаем задачу. Масса пакета с мукой – 2 кг. Узнай массу 4 таких пакетов.  Заносим данные в таблицу:                                                                                          (.)

Масса 1  пакета	Количество	Общая масса
2 кг	4п.	?

Устанавливаем взаимосвязь между понятиями «масса 1 пакета», «количество пакетов» и «масса всех пакетов» (общая масса). Рассуждаем и делаем вывод: чтобы найти массу всех предметов, нужно массу одного предмета умножить на количество предметов.

Стрелками обозначаю связь компонентов задачи (движение слева направо- умножаю) и выбор действия.

– Прочитаем вторую задачу. Масса 4 одинаковых пакетов с мукой – 8 кг. Узнай массу одного пакета.                (:)

Масса 1  пакета	Количество	Общая масса
?	4п.	8 кг

Сделаем вывод: чтобы найти массу одного предмета, нужно массу всех предметов разделить на количество предметов. Стрелками обозначаю связь компонентов задачи (движение справа  налево- делю) и выбор действия.

Аналогично работаем с третьей задачей.

Фрагменты уроков в 3 классе: решение составных задач на нахождение  массы. (слайды).

Я планирую решение таких задач на серии уроков с последующим усложнением работы

1 день-  первоначально в рабочем листе (экономим время на чертёж) дана готовая таблица. Учащиеся дополняют её из условия задачи. Работа с моделью позволяет ученикам яснее увидеть зависимости между данными и искомыми величинами и оценить задачу в целом. 

2 день- теперь предлагаем учащимся самостоятельно заполнить ячейки готовой  таблицы.

3 день- учащиеся самостоятельно озаглавливают и вносят данные в таблицу. Обращаем внимание учеников, если речь идёт о разных объектах, добавляем столбец наименование.

После заполнения таблицы (до решения) ученики самостоятельно проверяют заполнение таблицы по ключу. Анализируют и корректируют ошибки (в паре). Обсуждают план решения задачи и выполняют решение.

Каждый раз при решении задач с помощью таблицы обучающийся должен провести цепочку рассуждений (разбор задачи), которые приведут его к составлению плана решения задачи.

    Благодаря таблице текст превращается в информационную структуру со связями заданного вида.

3) Следующий этап-  проверка решения задачи- оценка информации.

Составление и решение обратной задачи.

При проверке решения задачи этим способом учащиеся, должны выполнить ряд действий: 1) подставить в текст задачи найденное число; 2) выбрать новое искомое; 3) сформулировать новую задачу; 4) решить составную задачу; 5) сравнить полученное число с тем данным первой задачи, которое было выбрано в качестве искомого, и на основе этого сравнения со ставить соответствующее умозаключения о правильности решения задачи.

Важно чтобы обучающиеся записывали полный ответ к задаче. Это приучает перед тем,  как написать ответ, еще раз прочитать вопрос задачи и спросить: «На все ли вопросы задачи я ответил?».

3. Организация дополнительной работы с решенной задачей. 

Также для развития читательской грамотности и умения решать текстовые задачи важно организовать дополнительную работу с решенной задачей.

Ученик научится решать задачи конкретного вида, когда пройдёт все этапы. Умение перейдёт в навык, когда ученик не только будет произвольно воспроизводить усвоенное, но и применять.  На этом этапе я провожу работу по изменению условия задачи, составление своей задачи по аналогии.  (Обучающие самостоятельно меняют условия задачи. Работа может быть организована в группах, парах или по рядам).

Данная таблица наглядно показывает, на каком этапе математическая и читательская грамотность соединяются – когда учащиеся начинают действовать.

Прием смыслового чтения (читательская грамотность)	Этап решения задач (математическая грамотность)	Умения учащихся (читательская грамотность)	Действия учащихся (читательская и математическая грамотность)
Поиск информации и понимание прочитанного	Анализ содержания задачи.  Поиск пути решения задачи и составление плана ее решения	Ориентироваться в содержании текста и понимать его целостный смысл, находить в тексте требуемую информацию.	Читают задачу. Находят и подчеркивают ключевые слова. По ключевым словам, пересказывают текст задачи.
Преобразование и интерпретация	Осуществление плана решения задачи.	Преобразовывать текст, используя новые формы представления информации.	Составляют краткую запись в виде таблицы и решают задачу.
Оценка информации	Проверка решения задачи.	Подвергать сомнению достоверность получаемой информации, обнаруживать её.	Подставляют полученный результат в текст вопроса.

Сделаю вывод: Успешное обучение в начальной и основной школе невозможно без сформированности у обучающихся читательской грамотности. На уроках математики активным приёмом работы с текстом является таблица. Она как модель помогает анализировать текст задачи, определить ход мыслительного процесса (верно выбрать действие) и, соответственно, решить задачу. Таблица будет помогать в обучении, если соблюдены основные принципы работы с ней.

1. Таблица  должна быть «живой», действенной моделью, создаваться самим учеником (совместно с учителем).
2. Принцип единообразия.  Величины, занесенные в первый и третий столбики таблицы, должны находиться в прямопропорциональной зависимости.
3. Таблица должна помогать анализу данных, не обременять решение.
4. Принцип преемственности. Обучение составлению таблиц должно начинаться в период обучения решению арифметических задач в начальных классах и продолжаться в 5 – 6 классах.

Важнейшей задачей современной школы является
формирование у учащихся умений самостоятельно
применять и приобретать знания. Но как это
сделать? Каждый учитель ищет свой путь
разрешения этой проблемы. Я вижу её решение в
использовании на уроках различных приёмов
систематизации и обобщения знаний.

Их регулярное применение позволяет
сформировать у учащихся умения устанавливать
логические связи между понятиями, тем самым
развивает логическое мышление, выступает
средством предупреждения и ликвидации
формализма в знаниях учащихся, позволяет
сформировать такую систему знаний, которая
представляется как динамичная, качественно
изменяющаяся.

Применяя различные приёмы систематизации и
обобщения знаний, учитель может разнообразить
работу на уроке, тем самым поддерживать интерес к
изучаемому предмету. Кроме того, эти приёмы носят
общепредметный характер, следовательно, их
применение способствует развитию общеучебных
навыков: работа с текстом, проведение
структурного анализа материала, составление
планов, конспектов, установление связей и
отношений между понятиями и представление их в
наглядной форме в виде схем, таблиц, логических
цепочек рассуждений. Математика как никакая
другая наука позволяет в полной мере
сформировать эти навыки. Таким образом, учитель с
одной стороны формирует прочные знания по
предмету, с другой – поддерживает интерес к
учению в целом.

Особое внимание стоит уделить таблицам, так как
их использование позволяет: развивать
логическое и аналитическое мышление, память,
формировать умения самостоятельно проводить
обобщение знаний, что способствует повышению
прочности и осознанности знаний.

Формирование навыка работы с таблицами
необходимо начинать как можно раньше: на первом
этапе – это заполнение предложенных таблиц, в
дальнейшем – их самостоятельное составление.

При регулярной работе с таблицами учащиеся
прекрасно сами формулируют алгоритм создания
таблиц:

• Выделить объекты.
• Выделить свойства объектов.
• Объекты и их свойства разнести по столбцам и
  строкам.
• Заполнить составленную таблицу.

Однако все таблицы должны отвечать
определённым требованиям: лаконичность и
наглядность. По характеру материала таблицы
можно разделить на систематизирующие и
сравнения. В систематизирующих таблицах можно
объединить величины, характеризующие
определённый класс явлений или других понятий
одного вида (Приложение 1). В
таблицах сравнения можно сопоставить или
ограничить схожие понятия (Приложение
2).

Как использовать таблицу? На этот вопрос каждый
учитель может сам найти ответ. Всё зависит от
цели, которую ставит педагог на уроке:
актуализации знаний, проверка ранее изученного
материала или его закрепление, обобщение и
систематизация. Рассмотрим пример использования
одной таблицы (Приложение 3).

Таблица может служить средством соотнесения
конкретных изучаемых вопросов с содержанием
всего раздела, осознания структуры изучаемой
темы целиком. Анализируя содержание таблицы,
ученик может оценивать вес каждого изучаемого
вопроса, более чётко представить процесс
изучения раздела целиком.

Ученики могут заполнить таблицу
непосредственно по мере изучения нового
материала: таблица может служить итогом
объяснения учителя, самостоятельного изучения
материала, результатом семинарского занятия или
практикума.

Для проверки уровня усвоения знаний можно
предложить заполнить всю таблицу или некоторые
её части по памяти.

При обобщении и систематизации знаний таблица
может служить средством подведения итогов
изучения темы. Повторяя основной пройденный
материал, учащиеся самостоятельно или при помощи
учителя могут заполнить предложенную таблицу,
либо могут сами составить таблицу по изученной
теме.

Кроме того, таблица может быть частью опорного
конспекта и служить опорой для самостоятельного
изучения темы и расширения знаний.

Подводя итог, можно сказать, что, используя
таблицы на уроках, мы можем добиваться:

• неформального усвоения темы;
• прочности знаний;
• осознанной работы с учебной литературой;
• самостоятельной ликвидации пробелов в своих
  знаниях или расширять и углублять их.

Приведу примеры таблиц, которые я использую в
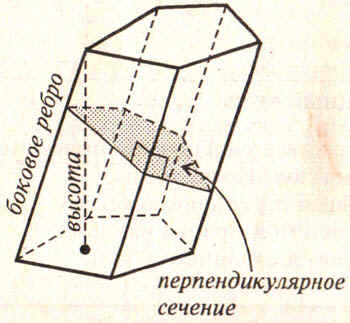
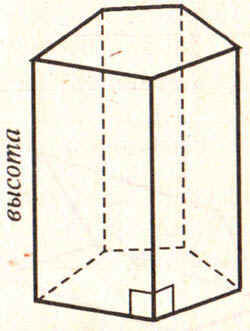
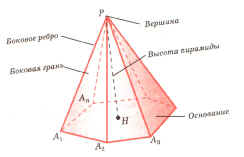
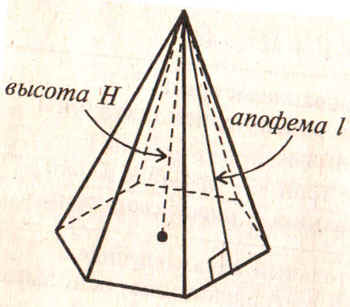
своей работе по теме “Многогранники” в 10 классе.
Это даст возможность составить более полное
представление об использовании таблиц в
обучении (Приложение 4).

Таблицы 1, 2, 3, 5 удобно заполнять в ходе
проведения практических работ. Для их проведения
потребуются наборы геометрических тел:
различные виды призм, пирамид. В этом случае
таблица может служить результатом
исследовательской работы. Применяя такие формы
обучения, есть реальная возможность изучить
большой объём теоретического материала за более
короткое время и больше времени отвести на
решение задач.