1 июля 2011
Elitarium.ru, 1 июля 2011г.
Предисловие редакции HT.ru:
Данная статья адресована, в первую очередь, маркетологам и социологам, которые занимаются проведением массовых опросов и исследований. Но нам бы хотелось, чтобы с этим материалом были знакомы наши hr-ы. Даже если Вы еще никогда не занимались проведением опросов в своей организации, поверьте, Вам предстоит когда-нибудь столкнуться с этой интереснейшей областью работы. И одной из первых проблем, которая встанет перед Вами, будет вопрос “Кого привлекать к опросу?”. Скажем так, данная статья не даст простого и четкого ответа на этот, в действительности, непростой вопрос. Но, прочитав ее, Вы сможете по-новому, осмысленнее и более профессионально взглянуть на тот фронт работ, который представляет собой проведение опросов. Например, Вы сможете предугадать, чьи ответы Вы получите в случае, когда опрос в организации будут проходить “все желающие”.
Редакция HT.ru
Автор статьи: Игopь Cтанислaвович Бepeзин, консультант по маркетинговым стратегиям, президент Гильдии мapкетoлoгов (г. Моcква).  Опрос и анкетирование являются ведущими, универсальными методами проведения социологических и маркетинговых исследований. Чаше всего, когда говорят о маркетинговом исследовании — сборе первичной информации, имеют в виду именно опрос или анкетирование, предполагающие прямое выяснение, непредвзятого мнения достаточно многочисленной группы респондентов.
Опрос и анкетирование являются ведущими, универсальными методами проведения социологических и маркетинговых исследований. Чаше всего, когда говорят о маркетинговом исследовании — сборе первичной информации, имеют в виду именно опрос или анкетирование, предполагающие прямое выяснение, непредвзятого мнения достаточно многочисленной группы респондентов.
Массовым считается опрос, в ходе которого путем личной беседы сотрудника исследовательской компании — интервьюера с носителями информации (респондентами), состоящей из нескольких десятков коротких вопросов, изучаются мнения нескольких сотен (тысяч) человек. Под анкетированием понимают безличную форму общения исследователей с носителями информации, при которой респонденты самостоятельно отвечают на вопросы анкеты, следуя содержащейся в ней инструкции и не вступая в непосредственный контакт с интервьюерами.
Конечной целью анкетирования и массового опроса является получение данных, характеризующих так называемую генеральную совокупность. Генеральная совокупность — это все представители какой-либо группы, носители какого-либо важного признака, например:
-
все российские избиратели;
-
все потенциальные потребители пива, проживающие в Перми;
-
все подростки (12-16 лет) Поволжского региона;
-
все учителя физики и химии, работающие в средних школах;
-
все домохозяйства, имеющие доход от 500 до 1 500 долл. в месяц;
-
все компании, занимающиеся розничной торговлей в Самаре и т. д. и т. п.
Для того чтобы опросить десятки или сотни тысяч, а тем более — миллионы человек (компаний), из которых может состоять генеральная совокупность, нужны сотни или даже тысячи интервьюеров. На проведение подобного исследования могут понадобиться десятки, если не сотни миллионов долларов и не менее полугода напряженной работы. Такое возможно только при переписи населения (проводящейся не чаще одного раза в 10 лет).
Однако в маркетинге этого и не требуется. Достаточно того, чтобы относительно небольшая выборка (от нескольких сотен до нескольких тысяч представителей) репрезентировала (выразила) мнение генеральной совокупности. Как такое возможно? На каком основании можно распространять данные, полученные от небольшой группы людей, на существенно (в десятки и сотни раз) большую группу? На основании гипотезы о том, что на поведение, знания, отношение потребителей к компании, товару, услуге или отдельных их компонентов оказывают влияние социально-демографические характеристики самих потребителей.
Иными словами, большинство представителей четко определенной социально-демографический группы будут сходным образом реагировать на внешние, в данном случае — рыночные стимулы: товар, цену, упаковку, рекламу и т. д. и т. п. И нет никакой необходимости опрашивать всех представителей этой группы, поскольку ее мнение (с допустимой погрешностью) может представить (репрезентировать) небольшая выборка из ее представителей.
Способы построения выборки
Существуют две группы методов построения выборки, в той или иной степени реализующих репрезентацию мнений и позиций генеральной совокупности: вероятностные и детерминированные.
Первая группа методов (вероятностные) базируется на использовании теории вероятности. В основе ее применения лежит постулат, что репрезентация будет достигнута в случае, если каждой единице генеральной совокупности обеспечено равновероятное попадание в выборку. Например, если генеральной совокупностью является все взрослое (16-85 лет) население города (200 тыс. человек), то каждому жителю должна быть обеспечена вероятность стать участником исследования(попасть в выборку), равная 1 / 200 000. В противном случае выборка будет не случайной, а смещенной, т. е. менее репрезентативной.
Реализовать это можно в случае, если все элементы генеральной совокупности могут быть тем или иным образом пронумерованы, а затем эти номера будут выбраны в определенной последовательности — «по воле случая». Например, в Москве около 2 500 средних школ, каждаяиз которых имеет свой номер. Мы могли бы выбрать наугад 100 номеров и провести опрос 100 директоров (завучей, учителей физики, классных руководителей 11-х классов и т. п.) в этих школах.
Эти 100 номеров мы можем выбрать с помощью таблицы или «генератора случайных чисел» (есть такая специальная компьютерная программа), а также с помощью «барабана» но принципу того, как это делается при проведении лотереи. Такие способы построения выборки называются «простой случайной выборкой». Каждый ее элемент отбирается независимо и имеет равную вероятность попасть в выборку.
Мы могли бы выбрать наугад любое число от 1 до 25, например— 12, а затем взять в выборку школы с номерами: 12, 37, 62, 87, 112, 137 и т. д. Такой метод построения называемся «систематической выборкой», первый элемент которой выбирается произвольно, а затем выбирают каждый i-й элемент.
Мы также могли бы сначала разделить эти школы на несколько страт (возможно, и пересекающихся), например, на школы физико-математические, спортивные, лингвистические и гуманитарные, а затем произвести случайную или систематическую выборку (по 20-30 школ) из каждой страты. Такой метод построения называется «стратифицированной выборкой».
Разновидностью стратифицированной выборки является «маршрутная выборка», суть реализации которой состоит в следующем. Город делится на 20-40 «секторов» по числу интервьюеров, задействованных и исследовании. Каждый интервьюер получает один сектор, маршрут обследования «своего» сектора и инструкцию по реализации простой случайной выборки. Например такую: «Начать обход с улицы Баумана, с дома № 2, третьего подъезда, второго этажа сверху, первой квартиры слева. Затем — дом № 4, второй подъезд, третий этаж, вторая квартира справа… Потом — переулок Комсомольский, нечетная сторона… Потом — тупик Коммунизма… и т. д.»
Наконец, мы могли бы разделить генеральную совокупность на непересекающиеся кластеры, к примеру, по муниципальным районам (их в Москве 125, и в каждом в среднем по 20 школ). Затем случайным образом выбрать пять районов и произвести обследование всех школ данного муниципального района. Такой метод построения называется «кластерной выборкой».
Тем не менее у вероятностных методов построения выборки есть один весьма существенный недостаток. Каждый из них исходит из предположения о том, что все элементы генеральной совокупности являются равнодоступными: и в «техническом» смысле (у всех есть телефон для телефонного опроса или доступ в Интернет), и в «психологическом», т. е. все респонденты с примерно равной вероятностью согласятся или откажутся принимать участие в исследовании. Однако это не так.
Граждане с относительно высокими доходами менее доступны для исследователей, чем те, чьи доходы невысоки. И нет никакой силы, которая могла бы заставить этих люден отвечать им вопросы социологов или маркетологов. Поэтому все выборки всегда смещены в сторону средне- и малообеспеченных групп населения. Во всех без исключения странах мира.
Менее образованные граждане идут на контакт с социологами менее охотно, чем лица с высшим образованием. Поэтому в большинстве выборок доля хорошо образованных граждан как правило существенно выше, чем в генеральной совокупности.
Никто из сотрудников исследовательских компаний не желает общаться с бомжами, алкоголиками, наркоманами, психо- и социопатами и прочими маргиналами. И у руководителя исследования нет решительно никаких возможностей заставить своих сотрудников делать это. А между прочим, к этим группам в России по взвешенным оценкам относится от 12 до 15% жителей Следовательно, любая выборка смещена в сторону «вменяемых» граждан.
Некоторые граждане боятся отвечать на вопросы, даже самые невинные. Таких людей немного, но они есть. А вот способов заставить их участвовать в опросе нет.
Наконец, есть люди, которые просто не желают участвовать в исследовании. У них есть время, они ничего не боятся, они все понимают, но на вопросы отвечать отказываются. И точка.
Таким образом, все выборки в маркетинге и социологии являются смещенными в сторону средне- и малообеспеченных, более образованных, контактных и вменяемых граждан. Они и репрезентируют общее мнение генеральной совокупности. И все исследователи рынка прекрасно это знают.
Преодолеть наложенные выше проблемы можно с помощью метода «квот», относящегося к детерминированным методам, при котором априори обеспечивается пропорциональное представительство носителей существенных признаков (пол, возраст, доход, образование и т. п.) генеральной совокупности в выборке.
Это наиболее эффективный, на наш взгляд, метод проведения массовых опросов. При его использовании существенно облегчается задача поиска корреляционных связей, сравнения различных типов (групп) потребителей между собой и экстраполяции выявленных закономерностей на генеральную совокупность.
Единственная, но весьма существенная трудность при реализации него метода состоит в том, что не всегда доподлинно известно распределение всех важных параметров в самой генеральной совокупности. В этом случае исследователь или консультант исследовательского проекта должен взять на себя смелость распределить квоты по своему усмотрению, в соответствии со своим видением, пониманием рынка.
Задача достижения строгой репрезентативности не всегда является важной. Иногда целесообразно воспользоваться существенно более простыми в реализации детерминированными методами:
-
нерепрезентативным, или произвольным, когда опрашивают того, кто «попался под руку» интервьюеру и согласился участвовать в опросе. Естественно, этот метод дает крайне ненадежные результаты. А вдруг под руку попадется рота солдат или команда баскетболисток! Однако его использование допустимо в исследованиях, носящих поисковый характер, не требующих большой точности, при проведении «пилотажа» анкеты. «Произвольность» можно компенсировать большим объемом выборки, из которой затем можно будет попробовать отобрать необходимое число «подходящих» анкет и составить уже из них репрезентативную в каких-то отношениях выборку;
-
поверхностным — когда отбор осуществляется по самым общим признакам, задаваемым исследователем интервьюерам в виде не очень строгого задания;
-
« воронки» — когда сначала отбираются наиболее «контактные», а затем среди них — наиболее «компетентные», подходящие респонденты;
-
« концентрации» — на представителях отдельных, сопоставимых сегментов рынка, среди которых проводят «сплошной» опрос. Например, школьный 11 «А» класс может представлять всех старшеклассников школы или даже города как «обычный», «типичный класс»;
-
«снежного кома» — когда начальная группа подбирается случайным образом, а дальнейший отбор ведется из кандидатов, указанных первыми респондентами, и т. д.
Достоверность и погрешности измерений
Под «достоверностью», уровнем достоверности понимают показатель вероятности того, что истинное значение изучаемого параметра генеральной совокупности попадет в доверительный интервал. Чем выше задаваемый уровень достоверности, тем больше должна быть выборка. Под доверительным интервалом понимают диапазон, в который попадет истинное значение изучаемого параметра генеральной совокупности при данном уровне достоверности. Чем он меньше, тем больше должна быть выборка.
К примеру, общероссийская городская выборка (14-65 лет) в 1 200 респондентов имеет доверительный интервал 4 процентных пункта при уровне достоверности 0,95. При ее проведении 15% участников опроса заявили, что за последние три месяца были в кинотеатре хотя бы один раз.
Эти данные позволяют нам утверждать с заданным уровнем достоверности, что от 11 до 19% жителей российских городов в возрасте от 14 до 65 лет были в кинотеатре хотя бы один раз за последние три месяца. Иными словами, можно сказать, что все значения между 11 и 19% в данном случае находятся в пределах «допустимой статистической погрешности». Если бы мы хотели задать доверительный интервал в 2 процентных пункта, то выборку (при прочих равных условиях) пришлось бы увеличить примерно в четыре раза.
Со стороны уровня достоверности эти данные означают, что если бы было проведено 100 независимых измерении (опросов) по 1200 респондентов в каждом, то в 95 из них значение доли ответов на вопрос о посещении кинотеатра не вышло бы за пределы доверительного интервала (в этом конкретном случае — 11-19%). А в пяти исследованиях или бы получены значения, выходящие за пределы доверительного интервала. Если бы нас устраивала достоверность на уровне 0,9, то опросить можно было бы 200 человек. Если нам нужна достоверность на уровне 0,99, то пришлось бы опросить более 10 тыс. человек.
Оптимальный размер выборки
Вот одна из формул расчета необходимого объема выборки, используемая при известном среднем отклонении (дисперсии) и заданных уровнях достоверности и точности:
N = (g2 * z2) / d2
где: N — искомый объем выборки; g — дисперсия признака, ожидаемое среднее отклонение получаемых результатов от ожидаемого среднего значения; z — коэффициент уровня достоверности (2 — для 0,95, 3 — для 0,99); d — уровень точности.
Допустим, мы изучаем поведение покупателей в продовольственном магазине, в частности, мы хотим определить среднюю сумму чека. Из бесед с владельцем магазина мы узнаем, что она может быть в районе 500-700 руб., а среднее отклонение (g) может составить 200 руб. В ходе опроса мы хотели бы определить среднее значение с точностью (d) до 20 руб. при уровне достоверности (z) в 0,95. Подставляем значения формулу и получаем:
40000 * 4 / 400 = 400.
То есть нам достаточно опросить 400 покупателей. Если бы мы хотели узнать среднюю сумму чека с точностью до 10 руб.. то нам пришлось бы опросить 1600 покупателей. Если бы при этом мы хотели получить уровень достоверности в 0,99, то количество покупателей, которых необходимо опросить, составило бы 3 500 человек. И наоборот: если нас устроила бы точность ±50 руб., то нам достаточно было бы опросить в заданных условиях всего 65 человек.
Практическое использование этой и других формул, которые здесь не будут приводиться, весьма затруднено следующими обстоятельствами:
-
Что делать, если мы не знаем даже приблизительно «ожидаемую среднюю» и среднюю дисперсию признака?
-
Что делать, если в анкете у нас 10 вопросов, по которым ожидаются различные средние, с различными средними дисперсиями?
-
Как быть в случае использования номинальных шкал?
-
Как быть в случае, если один вопрос предполагает два или три варианта ответа и т. д. и т. п.?
-
Для простых альтернативных вопросов по принципу «да/нет» используются одни формулы, для более сложных — другие.
-
Формулы необходимо корректировать в зависимости от количества столбцов в таблице «факторных распределении», а также в зависимости от распределения ответов (10 на 90 — это одно, а 45 на 55 — совсем другое дело).
-
Одни формулы учитывают размер генеральной совокупности, а другие (как приведенная выше) — нет. Есть много иных нюансов.
На практике сначала определяют количество респондентов, которое исследователи предполагают опросить с учетом временных и финансовых ограничений, задают уровень достоверности (обычно — 0,95), а затем уже рассчитывают доверительный интервал.
Определение необходимого и достаточного объема выборки происходит на основе опыта и неформальных «конвенций» исследователей между собой. Считается, и это многократно проверено на практике, что опрос 30-50 представителей конкретной, «узкой» социально-демографической группы населения, например «ярославских замужних женщин в возрасте 30-45 лет, имеющих одного ребенка, высшее образование и совокупный семейный доход в пределах от 1 500 до 3 000 долл. в месяц», можно распространять на всю эту группу, и допустимая ошибка (доверительный интервал) не превысит 4 процентных пунктов при уровне достоверности около 0,95.
Однако полученные данные нельзя распространять, например, на незамужних женщин того же возраста, имеющих такой же доход и уровень образования. А также на женщин, имеющих иной доход, возраст или уровень образования. И уж тем более — на мужчин.
Таким образом, если в задачу исследователя входит получение информации о мнениях, знаниях, поведении или отношении к некой проблеме всех ярославских женщин, и при этом все перечисленные выше социально-демографические факторы являются значимыми, необходимо построить такую выборку, в которой были бы представлены все «узко определенные» группы. В данном случае — две группы по семейному положению, три — по наличию и количеству детей, три возрастные, три доходные, две образовательные. Итого 108 групп, в каждой из которых должно быть не менее 30 представительниц. Всего — более 3 000 респондентов.
На самом деле едва ли найдется вопрос или проблема, на которые все пять факторов будут оказывать взаимное перекрестное воздействие. В большинстве случаев вполне можно было бы обойтись опросом 400-600 респонденток, а затем провести попарный (а не перекрестный) факторный анализ. То есть отдельно исследовать влияние факторов «возраст», «образование», «доход», «семейное положение», «дети». При этом выборка каждый раз разбивалась бы на две-три группы, наполнение которых было бы не меньше 100-150 респондентов.
Репрезентативная выборка, представляющая все население России, должна состоять из 3 600-9 000 человек и 180 групп (два пола, три возраста, два образовательных уровня, три доходные группы, пять типов поселений). Доверительный интервал будет в пределах ±3 процентных пункта. Это означает, что, к примеру, если 30% (12% или 45%) наших респондентов заявили, что регулярно употребляют в пищу майонез, то долю потребителей майонеза в России можно оценить в 27-33% (9-15 или 42-48% соответственно).
Размер выборки практически не зависит от размера генеральной совокупности. И в мегаполисе с населением более миллиона человек, и в уездном городе с населением в 35 тыс. человек для построения выборки, репрезентативной по одинаковому числу параметров, потребуется опросить одинаковое число респондентов.
От чего действительно зависит размер выборки — так это от числа параметров, по которым мы желаем добиться репрезентативности. Если нас устраивает репрезентативность только по полу и возрасту, то выборки в 400 человек в одном населенном пункте будет более чем достаточно. Если параметров три, количество респондентов придется увеличить до 600. Добиться репрезентативности выборки одновременно по пяти параметрам: полу, возрасту, доходу, образованию, сфере профессиональной деятельности — можно лишь на выборке из 1 000-1 200 человек в одном населенном пункте.
В вашей почте раз в неделю. А еще: новости, акции и мероприятия для HR.
1. Генеральная
совокупность и выборка.
2. Способы построения
выборки.
3. Определение
объема выборки.
1. Генеральная совокупность и выборка
Здесь мы рассмотрим,
каким образом можно получать информацию
о всей совокупности объектов на основе
изучения лишь части совокупности
объектов. Введем понятия.
Генеральная
совокупность
– исходная группа людей, организаций,
событий, текстов, относительно которых
мы хотим сделать выводы.
Выборка
– любая часть генеральной совокупности.
Пусть генеральной
совокупностью будут все избиратели
некоторого города. Тогда выборкой будет,
например, 100 взрослых людей, которых мы
встретили в течение получаса по дороге
с работы домой. Мы спрашиваем их, за
какую партию они собираются голосовать
на ближайших выборах в областную Думу.
Пусть выяснится, что 40 человек согласны
проголосовать за одну партию, а 60 человек
– за другую.
Можно ли на основании
результатов опроса данной части
генеральной совокупности сделать вывод,
что все избиратели города тоже собираются
проголосовать в пропорции 40 к 60?
Может получиться,
что среди городских избирателей больше
половины пожилых людей, а нам встретились
в основном молодые люди. Имеет ли это
значение? Какой должна быть выборка,
которая позволит более или менее
гарантированно делать выводы о генеральной
совокупности в целом?
Ясно одно: невозможно
физически опросить всех избирателей
города, поэтому мы должны научиться
получать знание о генеральной совокупности
на основе изучения ее части.
Эта ситуация – на
основе обозримой части судить о
необозримом целом – напоминает правило
«Искать там, где светлее, а не там, где
потеряли». И действительно: мы измеряем
то, что можно, чтобы получить представление
о том, что нужно.
С такой же ситуацией
мы уже сталкивались в случае
операционализации. Заменяли абстрактное
понятие показателем, который можно
измерить, и считали, что измеряем, пусть
косвенным образом, само абстрактное
понятие.
Задача заключается
в том, чтобы научиться строить такую по
составу выборку, которая, с одной стороны,
позволяла бы делать достоверные выводы
о генеральной совокупности, а с другой
стороны, была бы минимальной по размерам.
2. Способы построения выборки
Выборка называется
репрезентативной1,
если ее изучение позволяет получать
достоверное знание о генеральной
совокупности.
Дадим еще одно
определение: выборка называется
репрезентативной, если ее важные признаки
даются в той же пропорции, как в генеральной
совокупности.
Но для
репрезентативности, как мы только что
указали, нужно обеспечить определенный
состав выборки при минимальном объеме.
Требование противоречиво. Ведь очевидно,
что чем меньше выборка, тем меньше
вероятность того, что она будет близка
по своим свойствам к генеральной
совокупности. И наоборот, при большем
объеме она будет ближе по свойствам к
генеральной совокупности. Поэтому
уточняем, что речь идет о наименьшем
объеме, достаточном для
целей данного конкретного исследования.
В настоящем
параграфе мы рассмотрим сначала способы
формирования состава репрезентативной
выборки.
Для обеспечения
репрезентативности состав выборки
должен определяться на основе рандомизации,
или случайности. Выборка называется
случайной,
если любой
объект, а
также любое
сочетание объектов
генеральной совокупности имеют равные
возможности попасть в выборку.
Рассмотрим способы
формирования выборки, при которых будут
выполняться первое и второе условия.
1. Принцип
лотереи.
Допустим, генеральная совокупность
составляет тысячу человек, среди них
40% мужчин, 60% женщин, половина – с высшим
образованием, три четверти семейных, а
треть преподавателей вузов, а каждый
десятый является иностранцем. Нам нужно
отобрать выборку размером в двести
человек таким способом, чтобы в эту
выборку с одинаковой вероятностью могли
попасть любой мужчина, любая женщина,
любой человек с высшим образованием,
любой из имеющих семью, любой преподаватель
вуза и любой иностранец. А также любое
сочетание из мужчин, женщин, людей с
высшим образованием, семейных
преподавателей вузов и иностранцев.
Чтобы это осуществить,
мы выполняем простую операцию. Переписываем
на отдельных листочках имена всей тысячи
человек, листочки скручиваем, перемешиваем
в барабане и просим кого-нибудь вытащить
наугад двести листочков. От тщательности
перемешивания и зависит выполнение
названных выше условий.
Но ситуация может
оказаться более простой. Пусть в анкете
имеется вопрос о национальности
респондента и пять готовых вариантов
ответа, образующие номинальную шкалу:
калмык, русский, татарин, башкир, якут.
Нужно обеспечить случайный порядок
вариантов ответа, чтобы избежать так
называемого сдвига
в сторону ответной тенденции,
о котором шла речь в предыдущей теме.
Мы записываем
варианты ответа на листочках, скручиваем
их и перемешиваем в барабане, чтобы
вытащить листочки в случайной
последовательности. В этой последовательности
и расставляем варианты ответов на вопрос
о национальности респондента.
2. Использование
таблицы случайных чисел.
Принцип лотереи с барабаном не подходит,
когда исследуется генеральная совокупность
в несколько тысяч объектов. Ведь в таком
случае в барабан соответствующих
размеров надо сложить эти несколько
тысяч скрученных листочков, на каждом
из которых должны быть предварительно
написаны нужные имена. Поэтому используется
таблица случайных чисел, которая строится
особой компьютерной программой. Эту
таблицу можно найти в справочниках по
социологии. В настоящем учебном пособии
она дана в Приложении.
Приведем фрагмент
такой таблицы (табл. 7.1).
Таблица 7.1
Таблица
случайных чисел (фрагмент)
|
10097 66065 |
32533 74717 |
76520 34072 |
13586 76850 |
Допустим, что объем
генеральной совокупности включает N
объектов. А выборка составляет n
объектов. Наметим порядок действий.
Мы нумеруем все
объекты генеральной совокупности: 1, 2,
3, 4, 5…
Опираясь на таблицу,
по определенному правилу отбираем n
чисел, таких, которые по своей величине
не превышают N,
при этом
отбрасывая
повторяющиеся числа.
Пусть N
равно трехзначному числу 500. Будем
включать в нашу выборку три первые цифры
каждого пятизначного числа нашей
таблицы, двигаясь с первого числа вниз
по вертикали. Дойдя до конца первой
колонки, переходим к следующей, двигаясь
так же сверху по вертикали вниз. Выписываем
числа 100, 375, 084, 128, 310, 325, 048…, пропуская
числа, которые больше 500, например, числа
990, 660, 852… Но мы могли бы в пятизначных
числах таблицы использовать последние
три цифры: 097, 422, 019… Или средние цифры:
009, 280, 106, 357, 379, 253, 480, 252… Могли бы двигаться
по диагонали. Можно двигаться разными
способами, но если способ выбран, нужно
следовать ему до конца.
Дальше включаем
в выборку объекты генеральной совокупности,
соответствующие отобранному списку
номеров.
Но что делать, если
речь идет, например, о генеральной
совокупности всех избирателей города
численностью несколько сотен тысяч
человек? Можно, конечно, попробовать
составить общий список, определить
размеры выборки и дальше, используя
таблицу случайных чисел, определить
номера тех избирателей, которые войдут
в нашу выборку.
Но можно действовать
иначе. Пусть нужно получить выборку в
1000 человек. Мы берем список номеров
избирательных участков, который вполне
обозрим. Определяем номера, скажем, 10
участков при помощи таблицы случайных
чисел. Далее возьмем списки избирателей
в каждом из выбранных участков, ясно,
что и эти списки тоже будут вполне
обозримы. Из этих списков составляем
выборки, например, по 100 человек снова
на основе таблицы. Общая выборка включит,
таким образом, 1000 избирателей (10 х 100). В
дальнейшем этот метод мы рассмотрим
более подробно при описании кластерной
выборки.
Отправляться в
таблице можно от верхнего левого угла
или от левого края второй строки, вообще
от любого места. Выбор произволен. Но
дальше, как уже сказано выше, мы должны
двигаться систематически, и не метаться,
меняя правила на ходу.
3. При очень большой
генеральной совокупности можно
использовать метод систематической
случайной выборки.
Так действуют, когда каждый член
генеральной совокупности уже занесен
в единый список в виде телефонной книги,
списка студентов, списка избирателей,
членов какой-либо организации или
документов.
Предположим, что
мы работаем в избирательном штабе
кандидата в депутаты областного
Законодательного собрания. Нам нужно
каждый день определять, сколько из
избирателей округа готовы голосовать
за нашего кандидата, сколько собираются
голосовать за других кандидатов, и
сколько еще вообще не определились.
Мы берем телефонную
книгу и выявляем список номеров округа.
Делим этот список на равные части между
девушками-телефонистками (обычно это
студентки, обучающихся на специальности
«Социология»). Опытным путем определяем
среднее количество номеров, которые
физически сможет обзвонить за рабочий
день одна девушка-телефонистка. Делим
каждую часть общего списка на это
количество номеров и получаем шаг
движения по телефонной книге. Допустим,
этот шаг оказался равным 23.
Далее каждая
телефонистка, начав с первого номера в
ее списке, обзванивает избирателей с
шагом в 23 номера.
Таким образом, за
день охватывается весь округ в целом.
На другой день каждая телефонистка в
качестве исходного берет второй номер
в ее части списка и снова с шагом 23 номера
обзванивает избирателей.
Выясняются адреса
тех избирателей, которые вообще не
слышали о нашем кандидате в депутаты
или планируют голосовать за другого
кандидата. И по этим адресам срочно
выезжают представители избирательного
штаба нашего кандидата для разъяснения
преимуществ его программы.
У систематической
случайной выборки есть недостаток, она
в меньшей степени случайна, чем выбор
на основе лотереи или таблицы случайных
чисел. В результате может быть получена
менее репрезентативная выборка.
Например, проблема
может быть в том, что не все избиратели
имеют домашний телефон или телефонные
номера не всех избирателей присутствуют
в нашем списке. В результате не будет
гарантировано выполнение правила: любой
объект и любое сочетание объектов
генеральной совокупности должны иметь
равные возможности войти в выборку. Это
если речь идет о телефонных номерах.
Но покажем отсутствие
равных шансов попасть в выборку на
другом примере. Допустим, мы обследуем
уровень достатка семей в микрорайоне
из 10 пятиэтажных домах с 6 подъездами и
3 квартирами на каждом этаже1.
Всего получается в этих домах 900 квартир
(3 квартиры х 5 этажей х 6 подъездов х 10
домов). Это наша генеральная совокупность.
Пусть выборка
составит всего 60 квартир. Следовательно,
наш шаг должен быть равен 15 (900/60). Выбираем
произвольно в качестве исходного пункта
квартиру под номером 3 и двигаемся
систематически с шагом 15 квартир по
всему микрорайону. Допустим, обнаружилось,
что достаток в среднем получился по 4
тысячи рублей на одного члена семьи.
Через год мы
проверяем этот же микрорайон снова с
шагом 15 квартир, но для разнообразия
начинаем двигаться с 7 квартиры. И
выясняем, что теперь выходит по 5 тысяч
рублей на одного члена семьи.
Делаем вывод, что
за год благосостояние семей данного
микрорайона повысилось на четверть. Но
наш вывод будет неверен. Дело в том, что
семьи с разным достатком неодинаково
распределяются по этажам.
Практика показывает,
что семьи с меньшим достатком чаще живут
на первом и последнем этажах, а на
промежуточных этажах обитают чаще более
обеспеченные семьи. Поэтому в первом
обследовании, двигаясь с шагом 15, начиная
с 3-й квартиры, которая находится на
первом этаже, мы в каждом подъезде снова
будем оказываться на первом этаже,
поэтому наш опрос коснется только тех,
которые в среднем имеют 4 тысячи рублей
на одного члена семьи. А через год,
двигаясь с тем же шагом, но, начав с 7-й
квартиры, мы в каждом подъезде будем
оказываться на третьем этаже, жители
которого в среднем вполне могут иметь
5 тысяч рублей на одного члена семьи1.
А вот использование
принципа лотереи или таблицы случайных
чисел гарантировало бы равный шанс для
каждой семьи, независимо от этажа,
попасть в нашу выборку.
Таким образом,
идеалом являются выборка на основе
таблицы случайных чисел и лотереи, а
систематическая случайная выборка
может быть лишь приближением в той или
иной степени к этому идеалу2.
Очень часто ситуация
не позволяет применять рассмотренные
методы формирования выборки. Может не
существовать единый список генеральной
совокупности, объем генеральной
совокупности может быть известен только
приблизительно или постоянно меняется,
− респонденты женятся, переезжают,
умирают и т. д. Интересующие нас люди
могут жить слишком далеко друг от друга,
и с ними будет трудно связаться. В этих
случаях используется следующий метод,
который вполне сохраняет достоинства
случайного выбора.
4. Метод кластерной
выборки, или
многоступенчатого
случайного районирования.
Здесь выборка составляется не из
конкретных людей, а из мест жительства
населенного пункта. Удобство состоит
в том, что места жительства остаются
неизменными. Они нанесены на карту или
план города, распределены по кварталам,
участкам, округам, районам, домам.
Предположим, что
нам необходимо провести выборочное
исследование в масштабах всей страны.
Берем карту России
и делим ее на районы с более или менее
одинаковой численностью населения.
Обычно вся страна уже поделена на
избирательные округа с одинаковым
числом избирателей. Допустим, что таких
округов по стране 190.
1
Мы приписываем каждому округу номера
от 1 до 190 и, пользуясь таблицей
случайных чисел, отбираем несколько
округов.
В каждом отобранном
округе отбираются также случайным
образом несколько еще меньших единиц
территории с одинаковой численностью
населения. Они могут совпадать с
избирательными участками. Затем в этих
участках выбираются случайным образом
отдельные жилые единицы − дома, а затем
также методом случайного отбора –
квартиры. В результате мы получаем
совокупность отдельных жилых единиц,
общее количество которых можно подобрать
равным нужному объему выборки. Их жители
и будут объектами нашего исследования.
Допустим, что мы
выбрали из 190 всего 10 округов. В каждом
из них выбрали 5 избирательных участков,
в каждом из них выбрали 6 домов, а в каждом
из этих домов выбрали по 5 квартир.
Получили выборку из 1500 единиц (10 х 5 х 6
х 5).
Процедуру определения
величины выборки изобразить в виде
формулы:
N
= a
x
b
x
c
x
d…
Подбирая
соответствующим образом множители
a,
b,
c,
d…,
мы можем увеличить или уменьшить выборку.
Допустим, нам нужна выборка в 2500 единиц.
Соответственно, подбираем несколько
иные множители: 10 х 5 х 10 х 5.
Мы начинаем обходить
намеченные квартиры, и вот здесь мы
должны определиться, кого из членов
семьи анкетировать. Ведь анкетировать
нужно всего одного человека. Для этого
разрабатываются специальные карточки.
Пример такой
карточки см. на табл. 7.2.
Например, в квартире
проживают трое взрослых и среди них
двое мужчин. Определяем по карточке,
что интервью надо брать у старшего
мужчины. В случае проживания в квартире
двух людей, среди них одного мужчины,
определяем по карточке, что опрашивается
женщина.
Таблица 7.2
Карточка
выбора респондентов (один из вариантов)
|
Карта |
Количество |
||||
|
1 |
2 |
3 |
4 |
||
|
Количество |
0 |
Взрослый |
Старшая |
Средняя |
Вторая |
|
1 |
Взрослый |
Женщина |
Мужчина |
Средняя |
|
|
2 |
– |
Младший |
Старший |
Старшая |
|
|
3 |
– |
– |
Средний |
Самый |
|
|
4 |
– |
– |
– |
Второй |
5. Метод
стратифицированного
формирования выборки1
используется в случаях, когда чисто
случайная выборка будет содержать
слишком малое количество членов
интересующей нас подгруппы.
Предположим, что
мы хотим сравнить уровень достатка в
русских и немецких поселениях в Поволжье.
Пусть мы имеем генеральную совокупность
численностью 560 поселений. В ней немецких
поселений всего 112,
это и будет интересующая нас подгруппа.
Допустим, мы решили определить выборку
в 56 деревень и поселений, т. е. 1/10 часть
от генеральной совокупности. Тогда в
нашу выборку должно войти 55 русских
деревень (549/10) и всего одно немецкое
поселение (11/10). Очевидно, что сравнение
уровня достатка 55 русских деревень с
уровнем всего одного, причем случайно
отобранного немецкого поселения не
даст возможности сделать какое-либо
обобщение3.
Поэтому мы применяем
метод стратификации: формируем не одну
общую, а две отдельные выборки. Первая
– это случайная, но значимая выборка
из всего количества немецких поселений,
пусть эта выборка составит 5 объектов,
то есть почти половина от 11 поселений.
Вторая – случайная выборка из русских
деревень, она соответственно должна
составить 51 объект, чтобы суммарная
выборка все-таки составила 56 объектов.
В результате, сравнивая образ жизни в
обеих выборках (5 и 51), мы получаем
возможность делать какие-то выводы.
Но проблема состоит
в том, что соотношение обеих выборок
получилось ощутимо не равным: 0,5 для
немецких поселений (5/11) и 0,1 для русских
поселений (51/549). То есть исследовались
половина немецких поселений и лишь
каждое десятое русское поселение.
Следовательно, наши выводы будут
уязвимыми с точки зрения научной
объективности. Поэтому в данном случае
лучше всего просто описать методику,
на основе которой строились выборки, и
зафиксировать то, что удалось выяснить,
не делая каких-либо серьезных обобщений.
6. Квотная
выборка. Здесь члены выборки подбираются
из больших групп людей таким образом,
чтобы пропорции людей с нужными свойствами
− пол, возраст, образование, национальность
− соответствовали их пропорции в
генеральной совокупности. Например, мы
знаем, что в генеральной совокупности
20% людей в возрасте от 20 до 25 лет, 30% – с
высшим образованием, 62% семейных и т. д.
Из больших групп людей набирается
случайным образом выборка, в которой
будут выполнены интересующие нас
пропорции людей с данными свойствами.
Но здесь не гарантируется выполнение
правила: любой объект и любое сочетание
объектов генеральной совокупности
должны иметь равные возможности попасть
в нашу выборку. Поэтому данный метод
применяется для проведения поискового
либо пилотажного исследования, т. е. для
получения предварительных гипотез или
обкатки инструментария.
7. Экспертная
выборка.
Здесь сам исследователь отбирает объекты
из генеральной совокупности на основе
имеющихся в его распоряжении способов.
Например, необходимо
выбрать из 50 имеющихся в данной области
специалистов 10 человек для интервью.
Эти специалисты занимают, как правило,
важные посты и неохотно теряют время
на долгие беседы по вопросам, интересующим
только самого исследователя. Здесь
можно пойти по пути отбора тех, с кем
лично знаком исследователь, или тех, с
кем имеются общие знакомые, или тех, у
кого есть в данный момент свободное для
беседы время. Можно обратиться к тем,
кто не так давно отошел от дел и кому
самому интересно поделиться своими
наблюдениями над ситуацией в сфере, в
которой они недавно работали.
Последние три
выборки – стратифицированная, квотная
и экспертная – не являются действительно
репрезентативными, поэтому при изложении
результатов не стоит делать общих
выводов. Нужно просто описать то, что
получилось и выдвинуть предварительную
гипотезу для последующего действительно
репрезентативного исследования.
Методы выборки: Типы с примерами
Опубликовано 2023-02-11 19:53 пользователем

Выборка является важной частью любого исследовательского проекта. Правильный метод выборки может сделать или разрушить достоверность вашего исследования, и очень важно выбрать правильный метод для вашего конкретного вопроса. В этой статье мы подробно рассмотрим некоторые из наиболее популярных методов выборки и приведем реальные примеры того, как их можно использовать для сбора точных и надежных данных.
От простой случайной выборки до сложной стратифицированной выборки, мы рассмотрим плюсы, минусы и лучшие практики каждого метода. Итак, независимо от того, являетесь ли вы опытным исследователем или только начинаете свой путь, эта статья – обязательное чтение для всех, кто хочет освоить методы выборки. Давайте начнем!
Индекс содержания
- Что такое выборка?
- Типы выборки: методы выборки
- Типы вероятностной выборки с примерами:
- Использование вероятностной выборки
- Типы не вероятностной выборки с примерами
- Использование не вероятностной выборки
- Как вы решаете, какой тип выборки использовать?
- Разница между вероятностной и не вероятностной выборкой
- Вывод
Что такое выборка?
Выборка – это техника отбора отдельных членов или подмножества населения для того, чтобы сделать на их основе статистические выводы и оценить характеристики всего населения. Различные методы выборки широко используются исследователями в маркетинговых исследованиях, так что им не нужно изучать все население, чтобы получить действенные выводы.
Это также удобный и экономически эффективный метод, и поэтому он составляет основу любого плана исследования. Методы выборки могут быть использованы в программном обеспечении для проведения исследовательских опросов для получения оптимальных результатов.
Например, предположим, производитель лекарств хотел бы исследовать неблагоприятные побочные эффекты лекарства на население страны. В этом случае практически невозможно провести исследование, в котором участвовали бы все. В этом случае исследователь определяет выборку людей из каждой демографической группы и затем исследует их, получая ориентировочные данные о поведении препарата.
Узнайте больше об Аудитории
Типы выборки: Методы выборки
Выборка в исследованиях рыночных действий бывает двух типов – вероятностная и не вероятностная выборка. Давайте подробнее рассмотрим эти два метода выборки.
- Вероятностная выборка: Вероятностная выборка – это метод выборки, при котором исследователь выбирает несколько критериев и отбирает членов популяции случайным образом. При таком параметре отбора все члены имеют равную возможность участвовать в выборке.
- Невероятностная выборка: При невероятностной выборке исследователь случайным образом выбирает членов для исследования. Этот метод выборки не является фиксированным или заранее определенным процессом отбора. Это затрудняет для всех элементов населения равные возможности быть включенными в выборку.
В этом блоге обсуждаются различные вероятностные и не вероятностные методы выборки, которые вы можете применить в любом исследовании рынка.
Типы вероятностной выборки с примерами:
Вероятностная выборка – это метод, при котором исследователи выбирают образцы из большей совокупности на основе теории вероятности. Этот метод выборки учитывает каждого члена популяции и формирует выборки на основе фиксированного процесса.
Например, в популяции из 1000 человек каждый член имеет шанс 1/1000 быть отобранным для включения в выборку. Вероятностная выборка устраняет смещение выборки в популяции и позволяет включить в выборку всех членов.
Существует четыре типа методов вероятностной выборки:

- Простая случайная выборка: Одним из лучших методов вероятностной выборки, который помогает экономить время и ресурсы, является метод простой случайной выборки. Это надежный метод получения информации, при котором каждый отдельный член популяции выбирается случайно, чисто случайно. Например, в организации из 500 сотрудников, если команда HR решит провести мероприятия по сплочению коллектива, они, скорее всего, предпочтут выбирать фишки из миски. В этом случае каждый из 500 сотрудников имеет равную возможность быть отобранным.
- Кластерная выборка: Кластерная выборка – это метод, при котором исследователи делят всю совокупность на части или кластеры, представляющие совокупность. Кластеры определяются и включаются в выборку на основе таких демографических параметров, как возраст, пол, местоположение и т.д. Это позволяет создателю опроса сделать эффективные выводы из полученных данных.
Например, предположим, правительство Соединенных Штатов хочет оценить количество иммигрантов, проживающих на материковой части США. В этом случае они могут разделить его на кластеры, основанные на таких штатах, как Калифорния, Техас, Флорида, Массачусетс, Колорадо, Гавайи и т. д. Такой способ проведения опроса будет более эффективным, так как результаты будут распределены по штатам и предоставят глубокие данные об иммиграции. - Систематическая выборка: Исследователи используют метод систематической выборки для отбора членов выборки из популяции через регулярные промежутки времени. Он требует выбора начальной точки для выборки и размера выборки, который можно повторять через регулярные промежутки времени. Этот метод выборки имеет заранее определенный диапазон; следовательно, этот метод выборки наименее трудоемкий.
Например, исследователь намеревается собрать систематическую выборку из 500 человек в популяции численностью 5000 человек. Он/она пронумерует каждый элемент популяции от 1 до 5000 и выберет каждого 10-го человека для включения в выборку (Общая популяция/Размер выборки = 5000/500 = 10). - Стратифицированная случайная выборка: Стратифицированная случайная выборка – это метод, при котором исследователь делит популяцию на более мелкие группы, которые не пересекаются, но представляют всю популяцию. Например, исследователь, желающий проанализировать характеристики людей, принадлежащих к различным группам по годовому доходу, создает страты (группы) в соответствии с годовым доходом семьи. Например, менее $20 000, $21 000 – $30 000, $31 000 – $40 000, $41 000 – $50 000 и т. д. Таким образом, исследователь делает вывод о характеристиках людей, принадлежащих к различным группам доходов. Маркетологи могут проанализировать, на какие группы доходов ориентироваться, а какие исключить, чтобы создать дорожную карту, которая принесет плодотворные результаты.
Uses of probability sampling
Существует множество вариантов использования вероятностной выборки:
- Снижение погрешности выборки: При использовании метода вероятностной выборки погрешность выборки, полученной из совокупности, незначительна или вообще отсутствует. Выборка в основном отражает понимание и умозаключения исследователя. Вероятностная выборка приводит к более качественному сбору данных, поскольку выборка адекватно представляет население.
- Разнородное население: Когда население обширно и разнообразно, важно иметь адекватное представительство, чтобы данные не были перекошены в сторону одной демографической группы. Например, предположим, что компания Square хотела бы понять, какие люди могли бы использовать ее устройства в точках продаж. В этом случае поможет опрос, проведенный на выборке людей по всей территории США из разных отраслей промышленности и социально-экономического положения.
- Создание точной выборки: Выборка вероятностей помогает исследователям планировать и создавать точную выборку. Это помогает получить четко определенные данные.
Типы не вероятностной выборки с примерами
Не вероятностный метод – это метод выборки, который предполагает сбор обратной связи на основе возможностей исследователя или статистика по отбору выборки, а не на основе фиксированного процесса отбора. В большинстве ситуаций результаты опроса, проведенного с использованием не вероятностной выборки, приводят к искаженным результатам, которые могут не представлять желаемую целевую совокупность. Однако существуют ситуации, например, на предварительных этапах исследования или при ограничении затрат на проведение исследования, когда не вероятностная выборка будет гораздо полезнее, чем другой тип.
Четыре типа непроизводственной выборки лучше объясняют цель этого метода выборки:
- Выборка удобства: Этот метод зависит от легкости доступа к испытуемым, например, опрос покупателей в торговом центре или прохожих на оживленной улице. Обычно его называют выборкой удобства из-за того, что исследователю легко проводить его и вступать в контакт с испытуемыми. Исследователи практически не имеют полномочий для отбора элементов выборки, и он осуществляется исключительно на основе близости, а не репрезентативности. Этот метод не вероятностной выборки используется, когда существуют ограничения по времени и затратам на сбор обратной связи. В ситуациях с ограниченными ресурсами, например, на начальных этапах исследования, используется выборка по удобству.
Например, стартапы и НПО обычно проводят выборку по удобству в торговом центре для распространения листовок о предстоящих событиях или продвижения дела – они делают это, стоя у входа в торговый центр и раздавая брошюры случайным образом. - Суждение или целенаправленная выборка: Суждение или целенаправленная выборка формируется по усмотрению исследователя. Исследователи в обязательном порядке учитывают цель исследования, а также понимание целевой аудитории. Например, когда исследователи хотят понять ход мыслей людей, заинтересованных в получении степени магистра. Критерием отбора будет: “Заинтересованы ли вы в получении степени магистра в …?”, а те, кто ответит “нет”, будут исключены из выборки.
- Выборка снежного кома: Выборка снежного кома – это метод выборки, который исследователи применяют, когда субъектов трудно отследить. Например, опрос людей без жилья или нелегальных иммигрантов будет чрезвычайно сложным. В таких случаях, используя теорию снежного кома, исследователи могут отследить несколько категорий для опроса и получить результаты. Исследователи также применяют этот метод выборки, когда тема очень чувствительна и не обсуждается открыто – например, опросы для сбора информации о ВИЧ СПИДе. Не многие жертвы охотно ответят на вопросы. Тем не менее, исследователи могут связаться с людьми, которых они могут знать, или с волонтерами, связанными с этим делом, чтобы установить контакт с жертвами и собрать информацию.
- Квотная выборка: В квотной выборке при этом методе отбор участников происходит на основе заранее установленного стандарта. В этом случае, поскольку выборка формируется по определенным признакам, созданная выборка будет обладать теми же качествами, которые встречаются в генеральной совокупности. Это быстрый метод сбора выборки.
Uses of non-probability sampling
Невероятностная выборка используется для следующего:
- Создание гипотезы: Исследователи используют метод непропорциональной выборки для создания предположения, когда имеется ограниченная или вообще отсутствует предварительная информация. Этот метод помогает немедленно получить данные и создает базу для дальнейшего исследования.
- Исследовательские исследования: Исследователи широко используют этот метод выборки при проведении качественных исследований, пилотных исследований или исследовательских работ.
- Бюджет и временные ограничения: Невероятностный метод применяется, когда есть бюджетные и временные ограничения, и необходимо собрать некоторые предварительные данные. Поскольку схема опроса не является жесткой, проще выбрать респондентов случайным образом и попросить их пройти опрос или анкетирование.
Как вы решаете, какой тип выборки использовать?
Для любого исследования важно точно выбрать метод выборки, чтобы он соответствовал целям вашего исследования. Эффективность выборки зависит от различных факторов. Вот несколько шагов, которым следуют опытные исследователи, чтобы выбрать оптимальный метод выборки.
- Запишите цели исследования. Как правило, это должно быть сочетание стоимости, точности или аккуратности.
- Определите эффективные методы выборки, которые потенциально могут достичь целей исследования.
- Протестируйте каждый из этих методов и проверьте, помогают ли они достичь цели.
- Выберите метод, который лучше всего подходит для исследования.
Откройте силу точной выборки!
Разница между вероятностной и не вероятностной выборкой
Выше мы рассмотрели различные типы методов выборки и их подтипы. Однако, чтобы подытожить все обсуждение, ниже приведены существенные различия между вероятностными и не вероятностными методами выборки:
| Вероятностные методы выборки | Невероятностные методы выборки. | |
| Определение | Вероятностная выборка – это метод выборки, при котором выборки из большей совокупности отбираются с помощью метода, основанного на теории вероятности. | Невероятностная выборка – это метод выборки, при котором исследователь отбирает образцы на основе субъективного суждения исследователя, а не случайного отбора. |
| Альтернативно известный как | Случайный метод выборки. | Неслучайный метод выборки |
| Отбор популяции | Популяция отбирается случайным образом. | Население выбрано произвольно. |
| Натура | Исследование является окончательным. | Исследование является исследовательским. |
| Выборка | Поскольку существует метод определения выборки, демографические характеристики населения представлены убедительно. | Поскольку метод выборки произволен, демографические характеристики населения представлены почти всегда искаженно. |
| Время, затрачиваемое | На проведение исследования требуется больше времени, поскольку план исследования определяет параметры отбора до начала маркетингового исследования. | Этот тип выборочного метода является быстрым, поскольку ни выборка, ни критерии отбора выборки не определены. |
| Результаты | Данный тип выборки является полностью беспристрастным, следовательно, результаты также являются убедительными. | Данный тип выборки является полностью необъективным, следовательно, результаты также являются необъективными, что делает исследование спекулятивным. |
| Гипотеза | При вероятностной выборке существует основная гипотеза до начала исследования, и этот метод направлен на доказательство гипотезы. | При не вероятностной выборке гипотеза выводится после проведения исследования. |
Вывод
Теперь, когда мы узнали, как работают различные методы выборки, которые широко используются исследователями в маркетинговых исследованиях, чтобы им не нужно было исследовать все население для сбора действенных выводов, давайте рассмотрим инструмент, который может помочь вам управлять этими выводами.
понимает необходимость точного, своевременного и экономически эффективного метода отбора нужной выборки; именно поэтому мы предлагаем программное обеспечение Software – набор инструментов, позволяющих эффективно отбирать целевую аудиторию, управлять полученными данными в организованном, настраиваемом хранилище и управлять сообществом для обратной связи после проведения опроса.
Не упустите шанс повысить ценность исследований.
Попробуйте сегодня!
Рубрика:
- Бизнес
Ключевые слова:
- исследование рынка
Автор:
- Dan Fleetwood
Источник:
- questionpro
Перевод:
- Дмитрий Л
Приступим к изучению элементов математической статистики, в которой разрабатываются научно обоснованные методы сбора статистических данных и их обработки.
Пусть требуется изучить множество однородных объектов (это множество называют статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить соответствие детали стандартам, а количественным — контролируемый размер детали.
Лучше всего осуществить сплошное обследование, т. е. изучить каждый объект. Однако в большинстве случаев по разным причинам это сделать невозможно. Препятствовать сплошному обследованию может большое число объектов, их недоступность и т. п. Если, например, нужно знать среднюю глубину воронки при взрыве снаряда из опытной партии, то, проводя сплошное обследование, мы должны будем уничтожить всю партию.
Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.
Число объектов генеральной совокупности и выборки называется соответственно объемом генеральной совокупности и объемом выборки.
Пример. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 —объем генеральной совокупности, а 10 —объем выборки.
Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще используется бесповторная выборка. Если объем выборки составляет небольшую долю объема генеральной совокупности, то разница между повторной и бесповторной выборками незначительна
Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, или, как говорят, выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор осуществляется случайно. Например, для того чтобы оценить будущий урожай, можно сделать выборку из генеральной совокупности еще не созревших плодов и исследовать их характеристики (массу, качество и пр.). Если вся выборка будет взята с одного дерева, то она не будет репрезентативной. Репрезентативная выборка должна состоять из случайно выбранных плодов со случайно выбранных деревьев.

Статистическое распределение выборки. Полигон. Гистограмма
Пусть из генеральной совокупности извлечена выборка, причем 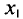 , наблюдалось
, наблюдалось 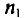 раз,
раз, 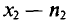 раз,
раз, 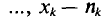 раз и
раз и 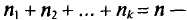 объем выборки. Наблюдаемые значения
объем выборки. Наблюдаемые значения 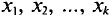 называются вариантами, а последовательность вариант, записанная в возрастающем порядке,— вариационным рядом. Числа наблюдений
называются вариантами, а последовательность вариант, записанная в возрастающем порядке,— вариационным рядом. Числа наблюдений 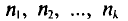 называют частотами, а их отношения к объему выборки
называют частотами, а их отношения к объему выборки 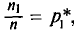
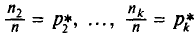 — относительными частотами. Отметим, что сумма относительных частот равна единице:
— относительными частотами. Отметим, что сумма относительных частот равна единице:
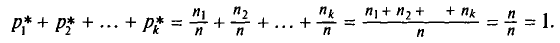
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.
Пример:
Перейдем от частот к относительным частотам в следующем распределении выборки объема n = 20:

Найдем относительные частоты:
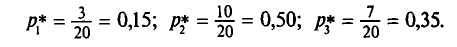
Поэтому получаем следующее распределение:

Для графического изображения статистического распределения используются полигоны и гистограммы.
Для построения полигона в декартовых координатах на оси Ох откладывают значения вариант 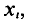 на оси Оу— значения частот
на оси Оу— значения частот 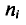 (относительных частот
(относительных частот 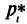 ).
).
Пример:
Рис. 14 представляет собой полигон следующего распределения:

Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов шириной h и находят для каждого частичного интервала 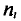 — сумму частот вариант, попавших в і-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами
— сумму частот вариант, попавших в і-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами 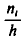 (или
(или 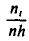 , где n —объем выборки). Площадь i-го частичного прямоугольника равна
, где n —объем выборки). Площадь i-го частичного прямоугольника равна 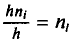
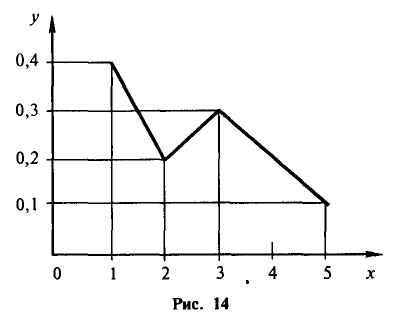
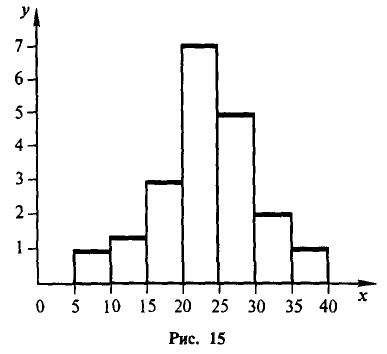
(или 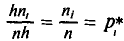 ). Следовательно, площадь гистограммы равна сумме всех частот (или относительных частот), т. е. объему выборки (или единице).
). Следовательно, площадь гистограммы равна сумме всех частот (или относительных частот), т. е. объему выборки (или единице).
Пример:
Рис. 15 показывает гистограмму непрерывного распределения объема n =100, заданного следующей таблицей:

Оценки параметров генеральной совокупности по ее выборке
Выборка как набор случайных величин
Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится известным значение х признака X этого объекта. Таким образом, мы можем рассматривать извлечение объекта из генеральной совокупности как испытание, X—как случайную величину, а х —как одно из возможных значений X.
Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного определения) параметров, которыми описывается это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение.
Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например значения количественного признака 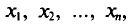 полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.
полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.
Опытные значения признака X можно рассматривать и как значения разных случайных величин 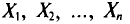 с тем же распределением, что и X, и, следовательно, с теми же числовыми характеристиками, которые имеет X. Значит,
с тем же распределением, что и X, и, следовательно, с теми же числовыми характеристиками, которые имеет X. Значит, 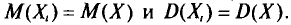 Величины
Величины 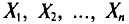 можно считать независимыми в силу независимости наблюдений. Значения
можно считать независимыми в силу независимости наблюдений. Значения 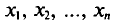 в этом случае называются реализациями случайных величин
в этом случае называются реализациями случайных величин 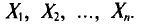 Отсюда и из предыдущего следует, что найти оценку неизвестного параметра — это значит найти функцию от наблюдаемых случайных величин
Отсюда и из предыдущего следует, что найти оценку неизвестного параметра — это значит найти функцию от наблюдаемых случайных величин 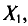
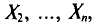 которая и дает приближенное значение оцениваемого параметра.
которая и дает приближенное значение оцениваемого параметра.
Генеральная и выборочная средние. Методы их расчета
Пусть изучается дискретная генеральная совокупность объема N относительно количественного признака X.
Определение:
Генеральной средней 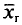 (или а) называется среднее арифметическое значений признака генеральной совокупности.
(или а) называется среднее арифметическое значений признака генеральной совокупности.
Если все значения 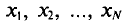 признака генеральной совокупности объема N различны, то
признака генеральной совокупности объема N различны, то
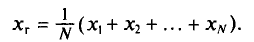
Если же значения признака 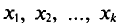 имеют соответственно частоты
имеют соответственно частоты 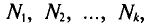 причем
причем  то
то
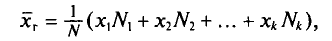
или

Как уже отмечалось (п. 1), извлечение объекта из генеральной совокупности есть наблюдение случайной величины X.
Пусть все значения 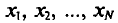 различны. Так как каждый объект может быть извлечен с одной и той же вероятностью 1/N, то
различны. Так как каждый объект может быть извлечен с одной и той же вероятностью 1/N, то
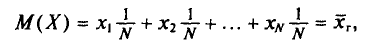
т. е.

Такой же итог следует, если значения 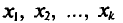 имеют соответственно частоты
имеют соответственно частоты 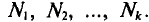
В случае непрерывного распределения признака X по определению полагают 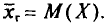
Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объема n.
Определение:
Выборочной средней 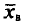 , называется среднее арифметическое значений признака выборочной совокупности.
, называется среднее арифметическое значений признака выборочной совокупности.
Если все значения 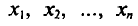 признака выборки объема n различны, то
признака выборки объема n различны, то
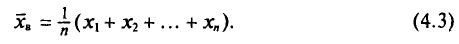
Если же значения признака  имеют соответственно частоты
имеют соответственно частоты 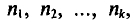 причем
причем  , то
, то
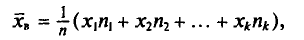
или

Пример:
Выборочным путем были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28^27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найдем выборочную среднюю 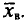
Согласно формуле (4.4), имеем:
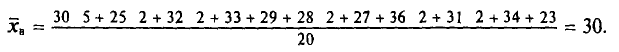
Итак, 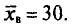
Далее, не уменьшая общности рассуждений, будем считать значения 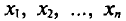 признака различными.
признака различными.
Разумеется, выборочная средняя для различных выборок того же объема n из той же генеральной совокупности будет получаться, вообще говоря, различной. И это не удивительно — ведь извлечение і-го по счету объекта есть наблюдение случайной величины 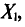 а их среднее арифметическое
а их среднее арифметическое
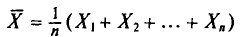
есть тоже случайная величина.
Таким образом, всевозможные получающиеся выборочные средние есть возможные значения случайной величины 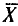 , которая называется выборочной средней случайной величиной.
, которая называется выборочной средней случайной величиной.
Найдем 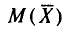 , пользуясь тем, что
, пользуясь тем, что 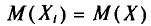 (см. п. 1).
(см. п. 1).
С учетом свойств математического ожидания (см. гл. II) получаем:
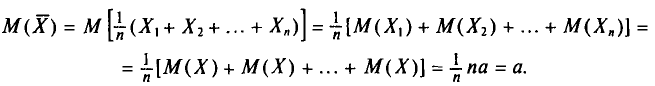
Итак, 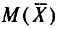 (математическое ожидание выборочной средней) совпадает с а (генеральной средней).
(математическое ожидание выборочной средней) совпадает с а (генеральной средней).
Теперь найдем 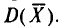 Так как
Так как 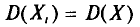 (п. 1) и
(п. 1) и 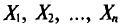 независимы, то, согласно свойствам дисперсии (см. гл. II), получаем
независимы, то, согласно свойствам дисперсии (см. гл. II), получаем
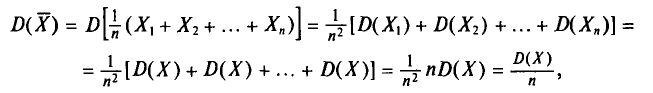
T. e.

Наконец, отметим, что если варианты 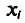 —большие числа, то для облегчения вычисления выборочной средней применяют следующий прием. Пусть С — константа.
—большие числа, то для облегчения вычисления выборочной средней применяют следующий прием. Пусть С — константа.
Так как
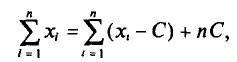
то формулу (4.3) можно преобразовать к виду
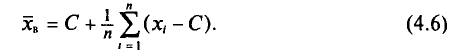
За константу С (так называемый ложный нуль) берут некоторое среднее значение между наименьшим и наибольшим значениями х, (і- 1, 2, …, n).
Пример:
Имеется выборка:
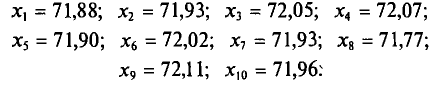
Требуется найти 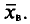
Возьмем С =72,00 и вычислим разности 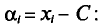
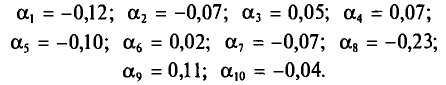
Их сумма: 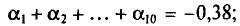 их среднее арифметическое
их среднее арифметическое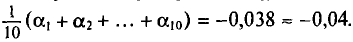 Выборочная средняя
Выборочная средняя
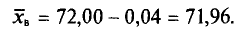
Генеральная и выборочная дисперсии
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику — генеральную дисперсию.
Определение:
Генеральной дисперсией D, называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней 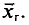
Если все значения 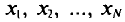 признака генеральной совокупности объема N различны, то
признака генеральной совокупности объема N различны, то
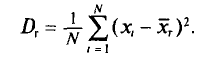
Если же значения признака 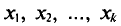 имеют соответственно
имеют соответственно
частоты 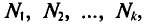 причем
причем  то
то
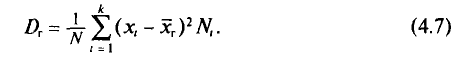
Пример:
Генеральная совокупность задана таблицей распределения:

Найдем генеральную дисперсию.
Согласно формулам (4.1) и (4.7), имеем:
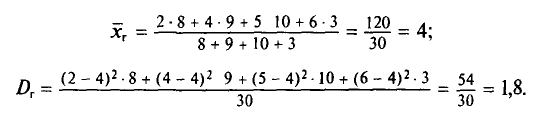
Генеральным средним квадратическим отклонением (стандартом) называется 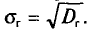
Пусть все значения 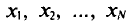 различны.
различны.
Найдем дисперсию признака X, рассматриваемого как случайная величина:
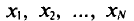
Так как 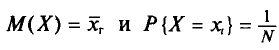 (см. п. 2), то
(см. п. 2), то
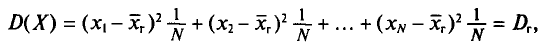
т. е.
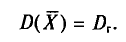
Таким образом, дисперсия D(X) равна 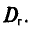
Такой же итог можно получить, если значения 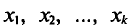 имеют соотвественно частоты
имеют соотвественно частоты 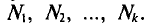
В случае непрерывного распределения признака X по определению полагают

С учетом формулы (4.8) формула (4.5) (п. 2) перепишется в виде
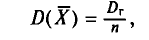
откуда 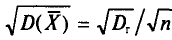 или
или 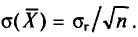 Величина
Величина 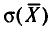 называется средней квадратической ошибкой.
называется средней квадратической ошибкой.
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 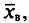 вводят выборочную дисперсию.
вводят выборочную дисперсию.
Определение:
Выборочной дисперсией 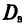 , называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней
, называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней 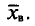
Если все значения 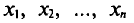 признака выборки объема n различны, то
признака выборки объема n различны, то
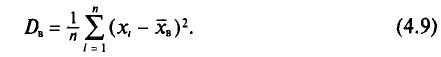
Если же значения признака 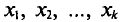 имеют соответственно частоты
имеют соответственно частоты 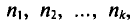 причем
причем 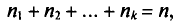 то
то
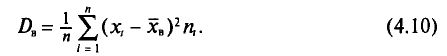
Пример:
Пусть выборочная совокупность задана таблицей распределения:

Найдем выборочную дисперсию. Согласно формулам (4.4) и (4.10), имеем:
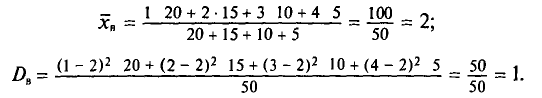
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии:
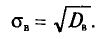
В условиях примера 2 получаем, что 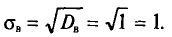
Далее, не уменьшая общности рассуждений, будем считать значения 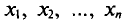 признака различными.
признака различными.
Выборочную дисперсию, рассматриваемую нами как случайная величина, будем обозначать 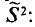
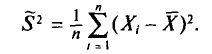
Теорема:
Математическое ожидание выборочной дисперсии равно 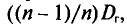 т.е.
т.е.
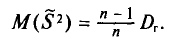
Доказательство:
С учетом свойств математического ожидания (см. гл. II) получаем
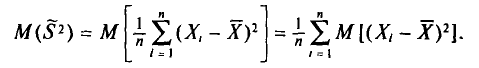
Вычислим одно слагаемое 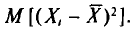 Имеем
Имеем
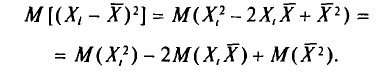
Вычислим по отдельности эти математические ожидания.
Согласно свойству I дисперсии (см. гл. И) и формулам (4.2), (4.8) имеем
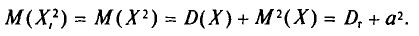
Далее, с учетом свойства 4 математического ожидания (см. гл. II)
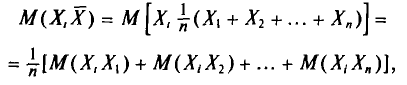
но слагаемое этой суммы, у которого второй индекс равен і, т.е. 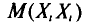 , равно
, равно 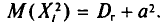 У всех остальных слагаемых
У всех остальных слагаемых 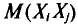 индексы разные. Поэтому в силу независимости
индексы разные. Поэтому в силу независимости 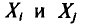 (см. гл. II)
(см. гл. II)
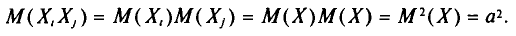
Так как имеется n-1 таких слагаемых, то
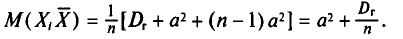
В силу свойства 1 дисперсии (см. гл. П) получаем
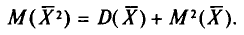
Нами уже найден (см. пп. 2 и 3):
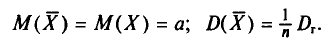
Поэтому
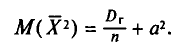
Таким образом,
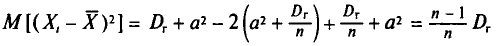
и не зависит от индекса суммирования і. Поэтому
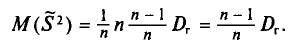
Что и требовалось доказать.
В заключение этого пункта отметим, что если варианты 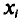 — большие числа, то для облегчения вычисления выборочной дисперсии
— большие числа, то для облегчения вычисления выборочной дисперсии 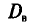 , формулу (4.9) преобразуют к следующему виду:
, формулу (4.9) преобразуют к следующему виду:
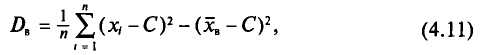
где С—ложный нуль.
Действительно, с учетом формулы (4.3) имеем
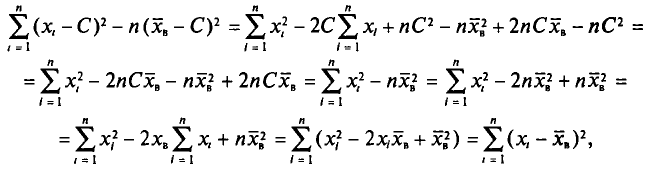
откуда
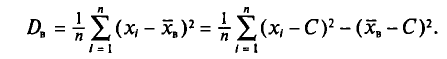
Пример:
Для выборки, указанной в примере 2 из п. 2, найдем 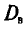 (ложный нуль остается прежним С= 72,00)
(ложный нуль остается прежним С= 72,00)
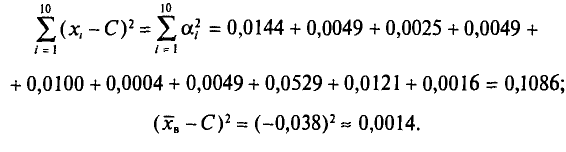
Наконец, согласно формуле (4.11)
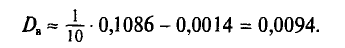
Оценки параметров распределения
Одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. При этом в теоретических рассуждениях считают, что генеральная совокупность бесконечна. Это делается для того, чтобы можно было переходить к пределу при 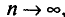 где n — объем выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. Например,
где n — объем выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. Например, 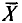 (см. п. 2) является оценкой генеральной средней, а
(см. п. 2) является оценкой генеральной средней, а 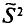 (см. п. 3) — оценкой генеральной дисперсии
(см. п. 3) — оценкой генеральной дисперсии 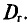 Обозначим через
Обозначим через 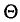 оцениваемый параметр, через
оцениваемый параметр, через 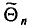 — оценку этого параметра
— оценку этого параметра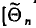 является выражением^ составленным из
является выражением^ составленным из 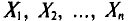 (см. п. 1)]. Для того чтобы оценка
(см. п. 1)]. Для того чтобы оценка 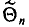 давала хорошее приближение, она должна удовлетворять определенным требованиям. Укажем эти требования.
давала хорошее приближение, она должна удовлетворять определенным требованиям. Укажем эти требования.
Несмещенной называют оценку 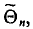 математическое ожидание которой равно оцениваемому параметру
математическое ожидание которой равно оцениваемому параметру 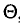 , т. е.
, т. е. 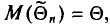 в противном случае оценка называется смещенной.
в противном случае оценка называется смещенной.
Пример:
Оценка 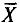 является несмещенной оценкой генеральной средней а, так как
является несмещенной оценкой генеральной средней а, так как 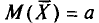 (см. п. 2).
(см. п. 2).
Пример:
Оценка 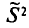 является смещенной оценкой генеральной дисперсии
является смещенной оценкой генеральной дисперсии 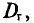 так как, согласно установленной выше теореме (см. п. 3),
так как, согласно установленной выше теореме (см. п. 3),
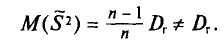
Пример:
Наряду с выборочной дисперсией 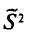 рассматривают еще так называемую исправленную дисперсию
рассматривают еще так называемую исправленную дисперсию 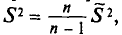 которая является также оценкой генеральной дисперсии. Для
которая является также оценкой генеральной дисперсии. Для 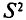 с учетом установленной выше теоремы (см. п. 3) имеем
с учетом установленной выше теоремы (см. п. 3) имеем
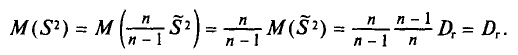
Таким образом, оценка 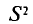 в отличие от оценки
в отличие от оценки 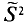 является несмещенной оценкой генеральной дисперсии. Явное выражение для
является несмещенной оценкой генеральной дисперсии. Явное выражение для 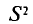 имеет вид
имеет вид
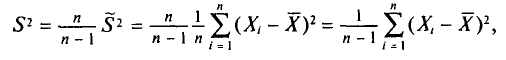
T. e.
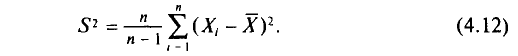
Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки для того, чтобы не делать систематической ошибки в сторону завышения или занижения.
Состоятельной называют такую оценку 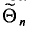 параметра
параметра 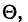 , что для любого наперед заданного числа
, что для любого наперед заданного числа 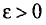 вероятность
вероятность 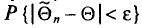 при
при 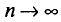 стремится к единице*. Это значит, что при достаточно больших n можно с вероятностью, близкой к единице, т. е. почти наверное, утверждать, что оценка
стремится к единице*. Это значит, что при достаточно больших n можно с вероятностью, близкой к единице, т. е. почти наверное, утверждать, что оценка 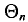 отличается от оцениваемого параметра
отличается от оцениваемого параметра 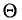 меньше, чем на
меньше, чем на 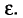
Очевидно, такому требованию должна удовлетворять всякая оценка, пригодная для практического использования.
Заметим, что несмещенная оценка 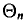 будет состоятельной, если при
будет состоятельной, если при 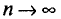 дисперсия стремится к нулю:
дисперсия стремится к нулю: 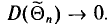 Это следует из неравенства Чебышева ((2.33) см. § 2.8, п. 1).
Это следует из неравенства Чебышева ((2.33) см. § 2.8, п. 1).
Пример:
Как было установлено (см. п. 3), 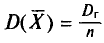 . Отсюда следует, что несмещенная оценка
. Отсюда следует, что несмещенная оценка 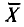 является и состоятельной, так как
является и состоятельной, так как
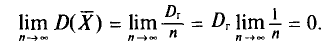
Можно показать, что несмещенная оценка 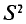 является также состоятельной. Поэтому в качестве оценки генеральной дисперсии принимают исправленную дисперсию. Заметим, что оценки
является также состоятельной. Поэтому в качестве оценки генеральной дисперсии принимают исправленную дисперсию. Заметим, что оценки 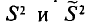 отличаются множителем
отличаются множителем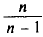 , который стремится к 1 при
, который стремится к 1 при 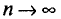 . На практике
. На практике 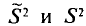 не различают при n > 30.
не различают при n > 30.
Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
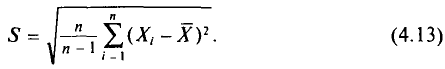
Левые части формул (4.12), (4.13), в которых случайные величины 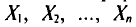 заменены их реализациями
заменены их реализациями 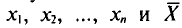 выборочной средней
выборочной средней 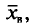 будем обозначать соответственно через
будем обозначать соответственно через 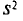 и s
и s
Отметим, что если варианты 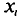 — большие числа, то для облегчения вычисления
— большие числа, то для облегчения вычисления 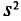 формулу для
формулу для 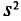 аналогично формуле (4.9) преобразуют к виду
аналогично формуле (4.9) преобразуют к виду
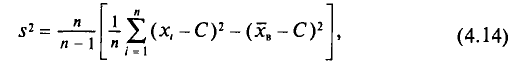
где С—ложный нуль.
Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями.
Ясно, что чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценка, обладающая таким свойством, называется эффективной.
Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности.
Пример:
С плодового дерева случайным образом отобрано 10 плодов. Их массы 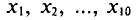 (в граммах) записаны в первой колонке приведенной ниже таблицы. Обработаем статистические данные выборки. Для вычисления
(в граммах) записаны в первой колонке приведенной ниже таблицы. Обработаем статистические данные выборки. Для вычисления 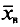 и s пo формулам (4.6) и (4.14) введем ложный нуль С=250 и все необходимые при этом вычисления сведем в указанную таблицу:
и s пo формулам (4.6) и (4.14) введем ложный нуль С=250 и все необходимые при этом вычисления сведем в указанную таблицу:
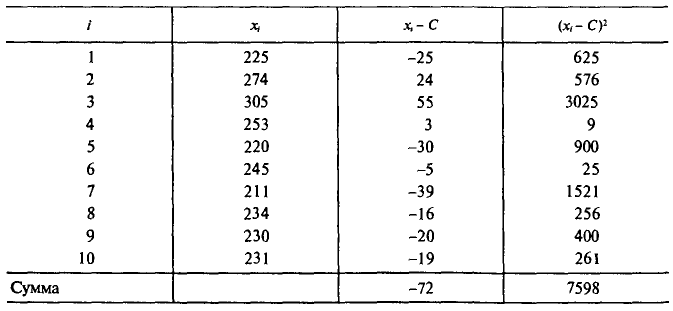
Следовательно,
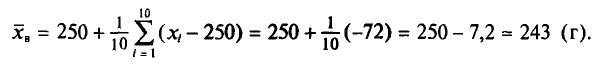
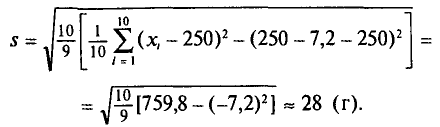
Отсюда 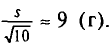
Итак, оценка генеральной средней массы плода равна 243 г со средней квадратической ошибкой 9 г.
Оценка генерального среднего квадратического отклонения массы плода равна 28 г.
Пример:
Через каждый час измерялось напряжение в электросети. Результаты измерений (в вольтах) представлены в следующей таблице:
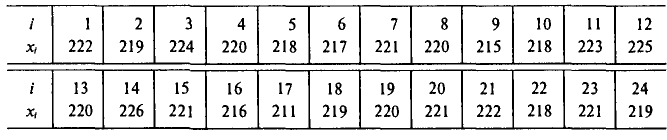
Найти оценки для математического ожидания и дисперсии результатов измерений. Оценки для математического ожидания и дисперсии найдем по формулам (6) и (14), положив С=220. Все необходимые вычисления приведены в нижеследующей таблице:
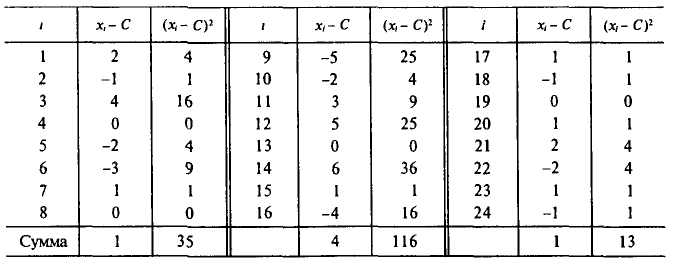
Следовательно,
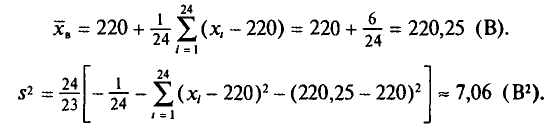
Доверительные интервалы для параметров нормального распределения
Пусть  — оцениваемый параметр,
— оцениваемый параметр,  — его оценка, составленная из
— его оценка, составленная из 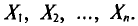
Если известно, что оценка  является несмещенной и состоятельной, то по данным выборки вычисляют значение
является несмещенной и состоятельной, то по данным выборки вычисляют значение  и считают его приближением истинного значения
и считают его приближением истинного значения  . При этом среднее квадратическое отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными. Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало.
. При этом среднее квадратическое отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными. Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало.
Если же о распределении имеется какая-либо информация, то можно сделать больше.
Здесь речь будет идти об оценке параметров а и 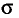 случайной величины, имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.
случайной величины, имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.
Пусть 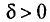 — некоторое число. Если выполняется неравенство
— некоторое число. Если выполняется неравенство 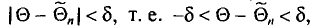 что можно записать в виде
что можно записать в виде 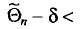
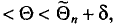 то говорят, что интервал
то говорят, что интервал 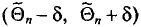 покрывает параметр
покрывает параметр  . Однако невозможно указать оценку
. Однако невозможно указать оценку  такую, чтобы событие
такую, чтобы событие 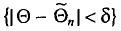 было достоверным, поэтому мы будем говорить о вероятности этого события. Число
было достоверным, поэтому мы будем говорить о вероятности этого события. Число 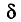 называется точностью оценки
называется точностью оценки 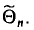
Определение:
Надежностью (доверительной вероятностью) оценки  параметра
параметра  0 для заданного
0 для заданного 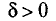 называется вероятность
называется вероятность  того, что интервал
того, что интервал 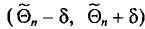 покроет параметр
покроет параметр  , т. е.
, т. е.
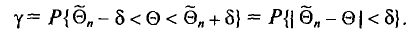
Заметим, что после того, как по данным выборки вычислена оценка  , событие
, событие 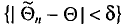 становится или достоверным, или невозможным, так как интервал
становится или достоверным, или невозможным, так как интервал 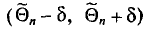 или покрывает
или покрывает  , или нет. Но дело в том, что параметр
, или нет. Но дело в том, что параметр  нам неизвестен. Поэтому мы называем надежностью
нам неизвестен. Поэтому мы называем надежностью  уже вычисленной оценки
уже вычисленной оценки  вероятность того, что интервал
вероятность того, что интервал 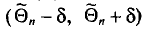 , найденный для произвольной выборки, покроет
, найденный для произвольной выборки, покроет  . Если мы сделаем много выборок объема n и для каждой из них построим интервал
. Если мы сделаем много выборок объема n и для каждой из них построим интервал 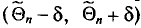 , то доля тех выборок, чьи интервалы покроют
, то доля тех выборок, чьи интервалы покроют  , равна
, равна  .
.
Иными словами,  есть мера нашего доверия вычисленной оценке
есть мера нашего доверия вычисленной оценке 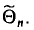
Ясно, что, чем меньше число 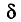 , тем меньше надежность
, тем меньше надежность  .
.
Определение:
Доверительным интервалом называется найденный по данным выборки интервал 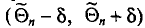 , который покрывает параметр
, который покрывает параметр  с заданной надежностью
с заданной надежностью  .
.
Надежность  обычно принимают равной 0,95 или 0,99, или 0,999.
обычно принимают равной 0,95 или 0,99, или 0,999.
Конечно, нельзя категорически утверждать, что найденный доверительный интервал покрывает параметр  . Но в этом можно быть уверенным на 95% при
. Но в этом можно быть уверенным на 95% при  = 0,95, на 99% при
= 0,95, на 99% при  =0,99 и т. д. Это значит, что если сделать много выборок, то для 95% из них (если, например,
=0,99 и т. д. Это значит, что если сделать много выборок, то для 95% из них (если, например,  = 0,95) вычисленные доверительные интервалы действительно покроют
= 0,95) вычисленные доверительные интервалы действительно покроют  .
.
Доверительный интервал для математического ожидания при известном
Доверительный интервал для математического ожидания при известном 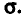
В некоторых случаях среднее квадратическое отклонение о ошибки измерения (а вместе с нею и самого измерения) бывает известно. Например, если измерения осуществляются одним и тем же прибором при одних и тех же условиях.
Итак, пусть случайная величина X распределена нормально с параметрами а и  , причем
, причем  известно. Построим доверительный интервал, покрывающий неизвестный параметр а с заданной надежностью
известно. Построим доверительный интервал, покрывающий неизвестный параметр а с заданной надежностью  . Данные выборки есть реализации случайных величин
. Данные выборки есть реализации случайных величин 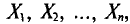 имеющих нормальное распределение с параметрами а и
имеющих нормальное распределение с параметрами а и  (§ 4.2, п. 1). Оказывается, что и выборочная средняя случайная величина
(§ 4.2, п. 1). Оказывается, что и выборочная средняя случайная величина 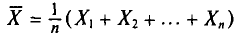 тоже имеет нормальное распределение (это мы примем без доказательства). При этом (см. § 4.2, пп. 2, 3)
тоже имеет нормальное распределение (это мы примем без доказательства). При этом (см. § 4.2, пп. 2, 3)
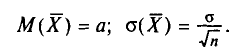
Потребуем, чтобы выполнялось соотношение 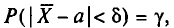 где
где  —заданная надежность. Пользуясь формулой (2.27) (§ 2.7, п. 2), получим
—заданная надежность. Пользуясь формулой (2.27) (§ 2.7, п. 2), получим
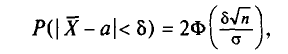
или
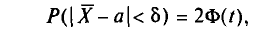
где

Найдя из равенства (4.15) 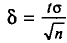 можем написать
можем написать
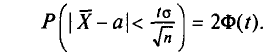
Так как Р задана и равна  , то окончательно имеем (для получения рабочей формулы выборочную среднюю заменяем на
, то окончательно имеем (для получения рабочей формулы выборочную среднюю заменяем на 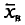 ):
):
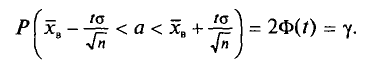
Смысл полученного соотношения таков: с надежностью у можно утверждать, что доверительный интервал 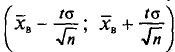 покрывает неизвестный параметр а; точность оценки
покрывает неизвестный параметр а; точность оценки 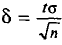 . Здесь число t определяется из равенства
. Здесь число t определяется из равенства 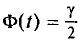 (оно следует из
(оно следует из 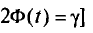 по таблице приложения 3.
по таблице приложения 3.
Как уже упоминалось, надежность  обычно принимают равной или 0,95 или 0,99, или 0,999.
обычно принимают равной или 0,95 или 0,99, или 0,999.
Пример:
Признак X распределен в генеральной совокупности нормально с известным  = 0,40. Найдем по данным выборки доверительный интервал для а с надежностью
= 0,40. Найдем по данным выборки доверительный интервал для а с надежностью  = 0,99, если n = 20,
= 0,99, если n = 20, 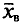 = 6,34.
= 6,34.
Для 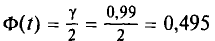 находим по таблице приложения 3
находим по таблице приложения 3
t=2,58. Следовательно, 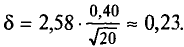 . Границы доверительного интервала 6,34 — 0,23 = 6,11 и 6,34 + 0,23 = 6,57. Итак, доверительный интервал (6,11; 6,57) покрывает а с надежностью 0,99.
. Границы доверительного интервала 6,34 — 0,23 = 6,11 и 6,34 + 0,23 = 6,57. Итак, доверительный интервал (6,11; 6,57) покрывает а с надежностью 0,99.
Доверительный интервал для математического ожидания при неизвестном
Доверительный интервал для математического ожидания при неизвестном 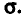 .
.
Пусть случайная величина X имеет нормальное распределение с неизвестными нам параметрами а и  . Оказывается, что случайная величина (ее возможные значения будем обозначать через t)
. Оказывается, что случайная величина (ее возможные значения будем обозначать через t)
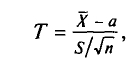
где n —объем выборки; 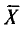 — выборочная средняя; S—исправленное среднее квадратическое отклонение, имеет распределение, не зависящее от а и
— выборочная средняя; S—исправленное среднее квадратическое отклонение, имеет распределение, не зависящее от а и  . Оно называется распределением Стьюдента*.
. Оно называется распределением Стьюдента*.
Плотность вероятности распределения Стьюдента дается формулой
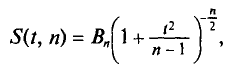
где коэффициент 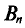 зависит от объема выборки.
зависит от объема выборки.
Потребуем, чтобы выполнялось соотношение
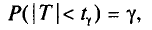
где  —заданная надежность.
—заданная надежность.
Так как S(t, n) — четная функция от t, то, пользуясь формулой
(2.15) (см. § 2.5), получим
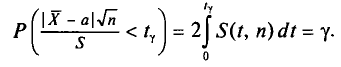
Отсюда
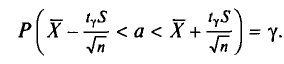
Следовательно, приходим к утверждению: с надежностью  можно утверждать, что доверительный интервал
можно утверждать, что доверительный интервал 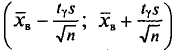 покрывает неизвестный параметр а, точность оценки
покрывает неизвестный параметр а, точность оценки 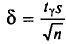 -. Здесь случайные величины
-. Здесь случайные величины 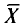 и S заменены неслучайными величинами
и S заменены неслучайными величинами 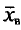 и s, найденными по выборке.
и s, найденными по выборке.
В приложении 4 приведена таблица значений 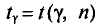 для различных значений n и обычно задаваемых значений надежности.
для различных значений n и обычно задаваемых значений надежности.
Заметим, что при 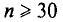 распределение Стьюдента практически не отличается от нормированного нормального распределения
распределение Стьюдента практически не отличается от нормированного нормального распределения
(см. § 2.7, п. 2). Это связано с тем, что 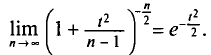
Пример. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 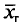 с надежностью
с надежностью  =0,99, если
=0,99, если 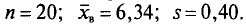 Для надежности
Для надежности  =0,99 и n = 20 находим по таблице приложения 4
=0,99 и n = 20 находим по таблице приложения 4 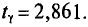 Следовательно,
Следовательно, 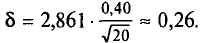 . Концы доверительного интервала 6,34-0,26 =
. Концы доверительного интервала 6,34-0,26 =
= 6,08 и 6,34 + 0,26 = 6,60. Итак, доверительный интервал (6,08; 6,60) покрывает 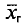 с надежностью 0,99.
с надежностью 0,99.
Доверительный интервал для среднего квадратического отклонения
Для нахождения доверительного интервала для среднего квадратического отклонения  будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим (пп. 2 и 3).
будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим (пп. 2 и 3).
С надежностью  можно утверждать, что доверительный интервал
можно утверждать, что доверительный интервал 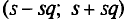 покрывает неизвестный параметр
покрывает неизвестный параметр  ; точность оценки
; точность оценки 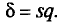
В приложении 5 приведена таблица значений 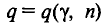 для различных значений n и обычно задаваемых значений надежности
для различных значений n и обычно задаваемых значений надежности  .
.
Пример:
Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для 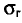 с надежностью
с надежностью  =0,95, если n = 20, s = 0,40.
=0,95, если n = 20, s = 0,40.
Для надежности  =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40 0,37 = 0,15. Границы доверительного интервала 0,40-0,15 = 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает
=0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40 0,37 = 0,15. Границы доверительного интервала 0,40-0,15 = 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает 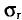 с надежностью 0,95.
с надежностью 0,95.
Пример:
На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратическое отклонение — 20 кг.
Определим: 1) доверительный интервал для математического ожидания а с надежностью 0,95; 2) доверительный интервал для среднего квадратического отклонения с той же надежностью.
При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.
Решение:
1) Согласно условиям задачи, 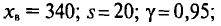 n = 20.
n = 20.
Пользуясь распределением Стьюдента, для надежности у=0,95 и n = 20 находим в таблице приложения 4 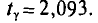 Следовательно,
Следовательно, 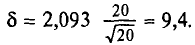 Границы доверительного интервала 340-9,4 =
Границы доверительного интервала 340-9,4 =
= 330,6 и 340 + 9,4 = 349,4. Итак, доверительный интервал (330,6; 349,4) покрывает а с надежностью 0,95.
Можно считать, что в данном случае истинная масса измерена 9 4 достаточно точно (отклонение порядка 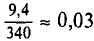 ).
).
2) Для надежности у =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 20 * 0,37 = 7,4. Границы доверительного интервала 20 — 7,4 = 12,6 и 20 + 7,4 = 27,4. Таким образом, 12,6 <  < 27,4, откуда можно заключить, что
< 27,4, откуда можно заключить, что  определено неудовлетворительно (отклонение порядка
определено неудовлетворительно (отклонение порядка 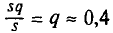 — почти половина!). Чтобы сузить доверительный интервал при той же надежности, необходимо увеличить число проб n.
— почти половина!). Чтобы сузить доверительный интервал при той же надежности, необходимо увеличить число проб n.
Примечание. Выше предполагалось, что q<1. Если q> 1, то, учитывая, что  >0, получаем 0<
>0, получаем 0< <s + sq. Значения q и в этом случае определяются по таблице приложения 5.
<s + sq. Значения q и в этом случае определяются по таблице приложения 5.
Пример:
Признак X генеральной совокупности распределен нормально. По выборке объема n = 10 найдено «исправленное» среднее квадратическое отклонение s = 0,16. Найдем доверительный интервал для 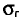 с надежностью 0,999.
с надежностью 0,999.
Для надежности у = 0,999 и n= 10 по таблице приложения 5 находим q=1,80.
Следовательно, искомый доверительный интервал таков’
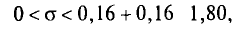
или
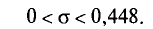
Оценка истинного значения измеряемой величины
Пусть проводится n независимых равноточных измерений* некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины 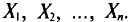 Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии
Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии 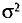 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются, следовательно, мы вправе использовать полученные в них предложения. Так как обычно
(измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются, следовательно, мы вправе использовать полученные в них предложения. Так как обычно  неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.
неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.
Пример:
По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений 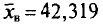 и «исправленное» среднее квадратическое отклонение s = 5,0. Требуется оценить истинное значение а измеряемой величины с надежностью у = 0,99.
и «исправленное» среднее квадратическое отклонение s = 5,0. Требуется оценить истинное значение а измеряемой величины с надежностью у = 0,99.
Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном  ) при помощи доверительного интервала
) при помощи доверительного интервала
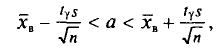
покрывающего а с заданной надежностью у=0,99.
Пользуясь таблицей приложения 4 по у=0,99 и n = 9, находим 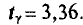
Найдем точность оценки:
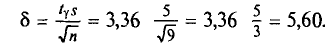
Границы доверительного интервала
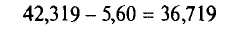
и
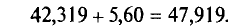
Итак, с надежностью у=0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719<а< 47,919.
Оценка точности измерений
В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения  случайных ошибок измерений. Для оценки
случайных ошибок измерений. Для оценки  используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то утверждение, приведенное в п. 4, применимо для оценки точности измерений.
используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то утверждение, приведенное в п. 4, применимо для оценки точности измерений.
Пример:
По 16 независимым равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s=0,4. Найдем точность измерений с надежностью у = 0,99.
Как отмечено выше, точность измерений характеризуется средним квадратическим отклонением о случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала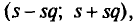 покрывающего
покрывающего  с заданной надежностью у=0,99 (см. п. 4). По таблице приложения 5 по у = 0,99 и n=16 найдем q = 0,70. Следовательно, искомый доверительный интервал таков:
с заданной надежностью у=0,99 (см. п. 4). По таблице приложения 5 по у = 0,99 и n=16 найдем q = 0,70. Следовательно, искомый доверительный интервал таков:
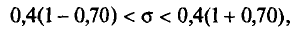
или
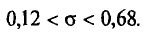
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров


Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:
 (в данной формуле не используется показатель объема генеральной совокупности N)
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p – ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p – ∆; p + ∆) = (20% – 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ – ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ – ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
