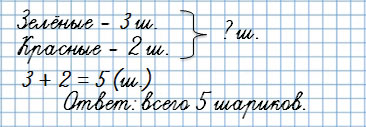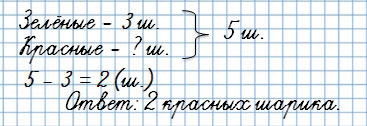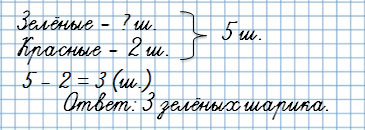|
Что значит “обратная задача” в математике (1, 2, 3, 4 класс)? Как записать и решить обратную задачу, пример? В математике обратная задача составляется на основании какой-либо имеющейся задачи. В обратных задачах искомые данные уже известны. Требуется найти одну из величин, которые были даны в условии исходной задачи. Пример 1 Исходная задача. В магазине яблоки стоят 120 рублей за 1 килограмм, а груши стоят 150 рублей за 1 килограмм. Требуется узнать, на сколько груши дороже яблок. Для решения этой задачи нужно найти разницу между 2 числами – стоимостью груш и стоимостью яблок. 150 – 120 = 30 (руб.) Таким образом, груши дороже яблок на 30 рублей. _ Обратная задача. Здесь нам будет известна разница в стоимости фруктов, то есть 30 рублей. Будем находить либо стоимость яблок, либо стоимость груш – то есть можно составить 2 разных обратных задачи. 1) Яблоки стоят 120 рублей, а груши на 30 рублей дороже. Сколько стоят груши? Решение: 120 + 30 = 150 (руб.) 2) Груши стоят 150 рублей, а яблоки на 30 рублей дешевле. Сколько стоят яблоки? Решение: 150 – 30 = 120 (руб.) Пример 2 Исходная задача. Покупатель хочет купить 500 грамм говядины, которая стоит 200 рублей за 1 килограмм. Сколько он должен заплатить? Для решения данной задачи нужно вспомнить соотношение между граммами и килограммами. 1 килограмм = 1000 грамм. 500 грамм – это ровно половина от 1000 грамм (или 1 килограмма): 500 / 1000 = 1/2. Таким образом, покупатель заплатит не 200 рублей, а только половину: 200 / 2 = 100 (руб.) _ Обратная задача. Здесь нам будет известна цена покупки, то есть 100 рублей. Можно найти, например, стоимость за 1 килограмм. Вот формулировка подобной задачи: Покупатель купил 500 грамм говядины за 100 рублей. Сколько стоит 1 килограмм говядины? Решение: 1) 1 килограмм – это 1000 грамм. 1000 / 500 = 2, то есть 1 килограмм будет в 2 раза больше, чем 500 грамм. 2) Стоимость 1 килограмма составляет 100 * 2 = 200 (руб.) модератор выбрал этот ответ лучшим Математический термин “обратная задача” включает два слова. С существительным задача все понятно. Возникает вопрос: что значит обратная. Данное прилагательное по отношению к задаче можно определить как противоположная или ведущая назад, к исходному состоянию. Для того, чтобы составить обратную задачу, нужно иметь задачу исходную. И исходную задачу необходимо решить. Это нужно для того, чтобы использовать полученный результат в качестве исходных данных для обратной задачи. Если сказать еще проще, то то, что дано ( известно ) в исходной задача, в обратной ей нужно будет искать. А решение исходной задачи станет тем, что известно по условию обратной задачи. Это мое определение термину “обратная задача”, простого определения для начальной школы я не нашла. Проще пояснить на примерах. Исходная задача: Мама купила 5 пирожных и 7 кексов к чаю. Сколько всего кексов и пирожных купила мама? Решение 5+7=12 (шт.) выпечки купила мама. Обратная ей задача: Обратных задач можно в этом случае составить две: 1) Мама всего купила 12 пирожных и кексов к чаю, из них 5 пирожных. Сколько кексов купила мама? Решение 12-5=7 (к.) купила мама. 2) Мама всего купила 12 пирожных и кексов к чаю, из них 7 кексов. Сколько пирожных купила мама? Решение 12-7=5 (п.) купила мама. Марина Вологда 3 года назад Обратная задача – это такая задача, в которой все искомые величины уже известны. Из этих известных величин и составляем обратную задачу. Например, нам дана задача: В автопарк заехало три красных машины и пять белых. Сколько всего машин заехало в автопарк? Решение: 3+5 = 8 машин. Составляем обратную задачу: 1) Сколько машин заехало в автопарк красного цвета, если известно, что всего машин было 8. А белых машин было 5. Решение: 8-5 = 3 машины красного цвета. 2) Известно, что в автопарк заехало 8 машин. Из них три были красного цвета. Остальные машины были белые. Сколько машин белого цвета? Решение: 8-3 = 5 машин белого цвета. Алиса в Стране 3 года назад Многие из нас, наверное, уже забыли, что такое обратная задача, но на самом деле ничего сложного в ней нет. Приведу пример. Допустим, у нас есть расстояние (путь) и время, за которое человек его прошел, все мы знаем, как просто определить скорость, нужно расстояние (путь) разделить на время. Так вот к этой элементарной задачке можно составить две обратные задачи: на определение пути (расстояния), если известна скорость и время (чтобы решить эту задачу, нужно скорость умножить на время): Второй обратной задачей будет задача на определение времени, если известно расстояние (путь) и скорость (нужно путь поделить на скорость): Не знаю, кто их назвал “обратными” потому что задача это всегда, как минимум, поиск третьего неизвестного по двум известным, и какая разница какое из них будет неизвестным. Составить их проще простого, просто поменять неизвестное с известным, ну и вероятно математическое действие будет другое – вместо сложения – вычитание, вместо деления – умножение (как и наоборот) Вот пример. У Васи было две конфеты, Валя дала Васе еще три конфеты, сколько у Васи конфет теперь? Ответ – пять. Якобы обратная задача. У Васи было пять конфет, две из которых были его, сколько конфет ему дала Валя что бы у него получилось пять? Ответ – три. Zummy out off 3 года назад Обратная задача в математике – это такая задача, которая составляется по исходной задаче, но ответ исходной задачи включается в условие обратной задачи, а требуется найти то, что было одним из условий исходной задачи. Составление обратных задач тренирует «мозги» для решения задач в математике. Пример составления обратной задачи. Исходная задача. У Маши было 20 рублей, она купила тетрадь за 12 рублей. Сколько денег осталось у Маши? Решение: 20-12=8. Ответ: 8 рублей осталось у Маши. Обратная задача. В условие задачи надо включить сумму сдачи 8 руб. Составляем задачу: Маша купила тетрадь за 12 руб и у неё осталась сдача 8 руб. Сколько денег было у Маши до покупки тетради? Решение: 12+8=20. Ответ: 20 рублей было у Маши. Бархатные лапки 3 года назад Обратная задача составляется на основе уже имеющейся решенной задачи. В обратной задаче требуется узнать то, что было известно в нашей задаче. Объясним, что такое обратная задача, на примере простейшей задачки для начальных классов. У Иры 10 яблок, у Маши 5 яблок. Нужно найти, сколько яблок у обоих девочек вместе. Это наша задача, решается она так: общее количество яблок равно: яблоки Иры плюс яблоки Маши = 5 + 10 + 15 Обратная задача к этой задаче: у двух девочек, Иры и Маши 15 яблок, сколько яблок у Иры, если у Маши 5 яблок. Решение: 15 – 5 = 10 яблок у Иры. Также обратную задачу можно составить и так: у Иры и Маши 15 яблок, сколько яблок у Маши, если у Иры 10 яблок. Решение: 15 – 10 = 5, у Маши 5 яблок. KritikSPb 4 года назад Обратная задача в математике требует найти то, что было известно в первоначальной задаче. То есть обязательным условием составления обратной задачи является наличие прямо задачи, от которой и отталкиваются для составления обратной. Например, первоначально известно, что человеку нужно дойти из дома до магазина. Расстояние 10 км. Идёт он со скоростью 5 км в час. Через сколько времени он будет на месте? Решение: 10 / 5 = 2 часа. А теперь обратная задача: За два часа человек дошёл от дома до магазина. Определите расстояние, если известно, что скорость человека 5 км в час. Решение: 2 * 5 = 10 км. Для составления обратной задачи необходимо решить исходную. Бекки Шарп 3 года назад Обратные задачи бывают в разных науках и в математике тоже. Обратная составляется на основании уже полученных данных. Когда то что требовалось найти уже известно. Например. У Миши было 7 яблок, а у Васи 8 яблок. Сколько всего было яблок у мальчиков. Решение: 7+8=15 (яблок) Обратная задача к нашей будет такая. Всего у Миши и Васи 15 яблок. У Миши – 7 яблок. Сколько у Васи яблок? Решение: 15-7=8 (яблок) Еще одна обратная задача к нашей. У Миши и Васи 15 яблок, у Васи – 8. Сколько яблок у Миши? Решение: 15-8=7 (яблок) Val111111 4 года назад Обратная задача- это когда то, что требовалось найти, теперь известно, а то, что было в дано нужно найти. Пример, есть три яблока. Два забрали. Сколько осталось? Обратная задачка: Забрали два яблока, осталось одно, сколько было? TheSun 3 года назад В обратной задаче неизвестным является дано, именно его и нужно найти. Но, при этом известен результат. Рассмотрим на примере. У Маши было 4 синих мяча и 3 зелёных мяча. Сколько всего у Маши мячей? 4+3=7 (шт.) мячей у Маши. Теперь обратная задача. У Маши всего 7 мячей. Из них синих мячей 4, а остальные мячи зелёного цвета. Сколько у Маши зелёных мячей? 7-4=3 (шт.) зелёных мяча у Маши. Знаете ответ? |
Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.
В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.
Решим задачу:
10 + 8 = 18 (д.)
Ответ: 18 детей в классе.
Составим вторую задачу.
В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?
Решим задачу:
18 – 10 = 8 (м.)
Ответ: 8 мальчиков в классе.
Составим третью задачу.
В классе 18 детей. Мальчиков 8, остальные – девочки. Сколько девочек в классе?
Решим задачу:
18 – 8 = 10 (д.)
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Тренировочные задания.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
Варианты ответов:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
Правильные варианты:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
Варианты ответов:
30, 20, ясных, пасмурных, июне
Правильный вариант:
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Обратные задачи
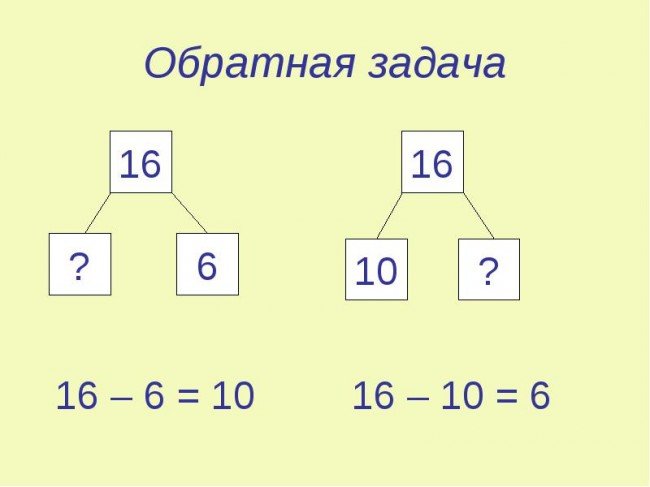
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.
Прямая задача:
У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?
Первая обратная задача:
У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?
Ты видишь, что известная величина – красные шарики – стала неизвестной.
А неизвестная величина – общее количество шариков – стало известной.
Вторая обратная задача:
У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?
Ты видишь, что известная величина – зелёные шарики – стала неизвестной.
А неизвестная величина – общее количество шариков – стало известной.
ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.
Советуем посмотреть:
Образцы оформления задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 48. Урок 25,
Петерсон, Учебник, часть 2
Страница 50. Урок 26,
Петерсон, Учебник, часть 2
Страница 53. Урок 27,
Петерсон, Учебник, часть 2
Страница 60. Урок 31,
Петерсон, Учебник, часть 2
Страница 63. Урок 32,
Петерсон, Учебник, часть 2
Страница 8. Урок 5,
Петерсон, Учебник, часть 3
Страница 25. Урок 13,
Петерсон, Учебник, часть 3
Страница 33. Урок 17,
Петерсон, Учебник, часть 3
Страница 65. Урок 33,
Петерсон, Учебник, часть 3
Страница 91. Повторение,
Петерсон, Учебник, часть 3
2 класс
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 17. ПР 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77. Урок 31,
Петерсон, Учебник, часть 2
Страница 12. Урок 4,
Петерсон, Учебник, часть 3
3 класс
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 21,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 35. Урок 13,
Петерсон, Учебник, часть 1
Страница 38. Урок 14,
Петерсон, Учебник, часть 1
Страница 40. Урок 15,
Петерсон, Учебник, часть 1
Страница 74. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 87,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2
Содержание
- Что означает обратная задача в математике?
- В данном случае, можно составить и решить две задачи обратные данной:
- Что значить решить задачу обратную данной
- Остались вопросы по теме? Наши репетиторы готовы помочь!
- Что такое задачи, обратные данной?
- Математика. 2 класс
Что означает обратная задача в математике?
Что такое обратная задача?
Начиная со второго класса, детям регулярно задают на дом задания. Большое внимание педагоги уделяют решению задач, ведь именно за них ребенок получает больше баллов на контрольных и тестах.
Понятие «обратная задача» знакомо всем ученикам школы, в которой учатся мои дети, даже тем, кто не любит математику и далек от нее.
По сути, обратная данной задача, — это задача в которой искомое и заданное поменялись местами. Для того чтобы решить ее, нужно для начала решить заданную.
В качестве примера рассмотрим задачу с решением в одно действие: На столе было 5 груш и 4 яблока, сколько фруктов было всего. Решение простое: 5+4=9.
В данном случае, можно составить и решить две задачи обратные данной:
- Всего на столе было 9 фруктов, из них 5 груш. Сколько было яблок?
- Всего на столе было 9 фруктов, из них 4 яблока. Сколько было груш?
Чем больше данных в задаче, тем больше обратных задач можно к ней составить.
Обратные задачи просты и понятны большинству учеников младших классов.
Если же ваш ребенок пропустил эту тему, не понимает, что от него требуется, научить его составлять обратные задачи не составит труда, так как данная тема легко воспринимается даже детьми с гуманитарным складом ума.
Достаточно интересна и познавательна для родителей тема: «Как помочь ребенку преодолеть школьные проблемы», рекомендую с ней, по желанию, ознакомиться.
Источник
Что значить решить задачу обратную данной
5. Задачи, обратные данной
1. Организационный этап
Ну, ребята, чур, молчок!
Начинается урок.
Приготовьте свои ушки и глазки,
Чтобы они могли всё видеть,
Слышать и запоминать.
Громко прозвенел звонок –
Начинается урок.
2. Этап подготовки учащихся к активному сознательному усвоению знаний
1. Целеполагание
Сегодня на уроке мы узнаем, что такое обратные задачи.
2. Устный счёт
Задание 1
Решите примеры. Дополните столбики одним своим примером. Запишите только ответы.
12 — 6 = 6 — У 5 + 7 = 12 — А 80 — 10 = 70 — О
13 — 6 = 7 — З 6 + 7 = 13 — Й 70 — 20 = 50 — Н
14 — 6 = 8 — Н 7 + 7 = 14 — К 60 — 30 = 30 — И
6, 7, 8, 9, 12, 13, 14, 15, 70, 50, 30, 10.
Расположите числа в порядке возрастания, чтобы узнать название города, по которому мы будем путешествовать сегодня на уроке.
6, 7, 8, 12, 13, 14, 30, 50, 70.
У З Н А Й К И Н О
Какое получилось слово?
В этом городе живут забавные человечки, которые очень любознательны и хотят все знать.
Задание 2
Чтобы попасть в город УЗНАЙКИНО нужно ответить на вопросы:
Назовите однозначные числа.
Назовите двузначные числа.
Назовите самое маленькое двузначное число.
Назовите самое маленькое однозначное число.
Назовите числа предшествующие числам: 6, 12, 30, 50, 70. 5, 11, 29, 49, 69.
Назовите числа, следующие за числами: 10, 15, 30, 50, 70. 11, 16, 31, 51, 71.
Назовите числа, которые находятся между числами 15 и 30. 16-29
А вот и наш помощник. Зовут его Путейка, потому что он очень любит путешествовать. Путейка познакомит вас с городом, расскажет интересные истории, проверит ваши знания.
Какой предмет помогал героям сказок находить нужное место?
Правильно, клубок ниток помогал героям сказок находить нужное место. Какой прибор помогает современным путешественникам?
Верно, компас помогает современным путешественникам. Что вы знаете о компасе? Компас – это устройство, облегчающее ориентирование на местности. Когда не было компаса, то люди ориентировались по солнцу, луне и звёздам, по местным признакам. А потом изобрели прибор, на котором изобразили четыре стороны света: Север, Юг, Запад, Восток. В центре компаса находится вращающаяся стрелка, 2 половины которой раскрашены в синий и красный цвет. Красная стрелка показывает на Юг, синяя – на Север.
Задание 3
Мы попали на улицу Сравнительную. Поставьте нужный знак, чтобы продолжить путешествие по улице.
1 дес… 10 1 дес = 10
1 р. …1 к. 1 р. > 1 к.
23… 32 23 4 дм
78 …75 78 > 75
Задание 4
Продолжим наш путь на общественном транспорте. Для этого нужно купить билет.
Сколько нужно получить сдачи с 10 рублей, если билет стоит 5 рублей? 5
Если билет стоит 6 рублей? 4
Если билет стоит 8 рублей? 2
Задание 5
Помогите Путейке сосчитать общественный транспорт, который находится на станции.
На станции находилось 5 автобусов, а троллейбусов на 6 больше. Сколько всего автобусов и троллейбусов на станции?
Решите задачу.
1) 5 + 6 = 11 (тр.)
2) 11 + 5 = 16 (м.)
3. Этап усвоения новых знаний
Мы прибыли на станцию «Задачкино». На этой станции мы узнаем, как решаются задачи, в которых число и результат меняются местами.
1. В апреле было 14 пасмурных дней и 16 ясных дней. Сколько дней в апреле?
2. В апреле 30 дней. Из них 14 дней были пасмурными. Сколько ясных дней было в апреле?
3. В апреле 30 дней. Ясными были 16 дней. Сколько пасмурных дней было в апреле?
Это одна и та же задача?
Нет, разные задачи.
Какая связь между задачами?
Говорится про одно и то же, но известное и неизвестное меняются.
Как вы думаете, эти задачи будут иметь одинаковое решение?
Давайте решим эти задачи.
Прочитайте 1 задачу.
Что известно? Пасмурных дней было 14. Ясных дней было 16.
Что спрашивается в задаче?
Каким действием решим задачу?
Прочитаем 2 задачу.
В чем сходство и в чем отличие этой задачи от предыдущей?
Что известно? В апреле 30 дней. Пасмурных дней было 14.
Что нужно узнать? Сколько ясных дней было в апреле.
Как решим эту задачу?
Прочитайте 3 задачу.
Как изменилось ее условие?
Какая будет краткая запись?
П. – ? дн.
Яс. – 16 дн. (общая скобка, 30 дн.)
Что нужно узнать?
Как решается эта задача?
Внимательно посмотрите на условия этих трех задач. Что вы о них можете сказать?
Они похожи. Что в этих задачах одинаково?
Данные, числа одинаковы. Чем задачи отличаются?
Ставятся вопросы разные. Что было известно, стало неизвестно и наоборот.
Сравните решения задач. Что одинаково?
Числа.
Чем отличаются?
Действиями. Другими словами, действия обратные.
Как назовем вторую и третью задачи по отношению к первой?
Задачи, обратные первой. Значит, что такое обратная задача?
Задачи, в которых объект (число) и результат меняются местами (известное становится не известным, а неизвестное известным), называются обратными первой.
Вместе с человечком мы добрались до остановки «Отдыхайкино».
4. Этап закрепления новых знаний
Мы добрались до улицы Решайкино. Как вы думаете, чем занимаются жители города на этой улице?
Правильно, они решают задачи. Давайте поможем им решить задачи.
Задание 1
1. В классе 20 учеников. 7 из них мальчики. Сколько девочек в классе?
2. В классе 7 мальчиков, а девочек на 6 больше. Сколько девочек в классе?
3. В классе 7 мальчиков и 13 девочек. Сколько всего детей в классе?
Найдите среди этих задач обратные.

Конечно № 1 и 3 – это обратные задачи. Объясните, почему вы так считаете?
Молодцы ребята, вы справились с заданием и попали на улицу Составляйкино.
Как думаете, чем занимаются жители города Узнайкино на этой улице?
Правильно, с забавными человечками мы будем составлять задачи обратные данной.
Задание 2
Прочитайте задачу.
В одном доме проживает 8 человечков, а в другом доме — 9. Сколько всего человечков проживает в двух домах?
Составим чертёж к задаче. Что известно в задаче?
Что спрашивается в задаче?
Как решается эта задача?
Ответ: 17 человечков.
Составим задачи, обратные данной. Не забывайте, что, решив исходную задачу, надо взять её ответ и включить его в новую задачу, не меняя сюжета, а одно из известных сделать искомым.
Задание 3
В двух домах проживает 17 человечков. В одном доме проживает 8 человечков. Сколько человечков проживает во втором?Составьте чертёж задачи.
Решите задачу.
Ответ: 9 человечков.
Составьте ещё одну задачу.
В двух домах проживает 17 человечков. В одном доме проживает 9 человечков. Сколько проживает в первом доме?
Составьте чертёж задачи.
Решите задачу.
Ответ: 8 человечков.
Чем отличаются схемы обратных задач от схемы данной задачи?
А если нет компаса и не светит солнце, можно ли как-то ещё сориентироваться на местности?
Как могут помочь знания о том, с какой стороны у деревьев растёт мох?
C какой стороны дерева муравьи строят муравейники?
В незнакомой такой обители
неприметно для нас живёт
Очень рыженький, очень маленький,
Муравьиный такой народ.
Озабоченный, сосредоточенный,
И у каждого ноша своя.
Ну, скажите, а вы разве видели
Безработного муравья? Р. Дерикот
Задание 4
Жители города Узнайкино говорят: «Трудолюбив, словно муравей».
Что значит эта поговорка?
Народ города предлагает вам потрудиться самостоятельно.
Самостоятельная работа
Задание 1
Человечек поймал 6 окуней и 8 лещей. Сколько всего рыб он поймал?
— Нарисовать схематический чертёж и решить задачу.
Проверьте себя и оцените свои успехи.
Задание 2
Решите задачи, обратные данной, используя чертежи.
14 — 6 = 8 (л.) 14 — 8 = 6 (ок.)
Ответ: 8 лещей. Ответ: 6 окуней.
Проверьте себя и оцените свои успехи.
5. Этап подведения итогов
Вот и подошло наше путешествие к концу.
С какими задачами мы познакомились сегодня на уроке?
Какие задачи называются обратными?
Еще раз запомните! Задачи, в которых объект (число) и результат меняются местами (известное становится не известным, а неизвестное известным), называются обратными первой.
Рефлексия
Понравилось вам наше занятие?
Выберите человечка, с которым вы хотели бы дружить.
Спасибо за урок!
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовиться к ЕГЭ, ОГЭ и другим экзаменам
Подготовиться к поступлению в любой ВУЗ страны
Источник
Что такое задачи, обратные данной?
Задачи, обратные данной — это задачи, в которых говорится об одном и том же, но известное и неизвестное меняются местами.
Поделиться в социальных сетях
Вашему вниманию представлена памятка по составлению схем-чертежей при решении простых и составных задач на.
Вашему вниманию представлен тренажёр «Отличник». Какие плюсы данного тренажёра? Во- первых, после.
Чтобы побеждать в математических олимпиадах, необходимо много трудиться. С этой целью предлагаю онлайн-.
Традиционно в школах сентябрь — это месяц входных контрольных работ. Цель такого вида контроля —.
ПАМЯТКА «РАБОТА НАД ОШИБКАМИ» (.
Отправляя сообщение, Вы разрешаете сбор и обработку персональных данных.
Политика конфиденциальности.
Я, Алегина Лилия Фаритовна, учитель начальных классов в режиме 24/7, человек, который стремится сделать обучение детей с 1 по 4 класс современным, интересным и познавательным!
Источник
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.
В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.
Ответ: 18 детей в классе.
Составим вторую задачу.
В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?
Ответ: 8 мальчиков в классе.
Составим третью задачу.
В классе 18 детей. Мальчиков 8, остальные — девочки. Сколько девочек в классе?
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
30, 20, ясных, пасмурных, июне
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
Источник
О.Д. Юрковец
студентка 5 курса ЛПИ Филиала СФУ
Г. Лесосибирска Российской федерации
МЕТОДИЧЕСКИЕ ПРИЕМЫ В
ОБУЧЕНИИ МЛАДШИХ ШКОЛЬНИКОВ СОСТАВЛЕНИЮ ТЕКСТОВЫХ ЗАДАЧ ОБРАТНЫХ ДАННЫМ
К сожалению, очень часто в обучении
детей решению задач учителя пользуются только показом способов решения
определенных видов задач и добиваются их закрепления решения механически, при
этом решение задач развивает логическое мышление, сообразительность, смекалку;
при работе над текстовой задачей у школьника идет формирование логического
умения проводить анализ и синтез, совершенствуется умение обобщать и
конкретизировать, раскрывать основное, выделять главное и отбрасывать
несущественное, второстепенное в тексте; воспитываются личностные качества –
воля, терпение, настойчивость.
С первых дней ребенка в школе его
учат решать текстовые задачи. Первые шаги при решении простых задач не вызывают
затруднения. При этом у многих возникают трудности при самостоятельном решении составных
задач, и из года в год эти дети испытывают всё большие затруднения. Главной причиной
этих трудностей является то, что у детей в значительной степени не сформировано
умение анализировать текст задачи, правильно выделять известное и неизвестное,
устанавливать взаимосвязи между ними, которые являются основой выбора действия
для решения текстовой задачи. Из-за этого же возникает сложность в составлении
текстовых задач обратных данным.
При изучении задач в курсе
математики, как простых, так и сложных, как обычных арифметических, так и
типовых оказывается высокоэффективным систематическое применение так
называемого метода обратных задач.
Положительный результат обучения
решению задач посредством преображения прямой задачи в обратные задачи
объясняется как первопричиной тем, что такого рода подход заставляет поднимать
из сферы подсознания максимальное разнообразие связей, заключенных в содержании
задачи. Это гарантирует – на языке дидактики – глубокое и прочное усвоение
материала.
Однако многие учителя не всегда
связывают составление и решение обратных задач с проверкой решения прямых
задач. Скорее всего, причинами этого является громоздкость метода и частичное
владение методикой составления обратных задач. Именно это не дает педагогу
полностью использовать возможности обратных задач, либо ведет лишь к
формальному выполнению проверки.
При выполнении проверки решения
прямой задачи способом составлением обратной задачи и ее решения, учащиеся
должны знать следующий алгоритм:
1. решить исходную задачу;
2. подставить результат в текст
исходной задачи в качестве известного данного;
3. обозначить новое неизвестное в
задаче;
4. составить новую задачу по
отношению к данной;
5. решить составленную задачу;
6. сравнить полученный результат с
тем данным, которое сделали неизвестным;
7. сделать соответствующий вывод
(если числовые значения совпадут, то задача решена верно).
Учащиеся очень редко допускают ошибки,
при составлении обратных задач к задачам, в основе решения которых лежат знания
конкретного смысла арифметических действий. Однако часто делают ошибки в
составлении обратных задач к задачам, в которых содержатся отношения «больше» и
«меньше», заменяя не полученные числа, а само отношение. Это говорит о том, что
у ребенка, который смог допустить такую ошибку, не сформировано понятие
«обратная задача».
Для устранения этой распространённой
ошибки важно использовать в сравнении кратких записей условия как прямой, так
и обратной задачи.
Схематическое изображение задачи
позволит школьнику пронаблюдать, что при составлении обратной задачи изменяются
только числовые значения, отношения в задаче остаются неизменными.
Бывает такое, что школьник, выполнив
решение задачи, и проверив ее решение действием, обратным к выполненному, не
составляет текст обратной задачи. Это приводит лишь к проверке правильности
вычисления, но не может помочь убедиться в правильности решения прямой задачи и
правильности выбора арифметического действия. Так же бывает, что задача
содержащая слова «улетели», «вышли в море», «съели» и т.д. вызывает затруднение
у учеников, у которых не сформирован конкретный смысл арифметических действий,
так как они, не вникая в условие данной задачи, выполняют ее решение действием
вычитания, хотя вопрос в задаче стоит, сколько всего выехало, улетело, ушло и
т.д.
Эту ошибку можно избежать, если ученик
при проверке решения задачи составит условие обратной задачи, а не остановится
на составлении только обратного действия.
Главная причина такого рода ошибок это
то, что у ученика не сформирован алгоритм проверки решения задачи. Алгоритм
проверки решения арифметических задач надо рассматривать специальным курсом,
раскрывая при этом содержание каждого действия, которое имеет место в процессе
проверки, при этом давать обоснование порядку их выполнения. Это приводит к
пониманию и осознанию приема работы.
Составление и решение обратных задач
это один из самых интересных способов проверки решения прямой задачи, а так же
творческая работа над ней. Благодаря ему можно насытить урок задачами.
П. М. Эрдниев в своей методике
рассматривает организацию работы над обратными задачами с первого класса. В его
методике имеются укрупненные задания, состоящие из выполнения трех
последовательных пунктов.
Проходя тему – задачи обратные
данным, по методике Эрдниева или по традиционной, у детей могут возникнуть
следующие трудности при формулировке текста обратных задач. Школьники часто
составляют обратную задачу по аналогии с прямой задачей.
Учащимся нужно рассказывать, про
существование различных формулировок задач, делая акцент на том, что задача
должна быть понятной всем, кто будет ее решать. Текст задачи должен быть
«красивым», «благозвучным», четко выраженным и без лишней информации.
Так же возможно использование при
работе над задачами краткой записи (в основном школьники ее и используют).
Можно применять мобильные схемы, например
такие как схемы С.Н. Лысенковой, смысл которых в смене чисел и знаков вопроса в
соответствующих «квадратиках» на демонстрационной схеме и на схемах на столах у
школьников.
Таким образом, существует большое многообразие
методов и приемов работы над текстовыми задачами обратными данным с младшими
школьниками. К сожалению, в настоящее время много учителей до сих пор не
понимают возможности и ценности использования обратных задач. Это объясняется многими
факторами: нехваткой времени, литературы и методик по этой теме и др. Так же мы
выяснили что, у детей при работе с обратными задачами возникает много ошибок,
избежать которых возможно при использовании определенных методов и приемов.
Можно утверждать, что применение обратных задач в работе с детьми, это и способ
проверки правильности решения прямой задачи, и способ развития творчества,
разносторонности, мотивации к учению и много другого у школьников.
Список использованной литературы:
Истомина Н.Б. Формирование умения
решать задачи различными способами// Начальная школа. 1985. №9.
Клименченко Д.В. Решение задач
различными способами// Начальная школа. 1986. №4.
Соснина Г.М. Один из способов
проверки решения задач // Начальная школа. 1983. №1.
© О.Д. Юрковец, 2018