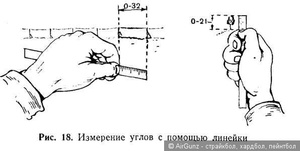
 Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.
- Действительно ли прямой угол?
- Что понадобится для определения прямого угла?
- Как можно вычислить прямой угол?
- Вывод
В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.
Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.
В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве – не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.
Действительно ли прямой угол?
 Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто “на глаз”. В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.
Что понадобится для определения прямого угла?
 Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Для вычисления прямого угла нужно взять:
- Карандаш;
- Строительную рулетку.
И всё. Вот так вот всё просто.
Как можно вычислить прямой угол?
Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.
Итак, нужно обозначить следующие шаги:
 Для начала стоит разобраться в том, почему принцип так обозначен – 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Для начала стоит разобраться в том, почему принцип так обозначен – 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;- Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра – предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
- В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
- После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
- Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.
Вывод
Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.
При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.
Как найти прямой угол
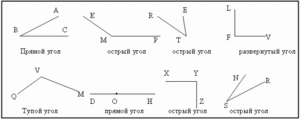
Существует несколько геометрических определений прямого угла:
– прямой угол – это смежный угол или угол, который равен смежному углу;
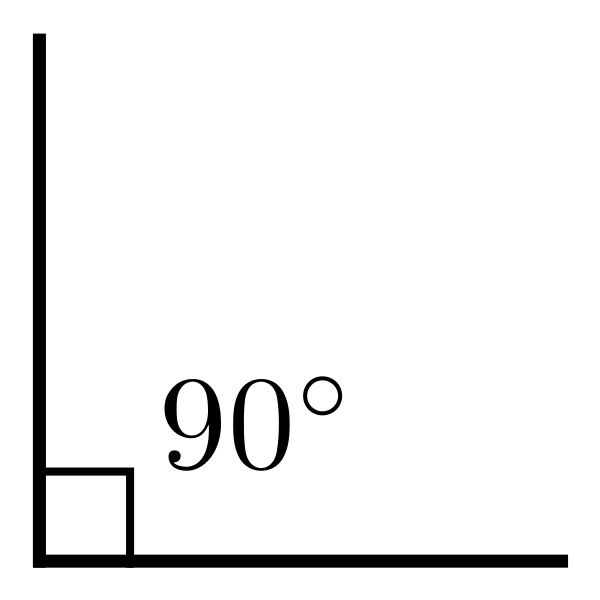
– прямым углом является угол, который равен 90 градусов;
– для вычисления прямого угла необходимы измерения углов- a и b;
– угол равный 90 градусов, составляющий четверть целого угла и половину развернутого называется прямым углом.
Инструкция
Данные понятия и определения указывают на то, что все без исключения прямые углы равны и любые два угла могут быть сравнимы. А само сравнение двух углов с прямым углом вводит понятие – острого и тупого угла.
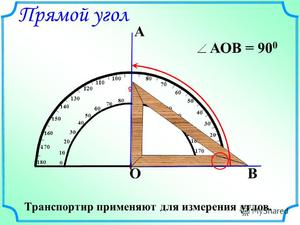
Для того, чтобы найти прямой угол, необходимо вводить измерение градуса угла с помощью транспортира, если он равен 90 градусов, то, следовательно, этот угол является прямым.
Ряд геометрических фигур имеет один или несколько прямых углов. К таким фигурам относятся прямоугольный треугольник (имеет одни прямой угол), параллелограмм (все углы его прямые), квадрат является ромбом, у которого все углы прямые, а также прямоугольная трапеция с одним прямым углом.
Построить прямой угол самостоятельно без геометрических инструментов можно с использованием отвеса (любая нитка с грузом), уровень для горизонтальной и стеклянная деталь для вертикальной поверхности.
Видео по теме
Источники:
- как вычислить прямой угол
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
В этом случае для построения прямого угла применяется всем известная формула Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Еще такое построение называют “египетским треугольником”, так как по такому же принципу строились углы пирамид. Натяните строительный шнур по главному фасаду одной из сторон будущего строения. Эта линия свое положение НЕ меняет. На шнуре, в точке где будет угол постройки привяжите еще один шнур и отойдите с ним в сторону, образуя другую, перпендикулярную сторону строения.На первом шнуре от точки, образующей угол отмерьте 4 метра. От этой же точки, но по другому шнуру отмерьте 3 метра. На совершенно отдельном шнуре зафиксируйте длину (расстояние) 5 метров (можно привязать яркие тесемки). Далее работают 2 человека. Один человек крайнюю точку пятиметрового шнура держит на шнуре главного фасада в точке 4 метра. Другой человекпостарается 5-и метровый шнур дотянуть до точки 3 м на другом шнуре.Вторая сторона на момент построения будет подвижной.Подтяните или отодвиньте боковую сторону так, чтобы крайние точки 5-иметрового и 3-х метрового шнура соединились. А угол между шнуром/линией главного фасада и линией бокового фасада у вас будет прямым, то есть 90 градусов. А по теореме это выглядит так – 4² (16) + 3² (9) = 5² (25) 25 = 25
автор вопроса выбрал этот ответ лучшим Rafail 8 лет назад Возьмите три брусочка (рейки, линейки, металлические полоски, какие-нибудь жесткие дюралевые элементы для строительства). Сделайте в них по два отверстия диаметром 4-6 мм. Расстояния между центрами отверстий должны относиться друг к другу как 3:4:5, (например 60 см, 80 см и 100 см, или 15 см, 20 см, 25 см). Скрепите брусочки винтами (болтами) в треугольник. Получится прямоугольный треугольник с прямым углом между короткими сторонами (катетами). Чем длиннее стороны треугольников тем точнее будет прямой угол. Но, слишком длинные брусочки могут оказаться кривыми, или прогнуться в процессе изготовления или эксплуатации. Другой вариант: берете три кусочка мягкой проволоки, с тем же соотношением длин, например 3 4 и 5 м, реально где-то на 10-20 см длиннее. На концах проволоки делаете кольца. Вбиваете в землю два колышка (кусочки труб), допустим, сначала на расстоянии ровно 3 м, накидываете кольца на колышки и сделав петлю где-нибудь в средней части проволоки “скруткой” выбираете излишек длины, чтобы проволока натянулась как можно прямее между колышками. Точно так же натягиваете другую проволоку на колышки с расстоянием между ними 4 м, и третью – с расстоянием 5 м. Теперь, в вершине требующегося прямого угла вбиваете один колышек. На него накидываете концы 3-х и 4-ж метровых проволок. Другие концы этих проволок продеваете в другие колышки, которые держат в руках Ваши помощники. кольца третьей проволоки (5 м) тоже продеваете в эти колышки. Затем помощники расходятся по требуемым направлениям и подбирают положения колышков, которые у них в руках (удерживая их строго вертикально) так, чтобы все три проволоки были натянуты. Когда такое положение достигнуто, угол будет близок к прямому. Можно и другие соотношения, лишь бы между ними соблюдалась теорема Пифагора, например 5, 12 и 13, или 7,24 и 25.
88SkyWalker88 5 лет назад Прямой угол можно построить, применяя теорему Пифагора. Кроме того, существует такое понятие как египетский треугольник. Еще древние египтяне, строя великие пирамиды, пользовались этим методом. Метод такой: натягиваем шнур, от точки, откуда будет начинаться угол, натягиваем другой шнур перпендикулярный этому. Далее на одной стороне нужно отсчитать три метра, а на другой – четыре метра. Затем берем еще один шнур (красного цвета) длиной ровно пять метров. Теперь пытаемся соединить крайние точки с помощью шнура красного цвета. При этом одна сторона нашего угла будет подвижной. Получаем прямой угол.
Ксарфакс 5 лет назад Для того, чтобы построить прямой угол на местности, можно воспользоваться Египетским треугольником, имеющим соотношение длин сторон как 3:4:5. В этом случае потребуется 3 колышка, а также 3 куска веревки – по 3, 4 и 5 метров. Алгоритм такой: 1) Сначала “натягиваем гипотенузу”. Для этого вбиваем в землю 2 колышка так, чтобы расстояние между ними было 5 метров (можно мерить либо по рулетке, либо по имеющейся верёвке). Закрепляем верёвку.
2) Теперь нужно разместить катеты (куски веревки по 3 и 4 метра) – так, чтобы они совпали вершинами между собой и с гипотенузой (понятно, нужна помощь нескольких человек). В этом случае получится искомый прямой угол. После этого вбиваем 3 колышек в то место, где катеты совпали и закрепляем верёвки. Кроме этого, иногда помогает примитивный вариант – обвести по какому-нибудь прямоугольному предмету. Или если есть доски, то нетрудно соотнести их между собой так, чтобы получился угол 90 градусов – если доски образуют прямой угол, то короткая часть первой доски (ширина) будет как бы продолжением длины другой доски.
Galina7v7 7 лет назад Кроме египетского треугольника,размеров которого немало,можно построить неполную окружность (примерно-полукруг),и провести прямую через центр окружности,это и будет диаметр,а 2 точки диаметра-концами лучей прямого угла.Вершина прямого угла может быть в любой удобной точке полуокружности.Доказательства того,что угол будет прямой,думаю,не требуются.А методика,как провести окружность на местности ,описана в литературе:вбивается колышек в землю,натягивается веревка удобного размера,и пошёл двигаться какой-то объект (человек,лошадь) по свободному концу верёвки,прочерчивая эту полуокружность (можно вбивать колышки через 10-15-25 см,как бы очкрчивая эту полуокружность(методов много).А потом на ней,где нужно отметить вершину прямого угла(можно в любом колышке),а лучи,на прямой -диаметре.То есть соединяя вершину с концами диаметр ,получим прямой угол.Если есть сомнения по поводу полуокружности,можно проводить целую окружность,но это затратно по времени.Достаточно немного больше полуокружности. Владмир8 4 года назад Только что родил способ построения прямого угла к условному забору или к прямой линии с помощью длинной неразмеченной (нерастяжимой) веревки.
Или можно растянуть веревку целиком от основания треугольника у забора до вершины и дальше – половина ляжет на сторону треугольника-далее узелок и колышек в земле- далее вторая половина веревки, как продолжение стороны. (Веревка в итоге получится прямой линией)
Основание- либо теорема об угле, вписанном в окружность (а вытянутая веревка- это и есть диаметр ее, а полверевки- радиус окружности- и точка пересечения-на заборе) Либо свойства прямоугольника- его диагонали равны и точкой пересечения делятся пополам.
Чтобы разметить прямой угол на местности не обязательно иметь транспортир или другие приспособления. Достаточно иметь три шнура и помнить теорему Пифагора. Есть очень удобные соседние числа – 3 и 4, квадраты которых в сумме дадут 25, то есть квадрат 5. А это значит, что есть прямоугольный треугольник со сторонами 3, 4 и 5 метров. При этом сторона в 5 метров окажется гипотенузой. Как же построить такой треугольник на местности? Вбиваем колышек в основание прямого угла. Привязываем к нему шнуры длиной 3 и 4 метра. Проводим сторону длиной например 4 метра и вбиваем второй колышек, закрепляем шнур. Привязываем к этому колышку шнур длиной 5 метров и острым колышком чертим небольшую дугу окружности на расстоянии 5 метров от вбитого колышка. Точно также проводим небольшую дугу радиусом 3 метра от первого колышка. Точка пересечения дуг и будет последней вершиной нашего прямоугольного треугольника.
fatalex 8 лет назад Ну, если говоря “на местности”, Вы предполагаете начертить прямой угол прямо на земле, к примеру размечая границы какого-то участка или фундамента будущего дома, то можно воспользоваться тремя колышками и шпагатом или верёвкой, длинна которой кратна 12 метрам. Говорят, этот метод был известен ещё в древнем Египте, а в его основе так называемое правило “золотого сечения”. “Золотое сечение” – это треугольник со сторонами, длинны которых соотносятся, как 3:4:5
Вот так, более подробно, использование этого метода на практике описывается в интернете:
Отсутствие транспортира вполне компенсирует теодолит. Ну и не забываем что диагонали прямоугольника равны между собой.
Проще простого. Сначала строим квадрат, натянув веревки по периметру. Чем больше будет квадрат, тем точнее будет построен прямой угол. Теперь промеряем диагонали нашего, пока еще якобы квадрата. Скорее всего у нас с первого раза получится ромб. Раздвигаем соответствующие углы квадрата, диагональ между которыми меньше. Делаем это пока обе диагонали не выровняться по длине. Как только это произойдет, мы получим правильный квадрат, а значит и четыре прямых угла. Как правило строили когда делают прямые углы меряют диагонали полученного прямоугольника. Если нужно сделать что-то маленькое, то можно этот прямой угол обвести по прямоугольному предмету. Самый простой способ это произвести замер диагоналей. Можно и с помощью веревки, смотрите какой вариант вам больше подходит.
moreljuba 5 лет назад Для этой цели я вам советую воспользоваться Египетским треугольником, а вернее соотношением его сторон, которое выглядит следующим образом 3 к 4 к 5. Берём колышки и натягиваем верёвкой сначала гипотенузу 5, а затем от неё натягиваем катеты. Так и получим прямой угол на местности. Знаете ответ? |
Приветствую Вас, уважаемые Читатели! Сразу хочу оговориться, что речь в этой статье будет идти про один из “идеальных” геометрических инструментов, задачи для построения с которым придумывали еще в древности.
Инструмент называется “двусторонняя линейка”. Линейка имеет фиксированную ширину а, и каких-либо требования к её углам не предъявляется. Например, моя линейка вообще имеет закругленные концы, в отличие от показанной выше:
Так что, даже отходя от требуемой геометрической “идеальности” инструмента, построить идеальный прямой угол или, например, провести перпендикуляр к прямой в произвольной точке будет не так просто, как кажется.
Что может идеальная двусторонняя линейка ?
Давайте перейдем к “правилам игры” – возможностям двусторонней линейки.С помощью этой линейки выполнимы следующие элементарные построения:
1) проводить прямую через две данные точки;
2) проводить прямую, параллельную данной и удаленную от нее на расстояние a;
3) через две данные точки A и B, где AB больше или равно a, проводить пару параллельных прямых, расстояние между которыми равно a (таких пар прямых две).
Этот функционал, кстати, позволяет проводить все построения доступные для классического тандема “циркуль-линейка”
Давайте начнем
Самая простая задача – построить прямой угол, скажем так, в произвольном месте плоскости. Для этого необходимы лишь две пары параллельных прямых. Точки их пересечения, как легко догадаться, образуют ромб,
диагонали которого пересекаются под прямым углом.
С этим справились, а теперь давайте рассмотрим, как построить перпендикуляр к произвольной прямой на плоскости?
Задача посложнее
Проведем произвольную прямую и отметим на ней точку А. Слева и справа от точки А построим две параллельные прямые, расстояние от которых до точки будет одинаковым и равно ширине линейки а:
Теперь возьмем нашу линейку и, регулируя угол наклона найдем такое положение, при котором через точки М1 и А могут “протиснуться” две параллельные прямые:
Верхняя точка пересечения как раз будет находиться на перпендикуляре к исходной прямой в точке А.
Это подтверждает тот факт, что лучи, выходящие из точки А в верхнюю полуплоскость по определению (и построению с равными интервалами а) являются биссектрисами соответствующих углов. Итак, задача решена!
Спасибо за внимание! А еще посмотрите, как найти центр окружности одним лишь циркулем!
TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.
Содержание материала
- Пошаговая инструкция
- Видео
- Листочек в клеточку
- Как можно вычислить прямой угол?
- Способы определения разворота
- Теорема Пифагора
- Египетский треугольник
- Равнобедренный треугольник
- Коротко главном
Пошаговая инструкция
1й способ. — С помощью «золотого», или «египетского», треугольника. Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град. Этим качеством широко пользовались древние египтяне и другие пракультуры.
Илл.1. Построение Золотого, или египетского треугольника
- Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров. Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок».
- Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
- Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
- В момент натяжения на линии границы – точка А, вбиваем колышек.
- Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
- После этого натягиваем мерку R5 – от А до В.
- В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника, со сторонами 3;4;5 и с прямым углом в точке О.
2й способ. С помощью циркуля.
Циркуль может быть веревочный или в виде шагомера. См: …простейший землемерный инструмент
Наш циркуль-шагомер имеет шаг в 1 метр.
Илл.2. Циркуль-шагомер
Построение – также по Илл.1.
- От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
- Ставим ногу циркуля в точку О.
- Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
- Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль.
- Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
- Проводим прямую (отрезок) через точки С и D.
- Все! Полученный отрезок, или прямая, — есть точное направление на север :). Простите, — на прямой угол.
- На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
- Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.
Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля
Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного. Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.
- Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.
Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки
- Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..
Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.
Листочек в клеточку
На листике в клеточку легко можно сделать замеры тех же стандартных углов, что и в предыдущем варианте.
- Определить 90 градусов будет легче всего – нужно просто нарисовать квадрат.
- Проведя в квадрате диагональ можно получить угол 45 градусов.
- Чтобы определить 30, 60 градусов нужно нарисовать прямоугольник (5 клеток в длину, 3 в высоту). Проведя в нем диагональ, получим угол 30 и 60 градусов. Если разделить линией угол 30 на 2 части, получим 15 градусов.
Полученные углы нужно вырезать и сравнить с заданным углом. Обычно, после прикладывания заготовок, получается, визуально определить примерные показатели.
Видео
Как можно вычислить прямой угол?
Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.
Итак, нужно обозначить следующие шаги:
 Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;- Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
- В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
- После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
- Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.
Способы определения разворота
Раньше распространенным решением как вывести угол 90 градусов, например, на фундаменте был обычный строительный уголок. Главное, чтобы он был проверен и соответствовал 90 градусам. Сегодня профессионалы для упрощения процесса и ускорения монтажных работ пользуются лазерными уровнями. Третий вариант – применение обычной измерительной рулетки.

Теорема Пифагора
С этой доказанной теоремой знаком каждый, кто учился в школе. Она применима только к треугольникам, в котором один из углов обязательно прямой. Прилегающие к нему стороны – катеты a и b, соединительный отрезок – гипотенуза (с). Формула выглядит так: a²+b²=c².
Удобство использования такого способа как найти прямой угол при строительстве в том, что наносить разметку можно в любом по площади помещении. Здесь даже допустимо наличие посторонних предметов. Главное, чтобы был доступ к углу и стенам, можно было свободно протянуть соединительную гипотенузу. Дополнительно понадобится только калькулятор, чтобы быстро произвести нужные вычисления.
Египетский треугольник
Золотой или Египетский треугольник – это фигура с прямым углом, у которой стороны равны 3, 4 и 5 частям. Удобство здесь заключается в том, что не нужно возводить параметры в квадратную степень и извлекать корни. Достаточно принять за часть ту или иную условную единицу. Это может быть как 1 см, так и 10 метров, что особенно удобно для решения как вывести угол 90 градусов на стенах из штукатурки.
Если имеются сомнения в справедливости утверждения про угол в 90 градусов, то можно его проверить с помощью теоремы Пифагора: 3*3+4*4= 5*5 или 9+16=25. Остается только начать применять эту методику на практике.
Равнобедренный треугольник
Здесь рассматривается для удобства формирования угла 90 градусов с помощью рулетки фигура с двумя сторонами, которые равны 100 см. Если между ними прямой разворот, то длина основы составит 141,4 см. Актуален такой подход в строительстве потому, что при увеличении метровых ориентиров в 2, 3 и более раз разница между размерами соединительного отрезка будет идентичной. То есть в прямоугольном равнобедренном треугольнике справедливы такие равенства:
- a и b равны 100*2=200 см – c=141,4*2=282,8 см;
- a и b равны 100*5=500 см – с= 141,4*5=707 см;
- a и b равны 100*2,2= 220 см – с=141,4*2,2=311,08 см.

Если проверить эти утверждения, то гипотенуза или основа равнобедренного треугольника с верхним прямым углом будет при округлении действительно равна 141,4 (141,421356…). С одной стороны – это простой и верный способ как проверить угол 90 градусов рулеткой по нанесенной разметке. Достаточно отмерять метровые участки и сделать только одно умножение 141,4 на число метров. Один только недостаток здесь все же есть. Если в квартире или доме погрешность будет несущественной из-за малых габаритов, то на крупных объектах отклонение из-за неточной гипотенузы может стать заметным.
Коротко главном
В интерьере часто приходится выводить прямые углы под мебель или сантехническое оборудование.
С помощью рулетки можно проверить разворот в 90 градусов тремя способами: стороны равны 3/4/5 частей, если между метровыми стенками соединительный отрезок составляет 141,4 см, применяя теорему Пифагора.
Также рулетки достаточно для формирования трех углов в 30, 45 и 60 градусов.
Дополнительно может понадобиться только калькулятор и карандаш для нанесения разметки.





