Как решать найти икс

Время чтения: 7 минут.

Если уравнения вызывают страх и ужас, то эта статья точно для тебя. Разберемся, что такое линейные уравнения и как быстро находить их корни.

Что такое линейные уравнения?

Для начала разберемся, что такое линейные уравнения и какой вид они имеют.

Линейное уравнение имеет вид: ax + b = 0, где a и b – это некоторые числа, а x – неизвестное.

Чтобы решить уравнение, нужно найти все его корни, либо доказать, что корней нет. Решением линейного уравнения является то число, которое обращает это уравнение в верное равенство (то есть правая часть становится равной левой части).

Правила переноса и деления

Чтобы научиться решать линейные уравнения, необходимо знать правила переноса членов уравнения из одной части в другую, а также правило деления всех частей уравнения на одно и то же число.

Правило переноса: При переносе члена уравнения из одной части уравнения в другую нужно менять знак на противоположный. Все члены с Х оставляем слева, а все числа – переносим вправо.

Правило деления: В уравнении можно разделить правую и левую часть на одно и то же число.

Алгоритм решения

Коротко алгоритм решения линейных уравнений можно записать так:

• Раскрыть все скобки (если они есть);
• Члены с Х перенести влево, а все числа – вправо;
• Сложить/вычесть все, что возможно, в каждой части уравнения;
• Найти корень уравнения.

Примеры решения линейных уравнений

Далее разберем примеры решения линейных уравнений, а после ты сможешь проверить свои знания и самостоятельно решить несколько подобных заданий.

А теперь проверь свои знания на заданиях ниже:

На этом все! Остались вопросы? Напиши о них в комментариях!👇

Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠

#впр #огэ #егэ #математика #репетитор #алгебра #геометрия #7класс #уравнения #линейныеуравнения

Решение простых линейных уравнений

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

−4x = 12 | : (−4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Перенести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

1. 4х + 8 = 6 − 7х
2. 4х + 7х = 6 − 8
3. 11х = −2
4. х = −2 : 11
5. х = −2/11

Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.

Пример 5. Решить:

1. 
2. 3(3х — 4) = 4 · 7х + 24
3. 9х — 12 = 28х + 24
4. 9х — 28х = 24 + 12
5. -19х = 36
6. х = 36 : (-19)
7. х = — 36/19

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

5х — 15 + 2 = 3х — 2 + 2х — 1

Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

Приведем подобные члены.

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 − 7х.

Нахождение неизвестного слагаемого, множителя: правила, примеры, решения

Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.

Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.

Нахождение неизвестного слагаемого

Допустим, у нас есть некоторое количество шариков в двух вазах, например, 9 . Мы знаем, что во второй вазе 4 шарика. Как найти количество во второй? Запишем эту задачу в математическом виде, обозначив число, которое нужно найти, как x. Согласно первоначальному условию, это число вместе с 4 образуют 9 , значит, можно записать уравнение 4 + x = 9 . Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x ? Для этого надо использовать правило:

Для нахождения неизвестного слагаемого надо вычесть известное из суммы.

В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения. Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если a + b = c , то c − a = b и c − b = a , и наоборот, из выражений c − a = b и c − b = a можно вывести, что a + b = c .

Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.

Возьмем то уравнение, что у нас получилось выше: 4 + x = 9 . Согласно правилу, нам нужно вычесть из известной суммы, равной 9 , известное слагаемое, равное 4 . Вычтем одно натуральное число из другого: 9 — 4 = 5 . Мы получили нужное нам слагаемое, равное 5 .

Обычно решения подобных уравнений записывают следующим образом:

1. Первым пишется исходное уравнение.
2. Далее мы записываем уравнение, которое получилось после того, как мы применили правило вычисления неизвестного слагаемого.
3. После этого пишем уравнение, которое получилось после всех действий с числами.

Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:

4 + x = 9 , x = 9 − 4 , x = 5 .

Мы можем проверить правильность полученного ответа. Подставим то, что у нас получилось, в исходное уравнение и посмотрим, выйдет ли из него верное числовое равенство. Подставим 5 в 4 + x = 9 и получим: 4 + 5 = 9 . Равенство 9 = 9 верное, значит, неизвестное слагаемое было найдено правильно. Если бы равенство оказалось неверным, то нам следовало бы вернуться к решению и перепроверить его, поскольку это знак допущенной ошибки. Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.

Нахождение неизвестного вычитаемого или уменьшаемого

Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.

Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.

Например, у нас есть уравнение x — 6 = 10 . Неизвестно уменьшаемое. Согласно правилу, нам надо прибавить к разности 10 вычитаемое 6 , получим 16 . То есть исходное уменьшаемое равно шестнадцати. Запишем все решение целиком:

x − 6 = 10 , x = 10 + 6 , x = 16 .

Проверим получившийся результат, добавив получившееся число в исходное уравнение: 16 — 6 = 10 . Равенство 16 — 16 будет верным, значит, мы все подсчитали правильно.

Переходим к следующему правилу.

Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.

Воспользуемся правилом для решения уравнения 10 — x = 8 . Мы не знаем вычитаемого, поэтому нам надо из 10 вычесть разность, т.е. 10 — 8 = 2 . Значит, искомое вычитаемое равно двум. Вот вся запись решения:

10 — x = 8 , x = 10 — 8 , x = 2 .

Сделаем проверку на правильность, подставив двойку в исходное уравнение. Получим верное равенство 10 — 2 = 8 и убедимся, что найденное нами значение будет правильным.

Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.

Нахождение неизвестного множителя

Посмотрим на два уравнения: x · 2 = 20 и 3 · x = 12 . В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.

Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.

Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a · b = c при a и b , не равных 0 , c : a = b , c : b = c и наоборот.

Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2 . Проводим деление натуральных чисел и получаем 10 . Запишем последовательность равенств:

x · 2 = 20 x = 20 : 2 x = 10 .

Подставляем десятку в исходное равенство и получаем, что 2 · 10 = 20 . Значение неизвестного множителя было выполнено правильно.

Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x · 0 = 11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на 0 , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.

Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от 0 . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.

Нахождение неизвестного делимого или делителя

Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.

Для нахождения неизвестного делимого нужно умножить делитель на частное.

Посмотрим, как применяется данное правило.

Решим с его помощью уравнение x : 3 = 5 . Перемножаем между собой известное частное и известный делитель и получаем 15 , которое и будет нужным нам делимым.

Вот краткая запись всего решения:

x : 3 = 5 , x = 3 · 5 , x = 15 .

Проверка показывает, что мы все подсчитали верно, ведь при делении 15 на 3 действительно получается 5 . Верное числовое равенство – свидетельство правильного решения.

Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.

Переходим к следующему правилу.

Для нахождения неизвестного делителя нужно разделить делимое на частное.

Возьмем простой пример – уравнение 21 : x = 3 . Для его решения разделим известное делимое 21 на частное 3 и получим 7 . Это и будет искомый делитель. Теперь оформляем решение правильно:

21 : x = 3 , x = 21 : 3 , x = 7 .

Удостоверимся в верности результата, подставив семерку в исходное уравнение. 21 : 7 = 3 , так что корень уравнения был вычислен верно.

Важно отметить, что это правило применимо только для случаев, когда частное не равно нулю, ведь в противном случае нам опять же придется делить на 0 . Если же частным будет нуль, возможны два варианта. Если делимое также равно нулю и уравнение выглядит как 0 : x = 0 , то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным 0 , с делимым, отличным от 0 , решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5 : x = 0 , которое не имеет ни одного корня.

Последовательное применение правил

Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.

У нас есть уравнение вида 3 · x + 1 = 7 . Вычисляем неизвестное слагаемое 3 · x , отняв от 7 единицу. Получим в итоге 3 · x = 7 − 1 , потом 3 · x = 6 . Это уравнение решить очень просто: делим 6 на 3 и получаем корень исходного уравнения.

Вот краткая запись решения еще одного уравнения ( 2 · x − 7 ) : 3 − 5 = 2 :

( 2 · x − 7 ) : 3 − 5 = 2 , ( 2 · x − 7 ) : 3 = 2 + 5 , ( 2 · x − 7 ) : 3 = 7 , 2 · x − 7 = 7 · 3 , 2 · x − 7 = 21 , 2 · x = 21 + 7 , 2 · x = 28 , x = 28 : 2 , x = 14 .

Как решать
показательные уравнения?

Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.

Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:

Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:

Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.

И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:

И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.

Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.

Простейшие показательные уравнения

Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:

Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:

Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.

Решим что-нибудь посложнее.

Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:

Мы применили свойство отрицательной степени по формуле:

Теперь наше уравнение будет выглядеть так:

Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:

Такое мы решать умеем, ведь это обыкновенное линейное уравнение.

Поздравляю, мы нашли корень нашего показательного уравнения.

Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:

Воспользуемся одним из свойств степеней ((a^n)^m=a^):

И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:

И еще один пример:

Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.

Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.

Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.

Общий метод решения показательных уравнений

Пусть у нас есть вот такой пример:

Где (a,b) какие-то положительные числа. ((a>0, ; b>0).

Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.

Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:

Раз основания одинаковые, то мы можем просто приравнять степени:

Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:

Замечаем, что (16=2*2*2*2=2^4) это степень двойки:

Основания одинаковые, значит можно приравнять степени:

$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$

Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).

Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:

(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):

Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):

Подставим данное преобразование в наш пример:

Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:

Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.

Кто забыл, что такое логарифм, можно посмотреть здесь.

Рассмотрим еще несколько аналогичных примеров.

Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:

Все эти варианты ответа верные, их можно смело писать в ответ.

И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).

Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:

Решение показательных уравнений при помощи замены

Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.

Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:

Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.

Квадратное уравнение, которое решается через дискриминант:

Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:

И второй корень:

И еще один пример на замену:

Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):

Подставим в исходное уравнение:

Теперь показательные функции одинаковы и можно сделать замену:

Обратная замена, и наше уравнение сводится к простейшему:

И второе значение (t):

Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):

Здесь нам придется воспользоваться свойствами степеней:

Разберем каждое слагаемое:

Теперь подставим получившееся преобразования в исходное уравнение:

Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):

Сделаем обратную замену:

И последний пример на замену:

Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:

Разберем каждое слагаемое нашего уравнения:

Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!

И последнее слагаемое со степенью:

Подставим все наши преобразования в исходное уравнение:

Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):

Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.

И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут

Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:

Воспользуемся формулой ((a*b)^n=a^n*b^n):

И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:

Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):

Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.

Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!

Для решения линейных уравнений используют два основных правила (свойства).

Свойство № 1
или
правило переноса

Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.

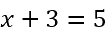
Вспомним, что у любого уравнения есть левая и правая часть.

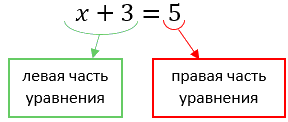
Перенесем число «3» из левой части уравнения в правую.

Так как
в левой части уравнения у числа «3»
был знак «+», значит в правую часть уравнения
«3» перенесется со знаком «−».

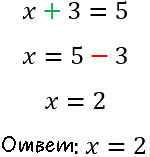
Полученное числовое значение «x = 2» называют корнем уравнения.

Рассмотрим другое уравнение.

5x = 4x + 9

По правилу переноса перенесем «4x» из правой
части уравнения в левую, поменяв знак на противоположный.

Несмотря на то, что перед «4x» не стоит никакого знака,
мы понимаем, что перед «4x» стоит знак «+».

5x = 4x + 9
5x = +4x + 9
5x − 4x = 9

Теперь приведем подобные и решим уравнение до конца.

5x − 4x = 9
x = 9

Ответ: x = 9

Свойство № 2
или
правило деления

Разберемся на примере, как использовать правило деления при решении линейных уравнений.

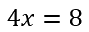
Число «4», которое стоит при «x»,
называют числовым коэффициентом при неизвестном.

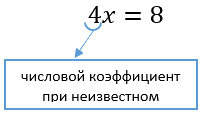
Между числовым коэффициентом и неизвестном всегда стоит действие умножение.

Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент
«1».

Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы
получить
«1»?».
Ответ очевиден, нужно разделить на «4».

Используем правило деления и разделим левую и правую части уравнения на «4».
Не забудьте, что делить нужно и левую, и правую части.

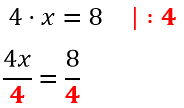
Используем сокращение дробей и решим линейное уравнение до конца.

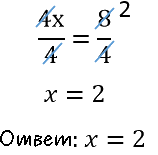
Как решить уравнение, если «x» отрицательное

Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Как, например, в уравнении ниже.

−2x = 10

Чтобы решить такое уравнение, снова зададим себе вопрос:
«На что нужно разделить «−2»,
чтобы получить «1»?». Нужно разделить на «−2».

−2x = 10         |:(−2)

=
                 
x = −5                 

Ответ: x = −5           

Примеры решения линейных уравнений

Рассмотрим другие примеры решения линейных уравнений. Обычно для решения уравнений нужно
применять оба свойства (правило переноса и правило деления).

Также требуется вспомнить правило раскрытия скобок и
правило приведения подобных.

• 
  25x − 1 = 9
  25x = 9 + 1
  25x = 10        |: 25

  =
  
  x =
  
  Ответ: x =

  ---

• 
  11(y − 4) + 10(5 − 3y) − 3(4 − 3y) = −6

  11y − 44 +
  50 −
  30y − 12
  + 9y = −6

  11y − 30y +
  9y −
  44 + 50 − 12 = −6

  20y − 30y + 6 − 12 = −6
  −10y − 6 = −6
  −10y = −6 + 6
  −10y = 0         |:(−10)
  =
  

  y = 0

  
  Ответ: y = 0

---

Ваши комментарии

Оставить комментарий:

---

Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид  

aх + b = 0, где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.

Например, все уравнения:

2х + 3= 7 – 0,5х;  0,3х = 0;  x/2 + 3 = 1/2 (х – 2) – линейные.

Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения.

Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.

А значение х = 3 не обращает  уравнение  3х + 7 = 13 в верное равенство, так  как  3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.

Решение любых линейных уравнений сводится к решению уравнений вида

aх + b = 0.

Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим

aх = ‒ b.

Если a ≠ 0, то х = ‒ b/a .

Пример 1. Решите уравнение 3х + 2 =11.

Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим 
3х = 11 – 2.

Выполним вычитание, тогда
3х = 9.

Чтобы найти х надо разделить произведение на известный множитель, то есть     
х = 9 : 3.

Значит, значение х = 3 является  решением или корнем уравнения.

Ответ: х = 3.

Если а = 0 и b = 0, то получим уравнение  0х = 0. Это уравнение имеет бесконечно много  решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения  является любое число.

Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.

Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
5х – 3х ‒ 2х =  – 12  ‒ 1 + 15 ‒ 2.

Приведем подобные члены:
0х = 0.

Ответ: х –  любое число.

Если а = 0 и b ≠ 0, то получим уравнение  0х = – b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но  b ≠ 0 .

Пример 3. Решите уравнение х + 8 = х + 5.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.

Приведем подобные члены: 
0х = ‒ 3.

Ответ: нет решений.

На рисунке 1 изображена схема решения линейного уравнения

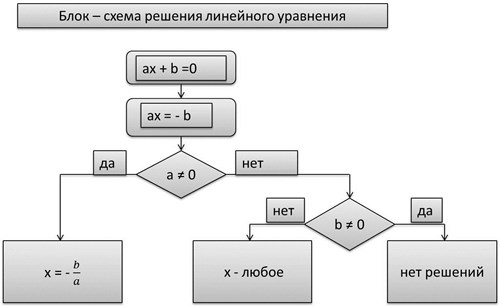
Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.

Пример 4. Пусть надо решить уравнение 

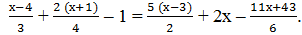
1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

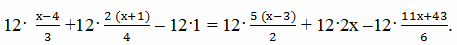
2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)

3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .

4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.

5) Приведем подобные члены:
‒ 22х = ‒ 154.

6) Разделим на  – 22 , Получим
х = 7.

Как видим, корень уравнения равен семи.

Вообще такие уравнения можно решать по следующей схеме:

а) привести уравнение к целому виду;

б) раскрыть скобки;

в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;

г) привести подобные члены;

д) решить уравнение вида aх = b,которое получили после приведения подобных членов.

Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2),  третьего (Пример. 1, 3) и даже с пятого этапа, как в примере 5.

СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).

Пример 5. Решите уравнение 2х = 1/4.

Находим неизвестное  х = 1/4 : 2,
х = 1/8 .

Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.

Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.

Решение

2х + 6 = 5 – 6х

2х + 6х = 5 – 6

8х = ‒1

х = ‒1 : 8

х = ‒ 0, 125

Ответ: ‒ 0, 125

Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.

Решение

– 30 + 18х = 8х – 7

18х  – 8х =  – 7 +30

10х = 23

х = 23 : 10

х = 2,3

Ответ: 2,3

Пример 8. Решите уравнение

 

Решение:

3(3х – 4) = 4 · 7х + 24

9х – 12 = 28х + 24

9х – 28х = 24 + 12

-19х = 36

х = 36 : (-19)

х = – 36/19

Ответ: – .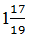 

Пример 9. Найдите f(6), если f (x + 2) = 3^7-х

Решение

Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.

Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.

Если х = 4, тогда
f(6) = 3^7-4 = 3³ = 27

Ответ: 27.

Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил.  Но если вдруг что-то еще непонятно – попробуй онлайн-занятие с репетитором (подробности тут + 🎁).

Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ. Буду рада Вам помочь!

Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решение простых уравнений  — одна из базовых тем для усвоения, при этом они являются достаточно мощным инструментом для решения большинства задач. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.

Уравнение — это равенство, содержащее в себе переменную. Значение данной переменной требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.

Переменную, входящую в уравнение, еще называют неизвестным.

Примеры:

• выражение 3+2=5 является равенством, так как при вычислении получаем 5=5
• выражение 3+х=5 является уравнением, так как содержит переменную х, значение которой можно найти.

Решить уравнение — значит найти такое значение х, чтобы равенство было верным.
То есть, в уравнении 3+х=5 значение будет равно 2 (х=2), чтобы получилось верное равенство.
При этом говорят, что 2 — это корень уравнения или решение уравнения 3+х=5.

Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.

Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.

Компоненты

Компонентами называются числа и переменные, которые входят в равенство:

• компоненты сложения — слагаемые и сумма;
• компоненты вычитания — уменьшаемое, вычитаемое и разность;
• компоненты умножения — множители и произведение;
• компоненты деления — делимое, делитель и частное.

Правила нахождения неизвестных

Чтобы выразить переменную через другие числа, нужно переменную оставить (или перенести) в левой части выражения, а все числа перенести в правую часть.

Решение простых уравнений подразумевает применение следующих правил:

1. чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
2. чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
3. чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
4. чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
5. чтобы найти неизвестное делимое, нужно частное умножить на делитель;
6. чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Примеры:

1. 3+х=5.
   Нужно задать вопрос: что сделать с числами 5 и 3, чтобы получить переменную х.
   Чтобы найти слагаемое, нужно из суммы вычесть известное слагаемое: х=5-3.
2. х-3=7
   Нужно задать вопрос: что сделать с числами 3 и 7, чтобы получить переменную х.
   Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое: х=7+3.
3. 8-х=6
   Нужно задать вопрос: что сделать с числами 8 и 6, чтобы получить переменную х.
   Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность: х=8-6.
4. 3×а=6 (а-переменная)
   Нужно задать вопрос: что сделать с числами 3 и 6, чтобы получить переменную а.
   Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель
5. а:4=3(а-переменная)
   Нужно задать вопрос: что сделать с числами 4 и 3, чтобы получить переменную а.
   Чтобы найти неизвестное делимое, нужно частное умножить на делитель: а=3*4
6. 12:а=3(а-переменная)
   Нужно задать вопрос: что сделать с числами 12 и 3, чтобы получить переменную а.
   Чтобы найти неизвестный делитель, нужно делимое разделить на частное: а=12:3.

Если неизвестное имеет коэффициент

Решение простых уравнений сводится к тому, что неизвестное нужно выразить через другие числа. Но чаще всего задаются уравнения, в которых неизвестное имеет коэффициент, например: 2х, 5х и т.д. В таких случаях неизвестное нельзя выразить сразу, поскольку оно содержит коэффициент. Поэтому нужно привести это уравнение к виду, в котором переменная будет выражена.

Рассмотрим пример: 2х+4=8.
В данном примере: 2x — первое слагаемое, 4 — второе слагаемое, 8 — сумма.

• Принимает слагаемое 2х за неизвестное слагаемое. Применяем правило нахождения неизвестного слагаемого: вычитаем из суммы известное слагаемое. Получаем: 2х=8-4 или 2*х=4.
• Мы получили новое уравнение . Теперь мы имеем дело с умножением. Применяем правило нахождения неизвестного множителя: произведение делим на известный множитель. Получаем: х=4:2; х=2
• Вычислим правую часть, получим значение переменной х.
• Проверяем: 2*2+4=8. Равенство верное.

Если уравнение имеет неизвестные с разными коэффициентами

Рассмотрим пример: a+2a+3a=30.
Cразу выразить неизвестное нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить. Для этого нужно сложить все неизвестные величины с коэффициентами: 1а+2а+3а=6а (а — это переменная с коэффициентом 1. который не пишется).
Получаем уравнение вида: 6*а=30. Его можно решить как простое уравнение. Получаем корень: а=5.

Равносильные уравнения

Уравнения называют равносильными, если их корни совпадают.

Из предыдущего примера: уравнение a+2a+3a=30 и уравнение 6а=30 являются равносильными.
Проверим это. Подставим корень сначала в уравнение a+2a+3a=30, а затем в уравнение 6а=30, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства.

Для удобства решения можно любое уравнение преобразовать в равносильное. Для этого можно применить законы математики и свойства уравнений.

Свойства уравнений

• Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
• Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.

Пример. Решить уравнение 5х-10=20.
Вычтем из обеих частей уравнения число 10, получим: 5х=20-10 или 5х=10.
В результате получилось равносильное уравнение , корень которого равен 2.

Пример. Решить уравнение 4(х+3)=20.
Раскроем скобки: 4х+12=20.
Вычтем из обеих частей уравнения число 12, получим: 4х=20-12 или 4х=8.
В результате получилось равносильное уравнение , корень которого равен 2.

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.

Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные числа.

Пример. Решить уравнение (1/4)х+5=6,5

• При решении уравнений, содержащих дробные выражения, сначала  принято упростить это уравнение.
• Для упрощения обе части уравнения можно умножить на 4: 4*(1/4)х+4*5=4*6,5 или х+20=26.
• В результате останется простейшее уравнение. Получаем, что корень равен 6.
• Вернемся к исходному уравнению  и подставим вместо x найденное значение. Получается верное числовое равенство. Значит уравнение решено правильно.

Пример. Решить уравнение 8х+16=56

• Для упрощения обе части уравнения можно разделить на 8: 8х:8+16:8=56:8 или х+2=7.
• В результате останется простейшее уравнение. Получаем, что корень равен 5.
• Вернемся к исходному уравнению  и подставим вместо x найденное значение. Получается верное числовое равенство. Значит уравнение решено правильно.

Если обе части уравнения умножить на минус единицу (поменять знаки), то получится уравнение равносильное данному.

Это правило следует из того, что если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю, то получится равносильное уравнение. Иногда это нужно для того, чтобы получить равносильное уравнение, которое проще решать.

Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.

При этом минус, стоящий перед переменной x, относится не к самой переменной x, а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать.

Пример. Решить уравнение: 2х-5х+10=4.

• Приведем подобные слагаемые:  -3х+10=4
• Перенесем второе слагаемое в правую часть: -3х=-6
• Для удобства умножим обе части на (-1). получим: 3х=6.
• Корень: х=2.

Уравнение имеет несколько корней

Уравнение может иметь несколько корней.

Рассмотрим уравнение: x(x + 9) = 0.
Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из множителей равен нулю.
То есть в уравнении x(x + 9) = 0 равенство будет выполняться, если x будет равен нулю или (x + 9) будет равно нулю. Таким образом, уравнение имеет два корня: 0 и −9.

Уравнение имеет бесконечно много корней

Уравнение может иметь бесконечно много корней, когда при подстановке подставив в такое уравнение любого числа, мы получим верное равенство.

Например: рассмотрим простое уравнение 6*(х+2)=6х+12. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 6х+12= 6х+12. Это равенство будет выполняться при любом х.

Уравнение не имеет корней

Бывает и так, что уравнение совсем не имеет  корней.

Например: уравнение х+2=х.
Данное уравнение не имеет корней, так как при любом значении х, левая часть уравнения всегда будет больше правой на 2.

Таким образом, мы рассмотрели в статье решение разных видов простых уравнений. Решение более сложных уравнений без знания данного материала практически невозможно.

Далее вы можете переходить к решению квадратных уравнений и решению систем линейных уравнений. 

Для решения уравнений вам также могут понадобится темы: раскрытие скобок и порядок действий в примерах.