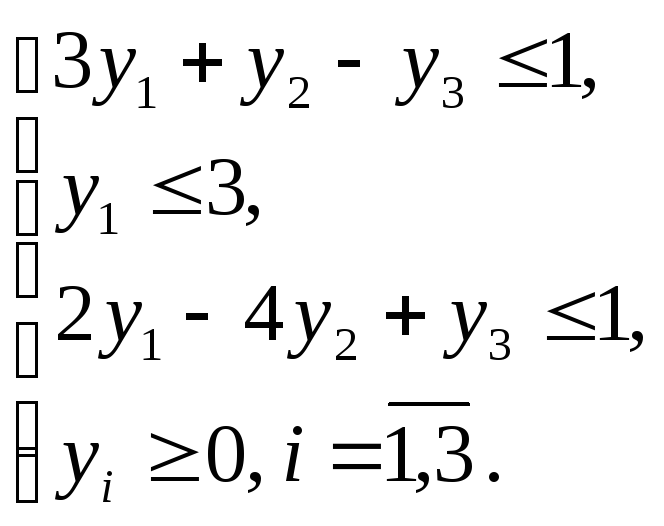Как решать составить двойственные задачи - Сайт, где вы сможете решить свои вопросы

Двойственная задача линейного программирования

Время на прочтение
9 мин

Количество просмотров 26K

Прочие статьи цикла

Обычно с задачей линейного программирования (ЗЛП) связана другая линейная задача, называемая двойственной. Обе эти задачи можно считать двойственными одну по отношению к другой, считать равносильными. Первая задача называется обычно исходной, или прямой, другая – обратной. Переменные, используемые в двойственной задаче называются двойственными или множителями Лагранжа. На них не накладывается ограничений по знаку. Рассматриваются двойственные критерии оптимальности. Специальные случаи называют симметричными двойственными задачами линейного программирования. Связь между оптимальными решениями двойственных задач устанавливается теоремой двойственности.

Теорема двойственности

Важнейшие свойства пары двойственных задач математического программирования сформулированы в трех основных теоремах.

Теорема двойственности

Допустимый вектор решения прямой задачи программирования оптимален тогда и только тогда, когда существует такой допустимый вектор решения двойственной задачи, что целевые функции прямой и двойственной задачи равны. Допустимый вектор двойственной задачи оптимален тогда и только тогда, когда существует допустимый вектор прямой задачи и целевые функции обеих задач равны.

Теорема существования решения

Если существуют допустимые векторы решений прямой и двойственной задач, то обе задачи имеют оптимальные векторы. Если одна из двух задач не имеет допустимого вектора, то ни одна из них не имеет оптимального вектора решения.

Теорема (принцип) дополняющей нежесткости

Если (x_Q, x_L) – оптимальное решение прямой задачи, а (y_Q, y_L) – решение двойственной задачи, то (x_Q, x_L, y_Q, y_L) – решение задачи Лагранжа. В частности, в этом случае удовлетворяются соотношения между переменными прямой и двойственной задач и условия дополняющей нежесткости.
Оптимальное решение прямой задачи программирования получается только при одном значении x_Q. Это справедливо и для переменной y_Q в двойственной задаче.

Теоремы двойственности

Основное неравенство двойственности. Для любых допустимых решений Х_<n>и Y_<n>пары двойственных ЗЛП имеет место неравенство

Экономически это означает, что для любого допустимого плана производства и любого дополнительного вектора оценок ресурсов (на складе) стоимость изготовленного продукта не превосходит оценки ресурсов.

Теорема существования (малая тероема двойственности)

Чтобы прямая и двойственная задачи имели opt решения, необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.

Теорема 1 двойственности.

Если одна из пары двойственных задач имеет opt решение, то и другая его имеет. Причем экспериментальные решения их целевых ф. равны; если же ЦФ одной из задач не ограничена, то система ограничений другой противоречива. Интерпретация: оптимальное использование ресурсов – opt план. Суммарная оценка ресурсов = оценке продукта полученного при opt плане. Любой другой план не рентабелен. C_j – стоимость единицы продукции (внешняя оценка) y_i – стоимость единицы ресурса (внутренняя оценка). Эти двойственные оценки выступают как инструменты балансирования затрат и результатов. Имеет место x_j <-> y_m +_j; x_n+i<-> y_i_.

Теорема 2 двойственности (о дополняющей нежесткости)

Для того, чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно выполнить условия:

То есть, если какое-либо ограничение одной ЗЛП обращается ее opt планом в строгое равенство, то соответствующая переменная двойственной задачи в ее opt плане равна нулю; если же какая-либо переменная opt-го решения одной ЗЛП положительна, то соответствующее ограничение в двойственной ЗЛП ее opt планом обращается в точное равенство.

Теорема Кёнига хорошо иллюстрирует использование принципа двойственности ЗЛП.

Формулирование теоремы. Максимальное число попарно неколлинеарных единиц любой булевой матрицы равно минимальному числу линий, покрывающих все единицы матрицы.

Доказательство. Для нахождения максимального числа попарно неколлинеарных единиц булевой матрицы достаточно сформулировать и решить линейную задачу:

Минимальное число линий, покрывающих все единицы матрицы [C_ij], найдем, решив линейную задачу:

Оптимальному решению (u*_i, v*_j) последней задачи отвечает минимальное покрытие, состоящее из множества строк I, для которых u*_i= 1 и столбцов J, для которых u*_j=1.

Матрицы А и А^Т коэффициентов (*), (**), (***) являются абсолютно унимодулярными, как матрицы двудольного графа. Поэтому условия целочисленности переменных заменяем на условие их неотрицательности, и тогда получаем пару двойственных задач линейного программирования и согласно теореме двойственности имеем:

Линией матрицы называется ее строка или столбец. Два элемента матрицы называются неколлинеарными, если они не лежат на одной линии.

Матрица называется абсолютно унимодулярной, если все ее ненулевые миноры равны 1, либо -1.

Следствие. Матрица инциденций неориентированного графа G абсолютно унимодулярна тогда и только тогда, когда G – двудольный граф. В двудольном графе все простые циклы имеют четкую длину

Принцип двойственности в задачах линейного программирования.

Предположим, что руководство предприятия из анализа конъюнктуры рынка продукции приняли решение: производство сократить, а от запасов сырья избавиться, (продать на рынке) и при этом не нанести себе убытков.

С этой целью руководство должно назначить стоимости y_i за единицу сырья вида S_i, стремясь при этом минимизировать общую стоимость сырья (чтобы быстрее продать сырье): Ф = Σ⁴_i=1 b_iy_i

Выручка предприятия от продажи сырья, расходуемого на единицу продукции П_i, составит: Σ⁴_i=1 a_ijy_i

И по условию она не должна быть меньше С_j (в противном случае предприятию выгоднее не продавать сырье, а использовать его для нужд производства, выпуска продукции).

Сформулируем исходную и двойственную задачи:

Обе задачи по отношению друг к другу называются двойственными или сопряженными. Анализ таблицы позволяет сделать выводы:

Если первая задача сформулирована на поиск максимума, то вторая формулируется на поиск минимума линейной функции.
Коэффициенты ЦФ первой задачи являются свободными членами системы ограничений второй.
Свободные члены системы ограничений первой задачи являются коэффициентами линейной системы во второй задаче.
Матрица коэффициентов второй задачи является транспонированной к матрице коэффициентов ограничений первой задачи.
Знаки неравенств в ограничениях второй задачи противоположны знакам неравенств в ограничениях первой задачи.

Оптимальный план X^opt_<n>одной из задач тесно связан с оптимальным планом Y^opt_<n> другой. Если одна из задач имеет решение, то другая также разрешена, причем для оптимальных клонов X^opt_<n> =<x₁, x₂,…x_n> и Y^opt_<m> =<y₁, y₂,…y_m> справедливо равенство Q( X^opt ) =Q’( Y^opt ). Если линейная форма одной из задач неограниченна, то условия другой задачи несовместны. Если A^-1 обратная матрица к матрице В, состоящей из векторов базиса оптимального плана исходной задачи, то оптимальный план двойственной задачи равен Y^opt_<m> =СВ ^-1, здесь С – вектор базисных переменных. Решение двойственной задачи получается в последней симплексной таблице исходной задачи, в (m+1) строке, в столбцах, соответствующих дополнительным параметрам.

Для того чтобы векторы X^opt_<n> =<x₁, x₂,…x_n> и Y^opt_<m> =<y₁, y₂,…y_m> были решениями пары задач, необходимо и достаточно, чтобы их компоненты удовлетворяли следующим условиям:

Эти условия называют принципом дополняющей нежесткости. Если исходная (прямая) задача задана в канонической форме, то двойственная к ней называется несимметричной. Для несимметричной двойственной задачи соблюдается условие y_i≥ 0.

Теория ЗЛП доказывает, что компоненты оптимальных планов взаимно двойственных задач, приведенных к каноническому виду, соответствуют одни другим. То есть базисные переменные основной задачи соответствуют свободным переменным двойственной задачи и наоборот, j = 1(1)n, x*_j y*_m _+j; x*_n+i y*_i ; i = 1(1)m.

Размерности в табличке m и n берутся в задаче для y-ков записанной в канонической форме.

Пример. Двойственный симплекс метод.

Исходная задача. Имеется три вида продуктов П_j, причем единица веса каждого из видов продуктов содержит a_ij единиц (питательных веществ). Для нормальной жизнедеятельности человек должен потреблять не менее b_i единиц вещества B_i в сутки. Стоимость единицы продукта П_j равняется C_j. Требуется составить оптимальный суточный рацион питания, т.е. найти количество x_j продукта, которое должен потреблять человек, чтобы стоимость питания была бы минимальной, если известно, что

такие значения его компонентов x_j, j = 1(1)3, которые минимизируют целевую функцию (Ц) Q = 3x₁+ 2x₂+ x₃ и удовлетворяют ограничениям неравенствам

0,3x₁+ 0,2x₂+ 0, 4x₃≥ 0,2;

0,4x₁+ 0,3x₂+ 0,45x₃≥ 0,5;

0,2x₁+ 0,3x₂+ 0, 1 x₃≥ 0,6;

0,1x₁+ 0,2x₂+ 0,05x₃≥ 0,1;

x_j ≥ 0;j = 1(1)3 = n

Для приведения задачи к каноническому виду введем дополнительные переменные x₄, x₅, x₆, x₇, переменных стало больше чем уравнений n – m = 7 – 4 = 3, следовательно, части из них (трем любым,) для получения решения можно задать произвольные значения (задают, как правило, нулевые значения), возникает число сочетаний из n по m вариантов. Система ограничений примет вид равенств

0,3x₁+ 0,2x₂+ 0,4x₃– x₄= 0,2;

0,4x₁+ 0,3x₂+ 0,45x₃– x₅= 0,5;

0,2x₁+ 0,3x₂+ 0,1x₃– x₆= 0, 6;

0,1x₁+ 0,2x₂+ 0,05x₃– x₇= 0, 1;

x_j ≥ 0; j = 1(1)3 = n, i = 1(1)4 = m.

Назначаем опорный план. Выбор в качестве базисных переменных x₄, x₅, x₆, x₇ приводит к недопустимому опорному плану. Так как знаки левой и правой частей различны. (Свободные переменные x₁ = x₂ = x₃= 0) Метод искусственного базиса приводит к увеличению числа неизвестных задач, что нежелательно. Анализ задачи показывает, что число уравнений в системе ограничений больше числа переменных. Поэтому попытаемся применить принцип двойственности, т.е. вначале решим двойственную ЗЛП, а затем найдем решение исходной.

Двойственная задача. Коэффициентами линейной формы в двойственной задаче выступают правые части b_i , i = 1(1)4 = m, исходной основной задачи. Переменные получают другие имена y₁, y₂, y₃, y₄, и формулируется двойственная задача иначе. Найти максимум линейной формы Q’:

Q’=0,2y₁+ 0,5y₂+ 0,6y₃+ 0,1y₄;

при ограничениях

0,3y₁+ 0, 4y₂+ 0,2y₃+ 0,1y₄≤ 3;

0,2y₁+ 0, 3y₂+ 0,3y₃+ 0,2y₄≤ 2;

0,4y₁+ 0,45y₂+ 0,1y₃+ 0,05y₄≤ 1;

y_i ≥ 0; i = 1(1)4.

Приведем задачу к каноническому виду, вводим дополнительные неотрицательные переменные y₅, y₆ , y₇:

Найти минимум ЦФ (знаки у коэффициентов ЦФ поменяли на противоположные): Q’= – 0,2y₁– 0,5y₂– 0, 6y₃– 0,1y₄;

при ограничениях (в ограничения добавили новые переменные):

0,3y₁+ 0, 4y₂+ 0,2y₃+ 0, 1y₄+ y₅= 3;

0,2y₁+ 0, 3y₂+ 0,3y₃+ 0, 2y₄+ y₆= 2;

0,4y₁+ 0,45y₂+ 0,1y₃+ 0,05y₄+ y₇= 1,

y_i ≥ 0; i = 1(1)7.

Задача решается симплекс методом. Исходный опорный план в качестве переменных может иметь y₅, y₆, y₇ и свободные переменные y₁= y₂= y₃= y₄= 0, т.е. Y_<7> = [0, 0, 0, 0, 3, 2, 1] .

Базисные переменные y₅, y₆, y₇и ЦФ выражаем через свободные переменные, т.е. из свободных членов (правых частей, обозначенных γ_i) вычитаем левые части ограничений

y₅= 3 – (0,3y₁+ 0,4y₂+ 0,2y₃+ 0,1y₄);

y₆= 2 – (0,2y₁+ 0,3y₂+ 0,3y₃+ 0,2y₄);

y₇= 1 – (0,4y₁+ 0,45y₂+ 0,1y₃+ 0,05y₆);

Q’₁=γ₀ – Σ⁴_i=1 γ_iy_i= 0 -(0,2y₁+ 0,5y₂+ 0, 6y₃+ 0,1y₄);

γ₀=0, так как ЦФ не содержит свободного члена.

и строим симплекс таблицу с двумя полуклетками. Направляющий столбец y₃, направляющая строка y₆.

Анализ таблицы показывает, что все коэффициенты ЦФ при свободных переменных положительны. Следовательно, план Y_<7> не является оптимальным, ЦФ можно уменьшить, увеличивая значения соответствующих свободных переменных.

Находим γ = max{γ_i} =max {0,2; 0,5; 0,6; 0,1} = 0,6. Переменную y₃ надо ввести в базис. После этого устанавливаем, существует ли оптимальный план. В направляющем столбце все коэффициенты положительны, следовательно, оптимальный план существует. В базисе есть переменные, которые можно уменьшать до нуля увеличивая значения y₃,тем самым минимизируя ЦФ. Раньше других в нуль обратиться переменная y₆ и ее исключаем из базиса.

После замены переменных в базисе переходим к новой симплексной таблице.

Анализ этой таблицы показывает, что все коэффициенты в выражении ЦФ свободных переменных отрицательны. Следовательно, опорный план Y_<7>= [0, 0, 20/3, 0, 5/3, 0, 1/3] является оптимальным. ЦФ при этом Q’₁= – 4 достигла наименьшего значения. Возвращаемся к двойственной задаче. Используя соответствие между оптимальными планами двойственных задач ЛП, определяем: базисными переменными в оптимальном плане будут x₂ x₄ x₅ x₇; их значения с противоположным знаком записаны в последней строке таблицы. Таким образом, X^opt_<n> =<0; 2; 0; 0; 2; 0; 1; 0; 1/30>, т.е. оптимальный рацион из двух единиц продукта П₂. Стоимость такого рациона минимальна и составляет 4 единицы. Это значение с противоположным знаком записано в той же таблице.

Литература

Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.
Квейд Э. Методы системного анализа // Новое в теории и практике управления производством в США.–М.: Прогресс, 1971.– с.78-99. .
Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.
Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.
Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.
Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.
Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.

Источник

Двойственные задачи линейного программирования

Двойственность является важным понятием в линейном программировании, имеющим экономическое (практическое) применение. Например, для задачи оптимального распределения ресурсов для производства некоторых видов товаров пара прямой и двойственной задачи принимает следующий экономический смысл:
Прямая задача: Сколько и какой продукции xj необходимо производить, чтобы при заданных доходах Cj и объемах ресурсов bi максимизировать доход от продажи продукции?
Двойственная задача: Какова должна быть “теневая” цена каждого ресурса yi, чтобы при заданных количествах bi и доходах Cj минимизировать затраты?

Для составления двойственных задач используют специальные правила, при решении же выбирают один из наиболее подходящих методов решения ЗЛП: симплекс-метод, графический метод. Более того, так как между парой двойственных задач существует связь, иногда достаточно решить только одну из задач, чтобы получить решение второй.

Примеры составления и решения двойственных задач линейного программирования приведены в этом разделе – изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий – Решение контрольных по линейному программированию.

Понравилось? Добавьте в закладки

Примеры составления и решения двойственных задач онлайн

Задача 1. Записать математическую модель двойственной ЗЛП по заданной прямой:

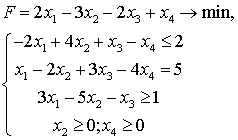
Задача 2. Составить задачу, двойственную исходной задаче:

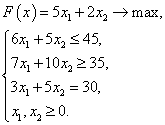
Задача 3. Решить задачу линейного программирования; составить задачу, двойственную данной, и также найти ее решение:

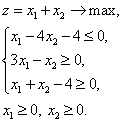
Качественно решаем задачи линейного программирования

Источник

Правила построения двойственной задачи.

Если
прямая задача на максимум, то двойственная
к ней – на минимум, и наоборот.
Если
прямая (двойственная) задача на максимум,
то ограничения-неравенства системы
представляются в виде неравенств типа
,
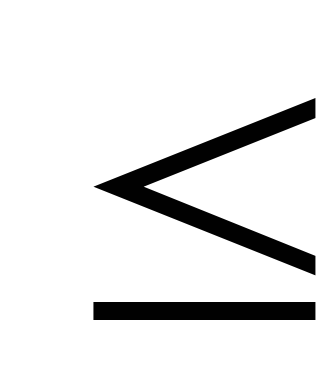если на минимум, то ограничения-неравенства
системы представляются в виде неравенств
типа.
Каждому
ограничению прямой задачи соответствует
переменная двойственной задачи, и
наоборот, каждому ограничению двойственной
задачи соответствует переменная прямой
задачи, следовательно, число ограничений
прямой задачи равно числу переменных
двойственной, а число ограничений
двойственной – числу переменных прямой.
Матрица
системы ограничений двойственной
задачи получается из матрицы системы
ограничений исходной задачи
транспонированием.
Свободные
члены системы ограничений прямой задачи
являются коэффициентами при соответствующих
переменных целевой функции двойственной
задачи, и наоборот, коэффициенты целевой
функции прямой задачи являются свободными
членами соответствующих ограничений
двойственной задачи.
Если
на переменную прямой задачи наложено
условие неотрицательности, то
соответствующее ограничение двойственной
задачи записывается как
ограничение-неравенство, если же нет,
то как ограничение-равенство.
Если
какое-либо ограничение прямой задачи
записано как равенство, то на
соответствующую переменную двойственной
задачи условие неотрицательности не
налагается.

Пример
1.24

Составить
задачу, двойственную к ЗЛП:

;

Решение

Воспользовавшись
правилами построения двойственной
задачи, получим следующую пару двойственных
ЗЛП:

прямая
задача

;

двойственная
задача

;

Пример
1.25

Составить
задачу, двойственную к ЗЛП, рассмотренной
в примере 1.8 (на максимум). Из решения
прямой задачи (пример 1.8) найти решение
двойственной задачи.

Решение

Исходная
ЗЛП:

Построим
пару двойственных ЗЛП:

прямая
задача

двойственная
задача

;

В
примере 1.6 было получено решение прямой
задачи графическим методом. Это
,.

Для
нахождения решения двойственной задачи
запишем обе задачи в канонической форме,
без учета неотрицательности исходных
переменных и добавляя во все ограничения
неотрицательные переменные. Если
переменная добавляется в ограничение-равенство,
то она равна нулю:

прямая
задача

двойственная
задача

;

Между
переменными двойственных задач существует
следующее соответствие:

Определим
из канонической формы прямой задачи,
какие переменные равны нулю в оптимальном
плане и из приведенного соответствия
определим отличные от нуля двойственные
переменные. Так

Для
нахождения отличных от нуля двойственных
переменных
ирешим систему уравнений, полученную из
системы ограничений канонической формы
двойственной задачи:

Откуда
.
Таким образом,,
или для двойственной задачи в симметричной
форме.
Причем.

Пример
1.26

Составить
задачу, двойственную к ЗЛП, примера
1.22. Из решения прямой задачи симплексным
методом (пример 1.22) найти решение
двойственной задачи.

Решение

Исходная
ЗЛП:

Построим
пару двойственных ЗЛП:

прямая
задача

двойственная
задача

;

Для
нахождения решения двойственной задачи
запишем обе задачи в канонической форме:

прямая
задача

двойственная
задача

;

Между
переменными двойственных задач существует
следующее соответствие:

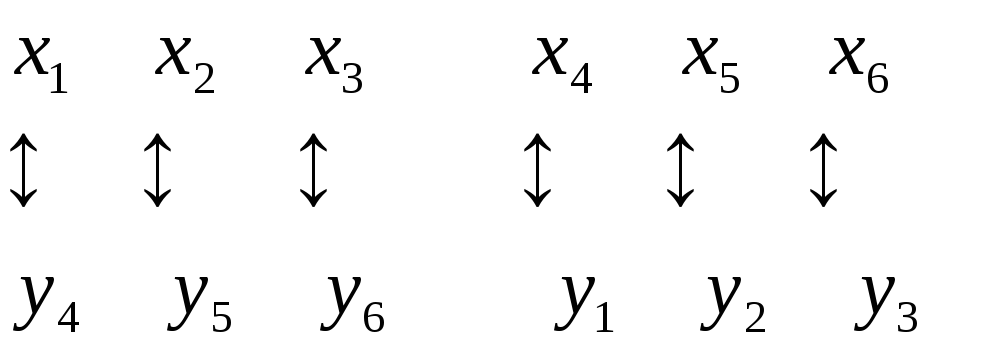
Для
нахождения оптимального плана двойственной
задачи воспользуемся симплексной
таблицей, в которой найден оптимальный
план прямой задачи (табл. 1.18). Двойственные
переменные, соответствующие базисным
переменным прямой задачи будут равны
нулю, а соответствующие свободным
переменным – будут равны абсолютной
величине оценок этих столбцов. Так
,,– базисные переменные, следовательно,
соответствующие им двойственные
переменные,,будут равны нулю, т.е.,,.
Найдем значения двойственных переменных,
соответствующих свободным переменным
прямой задачи:

Таким
образом,
,
или для двойственной задачи в симметричной
форме.
Причем.

Задачи

Составить
двойственные ЗЛП. Решая графическим
методом двойственную задачу, получить
решение прямой задачи (1.6.1
– 1.6.4).

1.6.1

;

1.6.3

;

1.6.2

;

1.6.4

;

1.6.5
–
1.6.10

Составить
двойственные ЗЛП к задачам 1.2.1 –
1.2.6
(соответственно).

1.6.11
–
1.6.28

Составить
двойственные ЗЛП к задачам 1.3.3 –
1.3.12,
1.4.1 –
1.4.8
(соответственно). Решая графическим
методом прямую задачу, получить решение
двойственной задачи.

1.6.29
–
1.6.38

Составить
двойственные ЗЛП к задачам 1.5.1 –
1.5.8
(соответственно). Решая симплексным
методом прямую задачу, получить решение
двойственной задачи.

1.6.39
–
1.6.41

Составить
двойственные ЗЛП к задачам 1.3.7, 1.3.8, и
1.3.11 (соответственно). Решая графическим
методом двойственную задачу, получить
решение прямой задачи.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Видео урока:

Из занятия 1 имеем прямую задачу линейного программирования.

Прямая задача ЛП

Записываем матрицу прямой задачи:

Матрица прямой задачи ЛП

Транспонируем полученную матрицу и получаем матрицу двойственной задачи: ТРАНСП(C12:G16)

Матрица двойственной задачи ЛП

Двойственная задача запишется в виде:

Двойственная задача ЛП

Запишем обе задачи:

Пара двойственных задач ЛП

Запишем матрицы соответствия переменных прямых и двойственных задач:

Матрицы соответствия переменных прямой и двойственной задач

Единица по диагонали означает соответствие:

x1↔ y5

x2↔ y6

x3↔ y7

и т. д.

Подпишем соответствующие переменные к последней симплекс-таблице из урока 3.

Последняя симплекс-таблица

Видим, что значения двойственных переменных совпадают со значениями,

полученными нами через надстройку «поиск решения»

Анализ устойчивости

Значения целевых функций для оптимальных планов двойственных задач совпадают F min = f max = 30,667.

Значения Y6=3,3 и Y8=3,0333 означают, что при производстве одного вида продукции 2-го и 4-го вида значение целевой функции уменьшится на 3,3 и 3,0333 денежных единиц соответственно.

Y5=Y7=0 означает, что производство 1-го и 3-го видов продукции является наиболее эффективным.

Значения Y2=0,1 и Y3=0,267 означают, что при увеличении запасов 2-го и 3-го видов сырья на одну весовую единицу, значение целевой функции возрастёт на 0,1 и 0,267 денежных единиц соответственно. Так же это означает дефицитность этих видов ресурсов, так как оценки выше нуля.

Y1=Y4=0 – это означает, что ресурсы 1-го и 4-го видов не являются дефицитными и их увеличение никак не повлияет на значение целевой функции.

Эти выводы действительны в пределах интервалах устойчивости изменения ресурсов и коэффициентов целевой функции.

Надстройка «поиск решения» автоматически считает интервалы устойчивости для коэффициентов целевой функции и ресурсов. Интервалы устойчивости показаны в столбцах «допустимое увеличение» и «допустимое уменьшение».

В следующей статье мы рассмотрим определение интервалов устойчивости ресурсов и коэффициентов целевой функции на основании последней симплекс-таблице из занятия 3.

Материал подготовлен сайтом: https://pro-smysl.ru/

Онлайн помощь в решении задач, консультации, создание обучающих роликов.

Подписывайтесь на наши каналы:

https://vk.com/sm_smysl

https://www.youtube.com/@SMYS_L

Источник

Двойственная задача^[1] для заданной задачи линейного программирования (ЛП, англ. Linear programming, LP) — это другая задача линейного программирования, которая получается из исходной (прямой) задачи следующим образом:

Каждая переменная в прямой задаче становится ограничением двойственной задачи;
Каждое ограничение в прямой задаче становится переменной в двойственной задаче;
Направление цели обращается – максимум в прямой задаче становится минимумом в двойственной, и наоборот.

Теорема о слабой двойственности утверждает, что значение двойственной задачи для любого допустимого решения всегда ограничено значением прямой задачи для любого допустимого решения (верхняя или нижняя граница, в зависимости от того, это задача максимизации или минимизации).

Теорема о сильной двойственности утверждает, что более того, если прямая задача имеет оптимальное решение, то двойственная задача имеет также оптимальное решение, и эти два оптимума равны^[2].

Эти теоремы принадлежат более широкому классу теорем двойственности в оптимизации. Теорема о сильной двойственности является одним из случаев, в котором разрыв двойственности (разрыв между оптимумом прямой задачи и оптимумом двойственной) равен 0.

О геометрическом смысле двойственной задачи можно почитать в книге Юдина и Гольштейна^[3]. Там же можно прочитать об экономическом смысле задачи^[4].

Построение двойственной задачи[править | править код]

Если дана прямая задача линейного программирования, для построения двойственной задачи может быть использован следующий алгоритм^[5].

Пусть прямая задача определена как:

Двойственная задача строится следующим образом.

Каждое ограничение прямой задачи становится двойственной переменной. Таким образом, получаем m переменных: ${displaystyle y_{1},ldots ,y_{m}}$ .
Знак ограничения каждой двойственной переменной «противоположен» знаку ограничения в прямой задаче. Таким образом, « ${displaystyle geqslant b_{j}}$ » становится ${displaystyle y_{j}leqslant 0}$ , « ${displaystyle leqslant b_{j}}$ » превращается в ${displaystyle y_{j}geqslant 0}$ , а « ${displaystyle =b_{j}}$ » превращается в ${displaystyle y_{j}in mathbb {R} }$ .
Целевая функция двойственной задачи равна (минимизировать) ${displaystyle b_{1}y_{1}+cdots +b_{m}y_{m}}$
Каждая переменная прямой задачи становится двойственным ограничением. Таким образом, получаем n ограничений. Коэффициент двойственной переменной в двойственных ограничениях равен коэффициенту переменной из ограничения прямой задачи. Таким образом, каждое ограничение i есть: ${displaystyle a_{1i}y_{1}+cdots +a_{mi}y_{m}lesseqqgtr c_{i}}$ , где символ перед $c_{i}$ аналогичен ограничению на переменную i в прямой задаче. Так, ${displaystyle x_{i}leqslant 0}$ превращается в « ${displaystyle leqslant c_{i}}$ », ${displaystyle x_{i}geqslant 0}$ превращается в « ${displaystyle geqslant c_{i}}$ », а ${displaystyle x_{i}in mathbb {R} }$ превращается в « ${displaystyle =c_{i}}$ ».

Из этого алгоритма легко видеть, что двойственная задача двойственной задачи совпадает с прямой задачей.

Векторные формулировки[править | править код]

Если все ограничения имеют один и тот же знак, можно представить вышеизложенный метод в более короткой форме с помощью векторов и матриц. Следующая таблица представляет связи между различными видами прямых и двойственных задач.

Прямая	Двойственная	Примечания
Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях	Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} ,mathbf {y} geqslant 0}$	Такая задача называется «симметричной» двойственной задачей
Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях	Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} =mathbf {c} ,mathbf {y} geqslant 0}$	Такая задача называется «асимметричной» двойственной задачей
Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях	Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} }$

Теоремы двойственности[править | править код]

Ниже мы предполагаем, что прямая задача поставлена как «Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях [ограничения]», а двойственная задача поставлена как «Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях [ограничения]».

Слабая двойственность[править | править код]

Теорема о слабой двойственности утверждает, что для каждого допустимого решения x прямой задачи и каждого допустимого решения y двойственной задачи: ${displaystyle mathbf {c} ^{T}mathbf {x} leqslant mathbf {b} ^{T}mathbf {y} }$ . Другими словами, значение целевой функции для каждого допустимого решения двойственной задачи является верхней границей целевой функции прямой задачи, а значение целевой функции любого допустимого решения прямой задачи является нижней границей для целевой функции двойственной задачи. Из этого следует, что

${displaystyle max _{mathbf {x} }mathbf {c} ^{T}mathbf {x} leqslant min _{mathbf {y} }mathbf {b} ^{T}mathbf {y} }$

В частности, если прямая задача не ограничена (сверху), то двойственная задача не имеет допустимого решения, а если не ограничена двойственная задача (снизу), то не имеет допустимого решения прямая задача.

Теорему о слабой двойственности относительно легко доказать^[6]. Предположим, что прямая задача линейного программирования звучит как «Максимизировать ${displaystyle mathbf {c} ^{T}mathbf {x} }$ при ограничениях ». Предположим, что мы создаём линейную комбинацию ограничений с положительными коэффициентами, такую, что коэффициенты при x не меньше ${displaystyle mathbf {c} ^{T}}$ . Эта линейная комбинация даёт нам верхнюю грань для целевой функции. Переменные y двойственной задачи являются коэффициентами этой линейной комбинации. Двойственная задача пытается найти такие коэффициенты, которые минимизируют результирующую правую часть. Это даёт задачу линейного программирования «Минимизировать ${displaystyle mathbf {b} ^{T}mathbf {y} }$ при ограничениях ${displaystyle mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} ,mathbf {y} geqslant 0}$ »^[7]. См. «Простой пример» ниже.

Сильная двойственность[править | править код]

Теорема о сильной двойственности утверждает, что границы, определяемые теоремой о слабой двойственности жёсткие, то есть

${displaystyle max _{mathbf {x} }mathbf {c} ^{T}mathbf {x} =min _{mathbf {y} }mathbf {b} ^{T}mathbf {y} }$

Теорему о сильной двойственности существенно труднее доказать. Обычно доказательство использует теорему о слабой двойственности в качестве леммы^[8].

Одно доказательство использует симплекс-метод и опирается на доказательство того, что, при подходящем правиле выбора выводимого столбца, он даёт правильное решение. Доказательство устанавливает, что, когда симплекс-метод завершается решением прямой задачи линейного программирования, можно из конечной таблицы прочесть решение двойственной задачи. Таким образом, после прогона симплекс-алгоритма мы получим решения как прямой, так и двойственной задачи одновременно^[9].

Другое доказательство использует лемму Фаркаша^[10]

Теоретическое приложение[править | править код]

Слабая двойственность имеет интересное теоретическое приложение — она показывает, что нахождение отдельного допустимого решения настолько же трудно, насколько нахождение оптимального допустимого решения. Предположим, что мы имеем систему предсказывания, что данная задача линейного программирования находит произвольное допустимое решение (если оно существует). Если задача звучит как «Максимизировать ${displaystyle mathbf {c} ^{mathbf {x} }}$ при ограничениях », мы можем построить другую задачу путём комбинирования её с двойственной ей задачей. Комбинированная задача имеет как x, так и y в качестве переменных:

Максимизировать 1

при ограничениях ${displaystyle mathbf {Ax} leqslant mathbf {b} ,mathbf {A} ^{T}mathbf {y} geqslant mathbf {c} ,mathbf {c} ^{T}mathbf {x} geqslant mathbf {b} ^{T}mathbf {y} ,mathbf {x} geqslant 0,mathbf {y} geqslant 0}$

Если комбинированная задача имеет допустимое решение (x,y), то по слабой двойственности ${displaystyle mathbf {c} ^{T}mathbf {x} =mathbf {b} ^{T}mathbf {y} }$ . Таким образом, x должно быть максимальным решением прямой задачи, а y должно быть минимальным решением двойственной задачи. Если комбинированная задача не имеет допустимого решения, то и прямая задача допустимого решения не имеет.

Примеры[править | править код]

Простой пример[править | править код]

Рассмотрим прямую задачу с двумя переменными и одним ограничением:

Максимизировать ${displaystyle 3x_{1}+4x_{2}}$

При условиях

${displaystyle {begin{aligned}&5x_{1}+6x_{2}=7\&x_{1}geqslant 0,x_{2}geqslant 0end{aligned}}}$

Применив вышеизложенный рецепт построения двойственной задачи, получим задачу с одной переменной и двумя ограничениями:

Минимизировать ${displaystyle 7y_{1}}$

При условиях

${displaystyle {begin{aligned}&&5y_{1}geqslant 3\&&6y_{1}geqslant 4\&&y_{1}in mathbb {R} end{aligned}}}$

Легко видеть, что максимум прямой задачи достигается, когда переменная x₁ минимизируется до её нижней границы (0), а переменная x₂ максимизируется до её верхней границы, заданной ограничением (7/6). Максимум равен .

Аналогично, минимум двойственной задачи достигается, когда y₁ минимизируется до его нижнего значения при ограничениях: первое ограничение даёт значение 3/5, в то время как второе даёт более строгую границу 4/6, так что фактический минимум равен 4/6 и минимум целевой функции равен .

Согласно теореме о сильной двойственности максимум прямой задачи равен минимуму двойственной.

Мы используем этот пример для иллюстрации доказательства теоремы о слабой двойственности. Предположим, что в прямой задаче линейного программирования мы хотим получить верхнюю границу целевой функции ${displaystyle 3x_{1}+4x_{2}}$ . Мы можем использовать ограничение, умноженное на некоторый коэффициент, скажем, y_1 . Для любого y_1 мы имеем: ${displaystyle y_{1}cdot (5x_{1}+6x_{2})=7y_{1}}$ . Теперь, если ${displaystyle y_{1}cdot 5x_{1}geqslant 3x_{1}}$ и ${displaystyle y_{1}cdot 6x_{2}geqslant 4x_{2}}$ , то ${displaystyle y_{1}cdot (5x_{1}+6x_{2})geqslant 3x_{1}+4x_{2}}$ , так что ${displaystyle 7y_{1}geqslant 3x_{1}+4x_{2}}$ . Следовательно, целевая функция двойственной задачи является верхней границей целевой функции прямой задачи.

Пример фермера[править | править код]

Рассмотрим фермера, который может выращивать пшеницу и ячмень на площади L, используя удобрения F и пестициды P.
Чтобы вырастить одну единицу пшеницы на единице площади, нужно использовать $F_{1}$ единиц удобрений и P_1 единиц пестицидов.

Прямой задачей будет решение фермера, сколько пшеницы ( $x_{1}$ ) и ячменя ( $x_{2}$ ) выращивать, если их продажные цены равны $S_{1}$ и $S_{2}$ за единицу.

Максимизировать:

${displaystyle S_{1}cdot x_{1}+S_{2}cdot x_{2}}$

(максимизировать доход от выращивания пшеницы и ячменя)

при ограничениях:

${displaystyle x_{1}+x_{2}leqslant L}$

(фермер не может использовать больше земли, чем у него есть)

${displaystyle F_{1}cdot x_{1}+F_{2}cdot x_{2}leqslant F}$

(фермер не может использовать больше удобрений, чем есть в наличии)

${displaystyle P_{1}cdot x_{1}+P_{2}cdot x_{2}leqslant P}$

(фермер не может использовать больше пестицидов, чем у него есть)

${displaystyle x_{1},x_{2}geqslant 0}$

(нельзя вырастить отрицательную величину зерна).

Для двойственной задачи предположим, что y единиц цены для каждой из этих видов продукта (входы) представлены группой планирования. Задачей группы планирования является минимизация полной стоимости производство продукции при заданных величинах потребления ресурсов с определением стоимости единицы ресурса (выход). Это соответствует следующей задаче линейного программирования:

Минимизировать

${displaystyle Lcdot y_{L}+Fcdot y_{F}+Pcdot y_{P}}$

(минимизировать полную стоимость производства продукции как «целевая функция»)

при ограничениях:

${displaystyle y_{L}+F_{1}cdot y_{F}+P_{1}cdot y_{P}geqslant S_{1}}$

(фермер должен получить не менее S₁ за единицу пшеницы)

${displaystyle y_{L}+F_{2}cdot y_{F}+P_{2}cdot y_{P}geqslant S_{2}}$

(фермер должен получить не менее S₂ за единицу ячменя)

${displaystyle y_{L},y_{F},y_{P}geqslant 0}$

(цены не могут быть отрицательными).

В матричной форме:

Минимизировать: ${displaystyle {begin{bmatrix}L&F&Pend{bmatrix}}{begin{bmatrix}y_{L}\y_{F}\y_{P}end{bmatrix}}}$

при условиях: ${displaystyle {begin{bmatrix}1&F_{1}&P_{1}\1&F_{2}&P_{2}end{bmatrix}}{begin{bmatrix}y_{L}\y_{F}\y_{P}end{bmatrix}}geqslant {begin{bmatrix}S_{1}\S_{2}end{bmatrix}},,{begin{bmatrix}y_{L}\y_{F}\y_{P}end{bmatrix}}geqslant 0.}$

Прямая задача имеет дело с физическими количествами, когда все величины ограничены и цены на единицу продукции известны. Задача состоит в определении, какие количества продукта произвести, чтобы максимизировать суммарный доход. Двойственная задача имеет дело с экономическими величинами. Задача состоит в том, чтобы при фиксированных ценах на продукцию и известных потреблениях ресурсов определить, какую ценовую схему установить, чтобы минимизировать суммарные затраты.

Каждой переменной в пространстве прямой задачи соответствует неравенство в пространстве двойственной задачи. Каждому неравенству в пространстве прямой задачи соответствует переменная в пространстве двойственной задачи.

Коэффициенты, которые ограничивают неравенства в пространстве прямой задачи, используются для вычисления целевой функции в двойственном пространстве. Коэффициенты, используемые для вычисления целевой функции, в пространстве прямой задачи ограничивают неравенства в пространстве двойственной задачи.

Как прямая, так и двойственная задачи используют одну и ту же матрицу. В пространстве прямой задачи эта матрица выражает потребление физических величин, необходимых для производства выходного продукта. В пространстве двойственной задачи матрица выражает создание экономических значений, ассоциированных с выходным продуктом из множеств входных цен на единицу продукции.

Поскольку каждое неравенство может быть заменено на равенство и дополнительную переменную, это означает, что каждая переменная прямой задачи соответствует двойственной дополнительной переменной, а каждая двойственная переменная соответствует прямой дополнительной переменной. Это отношение позволяет нам говорить о взаимодополнительности дополнительных переменных.

Недопустимая задача[править | править код]

Задача линейного программирования может также быть неограниченной или недопустимой. Теория двойственности говорит нам, что:

Если прямая задача является неограниченной, то двойственная задача недопустима;
Если двойственная задача является неограниченной, то прямая задача недопустима^[11].

Однако может быть, что обе задачи, как двойственная, так и прямая, недопустимы. Вот пример:

Приложения[править | править код]

Теорема о максимальном потоке и минимальном разрезе является специальным случаем теоремы о сильной двойственности — максимизация потока является прямой задачей линейного программирования, а минимизация разреза является двойственной задачей линейного программирования. См. теорему Форда — Фалкерсона.

Другие теоремы, связанные с графами, могут быть доказаны с помощью теоремы о сильной двойственности, в частности, теорема Кёнига^[12].

Теорема о минимаксе^[en] для игр с нулевой суммой может быть доказана с помощью теоремы о сильной двойственности^[13].

Альтернативный алгоритм[править | править код]

Иногда можно найти более интуитивный способ получить двойственную задачу без применения матрицы задачи. Рассмотрим следующую задачу линейного программирования:

Минимизировать ${displaystyle sum _{i=1}^{m}c_{i}x_{i}+sum _{j=1}^{n}d_{j}t_{j}}$

при условиях

${displaystyle sum _{i=1}^{m}a_{ij}x_{i}+e_{j}t_{j}geqslant g_{j},1leqslant jleqslant n}$

${displaystyle f_{i}x_{i}+sum _{j=1}^{n}b_{ij}t_{j}geqslant h_{i},1leqslant ileqslant m}$

${displaystyle x_{i}geqslant 0,,t_{j}geqslant 0,1leqslant ileqslant m,1leqslant jleqslant n}$

Мы имеем условий и все переменные неотрицательны. Нам нужно определить двойственных переменных: y_j и s_i. Мы получаем:

Минимизировать ${displaystyle sum _{i=1}^{m}c_{i}x_{i}+sum _{j=1}^{n}d_{j}t_{j}}$

при условиях

${displaystyle sum _{i=1}^{m}a_{ij}x_{i}cdot y_{j}+e_{j}t_{j}cdot y_{j}geqslant g_{j}cdot y_{j},1leqslant jleqslant n}$

${displaystyle f_{i}x_{i}cdot s_{i}+sum _{j=1}^{n}b_{ij}t_{j}cdot s_{i}geqslant h_{i}cdot s_{i},1leqslant ileqslant m}$

${displaystyle x_{i}geqslant 0,,t_{j}geqslant 0,1leqslant ileqslant m,1leqslant jleqslant n}$

${displaystyle y_{j}geqslant 0,,s_{i}geqslant 0,1leqslant jleqslant n,1leqslant ileqslant m}$

Поскольку это задача минимизации, нам хотелось бы получить двойственную задачу, которая является нижней границей прямой задачи. Другими словами, нам хотелось бы, чтобы сумма всех правых частей ограничений была максимальной при условиях, что для каждой переменной прямой задачи сумма её коэффициентов не превосходит коэффициента в линейной функции. Например, x₁ появляется в n+1 ограничениях. Если мы суммируем коэффициенты ограничения, мы получим ${displaystyle a_{1,1}mathbf {y} _{1}+a_{1,2}mathbf {y} _{2}+dots +a_{1,n}mathbf {y} _{n}+f_{1}mathbf {s} _{1}}$ . Эта сумма должна не превосходить c₁. Как результат мы получаем:

Максимизировать ${displaystyle sum _{j=1}^{n}g_{j}y_{j}+sum _{i=1}^{m}h_{i}s_{i}}$

при ограничениях

${displaystyle sum _{j=1}^{n}a_{ij}y_{j}+f_{i}s_{i}leqslant c_{i},1leqslant ileqslant m}$

${displaystyle e_{j}y_{j}+sum _{i=1}^{m}b_{ij}s_{i}leqslant d_{j},1leqslant jleqslant n}$

${displaystyle y_{j}geqslant 0,,s_{i}geqslant 0,1leqslant jleqslant n,1leqslant ileqslant m}$

Вычисления выше предполагают, что задача представлена в стандартной форме. Это предположение не влияет на общность рассуждений, так как любая задача линейного программирования может быть приведена к стандартному виду.

Интерпретации в реальной жизни[править | править код]

Теорема двойственности имеет экономическую интерпретацию. Если мы интерпретируем прямую задачу линейного программирования как классическую задачу «распределения ресурсов», её двойственную задачу можно интерпретировать как задачу «оценки ресурсов»^[14]. См. статью Теневая цена^ru_en. Об экономической интерпретации двойственной задачи можно почитать также в книге Лунгу^[15].

Теорема двойственности имеет и физическую интерпретацию^[16].

Примечания[править | править код]

↑ Иногда используется термин Сопряжённая задача, как, например, в книге Юдина и Гольштейна (Юдин, Гольштейн 1969, 149) или в книге Лунгу (Лунгу 2005, 67). Во второй книге прямая задача именуется также основной задачей.
↑ Gartner, Matousek, 2006, с. 81–104.
↑ Юдин, Гольштейн, 1969, с. 150-152 Пункт 5.2.
↑ Юдин, Гольштейн, 1969, с. 157-159 Пункт 5.5.
↑ Gartner, Matousek, 2006, с. 85.
↑ Доказательство очень близкого утверждения, из которого вытекает данная теорема можно найти в книге Юдина и Гольштейна (Юдин, Гольштейн 1969, 159, Лемма 5.1)
↑ Gartner, Matousek, 2006, с. 81–83.
↑ Доказательство можно найти в книге Юдина и Гольштейна, где она именуется «первой теоремой двойственности» (Юдин, Гольштейн 1969, 164, Теорема 6.1)
↑ Gartner, Matousek, 2006, с. 87–89.
↑ Gartner, Matousek, 2006, с. 81–94.
↑ Юдин, Гольштейн, 1969, с. 162, Лемма 5.3.
↑ A. A. Ahmadi Lecture 6: linear programming and matching. Princeton University (2016). Архивировано 21 сентября 2018 года.
↑ Gartner, Matousek, 2006, с. sub.8.1.
↑ В книге Юдина и Гольштейна для теневых цен используется термин предварительные оценки (факторов производства).
↑ Лунгу, 2005, с. 68 Пункт 5.4.
↑ Gartner, Matousek, 2006, с. 86–87.

Литература[править | править код]

Jiri Matousek, Bernd Gärtner. Understanding and Using Linear Programming. — Springer, 2006. — С. 81–104. — (Universitext).
Юдин Д.Б., Гольштейн Е.Г. Линейное программирование (теория, методы и приложения). — Москва: «Наука», 1969.
Лунгу К.Н. Линейное программирование. Руководство к решению задач. — М.: ФИЗМАТЛИТ, 2005. — ISBN 5-9221-0631-7.

Источник

Двойственная задача линейного программирования

Теорема двойственности

Двойственные задачи линейного программирования

Примеры составления и решения двойственных задач онлайн

Правила построения двойственной задачи.

Построение двойственной задачи[править | править код]

Векторные формулировки[править | править код]

Теоремы двойственности[править | править код]

Слабая двойственность[править | править код]

Сильная двойственность[править | править код]

Теоретическое приложение[править | править код]

Примеры[править | править код]

Простой пример[править | править код]

Пример фермера[править | править код]

Недопустимая задача[править | править код]

Приложения[править | править код]

Альтернативный алгоритм[править | править код]

Интерпретации в реальной жизни[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти в какой библиотеке журнал

Как найти длину дуги центрального угла

Как найти все слова в филворде

Добавить комментарий Отменить ответ