Цели урока:
- повторить правила раскрытия скобок и приведения подобных слагаемых;
- ввести определение линейного уравнения с одним неизвестным;
- познакомить учащихся со свойствами равенств;
- научить решать линейные уравнения;
- научить решать задачи на «было − стало».
Оборудование: компьютер, проектор.
Ход урока
I. Проверка предыдущего домашнего задания.
(устно, фронтально).
II. Повторение теоретического материала.
- Как найти неизвестное слагаемое? [От суммы отнять известное слагаемое]
- Как найти неизвестное уменьшаемое? [К вычитаемому прибавить разность]
- Как найти неизвестное вычитаемое? [От уменьшаемого отнять разность]
- Как найти неизвестный множитель? [Произведение разделить на известный множитель]
- Как найти неизвестное делимое? [Делитель умножить на частное]
- Как найти неизвестный делитель? [Делимое разделить на частное]
- Как раскрыть скобки, перед которыми стоит знак плюс? [Опустить скобки и этот знак плюс, переписать слагаемые с теми же знаками]
- Как раскрыть скобки, перед которыми стоит знак минус? [Опустить скобки и этот знак минус, переписать слагаемые с противоположными знаками]
- Как выглядит распределительное свойство умножения? [(a+b)∙c=ac+bc]
III. Устные задания по слайдам.
(слайд 2, слайд 3).
1) Раскройте скобки:
3+(х+2); 3-(х+2); 3+(х-7); 3-(х-7); 3+(-х+5); 3-(-х+5); -4(-5-х); 9(
; 9(
; 2(7+9х); 4(2-3х); -6(9-5х); -3(1+4х).
2) Приведите подобные слагаемые:
6b-b; 9,5m+3m; a –
a;
m-m; -4x-x+3; 7x-6y-3x+8y.
3) Упростите выражение:
2x-(x+1); n+2(3n-1); 5m-3(m+4).
IV. Новая тема. Решение линейных уравнений.
До сегодняшнего урока мы не умели решать уравнения, в которых неизвестное находилось слева и справа от знака равенства: 3x+7=x+15. Некоторые из нас постоянно забывают правила нахождения неизвестного слагаемого, уменьшаемого, вычитаемого. Сегодня мы постараемся разрешить все эти затруднения.
Уравнение, которое можно привести к виду ax=b, где a и b − некоторые числа (a0), называется линейным уравнением с одним неизвестным.
Линейные уравнения обладают свойствами:
- Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (стр. 229 учебника).
- Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак (стр. 230 учебника).
Рассмотрим план решения линейного уравнения:
| х-1+(х+2)=-4(-5-х)-5 х-1+х+2=20+4х-5 х+х-4х=20-5+1-2 -2х=14 х=14:(-2) х=-7 Ответ: -7. |
1) раскрыть скобки, если они есть; 2) слагаемые, содержащие неизвестное, перенести в левую часть равенства, а не содержащие неизвестное − в правую; 3) привести подобные слагаемые; 4) найти неизвестный множитель. |
Какими из свойств равенств мы воспользовались для решения уравнения? (вторым)
Рассмотрим примеры уравнений, при решении которых будет удобно воспользоваться и первым свойством.
№ 1317(а).
х+3=
х+5 │∙9 Удобно умножить на наименьшее общее кратное знаменателей дробей.
(
х+3)∙9=(
х+5)∙9 Далее − по плану.
7х+27=6х+45
7х-6х=45-27
х=18
Ответ: 18.
№1318(а).
-40∙(-7х+5)=-1600 │:(-40)
-7х+5=40
-7х=40-5
-7х=35
х=-5
Ответ: -5.
Не забывайте о том, что ответ может быть дробным числом.
V. Самостоятельная работа обучающего характера.
(Выполняется на листочках парами по карточкам.)
Для наиболее слабых учащихся:
Для средних учащихся:
Для сильных учащихся:
Сдать работы и тут же сверить ответы со слайдом 5.
VI. Решение задач на «было − стало».
Умея решать линейные уравнения по-новому, мы сможем справиться с новым для нас типом задач на «было – стало».
№1321. (слайд 6)
В первом бидоне в три раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько молока в каждом бидоне?
(Решает учитель, поясняя каждый шаг).
Решение.
Составим таблицу:
| 1 бидон | 2 бидон | |
| Было, л | 3х | Х |
| Стало, л | 3х-20 | х+20 |
По условию получаем уравнение:
3х-20=х+20
3х-х=20+20
2х=40
х=20(л) молока было в 1 бидоне.
3∙20=60(л) молока было во 2 бидоне.
Ответ: 60л и 20л.
№1324. (слайд 7)
На первую машину погрузили на 0,6т зерна больше, чем на вторую. Если бы на первую машину погрузили в 1,2 раза больше, а на вторую в 1,4 раза больше, то груза на обеих машинах было бы поровну. Сколько тонн груза погрузили на каждую машину?
(Решает у доски учащийся).
Решение.
| 1 машина | 2 машина | |
| Было, т | Х+0,6 | Х |
| Стало, т | 1,2(х+0,6) | 1, 4х |
По условию получаем уравнение:
1,2(х+0,6)=1,4х
1,2х+0,72=1,4х
1,2х-1,4х=-0,72
-0,2х=-0,72
х=-0,72:(-0,2)
х=3,6(т) зерна было на 2 машине.
3,6+0,6=4,2(т) зерна погрузили на 1 машину.
Ответ: 4,2т и 3,6т.
№1322.
Длина отрезка АВ на 2см больше, чем длина отрезка СD. Если длину отрезка АВ увеличить на 10см, а длину отрезка CD увеличить в 3 раза, то получатся равные результаты. Найдите длину отрезка АВ.
(Задача решается парами на местах. По окончании решения к доске для сверки вызывается один из учащихся.)
Решение.
| АВ | CD | |
| Было, см | х+2 | Х |
| Стало, см | (х+2)+10 | 3х |
По условию получаем уравнение:
(х+2)+10=3х
х+2+10=3х
х-3х=-2-10
-2х=-12
х=6(см) − CD.
6+2=8(см) − АВ.
Ответ: АВ= 8см.
Обратите внимание, что в ответ записываем только длину отрезка АВ («каков вопрос − таков ответ»).
Если останется время, решим №1340. (слайд 8)
Старинная задача.
− Скажи мне, учитель, сколько учеников посещают твою школу и слушают твои беседы.
− Вот сколько, − ответил учитель, − половина изучает математику, четверть − природу, седьмая часть проводит время в размышлении, и, кроме того, есть ещё три женщины.
Решение.
Пусть х − все ученики, из них:
Составим и решим уравнение:
│∙28
14х+7х+4х+84=28х
14х+7х+4х-28х=-84
-3х=-84
х=-84:(-3)
х=28
Ответ: всего 28 учеников.
VII. Подведение итогов.
(слайд 9)
- Какие уравнения называются линейными?
- Какие свойства уравнений мы изучили?
- Назовите план решения линейного уравнения.
- Назовите план решения задач на «было – стало».
VIII. Задание на дом.
п. 42, правила, №1342(г-ж), №1346, №1338.
№1342. Решите уравнения:
г) 25-3b=9-5b; д) 3+11у=203+у; е) 3∙(4х-8)=3х-6; ж) -4∙(-z+7)=z+17.
№1346.
На одной полке было в 3 раза больше книг, чем на другой. Когда с одной полки сняли 8 книг, а на другую положили 32 книги, то на полках стало книг поровну. Сколько книг было на каждой полке первоначально?
№1338. Докажите, что при любом значении буквы значение выражения:
- 5∙(7у-2)-7∙(5у+2) равно -24;
- 4∙(8a+3)-8∙(4a-3) равно 36.
Литература:
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс: учебник для общеобразовательных учреждений. − М.: Мнемозина, 2010.
- Семенов А.Л., Ященко И.В. и др. ГИА: 3000 задач с ответами по математике. Все задания части 1. − М.: Экзамен, 2013.
Презентация.
Задачи, решаемые с помощью уравнения: примеры, объяснение. Задачи по алгебре
Рано или поздно любому школьнику на уроках алгебры встречаются задачи, решаемые с помощью уравнения. Поначалу появление букв вместо привычных цифр и действия с ними ставят в тупик даже самых одарённых, но если разобраться, всё далеко не так сложно, как кажется на первый взгляд.
Алгоритм решения
Перед тем как перейти к конкретным примерам, необходимо понять алгоритм решения задач с помощью уравнений. В любом уравнении есть неизвестное, чаще всего обозначаемое буквой Х. Также и в каждой задаче есть то, что необходимо найти, то же самое неизвестное. Именно его и нужно обозначать как Х. А потом, следуя условию задачи, прибавлять, отнимать, умножать и делить – совершать любые необходимые действия.
После нахождения неизвестного обязательно выполнение проверки, чтобы быть уверенными, что задача решена правильно. Стоит заметить, что дети уже в начальной школе начинают решение задач с помощью уравнений. Примеры этому – те задачи, которые нужно решать отрезками, являющимися полнейшими аналогами буквенных неизвестных.
Основа основ – задача про корзины
Итак, попробуем же на практике применить решение задач с помощью уравнений, объяснение алгоритма которых было дано чуть выше.
Дана задача: Собрали некоторое количество корзин с яблоками. Сначала 3 корзины продали, потом дособирали ещё 8 корзин. В итоге получилось 12 корзин. Сколько корзин яблок собрали первоначально?
Начнём решение задачи с того, что обозначим неизвестное – то есть первоначальное количество корзин – буквой Х. Теперь начинаем составлять уравнение: Х (первоначальное количество) – 3 (проданные корзины) + 8 (те, которые собрали позже) = 12 (итоговое число корзин), то есть Х – 3 + 8 = 12. Решив простое уравнение, получим, что Х = 7. Обязательно выполняем проверку, то есть подставляем найденное число в равенство: 7 – 3 + 8 действительно равно 12, то есть задача решена верно.
Закрепление: концертные залы
Дана следующая задача: В двух концертных залах 450 мест. Известно, что в одном зале мест в 4 раза больше, чем в другом. Нужно узнать, сколько мест в каждом зале.
Для того чтобы решать подобные задачи по алгебре, снова нужно применить уравнение. Мы знаем, что сумма двух чисел, одно из которых в 4 раза больше другого, равна 450. Пусть число мест в меньшем зале, неизвестное, будет равно Х, тогда число мест в большем зале – 4 * Х = 4Х. Следовательно, 450 = Х + 4Х = 5Х. А дальше нужно решить стандартное уравнение 450 = 5Х, где Х = 450 / 5 = 90, то есть в меньшем зале 90 мест, значит в большем – 90 * 4 = 360. Чтобы убедиться, что задача решена правильно, можно проверить неравенство: 360 + 90 = 450, то есть ответ верный.
Классика: полки с книгами
Но задачи, решаемые с помощью уравнения, могут быть и посложнее. Например, есть три полки с книгами. На первой полке книг на 8 больше, чем на второй, а на третьей – в 3 раза больше, чем на второй, причём количество книг на первой и третьей полках равное. Сколько книг на каждой полке?
Понятно, что отталкиваться здесь нужно от второй полки, которая встречается в обоих условиях. Если мы обозначаем количество книг на ней за Х, то тогда на первой полке Х + 8 книг, а на третьей – Х * 3 книг, при этом Х + 8 = 3Х. Решив уравнение, получаем Х = 4. Выполняем проверку, подставляя неизвестное в равенство: 4 + 8 действительно равно 3 * 4, то есть задача решена правильно.
Практикуемся дальше: бобры
Как видите, решение задач с помощью уравнения гораздо легче, чем кажется на первый взгляд. Закрепим навыки работы с уравнениями ещё одной задачей. Первый бобр сгрыз за день какое-то количество деревьев. Второй бобр сгрыз в 6 раз больше. Третий бобр сгрыз в 2 раза больше деревьев, чем первый, но в 3 раза меньше, чем второй. Сколько деревьев сгрыз каждый бобр?
Задача не такая запутанная, какой кажется на первый взгляд. Для начала найдём неизвестное – в этой задаче это количество деревьев, сгрызенных первым бобром. Следовательно, второй бобр уничтожил 6 * Х деревьев, а третий – 2 * Х, причём это число в 3 раза меньше 6 * Х. Составляем уравнение: 6Х = 3 * 2Х. Решив его, получаем, что первый бобр погрыз всего одно дерево, тогда второй – 6, а третий – 2. Подставив числа в уравнение, понимаем, что задача решена верно.
Соотносим уравнения и условия
Если вам скажут: “К каждой задаче подберите соответствующее уравнение”, – не пугайтесь – это целиком и полностью реально.
Даны следующие уравнения:
Условия задач следующие:
- У мальчика было 6 яблок, а у девочки в два раза меньше, сколько было яблок у девочки?
- На столе лежат ручки и карандаши, известно, что ручек на столе 6, а карандашей на 2 меньше, сколько ручек и сколько карандашей на столе?
- У Вани на шесть монет больше, чем у Тани, а у Тани в два раза меньше, чем у Ани, сколько монет у каждого ребёнка, если у Вани и Ани одинаковое количество монет?
Составим уравнения по каждой из задач.
- В первом случае нам не известно число яблок у девочки, то есть оно равно Х, мы знаем, что Х в 2 раза меньше 6, то есть 6 = 2Х, следовательно, к этому условию подходит уравнение №2.
- Во втором случае за Х обозначается количество карандашей, тогда количество ручек Х + 2, но при этом мы знаем, что ручек 6, то есть Х + 2 = 6, значит сюда подходит третье уравнение.
- Что касается последней задачи, под номером 3, количество Таниных монет, которое встречается в двух условиях, является искомым неизвестным, тогда у Вани 6 + Х монет, а у Ани 2Х монет, то есть 6 + Х = 2Х – очевидно, что сюда подходит первое уравнение.
Если у вас есть задачи, решаемые с помощью уравнения, к которым необходимо подобрать соответствующее равенство, то составьте уравнение для каждой из задач, а потом уже соотносите то, что получилось у вас, с данными уравнениями.
Усложняем: система уравнений – конфеты
Следующий этап применения буквенных равенств в алгебре – это задачи, решаемые системой уравнений. В них имеется два неизвестных, причём одно из них выражается через другое на основании имеющихся данных. Известно, что у Паши и Кати вместе 20 конфет. Ещё известно, что если бы у Паши было на 2 конфеты больше, то у него было бы 15 конфет, сколько конфет у каждого?
В данном случае мы не знаем ни количество Катиных конфет, ни количество Сашиных конфет, следовательно, у нас два неизвестных, Х и Y соответственно. Вместе с тем, мы знаем, что Y + 2 = 15.
Составив систему, получаем два уравнения:
А дальше действуем по правилам решения систем: выводим Y из второго уравнения, получая Y = 15 – 2, а потом подставляем его в первое, то есть Х + Y = Х + (15 – 2) = 20. Решив уравнение, получаем Х = 7, тогда Y = 20 – 7 = 13. Проверяем правильность решения, подставив Y во второе уравнение: 13 + 2 действительно равно 15, то есть у Кати 7 конфет, а у Паши – 13.
Ещё сложнее: квадратные уравнения и земельный участок
Встречаются также и задачи по алгебре, решаемые квадратным уравнением. В них нет ничего сложного, просто стандартная система преобразовывается в квадратное уравнение в ходе решения. Например, дан участок земли площадью в 6 гектаров (60000 квадратных метров), забор, огораживающий его, имеет длину 1000 метров. Каковы длина и ширина участка?
Составляем уравнения. Длина забора является периметром участка, следовательно, если длину обозначить Х, а ширину Y, то 1000 = 2 * (Х + Y). Площадь же, то есть Х * Y = 60000. Из первого уравнения выводим Х = 500 – Y. Подставляя его во второе уравнение, получаем (500 – Y) * Y = 60000, то есть 500Y – Y 2 = 60000. Решив уравнение, получаем стороны равные 200 и 300 метрам – квадратное уравнение имеет два корня, один из которых зачастую не подходит по условию, например, является отрицательным, тогда как ответ должен быть числом натуральным, поэтому проверку проводить обязательно.
Повторяем: деревья в саду
Закрепляя тему, решим ещё одну задачу. В саду есть несколько яблонь, 6 груш и несколько вишнёвых деревьев. Известно, что общее количество деревьев в 5 раз больше, чем количество яблонь, при этом вишневых деревьев в 2 раза больше, чем яблоневых. Сколько деревьев каждого вида в саду и сколько в саду всего деревьев?
За неизвестное Х, как, наверное, уже понятно, обозначаем яблоневые деревья, через которые мы сможем выразить остальные величины. Известно, что Y = 2X, а Y + Х + 6 = 5Х. Подставив Y из первого уравнения, получаем равенство 2Х + Х + 6 = 5Х, откуда Х = 3, следовательно в саду Y = 3 * 2 = 6 вишнёвых деревьев. Проводим проверку и отвечаем на второй вопрос, складывая получившиеся величины: 3 + 6 + 6 = 3 * 5, то есть задача решена верно.
Контрольная: сумма чисел
Решение задач с помощью уравнения далеко не такое сложное, как кажется на первый взгляд. Главное – не ошибиться в выборе неизвестного и, что ещё важнее, правильно его выразить, особенно если речь идёт о системе уравнений. В завершение даётся последняя задача, гораздо более запутанная, чем представленные выше.
Сумма трёх чисел – 40. Известно, что Х = 2Y + 3Z, а Y = Z – 2 / 3. Чему равны Х, Y и Z?
Итак, начнём с избавления от первого неизвестного. Вместо Х подставляем в равенство соответствующее выражение, получаем 2Y + 3Z + Z + Y = 3Y + 4Z = 40. Далее заменяем также известный Y, получая равенство 3Z – 2 + 4Z = 40, откуда Z = 6. Возвращаясь к Y, находим, что он равен 5.2, а Х, в свою очередь, равен 18. С помощью проверки убеждаемся в истинности выражения, следовательно задача решена правильно.
Заключение
Итак, что же такое задачи, решаемые с помощью уравнения? Так ли они страшны, как кажется на первый взгляд? Ни в коем случае! При должной усидчивости разобраться в них не составляет никакого труда. А однажды поняв алгоритм, в дальнейшем вы сможете щёлкать подобные задачки, даже самые запутанные, как семечки. Главное – внимательность, именно она поможет правильно определить неизвестное и путём решения порой множества уравнений найти ответ.
Решение линейных уравнений. 6-й класс
Разделы: Математика
Класс: 6
Цели урока:
- повторить правила раскрытия скобок и приведения подобных слагаемых;
- ввести определение линейного уравнения с одним неизвестным;
- познакомить учащихся со свойствами равенств;
- научить решать линейные уравнения;
- научить решать задачи на «было − стало».
Оборудование: компьютер, проектор.
Ход урока
I. Проверка предыдущего домашнего задания.
II. Повторение теоретического материала.
- Как найти неизвестное слагаемое? [От суммы отнять известное слагаемое]
- Как найти неизвестное уменьшаемое? [К вычитаемому прибавить разность]
- Как найти неизвестное вычитаемое? [От уменьшаемого отнять разность]
- Как найти неизвестный множитель? [Произведение разделить на известный множитель]
- Как найти неизвестное делимое? [Делитель умножить на частное]
- Как найти неизвестный делитель? [Делимое разделить на частное]
- Как раскрыть скобки, перед которыми стоит знак плюс? [Опустить скобки и этот знак плюс, переписать слагаемые с теми же знаками]
- Как раскрыть скобки, перед которыми стоит знак минус? [Опустить скобки и этот знак минус, переписать слагаемые с противоположными знаками]
- Как выглядит распределительное свойство умножения? [(a+b)∙c=ac+bc]
III. Устные задания по слайдам.
(слайд 2, слайд 3).
1) Раскройте скобки:
3+(х+2); 3-(х+2); 3+(х-7); 3-(х-7); 3+(-х+5); 3-(-х+5); -4(-5-х); 9(
; 9(
; 2(7+9х); 4(2-3х); -6(9-5х); -3(1+4х).
2) Приведите подобные слагаемые:
6b-b; 9,5m+3m; a –
a;
m-m; -4x-x+3; 7x-6y-3x+8y.
3) Упростите выражение:
IV. Новая тема. Решение линейных уравнений.
До сегодняшнего урока мы не умели решать уравнения, в которых неизвестное находилось слева и справа от знака равенства: 3x+7=x+15. Некоторые из нас постоянно забывают правила нахождения неизвестного слагаемого, уменьшаемого, вычитаемого. Сегодня мы постараемся разрешить все эти затруднения.
Уравнение, которое можно привести к виду ax=b, где a и b − некоторые числа (a
Линейные уравнения обладают свойствами:
- Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (стр. 229 учебника).
- Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак (стр. 230 учебника).
Рассмотрим план решения линейного уравнения:
| х-1+(х+2)=-4(-5-х)-5 х-1+х+2=20+4х-5 х+х-4х=20-5+1-2 -2х=14 х=14:(-2) х=-7 Ответ: -7. |
1) раскрыть скобки, если они есть; 2) слагаемые, содержащие неизвестное, перенести в левую часть равенства, а не содержащие неизвестное − в правую; 3) привести подобные слагаемые; 4) найти неизвестный множитель. |
Какими из свойств равенств мы воспользовались для решения уравнения? (вторым)
Рассмотрим примеры уравнений, при решении которых будет удобно воспользоваться и первым свойством.
х+3=
х+5 │∙9 Удобно умножить на наименьшее общее кратное знаменателей дробей.
(

Решение текстовых задач с помощью линейных уравнений
Содержание
Раньше с помощью уравнений вы часто решали текстовые задачи, так как этот способ наиболее универсален и прост для нахождения ответа. В данном уроке:
- сформулируем основные понятия
- разберем алгоритм действий
- узнаем, на что обращать особое внимание
- прорешаем примеры таких задач
Для лучшего понимания темы вспомним, что такое текстовая задача:
Текстовая задача – описание с помощью слов какой-то ситуации, где в итоге требуется что-то из перечисленного:
— дать количественную характеристику какого-то элемента этой ситуации
— установить наличие какого-то отношения между элементами (либо его отсутствие)
— определить вид этого отношения
О том, что такое линейное уравнение, мы говорили в предыдущем уроке.
Решение задачи и математическая модель
Когда от нас требуется решить задачу, мы должны с помощью правильной цепочки действий над имеющимися в задании данными выполнить указанное в ней требование.
Почему важно научиться решать задачи? Часто они описывают какие-то реальные ситуации, которые вам будут попадаться в жизни дальше. И их придется решать.
В процессе нахождения ответов для разнообразных текстовых задач мы можем математическим языком (с помощью цифр) записать все данные. В результате перевода условия задачи из словесного в математический язык и получается уравнение. Это уравнение часто называют математической моделью ситуации.
Математическая модель — это способ описания реальной жизненной ситуации (задачи) с помощью математического языка.
Мы должны не просто составить уравнение по написанному в задаче условию, но и, конечно, решить его. То есть необходимо найти корень составленного уравнения. Но и найденный корень – это, как правило, еще не решение.
В младших классах вы находили ответы для задач попроще. Далее они станут сложнее и сложнее, и с найденным корнем уравнения нужно будет произвести какие-то дальнейшие действия. А потом необходимо обязательно удостовериться, не противоречит ли полученный ответ логике.
Важно: Иногда бывает, что у задачи нет правильного ответа и нужно быть особо внимательным при его формулировке.
Рассмотрим на самом простом примере
Несколько ребят на уроке труда собирали яблоки в саду около школы. Всего они насобирали $29$ кг яблок. Каждый из учеников собрал по $4$ кг яблок. Сколько ребят собирали яблоки в саду около школы?
Составим уравнение, обозначив количество учеников за $x$. Получим: $$4x = 29$$ $$x = frac <29><4>$$$$x = 7,25$$
У нас получилось нецелое число. Но может ли быть количество ребят нецелым числом? Конечно, нет, поэтому такая задача решения не имеет.
Ответ: решения нет.
Разберем другой пример.
Сейчас папе $46$ лет, а сыну $16$. Сколько лет назад папа был старше сына в $3$ раза?
Сначала найдем разницу в возрасте папы и сына: $$46-16 = 30$$ То есть, сын родился, когда папе было $30$ лет. Эта разница в возрасте будет сохраняться всю жизнь. Например, когда ребенку было $5$ лет, то папе все равно было на $30$ лет больше.
Теперь по условию задачи обозначим за $x$ возраст сына в момент, когда он был в 3 раза младше папы. Тогда папе в это же время было $3x$ лет. А разница между $3x$ и $x$, как мы выяснили, равна $30$ годам.
Составим уравнение: $$3x-x = 30$$ Упростим и решим его: $$2x = 30$$ $$x = 15 (лет)$$ Получили ли мы ответ? Еще нет, так как мы нашли только возраст сына. А в задаче требуется узнать, сколько лет назад случилась описанная ситуация. Если сейчас сыну $16$ лет, а тогда ему было $15$, то найдем разницу: $$16-15 = 1 (год)$$ То есть, мы выяснили, что папе было в $3$ раза больше, чем сыну один год назад. Это и будет ответом на нашу задачу.
Ответ: $1$ год назад.
Как видите, в данном задании найденный корень уравнения еще не был нужным нам ответом, и необходимо было решать дальше.
Важно: корень составленного к задаче уравнения – это часто еще не ответ на поставленный в ней вопрос!
Этапы решения заданий с помощью линейного уравнения
Все перечисленные в примерах выше действия для решения задач с помощью линейных уравнений мы можем свести к одному общему алгоритму:
- Выбрать, какую неизвестную величину обозначить за переменную $x$.
- Через введенную переменную выразить остальные неизвестные величины.
- На основе имеющихся данных составить уравнение и решить его.
- При необходимости найти другие неизвестные величины.
- Проанализировать, соответствуют ли полученные результаты смыслу задачи.
- Сформулировать и записать ответ.
Как правило, легче всего составить уравнение с помощью записи данных задачи в таблицу.
К примеру, решим такую задачу: в столовой на одной полке было в $2$ раза больше кружек, чем на другой. Перед очередным классом с первой полки взяли $16$ кружек, но потом на другую поставили $4$. В итоге на обеих полках оказалось одинаковое количество кружек. Найдите, сколько на каждой полке кружек было первоначально.
Решение. Обозначим исходное количество кружек на второй полке за $x$ и составим таблицу:
| Было | Стало | |
| $1$-я полка | $2x$ | $2x-16$ |
| $2$-я полка | $x$ | $x+4$ |
Так как по условию задачи кружек на обеих полках стало поровну, то $$2x-16 = x+4$$ Упростим и решим, перенеся $x$ влево, а $16$ вправо с противоположным знаком: $$2x-x = 16+4$$ $$x=20$$ Так мы нашли исходное количество кружек на второй полке. Тогда на первой полке было: $$20times 2 = 40 (кружек)$$
Ответ: на первой полке было $40$ кружек, а на второй $20$.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/627069
http://obrazavr.ru/algebra/7-klass-algebra/vyrazheniya-tozhdestva-uravneniya/uravneniya-s-odnoj-peremennoj/reshenie-tekstovyh-zadach-s-pomoshhyu-linejnyh-uravnenij/
[/spoiler]
|
Что значит “обратная задача” в математике (1, 2, 3, 4 класс)? Как записать и решить обратную задачу, пример? В математике обратная задача составляется на основании какой-либо имеющейся задачи. В обратных задачах искомые данные уже известны. Требуется найти одну из величин, которые были даны в условии исходной задачи. Пример 1 Исходная задача. В магазине яблоки стоят 120 рублей за 1 килограмм, а груши стоят 150 рублей за 1 килограмм. Требуется узнать, на сколько груши дороже яблок. Для решения этой задачи нужно найти разницу между 2 числами – стоимостью груш и стоимостью яблок. 150 – 120 = 30 (руб.) Таким образом, груши дороже яблок на 30 рублей. _ Обратная задача. Здесь нам будет известна разница в стоимости фруктов, то есть 30 рублей. Будем находить либо стоимость яблок, либо стоимость груш – то есть можно составить 2 разных обратных задачи. 1) Яблоки стоят 120 рублей, а груши на 30 рублей дороже. Сколько стоят груши? Решение: 120 + 30 = 150 (руб.) 2) Груши стоят 150 рублей, а яблоки на 30 рублей дешевле. Сколько стоят яблоки? Решение: 150 – 30 = 120 (руб.) Пример 2 Исходная задача. Покупатель хочет купить 500 грамм говядины, которая стоит 200 рублей за 1 килограмм. Сколько он должен заплатить? Для решения данной задачи нужно вспомнить соотношение между граммами и килограммами. 1 килограмм = 1000 грамм. 500 грамм – это ровно половина от 1000 грамм (или 1 килограмма): 500 / 1000 = 1/2. Таким образом, покупатель заплатит не 200 рублей, а только половину: 200 / 2 = 100 (руб.) _ Обратная задача. Здесь нам будет известна цена покупки, то есть 100 рублей. Можно найти, например, стоимость за 1 килограмм. Вот формулировка подобной задачи: Покупатель купил 500 грамм говядины за 100 рублей. Сколько стоит 1 килограмм говядины? Решение: 1) 1 килограмм – это 1000 грамм. 1000 / 500 = 2, то есть 1 килограмм будет в 2 раза больше, чем 500 грамм. 2) Стоимость 1 килограмма составляет 100 * 2 = 200 (руб.) модератор выбрал этот ответ лучшим Математический термин “обратная задача” включает два слова. С существительным задача все понятно. Возникает вопрос: что значит обратная. Данное прилагательное по отношению к задаче можно определить как противоположная или ведущая назад, к исходному состоянию. Для того, чтобы составить обратную задачу, нужно иметь задачу исходную. И исходную задачу необходимо решить. Это нужно для того, чтобы использовать полученный результат в качестве исходных данных для обратной задачи. Если сказать еще проще, то то, что дано ( известно ) в исходной задача, в обратной ей нужно будет искать. А решение исходной задачи станет тем, что известно по условию обратной задачи. Это мое определение термину “обратная задача”, простого определения для начальной школы я не нашла. Проще пояснить на примерах. Исходная задача: Мама купила 5 пирожных и 7 кексов к чаю. Сколько всего кексов и пирожных купила мама? Решение 5+7=12 (шт.) выпечки купила мама. Обратная ей задача: Обратных задач можно в этом случае составить две: 1) Мама всего купила 12 пирожных и кексов к чаю, из них 5 пирожных. Сколько кексов купила мама? Решение 12-5=7 (к.) купила мама. 2) Мама всего купила 12 пирожных и кексов к чаю, из них 7 кексов. Сколько пирожных купила мама? Решение 12-7=5 (п.) купила мама. Марина Вологда 3 года назад Обратная задача – это такая задача, в которой все искомые величины уже известны. Из этих известных величин и составляем обратную задачу. Например, нам дана задача: В автопарк заехало три красных машины и пять белых. Сколько всего машин заехало в автопарк? Решение: 3+5 = 8 машин. Составляем обратную задачу: 1) Сколько машин заехало в автопарк красного цвета, если известно, что всего машин было 8. А белых машин было 5. Решение: 8-5 = 3 машины красного цвета. 2) Известно, что в автопарк заехало 8 машин. Из них три были красного цвета. Остальные машины были белые. Сколько машин белого цвета? Решение: 8-3 = 5 машин белого цвета. Алиса в Стране 3 года назад Многие из нас, наверное, уже забыли, что такое обратная задача, но на самом деле ничего сложного в ней нет. Приведу пример. Допустим, у нас есть расстояние (путь) и время, за которое человек его прошел, все мы знаем, как просто определить скорость, нужно расстояние (путь) разделить на время. Так вот к этой элементарной задачке можно составить две обратные задачи: на определение пути (расстояния), если известна скорость и время (чтобы решить эту задачу, нужно скорость умножить на время): Второй обратной задачей будет задача на определение времени, если известно расстояние (путь) и скорость (нужно путь поделить на скорость): Не знаю, кто их назвал “обратными” потому что задача это всегда, как минимум, поиск третьего неизвестного по двум известным, и какая разница какое из них будет неизвестным. Составить их проще простого, просто поменять неизвестное с известным, ну и вероятно математическое действие будет другое – вместо сложения – вычитание, вместо деления – умножение (как и наоборот) Вот пример. У Васи было две конфеты, Валя дала Васе еще три конфеты, сколько у Васи конфет теперь? Ответ – пять. Якобы обратная задача. У Васи было пять конфет, две из которых были его, сколько конфет ему дала Валя что бы у него получилось пять? Ответ – три. Zummy out off 3 года назад Обратная задача в математике – это такая задача, которая составляется по исходной задаче, но ответ исходной задачи включается в условие обратной задачи, а требуется найти то, что было одним из условий исходной задачи. Составление обратных задач тренирует «мозги» для решения задач в математике. Пример составления обратной задачи. Исходная задача. У Маши было 20 рублей, она купила тетрадь за 12 рублей. Сколько денег осталось у Маши? Решение: 20-12=8. Ответ: 8 рублей осталось у Маши. Обратная задача. В условие задачи надо включить сумму сдачи 8 руб. Составляем задачу: Маша купила тетрадь за 12 руб и у неё осталась сдача 8 руб. Сколько денег было у Маши до покупки тетради? Решение: 12+8=20. Ответ: 20 рублей было у Маши. Бархатные лапки 3 года назад Обратная задача составляется на основе уже имеющейся решенной задачи. В обратной задаче требуется узнать то, что было известно в нашей задаче. Объясним, что такое обратная задача, на примере простейшей задачки для начальных классов. У Иры 10 яблок, у Маши 5 яблок. Нужно найти, сколько яблок у обоих девочек вместе. Это наша задача, решается она так: общее количество яблок равно: яблоки Иры плюс яблоки Маши = 5 + 10 + 15 Обратная задача к этой задаче: у двух девочек, Иры и Маши 15 яблок, сколько яблок у Иры, если у Маши 5 яблок. Решение: 15 – 5 = 10 яблок у Иры. Также обратную задачу можно составить и так: у Иры и Маши 15 яблок, сколько яблок у Маши, если у Иры 10 яблок. Решение: 15 – 10 = 5, у Маши 5 яблок. KritikSPb 4 года назад Обратная задача в математике требует найти то, что было известно в первоначальной задаче. То есть обязательным условием составления обратной задачи является наличие прямо задачи, от которой и отталкиваются для составления обратной. Например, первоначально известно, что человеку нужно дойти из дома до магазина. Расстояние 10 км. Идёт он со скоростью 5 км в час. Через сколько времени он будет на месте? Решение: 10 / 5 = 2 часа. А теперь обратная задача: За два часа человек дошёл от дома до магазина. Определите расстояние, если известно, что скорость человека 5 км в час. Решение: 2 * 5 = 10 км. Для составления обратной задачи необходимо решить исходную. Бекки Шарп 3 года назад Обратные задачи бывают в разных науках и в математике тоже. Обратная составляется на основании уже полученных данных. Когда то что требовалось найти уже известно. Например. У Миши было 7 яблок, а у Васи 8 яблок. Сколько всего было яблок у мальчиков. Решение: 7+8=15 (яблок) Обратная задача к нашей будет такая. Всего у Миши и Васи 15 яблок. У Миши – 7 яблок. Сколько у Васи яблок? Решение: 15-7=8 (яблок) Еще одна обратная задача к нашей. У Миши и Васи 15 яблок, у Васи – 8. Сколько яблок у Миши? Решение: 15-8=7 (яблок) Val111111 4 года назад Обратная задача- это когда то, что требовалось найти, теперь известно, а то, что было в дано нужно найти. Пример, есть три яблока. Два забрали. Сколько осталось? Обратная задачка: Забрали два яблока, осталось одно, сколько было? TheSun 3 года назад В обратной задаче неизвестным является дано, именно его и нужно найти. Но, при этом известен результат. Рассмотрим на примере. У Маши было 4 синих мяча и 3 зелёных мяча. Сколько всего у Маши мячей? 4+3=7 (шт.) мячей у Маши. Теперь обратная задача. У Маши всего 7 мячей. Из них синих мячей 4, а остальные мячи зелёного цвета. Сколько у Маши зелёных мячей? 7-4=3 (шт.) зелёных мяча у Маши. Знаете ответ? |
ЗАДАЧИ НА СООТНОШЕНИЕ БЫЛО – СТАЛО. Задача №1. Примеры | МАТЕМАТИКА 6 класс
Канал видеоролика: Математика online
Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

ЗАДАЧИ НА ВСТРЕЧНОЕ ДВИЖЕНИЕ. Задача №1. Примеры | МАТЕМАТИКА 6 класс
Математика online

ЗАДАЧИ НА СОВМЕСТНУЮ РАБОТУ. Задача №1. Примеры | МАТЕМАТИКА 6 класс
Математика online

ЗАДАЧИ НА СОВМЕСТНУЮ РАБОТУ. Задача №2 (ДВЕ ТРУБЫ НАПОЛНЯЮТ БАК). Примеры | МАТЕМАТИКА 6 класс
Математика online

ЗАДАЧИ НА РАБОТУ. Задача №2. Примеры | МАТЕМАТИКА 5 класс
Математика online
Облегчи жизнь другим ученикам – поделись! (плюс тебе в карму):
11.04.2020
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
Тема №8147
Решение задач по математике с помощью уравнений
Решение задач с помощью уравнений.
Чтобы решить задачу с помощью уравнения, надо:
1. Записать краткое условие в виде схемы, таблицы или произвольным образом;
2. Обозначить буквой х ту величину, которую надо найти в главном вопросе задачи; если таких величин несколько, то буквой х обозначается меньшая из них;
3. Записать все условия задачи с помощью х;
4. Составить и решить уравнение;
5. Ответить на главный вопрос задачи (найти все величины, о которых идет речь в главном вопросе).
6. Выполнить проверку решения;
7. Записать ответ.
Соотношение между величинами.
Задача (образец). Три школы получили 70 компьютеров. Вторая школа получила на 6 компьютеров больше первой, а третья – на 10 компьютеров больше второй. Сколько компьютеров получила каждая школа?
х 1 – ?
х+6 2 – ? на 6 к больше, чем 1
х+6+10 3 – ? на 10 к больше, чем 2
Пусть х к получила 1 школа, тогда (х+6)к получила 2 школа, (х+6+10)к получила 3 школа. Известно, что три школы получили 70 компьютеров. Составляем уравнение.
х+(х+6)+(х+6+10)=70
х+х+6+х+6+10=70
х+х+х=70-6-6-10
3х=48
х=48:3
х=16 (1 школа)
Сколько компьютеров получила 2 школа?
16+6=22 (к)
Сколько компьютеров получила 3 школа?
22+10=32 (к)
Ответ: 1 школа-16к, 2 школа-22к, 3 школа-32к.
Задачи для самостоятельного решения.
1 уровень.
1. Две бригады хлопкоробов собрали вместе 20,4ц хлопка за день. При этом первая бригада собрала на 1,52ц больше второй. Сколько хлопка собрала каждая бригада?
2. Два комбайнера убрали за день 64,2га. Сколько убрал каждый комбайнер, если первый убрал на 2,8га меньше второго?
3. Луч ОМ разделил развернутый угол АОВ на два угла АОМ и МОВ. Градусная мера угла АОМ в 3 раза больше градусной меры угла МОВ. Найдите, сколько градусов содержится в каждом из этих углов.
4. Новому заводу потребовались 840 рабочих следующих специальностей: токарей, слесарей, фрезеровщиков. При этом токарей потребовалось втрое, а слесарей вдвое больше, чем фрезеровщиков. Сколько токарей потребовалось для завода?
5. В товарном составе 60 крытых вагонов, цистерн и платформ. Цистерн на 4 меньше, чем платформ, а платформ на 22 меньше, чем крытых вагонов. Сколько цистерн в составе?
6. В трех ящиках было 76кг помидоров. Во втором ящике было в 2 раза больше помидоров, чем в первом, а в третьем — на 8кг больше, чем в первом. Сколько помидоров было в каждом ящике?
7. Периметр прямоугольника 84дм. Его ширина на 6дм меньше длины. Найдите стороны и площадь прямоугольника.
8 Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет каждому из них?
9. Кусок электропровода длиной 68м разрезали на четыре части. Первые две части были одинаковой длины, третья – в 2 раза больше первой, а четвертая — на Зм
длиннее второй. Какова длина каждой части?
2 уровень.
1. Для перевозки картофеля выделили две машины. На первую машину погрузили т 3 раза больше картофеля, чем на вторую. Сколько центнеров картофеля погрузили на каждую машину, если на вторую погрузили на 41,4ц меньше, чем на первую?
2. Шаг Пети на 12см длиннее шага Толи. Но 4 шага Пети короче 6 шагов Толи на 54см. Найдите длину шага каждого мальчика.
3. Во второй день со склада выдали в 2 раза больше проволоки, чем в первый день, а в третий — в 3 раза больше, чем в первый. Сколько килограммов проволоки выдали за три дня, если в первый день выдали на 30кг меньше, чем в третий?
4. Газовая туристская плитка и два баллона имеют массу 7кг. Масса плитки меньше массы баллона на 2кг. Найдите массу баллона.
3 уровень
1. Ребята собрали 65кг цветного металлического лома. Меди и алюминия вместе было собрано на 1кг больше, чем цинка, а отдельно меди было на 15кг больше, чем алюминия. Сколько килограммов каждого металла было собрано?
2. В клетке сидят фазаны и кролики. У них 19 голов и 62 ноги Сколько фазанов и сколько кроликов в клетке?
Изменение величин (было — стало).
Задача (образец). В двух сараях сложено сено, причем в первом сарае сена в 3раза больше, чем во втором. После того как из первого сарая увезли 20т сена, а во второй привезли 10т, в обоих сараях сена стало поровну. Сколько тонн сена было в каждом сарае?
|
Было |
Изменение |
Стало |
|
|
1сарай |
? 3х т в 3раза больше, чем во 2сарае |
-20 |
? (3х-20)т |
|
2 сарай |
? х т |
+10 |
? (х+10)т |
Пусть х т сена было во 2 сарае, тогда 3х т сена было в 1 сарае. После того как из первого сарая увезли 20т сена, а во второй привезли 10т, в обоих сараях сена стало поровну. Составляем уравнение.
3х-20=х+10
3х-х=10+20
2х=30
х=30:2
х=15 (2 сарай)
Сколько тонн сена было в 1 сарае?
15*3=45 (т)
Ответ: 1 сарай-45т
2 сарай-15т
Задачи для самостоятельного решения.
1 уровень.
1. В первом бидоне в 3 раза больше молока, чем во втором. Если из первого бидона перелить 20 л во второй, то молока в бидонах будет поровну. Сколько молока было в каждом бидоне?
2. Длина отрезка АВ на 2см больше, чем длина отрезка СВ. Если длину отрезка АВ
увеличить на 10см, а длину отрезка СD увеличить в 3 раза, то получатся равные результаты. Найдите длины данных отрезков.
3. Одно число больше другого в 4,5 раза. Если от большего числа отнять 54, а к меньшему прибавить 72, то получатся равные результаты! Чему равны эти числа?
4. На первом катере было в 2 раза больше людей, чем на втором. Когда на ближайшей пристани с первого катера сошло 98 человек, а со второго 16 человек, то на обоих катерах людей стало поровну. Сколько людей было на каждом катере первоначально?
5. В одном элеваторе было зерна й 3 раза больше, чем в другом. Из первого элеватора вывезли 960т зерна, а во второй привезли 240т, после чего в обоих элеваторах зерна стало поровну. Сколько зерна было первоначально в каждом элеваторе?
6. На железнодорожной станции стояли два состава, причем в одном из них было в 2 раза больше вагонов, чем в другом. Когда от первого состава отцепили 14 вагонов и прицепили их ко второму составу, то вагонов в составах стало поровну. Сколько вагонов было в каждом составе?
7. В одном куске в 2 раза больше полотна, чем в другом. Когда от меньшего куска отрезали !5м, от большего -— 45м. то полотне в обоих касках осталось погювну Сколько полотна было в каждом куске’7
2 уровень.
1. В двух кусках было поровну шелковой ткани. Когда от одного куска отрезали 10м, а от другого 40м, то в одном куске осталось вдвое больше ткани, чем в другом. Сколько ткани было в каждом куске9
2. . В двух бригадах было поровну рабочих. Когда в первую бригаду поступило 8 человек, а из второй ушли 2 человека, то в первой бригаде стало в 3 раза больше рабочих, чем во второй. Сколько рабочих было в каждой бригаде?
3. На станции стояло два товарных состава. Число вагонов в первом составе в 1,5 раза меньше числа вагонов во втором составе. От первого состава отцепили 5 вагонов и прицепили их ко второму составу. Теперь во втором составе стало вагонов в 2 раза больше, чем в первом. Сколько вагонов было в каждом составе?
4. В одной пачке было в 2,5 раза больше тетрадей, чем во второй. Когда из второй пачки переложили в первую 5 тетрадей, то во второй пачке стало тетрадей в 3 раза меньше, чем в первой. Сколько тетрадей было в каждой пачке?
5. На одной полке было в 3 раза больше книг, чем на другой. Когда с первой полки сняли 8 книг, а на другую положили 5 книг, то на второй полке стало на 17 книг меньше, чем на первой. Сколько книг было на каждой полке?
6. Для помощи в уборке урожая было выделено два отряда ребят. В одном отряде было в 3 раза больше ребят, чем во втором. Когда во второй отряд добавили еще 12 человек, то в двух отрядах стало 76 ребят. Сколько стало ребят во втором отряде?
1, На одной полке 42 книги, а на другой 34. Со второй полки сняли несколько книг, а с первой столько, сколько осталось на второй. После этого на первой полке осталось 12 книг. Сколько книг сняли со второй полки?
Задачи на движение.
Задача (образец) Два пешехода вышли одновременно навстречу друг из двух поселков и встретились через 3часа. Расстояние между поселками 30км. Найдите скорость каждого пешехода, если у одного она на 2км/ч меньше, чем у другого.
|
V (скорость) |
t (время) |
S (расстояние) |
|
|
1 пешеход |
? х км/ч |
3ч |
3х км |
|
2 пешеход |
? (х-2) км/ч на 2км/ч меньше, чем у 1 пешехода |
3ч |
3(х-2) км |
Пусть х км/ч скорость 1пешехода, тогда (х-2) км/ч скорость 2 пешехода. Известно, что они вместе прошли 30км. Составляем уравнение.
3х+3(х-2)=30
3х+3х-6=30
3х+3х=30+6
6х=36
х=36:6
х=6 (скорость 1пешехода)
Какова скорость 2 пешехода?
6-2=4 (км/ч)
Ответ: Скорость 1 пешехода-6км/ч
Скорость 2 пешехода-4км/ч
Задачи для самостоятельного решения.
1 уровень.
1. Два велосипедиста отправились одновременно навстречу друг другу из двух пунктов, расстояние между которыми 60 км, и встретились через 2 ч. Определите скорость каждого велосипедиста, если у одного она на 2 км/ч больше, чем у другого.
2. Два пешехода вышли одновременно навстречу друг другу из двух поселков и встретились через 3 ч. Расстояние между поселками 30 км. Найдите скорость каждого пешехода, если у одного она на 2 км/ч меньше, чем у другого.
3. Мотоциклист ехал 3 л по проселочной дороге и 0,5 ч по шоссе; всего он проехал 110 км. Скорость мотоциклиста на шоссе была на 10 км/ч больше, чем на проселочной дороге. С какой скоростью ехал мотоциклист по проселочной дороге, и с какой — по шоссе?
4. Велосипедист ехал 2 ч по лесной дороге и 1,5 ч по шоссе; всего он проехал 48 км. Скорость велосипедиста на шоссе была на 4 км/ч больше, чем на лесной дороге. С какой скоростью ехал велосипедист по шоссе, и с какой — по лесной дороге?
5. Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если они встретились через 2,5 ч после своего выхода.
6. Из двух пунктов, расстояние между которыми 210 км, вышли одновременно два электропоезда. Скорость одного из них на 5 км/ч больше скорости другого. Найдите скорость каждого электропоезда, если они встретились через 2 ч после своего выхода.
2 уровень.
1. Из Смоленска в Москву вышел поезд со скоростью 70 км/ч. Спустя. 1 ч 40 мин из Москвы в Смоленск отправился поезд, скорость которого 60 км/ч. Через сколько часов после выхода поезда из Смоленска произойдет встреча, если расстоянии между городами 420 км?
2. Из поселка в город выехал велосипедист. Спустя 44 мин вслед за ним выехал мотоциклист, скорость которого на 30 км/ч больше скорости велосипедиста. Через 36 мин после своего выхода мотоциклист, обогнав велосипедиста, находился от него на расстоянии 7 км. Найдите скорость велосипедиста.
3. Из пункта А в пункт В выехала грузовая машина. Спустя 1,2 ч вслед за ней выехал автобус. Через 0,8 ч после своего выхода он отставал от машины на 24 км. Найдите скорость автобуса, если известно, что она больше скорости грузовой машины на 30 км/ч.
Движение по воде.
Задача (образец).
Лодка может проплыть расстояние между двумя селениями, стоящими не берегу реки, за 4ч по течению реки и за 8ч против течения. Скорость течения реки 2 км/ч. Найдите собственную скорость лодки и расстояние между селениями.
|
v (скорость) |
t (время) |
s (расстояние) |
|
|
По течению реки |
(х+2) км/ч |
4ч |
4(х+2) км одинаковое |
|
Против течения реки |
(х-2) км/ч |
8ч |
8(х-2) км |
V собственная ? Х км/ч
V течения реки 2 км/ч
V по течению реки = V собственная + Vреки
V против течения реки = Vсобственная – V реки
Пусть х км/ч – собственная скорость, (х+2)км/ч скорость по течению реки,(х-2) км/ч скорость против течения реки.
Известно, что расстояние по течению и против течения одинаковое.
Составляем уравнение.
4(х+2) = 8(х-2)
4х+8 = 8х-16
4х-8х = -16-8
-4х = -24
х = -24:(-4)
х = 6 (собственная скорость)
Каково расстояние между селениями?
(6+2)*4=32(км)
Ответ: Собственная скорость 6 км/ч, Расстояние 32 км.
Задачи для самостоятельного решения.
1 уровень.
1. Лодка может проплыть расстояние между двумя селениями, стоящими на берегу реки, за 4 ч по течению реки и за 8 ч против течения. Скорость течения реки 2 км/ч. Найдите собственную скорость лодки и расстояние между селениями.
2. Лодка проплыла от одной пристани до другой против течения реки за 4 ч. Обратный путь занял у нее 3 ч. Скорость течения реки 1км/ч. Найдите собственную скорость лодки расстояние между пристанями.
3. По течению реки катер прошел за 7 ч столько же километров, сколько он проходит за 8 ч против течения. Скорость катера в стоячей воде 30 км/ч. Найдите скорость течения реки.
4. Расстояние по реке между пристанями равно 45 км. Одновременно навстречу друг другу вышли два катера, собственные скорости которых равны. Через 1,5 ч они встретились. Найдите собственные скорости катеров, если скорость течения реки равна 3 км/ч.
5. Из двух пунктов реки, расстояние между которыми равно 36 км, навстречу друг другу движутся две моторные лодки. Лодка, идущая по течению, собственная скорость которой 18 км/ч, до встречи шла 0,5 ч, другая лодка, собственная скорость которой равна 20 км/ч, до встречи шла 1,5 ч. Найдите скорость течения реки.
2 уровень.
1. Из двух пунктов реки навстречу друг другу движутся две моторные лодки, собственные скорости которых равны. Скорость течения реки равна 2 км/ч. До встречи лодка, идущая по течению, шла 0,9 ч, а другая лодка шла 1 ч. Найдите собственную скорость лодок, если лодка, идущая по течению, прошла на 2 км больше, чем другая лодка.
2. Из двух пунктов реки одновременно навстречу друг другу вышли две моторные лодки. Через 1,2 ч они встретились. Собственная скорость лодки, которая шла по течению реки, равна 18 км/ч, а лодки, которая шла против течения реки, равна 16 км/ч. До встречи одна лодка прошла на 9,6 км больше другой. Найдите скорость течения реки.
Работа по плану и фактически.
Задача (образец). Один автомат упаковывает в минуту на 2 пачки печенья больше, чем второй. Первый автомат работая 10 мин, а второй – 20 мин. Всего за это время было упаковано 320 пачек печенья. Сколько: пачек в минуту упаковывает каждый автомат?
|
Производительность |
Время |
Работа |
|
|
1 автомат |
?(х+2)п на 2 п больше, чем 2 |
10 мин |
? 10(х+2)п |
|
2 автомат |
? Х п |
20 мин |
? 20 х п |
Производительность – это работа за единицу времени.
Пусть х п производительность 2 автомата, тогда (х+2)п производительность 1 автомата.
Известно, что всего было упаковано 320 пачек. Составляем уравнение.
10(х+2)+20х = 320
10х+20+20х = 320
10х+20х = 320-20
х = 300:30
х = 10 (производительность 2 автомата)
Какова производительность 1 автомата?
10+2 = 12(п)
Ответ: 1 автомат упаковывает в минуту 12 пачек,
2 автомат упаковывает в минуту 10 пачек.
Задачи для самостоятельного решения.
1 уровень.
1. По плану тракторная бригада должна была вспахать поле за 14 дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану, и поэтому закончила пахоту за 12 дней. Сколько гектаров было вспахано? Найдите площадь поля.
2. Заказ по выпуску машин завод должен был выполнить за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана, а поэтому выполнил заказ за 18 дней. Сколько машин выпустил завод?
3. Колхоз должен был закончить сев за 5 дней. Колхозники засевали в день на 20 га больше, чем предполагалось по плану, а поэтому закончили сев за 4 дня. Сколько гектаров должен был засеять колхоз?
4. Заготовленного сена хватило на 180 дней. Если бы расход сена уменьшился бы на 32ц в день, то его хватило бы на 192 дня. Сколько центнеров сена было заготовлено на 1 день? Можно ли найти массу всего заготовленного сена?
5. Заготовленной кормовой свеклы хватит на 174 дня. Если бы расход свеклы увеличился на 12ц в день, то ее хватило бы на 168 дней. Сколько центнеров свеклы было заготовлено на 1 день? Можно ли узнать, сколько всего заготовлено свеклы?
6. От города до поселка автомобиль доехал за Зч. Если бы он увеличил скорость на 25 км/ч, то проехал бы это расстояние за 2ч. С какой скоростью ехал автомобиль и чему равно расстояние от поселка до города?
7. От турбазы до станции турист доехал на велосипеде за Зч. Пешком он смог бы пройти это расстояние за 7ч. Известно, что пешком он идет со скоростью на 8 км/ч меньшей, чем едет на велосипеде. С какой скоростью ехал турист и чему равно расстояние от турбазы до станции?
8. Турист шел от турбазы до станции со скоростью 6 км/ч. Если бы он шел со скоростью 4 км/ч, то затратил бы на дорогу на 1ч больше. Чему равно расстояние от турбазы до станции?
9. Грибник, выйдя из леса, направился к деревне. Он шел со скоростью 4 км/ч. Если бы он шел со скоростью 5 км/ч, то затратил бы на дорогу на 4 ч меньше. Какое расстояние прошел грибник от леса до деревни?
2 уровень.
1. Заказ по выпуску машин завод должен был выполнить за 20 дней. Но уже за 18 дней завод перевыполнил план на 6 машин, так как ежедневно выпускал по 3 машины сверх плана. Сколько машин выпустил завод?
2. Бригада рабочих должна была выполнить заказ за 5 дней. Ежедневно превышая норму на 18 деталей, она за 3,5 дней работы не только выполнила задание, но и изготовила 27 деталей сверх плана. Сколько деталей изготовила бригада?
3. Чтобы читать книгу в библиотеку, ученик должен был читать ежедневно по 40 страниц, но он читал в день на 15 страниц меньше и сдал книгу на 6 дней позже срока. За сколько дней ученик должен был прочитать книгу?
4. Путь от А до В автомобиль проезжает с определенной скоростью за 2,5 ч. Если он увеличит скорость на 20 км/ч, то за 2 ч пройдет путь, на 15 км больший, чем расстояние от А до В. Найдите – расстояние от А до В.
- 1
- 2
- 3
- 4
- 5
Категория: Математика | Добавил: Просмотров: 1 | Рейтинг: 3.5/2




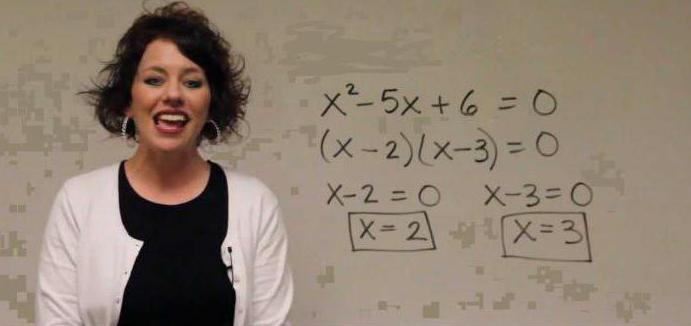

 ; 9(
; 9( ; 2(7+9х); 4(2-3х); -6(9-5х); -3(1+4х).
; 2(7+9х); 4(2-3х); -6(9-5х); -3(1+4х). a;
a;  m-m; -4x-x+3; 7x-6y-3x+8y.
m-m; -4x-x+3; 7x-6y-3x+8y. х+3=
х+3= х+5 │∙9 Удобно умножить на наименьшее общее кратное знаменателей дробей.
х+5 │∙9 Удобно умножить на наименьшее общее кратное знаменателей дробей.





