Как решать задачи с процентами найти процент

Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни.

Пока такие задачки остаются оторванными от реальности строчками в учебнике, их бывает сложно понять и тем более решить. Чтобы стало понятнее, мы вам сейчас покажем примеры из обычной жизни, где вам могут встретиться проценты. А еще просто и доступно объясним, как решать задачи на проценты. И все у вас станет на свои места.

Задачи про проценты вокруг нас

Давайте оглядимся по сторонам: значения в процентах указаны на упаковках с любыми продуктами. Значок процента «%» смотрит на нас с рекламных плакатов скидок и распродаж. В новостях проценты сразу бросаются в глаза, когда речь идет о повышении цен на товары или коммунальные услуги. Разве вы сможете расшифровать все эти послания, если не научитесь решать задачи с процентами? Но вы, конечно, научитесь – мы в вас верим.

А вот такая ситуация: вы купили что-нибудь через интернет и получили извещение от ближайшего почтового отделения. Или сами собираетесь послать подарок другу в другой город. Вам обязательно надо уметь разбираться с процентами, чтобы узнать, сколько денег почта захочет получить за свои услуги по пересылке.

Или возьмем банковские кредиты и ипотеку. Банки в договорах всегда пишут мелкими буквами всякие вещи, которые полезно понимать. Например, какой процент по кредиту придется заплатить банку кроме тех денег, которые вы у него «одолжили» и обязаны вернуть.

А самый близкий школьникам пример связан с ЕГЭ. Каждый год после экзаменов публикуют официальную статистику. В которой немало задействованы и проценты. И эти проценты имеют прямое отношение к будущим выпускникам. Например, процент ребят, сдавших экзамен по математике на «хорошо» и «отлично» косвенно говорит о том, сколько абитуриентов с высокими баллами могли подать документы в вузы на технические специальности. А еще на программирование, прикладную математику и т.п. Чем их больше, тем выше конкурс. Если сравнивать их результаты со своими оценками, можно прикинуть собственные шансы на поступление.

Что такое процент?

Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.

Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.

Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.

Типы задач на проценты

Раз мы уже договорились, что задачи на проценты – это задачи на дроби, такой тактики будем придерживаться и дальше.

Тип 1: Находим процент (дробь) от числа.

• Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
• Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.

Тип 2: Находим число по его проценту (дроби).

• Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
• Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

• Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
• Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.

Тип 4: Увеличиваем число на процент.

• Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
• Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.

Тип 5: Уменьшаем число на процент.

• Задача. Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
• Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.

Тип 6: Задачи на простые проценты.

• Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
• Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.

Тип 7: Задачи на сложные проценты.

• Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
• Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% – процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)^у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)³ = 38021,875 – искомая сумма.

Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще. Давайте решим задачу №3 про класс и процент девочек в нем, составив пропорцию.

• Решение. Обозначим искомый процент девочек в классе как х, общее количество учеников примем за 100%. Пропорция выглядит так:

30 – 100%
14 – х%

Перемножим крест накрест левую и правую части пропорции и получим, что 30* х = 14 * 100 («30 относится к х также, как 14 относится к 100»). Откуда найти х уже совсем несложно: х = 14 * 100/30 = 47%.

Задачи на проценты с решением

Давайте решим несколько задач для подготовки к ЕГЭ. Как вы сами видите, решать их совсем несложно. Сейчас просто закрепим материал.

Задача 1. После открытия торгов на бирже в понедельник акции некой компании выросли в цене на неизвестное количество процентов. А во вторник на то же самое количество процентов упали в цене. В итоге они подешевели на 4% по отношению к своей первоначальной стоимости в понедельник. На какой процент акции этой компании поднимались в цене в понедельник?

Решение. Пускай первоначальная стоимость акций это 1. В понедельник акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х). После чего они стали дешевле на 4%, т.е. стали стоить 0,96.

Отсюда 1 + х – х * (1 + х) = 0,96 ↔1 – х² = 0,96 ↔ х² = 0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.

Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте, на сколько процентов пять пар брюк стоят дороже, чем одно пальто.

Решение. Исходя из условия задачи, стоимость четырех пар брюк – это 92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это 23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 = 115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.

Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.

Решение. Из условия следует, что общий доход семьи находится в прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100% – 67%  – 6% = 27%.

Задача 4. В емкости находится 5 литров водного раствора с концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды. Раствор какой концентрации (с каким процентным содержанием вещества) получился после этого?

Решение. Опишем концентрацию вещества в растворе такой формулой: С = Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6 литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости увеличился. Но концентрация вещества понизилась (его объем остался неизменным). Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% = 0,6 /12 * 100% = 5%.

Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Решение. Исходя из условия, в абрикосах 10% питательного вещества, а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять 19/0,1 = 190 килограммов свежих абрикосов.

Заключение

Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить воображение, вы сможете щелкать такие задачки как орешки.

Вы даже можете составить задачу на проценты сами по нашим образцам. Кстати, будет очень хорошо, если вы так и поступите. Можете оставить нам свои задачи в комментариях – пускай другие наши читатели решат ваши задачи. А вы сможете решить те, что придумают они. Чтобы задач для подготовки к экзаменам получилось больше, расскажите про эту статью своим друзьям в социальных сетях.

Вот увидите, задачи на проценты вам придется решать еще много раз даже после того, как вы закончите школу. Они встречаются в физике, химии, биологии. Да и в повседневной жизни умение решать их может не раз пригодится. Не бойтесь сложных задач – мы всегда поможем вам найти к ним ключ.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

У очень многих детей и взрослых проблемы с задачами на проценты. Это одна из тех тем, которые хуже всего усваивают дети в школе. И в то же время — это одна из немногих тем, которая реально пригодится в жизни. Потому что проценты окружают нас в жизни везде. На кухне (рецепты, 7 % уксус и так далее), в магазинах (скидка 30% и т.д.), на работе (налог на доходы 13% и т.д.), в финансах (кредит под 8,5% годовых или депозит под 3% и так далее).

Короче говоря, с процентами надо уметь жить. Тем более считать их несложно. В мире есть всего три вида задач на проценты. Все остальные задачи со сложными процентами и так далее — это их производные. Если научиться решать простые три типа задач на проценты, то и с остальными проблем не будет.

Нахождение процентов от числа

Проще всего учиться не на яблоках и чем-то абстрактном, а на деньгах. Поэтому вот вам первая задача.

Муж заработал 6000 ₽, отдал жене, а жена в первый же день потратила 40% зарплаты в магазине. 25% от остатка отнесли в банк на погашение кредита за телевизор. Сколько денег осталось?

Всегда, когда мы работаем с процентами, мы должны сначала перевести их в части. Чтобы это сделать, делим на 100%, то есть 40% = 0,4.

1. Чтобы найти 40% от 6000 рублей, надо умножить одно на другое. 6000•0,4=2400 ₽ – потратила жена в магазине.

2. Теперь найдем сколько осталось денег: 6000-2400=3600 ₽.

3. 25% от этой сумму отнесли в банк. Как и в первом действии, переводим проценты в части и перемножаем: 3600•0,25=900 ₽.

4. 3600-900=2700 ₽ осталось у семьи до следующей зарплаты.

Задача про суровую российскую действительность, но для примера пойдет. Тут мы дважды искали процент от числа.

Нахождение числа по данной величине процентов

Завод изготовил 1200 боевых орудий. Это составило 30% от прошлогоднего гособоронзаказа. Какой был гособоронзаказ в прошлом году?

Чтобы не переводить проценты в части, можно использовать пропорцию, проценты там все равно сократятся. 1200 — это 30%, тогда 100% — это Х.

Как решать пропорции все должны знать. Это очень легко. Перемножаем крест на крест. Получаем Х•30%=1200•100%. Ну а дальше находим Х=1200•100:30=4000 (боевых орудий).

Как видите, снова ничего сложного.

Нахождение процентного соотношения двух величин

Папа зарабатывает 60 000 рублей в месяц, а мама — 15 000 рублей. Сколько процентов составляет папина зарплата относительно маминой и наоборот.

Снова про деньги, чтобы было понятней. В такого рода задачах надо сначала четко понять относительно чего мы считаем. Если мы считаем папину зарплату относительно маминой, значит мамину зарплату берем за 100%. А если мамину зарплату относительно папиной, то за 100% нужно обозначить папину зарплату.

1. Давайте сначала найдет папину зарплату относительно маминой. Мамина зарплата 15 000 ₽ — это 100%. А папина зарплата 60 000 ₽ — это Х%. Составляем пропорцию, как в предыдущей задаче, перемножаем крест на крест и находим ответ.

15•Х%=60•100%; Х=60•100%:15=400%. То есть папина зарплата составляет 400% от маминой. Иначе говоря, если переводить в части, папина зарплата в 4 раза больше.

Теперь найдем, какой процент составляет мамина зарплата относительно папиной. Теперь уже папину зарплату в 60 000 ₽ принимает за 100%, а мамину 15 000 рублей — за Х%.

Получаем 60•Х=15•100%; Х=15•100%:60=25%. То есть мамина зарплата составляет всего 25% от папиной зарплаты. А если перевести в части, но получим, 0,25, то есть в 4 раза меньше папиной.

Вот и все задачи на проценты. Других не бывает. Научитесь решать и жизнь наладится.

Ещё интересно: Как посчитать площадь многоугольника за 15 секунд в уме? Формула для ленивых

Как быстро в уме без калькулятора извлекать квадратные корни из больших чисел

Задача про партизан из Мурзилки 1944 года. Современные дети точно её не решат. Да и взрослые вряд ли

Рассмотрим три основных типа задач на проценты.

Нахождение процента от числа

Разбор примера

Предприятие изготовило за квартал 500 насосов, из которых
60% имели высшую категорию качества. Сколько насосов высшей категории качества
изготовило предприятие?

Решение:

Ответ: 300 насосов высшей категории качества.

Нахождение числа по его проценту

Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто
не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать
текст. Если вам встречаются слова «который», «что составляет» и «который составляет»,
скорее всего перед вами задача «число по его проценту».

Разбор примера

Ученик прочитал 138 страниц, что составляет 23%
числа всех страниц в книге. Сколько страниц в книге?

Решение:

Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую
прочитал ученик (138 страниц) составляет 23% от общего количества
страниц в книге.

Так как 138 стр. — это всего лишь часть, само количество
страниц, естественно, будет больше 138. Это поможет нам при проверке.

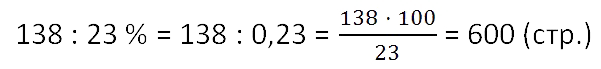
Проверка: 600 > 138 (это означает, что 138 является частью 600).

Ответ: 600 (стр.) — общее количество страниц в книге.

Сколько процентов одно число составляет от другого

Разбор примера

Из 200 арбузов 16 оказались незрелыми.
Сколько процентов всех арбузов составили незрелый арбузы?

Решение:

О чем спрашивают? О незрелых арбузах. Значит, 16
делим на общее количество арбузов и умножаем на 100%.

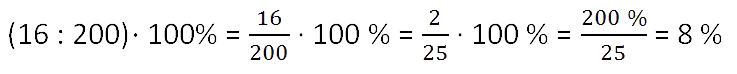
Ответ: 8% — составляют незрелые арбузы от всех арбузов.

---

Ваши комментарии

Оставить комментарий:

---

Проценты

• Нахождение процентов от числа
• Нахождение числа по его процентам
• Процентное отношение двух чисел
• Перевод процентов в десятичную дробь

Процент — это одна сотая часть числа. Отсюда следует, что два процента — это две сотых, двадцать процентов — двадцать сотых и так далее.

Слово  процент  обозначается знаком  %.  Так,  43%  какого либо числа означает  43 процента,  то есть    этого числа. Однако стоит обратить внимание, что в вычислениях знак  %  не пишется, он может быть записан в условии задачи и в окончательном результате.

Величина, от которой вычисляются проценты (например, цена, длина, количество конфет и т. д.), составляет  100  своих сотых долей, то есть  100%.

Чтобы найти один процент от числа, надо разделить это число на  100.

Нахождение процентов от числа

Чтобы найти некоторое число процентов от данного числа, нужно данное число разделить на  100  и умножить на число процентов.

Нахождение числа по его процентам

Чтобы найти число по данной величине его процентов, нужно эту величину разделить на число процентов и умножить на  100.

Процентное отношение двух чисел

Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на  100.

Перевод процентов в десятичную дробь

Чтобы перевести проценты в десятичную дробь, надо количество процентов разделить на  100.

Из данных примеров следует, что для перевода процентов в десятичные дроби, надо в числе, стоящем перед знаком  %,  перенести запятую на два знака влево.

Содержание

1. Что такое процент
2. Как вычесть проценты
3. Примеры решения задач с процентами
4. Как рассчитать процентное изменение
5. Распространенные ошибки при решении задач с процентами

Эта
статья посвящена решению задач на проценты. Ниже рассмотрены некоторые из этих задач.
Большинство задач на проценты связаны с нахождением процента от числа,
нахождением числа в процентах, представлением части в процентах или
представлением отношения между несколькими объектами, числами или величинами в
процентах.

Что такое процент

Процент – это способ расчета того, сколько
чего-то есть по отношению к целому.

Проценты очень широко используются как в математике, так и в
повседневных ситуациях, и они действительно полезны для понимания относительных
величин и привнесения их значимых.

Процент может быть записан несколькими способами. Один
из способов – изобразить его как десятичную дробь. Например, 24% также могут
быть записаны как 0,24. Можно найти десятичную версию процента, разделив
процент на 100.

Вот несколько распространенных способов использования
процентов в повседневной жизни:

• расчет
  того, насколько хорошо студент сдал тест;
• выяснение
  того, сколько НДС нужно заплатить при покупке;
• расчет
  того, сколько оставить в качестве чаевых в ресторане.

Проценты обычно представлены символом %, и
есть несколько основных правил, которые нужно понять, чтобы их правильно
рассчитать.

Процентные задачи –
это общие, повседневные реальные математические задачи. Таким образом, выделяют
три типа решений, о которых следует знать:

1. Поиск
   процента от целого (отсутствующая переменная – это часть, которая
   составляет заданный процент).
2. Поиск
   целого из процента (отсутствующей переменной является целое, из которого
   была взята процентная часть).
3. Поиск
   процента от целого и части (отсутствующей переменной является процентная
   сумма, равная соотношению детали к целому).

Используя процентную формулу, легко понять, как быстро
решить процентные проблемы. Нужно помнить, что общая алгебраическая формула
процента:%?В=П.

Формула
для поиска процента

Как указано, процент – это соотношение
желаемой детали по сравнению со всем продуктом, где100%представляет собой весь процент. Формула для поиска процента может быть записана математически как: П/В =%/100

Где:

• П – это
  часть.

• В – это
  все.

• % – это
  процент.

Как вычесть проценты

Чтобы вычесть один процент из другого, просто нужно игнорировать процентные знаки и относиться к ним как к целым числам.

Например, чтобы вычесть 20% из 50%, нужно сделать следующее: 50 – 20 = 30. Ответ – 30%.

Если вычитается процент из целого числа, сначала нужно преобразовать его в десятичную дробь.

Если попросят вычесть 25% из 45 (например, при расчете скидки), то нужно начать с преобразования 25% в десятичную дробь, что составляет 0,25.

Чтобы рассчитать сумму, которую следует вычесть, нужно умножить исходное число на десятичную дробь:

45 x 0,25 = 11,25

Затем вычесть эту сумму из базовой цифры:

45 – 11,25 = 33,75

Также можно взять десятичную дробь, вычесть ее из 1, а затем умножить
исходное число на него:

25% = 0,25

1 – 0,25 = 0,75

0,75 x 45 = 33,75

Примеры решения задач с процентами

Решенные образцы
задач с процентами помогут понять, как шаг за шагом решить различные
типы таких задач.

1. На выборах кандидат О получил 75% от общего числа
действительных голосов. Если 15% от общего числа голосов были признаны
недействительными, а общее количество голосов составляет 560000, нужно найти
количество действительных голосов, опрашиваемых в пользу кандидата.

Решение выглядит следующим образом:

Общее
количество недействительных голосов = 15% из 560000

= 15/100 ?
560000

= 8400000/100

= 84000

Общее
количество действительных голосов 560000 – 84000 = 476000

Процент
голосов, проголосовавших за кандидата А = 75%

Следовательно,
количество действительных голосов, проголосовавших за кандидата А = 75% от
476000

= 75/100 ?
476000

= 35700000/100

= 357000

2. У Гриши осталось 2100 рублей после того, как он потратил
30% денег, которые он взял в магазин. Сколько денег он взял с собой?

Пример решения:

Пусть деньги,
которые он взял в магазин, будут м.

Деньги,
которые он потратил = 30% от м

= 30/100 ? м

= 3/10 м

Деньги,
оставшиеся у него = м – 3/10 м = (10 м – 3 м)/10 = 7 м/10

Но деньги
остались у него = 2100 рублей.

Поэтому 7 м/10
= 2100 рублей.

м = 2100
рублей ? 10/7;

м = $ 21000/7;

м = 3000
рублей;

Таким образом,
деньги, которые он взял на покупки, составляют 3000 рублей.

3. Владелец магазина купил 600 яблок и 400 авокадо. Он
обнаружил, что 15% яблок и 8% авокадо были гнилыми. Нужно найти процент фруктов
в хорошем состоянии.

Решение:

Общее
количество купленных фруктов в магазине = 600 + 400 = 1000

Количество
гнилых яблок = 15% от 600

= 15/100 ? 600

= 9000/100

= 90

Количество
гнилых авокадо = 8% от 400

= 8/100 ? 400

= 3200/100

= 32

Следовательно,
общее количество гнилых фруктов = 90 + 32 = 122

Поэтому
количество фруктов в хорошем состоянии = 1000 – 122 = 878

Итак, процент
фруктов в хорошем состоянии = (878/1000 ? 100)%

=
(87800/1000)%

= 87,8%

4. На экзаменах было два
студента. Один из них получил на 9 баллов больше, чем другой, и его оценки
составили 56% от суммы их баллов. Итак, чему равны полученные ими баллы.

Решение: пусть их отметки будут (x +
9) и x.

Затем x + 9 = 56 (x +
9 + x) 100 25 (x + 9) = 14 (2x
 + 9);

3x = 99;

x = 33.

Итак, их баллы 42 и 33.

5. . Население города
увеличилось с 1 75 000 до 2 62 500 человек за десятилетие. Среднепроцентный
прирост населения в год?

Решение: увеличение через 10 лет =
(262500 – 175000) = 87500.

Увеличение %= (87500/175000 * 100)=50%

Требуемое среднее = (50/10)% = 5%

Как рассчитать процентное изменение

Процентное изменение равно изменению
данного значения. Можно найти его, разделив все значение на исходное значение,
а затем умножив его на 100. Формула решения задачи на процентное изменение следующая:

Для цены или процентного увеличения:

[(Новая цена – старая цена)/Старая цена] x
100;

Для снижения цены или процента:

[(Старая цена – новая цена)/Старая цена] x
100;

Вот пример увеличения цены/процента:

Телевизор стоил 100 тысяч рублей в прошлом
году, но теперь стоит 125 тысяч рублей. Чтобы определить повышение цены, нужно
вычесть старую цену из новой цены: 125 – 100 = 25. Затем разделить это на
старую цену: 25 разделить на 100 равно 0,25. Затем умножить это число на 100:
0,25 x 100 = 25, или 25%. Таким образом, цена на телевизор выросла на 25% за
последний год.

Пример снижения цены/процента:

В прошлом году телевизор стоил 100 тысяч
рублей, но теперь стоит всего 75 тысяч рублей. Чтобы определить снижение цены, нужно
вычесть новую цену из старой цены: 100 – 75 = 25. Затем разделить это число на
старую цену: 25 разделить на 100 равно 0,25. Затем умножить на 100: 0,25 x 100
= 25 или 25%. Это означает, что телевизор стоит на 25% меньше, чем в предыдущем
году.

Распространенные ошибки при решении задач с процентами

Рассмотрим наиболее распространенные ошибки:

• При
  сравнении процентов нужно убедиться, что есть общий базовый
  уровень (в противном случае проценты не будут связаны друг с другом).
• Одной из
  задач, в которой многие часто ошибаются, является увеличение процента
  из года в год. Например, у Алины 10 рублей, и каждый год это число увеличивается
  на 5%. Сколько у нее будет через 3 года? У некоторых людей может
  возникнуть соблазн сложить 5% в течение 3 лет, т.е. 15% и умножить 10 рублей
  на 15%. Это неправильно. Правильный способ решения таких задач – помнить,
  что каждый год начальные 10 рублей увеличивались на 5%. Таким образом, в
  конце первого года у Алины будет 10 рублей x 1,05 = 10,5 рублей. В конце 2
  года у нее будет 10,5 рублей x 1,05 = 11,025 и так далее. Важно добавить в
  каждый из этих шагов, чтобы получить правильный ответ.

Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со
всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.