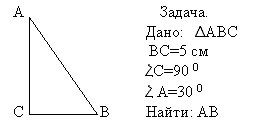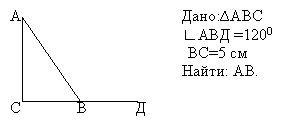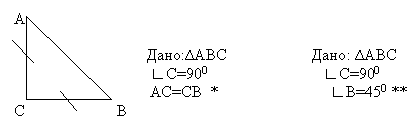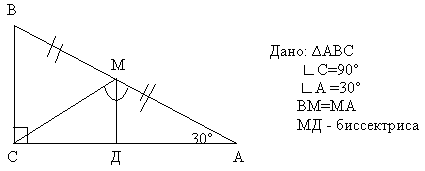Ключевые задачи на построение в 7 классе: 1) построить отрезок, равный данному; 2) построить угол, равный данному; 3) построить середину данного отрезка; 4) построить биссектрису данного угла; 5) построить треугольник, равный данному, или построить треугольник по трем заданным сторонам; 6) построить треугольник по двум сторонам и углу между ними; 7) построить треугольник по стороне и двум прилежащим к ней углам; 8) построить прямую, проходящую через данную точку, не принадлежащую данной прямой и перпендикулярную прямой; 9) построить прямую, проходящую через данную точку и параллельную данной прямой; 10) построить прямоугольный треугольник по гипотенузе и острому углу; 11) построить прямоугольный треугольник по гипотенуза и катету.
«Геометрия 7 ЗАДАЧИ на построение» содержат подробное указание «что делаем», «как делаем», а также показан пример «записи построения в тетради».
РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ НА ПОСТРОЕНИЕ
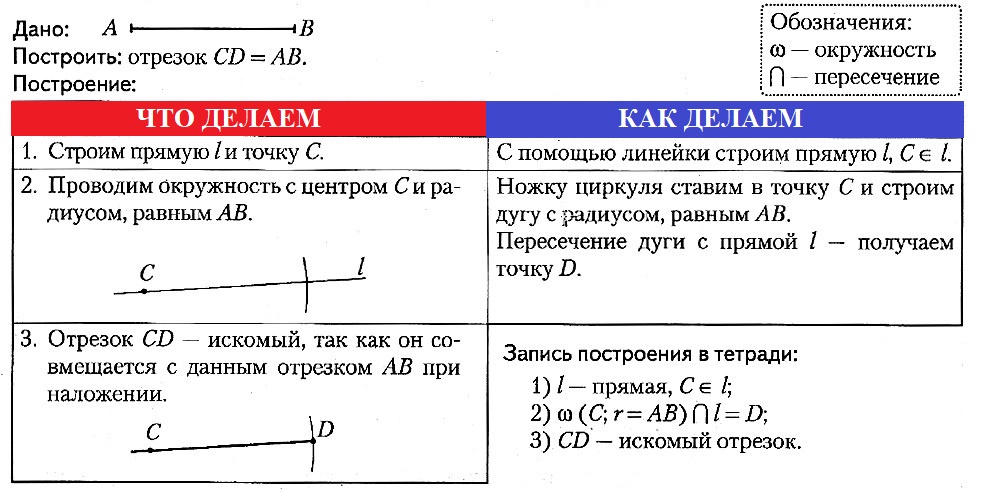
Опорная задача № 1.
Построить отрезок, равный данному.
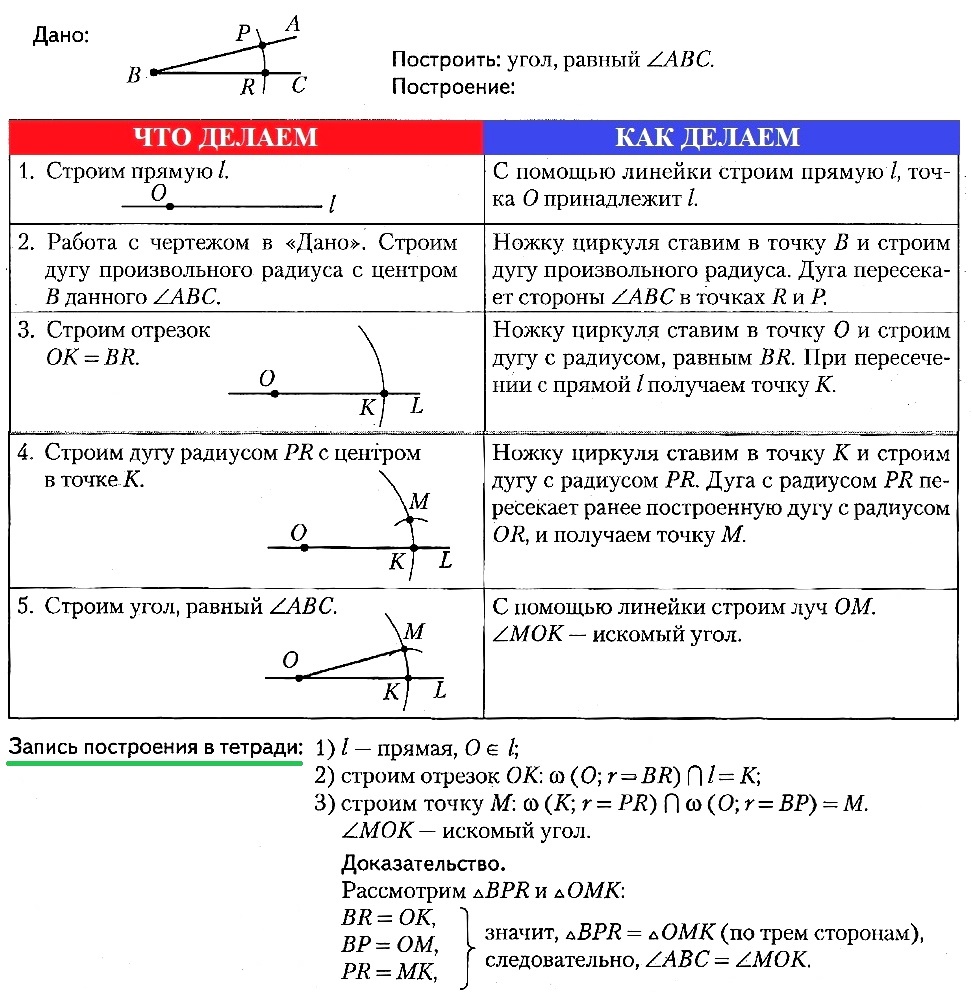
Опорная задача № 2.
Построить угол, равный данному.
Опорная задача № 3.
Построить середину данного отрезка.
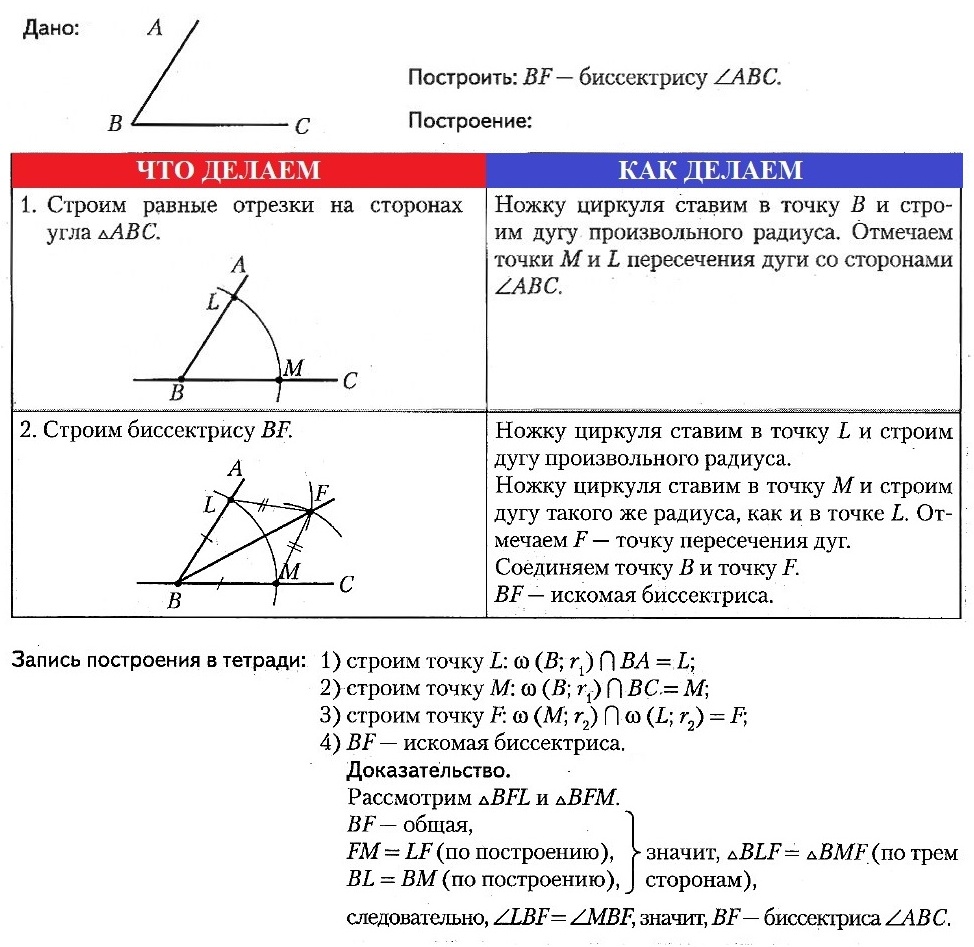
Опорная задача № 4.
Построить биссектрису данного угла.
Задача № 5.
Построить треугольник, равный данному, или построить треугольник по трем заданным сторонам.
Задача № 6.
Построить треугольник по двум сторонам и углу между ними.
Задача № 7.
Построить треугольник по стороне и двум прилежащим к ней углам.
Задача № 8.
Построить прямую, проходящую через данную точку, не принадлежащую данной прямой и перпендикулярную прямой.
Задача № 9.
Построить прямую, проходящую через данную точку и параллельную данной прямой.
Задача № 10.
Построить прямоугольный треугольник по гипотенузе и острому углу.
Задача № 11.
Построить прямоугольный треугольник по гипотенуза и катету.
Это конспект по теме «Геометрия 7 ЗАДАЧИ на построение». Выберите дальнейшие действия:
- Перейти к Конспекту учебника Геометрии 7 класс Мерзляк Глава 1
- Вернуться к Списку конспектов по геометрии
Цели:
- формировать умение применять полученные на
уроках знания в новой ситуации; - учить составлять геометрические задачи;
- развивать умение оценивать факты;
- развивать творческие способности и навыки
исследовательской деятельности; - формировать и развивать умение мыслить по
аналогии, умение обобщать, анализировать,
наблюдать и делать выводы; - воспитывать творческий подход к решению
математических задач.
Задача урока: создание ситуации на
уроке, в которой учащийся проявит себя и сам
проанализирует уровень сложности, на котором он
может работать
Оборудование: презентация,
раздаточный материал: каждому ученику карточки
“Секреты мастерства”, набор заказов для
умельца, для подмастерья, для мастера.
Для создания соответствующей атмосферы:
- “Вещь, созданная руками Мастера, радует
окружающих и приносит уважение своему
создателю” Н. Конышева - “Кто красотой гордиться, кто славой, кто
уменьем:
Да здравствует Мастер, гордящийся уменьем!” Н.
Матвеева - “Для подмастерья выше счастья нет,
чем гнаться с тонкой кисточкой учёбы
За смелой кистью Мастера вослед!”
Тип урока: комбинированный.
Вид урока: урок-мастерская.
Формы работы на уроке: фронтальная,
индивидуальная, работа в парах.
На уроке использована методика обратного
поэтапного формирования способа действий.
План урока.
- Организационный момент.
- Сообщение темы и цели урока.
- Актуализация знаний учащихся Повторение
изученного. - Отработка приёмов составления геометрических
задач. - Творческая самостоятельная работа.
- Презентация работ. Подведение итогов.
- Задание на дом.
Ход урока
1. Организационный момент. Приём
отсроченной мотивации.
Я приглашаю Вас на урок геометрии, в мастерскую.
Скажите, а чем занимаются в мастерской?
А что можно мастерить на уроке геометрии?
2. Сообщение темы и цели урока.
Как бы вы сформулировали тему нашего урока?
В мастерской творит Мастер. Мы шагнём по
ступеням мастерства.
“Шагнуть вперёд можно лишь тогда, когда нога
отталкивается от чего-то, движение от ничего или
из ничего невозможно:” Василий Белов (русский
писатель)
Нам есть от чего оттолкнуться – от знаний.
Как настоящим мастерам нам понадобятся
инструменты.
С помощью чего можно составлять задачи?
Какие инструменты нам необходимы?
Теоремы, определения, свойства геометрических
фигур.
Проверим готовность наших инструментов.
3. Повторение изученного.
Приготовьтесь к сборке набора инструментов. На
наборном полотне в ячейках изображены чертежи.
Разложи теоремы, определения в соответствии с
чертежами.
Если вы сложили правильно, то узнаете, что можно
открыть с помощью инструментов. Это “секреты
мастерства”.
Лото “Секреты мастерства” (Приложение 1)
4. Обучение приёмам составления задач.
“Для подмастерья выше счастья нет,
чем гнаться с тонкой кисточкой учёбы
За смелой кистью Мастера вослед!”
Мастерство давало человеку достоинство и
приносило уважение окружающих.
У каждого Мастера есть свои секреты.
Раскроем и мы секреты мастерства составления
геометрических задач.
Приготовьте листы “Секреты мастерства” (Приложение 2)
Как создать геометрическую задачу?
– сконструировать чертёж;
– определить данные;
– получить возможные следствия и их
обоснования;
– на основе полученных следствий выдвинуть
требование к задаче.
Возьмём заготовку – простую задачу и путём
преобразований из простой задачи смастерим
более сложную, то есть с точки зрения геометрии
более красивую задачу. И чем сложнее задачу мы
сможем составить, чем больше знаний мы привлечём,
тем ценнее будет наше изделие.
Мастер-класс. Секрет первый. (Приложение 2)
Решение:
1. ВС = 1/2 АВ (свойство катета, лежащего против
угла 300)
АВ = 5 * 2=10 см
Ответ: АВ = 10 см.
Перепрячем в этой задаче условие А=300 следующим образом: пусть
нам известно В=600.
Тогда чтобы решить задачу надо сначала
вычислить угол А. Как это сделать?
На основании какого свойства?
Свойство острых углов прямоугольного
треугольника.
90 0– 600=300.
Теперь наша задача решается в два шага.
Перепрячем ещё раз данное – пусть угол АВД=1200.
Этот угол внешний для АВС.
Необходимо применить свойство внешнего угла
треугольника.
Теперь задача решается в 3 шага.
Выглядит она так:
Решение:
1. АВС= 1800 –
АВД (свойство внешнего угла)
АВС= 1800-1200=600
2. ВАС=900 –
АВС
ВАС= 900 – 600=300
(свойство острых углов прямоугольного
треугольника)
3. ВС=1/2 АВ (свойство катета, лежащего против угла
300) АВ=5 * 2=10 см
Ответ: АВ=10 см.
Рецепт
- Составь простую задачу.
- Перепрячь одно (несколько) данных с помощью,
какой-либо теоремы. - Сформулируй новую более сложную задачу.
Поиграем в прятки по правилу: данное задачи
прячем с помощью какой-либо теоремы, свойства,
определения.
Теперь, чтобы от утверждения **перейти к
утверждению *надо применить
а) свойство острых углов прямоугольного
треугольника;
б) признак равнобедренного треугольника.
Секрет второй “Обработка данных”. (Приложение
2)
Как создать геометрическую задачу?
- Сконструируй чертёж.
- Определить данные.
- Получить возможные следствия и их обоснования.
- На основе полученных следствий выдвинуть
требование к задаче.
Задача
Утверждение обоснование
1. ВС = 1/2 АВ, АВ = 4 * 2 = 8 см Свойство катета,
лежащего против угла в 30о
2. ВМ = МА по условию
3. СМ – медиана по определению
4. СМ = МА свойство медианы прямоугольного
треугольника
5. СМА – равнобедренный
по определению
6. МД – биссектриса по условию
7. МД – высота свойство биссектрисы
равнобедренного треугольника
8. МДА – прямоугольный
МД СА
9. МД = 1/2 МА , МА= 4 см, МД = 2 см свойство медианы
прямоугольного треугольника.
Это пока ещё не задача- это геометрическая
конструкция.
Для того чтобы получилась задача – выдвинем
требование к её решению.
Если мы потребуем доказать, что СМА – равнобедренный, сколько шагов
будет иметь решение? (5 шагов)
А если мы потребуем найти МД, сколько шагов
придётся выполнить? (9 шагов)
Задача готова!
5. Творческая самостоятельная поуровневая
работа.
Неленивого человека в старину называли
умельцем. Почти каждый умелец становился
подмастерьем, но только самые старательные –
мастерами!
У каждого из вас на столе лежит заказ на
изготовление задачи.
Решите сами, какой заказ вам по силам. (Приложение 3)
- Заказ для умельца – ремонт задачи (вставить
пропуски); - заказ для подмастерья – составить задачу по
готовому чертежу; - заказ для мастера – сконструировать свою
задачу.
За выполнение заказа
- умелец может заработать 3 балла,
- подмастерье – 4 балла,
- мастер- 5 баллов.
Настоящий Мастер дарит результаты своего труда
окружающим. По окончанию работы я предлагаю Вам
свою работу поместить на выставку и презентовать
их.
У вас всё получится! Удачи! Приступайте к
работе.
6. Выставка работ. Подведение итогов.
” Кто красотой гордиться, кто славой, кто
уменьем:
Да здравствует Мастер, гордящийся уменьем!” Н.
Матвеева
Будьте
- Мудрыми
- Активными
- Смелыми
- Терпеливыми
- Ещё Решительными
И тогда каждый из Вас станет МАСТЕРОМ!
За работу хотелось бы отметить самых успешных и
старательных!
Им присваивается звание “Мастер задач”.
7. Задание на дом.
Смастерить геометрическую задачу.
Урок окончен!
Решение задач с помощью линейных уравнений с одной переменной
Алгоритм решения текстовой задачи с помощью уравнения
Алгоритм решения текстовой задачи с помощью уравнения:
- Проанализировать условие задачи, обозначить неизвестное буквой и составить уравнение.
- Решить полученное уравнение.
- Истолковать результат в соответствии с условием задачи.
Задачи с решениями
Задача 1. Одна сторона треугольника в два раза больше другой и на 3 см меньше третьей. Найдите стороны треугольника, если его периметр равен 43 см.
Пусть сторона AB=x.
Периметр треугольника: P = AB+AC+BC = x+2x+(2x+3) = 43
$$5x+3 = 43 iff 5x = 40 iff x = 40:5 = 8$$
AB = x = 8 см, AC = 2x = 16 см, BC = 2x+3 = 19 см
Ответ: 8 см, 16 см и 19 см
Задача 2. Расстояние между двумя станциями поезд может пройти со скоростью 70 км/ч на полчаса быстрее, чем со скоростью 60 км/ч. Найдите это расстояние.
Пусть x – расстояние между станциями.
По условию разность затраченного времени:
Решаем: $ frac <60>- frac <70>= frac<1> <2>| times 420 iff 7x-6x = 210 iff x = 210 $
Расстояние между станциями 210 км
Задача 3. Бригада должна была изготовить детали за 5 дней, но выполнила работу за 4 дня, т.к. изготавливала каждый день на 12 деталей больше. Сколько деталей изготовила бригада?
Пусть x – количество изготовленных деталей.
Количество деталей в день, шт./дни
Количество дней, дни
По условию разность между количествами деталей в день:
Решаем: $ frac <4>- frac <5>= 12 | times 20 iff 5x-4x = 240 iff x = 240 $
Бригада изготовила 240 деталей.
Ответ: 240 деталей
Задача 4. Сумма двух чисел равна 90. Если большее из них разделить на меньшее, то частное равно 3 и в остатке 6. Найдите эти числа.
Пусть x – меньшее число. Тогда большее равно 90-x. По условию: 90-x = 3x+6
$$ 90-6 = 3x+x iff 4x = 84 iff x = 21 $$
Меньшее число x = 21, большее число 90-x = 69.
Задача 5. Матери 37 лет, а дочери 13 лет. Когда дочь была или будет втрое младше матери? А вдвое?
Пусть x – число прошедших лет. Возраст матери станет 37+x, дочери 13+x.
$$ frac<37+x> <13+x>= 3 iff 37+x = 3(13+x) iff 37+x = 39+3x iff 37-39 = 3x-x iff $$
$$ iff 2x = -2 iff x = -1 $$
Дочь была втрое младше матери 1 год тому назад.
$$ frac<37+x> <13+x>= 2 iff 37+x = 2(13+x) iff 37+x = 26+2x iff 37-26 = 2x-x iff $$
Дочь будет вдвое младше матери через 11 лет.
Ответ: год назад; через 11 лет
Задача 6. Сколько лет отцу и сыну, еcли в позапрошлом году сын был младше в 5 раз, а в следующем будет младше в 4 раза?
Пусть x – возраст сына в этом году.
Возраст сына, лет
Возраст отца, лет
И для отца, и для сына пройдёт три года:
$$ 4(x+1)-5(x-2) = 3 iff 4x+4-5x+10 = 3 iff 4x-5x = 3-14 iff -x = -11 $$ $$ x = 11 $$
Сейчас сыну 11 лет.
В следующем году отцу будет 4(x+1)=4∙12=48 лет. Значит, сейчас отцу 47 лет.
Ответ: 11 лет и 47 лет.
Задача 7. Сумма цифр данного двузначного числа равна 7. Если эти цифры поменять местами, то получится двузначное число на 9 больше данного. Найдите данное число.
Пусть x – первая цифра данного числа, число десятков.
По условию разность чисел:
$$ (70-10x+x)-(10x+7-x) = 9 iff 70-9x-9x-7 = 9 iff $$ $$ iff -18x = 9-63 iff -18x = -54 iff x = 3 $$
Первая цифра x = 3, вторая цифра 7-x = 4.
Данное число 34.
Задача 8. По расписанию автобус должен ехать от посёлка до станции со скоростью 32 км/ч и приезжать на станцию за полчаса до отхода поезда. Но из-за ненастной погоды автобус ехал со скоростью на 7 км/ч меньше и опоздал к поезду на 12 мин. Чему равно расстояние от посёлка до станции?
Пусть x – расстояние от посёлка до станции.
Разность по времени между расписанием и фактическим прибытием:
30 мин+12 мин = 42 мин = $frac<42><60>$ ч = 0,7 ч
$ frac<25>- frac <32>= 0,7 | times 32 cdot 25 $
$ 32x-25x = frac<7> <10>cdot 32 cdot 25 = 7 cdot 16 cdot 5 $
$ 7x = 7 cdot 16 cdot 5 iff x = 16 cdot 5 = 80 $
Расстояние 80 км.
Задача 9*. Если к двузначному числу приписать справа и слева цифру 4, то получится число в 54 раза больше исходного. Найдите исходное двузначное число.
Пусть x – исходное число.
Если приписать по 4 слева и справа, в полученном четырёхзначном числе первая 4 указывает на количество тысяч, число x – на количество десятков, последняя 4 – на количество единиц. Соотношение чисел:
Решаем: $ 4004+10x = 54x iff 4004=44x iff x = frac<4004> <44>= frac<1001> <11>= 91 $
Исходное число x = 91.
Задача 10. Для проведения экзамена закуплены тетради. Если их сложить в пачки по 45 штук, останется одна лишняя тетрадь, а если сложить в пачки по 50 штук, то в одной пачке не будет хватать 4 тетради. Сколько тетрадей было куплено, если пачек по 45 тетрадей получается на одну больше, чем пачек по 50 тетрадей?
Задачи, решаемые с помощью уравнения. 7-й класс
Разделы: Математика
Класс: 7
- Проверка практических умений и навыков решения задач на составление уравнения.
- Активизация учебной деятельности учащихся путём общения в динамических парах, когда каждый учит каждого.
- Воспитывать ответственное отношение к учебному труду, развивать логическое мышление, любознательность, умение проверять и оценивать выполненную работу.
Коллективным способом обучения (А. Г. Ривин и В.К. Дьяченко) является такая его организация, при которой обучение осуществляется путём общения в динамических парах, когда каждый учит каждого.
I. Работа начинается с ввода или так называемого “запуска” раздела.
Обобщение и систематизация знаний по теме “ Задачи, решаемые с помощью уравнения”.
1. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
Пусть собственная скорость теплохода – Х км/ч. Заполним таблицу значений трёх величин.
| Скорость (км/ч) | Время (ч) | Расстояние (км) | |
| По течению | Х + 2 | 9 | 9(Х + 2) |
| Против течения | Х – 2 | 11 | 11(Х – 2) |
На основании условия задачи составим уравнение:
9(Х + 2) = 11(Х – 2), которое имеет единственный корень 20.
Собственная скорость теплохода 20 км/ч.
2. Увеличив среднюю скорость с 250 до300 м/мин, спортсменка стала пробегать дистанцию на 1 мин быстрее. Какова длина дистанции?
Пусть Х мин – время, за которое спортсменка пробегала дистанцию со скоростью 300 м/мин, тогда Х +1 мин – время, за которое спортсменка пробегала дистанцию со скоростью 250 м/мин. Составим уравнение:
250(Х + 1) = 300Х , которое имеет единственный корень 5.Найдём длину дистанции 300Х = 300×5 = 1500 м.
3. В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?
Пусть в первую бригаду привезли Х кг раствора, тогда во вторую – Х + 50 кг. Заполним таблицу значений величин для двух бригад:
| Привезли(кг) | Расход(кг)за 1 час | Время (ч) | Осталось раствора(кг) | |
| 1-я бригада | Х | 150 | 3 | Х – 450 |
| 2-я бригада | Х + 50 | 200 | 3 | Х + 50 – 600 |
По условию задачи в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Составим уравнение:
Х – 450 = (Х + 50 – 600)×1,5 , имеющее единственный корень 750. 750 кг раствора привезли в первую бригаду, а во вторую привезли 750 + 50 = 800 кг.
4. (Задача Э.Безу) По контракту работникам причитается 48 франков за каждый отработанный день, а за каждый неотработанный день с них вычитается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько дней они отработали в течение этих 30 дней?
Пусть работники отработали Х дней, тогда они не работали (30 – Х) дней. Составим уравнение:
48Х – 12 (30 – Х) = 0.
Решив это уравнение, получим Х = 6, то есть они отработали 6 дней.
5. Книгу в 296 страниц ученик прочитал за три дня. Во второй день он прочитал на 20% больше, чем в первый, а в третий – на 24 страницы больше, чем во второй. Сколько страниц прочитал ученик в первый день?
Пусть в первый день ученик прочитал Х страниц, тогда во второй день ученик прочитал Х + 0,2Х = 1,2Х страниц, а в третий день прочитал 1,2Х + 24. Составим уравнение:
Х + 1,2Х +1,2Х + 24 = 296. Решив это уравнение, получим Х = 80, то есть ученик прочитал в первый день 80 страниц.
6. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
Пусть грелось Х кошек, тогда у этих кошек 2Х ушей и 4Х лап. Составим уравнение:
4Х – 2Х = 10. Решив это уравнение, получим Х = 5,то есть 5 кошек грелось на солнышке.
II. Самостоятельная работа учащихся.
Каждый ученик получает индивидуальную карточку с задачами. Правильность решения проверяет преподаватель, при необходимости он оказывает помощь в решении. После проверки ученику выставляется в оценочный лист плюс или оценка.
Примеры карточек для первой группы:
1. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней второй догонит первого?
2. Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?
Ответ: № 1 – 8 дней, № 2 – 9 дней.
1. Кооператив наметил изготовить партию мужских сорочек за 8 дней. Выпуская в день на 10 сорочек больше, чем предполагалось, он выполнил план за один день до срока. Сколько сорочек в день должен был выпускать кооператив?
2. На ферме 1000 кроликов и кур, у них 3150 ног. Сколько кроликов и сколько кур на ферме?
Ответ: № 1 – 70 сорочек, № 2 – 575 кроликов и 425 кур..
1. Из пункта А вышла грузовая машина со скоростью 60км/ч. Через 2 ч вслед за ней из пункта А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?
2. Чтобы выполнить задание в срок, токарь должен изготавливать по 24 детали в день. Однако он ежедневно перевыполнял норму на 15 деталей и уже за 6дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?
Ответ: № 1 – 360 км, № 2 – 408 деталей.
1. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком расстоянии от турбазы был сделан привал?
2. На одном складе было 185 т угля, а на другом – 237 т. Первый склад стал отпускать ежедневно по 15 т угля, а второй – по 18 т. Через сколько дней на втором складе угля будет в полтора раза больше, чем на первом?
Ответ: № 1 – 9 км, № 2 – 9 дней.
Примеры карточек для второй группы:
1. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В , отстоящего от пункта А на расстоянии 60 км/ч, выехал мотоциклист. Велосипедист ехал со скоростью 12 км/ч, а мотоциклист – со скоростью 30 км/ч. На каком расстоянии от пункта А мотоциклист догонит велосипедиста?
2. Три бригады изготовили 65 деталей. Первая бригада изготовила на 10 деталей меньше, чем вторая, а третья – 30% того числа деталей, которые изготовили первая и вторая детали вместе. Сколько деталей изготовила каждая бригада?
Ответ: № 1 – 40 км, № 2 – 20, 30, 15 деталей.
1. Расстояние между пристанями М и N равно 162 км. От пристани М отошёл теплоход со скоростью 45 км/ч. Через 45 мин от пристани N навстречу ему отошёл другой теплоход, скорость которого 36 км/ч. Через сколько часов после отправления первого теплохода они встретятся?
2. Бригада рабочих должна была изготовить определённое количество деталей за 20 дней. Однако она ежедневно изготавливала на 70 деталей больше, чем планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось изготовить 140 деталей. Сколько деталей должна была изготовить бригада?
Ответ: № 1 – 2 
1. От пристани А отошел теплоход со скоростью 40 км/ч. Через 1 
2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Ответ: № 1 – 2 ,5 ч; 150 км, № 2 – 4 овцы и15 кур.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?
2. За 4 ч катер проходит по течению расстояние, в 2,4 раза большее, чем за 2 ч против течения. Какова скорость катера в стоячей воде, если скорость течения 1,5 км/ч?
Ответ: № 1 – 7 монет, № 2 – 16,5 км/ч.
Примеры карточек для третьей группы:
1. Со станции М и N, расстояние между которыми 380 км, одновременно навстречу друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам оставалось пройти до встречи 30 км. Найдите скорость поездов.
2. В одном резервуаре 380 м³ воды, а в другом 1500 м³. В первый резервуар каждый час поступает 80 м³ воды, а из второго каждый час выкачивают 60 м³. Через сколько часов воды в резервуаре станет поровну?
Ответ: № 1 – 85 и 90км/ч, № 2 – 56 ч.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?
2. Скашивая ежедневно по 60 га вместо 50 га, бригада сумела скосить луг на один день быстрее, чем планировалось. Какова площадь луга?
Ответ: № 1 – 7 монет, № 2 – 300 га.
1. (Старинная задача.) Летели галки, сели на палки: по две сядут – одна палка лишняя, по одной сядут – одна галка лишняя. Сколько было галок и сколько палок?
2. Турист рассчитал, что если он будет идти к железнодорожной станции со скоростью 4км/ч, то опоздает к поезду на полчаса, а если он будет идти со скоростью 5км/ч, то придёт на станцию за 6 мин до отправления поезда. Какое расстояние должен пройти турист?
Ответ: № 1 – 4 галки и 3 палки, № 2 – 12 км.
1. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было орехов?
2. К числу приписали справа нуль. Число увеличилось на 405. Найдите первое число.
Ответ: № 1 – 83 ореха, № 2 – 45.
Раздел считается введённым в работу, если каждая карточка с заданиями выполнена хотя бы одним учеником.
III. Работа в группах.
Затем работа классного коллектива выглядит так: организуется 3–4 группы по 4 человека (можно до 7 человек). В группе у каждого ученика своя карточка, за которую ученик уже получил плюс или оценку в оценочный лист. Каждый в группе выбирает партнёра, и они меняются карточками. Школьники работают в парах (решают карточку своего партнера полностью), затем пары в группе меняются. Если необходима помощь, то происходит взаимообучение. Если помощь не нужна, то после выполнения задания происходит взаимопроверка и делается отметка в оценочный лист. Потом пары меняются, и процесс продолжается до тех пор, пока каждый ученик не выполнит задания других учеников группы. Затем подводится итог, и выставляется общая оценка.
| №1 | №2 | №3 | №4 | Итоговая оценка |
| Лаптева Алина | 5 | |||
| Борзенков Егор | 3 | |||
| Мартышин Сергей | 4 | |||
| Казакова Виктория | 3 |
По диагонали оценка выставлена учителем. За выполнение карточки № 1оценка выставляется Лаптевой А., № 2 – Борзенковым Е., № 3 – Мартышиным С., № 4 – Казаковой В..
Решение задач по геометрии 7 класс, объяснение тем, объяснение задач
В 7 классе ученики начинают изучать новый предмет — геометрию. До этого они уже знакомились с некоторыми геометрическими понятиями, но не так подробно. Чтобы в дальнейшем не возникали трудности с усвоением информации, следует с самого начала усвоить основные моменты: уметь различать типы фигур, знать основные их свойства, выучить теоремы, признаки фигур. В 7 классе изучаются простейшие объекты: точка, луч, отрезок, прямая и т.д. Кроме этого, в учебниках подробно рассматривается треугольник.
Чтобы помочь ученику с усвоением основных тем по геометрии, ниже рассмотрено их содержание, представлены рисунки фигур и задачи по темам треугольников.
Основные темы по геометрии 7 класс
Ученику 7 класса предстоит познакомиться со следующими основными разделами учебника по геометрии:
Геометрия 7 класс объяснение основных тем, понятно для детей
первые геометрические объекты
Начать стоит с самого понятия «геометрия». С древнегреческого слово переводится как земля и измерение. Эта древнейшая наука, которая появилась в связи с необходимостью строить здания, дороги, измерять объекты и прокладывать границы.
О равных треугольниках. Равнобедренный треугольник
Треугольником принято считать фигуру, которая состоит из 3-х точек. Причем точки эти не должны лежать на одной прямой, а соединяются они отрезками.
Сумма всех углов в треугольнике равняется 180º. Знание этого факта пригодится при решении задач на нахождение углов.
Треугольники можно различать по двум признакам: размеру сторон и размеру углов.

Если один треугольник (назовем его CFD) наложить на другой (C1F1D1) и они будут соответствовать друг другу, то треугольники равны. У равных фигур все элементы равны.
Чтобы понять, равны ли треугольники, познакомимся с признаками равенства этих фигур.
Остановимся отдельно на равнобедренных треугольниках. Если 2 стороны треугольники равны, то его называют равнобедренным.
На заметку! Если равны все стороны, а не только две, то треугольник уже равносторонний, а не равнобедренный.

- 2 угла в нем равны;
- биссектриса одновременно является высотой и медианой;
- медиана — биссектриса и высота;
- высота, соответственно — медиана и биссектриса.


параллельные прямые

Чтобы понять, параллельны ли прямые, нужно усвоить 3 основных признака.

прямоугольный треугольник и его свойства
Прямоугольным называют треугольник, в котором один из углов равен 90º. Рассмотрим название сторон такой фигуры.
Геометрия 7 класс задача по теме треугольники, пояснение решения задач
Решим несколько задач про треугольники:
- нахождение периметра;
- доказательство равенства треугольников.



Сумму периметра АВС также записали с помощью сложения сторон. Затем упростили это сложение, записав: 32 = 2 АВ + 2 ВМ (так как АВ и АС равны — равнобедренный треугольник; ВМ и СМ тоже равны). Потом эту запись сократили, разделив на 2.
Вышло, что сумма двух сторон равна 16 см. Остается найти третью сторону (АМ). Она входит в треугольник АВМ, периметр которого равен 24 см. Тогда, чтобы найти третью сторону (АМ, нужно просто 24 отнять 16, вышло 8 см. В примере подставили в уравнение, чтобы не запутаться.
Решим задачу на нахождение угла в треугольнике.
Чтобы найти угол С в задаче потребовалось узнать, чему равен угол В. По условиям известно, что внешний В равняется 110º. Знаем, что развернутый угол равняется 180º (это внешний и внутренний угол В в сумме). Поэтому от 180 отнимаем 110. Получается угол В = 70º.
Треугольник равнобедренный, значит углы при основании одинаковые ⇒ угол В = углу А = 70º.
Поскольку сумма углов треугольника равна 180º (по правилу), значит угол С = 180 — углы А и В = 180 — 70 — 70 = 40°.

Геометрия 7 класс тест по теме треугольник
Закрепим материал по треугольникам, решив несколько тестовых заданий.
- Как называется сумма всех сторон в треугольнике?
а) площадь;
б) периметр;
в) медиана
2. Треугольник называется равнобедренным, если:
а) у него есть основание;
б) все стороны равны;
в) две стороны равны
3. Если в равнобедренном треугольнике к основанию провести высоту, то чем еще она будет являться?
а) биссектрисой;
б) медианой;
в) медианой и биссектрисой;
г) только высотой
4. Сколько всего признаков равенства треугольников?
5. В треугольнике можно провести ___ медиан (-ы)
а) одну;
б) множество;
в) три;
г) две
6. Как называются стороны прямоугольного треугольника, которые образуют угол 90º?
а) гипотенузы;
б) катеты;
в) высоты
7. Про что гласит 3-й признак равенства треугольников?
а) про стороны;
б) про сторону и углы;
в) про угол и стороны
8. Под каким углом в любом треугольнике проходит высота?
а) это зависит от вида треугольника
б) под углом 45 градусов;
в) 90 градусов
9. По каким признакам различаются виды треугольников?
а) по размеру сторон;
б) по размеру углов;
в) по размеру сторон и углов;
г) по периметру и площади
10. Чему равна сумма двух острых углов прямоугольного треугольника?
а) 90 градусов;
б) 180 градусов;
в) 60 градусов
Ответы: 1 — б; 2 — в; 3 — в; 4 — б; 5 — в; 6 — б; 7 — а; 8 — в; 9 — в; 10 — а.
7 класс геометрия сложная тема, разъяснить подробно для детей
Решим более сложную задачу, где есть и доказательство равенства треугольников, и поиск углов. Алгоритм решения задачи:
Шаг 1. Начертим, согласно условиям. Дается треугольник АВС, в котором провели медиану (вспоминаем, что медиана делит сторону пополам). В нашей задаче медиана AD уходит за пределы треугольника, создавая дополнительный отрезок DE (он равен AD). Получился треугольник, из которого проведена медиана.
Шаг 2. Первая задача — доказать равенство треугольников ABD и ECD: соединим точку Е и С, чтобы получился треугольник.
Шаг 3. По условиям AD и DE равны (одна сторона треугольника равна другой стороне ⇒ AD = DE
Шаг 4. Получается BD = DC, так как медиана разделила BC пополам (выходит, еще одни стороны треугольников равны).
Шаг 5. Рассмотрим углы между сторонами (на рис. обозначены цифрами 1 и 2). Они вертикальные, так как образовались двумя прямыми. Следовательно, они равны.
Из первого признака равенства треугольников знаем, что если 2 стороны и угол между этими сторонами одного треугольника равен этим показателям во втором, то они равные. Пункт а доказан. Переходим к б.
Шаг 1. Нам нужно найти угол АСЕ. Из рисунка видно, что он состоит из 2-х маленьких углов, получается: угол АСЕ равен сумме углов DCA и DCE.
Шаг 2. По условиям мы знаем, чему равен DCA, осталось найти второй. Так как равенство треугольников доказали, значит воспользуемся правилом: напротив равных сторон треугольников лежат и равные углы. AD напротив ABD; DE напротив DCE. Выходит: угол ABD = углу DCE = 40 градусам (по условию).
Шаг 3. Маленькие углы известны, найдем тот, который требуется: угол ACE = 56º + 40º = 96º.
Равенство доказали, угол нашли. Задание выполнено.
Еще пара видеороликов про решение задачи с прямоугольным треугольником, а также вся геометрия за 7 класс в одной задаче.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/592484
[/spoiler]
Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?

Вам понадобится
- Учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик
Инструкция
Внимательно прочитайте условие задачи.
Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи. Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками.
Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.
Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы.
Рассмотрите примеры решения задач по этой теме. В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».
Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.
Полезный совет
Не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное. Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.
Источники:
- задачи по геометрии 7 класс
Методические
рекомендации решения задач на построение
Рассмотрим этапы выполнения интересных
задач на построение. Такой разбор решений задач поможет ученикам самостоятельно
проанализировать и выполнить построения, работая на дистанционном обучении.
Характеристика
задания: Решить задачу на построение – это значит найти способ построения
фигуры только с помощью циркуля и линейки без делений. Другие чертежные
инструменты не используются.
Задача
1 (№ 285, учебник Геометрия 7-9 класс, Л.С. Атанасян и др):
Даны пересекающиеся прямые а и b
и отрезок PQ. На прямой а постройте точку, удаленную от
прямой b на расстояние PQ.
Анализ
задачи:
Подумаем, где
расположены все точки, которые находятся на одном и том же расстоянии от прямой
b? Все точки плоскости, расположенные по одну сторону от прямой b
и равноудаленные от нее, лежат на прямой, параллельной прямой b.
Наша задача
свелась к задаче построения прямой (назовем ее d), параллельной прямой b,
и удаленной от прямой b на расстояние PQ. Любая точка прямой d
находится на расстоянии PQ от прямой b. Искомая точка есть точка
пересечения прямых а и d.
Выполнение
задания
Дано:
прямые а и b, а ∩ b = С; отрезок PQ.
Построить: точку А (А Є а), такую, что расстояние
от А до прямой b равно PQ.
Построение:
1.
Отметим произвольную точку К на прямой b; построим
прямую с, перпендикулярную прямой b и проходящую через
точку К. (задача построения перпендикулярных прямых рассмотрена в п. 23
учебника)

b, К Є с
2. Отложим
от точки К на прямой с отрезок KL, равный отрезку PQ.

= PQ
3. Построим
прямую d, перпендикулярную прямой с и проходящую через
точку L.

с = L
Две прямые d и b, перпендикулярные третьей
прямой с, параллельны друг другу.
Расстояние между прямыми d и b равно KL и
равно PQ.
d с, b с, следовательно
d ║ b, KL = PQ.
4.
Прямые d и а пересекаются в точке А. Точка
А – искомая, так как лежит на прямой а и удалена от прямой b на
расстояние PQ, так как принадлежит прямой d.
d
∩ а = А, А Є а, А Є d, KL = PQ.
5.
Задача имеет два решения, так как отрезок KL можно отложить вдоль
прямой с в разные стороны от точки К.