Как решать задания найти площадь четырехугольника

Задачи на площадь четырехугольников на три уровня
тренажёр по геометрии (8 класс) на тему

Задачи на нахождение площади четырехугольников на 3 уровня

Скачать:

Вложение	Размер
zadachi_na_ploshchad_po_urovnyam.docx	15.04 КБ

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Предварительный просмотр:

Задачи 1 уровня

1.Найдите площадь прямоугольника, если его длина 2 дм, а ширина 4 см.

2.Найдите площадь параллелограмма, если одна из его сторон равна 6 см , а высота, проведенная к этой стороне, равна 9 см.

3.Катеты прямоугольного треугольника 12 и 8см. Найдите площадь треугольника.

4.Найдите площадь прямоугольника, если его длина 110 см, а ширина 10 м.

5.Найдите площадь прямоугольной трапеции, если основания равны 8 см и 10 см, а боковая сторона, перпендикулярная нижнему основанию равно 5 см.

6.Найдите площадь прямоугольника, если его длина 15 дм, а ширина 20 м.

7.Основания трапеции 6см и 8 см, высота 2 см. Найдите площадь трапеции.

8.Основания трапеции 9 см и 1 см, высота 4 см. Найдите площадь трапеции.

9.Основание треугольника 16, а высота, проведенная к основанию 5. Найдите площадь треугольника.

10.Основание параллелограмма равно 20, а высота, проведенная к основанию равна 7. Найдите площадь параллелограмма.

Задачи 2 уровня.

1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

2.Найдите площадь ромба с диагоналями 5см и 8 см.

3.Стороны параллелограмма равны 10 см и 18 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

4.Периметр квадрата 40 см. Найдите его площадь.

5.Площадь квадрата 81 кв. см. Найдите его периметр.

6.Найдите площадь прямоугольного треугольника, если его катеты 8 см и 15 см.

7.Основание равнобедренного треугольника 16 см, а медиана, проведенная к основанию, равна 6 см. Найдите площадь треугольника.

8.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.

Задачи 3 уровня.

1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

2.Высоты параллелограмма равны 3 см и 4 см, острый угол между сторонами равен 30 градусов. Найдите площадь параллелограмма.

3.Найдите площадь трапеции со сторонами 6 см, 6 см, 10см и 14 см, если угол между боковой стороной и нижнем основанием 30 градусов.

4.Стороны параллелограмма равны 8 см и 15 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

5.Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если его катеты 8 см и 6 см., а гипотенуза равна 10 см

По теме: методические разработки, презентации и конспекты

Площади четырехугольников

Материал для обобщающего урока по теме “Площади четырехугольников” для 8 класса, представляющий различные формы работы с обучающимися.

Зачет по геометрии в 8 классе по теме “Площади четырехугольников”

Карточка для зачета , 2 варианта.

Разработка урока-соревнования в 8 классе по геометрии на тему “Четырехугольники. Свойства, признаки и площади четырехугольников”

Материал урока систематизирует и обобщает знания о четырехугольниках, их свойствах, признаках, площадях.

Презентация. Решение задач на вычисление площадей четырехугольников.

Данная презентация содержит задачи на вычисление площадей многоугольников: прямоугольника, параллелограмма, а также треугольника, трапеции с применением свойств площадей многоугольников, свойств.

Учебный элемент к уроку геометрии по теме: “Четырехугольники. Формулы для нахождения площадей четырехугольников “

Учебный элемент содержит теоретический материал по данной теме и примеры задач.

Урок геометрии в 8 классе “Решение задач на вычисление площади четырехугольников”

Урок обобщения по теме “Площадь четырехуголников”.

Урок по теме “Решение задач на вычисление площади четырехугольников”

Разделы: Математика

Урок рассчитан на один академический час и проводится после того, как изучены формулы для вычисления площадей треугольников, прямоугольника, квадрата, параллелограмма и трапеции.

1. Образовательные: повторить ранее изученные формулы для вычисления площадей выпуклых фигур, вывести и научиться пользоваться формулами для вычисления площадей выпуклых четырехугольников, имеющих перпендикулярные диагонали;
2. Развивающие: развитие логического мышления, памяти, внимания, выработка математической зоркости;
3. Воспитательные: воспитание трудолюбия, интереса к предмету, умение внимательно выслушивать ответы одноклассников.

1. Организационный момент.
2. Устная работа.

Проводится по чертежам, выведенным с проектора на экран.

Задание. Для каждой из геометрических фигур найти площадь, назвав используемую формулу. Опрос ведется фронтально, учащиеся могут отвечать по желанию.

Учитель обращает внимание учащихся на то, что до сих пор, в основном, площади фигур вычислялись по двум элементам: основанию и высоте, проведенной к основанию. Однако, в случае, если в четырехугольнике диагонали взаимно перпендикулярны, его площадь можно вычислить, зная длины диагоналей.

Учитель просит учащихся сформулировать тему урока. Учащиеся предлагают свои варианты темы урока. Принимается такая: «Вычисление площади выпуклого четырехугольника, имеющего взаимно перпендикулярные диагонали».

Задача. Доказать, что площадь выпуклого четырехугольника, имеющего взаимно перпендикулярные диагонали, равна половине произведения его диагоналей.

Запись на доске.

ABCD – вып. четырехугольник,

S_ABCD=1/2 ACBD.

S_ABC=1/2 ACBО, т.к. BO является высотой в ABC,

S_ABC=1/2 ACDO, т.к. DO является высотой в ADC.

1. S_ABCD= S_ABC+ S_ADC = 1/2 ACBО + 1/2 ACDO = 1/2 AC(BO+DO)= 1/2 ACBD, ч.т.д.

Учитель. Какие вы знаете четырехугольники с взаимно-перпендикулярными диагоналями?

Ученик. Ромб и квадрат.

Учитель. Давайте запишем формулы в общем виде для вычисления площадей ромба и квадрата для их диагоналей.

Запись на доске:

Учитель. Что можно сказать о диагоналях квадрата, кроме того, что они взаимно перпендикулярны?

Ученик. Диагонали квадрата равны, то есть d₁ = d_2.

Учитель просит ученика записать формулу для вычисления площади квадрата по его диагонали.

Ученик пишет на доске:

S_{квадрата} = ½ d 2 , где d – диагональ квадрата.

Учитель. Приведите свои примеры использования выведенных формул.

Ученик. Найти площадь ромба, если его диагонали равны 3см и 6см.

Решение: S=1/2 36 = 9 (см 2 ).

Ученик. Найти площадь квадратного участка земли, если его диагональ равна 10м.

Решение: S=1/2 10 2 =50 (м 2 ).

Учитель. Придумайте обратные задачи.

Ученик. Найти одну из диагоналей ромба, если его площадь равна 20 см 2 , а вторая диагональ 8 см.

Решение: d₁= 2S/d₂, d₁= 220/8 = 5 (см)

Ученик. Найти диагональ квадрата, если его площадь равна 18 см 2 .

Решение: d 2 =2S, d 2 =36, d=6(см).

Учитель. Давайте теперь решим более сложную задачу, в которой известны площадь ромба, а также соотношение между длинами диагоналей, а требуется найти диагонали.

(На эту задачу лучше вызвать сильного ученика, т.к. она решается с помощью уравнения и является сложной для слабых учеников). Во время обдумывания решения предложенной задачи средними и сильными учениками класса, слабые получают карточки-задания на отработку выведенных формул. Каждая карточка содержит по 2 простые задачи типа:

Вычислить площадь ромба, если одна из его диагоналей равна 5 см, а другая в 4 раза больше.

Вычислить диагональ квадрата, если его площадь равна 32 см 2 .

Задача (для средних и сильных учеников).

Одна из диагоналей ромба, площадь которого равна 27 см 2 , в 1,5 раза больше другой диагонали. Найти диагонали этого ромба.

Ученик записывает на доске:

1. S_ABCD = 1/2 ACBD.

Пусть BD = x см, тогда AC = 1,5x см. Т.к. по условию задачи S_ABCD = 27 см 2 , то получаем уравнение:

1/21,5xx = 27,

x=6 ( x=-6 не подходит по смыслу задачи).

1. BD = 6 см, AC = 1,56= 9 см.

Ответ : 6 см и 9 см.

Учитель. Какие новые формулы мы сегодня узнали?

Ученик. Формулы для вычисления площадей выпуклых четырехугольников, имеющих взаимно-перпендикулярные диагонали, в частности, для ромба и квадрата.

Учитель. Какая еще из известных вам геометрических фигур может иметь взаимно-перпендикулярные диагонали?

Учитель. Верно, значит можно вычислить и площадь трапеции, если у нее взаимно-перпендикулярные диагонали. Этими формулами можно пользоваться наряду с ранее изученными.

1. Домашнее задание (творческое).

• Придумать по 2 задачи (2 прямые и 2 обратные) на применение изученных формул и записать их с решениями. Чем сложнее задача, тем выше оценка.
• Для слабых учеников (у кого не получится придумать задачи):

Задача. Найти площадь трапеции, если ее диагонали взаимно перпендикулярны, а их длины равны 10 см и 16 см.

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

[spoiler title=”источники:”]

http://urok.1sept.ru/articles/523943

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/

[/spoiler]

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Урок рассчитан на один
академический час и проводится после того,
как изучены формулы для вычисления
площадей треугольников, прямоугольника,
квадрата, параллелограмма и трапеции.

Цели урока:

1. Образовательные: повторить ранее
   изученные формулы для вычисления
   площадей выпуклых фигур, вывести и
   научиться пользоваться формулами для
   вычисления площадей выпуклых
   четырехугольников, имеющих
   перпендикулярные диагонали;
2. Развивающие: развитие логического
   мышления, памяти, внимания, выработка
   математической зоркости;
3. Воспитательные: воспитание трудолюбия,
   интереса к предмету, умение внимательно
   выслушивать ответы одноклассников.

Необходимое оборудование:

• компьютер,

• проектор.

Ход урока.

1. Организационный момент.
2. Устная работа.

Проводится по чертежам,
выведенным с проектора на экран.

Задание. Для каждой из
геометрических фигур найти площадь, назвав
используемую формулу. Опрос ведется
фронтально, учащиеся могут отвечать по
желанию.

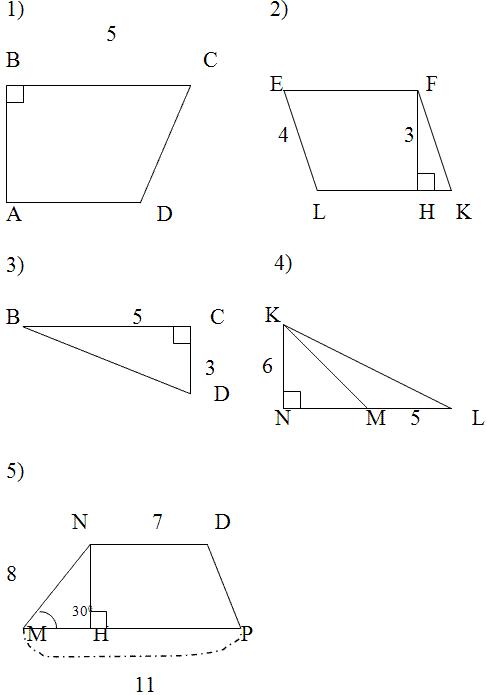
1. Введение новых знаний.

Учитель обращает внимание
учащихся на то, что до сих пор, в основном,
площади фигур вычислялись по двум
элементам: основанию и высоте, проведенной
к основанию. Однако, в случае, если в
четырехугольнике диагонали взаимно
перпендикулярны, его площадь можно
вычислить, зная длины диагоналей.

Учитель просит учащихся
сформулировать тему урока. Учащиеся
предлагают свои варианты темы урока.
Принимается такая: «Вычисление площади
выпуклого четырехугольника, имеющего
взаимно перпендикулярные диагонали».

Задача. Доказать, что площадь
выпуклого четырехугольника, имеющего
взаимно перпендикулярные диагонали, равна
половине произведения его диагоналей.

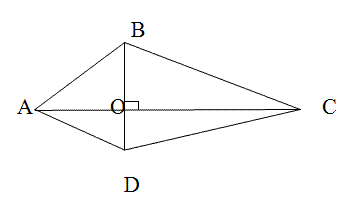
Запись на доске.

Дано:

ABCD – вып. четырехугольник,

AC ┴ BD.

Доказать:

S_ABCD=1/2 ACBD.

Доказательство:

1. пусть AC ∩ BD = O, тогда

S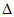_ABC=1/2
ACBО,
т.к. BO является высотой в 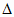ABC,

S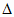_ABC=1/2
ACDO,
т.к. DO является высотой в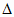
ADC.

1. S_ABCD= S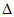_ABC+
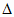   S_ADC
   = 1/2 ACBО
   + 1/2 ACDO
   = 1/2 AC(BO+DO)=
   1/2 ACBD,
   ч.т.д.

Учитель. Какие вы знаете
четырехугольники с взаимно-перпендикулярными
диагоналями?

Ученик. Ромб и квадрат.

Учитель. Давайте запишем
формулы в общем виде для вычисления
площадей ромба и квадрата для их диагоналей.

Запись на доске:

S_ромба=1/2d₁d₂, где
d_1, d₂ – диагонали ромба.

Учитель. Что можно сказать о
диагоналях квадрата, кроме того, что они
взаимно перпендикулярны?

Ученик. Диагонали квадрата
равны, то есть d₁ = d_2.

Учитель просит ученика
записать формулу для вычисления площади
квадрата по его диагонали.

Ученик пишет на доске:

S_{квадрата} =
½ d², где d – диагональ квадрата.

1. Закрепление выведенных формул.

Учитель. Приведите свои
примеры использования выведенных формул.

Ученик. Найти площадь ромба,
если его диагонали равны 3см и 6см.

Решение: S=1/2 36
= 9 (см²).

Ученик. Найти площадь
квадратного участка земли, если его
диагональ равна 10м.

Решение: S=1/2 10²=50
(м²).

Учитель. Придумайте обратные
задачи.

Ученик. Найти одну из
диагоналей ромба, если его площадь равна 20
см², а вторая диагональ 8 см.

Решение: d₁= 2S/d₂, d₁= 220/8
= 5 (см)

Ученик. Найти диагональ
квадрата, если его площадь равна 18 см².

Решение: d²=2S, d²=36, d=6(см).

Учитель. Давайте теперь решим
более сложную задачу, в которой известны
площадь ромба, а также соотношение между
длинами диагоналей, а требуется найти
диагонали.

(На эту задачу лучше вызвать
сильного ученика, т.к. она решается с
помощью уравнения и является сложной для
слабых учеников). Во время обдумывания
решения предложенной задачи средними и
сильными учениками класса, слабые получают
карточки-задания на отработку выведенных
формул. Каждая карточка содержит по 2
простые задачи типа:

1. Вычислить площадь ромба, если
   одна из его диагоналей равна 5 см, а другая
   в 4 раза больше.

2. Вычислить диагональ квадрата,
   если его площадь равна 32 см².

Задача (для средних и сильных
учеников).

Одна из диагоналей ромба, площадь
которого равна 27 см², в 1,5 раза больше
другой диагонали. Найти диагонали этого
ромба.

Ученик записывает на доске:

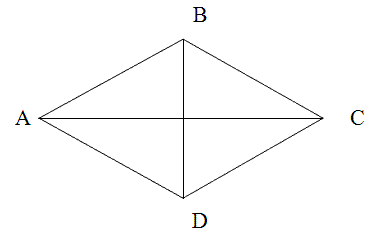
Дано:

ABCD – ромб,

AC = 1,5 BD,

S_ABCD = 27 см².

Найти:

AC, BD.

Решение:

1. S_ABCD = 1/2 ACBD.

Пусть BD = x см, тогда AC = 1,5x см. Т.к.
по условию задачи S_ABCD = 27 см², то
получаем уравнение:

1/21,5xx
= 27,

1,5x²=54,

x²=36,

x=6 ( x=-6 не подходит по смыслу
задачи).

1. BD = 6 см, AC = 1,56=
   9 см.

Ответ : 6 см и 9 см.

1. Итог урока.

Учитель. Какие новые формулы
мы сегодня узнали?

Ученик. Формулы для вычисления
площадей выпуклых четырехугольников,
имеющих взаимно-перпендикулярные
диагонали, в частности, для ромба и квадрата.

Учитель. Какая еще из известных
вам геометрических фигур может иметь
взаимно-перпендикулярные диагонали?

Ученик. Трапеция.

Учитель. Верно, значит можно
вычислить и площадь трапеции, если у нее
взаимно-перпендикулярные диагонали. Этими
формулами можно пользоваться наряду с
ранее изученными.

1. Домашнее задание (творческое).

• Придумать по 2 задачи (2 прямые и 2
  обратные) на применение изученных формул
  и записать их с решениями. Чем сложнее
  задача, тем выше оценка.
• Для слабых учеников (у кого не получится
  придумать задачи):

Задача. Найти площадь трапеции,
если ее диагонали взаимно перпендикулярны,
а их длины равны 10 см и 16 см.

Задачи 1 уровня

1.Найдите площадь прямоугольника, если его длина 2 дм, а ширина 4 см.

2.Найдите площадь параллелограмма, если одна из его сторон равна 6 см, а высота, проведенная к этой стороне, равна 9 см.

3.Катеты прямоугольного треугольника 12 и 8см. Найдите площадь треугольника.

4.Найдите площадь прямоугольника, если его длина 110 см, а ширина 10 м.

5.Найдите площадь прямоугольной трапеции, если основания равны 8 см и 10 см, а боковая сторона, перпендикулярная нижнему основанию равно 5 см.

6.Найдите площадь прямоугольника, если его длина 15 дм, а ширина 20 м.

7.Основания трапеции 6см и 8 см, высота 2 см. Найдите площадь трапеции.

8.Основания трапеции 9 см и 1 см, высота 4 см. Найдите площадь трапеции.

9.Основание треугольника 16, а высота, проведенная к основанию 5. Найдите площадь треугольника.

10.Основание параллелограмма равно 20, а высота, проведенная к основанию равна 7. Найдите площадь параллелограмма.

_______________________________________________________________________________________

Задачи 2 уровня.

1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

2.Найдите площадь ромба  с диагоналями  5см и 8 см.

3.Стороны параллелограмма равны 10 см и 18 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

4.Периметр квадрата 40 см. Найдите его площадь.

5.Площадь квадрата 81 кв. см. Найдите его периметр.

6.Найдите площадь прямоугольного треугольника, если его катеты 8 см и 15 см.

7.Основание равнобедренного треугольника 16 см, а медиана, проведенная к основанию, равна 6 см. Найдите площадь треугольника.

8.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.

_____________________________________________________________________________________

Задачи 3 уровня.

1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

2.Высоты параллелограмма равны 3 см и 4 см, острый угол между сторонами равен 30 градусов. Найдите площадь параллелограмма.

3.Найдите площадь трапеции со сторонами 6 см, 6 см, 10см и 14 см, если угол между боковой стороной  и нижнем основанием 30 градусов.

4.Стороны параллелограмма равны 8 см и 15 см и угол между ними 150 градусов. Найдите площадь параллелограмма.

5.Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если его катеты 8 см и 6 см., а гипотенуза равна 10 см

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Содержание страницы:

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

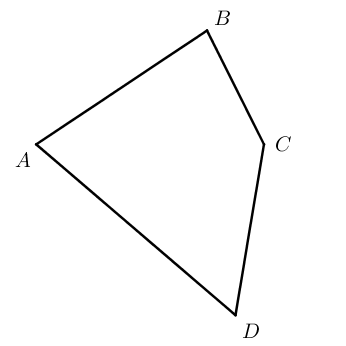
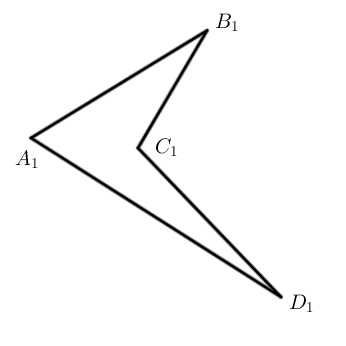
Четырехугольники бывают выпуклые  ( A B C D )  и невыпуклые  ( A 1 B 1 C 1 D 1 ) .

Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон:  A B  и  A D ,   A B  и  B C ,   B C  и  C D ,   C D  и  A D .

Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон:  A B  и  C D ,   B C  и  A D .

Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин:  A  и  C ,   B  и  D .

Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины.  A C  и  B D  – диагонали четырехугольника  A B C D .

Диагонали выпуклого четырехугольника пересекаются в одной точке.

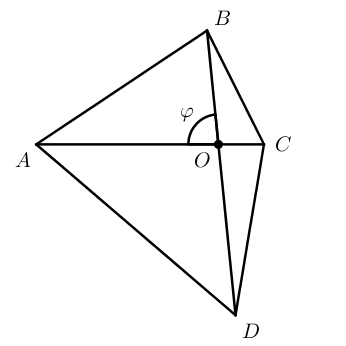
Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где  d 1  и  d 2  – диагонали четырехугольника,  φ  – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов: параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций: произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Параллелограмм

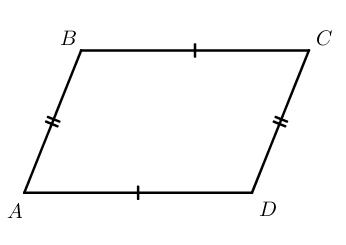
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

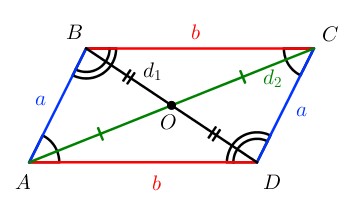
• Противолежащие стороны равны.
• Противоположные углы равны.
• Диагонали точкой пересечения делятся пополам.
• Сумма углов, прилежащих к одной стороне, равна  180 ° .
• Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )

Площадь параллелограмма можно найти по трём формулам.

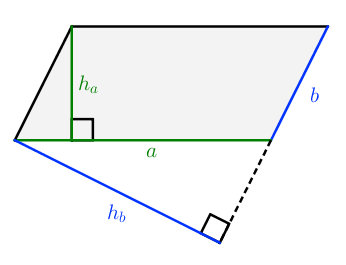
S = a ⋅ h a = b ⋅ h b

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

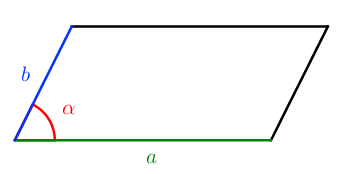
S = a ⋅ b ⋅ sin α

Как произведение двух смежных (соседних) сторон на синус угла между ними.

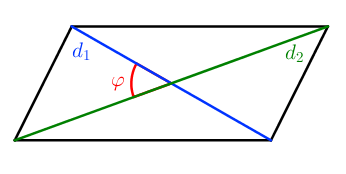
S = 1 2 ⋅ d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Ромб

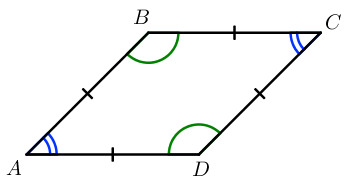
Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

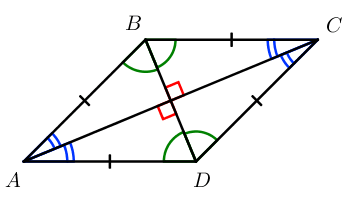
• Диагонали пересекаются под прямым углом.
• Диагонали являются биссектрисами углов, из которых выходят.
• Сохраняются все свойства параллелограмма.

Площадь ромба можно найти по трём формулам.

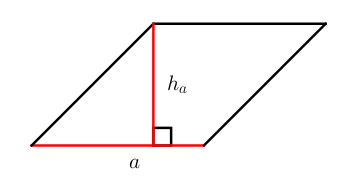
S = a ⋅ h

Как произведение стороны ромба на высоту ромба.

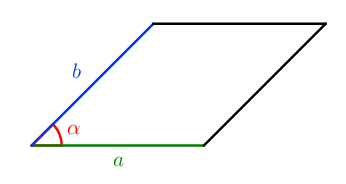
S = a 2 ⋅ sin α

Как квадрат стороны ромба на синус угла между двумя сторонами.

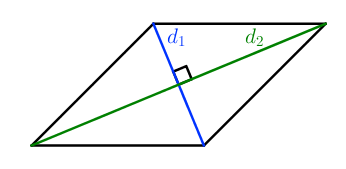
S = 1 2 ⋅ d 1 ⋅ d 2

Как полупроизведение диагоналей ромба.

Прямоугольник

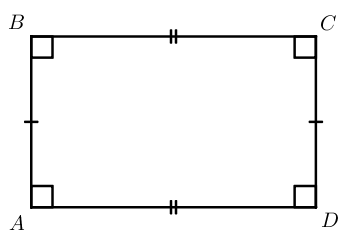
Прямоугольник – это параллелограмм, у которого все углы равны  90 ° .

Свойства прямоугольника:

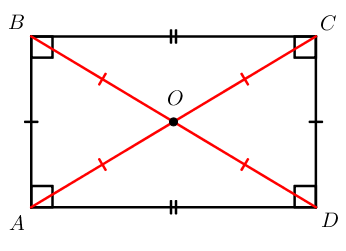
• Диагонали прямоугольника равны.
• Сохраняются все свойства параллелограмма.

Площадь прямоугольника можно найти по двум формулам:

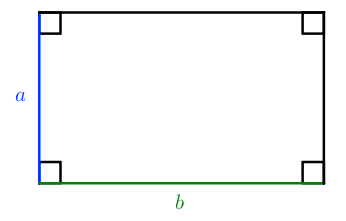
S = a ⋅ b

Как произведение двух смежных (соседних) сторон прямоугольника.

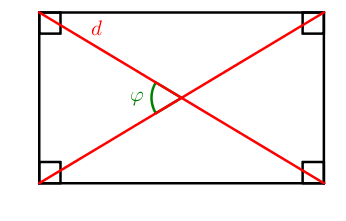
S = 1 2 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Квадрат

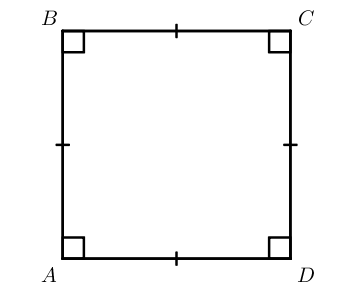
Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

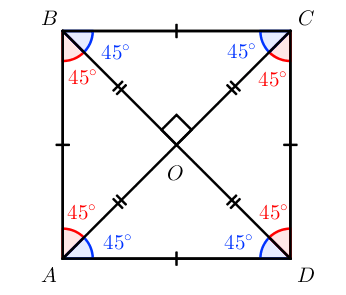
• Сохраняет свойства ромба.
• Сохраняет свойства прямоугольника.

Площадь квадрата можно вычислить по двум формулам:

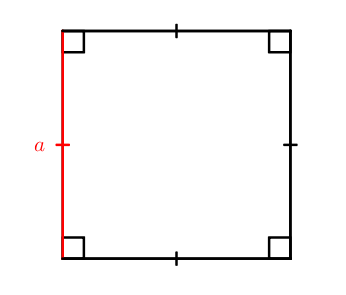
S = a 2

Как квадрат стороны.

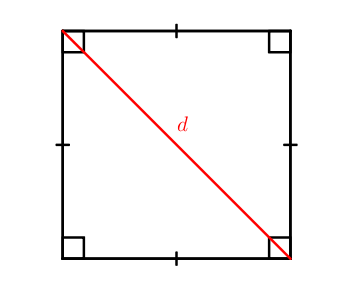
S = d 2 2

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

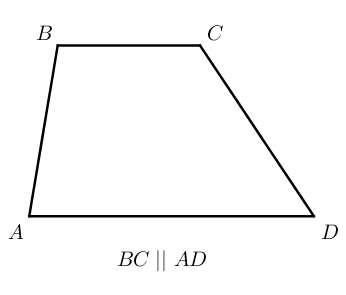
Стороны, которые параллельны друг другу называются основаниями, другие две стороны называются боковыми сторонами.

B C  и  A D  – основания,  A B  и  C D  – боковые стороны трапеции  A B C D .

Свойства трапеции:

сумма углов, прилежащих к боковой стороне, равна  180 ° .

∠ A + ∠ B = 180 °

∠ C + ∠ D = 180 °

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

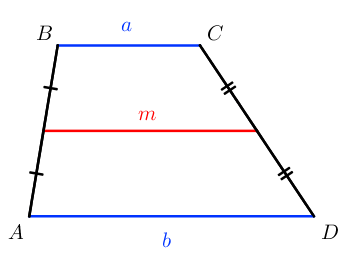
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

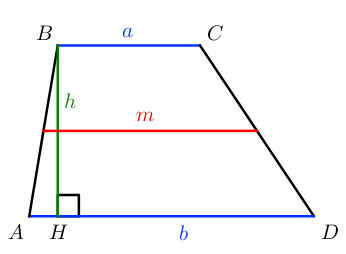
S = a + b 2 ⋅ h = m ⋅ h

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

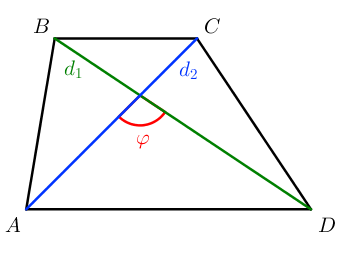
S = 1 2 d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

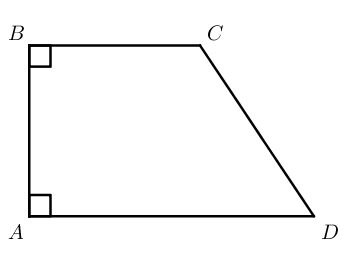
Прямоугольная трапеция – трапеция, у которой два угла прямые.

Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

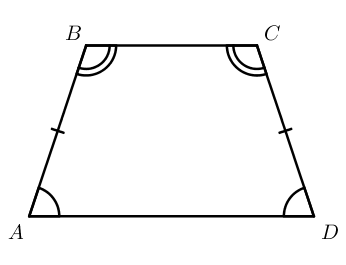
Свойство равнобокой трапеции: углы при основании равны

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с четырехугольниками

Скачать домашнее задание к уроку 4.