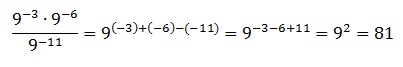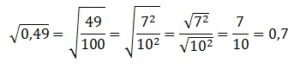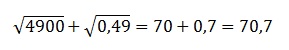Как решать задания найти значение выражения - Сайт, где вы сможете решить свои вопросы

Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.

Поиск значения числовых выражений

Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.

Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:

Числа (целые, дробные и т.д.);
Знаки: «+», «—», «•» и «÷».

Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.

Пример 1. Решение числового выражения

Задача. Решить:

20 — 2 • 10 ÷ 5 — 4 = ?

Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:

20 — 4 — 4 = ?

Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.

Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.

Ответ. 12

Пример 2. Решение числового выражения

Задача. Решить:

0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?

Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:

0,2 — (— 20) + 10

Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:

0,2 + 20 + 10 = 30,2

Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2

Ответ. 30,2

Находим значение выражения со скобками

Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.

Пример 3. Значение числового выражения со скобками

Задача. Решить:

5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?

Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:

7 — 2 • 3 = 7 — 6 = 1
6 — 4 = 2

Когда скобки решены, подставляем полученные значения в наш пример:

5 + 1 • 2 ÷ 2

Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:

1 • 2 = 2
2 ÷ 2 = 1

Упрощенное выражение выглядит следующим образом:

5 + 1 = 6

Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6

Ответ. 6

Значение числового выражения со скобками

Задача. Решить:

4 + (3 + 1 + 4 • (2+3)) = ?

Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:

3 + 1 + 4 • (2+3)

В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:

2 + 3 = 5

Теперь можем подставить определенное значение в общую скобку:

3 + 1 + 4 • 5

Начинаем решение с умножения и далее слева направо:

4 • 5 = 20
3 + 1 = 4
4 + 20 = 24

Далее подставляем полученный ответ вместо большой скобки и получаем:

4 + 24 = 28

Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28

Ответ. 28

Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.

Поиск значения выражения с корнями

Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:

Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
Извлекаем корень из числа, которое получили в результате решения обычного примера.

Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.

Значение числового выражения с корнями

Задача. Решить:

√ 2² • 2² • 3² = ?

Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:

√2² • √2² • √3² = ?

Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:

2 • 2 • 3 = 12

Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12

Ответ. 12

Нет времени решать самому?

Наши эксперты помогут!

Находим значение числовых выражений со степенями

Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.

Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].

Задача. Решите:

[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]

Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:

[(a cdot b)^{r}=a^{r} cdot b^{r}]

Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:

[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]

Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:

[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]

Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]

Ответ. 21

Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:

[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]

Ответ. 21

Задача. Решить:

[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]

Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25

Выражения с дробями

Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.

Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.

Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.

Задача. Решить:

[ 6 frac{2}{13}+4 frac{1}{13}=? ]

Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:

[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]

Теперь выполняем вычисления в знаменателе и числителе и находим ответ:

[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]

Ответ. [10 frac{3}{13}]

Примеры(2):

Задача. Решить:

[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]

Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:

[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]

Теперь можем придать нашему первоначальному выражению следующий вид:

[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]

Ответ. [-frac{3}{4}].

Выражения с логарифмами

Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.

Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).

В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.

Задача. Решить:

[log _{27} 81+log _{27} 9=?]

Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:

Это позволит нам решить пример следующим образом:

Ответ. 2

Решаем выражения с тригонометрической функцией

Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:

Синус;
Косинус;
Котангенс;
Тангенс;
Секанс;
Косеканс.

Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.

В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.

Задача. Решить:

[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]

Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:

sin217 — sin (90 + 127) = cos127

Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:

[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]

Вспоминаем, что по тригонометрическому тождеству sin²a+ cos² a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin²127+ cos²127) преобразуем в единицу и получаем:

[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]

Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.

Задача. Решить:

[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]

Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:

[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]

Ответ. — 6.

Общий случай: находим значения выражений с дробями, функциями, степенями и не только

Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:

Степени;
Скобки;
Корни;
Функции и т.д.

Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.

Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:

Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.

Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.

Задача. Решить:

[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]

Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:

[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]

Со знаменателем дела обстоят куда проще:

[ ln e^{2}=2 ]

Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27

Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.

Как найти значение выражения числителя дроби, подкорневого значения рационально?

Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.

Правило 1. Когда произведение равно нулю

Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.

Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.

Правило 2. Группировка и вынесение чисел

Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.

Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]

Решение примеров с переменными

Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.

Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:

2x — y = 2 • 2,5 — 2 = 3

При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.

Источник

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения $frac{2,88cdot 44,5}{0,288cdot 4,45}.$

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

$frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.$

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения $7frac{9}{13}:frac{5}{13}.$

$7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.$

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

$left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0$ .

3. Вычислите .

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:

Упростим множители:

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=$

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=$

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

$a^{m}cdot a^{n}=a^{m+n}.$

$frac{a^{m}}{a^{n}}=a^{m-n}.$

$left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.$

$a^{n}b^{n}=left ( ab right )^{n}.$

$frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.$

5. Найдите значение выражения: $frac{a^{8,9}}{a^{4,9}}$ при a=4.

$frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.$

Применили формулу частного степеней $frac{a^{m}}{a^{n}}=a^{m-n}.$

Ответ: 256.

6. Вычислите $left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.$

$left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=$

$=left (2^{frac{1}{2}} right )^{2}=2.$

Ответ: 2.

7. Вычислите $frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}$ , если .

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

$frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.$

Ответ: 4,5.

8. Вычислите $0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.$

$0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.$

Применили формулу для произведения степеней: $a^{m}cdot a^{n}=a^{m+n}.$

Ответ: 12.

9. Вычислите $frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.$

$frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.$

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

$log _{a}b=cLeftrightarrow a^{c}=b$ .

При этом > 0, > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: $boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.$

Логарифм произведения равен сумме логарифмов: $boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.$

Логарифм частного равен разности логарифмов: $boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.$

Формула для логарифма степени: $boldsymbol{log _{a}b^{m}=mlog_{a}b}.$

Формула перехода к новому основанию: $boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.$

10. Вычислите: $log _{5}7cdot log _{7}25$ .

$log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.$

Снова формула перехода к другому основанию.

$log _{a}b=frac{1}{log _{b}a}$ , поэтому
$log _{a}bcdot log _{b};a=1.$

11. Найдите $log _{a}frac{a^{6}}{b^{4}}$ , если $log _{a}b=-2$ .

$log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.$

12. Найдите значение выражения $frac{log _{2}80}{3+log _{2}10}$ .

$frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.$

13. Найдите значение выражения $frac{log _{9}sqrt[10]{8}}{log _{9}8}$ .

$frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1$ .

14. Найдите значение выражения $left ( 1-log _{3}18 right )left ( log _{6}54 -1right )$ .

$left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.$

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: $44sqrt{3}tgleft ( -480^{circ} right ).$

$44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.$

16. Найдите , если $sin alpha =-frac{2sqrt{2}}{3}$ и $alpha in left ( frac{3pi }{2};;2pi right )$ .

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.$

Т.к. $alpha in left ( frac{3pi }{2};;2pi right )$ , то $cos alpha =frac{1}{3}.$
$3cos alpha =3cdot frac{1}{3}=1.$

17. Найдите , если $sin alpha =-frac{1}{sqrt{5}}$ и

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.$

Т.к. , то
$cos alpha =frac{2}{sqrt{5}}.$

$tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.$

18. Найдите значение выражения: $frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.$

$frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=$

$=frac{26cos 14^{circ}}{cos 14^{circ}}=26.$

Применили формулу приведения.

19. Упростите выражение: $frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.$

$frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.$

Применили формулу приведения.

20. Найдите , если .

$2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.$

21. Вычислите $frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }$ , если

$frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=$

$=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.$

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти $sqrt{a^{2}}$ .

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}$ при .

Запомним: $sqrt{a^{2}}=left | a right |.$

$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |$ .

Если , то и .

При этом и .

При получаем: .

Ответ: 2.

23. Найдите значение выражения

$x+sqrt{x^{2}-24x+144}$ при xleq 12 .

При xleq 12 получим:

$x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.$

Ответ: 12.

24. Найдите $frac{gleft ( 5-x right )}{gleft ( 5+x right )}$ , если , при .

Что такое ? Это функция, каждому числу ставящая в соответствие число . Например, ;

Тогда:

Заметим, что .

Значит, при
$frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1$ .

25. Найдите $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ , если $pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ , при .

$pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ — функция, каждому числу b ставящая в соответствии число
$left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ .

Тогда при bneq 0.

$pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right )$ , и значение выражения $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ равно 1.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями. При выполнении задания №8 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений. В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости. Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.

Теория к заданию №8

Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:

Кроме этого, нам понадобятся формулы сокращенного умножения:

Квадрат суммы

(a + b)² = a² + 2ab + b²

Квадрат разности

(a – b)² = a² – 2ab + b²

Разность квадратов

a² – b² = (a + b)(a – b)

Куб суммы

(a + b)³ = a³ + 3a²b + 3ab² + b³

Куб разности

(a – b)³ = a³ – 3a²b + 3ab² – b³

Сумма кубов

a³ + b³ = (a + b)( a² – ab + b²)

Разность кубов

a³ – b³ = (a – b)( a² + ab + b²)

Правила операций с дробями:

Задание 8OM21R

Найти значение выражения

(3∙8)737∙85

В числителе дроби возведем в степень каждый множитель:

(3∙8)737 ∙85=37∙8737∙85

Теперь сократим (выполним деление степеней), сократятся 37 полностью, а при сокращении на 85 по свойству степеней останется 82, возведем 8 во вторую степень, получим 64, т.е.

(3∙8)737 ∙85=37∙8737∙85=82=64

Ответ: 64

pазбирался: Даниил Романович | обсудить разбор

Задание OM1306o

Найдите значение выражения:

Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

сокращаем выражение на (a–5b):

Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):

Подставим полученные значения в выражение и найдем конечный результат:

Ответ: 39

pазбирался: Даниил Романович | обсудить разбор

Задание OM1305o

Найдите значение выражения при x = 12:

Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

Подставляем числовое значение для х в полученное выражение и находим результат:

Ответ: 0,6

pазбирался: Даниил Романович | обсудить разбор

Задание OM1304o

Найдите значение выражения

где a = 9, b = 36

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю – это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

9b² + 5a – 9b²

Приведем подобные слагаемые – это 9b² и – 9b², в числителе остается 5a. Запишем конечную дробь:

5a/b

Вычислим её значение, подставив числа из условия:

5•9/36 = 1,25

Ответ: 1,25

pазбирался: Даниил Романович | обсудить разбор

Задание OM1303o

Найдите значение выражения:

при x = √45 , y = 0,5

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель – это 15 x y, для этого необходимо первую дробь домножить на 5 y – и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y – (3 x + 5 y) = 5 y – 3 x – 5 y = – 3 x

Тогда дробь примет вид:

Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: – 1/5 y

Подставим значение y = 0,5: – 1 / (5 • 0,5) = – 1 / 2,5 = – 0,4

Ответ: -0,4

pазбирался: Даниил Романович | обсудить разбор

Задание OM1302o

Найдите значение выражения:

при a = 13, b = 6,8

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

Сокращаем (a-b):

И получаем:

a/2

Подставляем значение a = 13:

13 / 2 = 6,5

Ответ: 6,5

pазбирался: Даниил Романович | обсудить разбор

Задание OM1301o

Найдите значение выражения: (x + 5)² – x (x- 10) при x = – 1/20

В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:

(x + 5)² – x (x – 10) = x² + 2 • 5 • x + 25 – x²+ 10x

Затем приведем подобные слагаемые:

x² + 2 • 5 • x + 25 – x²+ 10x = 20 x + 25

Далее подставим x из условия:

20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24

Ответ: 24

pазбирался: Даниил Романович | обсудить разбор

Задание OM0807o

Найдите значение выражения:

Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

Ответ: 81

pазбирался: Даниил Романович | обсудить разбор

Задание OM0806o

Найдите значение выражения:

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:

По аналогии извлекаем и 2-й корень:

В итоге получаем:

Ответ: 70,7

pазбирался: Даниил Романович | обсудить разбор

Задание OM0805o

Значение какого из выражений является рациональным числом?

√6-3
√3•√5
(√5)²
(√6-3)²

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ: 3

pазбирался: Даниил Романович | обсудить разбор

Задание OM0804o

Какое из данных ниже чисел является значением выражения?

Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:

16 – 14 = 2

Суммарно наши действия выглядят так:

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор

Задание OM0803o

Какое из данных чисел является рациональным?

√810
√8,1
√0,81
все эти числа иррациональны

Для решения этой задачи нужно действовать следующим образом:

Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:

0,9

Рассмотри каждое из них:

0,9 = √(0,9)² = √0,81

90 = √(90²) = √8100

Следовательно, число √0,81 является рациональным, остальные же числа

√810
√8,1

хотя и похожи на форму 9 в квадрате, не являются рациональными.

Таким образом, правильный ответ третий.

Ответ: √0,81

pазбирался: Даниил Романович | обсудить разбор

Задание OM0802o

Значение какого из данных ниже выражений является наибольшим?

3√5
2√11
2√10
6,5

Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:

3√5

Переносим 3 под корень:

3√5 = √(3² •5) = √(9•5) = √45

2√11

Переносим 2 под корень:

2√11 = √(2² • 11) = √(4 • 11) =√44

2√10

Переносим 2 под корень:

2√10 = √(2² • 10) = √(4 • 10) =√40

Возводим 6,5 в квадрат:

6,5 = √(6,5²) = √42,25

3-2

Посмотрим на все получившиеся варианты:

3√5 = √45
2√11 = √44
2√10 = √40
6,5 = √42,25

Следовательно, правильный ответ первый.

Ответ: 3√5

pазбирался: Даниил Романович | обсудить разбор

Задание OM0801o

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11ⁿ?

121ⁿ
11ⁿ⁺²
11²ⁿ
11ⁿ⁺³

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

при умножении степени складываются
приделении степени вычитаются
при возведении степени в степень степени перемножаются
при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11².

121 • 11ⁿ= 11² • 11ⁿ

С учетом правила умножения, складываем степени:

11² • 11ⁿ= 11ⁿ⁺²

Следовательно, нам подходит второй ответ.

Ответ: 2

pазбирался: Даниил Романович | обсудить разбор

Источник

В задании № (6) ОГЭ нужно найти значение числового выражения.

Пример:

найди значение выражения

1,2×(18+0,015)

За правильное выполнение задания даётся (1) первичный балл. За неправильное ставится (0) баллов.

Алгоритм выполнения задания

Определяем порядок вычислений, если нужно выполнить несколько математических действий.

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Проводим вычисления строго по порядку, не округляя.
Записываем ответ.

Обрати внимание!

Ответом является число или последовательность цифр, которую необходимо записать без пробелов, запятых и других дополнительных символов. Если получилась обыкновенная дробь, то ответ запиши в виде десятичной.

Как решить задание из примера?

Определим, в каком порядке выполним вычисления 1,2×(18+0,015).
Сначала — действие в скобках (сложение), а затем — умножение.
Чтобы выполнить сложение, переведём 18 в десятичную дробь (нужно числитель разделить уголком на знаменатель без остатка). 1,0−8¯8¯0,12520−16¯40−40¯018=0,125.
Выполним сложение двух десятичных дробей. 0,125+0,015 (=) 0,14.
Выполним умножение. 1,2
·0,14=0,168.
Запишем ответ в виде десятичной дроби, не округляя.
Ответ: 0,168.

Источник

Поиск значения числовых выражений

Значение числового выражения со скобками

Поиск значения выражения с корнями

Значение числового выражения с корнями

Находим значение числовых выражений со степенями

Выражения с дробями

Выражения с логарифмами

Решаем выражения с тригонометрической функцией

Общий случай: находим значения выражений с дробями, функциями, степенями и не только

Как найти значение выражения числителя дроби, подкорневого значения рационально?

Правило 1. Когда произведение равно нулю

Правило 2. Группировка и вынесение чисел

Решение примеров с переменными

Теория к заданию №8

Вам также может понравиться

Как найти образ биоса

Как найти адрес видео по ссылке

Как найти фокальное расстояние эллипса

Добавить комментарий Отменить ответ