Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике
В задании №1 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Уравнения, сводящиеся к квадратным
1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:
Выбираем меньший корень.
Ответ: – 6,5.
2. Решите уравнение
Возведем в квадрат левую часть уравнения. Получим:
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:
Это довольно простой тип уравнений. Главное – внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.
4. Решите уравнение:
Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит,  .
.
Возведём обе части уравнения в квадрат:
Условие  при этом выполняется.
при этом выполняется.
5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:
Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

Мы получили, что . Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов.

Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение
Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
8. Решите уравнение
Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
9. Решите уравнение
Представим в виде степени с основанием 3 и воспользуемся тем, что
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел;
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений:  . Значит,
. Значит, 
Представим 2 в правой части уравнения как – чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом 
11. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:


12. Решите уравнение:
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.


13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: и
Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? – Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену Получим:

Получаем решения: Вернемся к переменной x.
Поделим обе части уравнения на и умножим на 4.
Первой серии принадлежат решения
Вторая серия включает решения
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это
15. Решите уравнение В ответе напишите наименьший положительный корень.
Сделаем замену Получим: Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на
Выпишем несколько решений уравнения и выберем наименьший положительный корень:
Наименьший положительный корень
Мы разобрали основные типы уравнений, встречающихся в задании №1 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!
Задание №7 ЕГЭ по математике базового уровня
Простейшие уравнения
В задании №7 базового уровня ЕГЭ по математике необходимо решить
Простейшие (Protozoa) – тип одноклеточных животных.
Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня
Вариант 7МБ1
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Алгоритм выполнения
- Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
- Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
- Преобразовать левую часть.
- Преобразовать правую часть.
- Решить уравнение относительно x, то есть найти неизвестный множитель.
Решение:
Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.
(x + 3) 2 = x 2 + 2 · x · 3 + 3 2 = x 2 + 6x + 9
Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.
(x – 9) 2 = x 2 – 2 · x · 9 + 9 2 = x 2 – 18x + 81
После преобразования выражение примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x 2 + 6x + 9 = x 2 – 18x + 81
Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.
x 2 + 6x – x 2 + 18x = 81 – 9
Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.
x 2 + 6x – x 2 + 18x = (x 2 – x 2 ) + (6x +18x) = 0 + 24x = 24x
Выражение примет вид:
Преобразуем правую часть. 81 – 9 = 72
Выражение примет вид:
Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
Решение в общем виде:
Вариант 7МБ2
Алгоритм выполнения
- Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
- Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
- Преобразовать левую часть.
- Преобразовать правую часть.
- Решить уравнение относительно x, то есть найти неизвестный множитель.
Решение:
Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.
(x + 2) 2 = x 2 + 2 · x · 2 + 2 2 = x 2 + 4x + 4
Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.
(x – 8) 2 = x 2 – 2 · x · 8 + 8 2 = x 2 – 16x + 64
После преобразования выражение примет вид:
x 2 + 4x + 4 = x 2 – 16x + 64
Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.
x 2 + 4x – x 2 + 16x = 64 – 4
Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.
x 2 + 4x – x 2 + 16x = (x 2 – x 2 ) + (4x +16x) = 0 + 20x = 20x
Выражение примет вид:
Преобразуем правую часть. 64 – 4 = 60
Выражение примет вид:
Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
Решение в общем виде:
Вариант 7МБ3
Алгоритм выполнения
- Перенести вычитаемое в правую сторону равенства с противоположным знаком.
- Преобразовать правую часть с учетом свойства: logax + logay = loga (x · y).
- Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
- Решить уравнение относительно x.
Решение:
Вариант 7МБ4
Найдите корень уравнения 3 x− 3 = 81.
Алгоритм выполнения
- Привести выражения в степенях к одинаковому основанию. В данном случае – это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
- Когда основания равны, можно приравнять значения степеней
Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором – 9, при третьем – три.
Значит, 81 это три в четвертой степени. Запишем это:
Решение:
Ответ: 7
Вариант 7МБ5
Найдите корень уравнения log2( x − 3) = 6 .
Алгоритм выполнения
- Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.
Решение:
Вариант 7МБ6
Найдите отрицательный корень уравнения x 2 − x − 6 = 0.
Алгоритм выполнения
- Вычислить дискриминант
- Найти корни
- Выбрать необходимый корень
Решение:
D = -(1) 2 − 4 • 1 • (-6) = 25
Так как нам необходим отрицательный корень – ответ -2
Вариант 7МБ7
Решите уравнение х 2 = –2х + 24.
Если уравнение имеет больше одного
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Алгоритм выполнения
- Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
- Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
- Записываем в качестве ответа большее из полученных 2 чисел.
Решение:
Поскольку требуется указать больший из корней, то ответом будет 4.
Вариант 7МБ8
Найдите корни уравнения 4 х–6 = 64.
Алгоритм выполнения
- Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
- Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
- Находим корень ур-ния.
Решение:
Вариант 7МБ9
Найдите корень уравнения log3 (2x – 5) = 2.
Алгоритм выполнения
- Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов logxx=1 и logxy n =nlogxy.
- Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
- Решаем полученное линейное ур-ние.
Решение:
Вариант 7МБ10
Найдите корень уравнения 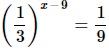
Алгоритм выполнения
- Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а) х =а –х .
- Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
- Решаем полученное линейное ур-ние.
Решение:
Вариант 7МБ11
Найдите корень уравнения (х – 8) 2 = (х – 2) 2 .
Алгоритм выполнения
- Раскрываем скобки слева и справа, используя ф-
Луб – это сложная проводящая ткань, по которой продукты фотосинтеза (органические вещества) транспортируются из листьев ко всем органам растения (к корневищам, плодам, семенам и т. д.).
Решение:
х 2 – 2 · х ·8 + 8 2 = х 2 – 2 · х · 2 + 2 2
Вариант 7МБ12
Найдите корень уравнения 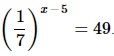
Алгоритм выполнения
- Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а) х =а –х .
- Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
- Решаем его.
Решение:
Вариант 7МБ13
Решите уравнение х 2 – 25 = 0
Алгоритм выполнения
- Переносим 25 в правую часть ур-ния.
- Выражаем из ур-ния х путем извлечения корня из 25.
- Определяем корни, сравниваем их, определяем больший.
Решение:
Для ответа берем 5.
Вариант 7МБ14
Найдите корень уравнения 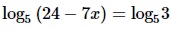
Алгоритм выполнения
- Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
- Решаем полученное линейное ур-ние.
Решение:
Вариант 7МБ15
Найдите корень уравнения 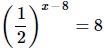
Алгоритм выполнения
- Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а) х =а –х .
- Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
- Решаем его.
Решение:
Вариант 7МБ16
Найдите корень уравнения 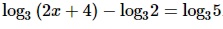
Алгебра 7 Дорофеев КР-04
Контрольная 4 по алгебре 7 класс (УМК Дорофеев).
Алгебра 7 Дорофеев КР-04. Контрольная работа по алгебре «Уравнения» с ОТВЕТАМИ на все 4 варианта. Цитаты из пособия «Алгебра. Контрольные работы 7 класс» (авт. Л.В. Кузнецова и др.), которое используется в комплекте с учебником «Алгебра 7 класс / Г.В. Дорофеев и др. — М.: Просвещение». Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных рекомендуем купить указанное пособие.
Контрольная работа «Уравнения» с ответами
В контрольной работе проверяются умения:
- определять, является ли число корнем уравнения;
- применять правила преобразования уравнения;
- составлять уравнение по условию задачи;
- решать уравнения;
- решать задачи с помощью уравнения.
Контрольная работа по алгебре (образец)
7 класс (Дорофеев). КР-04.


КР-04. Уравнения
Вариант 1
1 Какие из чисел: -2; -1; 0, 1; 2 — являются корнями уравнения х 2 — х — 2 = 0?
2 Найдите корень уравнения: а) 2х/3 = 6; б) 5 — 0,2х = 1; в) Зx — 7 = х — 11.
3 Составьте уравнение по условию задачи и решите её: «Масса яблок составляет 3/10 от массы фруктового салата. Сколько получится салата, если имеется 150 г яблок?»
4 Решите уравнение: а) (8 — Зх) — (4 + 2х) = 9; б) x/3 + x/6 = 1.
5 Решите задачу с помощью уравнения: «Груша тяжелее сливы в 5 раз. Сколько весит груша и сколько слива, если 4 такие груши и 14 таких слив вместе весят 1 кг 700 г?»
6 Решите уравнение относительно х: 4а — 3x = с – 6x.
7 При каком значении х выражения 3х + 5 и 2х — 6 имеют противоположные значения?
Дополнительное задание. *8. Решите задачу, составив уравнение: «Шнур длиной 7,2 м разрезали на две части. Определите длину каждой части, если известно, что одна из них на 20% короче другой».
Вариант 2
1 Какие из чисел: -3; -1; 0; 1; 3 — являются корнями уравнения х 2 + 2х — 3 = 0?
2 Найдите корень уравнения: а) 3x/5 = 15; б) 7 — 0,3x = 1; в) 3 + 5x = 2х — 6.
3 Составьте уравнение по условию задачи и решите её: «Масса изюма составляет 3/20 от массы фруктовой смеси. Сколько получится фруктовой смеси, если имеется 90 г изюма?»
4 Решите уравнение: а) (x — 3) — (3x — 4) = 15; б) x/2 + x/3 = 10.
5 Решите задачу с помощью уравнения: «Тетрадь легче альбома на 120 г. Сколько весит тетрадь и сколько альбом, если 10 таких тетрадей и 5 таких альбомов вместе весят 1 кг 500 г?»
6 Решите уравнение относительно x: 4х — b = 2х — 3с.
7 При каком значении x выражения 2х — 3 и 3x + 5 имеют противоположные значения?
Дополнительное задание. *8. Решите задачу, составив уравнение: «Ленту длиной 7,2 м разрезали на две части. Определите длину каждой части, если известно, что одна из них на 40% длиннее другой».
[spoiler title=”источники:”]
http://algeomath.ru/algebra-7-dorofeev-kr-04/
[/spoiler]

СДАМ ГИА: РЕШУ ВПР
Образовательный портал для подготовки к работам
Математика для 7 класса
математика–7
≡ Русский язык
Русский язык–2
Русский язык–4
Русский язык–5
Русский язык–6
Русский язык–7
Русский язык–8
≡ Математика
Математика–4
Математика–5
Математика–6
Математика–7
Математика–7 угл.
Математика–8
Математика–8 угл.
≡ Физика
Физика–7
Физика–7 угл.
Физика–8
Физика–8 угл.
Физика–11
≡ Биология
Биология–5
Биология–6
Биология–6 (конц.)
Биология–7
Биология–8
Биология–8 (конц.)
Биология–11
≡ География
География–6
География–7
География–8
География–11
≡ История
История–5
История–6
История–7
История–8
История–11
≡ Обществознание
Обществознание–6
Обществознание–7
Обществознание–8
Окружающий мир–4
≡ Химия
Химия–8
Химия–11
≡ Английский язык
Английский язык–7
Английский язык–11
≡ Немецкий язык
Немецкий язык–7
Немецкий язык–11
Французский язык
сайты – меню – вход – новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
О работе
Каталог заданий
Варианты
Ученику
Учителю
Школа
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
На сайте что-то не так? Отключите адблок
Новости
1 мая
Новый сервис: можно исправить ошибки!
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
26 марта
Появились каталоги ВПР по углубленной физике для 7 и 8 класса
6 марта
Изменения ВПР 2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
ЧУЖОЕ НЕ БРАТЬ!
Семёнова, не укради!
Все новости
Наша группа
Каталог заданий.
Задания для подготовки
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 9 № 8 

i
Решите уравнение 2 + 3x = − 2x − 13.
Источник: Демонстрационная версия ВПР по математике 7 класс 2018−2023
Решение
·
Помощь
2
Тип 9 № 805 

Найдите корни уравнения
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение
·
Помощь
3
Тип 9 № 808 

Решите уравнение
Решение
·
Помощь
4
Тип 9 № 809 

Решите уравнение
Решение
·
Помощь
5
Тип 9 № 816 

Решите уравнение
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
|
Контрольная работа по теме: «Решение уравнений» |
Контрольная работа по теме: «Решение уравнений» |
|
ВАРИАНТ 1 1. Решите уравнения: а) 13х– 26 = -130; б) 5х −3 = 3х −11; в)24(х +2) = 6(х −4); г) Решите задачу с помощью уравнения: 2. В одной бочке в 3 раза больше бензина, чем в другой. Если из первой бочки отлить 78 л бензина, а во вторую добавить 42 л, то бензина в бочках будет поровну. Сколько бензина в каждой бочке? 3. Найдите корень уравнения 4. Теплоход за 7 ч проходит такой же путь, как катер за 4 ч. Найдите скорость теплохода, если она меньше скорости катера на 24 км/ч. 5. а) 4(0,2x – 7) – 5(0,3x + 6) = 5; б) 6y – 20 = 2(5y – 10) – 4y; в) 6(1 + 5v) = 5(1 + 6v). |
ВАРИАНТ 2 1. Решите уравнение: а) 17х– 34 = –170; б) 7х + 5 = 9х – 11; в) 5(х −6) = 15(х −8); г) Решите задачу с помощью уравнения: 2. В одном зале кинотеатра в 2 раза больше зрителей, чем в другом. Если из первого зала уйдут 37 человек, а во второй придут 50, то зрителей в обоих залах будет поровну. Сколько зрителей в каждом зале? 3. Найдите корень уравнения 4. Скорость автобуса на 26 км/ч меньше скорости легкового автомобиля. Автобус за 5 ч проходит такой же путь, как легковой автомобиль за 3 ч. Найдите скорость автобуса. 5. а) 3(0,4x + 7) – 4(0,8x – 3) = 2; б) 2x + 5 = 2(x + 1) + 11; в) 15(v + 2) – 30 = 15v. |
|
Контрольная работа по теме: «Решение уравнений» |
Контрольная работа по теме: «Решение уравнений» |
|
ВАРИАНТ 1 1. Решите уравнения: а) 13х– 26 = -130; б) 5х −3 = 3х −11; в)24(х +2) = 6(х −4); г) Решите задачу с помощью уравнения: 2. В одной бочке в 3 раза больше бензина, чем в другой. Если из первой бочки отлить 78 л бензина, а во вторую добавить 42 л, то бензина в бочках будет поровну. Сколько бензина в каждой бочке? 3. Найдите корень уравнения 4. Теплоход за 7 ч проходит такой же путь, как катер за 4 ч. Найдите скорость теплохода, если она меньше скорости катера на 24 км/ч. 5. а) 4(0,2x – 7) – 5(0,3x + 6) = 5; б) 6y – 20 = 2(5y – 10) – 4y; в) 6(1 + 5v) = 5(1 + 6v). |
ВАРИАНТ 2 1. Решите уравнение: а) 17х– 34 = –170; б) 7х + 5 = 9х – 11; в) 5(х −6) = 15(х −8); г) Решите задачу с помощью уравнения: 2. В одном зале кинотеатра в 2 раза больше зрителей, чем в другом. Если из первого зала уйдут 37 человек, а во второй придут 50, то зрителей в обоих залах будет поровну. Сколько зрителей в каждом зале? 3. Найдите корень уравнения 4. Скорость автобуса на 26 км/ч меньше скорости легкового автомобиля. Автобус за 5 ч проходит такой же путь, как легковой автомобиль за 3 ч. Найдите скорость автобуса. 5. а) 3(0,4x + 7) – 4(0,8x – 3) = 2; б) 2x + 5 = 2(x + 1) + 11; в) 15(v + 2) – 30 = 15v. |
Контрольная работа по математике в 6 классе с ответами «Решение уравнений и решение задач с помощью уравнений». Методическое пособие для УМК Мерзляк, Полонский, Якир. Цитаты из пособия использованы в учебных целях. Мерзляк 6 класс Контрольная 10 Варианты 1-2.
Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ)
Математика 6 класс (Мерзляк)
Контрольная № 10. Варианты 1-2
Решение уравнений и решение задач с помощью уравнений

Другие варианты: К-10 Варианты 3-4
Решения и Ответы на Вариант 1
№ 1. Решите уравнение 13х + 10 = 6х – 4.
ОТВЕТ: x = –2.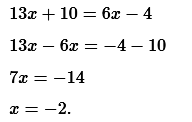
№ 2. В трёх ящиках лежит 75 кг апельсинов. Во втором ящике апельсинов в 4 раза больше, чем в первом, а в третьем – на 3 кг меньше, чем в первом. Сколько килограммов апельсинов лежит в первом ящике?
ОТВЕТ: 13 кг.
Смотреть РЕШЕНИЕ задачи № 2 в тетради

№ 3. Найдите корень уравнения: 1) 0,4(х – 3) + 2,5 = 0,5(4 + х); 2) (х – 4)/4 = (х + 3)/7.
ОТВЕТ: 1) –7; 2) 13 1/3.
Смотреть РЕШЕНИЕ задачи № 3 в тетради
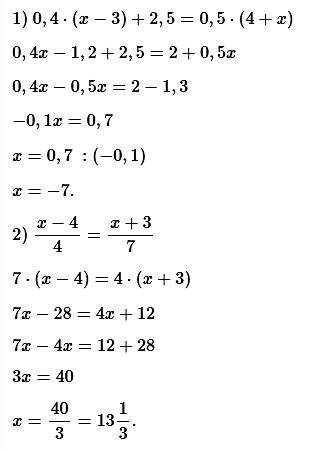
№ 4. У Пети и Васи было поровну денег. Когда Петя потратил на покупку книг 400 р., а Вася – 200 р., то у Васи осталось денег в 5 раз больше, чем у Пети. Сколько денег было у каждого из них вначале?
ОТВЕТ: по 450 руб.
Смотреть РЕШЕНИЕ задачи № 4 в тетради

№ 5. Решите уравнение (4у + 6) (1,8 – 0,2у) = 0.
ОТВЕТ: –1,5; 9.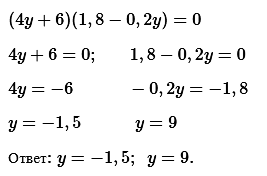
Решения и Ответы на Вариант 2
№ 1. Решите уравнение 17х – 8 = 20х + 7.
ОТВЕТ: –5.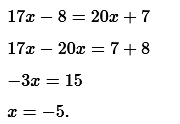
№ 2. Три брата собрали 88 кг яблок. Старший собрал в 3 раза больше, чем младший, а средний – на 13 кг больше, чем младший. Сколько килограммов яблок собрал младший брат?
ОТВЕТ: 15 кг.
Смотреть РЕШЕНИЕ задачи № 2 в тетради

№ 3. Найдите корень уравнения: 1) 0,6(х – 2) + 4,6 = 0,4(7 + х); 2) (х – 1)/(5 – х) = 2/9.
ОТВЕТ: 1) –3; 2) 19/11.
Смотреть РЕШЕНИЕ задачи № 3 в тетради
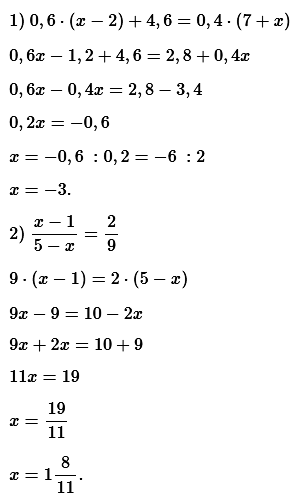
№ 4. В двух цистернах было поровну воды. Когда из первой цистерны взяли 54 л воды, а из второй – 6 л, то в первой цистерне осталось в 4 раза меньше воды, чем во второй. Сколько литров воды было в каждой цистерне вначале?
ОТВЕТ: 70 л.
Смотреть РЕШЕНИЕ задачи № 4 в тетради

№ 5. Решите уравнение (3х + 42)(4,8 – 0,6х) = 0.
ОТВЕТ: –14; 8.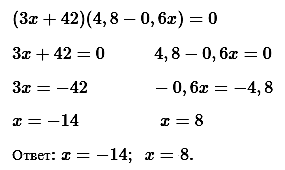
Другие варианты: К-10 Варианты 3-4
Вы смотрели: Мерзляк 6 класс Контрольная 10 в 4-х вариантах (Варианты 1-2). Контрольная работа по математике в 6 классе «Решение уравнений и решение задач с помощью уравнений» УМК Мерзляк, Полонский, Якир.
Вернуться к Списку контрольных работ из Методического пособия для УМК Мерзляк (ответов нет)
Перейти к ещё двум вариантам контрольной работы № 10 из Дидактических материалов для УМК Мерзляк (с ответами)
(с) Цитаты из пособия «Математика 6 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.
Самостоятельная работа по математике в 6 классе «Решение уравнений» по УМК Мерзляк в 4 вариантах с ответами. Цитаты из пособия «Математика 6 класс. Дидактические материалы / Мерзляк и др.» использованы в учебных целях. Математика 6 Самостоятельная 38: Решение уравнений. Используется в комплекте с учебником «Математика 6 класс» авторов: Мерзляк, Полонский, Якир.
Вернуться к Списку самостоятельных работ (ОГЛАВЛЕНИЕ)
Самостоятельная работа по математике:
Решение уравнений. Вариант 1

Самостоятельная № 38. Варианты 2, 3, 4
Нажмите на спойлер, чтобы увидеть задания Вариантов 2-4

ОТВЕТЫ на самостоятельную работу
СР-38. Ответы на Вариант 1
№ 200. Решите уравнение: 1) 2х = 18 – х; 2) 7х + 3 = 30 – 2х; 3) 7 – 2х = 3х – 18; 4) 0,2х + 2,7 = 1,4 – 1,1х; 5) 5,4 – 1,5х = 0,3х – 3,6; 6) 3/8 • х + 15 = 1/6 • х + 10.
ОТВЕТ: 1) 6; 2) 3; 3) 5; 4) –1; 5) 5; 6) –24.
№ 201. Найдите корень уравнения: 1) 3(х – 2) = х + 2; 2) 5 – 2(х – 1) = 4 – х; 3) (7x + 1) – (9х + 3) = 5; 4) 3,4 + 2у = 7{у – 2,3); 5) 0,2(7 – 2у) = 2,3 – 0,3(у – 6); 6) 2/3 • (х/3 – 1/2) = 4х + 2 1/2.
ОТВЕТ: 1) 4; 2) 3; 3) –3,5; 4) 3,9; 5) –27; 6) –3/4.
№ 202. Решите уравнение: 1) 4(5х + 2) = 10(2х – 3) + 15; 2) 2(7х – 7) = 7(2х – 3) + 7.
ОТВЕТ: 1) нет решений; 2) любое число.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ
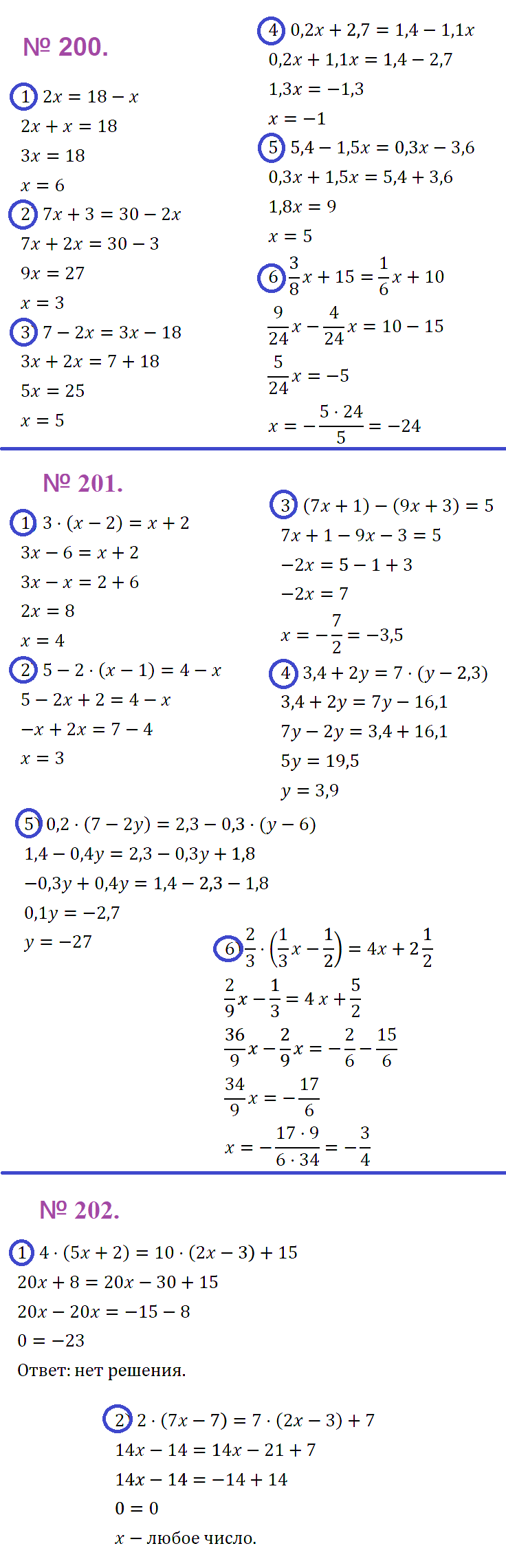
СР-38. Ответы на Вариант 2
№ 200. Решите уравнение: 1) 4х = 24 + х; 2) 8х – 8 = 20 – 6х; 3) 9 – 4х = 3х – 40; 4) 0,6х – 5,4 = –0,8х + 5,8; 5) 4,7 – 1,1х = 0,5x – 3,3; 6) 5/6 • х + 16 = 4/9 • х + 9.
ОТВЕТ: 1) 8; 2) 2; 3) 7; 4) 8; 5) 5; 6) –18.
№ 201. Найдите корень уравнения: 1) 4(х – 3) = х + 6; 2) 4 – 6(х + 2) = 3 – 5х; 3) (5x + 8) – (8x + 14) = 9; 4) 2,7 + 3у = 9(у – 2,1); 5) 0,3(8 – 3у) = 3,2 – 0,8(у – 7); 6) 5/6 • (х/3 – 1/5) = 3х + 3 1/3.
ОТВЕТ: 1) 6; 2) –11; 3) –5; 4) 3,6; 5) –64; 6) –9/7 = –1 2/7.
№ 202. Решите уравнение: 1) 4(х – 1) = 2(2х– 8) + 12; 2) 7(4х – 1) = 6 – 2(3 – 14х).
ОТВЕТ: 1) любое число; 2) нет решений.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ

СР-38. Ответы на Вариант 3
№ 200. Решите уравнение: 1) 6х = 28 – х; 2) 9х – 26 = 30 – 5х; 3) 7 – Зх = 6х – 56; 4) 0,9х – 7,4 = –0,4х + 4,3; 5) 5,8 – 1,6х= 0,3х– 1,8; 6) 3x/8 + 19 = 7x/12 + 24.
ОТВЕТ: 1) 4; 2) 4; 3) 7; 4) 9; 5) 4; 6) –24.
№ 201. Найдите корень уравнения: 1) 5(х – 4) = х + 8; 2) 9 – 7(х + 3) = 5 – 6х; 3) (7х + 9) – (11х – 7) = 8; 4) 19,6 + у = 7(1,2 – y); 5) 0,4(6 – 4у) = 0,5(7 – 3у) – 1,9; 6) 3/4 • (x/6 – 1/3) = 2x – 11 1/2.
ОТВЕТ: 1) 7; 2) –17; 3) 2; 4) –1,4; 5) 8; 6) 6.
№ 202. Решите уравнение: 1) 3(х + 6) = х + 2(х + 9); 2) 2(8х – 7) = 18 – 4(5 – 4х).
ОТВЕТ: 1) любое число; 2) нет решений.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ

СР-38. Ответы на Вариант 4
№ 200. Решите уравнение: 1) 11x = 36 – x; 3) 8 – 4x = 2x – 16; 2) 9x + 4 = 48 – 2x; 4) 0,4x + 3,8 = 2,6 – 0,8x; 5) 6,8 – 1,3х = 0,6х – 2,7; 6) 4x/9 + 14 = х/6 + 9.
ОТВЕТ: 1) 3; 2) 4; 3) 4; 4) –1; 5) 5; 6) –18.
№ 201. Найдите корень уравнения: 1) 4(х – 6) = x – 9; 2) 6 – 3(х + 1) = 7 – 2х; 3) (8x + 3) – (10x + 6) = 9; 4) 3,5 – х = 8(x + 2,8); 5) 0,3(6 – 2у) = 4,5 – 0,7(y + 9); 6) 3/5 • (7x/9 – 1/3) = x – 2 1/3.
ОТВЕТ: 1) 5; 2) –4; 3) –6; 4) –2,1; 5) –36; 6) 4.
№ 202. Решите уравнение: 1) 8(5 – 3x) = 6(2 – 4x) + 7; 2) 5(x – 12) = 6(x – 10) – x.
ОТВЕТ: 1) нет решений; 2) любое число.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ
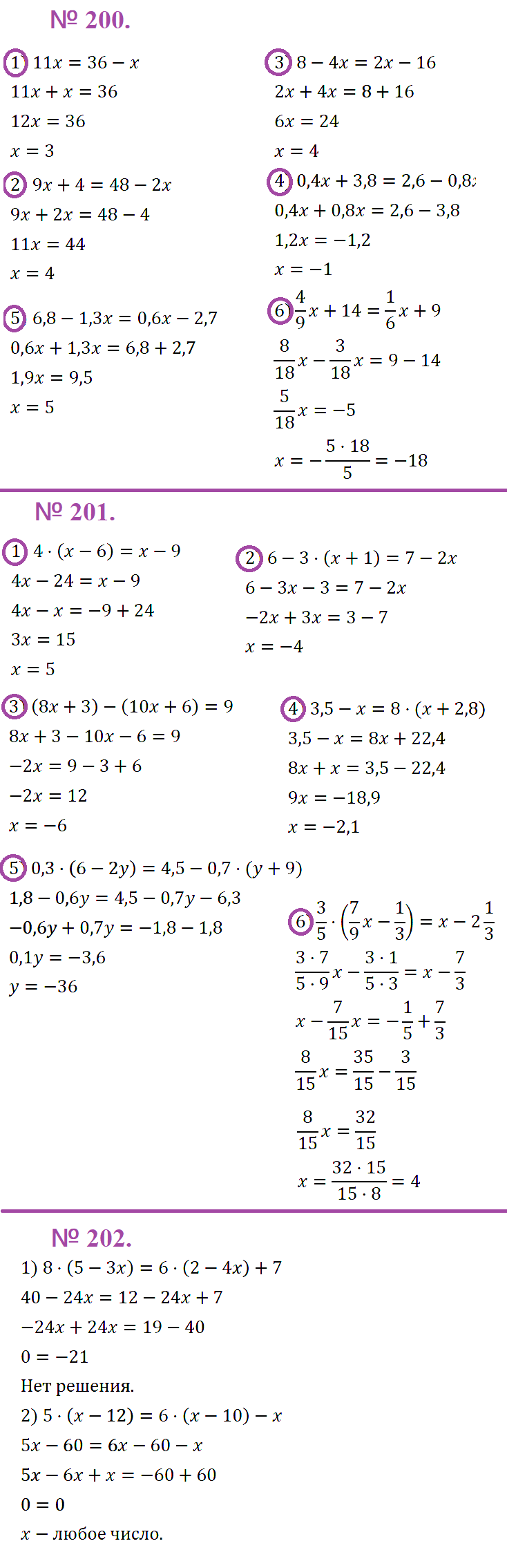
Вы смотрели «Самостоятельные работы. Математика 6 Самостоятельная № 38: Решение уравнений». Цитаты упражнений из пособия для учащихся «Математика 6 класс. Дидактические материалы / Мерзляк и др.», которое используется в комплекте с учебником «Математика 6 класс» авторов: Мерзляк и др.
Вернуться к Списку самостоятельных работ по математике в 6 классе (УМК Мерзляк)
