Как решить найдите площадь поверхности многогранника

Сайты, меню, вход, новости

Приветствую, сообщество Хакнем!

Сегодня в рубрике #хакнем_математика продолжим цикл статей, посвященных решению задач из ОГЭ и ЕГЭ по математике. Иногда в комментариях читатели спрашивают — зачем вы это пишите, и кому это нужно? Отвечаю — поверьте, кому-то это точно нужно! И даже, если моя статья поможет хоть 5-ти учащимся, я буду рада.

Недавно мой сын 11-классник пришёл ко мне с вопросом по задаче 8 (стереометрия) из ЕГЭ профильного уровня: «Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится». Вот эта задача:

Задача 1

При решении этой задачи нам необходимо знать одну лишь формулу — формулу нахождения площади полной поверхности прямоугольного параллелепипеда с измерениями a, b, c: S = 2 ×(ab+ bc+ ac).

Как рассуждал сын? Он нашёл площадь нижнего параллелепипеда и площадь верхнего, и сложил результаты:

1. Площадь нижнего с измерениями 5×4×3 равна: S = 2 (5×4 + 4×3 + 5×3) = 94

2. Площадь верхнего с измерениями 3×2×3 равна: S = 2 (3×2 + 2×3 + 3×3) = 42

Если сложить эти два результата, получится 136. Где же ошибка?

Ошибка в том, что в найденных площадях и нижнего и верхнего параллелепипедов содержится площадь прямоугольника со сторонами 2×3 (S = 6, показана на рисунке красным, которая в площадь поверхности многогранника не входит.

Таким образом, из полученного результата надо вычесть две таких площади: 136 – 2×6 = 124. Ответ: 124.

Разберём ещё подобные задачи.

Задача 2

Решение:

Чтобы упростить решение задачи, достроим наш многогранник до параллелепипеда с измерениями 2×1×3.

Его площадь равна: S = 2 × (2×1 + 1×3 + 2×3) = 22.

Осталось вычесть площади «лишних» прямоугольников. Посмотрите на рисунок:

• прямоугольник (его площадь), показанный розовой штриховкой, оставляем, так он входит в многогранник;
• голубой тоже нужен;
• а вот 2 зелёных (со сторонами 1 × 2) — лишние, их площади нужно вычесть.

Итак, S = 22 – 2 × (1×2) = 22 – 4 = 18.

Ответ: 18.

Задача 3

Решение:

А эту задачу решим немного другим способом. Если вы внимательно посмотрите на рис. в условии, то увидите, что это параллелепипед с вырезанным уголком (ну или с вдавленным). И если бы была такая возможность, и мы могли бы взять за уголок и потянуть, как показано стрелкой на рисунке, то параллелепипед станет «целым».

А это значит, чтобы найти искомую площадь поверхности многогранника нужно найти площадь поверхности прямоугольного параллелепипеда с измерениями 5×5×3:

S = 2 × (5×5 + 5×3 + 5×3) = 110.

Ответ: 110.

Задача 4

Решение:

Достроим снова для наглядности многогранник до прямоугольного параллелепипеда с измерениями 4×6×4. Его площадь:

S = 2×(4×6 + 6×4 + 4×4) = 128.

• площадь жёлтого прямоугольника уже вошла в найденную площадь поверхности параллелепипеда;
• 2 площади зелёных прямоугольников со сторонами 1×4 (S = 4) нужно добавить к найденной площади параллелепипеда;
• 2 площади сиреневых прямоугольников со сторонами 1×2 (S = 2) — лишние, и поскольку они вошли в площадь параллелепипеда, а в искомом многограннике их на самом деле нет, то их вычтем.

Итак, S = 128 + 2×4 – 2×2 = 132.

Ответ: 132.

А в заключении приведу задачу с условием и рисунком, что и в задаче 1, но найти нужно объём многогранника.

Задача 5.

Решение:

Здесь всё намного проще. Достаточно найти объёмы 2-х параллелепипедов с измерениями 4×5×3 и 3×2×3 и сложить их.

Вспоминаем, что объём прямоугольного параллелепипеда с измерениями a, b, c находится по формуле: V = a×b×c.

V1 = 4 × 5 × 3 = 60;

V2 = 3 × 2 × 3 = 18;

V = 60 + 18 = 78.

Ответ: 78.

Не путайте на экзамене объём и площадь поверхности.

Вы всегда можете распечатать решение этих задач из Дзен или скопировать себе ссылку на статью, а при подготовке к экзамену ещё раз перечитать решение и вспомнить.

Удачи!

Кстати, принесла эти задачи своим коллегам на работу (не в школу, так как моя работа никак с ней не связана), так вот они с интересом эти задачки порешали. В ход пошли различные подручные “модели” и сложенные фигурки из бумаги. Ведь самое сложное в них — понять что лишнее, а что уже входит. Хорошая гимнастика ума!

Если нашли ошибку или опечатку, пишите в комментариях, буду благодарна.

#хакнем_математика (👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳

Автор: #ирина_чудневцева координатор канала Хакнем Школа, 42 года, город Ярославль

Похожие статьи автора:

Если у вас есть познавательный материал, тёплые воспоминания и интересные истории из школьной жизни, которые вы хотели бы опубликовать в нашем канале, или вы просто хотите стать автором канала, напишите нам об этом 👉 story@haknem.com

Такое задание можно выполнить несколькими способами:

а) Вычислить отдельные составляющие многогранника без достроения

б) Достроить до полноценной фигуры (параллелепипеда) и вычесть площадь поверхности фигуры, которую мы “приклеили” в изначально заданному многограннику

Воспользуемся первым способом:

Разметим поверхности для удобства как показано на рисунке и по отдельности вычислим площади составляющих общую поверхность поверхностей составляющих, после чего сложим полученные площади и получим ответ.

S1 = 1*2 = 2

Таких поверхностей у нас две => S1*2 = 2*2 = 4

S2 = 1*1 = 1

Аналогично, две поверхности => S2*2 = 1*2 = 2

S3 = 2*1 = 2

S4 = 1*2 = 2

Две поверхности => S4*2 = 2*2 = 4

S5 = 1*1 = 1

Аналогично, S5*2 = 1*2 = 2

S6 = 2*1 = 2, S6*2 = 2*2 = 4

Теперь сложим все площади: 4 + 2 + 2 + 4 + 2 + 4 = 18

Площадь поверхности многогранника. В данной рубрике в опубликованных статьях “Общий обзор. Формулы стереометрии“ и “Что ещё необходимо знать для решения по стереометрии“ мы уже рассмотрели теоретические моменты, которые необходимы для решения.

В составе  ЕГЭ по математике имеется целый ряд задач на определение площади поверхности и объема составных многогранников. Это, наверное, одни из самых простых задач по стереометрии. НО! Имеется нюанс. Не смотря на то, что сами вычисления  просты, ошибку при решении такой задачи допустить очень легко.

В чём же дело? Далеко не все обладают хорошим пространственным мышлением, чтобы сразу увидеть все грани и параллелепипеды из которых «состоят» многогранники. Даже если вы умеете делать это очень хорошо, можете мысленно сделать такую разбивку,  всё-таки следует не торопиться и воспользоваться рекомендациями из этой статьи.

Кстати, пока работал над данным материалом, нашёл ошибку в одной из задач на сайте. Нужна внимательность и ещё раз внимательность, вот так.

Итак, если стоит вопрос о площади поверхности, то на листе в клетку постройте все грани многогранника, обозначьте размеры. Далее внимательно вычисляйте сумму площадей всех полученных граней. Если будете предельно внимательны при построении и вычислении, то ошибка будет исключена.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

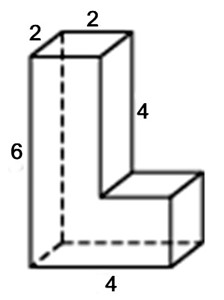
Используем оговоренный способ. Он  нагляден. На листе в клетку строим все элементы  (грани) в масштабе. Если длины рёбер будут большими, то просто подпишите их.

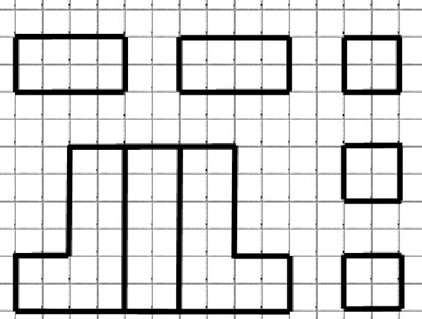
Ответ: 72

Решите самостоятельно:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

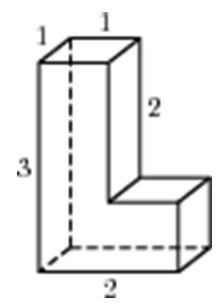
Посмотреть решение

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

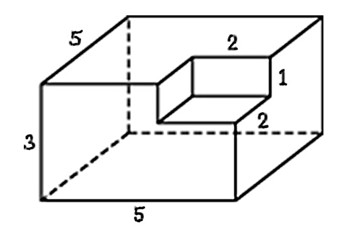
Посмотреть решение

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Посмотреть решение

Ещё задачи 25881, 77155, 77156.  В них приведены решения другим способом (без построения), постарайтесь разобраться — что откуда взялось. Также решите уже представленным способом.

* * *

Если требуется найти объём составного многогранника. Разбиваем многогранник на составляющие его параллелепипеды, записываем внимательно длины их рёбер и вычисляем.

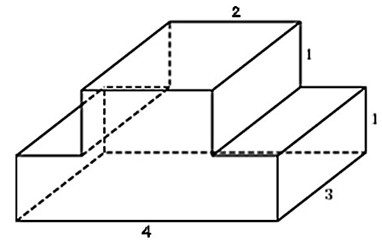
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Объем многогранника, изображенного на рисунке равен сумме объёмов  двух многогранников с рёбрами 6,2,4 и 4,2,2

Ответ: 64

Решите самостоятельно:

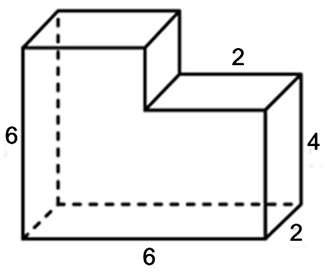
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Посмотреть решение

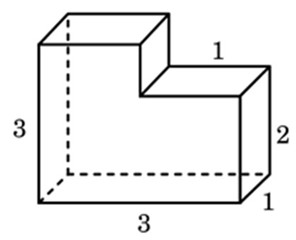
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

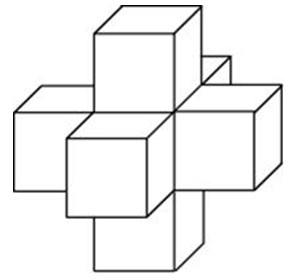
Посмотреть решение

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

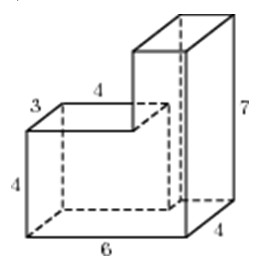
Посмотреть решение

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

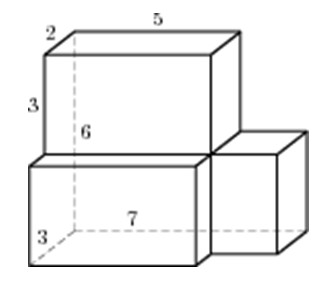
Посмотреть решение

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

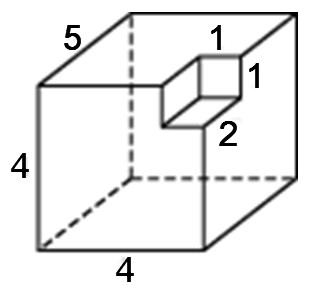
Посмотреть решение

Казалось бы, данные задачи можно вообще не рассматривать, они же просты и понятны. Но в их решении важна практика. Повторюсь, что ошибиться очень легко, попрактикуйтесь с подобными задачами и вы убедитесь.

В открытом банке задач много примеров аналогичных задач (смотрите здесь и здесь). Договоритесь с одноклассниками решить одни  и те же задачи, затем сверьтесь.

Мы продолжим рассматривать задачи данной части, не пропустите! Успехов вам!!!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Практикум по теме «Площадь поверхности составного многогранника»
15 января 2020 г. 11 класс

Цель: практическое закрепление ЗУН.

Задачи из открытого банка задач.

1. Задание 8 № 25541

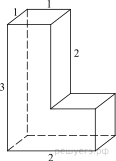Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 2, 3, 1 и двух площадей
прямоугольников со сторонами 2, 1:

Ответ: 18.

2. Задание 8 № 25561

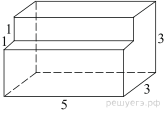Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 3, 5 и двух площадей
квадратов со стороной 1:

Ответ: 76.

3. Задание 8 № 25581

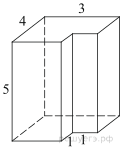Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух
квадратов со стороной 1:

Ответ: 92.

4. Задание 8 № 25601

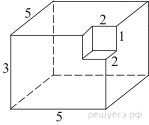Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:

Ответ: 110.

5. Задание 8 № 25621

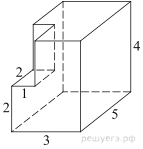Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:

Ответ: 94.

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней
данного многогранника, и смиритесь:

6. Задание 8 № 25641

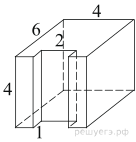Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 6, 4, 4 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 2:

Ответ: 132.

7. Задание 8 № 25661

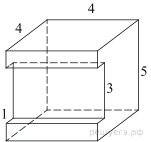Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 4, 4, 5 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 3:

Ответ: 114.

8. Задание 8 № 25681

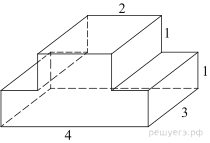Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
прямоугольников со сторонами 1, 3, 4 и 1, 2, 3, уменьшенной на удвоенную
площадь прямоугольника со сторонами 2, 3:

Ответ: 48.

9. Задание 8 № 25701

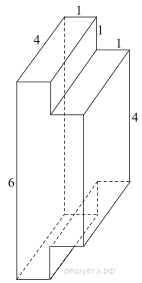
Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь
квадрата стороной 4:

Ответ: 84.

Приведем другое решение

Площадь поверхности заданного многогранника равна площади
прямоугольного параллелепипеда с ребрами 6, 4, 2 уменьшенной на 4 площади
квадратов со стороной 1:

10. Задание 8 № 25721

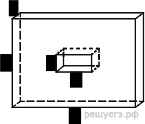Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной
на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького
параллелепипеда, излишне учтенной при расчете площадей поверхности
параллелепипедов:

Ответ: 96.

11. Задание 8 № 25881

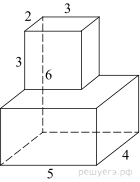Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов со сторонами 2, 3, 3 и 5, 4, 3 уменьшенной на удвоенную
площадь прямоугольника со сторонами 3, 2:

Ответ: 124.

12. Задание 8 № 27071

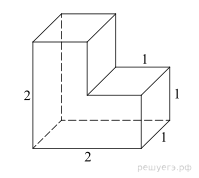Найдите площадь
поверхности многогранника, изображенного на рисунке, все двугранные углы
которого прямые.

Решение.

Площадь поверхности заданного многогранника складывается из
четырех площадей квадратов со стороной 1, двух прямоугольников со сторонами 1 и
2 и двух граней (передней и задней), площади которых в свою очередь
складываются из трех единичных квадратов каждая. Всего 4 + 4 + 6 = 14.

Ответ: 14.

13. Задание 8 № 27158

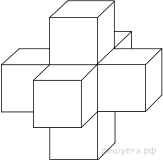Найдите площадь
поверхности пространственного креста, изображенного на рисунке и составленного
из единичных кубов.

Решение.

Поверхности креста составлена из шести поверхностей кубов, у
каждого из которых отсутствует одна грань. Тем самым, поверхность креста
состоит из 30 единичных квадратов, поэтому ее площадь равна 30.

Ответ: 30.

14. Задание 8 № 77155

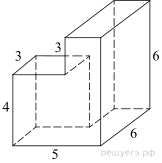Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника равна сумме площадей
поверхностей прямоугольных параллелепипедов с рёбрами 6, 6, 2 и 3, 3, 4,
уменьшенной на две площади прямоугольников со сторонами 3 и 4:

Ответ: 162.

15. Задание 8 № 77156

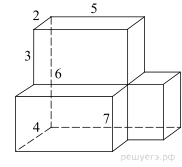Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих ее параллелепипедов с ребрами 2, 5, 6; 2, 5, 3 и 2, 2,
3, уменьшенная на удвоенные площади прямоугольников со сторонами 5 ,3 и 2, 3:

Ответ: 156.

16. Задание 8 № 77157

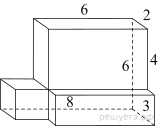Найдите площадь
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих его параллелепипедов с измерениями 2, 4, 6; 1, 6, 2 и 2, 2, 2:

Ответ: 152.

17. Задание 8 № 512330

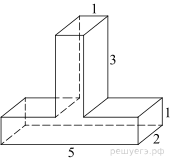Найдите площадь
поверхности многогранника, изображённого на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника складывается из площадей
двух параллелепипедов со сторонами 1, 3, 2 и 1, 2, 5 за вычетом двух площадей
прямоугольников со сторонами 2 и 1, которые учитываются дважды в представленном
многограннике: 

Ответ: 52