На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно осуществить поиск и определить оптимальное значение какого-либо параметра или количество. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно нами строится выражение этих значений в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).
В этом материале мы расскажем, как найти наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x), чтобы вам не нужно было искать это самостоятельно онлайн.
Основные определения
Начнем, как всегда, с формулировки основных определений: какое значение называют максимальным и минимальным?.
Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Минимальное значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее наибольшее число, которое она может принимать на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или то, что больше всего, значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы можем определить наибольшее или найти наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с интервалом, не имеющим конца. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения (мало и много). В этих случаях определить или найти наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
Как найти наибольшее и наименьшее значение функции на отрезке?
В этом пункте мы приведем последовательность действий, которую нужно выполнить, чтобы найти наибольшее значение функции на некотором отрезке или как найти наименьшее значение функции.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
Ответ: Для отрезка [1;4] – max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] – max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнавать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный (квадратичный) трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определяться с наименьшим значением функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.
Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Наибольшее и наименьшее значение функции
Как найти?
Постановка задачи
Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $
План решения
Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $
- Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
- Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
- Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
- Выбираем критические точки, принадлежащие отрезку $ [a,b] $
- Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $
Примеры решений
| Пример 1 |
| Найти наибольшее и наименьшее значение функции $ y = 2x^3 – 3x^2 – 4 $ на отрезке $ [0;2] $ |
| Решение |
|
Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 – 3x^2 – 4)’ = 6x^2 – 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 – 6x = 0 $$ $$ 6x(x – 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 – 3 cdot 0^2 – 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 – 3 cdot 1^2 – 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 – 3 cdot 2^2 – 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M = 0, m = -5 $$ |
| Пример 2 |
| Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $ |
| Решение |
|
Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $. |
| Ответ |
| $$ m = 0, M = 1 $$ |
Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Образовательные задачи урока.
- повторить необходимые и достаточные условия
существования точек экстремума, понятия:
стационарные и критические точки; - ввести алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке - сформировать умение решать задачи на
нахождение наибольшего и наименьшего значения
степенной функции на отрезке с помощью
производной. - разобрать прототипы задач № 1 В14
экзаменационной работы в формате ЕГЭ. - Продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения писать
необходимом темпе.
Воспитательные задачи:
- cодействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - cодействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм; - cодействовать профилактике утомляемости
школьников, используя разнообразные виды работы
на уроке.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Актуализация знаний учащихся.
Повторить с учащимися основные понятия прошлых
уроков: точки экстремума, каково достаточное
условие точек экстремума, стационарные точки и
критические точки (учащихся отвечают с места)
Повторить таблицу производных основных
функций и основные правила нахождения
III. Изучение нового материала.
Алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке
(учащиеся записывают себе в тетрадь).
Пусть функция 
непрерывна и дифференцируема на
отрезке 
, то
для нахождения наибольшего и наименьшего
значения функции на отрезке нужно:
- найти производную функции, найти стационарные
точки (решаем уравнение, приравнивая производную
к нулю) - среди полученных стационарных точек выбрать те,
которые принадлежат отрезку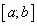
- найти значение в стационарных точках и в концах
отрезка, то есть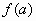
и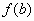 
. - среди полученных значений выбрать наибольшее
или наименьшее.
и 
.Записать схему нахождения наибольшего и
наименьшего значения функции на отрезке в
тетради (учитель оформляет схему на доске):
Пусть
непрерывна на 
и дифференцируема. Тогда, для нахождения 
или 
:
- Находим
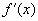
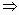
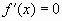
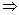находим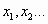 
- Проверяем принадлежность 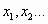отрезку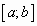
- Находим
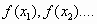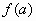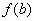, , . - Среди полученных значений выбираем
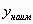или 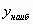. - Записываем ответ (Акцентировать внимание, что в
ответе должно быть записано либо целое число,
либо конечная десятичная дробь).
находим 
отрезку 
, 
, 
.Пример № 1. Найти наименьшее значение функции
на отрезке 
. (Учитель
совместно с учащимися записывает решение на
доске последовательно проговаривая каждый пункт
алгоритма).
Решение:
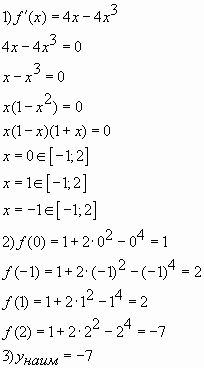
Ответ: 
Пример № 2. Найти наибольшее значение
функции 
на
отрезке 
Решение:
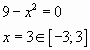
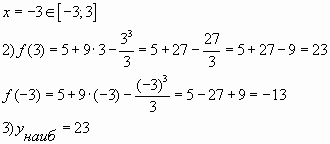
Ответ: 23
Пример № 3. Найдите наименьшее значение
функции 
на
отрезке 
.
Решение:
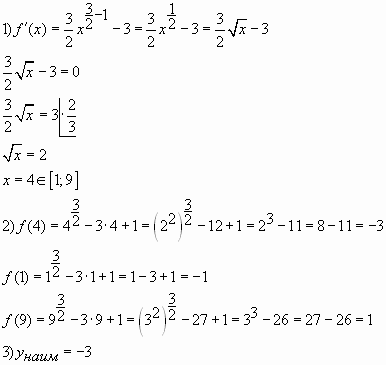
Ответ: -3
Пример № 4. Найдите наибольшее
значение функции 
на отрезке 
.
Решение:
Упростим функцию 
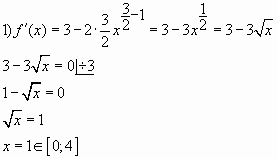
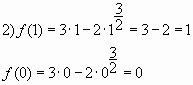
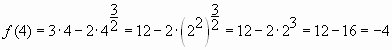
Ответ: 1
IV. Закрепление материала.
- Найдите наименьшее значение функции
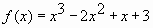на отрезке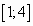 
- Найдите наименьшее значение функции
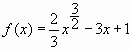на отрезке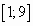 - Найдите наименьшее значение функции
на отрезке
на отрезке 
на отрезке 
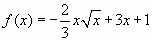на отрезке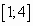 
V. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Выставить отметки за урок.
VI. Домашнее задание:
- Найдите наименьшее значение функции
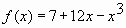на отрезке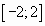 
- Найдите наибольшее значение функции
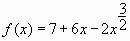на отрезке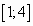 - Найдите наибольшее значение функции
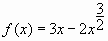на отрезке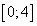 - Найдите наименьшее значение функции
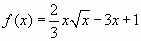на отрезке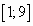 - Найти наибольшее значение функции
на отрезке 
на отрезке 
на отрезке 
на отрезке 
на отрезке 
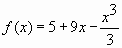на отрезке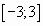 
Урок № 2. “Нахождение наибольшего и
наименьшего значения функций 
и 
на отрезке 
.
Тип урока: комбинированный.
Образовательные задачи:
- обеспечить повторение в ходе урока алгоритма
нахождения наибольшего и наименьшего значения
функции на отрезке; - продолжить формирования навыка применения
этого алгоритма при решении второго типа задач
экзаменационных вариантов ЕГЭ; - продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения в
необходимом темпе читать и писать, анализировать
условия задачи.
Воспитательные задачи:
- содействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - содействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм. умение
слушать товарищей; - содействовать профилактике утомляемости
школьников.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Проверка домашнего задания. Фронтальная
проверка домашнего задания. Если у большинства
учащихся возникли вопросы, разобрать на доске
решение конкретного задания, если лишь у
некоторых, объяснить в индивидуальном порядке,
предварительно схематично обговорив решение у
доски.
III. Актуализация знаний. Повторить еще раз
алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке с оформлением схемы
на доске.
Повторить следующие формулы для дальнейшего
изучения материала:
, 
, 
Решить на повторение примеры (1 учащийся пишет
решение на доске с комментариями по решению,
остальные записывают себе в тетради).
IV. Решение новых прототипов задач (разбирает
решение учитель)
Пример № 1. Найти наименьшее значение
функции 
на
отрезке 
Решение
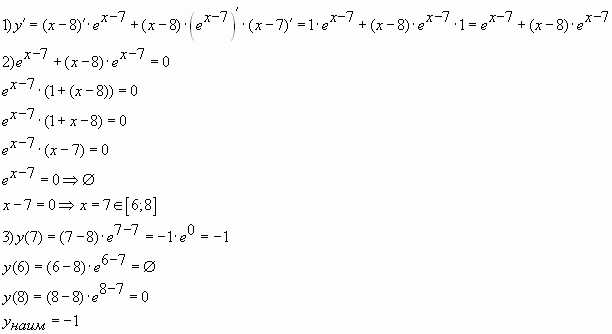
Ответ: –1
Пример № 2. Найти наименьшее значение
функции 
на
отрезке 
Решение. Преобразуем и упростим функцию 
, используя
свойство логарифмов 
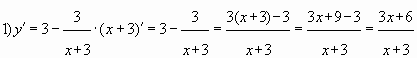
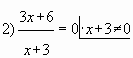
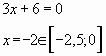
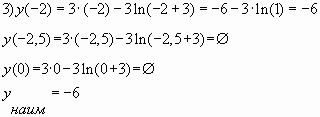
Ответ: -6
V. Закрепление материала (самостоятельное
решение задач учащимися у доски).
Пример № 3. Найти наибольшее значение функции
на отрезке 
Решение.
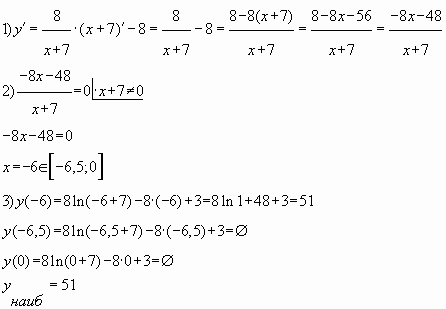
Ответ: 51
Пример № 4. Найти наименьшее значение функции
на отрезке 
Решение.
(
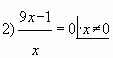
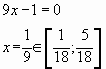
, так как 
)
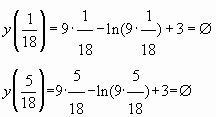
Ответ: 4
Пример № 5. Найти наименьшее значение функции
на отрезке 
Решение
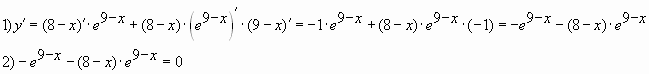
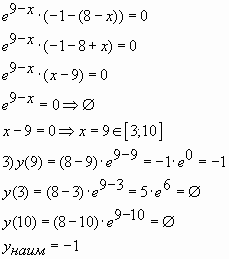
Ответ: -1
Пример № 6. Найти наибольшее значение функции
на отрезке 
Решение:
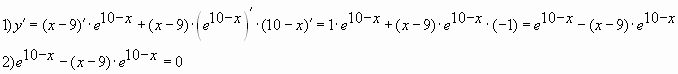
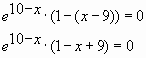
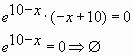
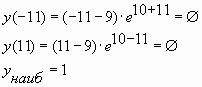
Ответ: 1
Пример № 7: Найдите наибольшее значение
функции 
на
отрезке 
Решение
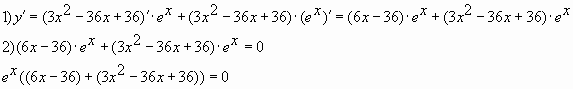
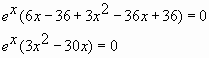
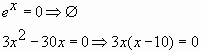
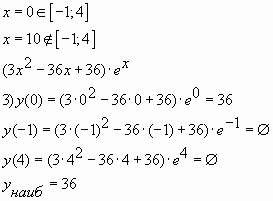
Ответ: 36
VI. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Проговорить основные алгоритмы решения тех
примеров, которые изучены на уроке.
VII. Домашнее задание по вариантам.
Экстремумы функции
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word. Если же задана функция f(x,y), следовательно, необходимо найти экстремум функции двух переменных. Также можно найти интервалы возрастания и убывания функции.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Необходимое условие экстремума функции одной переменной
Уравнение f’0(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) < 0
то точка x* – локальный (глобальный) максимум.
Пример №1. Найти наибольшее и наименьшее значения функции:
на отрезке [1; 3].
Решение.
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)=5/2, f(3)=3 8/81
Ответ: fmin=5/2 при x=2; fmax=9 при x=1
Пример №2. С помощью производных высших порядков найти экстремум функции y=x-2sin(x).
Решение.
Находим производную функции: y’=1-2cos(x). Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=±π/3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x=π/3+2πk, k∈Z – точки минимума функции; , значит x=-π/3+2πk, k∈Z – точки максимума функции.
Пример №3. Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0, то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x – первое слагаемое. Тогда (49-x) – второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x – x2
Наибольший объем цилиндра
Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R.
Решение:
Объем цилиндра равен: V = πr2H
где H = 2h,
Подставим эти значения в целевую функцию.
V → max
Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервиса Производная онлайн
и приравняем ее к нулю.
dV/dh = 2πR2 – 6πh2
dV/dh = 0
2πR2 – 6πh2 = 0 или R2 = 3h2
Откуда
При высоте и радиусе основания размеры цилиндра будут наибольшими.
