Прямоугольная трапеция особенна тем, что имеет сторону, перпендикулярную двум неравным основаниям фигуры. Важным признаком является и наличие двух прямых смежных углов. Поиск площади прямоугольной трапеции возможен по любой из общих формул, предназначенных для данного вычисления любых трапеций (прямоугольной, равнобедренной, произвольной).
5 способов вычисления:
- через три стороны трапеции;
- умножив высоту трапеции на среднюю линию;
- через основание и углы;
- через диагонали и углы между ними;
- через четыре стороны.
Вычисление площади трапеции через три её стороны (основания и перпендикулярную сторону) подходит только для прямоугольных трапеций.
Площадь прямоугольной трапеции по трём сторонам
Значение высоты прямоугольной трапеции совпадает со значением её стороны, перпендикулярной основаниям фигуры. Площадь такой фигуры можно найти через три известных стороны.
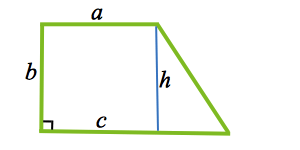
a – малое основание;
b – перпендикулярная сторона;
c – большое основание;
h – высота.
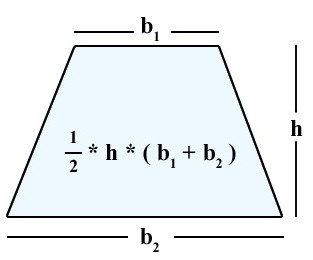
Рисунок 1. Прямоугольная трапеция. Высота h.
[boldsymbol{S}=frac{mathbf{1}}{mathbf{2}} *(boldsymbol{a}+boldsymbol{c}) * boldsymbol{b}, text { где } mathbf{S}], где S – площадь прямоугольной трапеции.
Если половину суммы малого и большого основания умножить на перпендикулярную сторону трапеции или высоту, в результате получается площадь.
Задача.
Найдите площадь прямоугольной трапеции S, если малое основание a составляется 4,84 см, а большое с – 7,88 см, перпендикулярная основаниям высота b равна 4,64 см.
Решение:
Основываясь на данные о трёх её сторонах, по соответствующей формуле найдём площадь.
[boldsymbol{S}=frac{1}{2} *(4,84+7,88) * 4,64=mathbf{2 9}, mathbf{5 1} text { кв.см }]
Ответ: Площадь прямоугольной трапеции равна 29,51 кв.см.
Площадь прямоугольной трапеции по высоте и средней линии
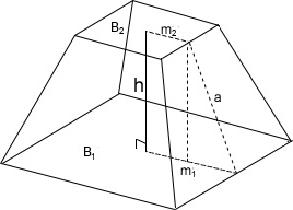
Для расчета площади потребуются данные о высоте трапеции и линии, проведенной посередине фигуры. Произведение этих величин и составит площадь. Рассмотрим рисунок 2.
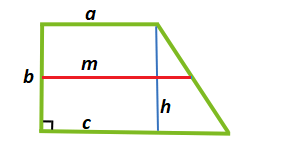
[boldsymbol{S}=boldsymbol{m} * boldsymbol{h}], где S – площадь фигуры, m – средняя линия, а h – высота, которую можно заменять на перпендикулярную основаниям сторонуb.
Задача.
Найдите площадь прямоугольной трапеции S, зная высоту h – 4,64 см и среднюю линию m – 6,36 см.
Решение:
Найдём площадь трапеции путём умножения известных величин.
[boldsymbol{S}=4,64 * 6,36=29,51 text { кв.см }]
Ответ: S = 29,51 кв.см.
Вычисление площади по основаниям и углам
Зная значения оснований трапеции и углов при них, для вычисления площади нужно половину разницы квадратов оснований фигуры умножить на частное из произведения синусов углов при основании и синуса суммы этих углов. Рассмотрим рисунок 3.
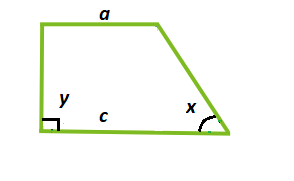
[S=frac{1}{2} *left(c^{2}-a^{2}right) * frac{sin (y) * sin (x)}{sin (y+x)}], где S – площадь; с – большое основание;a – малое основание;
y, x – первый и второй угол при основании.
Задача.
Как узнать площадь прямоугольной трапеции S по формуле оснований и углов, если малое снование a равно 4,84 см, а большое с – 7,88 см, первый угол при основании y прямой, а второй x равен 56,8о?
Решение:
Рассчитаем площадь трапеции, используя данные об основаниях и углах при большом основании.
[boldsymbol{S}=frac{1}{2} *left(7,88^{2}-4,84^{2}right) * frac{sin (90) * sin (56,8)}{sin (90+56,8)}=mathbf{2 9 , 4 8} mathbf{кв.см}]
Ответ: S = 29.48 кв.см.
Нет времени решать самому?
Наши эксперты помогут!
Площадь прямоугольной трапеции через диагонали и углы между ними
Умножив синус угла, образованный на пересечении диагоналей, на произведение диагоналей, делённое пополам, получим площадь прямоугольной трапеции.
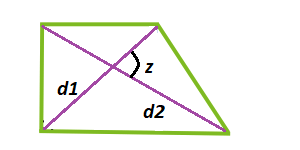
[S=frac{1}{2} * d 1 * d 2 * sin (x)], где S – площадь; d1 – диагональ 1; d2 – диагональ 2; z – угол между диагоналями.
Задача.
Найдите площадь прямоугольной трапеции, имя данные первой диагонали d1, второй – d2 и угла между ними z. d1 = 2,23 см; d2 = 2,65 см, z = 57o.
Решение:
Пользуясь формулой расчёта площади, при известных диагоналях и углу между ними, составим решение.
[boldsymbol{S}=frac{1}{2} * 2,23 * 2,65 * sin (57)=mathbf{2}, mathbf{4 8} mathbf { кв.см }]
Ответ: S=2,48 кв.см
Площадь прямоугольной трапеции, исходя из значения всех её сторон
Если известны показатели всех сторон прямоугольной трапеции, то вычислить её площадь можно по формуле, приведённой ниже.
[left.S=frac{a+c}{2} * sqrt{e^{2}-left(frac{(c-a)^{2}+e^{2}-b^{2}}{2 *(c-a)}right.}right)^{2}], где a – малое основание; c – большое основание; b – перпендикулярная основаниям сторона; e – неперпендикулярная боковая сторона.
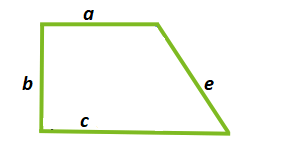
Задача.
Дано: a = 3 см; b = 3 см; c = 5 см; e = 3,5 см.
Найти: площадь трапеции S.
Решение: применяя формулу расчёта площади по всем сторонам фигуры, найдём площадь трапеции.
[S=frac{3+5}{2} * sqrt{3,5^{2}-left(frac{(5-3)^{2}+3,5^{2}-3^{2}}{2 *(5-3)}right)^{2}}=11,98 mathbf { кв.см} .]
Ответ: S = 11,98 кв.см.
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
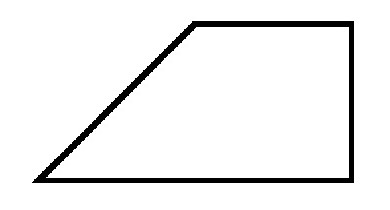
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
| Величина | Ее обозначение |
| a | большее основание |
| b | меньшее основание прямоугольной трапеции |
| c, h | перпендикулярная к основаниям боковая сторона, высота |
| d | наклонная боковая сторона |
| α | острый угол |
| β | тупой угол |
| м | средняя линия трапеции |
| д1 | меньшая диагональ |
| д2 | большая диагональ |
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
c = h.
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a – b) * tg α;
c = √ (d2 – (a – b)2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
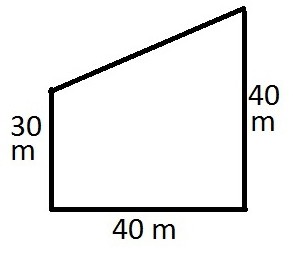
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a – b) /cosα;
d = c / sin α;
d = √ (c2 + (а – b)2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
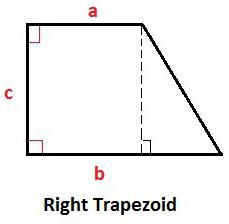
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с2 + b2)
или по-другому, заменив «с» на «h»:
d1 = √ (h2 + b2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с2 + b2) или d2 = √ (h2 + а2).
Задача №1
Условие. Площадь прямоугольной трапеции известна и равна 120 дм2. Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с2 + (а – b)2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а – b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2.
Необходимо сделать преобразования, подставив вместо с его значение из условия – 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см2.
Ответ. Искомая площадь 36 см2.
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
Прямоугольная трапеция является трапецией, у которой одна из боковых сторон перпендикулярна основаниям. Средняя линия прямоугольной трапеции равна половине суммы ее оснований. (рис.105.1)
m=(b+d)/2
Высота прямоугольной трапеции равна ее боковой стороне-перпендикуляру. Следовательно, площадь трапеции, которая обычно равна произведению высоты на среднюю линию, преобразуется в произведение боковой стороны на среднюю линию. (рис.105.2)
S=hm=am=(a(b+d))/2
Вторая боковая сторона прямоугольной трапеции, находящаяся под углом к основаниям, отличным от 90 градусов, вычисляется по теореме Пифагора в прямоугольном треугольнике с высотой.
c=√(h^2+〖(d-b)〗^2 )=√(a^2+〖(d-b)〗^2 )
Периметр такой трапеции вычисляется также как обычной, сложением всех ее сторон.
P=a+b+c+d=a+b+d+√(a^2+〖(d-b)〗^2 )
Обе диагонали прямоугольной трапеции являются гипотенузами в прямоугольных треугольниках со стороной, перпендикулярной основаниям. Поэтому вычислить их становится возможным, используя теорему Пифагора. (рис.105.3)
d_1=√(a^2+b^2 )
d_2=√(a^2+d^2 )
Если боковые стороны прямоугольной трапеции в сумме дают то же, что и основания, то внутри такой трапеции можно вписать окружность. Радиусом вписанной окружности будет служить половина высоты или, в данном случае, половина квадратного корня из произведения оснований.
r=√bc/2
Вокруг прямоугольной трапеции нельзя описать окружность, для этого она должна стать либо равнобокой трапецией, либо прямоугольником
|
Площадь прямоугольной трапеции найти очень просто: достаточно вспомнить, из что представляет собой эта геометрическая фигура. Трапеция состоит из двух параллельных и двух боковых сторон, причем одна из боковых сторон имеет угол в 90 градусов. Найти площадь трапеции можно по следующим формулам:
модератор выбрал этот ответ лучшим
[пользователь заблокирован] 7 лет назад Площадь трапеции равна полусумме её оснований, умноженной на высоту данной трапеции: S=(( AD+ВС) :2)хВН, Высотой трапеции является любой перпендикуляр , относительно основаниям трапеции, проведенный из любой точки от одного основания трапеции до другого. Площадь равнобедренной трапеции можно найти и по формуле: S=4r:sina; в этой формуле r– это радиус вписанной в равнобедренную трапецию окружности, sina – угол при основании. Площадь трапеции равна произведению средней линии трапеции и её высоты: S=mh, где h– это высота трапеции, m– её средняя линия. Есть и ещё одна формула, по которой возможно найти площадь трапеции. В данной формуле:
a и b– это основания, с и d– боковые стороны трапеции. Что такое прямоугольная трапеция? Это фигура, у которой две стороны параллельны, третья перпендикулярна первым двум, а четвёртая расположена под определённым, не прямым углом. Рисунок:
На рисунке вы видите прямоугольную трапецию. Две стороны у неё параллельны (a и c). Сторона b перпендикулярна, а четвёртую сторону мы даже можем не обозначать, так как она нам не понадобится для расчётов. Теперь посмотрите, что будет, если справа достроить к четвёртой стороне два отрезка так, как изображено на рисунке красным цветом. То есть отрезки должны быть параллельны противоположной стороне трапеции. Как вы видите, получился прямоугольник большей площади, чем наша трапеция. Затем ещё проведём из правого верхнего угла трапеции вниз отрезок, перпендикулярный нижней стороне. Таким образом наш большой прямоугольник делится на два поменьше. Левый цельный, а правый – состоящий из треугольников. Площадь трапеции складывается из суммы площади левого прямоугольника и из площади треугольника: Sтрап = Sab + Sтреуг Площадь левого прямоугольника равна произведению a на b: Sab = a * b А площадь треугольника равна одной второй от площади правого прямоугольника, то есть её половине. Вертикальная сторона этого прямоугольника равна b, а горизонтальная равна разности между большей из параллельных сторон трапеции и меньшей, то есть вертикальная сторона равна c-a. Получается, что площадь правого прямоугольника равна b(c-a). Таким образом площадь треугольника равна: Sтреуг = b(c-a)/2 А искомая площадь трапеции: Sтрап = ab + b(c-a)/2 Ответ: Площадь прямоугольной трапеции равна ab + b(c-a)/2
Nonsense 7 лет назад Вот так выглядит прямоугольная трапеция (ПТ), у неё одна из боковых сторон равна высоте и образует с основаниями прямой угол (90º):
Площадь ПТ — половина суммы длин оснований, умноженная на высоту:
Или произведение средней линии на высоту:
Или половина произведения диагоналей на синус угла между ними:
Или, если диагонали трапеции перпендикулярны, то просто, половине их произведения:
Или полупериметру, помноженному на радиус вписанной окружности:
Или иначе, положив что AD=a, BC=b, CD=c, и AB=h(высота)=2r(двойной радиус или диаметр вписанной окружности):
Или удвоенное произведение радиуса вписанной окружности и средней линии:
Galina7v7 7 лет назад Для ответа именно на этот вопрос- “как найти площадь прямоугольной трапеции АВСД “(АВ | АД) достаточно знать: 1)2 основания ВС =b и АД =а.2)Высоту трапеции АВ=hФормула площади S прямоугольной трапеции: S = (a+b)*h/2То есть необходимо знать или найти 3 параметра трапеции: оба основания, и боковую сторону, которая перпендикулярна обоим основаниям. Трапеция которая имеет прямые (90 градусов) углы при боковой стороне называется прямоугольной.
Площадь прямоугольной трапеции равна сумме площадей прямоугольника с меньшем основанием a и высотой h и прямоугольного треугольника с основанием с и высотой h. А теперь посчитаем: площадь прямоугольника равна a*h, а площадь прямоугольного треугольника равна c*h/2 (сторона с=b-a) = (b-a)*h/2 таким образом площадь любой прямоугольной трапеции можно написать в виде: S(трапеции)=a*h+(b-a)*h/2=(2a*h+(b-a)*h)/2=h(2а+b-a)/2=h(а+b)/2. а+b у нас сумма оснований трапеции, поэтому площадь прямоугольной трапеции равна сумме оснований умноженной на половину высоты трапеции
Virineya 7 лет назад Трапеция – это четырехугольник с двумя параллельными друг другу сторонами, являющиеся её основаниями, а две наклонные стороны – её боковыми. Прямоугольная трапеция – это фигура, у которой хотя бы одна сторона имеет угол 90 градусов. Хотя у данной фигуры минимум 2 прямых угла; это трапеция, у которой одна сторона перпендикулярна двум основаниям. Площадь прямоугольной трапеции ( по сути, ничем не отличается от формулы вычисления площади обычной трапеции, но одна из сторон является высотой): произведение 1/2 суммы её двух оснований и высоты, которая может являться одной из боковых сторон фигуры. Определяется по формуле: S = 1/2 · (a + b) · h
stalonevich 8 лет назад У этой фигуры имеются две параллельные стороны (a и b), а также 2 боковые. Для решения необходимо провести высоту, или же эта будет одна из боковых сторон фигуры, которая имеет угол в 90 градусов (пусть будет h), тогда формула имеет вид.
Oleg74 9 лет назад Если взять два основания А и В, которые в геометрической фигуре ” трапеция ” всегда параллельны, сложить их, потом разделить эту сумму пополам и умножить полученный результат на высоту H трапеции, то получим площадь S трапеции.
Стрымбрым 9 лет назад Как мы знаем, трапецией называется геометрическая фигура, которая образована четырьмя отрезками, два из которых параллельны между собой. Площадь трапеции определяется, как полусумма оснований, помноженная на высоту.
Площадь трапеции = H (A + C) / 2 где А и С – длина каждого основания трапеции А Н – это высота Напомним, что основания – это две параллельные стороны трапеции. Высота трапеции – перпендикулярна двум основаниям.
Katalina 8 лет назад Мне, если сказать честно, для ответа на этот вопрос пришлось освежить память и покопаться в интернете. Так вот, площадь прямоугольной трапеции равна деленной пополам сумме оснований, умноженной на высоту.
Гульнара Римовна 9 лет назад Допустим, что основания этой трапеции а( меньшее основание )и в( большее основание), высота- h. тогда, чтобы найти s можно поступить и по- другому. S=a*h+h*(b-a)/2 nastasykos 9 лет назад площадь прямоугольной трапеции равна полусумме оснований умноженной на высоту трапеции Sveta2013 9 лет назад сумму оснований умножить на высоту и поделить пополам Знаете ответ? |
Примечание. Это часть урока с задачами по геометрии (раздел прямоугольная трапеция). Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”
См. также: трапеция и ее свойства.
Прямоугольная трапеция
Прямоугольная трапеция – это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже – свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
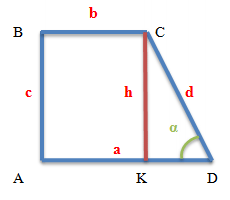
Формулы для прямоугольной трапеции
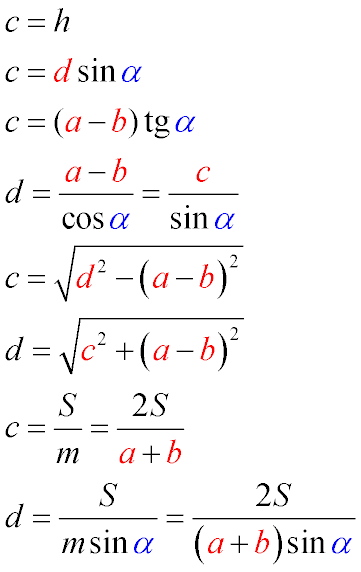 Обозначения формул даны на чертеже выше.
Обозначения формул даны на чертеже выше.
a и b – основания трапеции
с – боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d – боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α – острый угол при большем основании трапеции
m – средняя линия трапеции
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD – прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона,
перпендикулярная
основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD – прямоугольный. Поскольку трапеция – прямоугольная, то длина KD – это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая
не перпендикулярна
основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая
не перпендикулярна
основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее – следствие из теоремы Пифагора – из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее – следствие из теоремы Пифагора – находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая
не перпендикулярна
основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция – это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе “Трапеция”.
Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона – наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет
∠A.
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD
2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка
AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a – b.
то есть
122 + (a – b)2 = (a + b)2
откуда
144 + a2 – 2ab + b2 = a2 + 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см
2 .
0
Диагонали трапеции |
Описание курса
| Равнобокая (равнобедренная) трапеция
























