Как с помощью графика функции найти рисунок

Поиск изображения по графику оригинала

Пр.9
По данному графику оригинала найти
изображение.

Построим аналитическое
выражение для данной функции,

на
основе общего уравнения прямой, проходящей
через

две
точки (t₁,
y₁)
, (t₂,
y₂)

=

( 5 )

и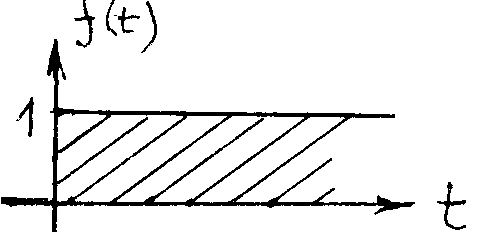
свойств единичной функции
(t
– а) =

(t)

(t)
–
(t
– а)

Решение.
Функцию на интервале [0 , a]
описывает разность двух единичных
функций
(t)
–
(t
– а) . Первую наклонную определим из ( 5
) по точкам (2а,
0), (а,
1): y
=-
(t
– 2a).
Для перехода от бесконечной прямой к
отрезку на интервале [a,
3a]
умножим уравнение на разность(t
-а) –(t
-3а)
Вторую наклонную определим из ( 5 ) по
точкам (4а,0)
, (3а,-1):
y
=(t
– 4a),
и умножим уравнение на
(t
– 3а).
Сумма этих трех выражений определит
аналитический вид функции

f(t)
=
(t)
–
(t
– а) –

(t
– 2a)
[(t
– а) –
(t
– 3а)]
+

(t
– 4a)
[(t
– 3а)]

Представим
f(t)
в виде суммы слагаемых двух типов
(t
– b)
и (t
– b)(t
– b)

f(t)
=(t)
–(t
– а) –(t
– a)(t
– а) +(t
– а) +(t
– 3a)(t
– 3а)
+(t
– 3а)+

+

(t
– 3a)
(t
– 3а)
–
(t
– 3а)
=
(t)
–
(t
– a)(t
– а)
+
(t
–
3a)(t
– 3а)

С
помощью соотношений Пр.8 совершим
переход к искомому изображению

F(t)
=:

–

+
.

Таблица
изображений

№	f(t) при t>0	F(p)	№	f(t) при t>0	F(p)
1	1		9	t cos at
2			10	t sin at
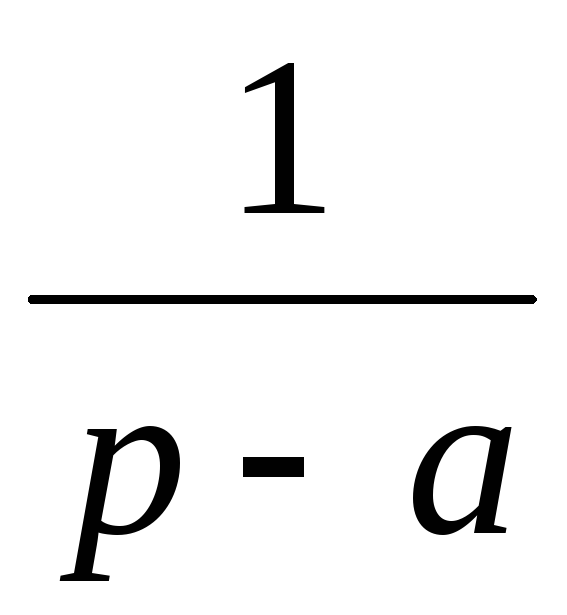
3	eat		11
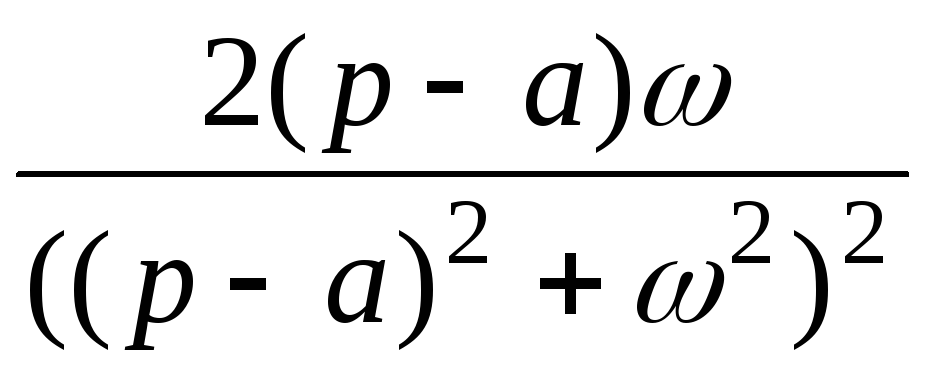
4	cos at		12
5	sin at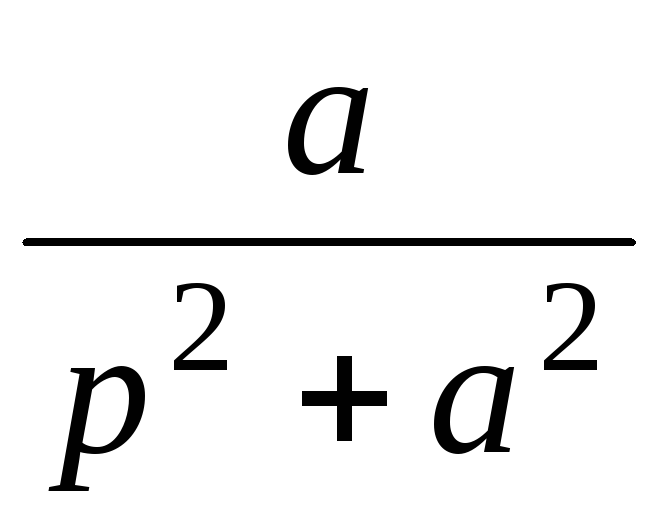		13
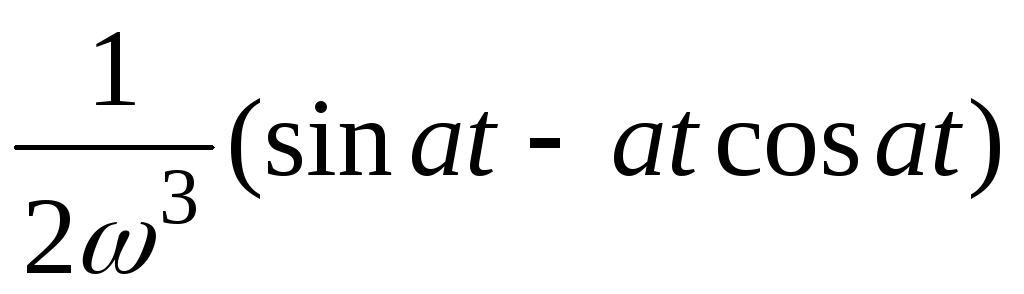
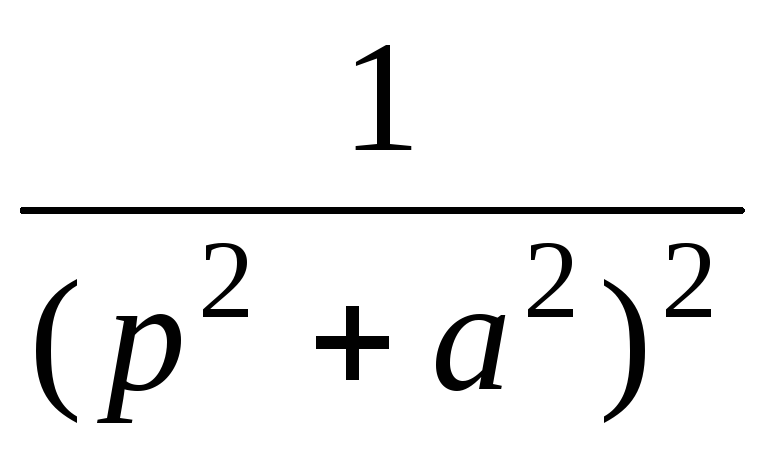
6	ezt cos at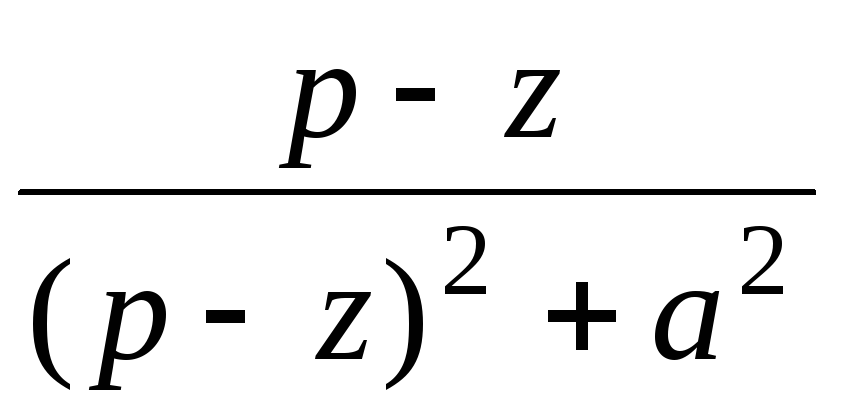		14
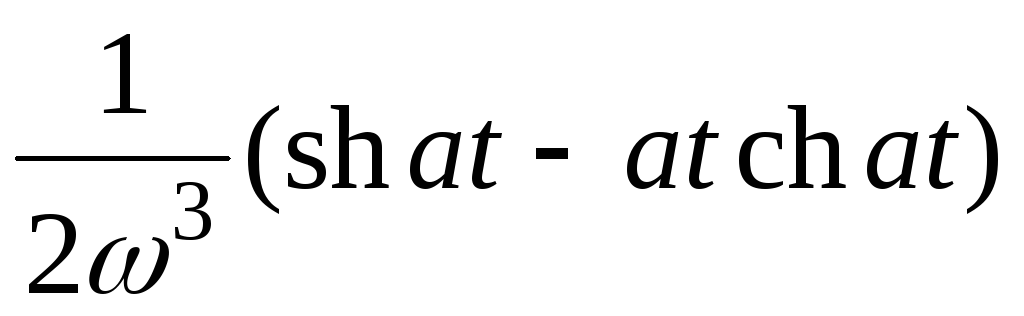
7	ezt sin at		15
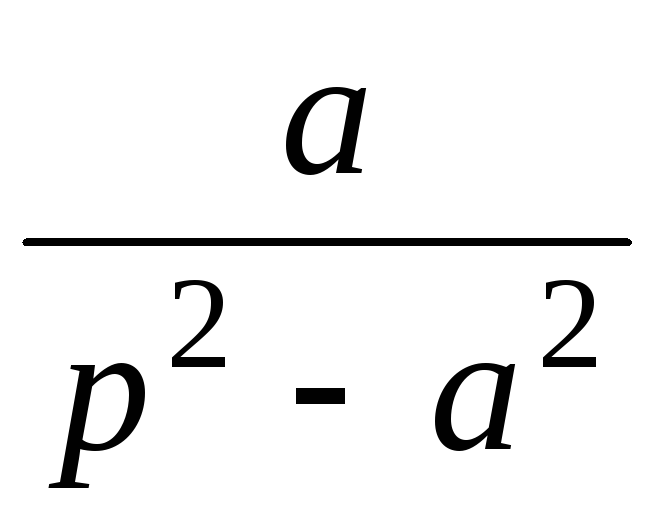
8	eat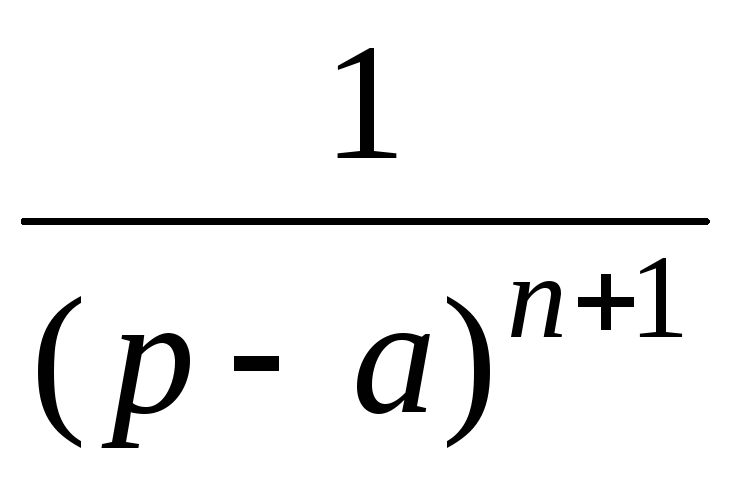		16

Отыскание оригинала по изображению

Если
изображение является дробно-рациональной
функцией F(p)
=

и m
< n
,
то многочлен
знаменателя представим в виде произ-ведения
линейных множителей

=
.
Корни
многочлена p_i
могут
быть
действительными числами, комплексными
числами и кратными. Комплексные корни
входят сопряженными парами и приводят
к трехчленам типа ( p²
+
p
+
).
В результате F(p)
представ-ляется в виде суммы
элементарных
дробей типа
,

(метод неопределенных коэффициентов).
Комбинируя эти дроби, можно пытаться
построить изображения основных
элементарных функций и затем по таблице
восстановить оригинал.

Пр.
10 Найти оригинал функции F(p)
=
.

=
=

+ ½=:
e^tcos
2t
+ ½ e^tsin
2t

Пр.
11 Найти оригинал функции F(p)
=

.

=

=

+

= =

p²
| A + B = 0

p¹
| 2A – 2B + C = 0

A = 1/12 , B = -1/12 , C = – 1/3

p⁰
| 4A – 2C = 1

=

–

=

–

Из
формул
№ 3, 6, 7

оригинал
f(t)
=e^2t
–

e^-t
(cos t+
sin t)
.

Если
в F(p)
только простые нули :
=

,
то разложение
изображения упрощается

F(p)
=

, где

( 6 )

Пр.12
Найти оригинал функции F(p)
=

Вычисляем
производную от знаменателя

= [ p(p
– 1)(p
– 2)(p
– 3) ]` =

=
(p
– 1)(p
– 2)(p
– 3) + p(p
– 2)(p
– 3) + p(p
– 1)(p
– 3) +
p(p
– 1)(p
– 2),

находим
её значения в нулевых точках v₄`(0)
= – 6 , v<sub>4</sub>`(1)
= 2 , v₄`(2)
= – 2 , v<sub>4</sub>`(3)
= 6 , определяем коэффициенты A₀
= – 1/6 , A₁
= 1, A₂
= – 3/2, A₃
= 2/3

и
по формуле ( 6 ) расписываем разложение
изображения на простые дроби

F(p)
=

=:

+

–

+
.

Если
F(p)
разлагается в сходящийся ряд

F(p)
=

+

+

+ . . . +

+ . . . ,

то
его оригинал находится по формуле

f(t)
=

+

+

+ . . . +

+ . . .

Этот
ряд сходится при всех значениях t
.

Пр.13
Найти оригинал функции F(p)
=
.

Используем
формулу для суммы бесконечной
геометрической прогрессии

==

–

+

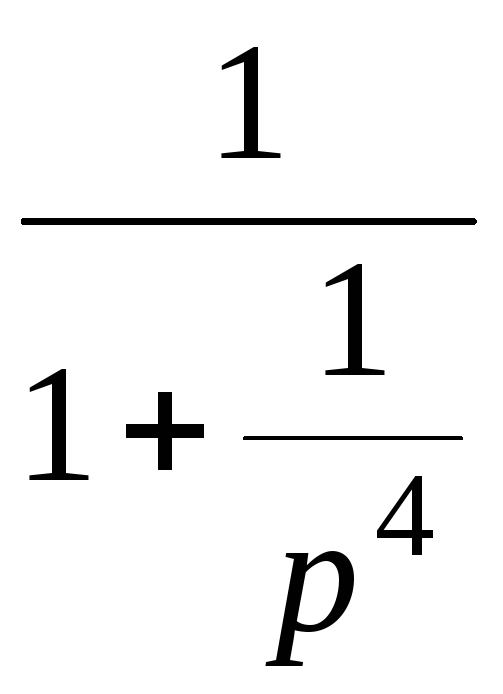– . . . Этот ряд сходится при |p|
> 1

По
формуле № 2 получаем оригинал f(t)
=

–

+

–

+ . . .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Интегрированный урок (алгебра + информатика) по теме «Рисуем графиками функций». 8-й класс

Класс: 8

Тема (математика): Преобразования графиков функций.

Тема (информатика): Построение графиков в MS Excel.

Цели урока:

• Образовательные:
  • повторение знаний по преобразованию графиков функций,
  • применение приобретенных умений и навыков графического изображения в процессе решения задач по математике и информатике;
  • формирование практических навыков построения графиков в программе Excel.
• Развивающие:
  • развитие умений выделять главное,
  • развитие речи, эмоций, логического мышления учащихся,
  • активизация познавательной и творческой активности учащихся.
• Воспитательные:
  • формирование интереса к предмету, навыков контроля и самоконтроля, чувства ответственности, самостоятельности, деловых и коммуникативных качеств учащихся.

Задачи урока:

• Повторить виды преобразований графика функции y = f(x):
  • y = – f(x) ;
  • y = kf(x);
  • y = f(x) + а;
  • y = f(x – b);
  • y = f(x – b) + а.
• Использовать изученные виды преобразований для построения рисунка с помощью графиков.
• Использовать умения построения графиков в одной системе координат с помощью программы Excel для получения некоторого изображения.
• Продолжить формирование у учащихся потребности использования информационных технологий в решении графических заданий по математике.
• Продемонстрировать применение полученных знаний на практике и для решения задач из смежных дисциплин.

Структура урока:

1. Организационный момент (объявление темы, цели и задач урока).
2. Актуализация знаний (повторение видов преобразований графиков функций)
3. Повторение темы «Преобразования графиков функций»:
   • выполнение задания на построение графиков функций с помощью различных видов преобразований;
   • построение рисунка в тетради с помощью графиков функций на заданной области определения.
4. Повторение темы «Построение графиков функций с помощью программы Excel:
   • повторение особенностей ввода формул и построения графиков в программе Excel.
   • практическая работа «Рисуем графиками функций в программе Excel».
   • проверка практической работы, анализ ошибок и выставление оценок.
5. Постановка домашнего задания.
6. Подведение итогов урока, рефлексия.

1. Организационный момент

Сегодня мы проводим интегрированный урок, в ходе которого попробуем совместить два предмета: математику и информатику. Нам предстоит повторить преобразования графиков функций и использовать эти знания для выполнения заданий по математике и информатике на построение различных изображений.

2. Актуализация знаний

Для повторения изученных видов преобразований графиков необходимо выполнить предложенное задание.

Задание для фронтальной работы: установите соответствие между предложенными графиками и формулами функций, дайте характеристику данному виду преобразований (рис.1, 2).

3. Повторение темы «Преобразования графиков функций»

Применение рассмотренных видов преобразований осуществляется при выполнении двух следующих заданий, которые учащиеся выполняют в тетрадях. Один ученик выполняет задание на интерактивной (либо обычной) доске. Графики обозначаются разными цветами.

Задание 1: постройте графики функций с помощью изученных видов преобразований

Первый график должен быть построен обязательно на доске, второй рассчитан на учеников, быстро выполнивших задание, либо может быть использован как резервный в конце урока для самостоятельной работы учащихся, быстро справившихся с практической работой.

Задание 2: Постройте рисунок с помощью графиков функций (рис.3):

Графики 4),5),6),7) до пересечения с графиком
А теперь попробуем получить рисунки в программе Excel.

4. Повторение темы «Построение графиков функций с помощью программы Excel:

Для повторения темы на данном этапе урока необходимо провести фронтальный опрос учащихся с целью актуализации знаний по информатике, необходимых для выполнения практической работы.

Вопросы для устной фронтальной работы:

• Как задать диапазон значений для переменной Х?
• Как задать диапазон значений для переменной У?
• Как показать, что в ячейку будет введена формула?
• Какие правила ввода формул вы знаете?
• Какими символами обозначаются действия умножения, деления, возведения в степень?
• Может ли формула в программе Excel содержать переменную Х? А что вместо Х она должна содержать?
• Как построить несколько графиков в одной системе координат?
• Какой тип диаграмм надо выбрать для построения графика функции?
• Как изменить цвет графика?

Практическая работа «Рисуем графиками функций в программе Excel».

Все ученики получают карточки с заданиями. Задания (зонтик, очки, кит) берутся из источника [6]. В одной системе координат необходимо построить графики всех функций на указанных промежутках. Если все будет выполнено верно, то получится картинка. За работу каждому будет выставлена отметка с учетом объема выполненной работы и допущенных ошибок. Работу сохранить на Рабочий стол и не закрывать.

На данном этапе учащиеся осуществляют самоконтроль:

• определяют, какие элементы рисунка «не вписываются» в общую картину,
• чем это было вызвано (ошибки при вводе формулы, при задании диапазона значений и т.п.), опираясь на полученные на уроках математики знания о различных видах преобразований, вносят изменения и оценивают, как они повлияют на вид рисунка. Во время работы учитель проходит по классу и оценивает работу учащихся.

На следующем этапе учитель показывает с помощью проектора, какие рисунки должны получиться у учащихся, объявляет оценки за выполненную работу, проводит с помощью учеников анализ типичных неточностей и ошибок.

5 . Постановка домашнего задания

По алгебре (творческое задание): придумать рисунок с помощью графиков 7-8 функций. Изобразить его в координатной плоскости, записать используемые функции на заданной области определения.
По информатике: построить с помощью программы Excel рисунок по заданным формулам функций из того же источника [6] (бабочка и лягушка).

6. Подведение итогов урока, рефлексия

Подведение итогов урока осуществляется в форме беседы, в ходе которой обсуждается вопрос: в каких сферах человеческой деятельности могут применяться графики функций.
На этапе рефлексии ученикам предоставляется возможность оценить свою работу, а также ответить на вопросы: получилось ли достигнуть цели урока, достаточно ли было знаний для выполнения предложенных заданий, какие задания требуют дополнительного внимания.

Список использованной литературы

1. Алгебра,8 класс: учеб. для учащихся общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е.Феоктистов.–10-е изд., испр. – М.: Мнемозина, 2010.–384с.
2. Босова Л.Л. Информатика и ИКТ: учебник для 7 класса / Л.Л. Босова. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2010. – 229 с.
3. Цукарь А.Я. Рисуем графиками функций // Математика в школе. – 1999. – №4. – с. 80-81

Рисуем картинки с помощью кривой Гильберта

В субботу на прошлой неделе «дело было вечером, делать было нечего», и мы с хабраюзером sourcerer разговаривали не понятно о чём. И почему-то речь зашла речь о задаче обратной к задаче построения графика функции по её выражению. То есть, например, у нас есть выражение y(x) = (cos 0,5 x ⋅ cos 200x + |x| 0,5 − 0,7)(4 − x 2 ) 0,01 . График такой функции чем-то напоминает сердечко. Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.

Какие-нибудь ряды Фурье вспоминать не хотелось, а хотелось чего-то простого и красивого. Мы начали вспоминать известные нам результаты, связанные с этим вопросом. В результате получилась программка, которая по изображению генерирует ломаную линию, чем-то напоминающую исходное изображение. На примере котёнка по имени Гав это выглядит примерно так (смотреть лучше издалека):

Если интересно как такое сделать, а также узнать про формулу конопли, формулу, график которой является этой же формулой, то добро пожаловать под хабракат. (Будет много картинок.)

Итак, вспомним некоторые результаты.

Формула Таппера. Рассмотрим неравенство
, и пусть число k равно
48584506361897134235820959624942020445814005879832445494830930850619347
04708809928450644769865524364849997247024915119110411605739177407856919
75432657185544205721044573588368182982375413963433822519945219165128434
83329051311931999535024137587652392648746133949068701305622958132194811
13685339535565290850023875092856892694555974281546386510730049106723058
93358605254409666435126534936364395712556569593681518433485760526694016
12512669514215505395545191537854575257565907405401579290017659679654800
64427829131488548259914721248506352686630476300.

Оказывается множество точек (x, y − k) удовлетворяющих этому неравенству и таких, что 0 ≤ x ≤ 106 и k ≤ y ≤ k + 17, выглядит следующим образом:

А это снова само неравенство. Понятно, конечно, что просто-напросто в числе k зашифровано изображение, но тем не менее результат очень красивый и не понятно как такое вообще можно было придумать.
Более подробно можно почитать в википедии: Tupper’s self-referential formula, а мы перейдём от частных результатов к массовым методам.

Системы итерируемых функций. Наверное, каждый, кто хоть немножко сталкивался с фракталами, знает, что такое системы итерируемых функций. СИФ позволяет с помощью пары десятков чисел получать картинки очень похожие на реальные листья, деревья, ветки:

Идея о том, что можно попытаться решить обратную задачу — по заданному изображению получить набор чисел, описывающих СИФ, позволила Майклу Барнсли придумать фрактальное сжатие. Какая-то попытка рассказать о фрактальном сжатии уже предпринималась на хабре: Основы фрактального сжатия изображений. Но тем, кто хочет разобраться детально порекомендую первую половину книги «Фракталы и вейвлеты для сжатия изображений в действии» С. Уэлстида.

Фрактальные строки. На самом деле в алгоритме фрактального сжатия используются не системы итерируемых функций, а так называемые системы частичных итерируемых функций. Тем не менее есть класс изображений, для которых легко придумать именно СИФ, аттракторами которых они являются. Такими изображениями являются фрактальные строки. Фрактальная строка — это слово, каждая буква которого состоит из уменьшенных копий данного слова и так далее. На примере слова «ХАБР» это выглядит как-то так:

Несложно понять как такое сделать для произвольного слова, достаточно потратить немного времени, чтобы представить каждое слово в виде набора параллелограммов. Как минимум лет пять назад это было сделано. Подробное описание и код можно найти в статье Фрактальные строки.

Портрет В.-Й. Мёллера. Листая книгу «Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая» М. Шредера, можно наткнуться на следующую иллюстрацию:

Выглядит это очень симпатично, и понятно, что такое можно сделать с произвольным изображением. О том, как это было нарисовано, в книге не рассказывается, но не сложно догадаться самому.

Для начала нужно взять алгоритм построения кривой Гильберта. Но не с помощью каких-нибудь L-систем, а честный рекурсивный алгоритм. А дальше модифицируем его следующим образом. Если яркость квадратика больше заданного порога и в четырёх его подквадратиках кривую рисовать не нужно, то считаем, что и в самом квадратике рисовать кривую не нужно. Хотя наверное проще понять из кода, приведённого ниже.

Перед тем, как изображение скармливалось программке, оно переводилось в оттенки серого и опытным путём подстраивалась яркость и контрастность. Например, вот что получилось, когда программку натравили на тукса:

Если кто-то знает ещё какие-то красивые результаты из обсуждаемой области, то напишите об этом, пожалуйста, в комментариях.

Проектная работа по теме «Построение рисунков с помощью графиков функций» (9 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Задания группам.docx

Построить рисунок «Зонтик» [5] по заданным уравнениям графиков функций:

у = (-1/18) х 2 +12, xϵ[ -12;12 ] ;

у = (-1/8) х 2 +6, xϵ[ -4;4 ] ;

у = (-1/8) (х+8) 2 , xϵ 12; -4 ] ;

у = (-1/8) (х-8) 2 , xϵ[ 4;12 ] ;

у = 2(х+3) 2 -9, xϵ [ -4; -0,3 ] ;

у = 1,5(х+3) 2 -10, xϵ [ -4; -0,2 ] .

Построить рисунок «Очки» [5] по заданным уравнениям графиков функций:

у = (-1/16) (х+5) 2 +2, xϵ [ -9; -1 ] ;

у = (-1/16) (х-5) 2 +2, xϵ[ 1;9 ] ;

у = (1/4) (х+5) 2 -3, xϵ [ -9; -1 ] ;

у = (1/4) (х-5) 2 -3, xϵ[ 1;9 ] ;

у = -(х+7) 2 +5, xϵ [ -9; -6 ] ;

у = — (х-7) 2 +5, xϵ [ 6; 9 ] ;

у = 0,5х 2 +1,5, xϵ [ -1; 1 ] .

Построить рисунок «Лягушка» [5] по заданным уравнениям графиков функций:

у = (-3/49) х 2 +8, xϵ[ -7;7 ] ;

у = (4/49) х 2 +1, xϵ[ -7;7 ] ;

у = -0,75 (х+4) 2 +11, xϵ [-6,8; -2];

у = -0,75 (х-4) 2 +11, xϵ [2;6,8];

у = -(х+4) 2 +9, xϵ [-5,8; -2,8];

у = — (х-4) 2 +9, xϵ [2,8;5,8];

у = (4/9) х 2 -5, xϵ [-4;4].

у = (4/9) х 2 -9, xϵ [-5,2;5,2];

у = (-1/16) (х+3) 2 -6, xϵ [-7; -2,8];

у = (-1/16) (х-3) 2 -6, xϵ [2,8;7];

у = (1/9) (х+4) 2 -11, xϵ [-7;0];

у = -(1/9) (х-4) 2 -11, xϵ [0;7];

у = -(х+5) 2 , xϵ [-4,5; -7];

у = — (х-5) 2 , xϵ [4,5;7];

у = (2/9) х 2 +2, xϵ [-3;3].

Построить рисунок «Динозаврик» [5] по заданным уравнениям графиков функций:

у = (-1/8) х 2 +5, xϵ[ -5,2;4 ] ;

у = (-5/16) (х-8) 2 +8, xϵ[ 4;12 ] ;

у = -0,5 (х+7) 2 +3, xϵ [ -9; -5 ] ;

у = -0,5 (х-10) 2 +1, xϵ[ 8;12 ] ;

у = (х+3) 2 -7, xϵ [ -5; -1 ] ;

у = (х-4) 2 -7, xϵ[ 2;6 ] ;

у = (4/9) (х-0,5) 2 -4, xϵ[ -1;2 ] ;

у = 0,5(х-11) 2 -7, xϵ [9;13].

Построить рисунок «Верблюд» [5] по заданным уравнениям графиков функций:

у = -0,5х 2 +4, xϵ[ -2;2 ] ;

у = -0,5(х+4) 2 +4, xϵ [ -6; -2 ] ;

у = 0,5 (х-3) 2 +1,5, xϵ[ 2;6 ] ;

у = -0,5 (х-8) 2 +8, xϵ[ 6;10,5 ] ;

у = (х-9,5) 2 +4, xϵ[ 8,5;10,5 ] ;

у = -0,5(х-8,5) 2 +5, xϵ[ 4;8,5 ] ;

у = (1/8) (х+3) 2 -5, xϵ[ -7;1 ] .

у =-0,25 (х+6) 2 +2, x ϵ [ -11; -6 ] ;

у = 3 (х+6), xϵ [ -8; -7 ] ;

Выбранный для просмотра документ Карта проекта. Группа 1. Построение рисунков с помощью графиков.docx

по теме «Построение рисунков с помощью графиков функций»

Цель работы: применение навыков построения графиков.

Оборудование: шаблоны графиков функций, линейка, карандаш, «Учебное электронное издание математика 5-11».

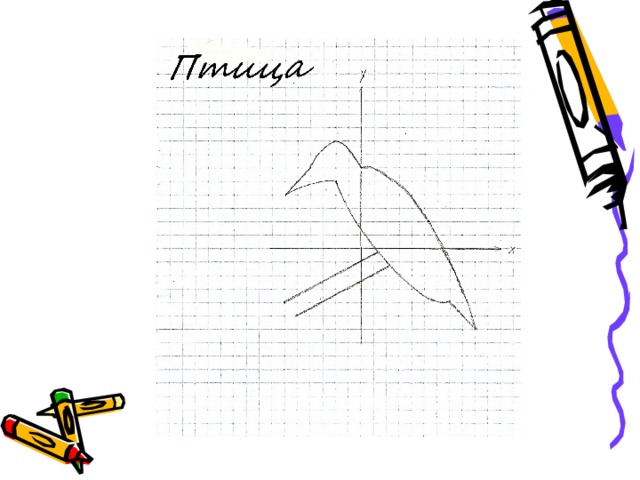
Построить рисунок «Птица» по заданным уравнениям графиков функций:

у = (-4/27) х 2 +6, xϵ[0 ;9 ] ;

у = (1/9) (х-7) 2 -4, xϵ[ -2;7 ] ;

у = -0,5(х+2) 2 +8, xϵ[ -4;0 ] ;

у = (-1/16) (х+2) 2 +5, xϵ[ -6;2 ] ;

Распределить обязанности в группе:

А) представление теоретического материала по теме «Функция»;

Б) изготовление шаблонов парабол (уравнения №1-№4);

В) Заполнение таблицы №1 для построения рисунка;

Г) Построение рисунка с помощью шаблонов и линейки;

Д) Построение рисунка с помощью пособия «Учебное электронное издание математика 5-11»;

Е) Представление результатов работы в группе.

2. Выполнение работы:

2.1. Актуализация теоретических знаний по теме «Функция».

2.2. Изготовление шаблонов парабол

2.3. Заполнение таблицы №1

Вид графика (парабола, прямая)

Шаблон у=ах 2 , а

Ветви направлены (вверх, вниз)

2.4. Построение рисунка на координатной плоскости с помощью шаблонов и линейки.

2.5. Построение рисунка с помощью пособия «Учебное электронное издание математика 5-11».

3. Представление результатов работы группы.

Выбранный для просмотра документ Презентация. Построение рисунков с помощью графиков. Ржевская Диана, сош 31.pptx

Описание презентации по отдельным слайдам:

Выполнила РЖЕВСКАЯ ДИАНА ученица 9 А класса БОУ СОШ № 31 МО Динской район Руководитель проекта Баранова М.Н. учитель математики БОУ СОШ № 31 МО Динской район XXV районная научно-практическая конференция учащихся 9-11 классов Построение рисунков с помощью графиков функций

Графики живых организмов

Берёзовый долгоносик вырезает из листа колыбельку для своего детёныша в форме эволюты

Форму логарифмической спирали имеют: галактика, паутина паука, раковина улитки, рога козлов,…

Использование графиков в деятельности человека

Использование оптического свойства параболы

Всякий ли объект может быть описан с помощью уравнений графиков функций? Гипотеза:

Доказать, что любой объект можно описать с помощью уравнений графиков функций. Цель работы:

Изучение теоретического материала по темам «Графики функций», «Преобразования графиков функций». Построение рисунков по заданным уравнениям графиков функций. Описание рисунка «Черепашка» с помощью уравнений графиков функций. Проверка правильности выполнения практических заданий с помощью компьютерной программы «Учебное электронное издание, математика 5-11». Задачи:

Уравнение и график линейной функции: у=кх+в; график – прямая. Уравнение и график квадратичной функции: у=а(х-n)²+m; график – парабола. Преобразования графиков: перенос вдоль оси Ох и Оу. Поиск графиков, не изучаемых в школьном курсе. Изучение теоретического материала.

Трёх лепестковая роза . Лемниската Бернулли

Выполнение практической работы №1 «Построение рисунков с помощью графиков функций» и проверка её результатов с помощью компьютерной программы «Учебное электронное издание, математика 5-11». Построение рисунков по заданным уравнениям графиков функций.

1.у = (-4/27)х² +6, х є [0;9]; 2.у = (1/9)(х – 7)² — 4, х є [-2;7]; 3.у = -0,5(х + 2)² + 8,x є [-4;0]; 4.у = (-1/16)(х + 2)² +5, x є [-6;2]; 5.y = x + 10, x є [-6;-4]; 6.y = -x = 3, x є [7;9]; 7.y = 0.5x – 1, x є [-6;1]; 8.y = 0.5x – 2.5, x є [-5;2]. Задание №1. построить рисунок «Птица» по заданным уравнениям графиков функций:

Практическая работа №2 «Описание рисунка «Черепашка» с помощью уравнений графиков функций».

Найдем координаты точек А1 и В1 в системе координат О1х1у1 А1(-2,6;-1), В1(0;0) -1,3=а*(-2,6)2 -1=а*6,76 а=-1/6,76=-100/676=-50/338=-25/169 у=-25/169 х2 Найдем координаты вершины В1 в системе координат Оху (9;11,8) у=-25/169(х-9)2+11,8 Промежуток [6,4; 10,8] Фрагмент рисунка напоминает параболу.

Этот участок напоминает прямую. А2(х2;у2) ; А4(х4;у4) А2(14,6; 6,8) ; А4(14,9; 6) у=(х-х2)(у4-у2)/(х4-х2)+у2 у=(х-14,6)(6-6,8)/(14,9-14,6)+6,8 Промежуток [14,6; 14,9] Фрагмент рисунка А2А4

С помощью программы «Учебное электронное издание математика 5-11 » получен рисунок «Черепашка».

Вывод: Любой объект можно описать с помощью уравнений графиков функций.

ученными было установлено, что с помощью математических уравнений можно описать движение животного (кошки). Почти 40 лет назад, 1968 год… Группа под руководством Николая Николаевича Константинова создает математическую модель движения животного (кошки).Машина БЭСМ-4, выполняя написанную программу решения обыкновенных (в математическом смысле слова) дифференциальных уравнений, рисует мультфильм «Кошечка», содержащий даже по современным меркам удивительную анимацию движений кошки, созданную компьютером. При изучении теоретического материала, я узнала, что

Выбранный для просмотра документ Проектная работа. Построение рисунков. Ржевская Диана. сош 31.docx

XXV районная научно-практическая конференция

школьников Динского района

Построение рисунков с помощью графиков функций.

ученица 9а класса

МО Динской район.

МО Динской район

к работе по теме «Построение рисунков с помощью графиков функций» ученицы 9а класса БОУ СОШ №31 МО Динской район

Тема работы «Построение рисунков с помощью графиков функций» для школы актуальна. В работе раскрывается проблема: можно ли описать окружающие нас объекты с помощью графиков функций?

Цель работы: описать рисунок «Черепашка» с помощью уравнений графиков функций.

Для этого ученицей изучен теоретический материал по темам «Графики элементарных функций», «Преобразования графиков функций». Найден дополнительный иллюстративный материал по теме работы.

Цель практической работы №1 – отработка навыков построения графиков. Её выполнение позволило ученице применить свои теоретические знания на практике при построении рисунков.

В практической работе №2 Диана самостоятельно описала рисунок «Черепашка» с помощью уравнений графиков функций (линейной и квадратичной). Проверила правильность выполнения всех заданий практических работ с помощью программы «Учебное электронное издание математика 5-11» /Дрофа –ДОС для НФПК/.

Цель работы достигнута. Рисунок «Черепашка» описан с помощью графиков функций. Сделан вывод о том, что при выполнении рисунка достаточно использовать лишь линейные функции.

Учитель математики БОУ СОШ №31

МО Динской район М.Н. Баранова

Практическая работа №1 «Построение рисунков с помощью графиков функций»……………………………………………………………..5

3. Практическая работа №2 «Создание рисунка «Черепашка» и описание его с помощью уравнений графиков функций»………………………………8

Е) Приложение №6 (шаблоны графиков функций)………………………27

Функция – это одно из основных математических понятий, выражающее зависимость между переменными [1].

График функции – это один из способов представления функции. Представить какую-либо функцию можно разными способами. Например, табличным или графическим [1].

Табличный способ предпочитают тогда, когда трудно вычислять значения функции [1].

Графический способ представления функции – самый наглядный. График функции – это линия, дающая цельное представление о характере изменения её уравнения [1].

В школьной программе мы изучаем самые простейшие графики и их преобразования.

Помимо графиков функций, изучаемых нами в школе, существую и другие, интересные и «красивые» графики. Например, кардиоида, астроида, декартов лист, лемниската Бернули, спираль Архимеда и другие (Приложение №1) [2].

Живая природа демонстрирует нам многочисленные графики живых организмов. Например, березовый долгоносик, изготовляя колыбельку для своего детёныша, на листке вырезает эволюту. Паук плетёт паутину, которая выглядит как логарифмическая спираль [3].

Если взглянуть на форму многих галактик, то можно обнаружить, что некоторые из них имеют форму логарифмической спирали. Галактика млечный путь – типичная спиральная галактика [3]. (Приложение 2).

Но форму логарифмической спирали имеют не только объекты астрономии, но и, например: рога козлов, паутина, ракушки многих улиток, расположение семечек в цветке подсолнуха. Так же широкое применение нашла логарифмическая спираль в экономике [3].

Так же было установлено, что с помощью математических уравнений можно описать движение. Так, существуют математические уравнения колебания струны, математического маятника и другие.

Почти 40 лет назад, 1968 год… группа под руководством Николая Николаевича Константинова создает математическую модель движения животного (кошки). Машина БЭСМ -4, выполняя написанную программу решения обыкновенны (в математическом смысле слова) дифференциальных уравнений, рисует мультфильм «Кошечка» (Приложение№3), содержащий даже по современным меркам удивительную анимацию движений кошки, созданную компьютером.

В этой работе рассматриваются различные элементарные функции. Работа включает в себя две практические работы: «Построение рисунков с помощью графиков функций», «Создание композиции «Черепашка» и описание её с помощью уравнений графиков функций».

Я представляю два варианта выполнения рисунков: ручной и электронный. Электронный вариант осуществлён с помощью программы «Учебное электронное издание математика 5-11».

Цель этих практических работ: применение навыков построения, преобразования графиков функций при создании рисунков и применение навыков преобразования графиков функций при составлении композиции.

Практическая работа №1

Тема: «Построение рисунков с помощью графиков функций».

Цель работы: применение навыков построения графиков.

Оборудование: шаблоны графиков функций, линейка, карандаш, «Учебное электронное издание математика 5-11».

Построить рисунок «Птица» [4] по заданным уравнениям графиков функций:

Проектная работа Рисунки в графиках Авторы: Расулова Лейла Руководитель: Зенина Е.Н. (Данилина Е.Н.) МОУ «Гимназия №4» 2019-2020 уч.год.

Введение.

Тема нашего проекта называется «Рисунки в графиках». Мы выбрали этот проект так как знали, что существует декартова система координат на плоскости и умели строить некоторые графики функций. Нам стало интересно сможем ли мы построить различные фигуры с помощью известных нам графиков? Эти вопросы нас заинтересовали и мы решили работать над данным проектом.

Таким образом, мы поставили перед собой цель: научиться строить фигуры с помощью графиков функций в декартовой системе координат.

Для достижения цели, мы наметили план работы и сформулировали задачи, способствующие раскрытию творческих способностей каждого из нас, взаимопонимания, индивидуальности.

Задачи проекта:

• научиться строить фигуры с помощью графиков в декартовой системе координат, расширив свой кругозор и продолжив работу над графической культурой;
• научиться работать с различными источниками информации;
• научиться составлять презентации, используя навыки работы с компьютером;
• научиться выступать перед аудиторией.

В процессе работы над проектом, мы обращались к математическому словарю, учебникам по высшей математике, методической литературе, интернету. Построили каждый по двефигуры в системе координат с помощью графиков функций, и одну общую фигуру, описали их и выполнили соответствующие построения, т.е. выполнили творческие работы, наглядно показав степень овладения полученной информацией.

Элементарные функции и их графики.

1). Пропорциональные величины . Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:

y = k x, где k – постоянная величина ( коэффициент пропорциональности ).

График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол , тангенс которого равен k : tan = k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3.

2. Линейная функция . Если переменные y и x связаны уравнением 1-ой степени:A x + B y = C , где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае – нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.

3. Обратная пропорциональность . Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x , где k – постоянная величина. График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью ( о конических сечениях см. раздел «Конус» в главе «Стереометрия» ). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.

4. Квадратичная функция . Это функция: y = ax ² + bx + c, где a, b, c – постоянные, a 0. В простейшем случае имеем: b = c = 0 и y = ax². График этой функции квадратная парабола – кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.

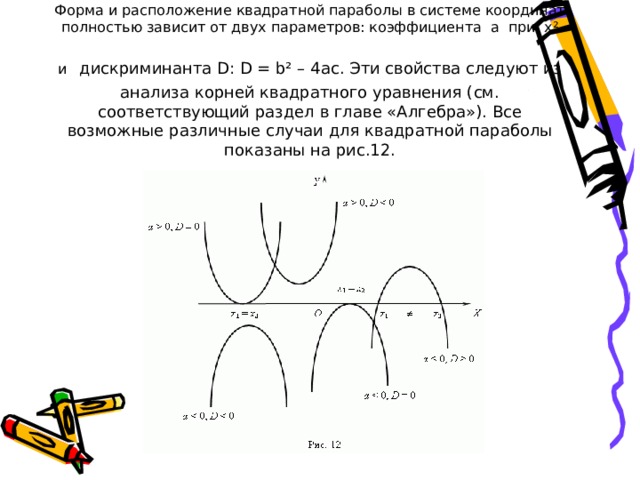
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x² и дискриминанта D: D = b² – 4ac. Эти свойства следуют из анализа корней квадратного уравнения (см. соответствующий раздел в главе «Алгебра»). Все возможные различные случаи для квадратной параболы показаны на рис.12.

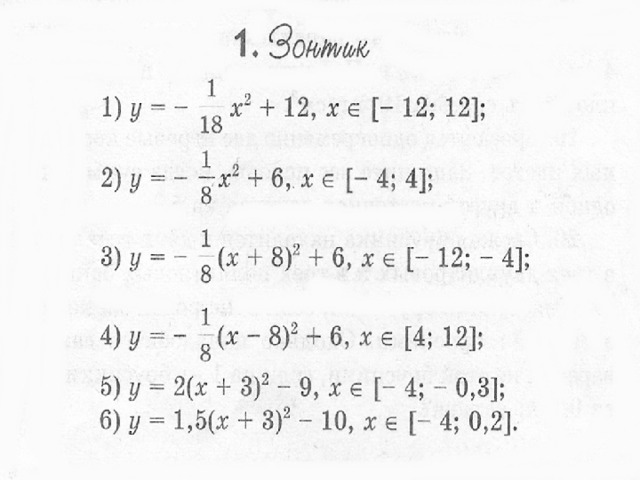
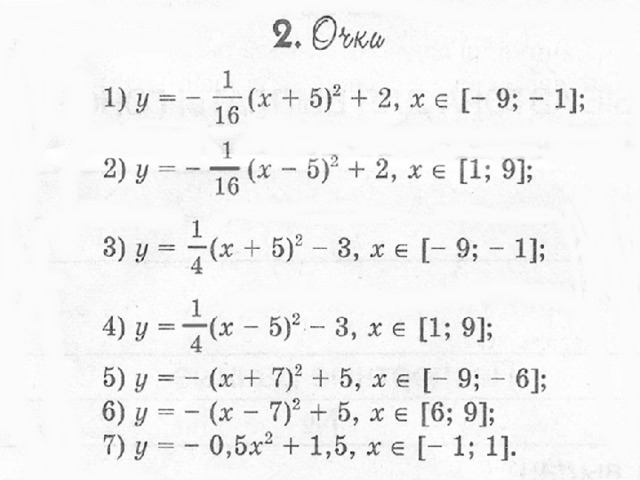
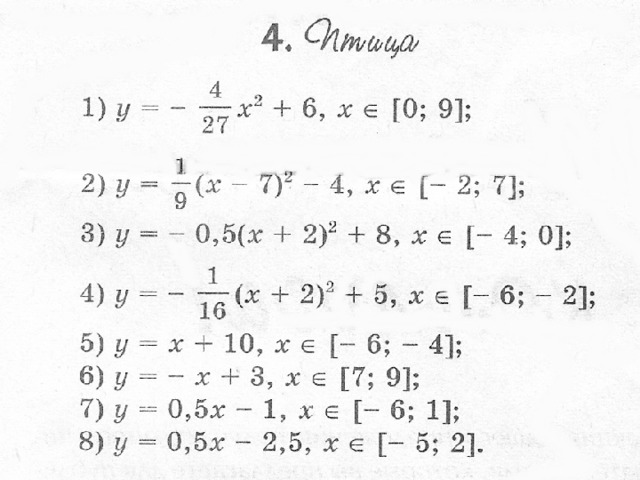
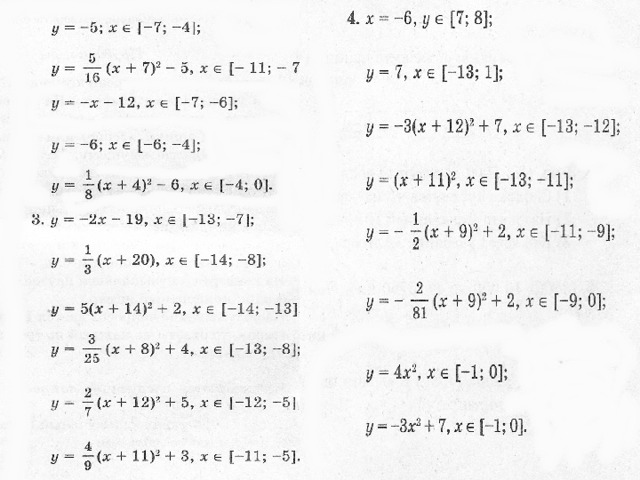
Заключение. Таким образом, при работе над проектом «Рисунки в графиках» мы научились строить фигуры с помощью графиков функций, заданных каждый своей формулой на рассматриваемых промежутках.

При выполнении творческих работ, мы:

• придумали и построили каждый свой рисунок;
• описали этот рисунок;
• проверили друг у друга выполненные творческие работы и внесли, если это необходимо, соответствующие коррективы;
• оформили результаты на листах;
• составили презентации своих творческих работ.

Выполняя творческие работы, мы закрепили навыки вычислительной техники; показали степень овладения графической культурой, хотя это было нелегко.

Наш проект имеет свою практическую направленность:

• создание дидактического материала;
• расширение кругозора;
• закрепление навыков графических построений;
• использование материалов проектной работы при проведении уроков;
• поиск и отбор информации.

Спасибо за внимание