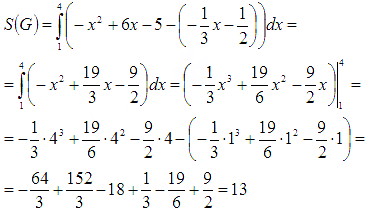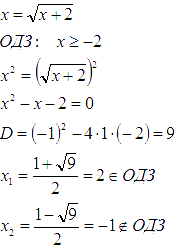В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S(G)=∫abf(x)dx для непрерывной и неотрицательной функции y=f(x) на отрезке [a;b],
S(G)=-∫abf(x)dx для непрерывной и неположительной функции y=f(x) на отрезке [a;b].
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y=f(x) или x=g(y).
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
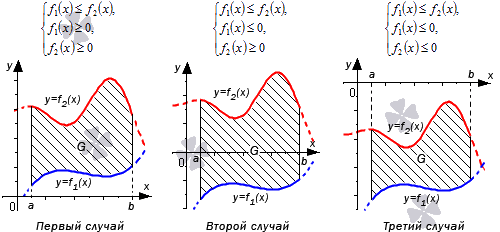
Пусть функции y=f1(x) и y=f2(x) определены и непрерывны на отрезке [a;b], причем f1(x)≤f2(x) для любого значения x из [a;b]. Тогда формула для вычисления площади фигуры G, ограниченной линиями x=a, x=b, y=f1(x) и y=f2(x) будет иметь вид S(G)=∫abf2(x)-f1(x)dx.
Похожая формула будет применима для площади фигуры, ограниченной линиями y=c, y=d, x=g1(y) и x=g2(y): S(G)=∫cd(g2(y)-g1(y)dy.
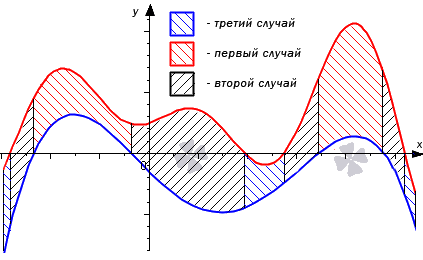
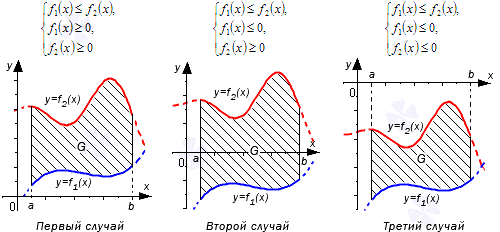
Разберем три случая, для которых формула будет справедлива.
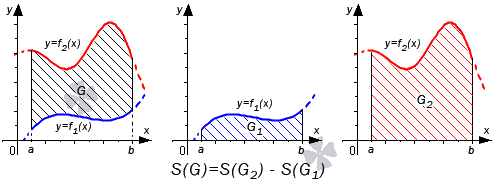
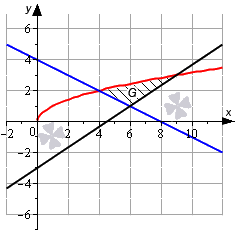
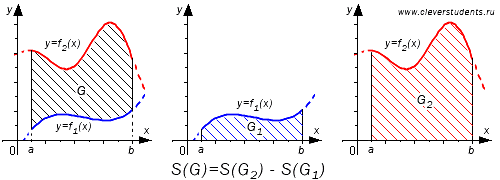
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G1 равна площади фигуры G2. Это значит, что
Поэтому, S(G)=S(G2)-S(G1)=∫abf2(x)dx-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx.
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
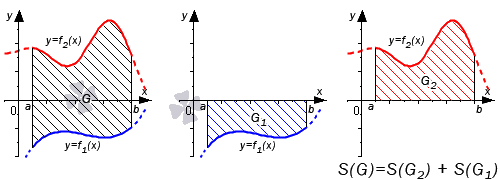
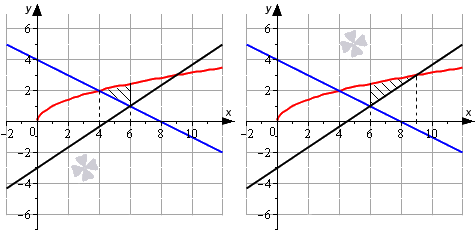
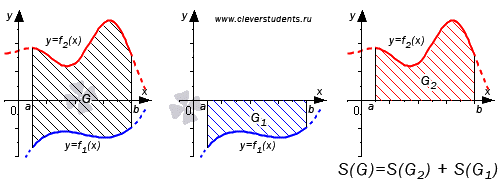
Во втором случае справедливо равенство: S(G)=S(G2)+S(G1)=∫abf2(x)dx+-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx
Графическая иллюстрация будет иметь вид:
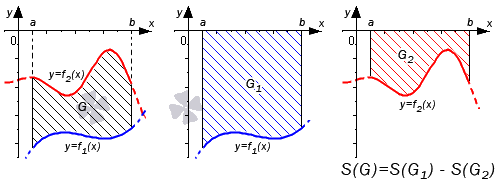
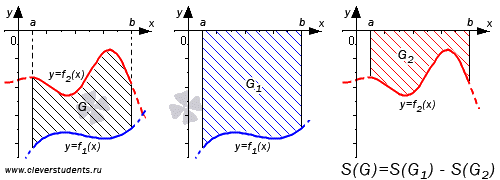
Если обе функции неположительные, получаем: S(G)=S(G2)-S(G1)=-∫abf2(x)dx–∫abf1(x)dx=∫ab(f2(x)-f1(x))dx . Графическая иллюстрация будет иметь вид:
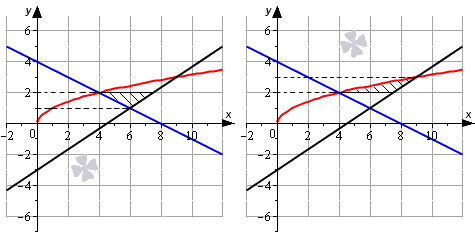
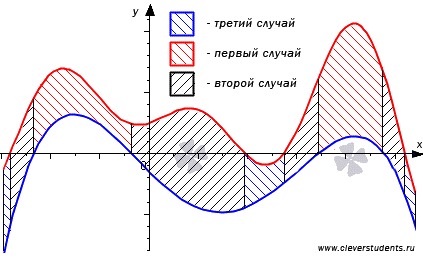
Перейдем к рассмотрению общего случая, когда y=f1(x) и y=f2(x) пересекают ось Ox.
Точки пересечения мы обозначим как xi, i=1, 2,…, n-1. Эти точки разбивают отрезок [a; b] на n частей xi-1; xi, i=1, 2,…, n, где α=x0<x1<x2<…<xn-1<xn=b. Фигуру G можно представить объединением фигур Gi, i=1, 2,…, n. Очевидно, что на своем интервале Gi попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S(Gi)=∫xi-1xi(f2(x)-f1(x))dx, i=1, 2,…, n
Следовательно,
S(G)=∑i=1nS(Gi)=∑i=1n∫xixif2(x)-f1(x))dx==∫x0xn(f2(x)-f(x))dx=∫abf2(x)-f1(x)dx
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
Формулу S(G)=∫abf2(x)-f1(x)dx можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y=f(x) и x=g(y).
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
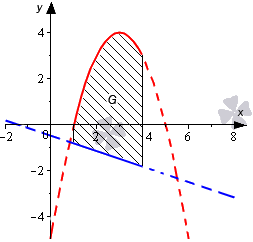
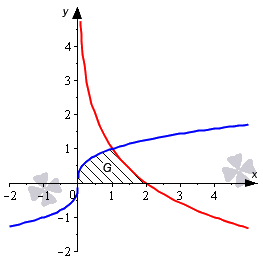
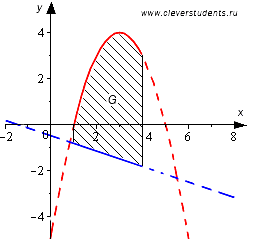
Необходимо определить площадь фигуры, которая ограничена параболой y=-x2+6x-5 и прямыми линиями y=-13x-12, x=1, x=4.
Решение
Изобразим линии на графике в декартовой системе координат.
На отрезке [1;4] график параболы y=-x2+6x-5 расположен выше прямой y=-13x-12. В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S(G)=∫14-x2+6x-5–13x-12dx==∫14-x2+193x-92dx=-13×3+196×2-92×14==-13·43+196·42-92·4–13·13+196·12-92·1==-643+1523-18+13-196+92=13
Ответ: S(G)=13
Рассмотрим более сложный пример.
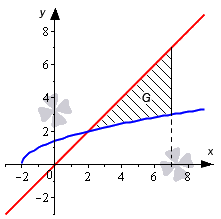
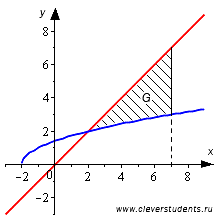
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x+2, y=x, x=7.
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x=7. Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y=x и полу параболы y=x+2. Для нахождения абсциссы используем равенства:
y=x+2ОДЗ: x≥-2×2=x+22×2-x-2=0D=(-1)2-4·1·(-2)=9×1=1+92=2∈ОДЗx2=1-92=-1∉ОДЗ
Получается, что абсциссой точки пересечения является x=2.
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y=x+2 , y=x пересекаются в точке (2;2), поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [2;7] график функции y=x расположен выше графика функции y=x+2 . Применим формулу для вычисления площади:
S(G)=∫27(x-x+2)dx=x22-23·(x+2)3227==722-23·(7+2)32-222-23·2+232==492-18-2+163=596
Ответ: S(G)=596
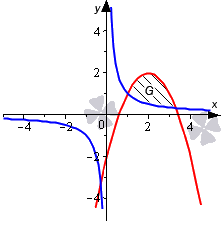
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y=1x и y=-x2+4x-2.
Решение
Нанесем линии на график.
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1x и -x2+4x-2. При условии, что x не равно нулю, равенство 1x=-x2+4x-2становится эквивалентным уравнению третьей степени -x3+4×2-2x-1=0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х=1: -13+4·12-2·1-1=0.
Разделив выражение -x3+4×2-2x-1 на двучлен x-1, получаем: -x3+4×2-2x-1⇔-(x-1)(x2-3x-1)=0
Оставшиеся корни мы можем найти из уравнения x2-3x-1=0:
x2-3x-1=0D=(-3)2-4·1·(-1)=13×1=3+132≈3.3 ; x2=3-132≈-0.3
Мы нашли интервал x∈1; 3+132, на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S(G)=∫13+132-x2+4x-2-1xdx=-x33+2×2-2x-ln x13+132==-3+13233+2·3+1322-2·3+132-ln3+132—133+2·12-2·1-ln 1=7+133-ln3+132
Ответ: S(G)=7+133-ln3+132
Необходимо вычислить площадь фигуры, которая ограничена кривыми y=x3, y=-log2x+1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y=-log2x+1 из графика y=log2x, если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у=0.
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y=x3 и y=0 пересекаются в точке (0;0). Так получается потому, что х=0 является единственным действительным корнем уравнения x3=0.
x=2 является единственным корнем уравнения -log2x+1=0, поэтому графики функций y=-log2x+1 и y=0 пересекаются в точке (2;0).
x=1 является единственным корнем уравнения x3=-log2x+1. В связи с этим графики функций y=x3 и y=-log2x+1 пересекаются в точке (1;1). Последнее утверждение может быть неочевидным, но уравнение x3=-log2x+1 не может иметь более одного корня, так как функция y=x3 является строго возрастающей, а функция y=-log2x+1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x∈0; 1, а вторая ниже красной линии на отрезке x∈1;2. Это значит, что площадь будет равна S(G)=∫01x3dx+∫12(-log2x+1)dx.
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x∈0; 2, а вторая между красной и синей линиями на отрезке x∈1; 2. Это позволяет нам найти площадь следующим образом:
S(G)=∫02x3dx-∫12×3-(-log2x+1)dx
В этом случае для нахождения площади придется использовать формулу вида S(G)=∫cd(g2(y)-g1(y))dy. Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y.
Разрешим уравнения y=x3 и -log2x+1 относительно x:
y=x3⇒x=y3y=-log2x+1⇒log2x=1-y⇒x=21-y
Получим искомую площадь:
S(G)=∫01(21-y-y3)dy=-21-yln 2-y4401==-21-1ln 2-144–21-0ln 2-044=-1ln 2-14+2ln 2=1ln 2-14
Ответ: S(G)=1ln 2-14
Необходимо вычислить площадь фигуры, которая ограничена линиями y=x, y=23x-3, y=-12x+4.
Решение
Красной линией нанесем на график линию, заданную функцией y=x. Синим цветом нанесем линию y=-12x+4, черным цветом обозначим линию y=23x-3.
Отметим точки пересечения.
Найдем точки пересечения графиков функций y=x и y=-12x+4 :
x=-12x+4ОДЗ: x≥0x=-12x+42⇒x=14×2-4x+16⇔x2-20x+64=0D=(-20)2-4·1·64=144×1=20+1442=16; x2=20-1442=4Проверка:x1=16=4, -12×1+4=-12·16+4=-4⇒x1=16 не является решением уравненияx2=4=2, -12×2+4=-12·4+4=2⇒x2=4 является решением уравниния ⇒(4; 2) точка пересечения y=x и y=-12x+4
Найдем точку пересечения графиков функций y=x и y=23x-3:
x=23x-3ОДЗ: x≥0x=23x-32⇔x=49×2-4x+9⇔4×2-45x+81=0D=(-45)2-4·4·81=729×1=45+7298=9, x245-7298=94Проверка:x1=9=3, 23×1-3=23·9-3=3⇒x1=9 является решением уравнения ⇒(9; 3) точка пересечания y=x и y=23x-3×2=94=32, 23×1-3=23·94-3=-32⇒x2=94 не является решением уравнения
Найдем точку пересечения линий y=-12x+4 и y=23x-3:
-12x+4=23x-3⇔-3x+24=4x-18⇔7x=42⇔x=6-12·6+4=23·6-3=1⇒(6; 1) точка пересечения y=-12x+4 и y=23x-3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
Тогда площадь фигуры равна:
S(G)=∫46x–12x+4dx+∫69x-23x-3dx==23×32+x24-4×46+23×32-x23+3×69==23·632+624-4·6-23·432+424-4·4++23·932-923+3·9-23·632-623+3·6==-253+46+-46+12=113
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
Тогда решим уравнение линии относительно x, а только после этого применим формулу вычисления площади фигуры.
y=x⇒x=y2 красная линияy=23x-3⇒x=32y+92 черная линияy=-12x+4⇒x=-2y+8 синяя линия
Таким образом, площадь равна:
S(G)=∫1232y+92–2y+8dy+∫2332y+92-y2dy==∫1272y-72dy+∫2332y+92-y2dy==74y2-74y12+-y33+3y24+92y23=74·22-74·2-74·12-74·1++-333+3·324+92·3–233+3·224+92·2==74+2312=113
Как видите, значения совпадают.
Ответ: S(G)=113
Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
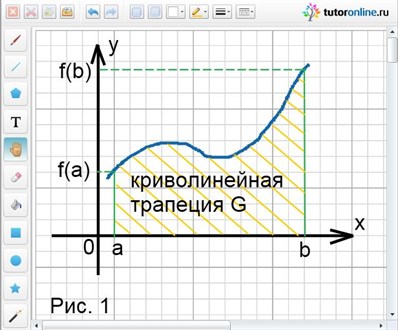
Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃаb f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃаb f(x)dx.
Таким образом, S(G) = ʃаb f(x)dx.
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃаb f(x)dx.
Пример 1.
Вычислить площадь фигуры, ограниченной линиями у = х3; у = 1; х = 2.
Решение.
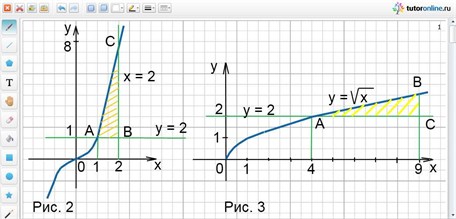
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃаb f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х3,
{у = 1.
Таким образом, имеем х1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = SDACE – SDABE = ʃ12 x3 dx – 1 = x4/4|12 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃаb(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫49 (√x – 2)dx = ∫49 √x dx –∫49 2dx = 2/3 x√х|49 – 2х|49 = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).
Ответ: S = 2 2/3 кв. ед.
Пример 3.
Вычислить площадь фигуры, ограниченной линиями у = х3 – 4х; у = 0; х ≥ 0.
Решение.
Построим график функции у = х3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции уmin = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х3 – 4х = 0 или х(х2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х1 = 0, х2 = 2, х3 = -2 (не подходит, т.к. х ≥ 0).
Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.
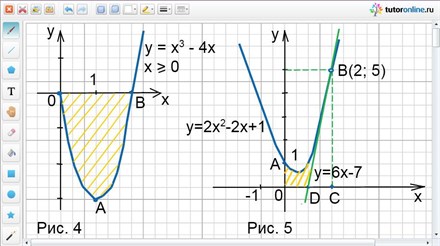
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ02 (x3 – 4x)dx|.
Имеем: ʃ02 (x3 – 4х)dx =(x4/4 – 4х2/2)|02= -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х2 – 2х + 1 в точке с абсциссой х₀ = 2.
Так как производная y’ = 4x – 2, то при х0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у0 = 2 · 22 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Гу = 2х2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х2 – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:
xb = -b/2a;
xb = 2/4 = 1/2;
yb = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: SОAВD = SOABC – SADBC.
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле SADBC = 1/2 · DC · BC. Таким образом,
SADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
Далее:
SOABC = ʃ02(2x2 – 2х + 1)dx = (2x3/3 – 2х2/2 + х)|02 = 10/3 (кв. ед.).
Окончательно получим: SОAВD = SOABC – SADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Определение значения площади фигуры, ограниченной линиями y=f(x), x=g(y)
При помощи основных формул и значений интегралов, можно определить площадь криволинейной трапеции G. Для этого используются следующий перечень формул:
[
S(G)=int_{a}^{b} f(x) d x
]
Формула, для определения непрерывной и положительной функции, следующего вида: y=f(x) на промежутке [a;b].
[
S(G)=-int_{a}^{b} f(x) d x
]
Для непрерывной и функции с отрицательными показателями, вида: y=f(x) на числовом промежутке [a;b].
Однако, когда необходимо решить задачи с определением площади фигур, очень часто возникает необходимость применять более сложные фигуры.
Для этого используют фигуры, площади которых ограничены линиями, которые представлены в виде функций следующего типа: как y=f(x) или x=g(y).
Доказательство данных функций подробно описывается для трех случаев, параллельно изображая весь процесс решения графиками на координатной прямой.
Первый вариант:
В данной ситуации, обе функции имеют положительные характеристики, в силу свойства целостности площади. Следовательно, сумма для площадей исходной фигуры, обозначенной G и криволинейной геометрической трапеции G1 равняется значению площади фигуры G2. Из этого следует:
[
S(G)=Sleft(G_{2}right)-Sleft(G_{1}right)=int_{a}^{b} f_{2}(x) d x-int_{a}^{b} f_{1}(x) d x=int_{a}^{b}left(f_{2}(x)-f_{1}(x)right) d x
]
Второй вариант:
Таким же образом, как и в первом случае, можно доказать равенство, которое характерно для второго варианта.
[
S(G)=Sleft(G_{2}right)+Sleft(G_{1}right)=int_{a}^{b} f_{2}(x) d x+left(-int_{a}^{b} f_{1}(x) d xright)=int_{a}^{b}left(f_{2}(x)-f_{1}(x)right) d x
]
Графически данная ситуация будет выглядеть следующим образом.
Третий вариант:
Для данного варианта характерно две функции, отрицательные по своим значениям.
Формула, которая применяется для доказательства, выглядит следующим образом:
[
S(G)=Sleft(G_{1}right)-Sleft(G_{2}right)=-int_{a}^{b} f_{1}(x) d x-left(-int_{a}^{b} f_{2}(x) d xright)=int_{a}^{b}left(f_{2}(x)-f_{1}(x)right) d x
]
Для более понятно и доступного восприятия, лучше всего данное доказательство изображать в виде графического рисунка.
Нет времени решать самому?
Наши эксперты помогут!
Общий случай, для определения площади фигуры
Общий случай для фигуры, когда функция имеет вид: [y=f_{1}(x) text{ и } y=f{2}(x)] и пересекают ось значений на координатной прямой.
Точки, которые пересекают вышеуказанные функции, можно обозначать следующими показателями: [x_{i}, quad i=1,2, ldots, n-1]. Данные точки, разделяют промежуток значений (a и b) на несколько частей, которые можно обозначить как n. Значение а всегда равняется b. Заданную фигуру, площадь которой нужно определить, можно обозначить как объединение двух фигур. На интервале, где располагается геометрическая фигура, она попадает под один из трех вариантов, которые были рассмотрены ранее.
[
Sleft(G_{i}right)=int_{x_{i-1}}^{x_{i}}left(f_{2}(x)-f_{1}(x)right) d x, quad i=1,2, ldots, n
]
Следовательно, можно составить и записать следующее выражение:
[S(G)=sum_{i=1}^{n} Sleft(G_{i}right)=sum_{i=1}^{n} int_{x_{i-1}}^{x_{i}}left(f_{2}(x)-f_{i}(x)right) d x=int_{x_{0}}^{x_{0}}left(f_{2}(x)-f_{1}(x)right) d x=int_{a}^{b}left(f_{2}(x)-f_{1}(x)right) d x]
Для последнего перехода функции справедливо пятое свойство интегральных значений.
Из этого следует, что заданная формула: [S(G)=int_{a}^{b}left(f_{2}(x)-f_{1}(x)right) d x] является доказанной.
Примеры вычисления площади стороны фигуры
Необходимо определить вычислить площадь фигуры ограниченной линиями геометрической фигуры, которая ограничена параболой:
[y=-x^{2}+6 x-5] и прямыми линиями: [y=-frac{1}{3} x-frac{1}{2}], [, x=1, x=4].
На протяжении всего отрезка [1;4] график в виде параболы равен функции:
[y=-x^{2}+6 x-5] и расположен выше прямой: [y=-frac{1}{3} x-frac{1}{2}]
Следователь, применяя все известные формула и используя алгоритм решения, для определения площади фигуры. Можно определить значение определенного интеграла по формуле Ньютона-Лейбница:
Определим значение площади фигуры, которая ограничена линиями, со следующими значениями:
[
y=sqrt{x+2}, quad y=x, quad x=7
]
Для вычисления необходимо выяснить предел интегрирования. Так как дана только одна прямая равная 7.
Для этого необходимо построить график, со всеми известными данными.
Согласно графику, можно сделать вывод, что нижний предел интегрирования, для определения площади, будет являться точка пересечения графика прямой
y=x и значения половины параболы [y=sqrt{x+2}]
Значение данной точки можно вычислить из следующего равенства:
Исходя из вычислений, приведенных выше, можно сделать вывод, что абсциссой точки, где происходит пересечение, будет являться значение 2.
В данном примере и графике видно, что все линии пересекаются в точках на промежутке (2;2).
График функции y=x располагается выше графической функции [y=sqrt{x+2}], которой характерен интервал (2;7).
Для определения площади используем формулу:

Содержание:
- Примеры с решением
Пусть требуется найти площадь фигуры, ограниченной графиками функций 



Каждую площадь можно вычислить как определенный интеграл на заданном промежутке.
Эти суждения можно обобщить следующим образом. 
Так как функции 






По этой ссылке вы найдёте полный курс лекций по высшей математике:
Графики функций не имеют общих точек.
Примеры с решением
Пример 1.
Найдите площадь, ограниченную графиками функций 


Решение:
=
Графики функций пересекаются в двух точках.
Пример 2.
Найдите площадь, ограниченную графиками функций
Решение:
Найдем абсциссы точек пересечения графиков функций.


Полученные значения
Возможно вам будут полезны данные страницы:
Пример 3.
Найдите площадь, заключенную между графиками функций 

Решение:
Найдем абсциссы точек пересечени графиков.
Значит, графики пересекаются в точках с абсциссами 







! Вычислите требуемую площадь при помощи интеграла

Пример 4.
Члены школьного клуба юных конструкторов работают над созданием нового двигателя для автомобиля, который будет меньше засорять окружающую среду. Для нового мотора изменение количества частиц (млрд), загрязняющих атмосферу, в 


a) В какой год они будут выбрасывать в атмосферу одинаковое количество частиц?
b) Какова разница между количеством вредных частиц, выброшенных в атмосферу, за этот период
Решение:
а) при 


Значение 

Пример 5.
Вычислить площадь фигуры, ограниченной параболой 

Решение:
Сначала схематически изобразим эту площадь. Из рисунка видим
что заданные кривые ограничивают две различающиеся плоские фигуры (меньшую и большую). Каждая из этих фигур, в свою очередь, состоит из двух симметричных относительно оси 
Поэтому достаточно вычислить площадь верхней части каждой фигуры и затем умножить ее на два.
Найдем сначала площадь меньшей фигуры. Преобразуем уравнение окружности и определим координаты ее центра и величину радиуса.

Следовательно, центр окружности находится в точке 



уравнений
Найдем уравнение границы 



по этой же причине уравнение нижней части границы 

По формуле (1) находим

но 
– это площадь четверти окружности. Площадь всей окружности равна 

Теперь, чтобы найти площадь большей фигуры, необходимо из площади круга вычесть площадь меньшей фигуры:
Проверим значение первого интеграла







Пример 6.
Вычислить площадь фигуры, ограниченной линиями 
Решение:
Второе уравнение запишем так 









Ветви второй параболы направлены также влево, а ее вершина совпадает с началом координат.
Определим точки пересечения этих кривых из решения системы

Одна точка пересечения 

Изобразим эту фигуру на чертеже. Здесь проще вычислить площадь по формуле (2) т. е.
Лекции:
- Подобие фигур
- Элементарные функции
- Пересекающиеся плоскости
- Как найти производную: примеры решения
- Дифференциальные уравнения примеры решения
- Производная сложной функции
- Многоугольники
- Арифметические операции над пределами
- Метод Гаусса: пример решения
- Производные показательной и логарифмической функций
Вычислить площадь фигуры, ограниченной линиями
Данный калькулятор поможет найти площадь фигуры, ограниченной линиями.
Для того чтобы вычислить площадь фигуры, ограниченной линиями, применяется одно из свойств интеграла. Это свойство аддитивности площадей, интегрируемых на одном и том же отрезке функции.
Аддитивность означает, что площадь замкнутой области, составленных из нескольких фигур, не имеющих общих внутренних точек, равна сумме площадей этих фигур. Интеграл равен площади криволинейной трапеции, ограниченной графиками функций. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.
Калькулятор поможет вычислить площадь фигуры ограниченной линиями онлайн.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»