Как с помощью тангенса найти котангенс

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.

(sin^2⁡ 776^° +cos^2⁡ 776^° =1)
(tg, 3xcdot ctg, 3x=1)

Но:

(sin^2⁡x+cos^2⁡3x≠1)
(tg, xcdot ctg, y≠1)

Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.

Примеры применения формул связи

Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения, заменяя одну функцию другой и так далее.

Пример. Найдите (5sin⁡,α), если (cos,⁡α=frac{2sqrt{6}}{5}) и (α∈(frac{3π}{2};2π)). 
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:

(sin^2α+cos^2⁡α=1).

Подставим вместо косинуса его значение:

(sin^2⁡α+)((frac{2sqrt{6}}{5}))(^2=1)
(sin^2⁡α+)(frac{4cdot 6}{25})(=1)
(sin^2⁡α+)(frac{24}{25})(=1)
(sin^2⁡α=1-)(frac{24}{25})
(sin^2⁡α=)(frac{1}{25})
(sin⁡α=±)(frac{1}{5})

Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt{a})  и (x_2=-sqrt{a}). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»

Вернемся к задаче. Получилось, что синус может иметь значение (frac{1}{5}), а может (-)(frac{1}{5}). И какое значение нам надо выбрать – с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac{3π}{2};2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac{3π}{2};2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,⁡α=-frac{1}{5}) т.е. (5sin,⁡α=5cdot(-frac{1}{5})=-1).

Ответ: (-1).

Пример.Найдите (tg,α), если (cos,⁡α=)(frac{sqrt{10}}{10}) и (α∈(frac{3π}{2};2π)). 
Решение. Есть 2 пути решения этой задачи:

– напрямую вычислить тангенс через формулу (tg^2α+1=)(frac{1}{cos^2⁡α});
– сначала с помощью тождества (sin^2⁡α+cos^2⁡α=1) найти (sin⁡,α), а потом через формулу (tg,α=)(frac{sin⁡,α}{cos⁡,α}) получить тангенс.

В учебниках обычно идут первым путем, поэтому мы пойдем вторым.

Вычисляем синус:

(sin^2⁡α+)((frac{sqrt{10}}{10})^2)(=1)
(sin^2⁡α+)(frac{10}{100})(=1)
(sin^2⁡α+)(frac{1}{10})(=1)
(sin^2⁡α=1-)(frac{1}{10})
(sin^2⁡α=)(frac{9}{10});
(sin⁡,α=±)(frac{3}{sqrt{10}})

Опять (α∈(frac{3π}{2};2π)), значит в итоге синус может быть только отрицательным. То есть, (sin⁡,α=-)(frac{3}{sqrt{10}}).
А теперь вычисляем тангенс: (tg,α=-)(frac{3}{sqrt{10}})(:)(frac{sqrt{10}}{10})(=)(-frac{3}{sqrt{10}}cdotfrac{10}{sqrt{10}})(=-)(frac{30}{10})(=-3).

Ответ: (-3).

Пример. Известно, что (tg,α=-frac{3}{4}) и (frac{π}{2}<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:

(ctg, α=)(frac{1}{tg, α})
(ctg,α=1:(-frac{3}{4})=1cdot(-frac{4}{3})=-frac{4}{3}).

Теперь вычислим косинус по упомянутой выше формуле:

(tg^2 α+1=)(frac{1}{cos^2⁡α})
((-)(frac{3}{4}))(^2+1=)(frac{1}{cos^2⁡α})
(frac{9}{16})(+1=)(frac{1}{cos^2⁡α})
(frac{9+16}{16})(=)(frac{1}{cos^2⁡α})
(frac{25}{16})(=)(frac{1}{cos^2⁡α})
(cos^2⁡α=)(frac{16}{25})
(cos⁡α=±)(frac{4}{5})

Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac{π}{2};π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,⁡α=-)(frac{4}{5}).

Осталось найти синус:

(sin^2⁡α+cos^2⁡α=1)
(sin^2⁡α+(-)(frac{4}{5})()^2=1)
(sin^2⁡α+)(frac{16}{25})(=1)
(sin^2⁡α=1-)(frac{16}{25})
(sin^2⁡α=)(frac{9}{25})
(sin,⁡α=±)(frac{3}{5})

Опять используем круг, чтобы определить знак.

Получается, что (sin,⁡α=)(frac{3}{5}).

Ответ: (ctg,α=-)(frac{4}{3});   (cos,⁡α=-)(frac{4}{5});    (sin,α=)(frac{3}{5}).

Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2⁡α+13 cos^2⁡α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2⁡α+13 cos^2⁡α=6) синус заменим на косинус:

(5(1-cos^2⁡α)+13 cos^2⁡α=6)
(5-5 cos^2⁡α+13 cos^2⁡α=6)
(5+8 cos^2⁡α=6)
(8 cos^2⁡α=1)
(cos^2⁡α=)(frac{1}{8})

Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=)(frac{1}{cos^2⁡α}) :

(tg^2 α+1=1:)(frac{1}{8})
(tg^2 α+1=1cdot)(frac{8}{1})
(tg^2 α+1=8)
(tg^2 α=7)

Ответ: (7).

Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac{1}{sin^2 α})(-ctg^2 α-cos^2 β).
Решение.

(frac{1}{sin^2 α})(-ctg^2 α-cos^2 β)		Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.
(=)(frac{1}{sin^2 α})(-)(frac{cos^2⁡α}{sin^2 α})(-cos^2 β=)		Приводим дроби к общему знаменателю.
(=)(frac{1-cos^2⁡α}{sin^2 α})(-cos^2 β=)		(1-cos^2⁡α) можно заменить на (sin^2 α).
(=)(frac{sin^2 α}{sin^2 α})(-cos^2 β=)		Сокращаем синусы.
(=1-cos^2 β=sin^2 β).

Пример. Докажите тождество (frac{cos^4⁡α-sin^4⁡α}{(1-sin⁡α)(1+sin⁡α)})(+2tg^2 α=)(frac{1}{cos^2 α}).
Решение.

(frac{cos^4⁡α-sin^4⁡α}{(1-sin⁡α)(1+sin⁡α)})(+2tg^2 α=)(frac{1}{cos^2 α})		Чтобы доказать это тождество, будем преобразовывать левую часть, пытаясь свести ее к правой. Поехали. Разложим числитель левой дроби по формуле разности квадратов, а знаменатель, наоборот, соберем по ней же.
(frac{(cos^2⁡α-sin^2⁡α )(cos^2 α+sin^2⁡α)}{1-sin^2⁡α})(+2tg^2 α=)(frac{1}{cos^2 α})		Очевидно, что вторая скобка числителя равна (1) (по основному тригонометрическому тождеству), а знаменатель можно заменить на (cos^2 α).
(frac{cos^2⁡α-sin^2⁡α}{cos^2 α})(+2tg^2 α=)(frac{1}{cos^2 α})		Теперь разложим тангенс по формуле (tg, α=)(frac{sin⁡,α}{cos,⁡α}).
(frac{cos^2⁡α-sin^2⁡α}{cos^2 α})(+2)(frac{sin^2⁡α}{cos^2⁡α})(=)(frac{1}{cos^2 α})		Приводим дроби к общему знаменателю.
(frac{cos^2⁡α-sin^2⁡α+2 sin^2⁡α}{cos^2 α})(=)(frac{1}{cos^2 α})		Приводим подобные слагаемые.
(frac{cos^2⁡α+sin^2⁡α}{cos^2 α})(=)(frac{1}{cos^2 α})		И вновь нас выручает основное тригонометрическое тождество
(frac{1}{cos^2 α}) (=)(frac{1}{cos^2 α})

Левая часть полностью идентична правой, то есть тождество доказано.

Как доказать все формулы связи

Как найти синус, если известен тангенс? Как найти косинус, если известен тангенс? довольно часто при решении уравнений и упрощении тригонометрических выражений требуется найти синус или косинус через тангенс. Для этого существуют специальные формулы. Итак, для нахождения косинуса нужно извлечь квадратный корень из дроби в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате. А вот для того, чтобы найти синус нужно извлечь квадратный корень из выражения один минус дробь в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате. Но нужно обратить на знак синуса и косинуса, в зависимости от того в какой четверти находится угол. И если синус находим, то в 3 и 4 четвертях он будет отрицателен, а если косинус, то во второй и третьей. система выбрала этот ответ лучшим Ксарф­акс [156K] 4 года назад  Косинус через тангенс Для того, чтобы найти значение косинуса по известному тангенсу, нужно воспользоваться одним из тригонометрических тождеств. Сумма квадрата тангенса и единицы равна отношению единицы и квадрата косинуса. Отсюда можно выразить косинус: Наличие знака ± связано с тем, что в одних четвертях косинус угла может быть положительным, а в других – отрицательным. То есть в условии задачи должна оговариваться четверть, в которой находится угол. ** Пример. tgα = 1/√3, α находится в 1 четверти (0 < α < 90). Найдём косинус: cosα = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2. Итак, если тангенс равен 1/√3, то косинус равен √3/2. Нетрудно догадаться, что мы имели дело с углом 30°. Синус через тангенс Здесь также понадобятся тригонометрические тождества. Можно пойти двумя путями: 1) Выразить котангенс через тангенс и найти синус по котангенсу. 2) Найти косинус по тангенсу, а затем воспользоваться основным тригонометрическим тождеством. ** Пример. tgα = √3, α находится в 1 четверти (0 < α < 90). Найдём котангенс: ctga = 1 / tgα = 1 / √3. Теперь найдём синус: sina = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2. Или: cosa = √ ( 1 / (1 + 3)) = √ (1/4) = 1/2. sina = √ (1 – 1/4) = √ (3/4) = √3/2. Таким образом, если тангенс равен √3, то синус равен √3/2. Здесь также понятно, что это угол 60°. Серге­йНико­лаев [127K] 5 месяцев назад  Для этого существуют вполне определённые математические тригонометрические формулы. Например, косинус любого угла можно найти, зная его тангенс, исходя из соотношения что он равен корню квадратному из дроби, в числителе которой будет единица, а в знаменателе квадрат тангенса плюс единица. Только надо учитывать момент, что он может быть положительным и отрицательным. Зная косинус, несложно вычислить и синус любого угла, если вспомнить, что сумма их квадратов всегда равна единице. Также можно найти котангенс этого угла, разделив 1 на тангенс, а дальше воспользоваться аналогичной приведённой в первом абзаце формулой для синуса и котангенса. Optor­ius [13.8K] 6 месяцев назад  Синус и косинус через тангенс можно найти: 1 – По таблице значений тригонометрических функций некоторых углов. 2 – Через вычисления по формулам тригонометрических тождеств. Сначала находим косинус, затем по нему синус. 3 – Через универсальные тригонометрические подстановки (полуугловые подстановки). Такой способ обычно используют при вычислении интегралов, он дает приближенный результат. Для примера: Возьмем tg = √3. По таблице sin = √3/2 ≈ 0,866. По второму способу sin = √(1-1/4) ≈ 0,866. По третьему способу sin = √3/(7/4) ≈ 0,9897. Дмитр­ий Подко­паев [95] 2 года назад  Приведу на всякий случай, на мой взгляд, наиболее общий способ нахождения синуса и косинуса по тангенсу. Как говорится определил знак подставил в выражение и получил ответ. В алгебре и геометрии очень часто при решении задач используются тригонометрические формулы, которые чаще называют тригонометрическими тождествами. Из любого тригонометрического тождества несложно вывести новую формулу, необходимую для нахождения одной из величин, входящих в его состав. ****************­*****************­*****************­*****************­***** Для того, чтобы найти косинус угла, зная его тангенс, возьмем тригонометрическое тождество: . Из данного тождества выводим новую формулу для вычисления косинуса: Не забываем, что косинус может принимать как положительные, так и отрицательные значения в зависимости от четверти нахождения угла. ****************­*****************­*****************­*****************­***** Для вычисления синуса угла через его тангенс можно действовать по-разному. Например, вычислить по выведенной выше формуле косинус угла, а затем воспользоваться еще одним тригонометрическим тождеством и вывести из него формулу для вычисления синуса угла: Алиса в Стран­е [363K] 3 года назад  В тригонометрических тождествах нет, конечно, ничего сложного, вот только запомнить их все так, чтобы не пользоваться справочными материалами, обычному человеку достаточно трудно, поэтому всегда приходится где-то искать эти формулы. Вот одна из них: Из нее то мы и будем получать формулу для выполнения задания из вопроса, а именно – нахождения косинуса через тангенс, проведя несложные преобразования, получим: Как видите, действительно все очень просто. Теперь, найдя косинус, воспользуемся основным тригонометрическим тождеством, преобразуем его, чтобы найти синус через уже найденный косинус, формула такая: RIOLI­t [176K] 5 лет назад  конечно тангенс угла- это отношение синуса этого угла к косинусу того же угла- условно- а/б= с и а= с*в, в= а/с, сразу видно, что, кроме с, что- нибудь еще должно быть дано иначе не расколоть задачку, разве с будет равно 1 или еще какому замечательному значению, позволяющему определить величину угла угла. Krust­all [125K] 8 месяцев назад  Синус, косинус и тангенс являются тригонометрическими функциями. Исторически они возникли как отношения между сторонами прямоугольного треугольника, поэтому их удобнее вычислять через прямоугольный треугольник. Однако через него могут быть выражены только тригонометрические функции острых углов. Для тупых углов вам нужно будет вставить окружность. Иногда, необходимо найти синус или косинус через тангенс. Для этого существуют специальные формулы. Итак, чтобы найти косинус, нужно извлечь квадратный корень из дроби, в числителе которой единица, а в знаменателе выражение единица плюс тангенс к квадрату. Но чтобы найти синус, нужно извлечь квадратный корень из выражения один минус дробь в числителе которого единица, а в знаменателе выражение равно единице плюс касательная к квадрату. Но нужно обращать внимание на знак синуса и косинуса в зависимости от того, в какой четверти находится угол. И если мы найдем синус, то в 3-й и 4-й четвертях он будет отрицательным, а если косинус – во 2 и 3. Если говорить о тангенсе угла, то является отношением синуса по отношению к косинусу. Так, следует воспользоваться тригонометрическим тождеством. Согласно ему выводится формула, которую используем для того, чтобы вычислить косинус. Вы можете вычислить по формуле, а также воспользуюсь еще 1 тригонометрическим тождеством, выведя формула вычислить: Лара Изюми­нка [59.8K] 2 года назад  Итак , чтобы найти синус нужно взять корень из выражения 1 деленное на 1 плюс тангенс в квадрате. Далее по основному тригонометрическому тождесьву можно найти косинус. Для этого нужно извлечь квадратный корень их 1 минус только что найденнный синус в квадрате. sin=sqrt(1/(1+((1/tg)**2))) cos=sqrt(1/(1+((1/ctg)**2))) Знаете ответ?

Смотрите также: Что такое тангенс, катангенс, синус, косинус, секанс, касеканс? Как найти тангенс, если известен косинус и синус? Как выучить значения косинусов, синусов, тангенсов? Какова этимология слов “тангенс, котангенс, синус, косинус, тон”? А вам в жизни когда нибудь приходились столкнуться с косинусами, синусами? Как легко запомнить тригонометрический круг (единичную окружность)? Как узнать синус угла в треугольнике если известны синусы остальных углов? Определите знак выражения и как вы нашли? Sin имеет много рациональных значений, а в таблицах мало, почему (см.)? Для чего и где нужны математические Sin и Cos?

Определение котангенса угла

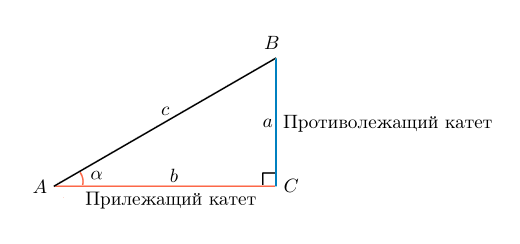
Котангенс является обратно пропорциональной величиной к тангенсу. То есть, это отношение прилежащего катета к противолежащему.

Для простоты запоминания можно дать такое определение: котангенс угла — это отношение ближнего от рассматриваемого угла катета к дальнему катету.

В случае с рисунком, описанным выше: ctg⁡α=bactgalpha=frac{b}{a}

ctg⁡α=cos⁡αsin⁡αctgalpha=frac{cosalpha}{sinalpha}

Задача 1

Пусть в прямоугольном треугольнике синус угла равен 0.200.20, а косинус этого угла равен 0.980.98. Найдите котангенс данного по условию угла.

Решение

sin⁡α=0.20sinalpha=0.20
cos⁡α=0.98cosalpha=0.98

ctg⁡α=cos⁡αsin⁡α=0.980.20=4.9ctgalpha=frac{cosalpha}{sinalpha}=frac{0.98}{0.20}=4.9

Ответ

4.94.9

После того, как мы изучили и тангенс, и котангенс, можно рассмотреть еще одно тождество:

Связь тангенса с котангенсом

tg⁡α⋅ctg⁡α=1tgalphacdotctgalpha=1

Вывод его прост:

tg⁡α⋅ctg⁡α=sin⁡αcos⁡α⋅cos⁡αsin⁡α=1tgalphacdotctgalpha=frac{sinalpha}{cosalpha}cdotfrac{cosalpha}{sinalpha}=1

Благодаря ему можно быстро и без каких-либо трудностей вычислять одну из этих величин.

Задача 2

Каков тангенс угла, если его котангенс равен 4.54.5?

Решение

ctg⁡α=4.5ctgalpha=4.5

tg⁡α⋅ctg⁡α=1tgalphacdotctgalpha=1

tg⁡α⋅4.5=1tgalphacdot4.5=1

tg⁡α=14.5tgalpha=frac{1}{4.5}

tg⁡α≈0.22tgalphaapprox0.22

Ответ

0.220.22

Еще одно тождество помогает решить задачи, связанные с котангенсом:

1+ctg⁡2α=1sin⁡2α1+ctg^2alpha=frac{1}{sin^2alpha}

Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат синуса.

Задача 3

Найдите котангенс угла, если квадрат его синуса равен 0.490.49.

Решение

sin⁡2α=0.49sin^2alpha=0.49

1+ctg⁡2α=1sin⁡2α1+ctg^2alpha=frac{1}{sin^2alpha}

1+ctg⁡2α=10.491+ctg^2alpha=frac{1}{0.49}

1+ctg⁡2α≈2.041+ctg^2alphaapprox2.04

ctg⁡2α≈1.04ctg^2alphaapprox1.04

ctg⁡α≈1.02ctgalphaapprox1.02

Ответ

1.021.02

Решение задач по математике недорого от экспертов биржи!

Тест по теме «Вычисление котангенса»

Данная статья посвящена разбору такой темы, как универсальная тригонометрическая подстановка. Суть данного термина состоит в том, что мы находим значение любой тригонометрической функции (sin α, cos α, tg α, ctg α) через формулу тангенса половинного угла. Этот вариант намного проще и рациональнее, так как выполнять дальнейшие вычисления легче без корней, а с целыми числами.

Мы подробно рассмотрим этот раздел. Для начала мы расскажем вам о формулах тангенса половинного угла, которой мы будем часто пользоваться. После мы перейдем к практическому применении формул, рассмотрим несколько примеров использования универсальной тригонометрической подстановки.

Универсальная тригонометрическая подстановка для sin α, cos α, tg α, ctg α

Во введении мы рассказали, что основной темой этого раздела станет основная тригонометрическая подстановка. Для начала запишем и разберем формулы, с помощью которых можно выразить sin α, cos α, tg α, ctg α через тангенс половинного угла α2 .

sin α=2·tgα21+tg2α2,  cos α=1-tg2α21+tg2α2tg α=2·tgα21-tg2α2,    ctg=1-tg2α22·tgα2

Указанные формулы будут правильны для всех углов α . Для работы в задаче должен быть определен входящие тангенсы и котангенсы.

Формулы для sin α и cos α, sin α=2·tgα21+tg2α2 и   cos α=1-tg2α21+tg2α2 имеют место для a≠π+2π·z , где z – любое целое число, так как при a=π+2π·z,  tg α2 не определен.

Формула tg α=2·tgα21-tg2α2 справедлива для α≠π2+π·z и a≠π+2π·z , так как при a=π2+π·z не определен tg αЗнаменатель дроби обращается в нуль, а при α=π+2π·z не определен tg α2 .

Формула ctg=1-tg2α22·tgα2 , выражающая ctg через tg α2 , справедлива для a≠π·z , так как при a=π·z не определен ctg, при a=π+2π·z не определен tg α2, а при α=2π·z знаменатель дроби обращается в нуль.

Вывод формул

Разберем вывод формул, выражающих sin α, cos α, tg α, ctg α через тангенс половинного угла. Начнем с формул для синуса и косинуса. Представим синус и косинус по формулам двойного угла как sin α=2·sin α2·cosα2 и cos α=cos2α2-sin2α2 соответственно. Теперь выражения 2·sinα2·cosα2 и cos2α2-sin2α2 запишем в виде дробей со знаменателем 1 как 2·sinα2·cosα21 и cos2α2-sin2α21 . Воспользуемся основным тождеством из тригонометрии и заменим единицы в знаменателе на сумму квадратов sin и cos, после чего получаем 2·sinα2·cosα2sin2α2+cos2α2 и cos2α2-sin2α2sin2α2+cos2α2

Для решения данного выражения необходимо числитель и знаменатель полученных дробей разделить на cos2α2 (его значение не равно нулю при условии α≠π+2π·z ). Вся формула будет выглядеть так sin α=2·sinα2·cosα2=2·sinα2·cosα2sin2α2+cos2α2=2·sinα2·cosα2cos2α2sin2α2+cos2α2cos2α2=2·sinα2cosα2sin2α2сos2α2+cos2α2сos2α2=2·tgα2tg2α2+1 

и cos α=cos2α2-sin2α2=cos2α2-sin2α21=cos2α2-sin2α2sin2α2+cos2α2==cos2α2-sin2α2cos2α2sin2α2+cos2α2cos2α2=cos2α2cos2α2-sin2α2cos2α2sin2α2cos2α2+cos2α2cos2α2=1-tg2α2tg2α2+1

Мы закончили вывод формул для sin и cos, завершив все вычислительные действия.

Следующий шаг – это вывод определенных формул для нахождения tg и ctg.

Взяв за основу описанные выше примеры tg α=sin αcos α и ctg α=cos αsin α , мы сразу получаем формулы, которые выражают тангенс и котангенс через тангенс половинного угла:

tg α=sin αcos α=2·tg α21+tg2 α21-tg2 α21+tg2 α2=2·tg α21-tg2 α2;

ctg α= cos αsin α=1-tg2 α21+tg2 α22·tg α21+tg2 α2=1-tg2 α22·tg α2;

В этом разделе мы нашли все формулы, которые нам потребуются для выражения основных тригонометрических функций.

Примеры использования в задачах и упражнениях

Для начала рассмотрим пример применения универсальной тригонометрической подстановки при преобразовании выражений.

Вспомним, что во введении мы подробно рассказали, как менять sin α, cos α, tg α, ctg α в частных случаях. Она заключается в том, чтобы преобразовать первоначальное рациональное выражение, содержащее sin, cos, tg и ctg, к выражению с одной функцией благодаря формуле. Это намного проще и понятнее. Мы выражаем все формулы через tg половинного угла. Данное преобразование обязательно пригодится при решении разнообразных уравнений и задач, интегрировании основных функций sin α, cos α, tg α, ctg α.