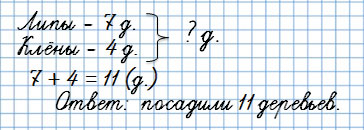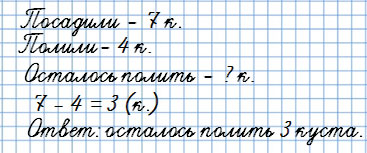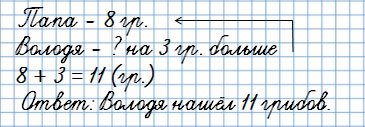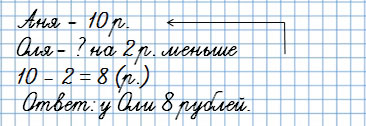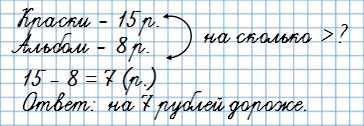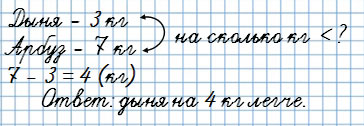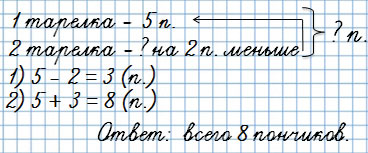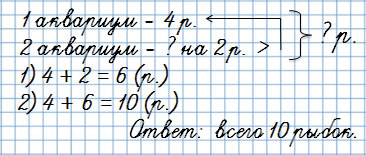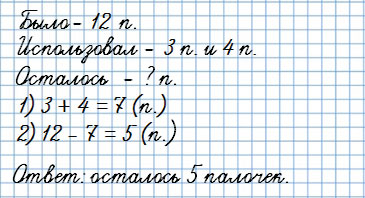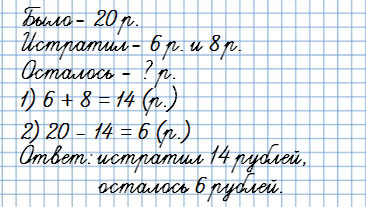- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе “Задачи” мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть “Сколько всего?”
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
В вопросе “Сколько … осталось?”
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии “на … больше”
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
В условии “на … меньше”
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
В вопросе “На сколько больше…?”
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
“На сколько меньше…?”
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии “Было…Стало…”
В вопросе “Сколько добавили?”
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии “Было… Осталось…”
В вопросе “Сколько уехало?”
“Сколько человек вышло?”
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии “Убрали… Осталось…”
В вопросе “Сколько было сначала?”
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором – на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
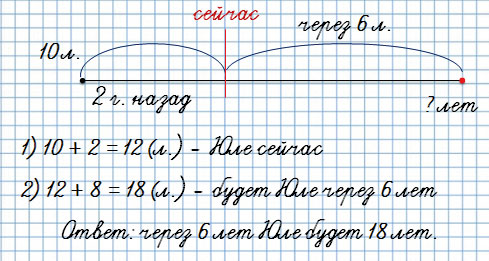
Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 19,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 25,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 4,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 55,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 61,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 37. ПР 4. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 100,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 40,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 4,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 37,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 399,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 108,
Мерзляк, Полонский, Якир, Учебник
Номер 248,
Мерзляк, Полонский, Якир, Учебник
Номер 320,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 496,
Мерзляк, Полонский, Якир, Учебник
Номер 500,
Мерзляк, Полонский, Якир, Учебник
Номер 508,
Мерзляк, Полонский, Якир, Учебник
Номер 727,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 365,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 366,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 382,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 390,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 391,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 392,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 393,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 436,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 450,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 453,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Математическое образование необходимо как
часть общей культуры для всех учащихся, а поэтому
изучение математики в колледже в группах,
готовящих квалифицированных бухгалтеров,
товароведов на базе основной школы с получением
среднего образования и специальности, является
необходимым. Уровень математического
образования, обеспечиваемый введением новых
программ, становится одним из важных элементов
подготовки учащихся, к общественно полезной
деятельности. Задача для преподавателя
математики в колледже непростая: в кратчайший
срок, за один год, в отведенное по учебному плану
время, а это в пределах 180 часов изучить
программный материал в объеме математики 10-11
классов. И не только изучить, но и вооружить
мобильными, ровными знаниями, которые при
переходе на дальнейшую ступень учебы будут сразу
востребованы при изучении высшей математики в
технологических и бухгалтерских группах.
Цель преподавания заключается в том, чтобы
учащийся овладел математикой. Термин “овладел”
очень растяжимый. Во-первых, учащийся должен
нечто знать. Во-вторых, он должен на некоторую
глубину понимать, т.е. под знанием
подразумевается не только умение повторить
формулировку, а мотивировать, почему так, а не
иначе. В-третьих, учащийся должен уметь применять
изученную им математику по профилю
специальности.
Для достижения этих целей необходимо изучать
теорию и решать задачи. Решая задачи, применяем
теорию и тем самым познаем ее. Изучать
математику, не решая задач, совершенно
бесполезно. В этом вряд ли кто-то сомневается, но
многие неправильно понимают роль задач. Обучение
математике нельзя разделить на теорию и решение
задач. Невозможно без решения задач усвоить
теорию. Цель не в том, чтобы ученик решил задачу
(т.е. получил ответ), а в том чтобы получил от этой
задачи пользу, т.е. продвинулся на одну ступеньку
по длинной лестнице овладения математикой. Цель
не в ответе, а в процессе решения. Решая задачи
учащийся приобретает новые знания и навыки,
развивает в себе настойчивость, приобщается к
математическому творчеству.
Наиболее эффективно и результативно развитие
математического творчества проявляется при
составлении математических задач
преподавателем и учащимися, где отражается
систематическое применение материалов по
специальности, элементов производственного
процесса. Математическое творчество
прослеживается на всех этапах составления задач
по математике. Целесообразно давать учащимся
задания на составление задач, связанных с той или
другой специальностью, чтобы при их решении
нужно было использовать изучаемый на уроках
материал. Например, предлагаются для групп по
специальности “товароведение” задачи на
нахождение процентного содержания вещества,
расчет наибольшего и наименьшего значения
количества материала. Для групп по специальности
“экономика и бухгалтерский учет” предлагаются
задачи на определение величины дохода и
возвращаемого займа, расчет прибыли, общей суммы
дохода предприятия и т. д. После решения подобных
задач учащиеся более подробно узнают об
особенностях и значимости выбранной профессии, о
трудностях в работе, об оплате.
Основным исходным положением, затрагивающим
профессиональную направленность курса
математики, является прикладная значимость
знаний в практической деятельности. Прикладная
направленность математических знаний означает
осуществление реализации профессиональной
подготовки. К основным направлениям этой работы
в процессе обучения математике можно отнести
следующие:
- усиление в аспекте прикладной ориентации
взаимосвязи математики и других смежных
дисциплин; - сближение методов решения учебных задач с
методами, применяемыми на практике; - раскрытие своеобразия отражения математикой
законов действительности; - формирования у учащихся умений строить
математические модели; - изучение впечатлений учащихся, сложившихся в
результате наблюдения трудового процесса, и учет
обобщенных результатов при объяснении нового
материала; превращение материалов наблюдения в
средство повышения эффективности уроков
математики; - систематическое использование на уроках
математики материала по специальности,
элементов производительного процесса; - ознакомление учащихся средствами математики с
особенностями выбранной ими специальности;
Каждая решаемая задача имеет методическую
цель. Поэтому преподаватель должен стремиться не
к тому, чтобы задача была решена быстро и
безошибочно или только на развитие тренировки, а
к тому, чтобы она была решена творчески и чтобы из
нее выжить как можно больше пользы для
математического развития ученика.
Под составлением задачи по математике надо
понимать не простую репродукцию задачи из
сборника или учебного пособия, а самостоятельную
постановку и решение проблемы учащимися, которая
в общем случае решается с помощью логических
умозаключений, математических действий на
основе законов и методов математики.
Понимание взаимосвязи решения и составления
задач позволит преподавателю добиться повышения
эффективности и результативности составления и
решения задач.
Последовательность операций в процессе
составления задач сводится к следующим:
- обнаружение и наличие математической задачной
ситуации; - выявление и анализ элементов задачной ситуации
(первичная модель задачи); - краткая запись условия задачи с выполнением
рисунка, чертежа, графика или схемы; - вторичный анализ условия с выделением теории и
законов, описывающих задачную ситуацию; - упрощение условия, дополнение условия
недостающими данными, постоянными; - выбор методов, приемов, способов решения задачи;
- выделение звеньев (уравнений, выводов и т. д.);
- нахождение и осуществления решения в общем
виде; - анализ модели задачи, ее точная формулировка и
корректирование; - проверка и оценка условия задачи;
- исследование задачи, ее окончательная редакция,
обсуждение, выделение и постановка новых
задачных ситуаций;
Для составления и решения математических задач
служат основой именно факты из практической
деятельности человека для удовлетворения
человеческих потребностей. Мировоззренческая
направленность задачного подхода к
математическому образованию требует:
- целостного видения предмета математики на
каждом этапе с углублением картины
математической реальности от этапа к этапу; - “соразмерность” человеку, его потребностям,
эмоциональной и интеллектуальной сферам; - отражение мировоззренческих идей и выводов;
Можно выделить следующие виды заданий на
составление задач:
- на установление аналогичных задач;
- на отыскание, составление подзадач;
- на дополнение данных по неполной ситуации;
- с другими численными данными;
- по схеме условия в общем виде;
- на отыскание, составление обратных задач;
- на отбор данных по избыточной ситуации;
- на постановку вопроса к условию;
- по схеме-решения в общем виде;
Предлагаемые учащимся преподавателем задания
на составление по ситуациям в учебном материале:
- по рисункам учебника, пособия, задачника и т.д.;
- по тексту учебника, пособия;
- по материалам по профилю специальности;
- итоговое по теме, по материалам экзаменационных
билетов; - по графикам и схемам учебника, пособия,
задачника; - по данной задачной ситуации;
В обучении и решении математических задач в
среднем специальном заведении схемы
“преподаватель-ученик”,
“преподаватель-задача”, “ученик-задача”
выступают в качестве составных взаимосвязанных
и взаимообусловленных элементов современной
концепции обучения математики: преподавания,
учения и содержания изучаемого. Выделенные схемы
включают в себя как прямые, так и обратные связи.
Традиционное обучение решению математических
задач в колледже предусматривает
целенаправленное воздействие преподавателя на
ученика непосредственно
(“преподаватель-ученик”) или через задачу
(“преподаватель–задача–ученик”). Составление
математических задач позволяет осуществить
эффективные и результативные обратные связи не
только на уровне схемы, но и в рамках общей схемы
“преподаватель-ученик-задача – преподаватель”.
При этом по заданию преподавателя учащийся
составляет задачу и предъявляет ее снова
преподавателю. Так, в идеальном случае, ученик по
требованию преподавателя составляет и решает
задачу под его контролем. Но, самостоятельное,
творческое составление математических задач
достигается постепенным овладением всего
процесса составления в ходе выполнения
специальных заданий. Знания о задачах, приемах их
постановки, формулировки и решения,
актуализированными заданиями на составление
задач, представляют собой содержание обучения
составлению. Это содержание, вместе с
преподаванием и учением, определяют структуру
обучения составлению математических задач.
Преподаватель ставит задание перед учащимися с
требованием составить (полностью или частично) и
решить задачу; ученик составляет и решает задачу,
а саму задачу и ее решение предоставляет
преподавателю для проверки с возможным
последующим включением в учебно-воспитательный
процесс по традиционной схеме.
В перспективе, при овладении учащимися
достаточно высокого уровня в составлении
математических задач, по требованию
преподавателя ученик сам выбирает задачную
ситуацию, составляет, решает ее, а преподаватель
проверяет и осуществляет отбор для дальнейшего
использования.
Общая структура методики составления задач по математике
Математическое образование необходимо как часть общей культуры для всех учащихся, а поэтому изучение математики в колледже в группах, готовящих квалифицированных специалистов на базе основной школы с получением среднего образования и специальности, является необходимым. Уровень математического образования, обеспечиваемый введением новых программ, становится одним из важных элементов подготовки учащихся к общественно полезной деятельности. Задача для преподавателя математики в колледже непростая: в кратчайший срок, в отведенное по учебному плану время, а это в пределах 180 часов изучить программный материал в объеме математики 9 классов. И не только изучить, но и вооружить мобильными, ровными знаниями, которые при переходе на дальнейшую ступень учебы будут сразу востребованы.
Цель преподавания заключается в том, чтобы учащийся овладел математикой. Термин “овладел” очень растяжимый. Во-первых, учащийся должен нечто знать. Во-вторых, он должен на некоторую глубину понимать, т.е. под знанием подразумевается не только умение повторить формулировку, а мотивировать, почему так, а не иначе. В-третьих, учащийся должен уметь применять изученную им математику по профилю специальности.
Для достижения этих целей необходимо изучать теорию и решать задачи. Решая задачи, применяем теорию и тем самым познаем ее. Изучать математику, не решая задач, совершенно бесполезно. В этом вряд ли кто-то сомневается, но многие неправильно понимают роль задач. Обучение математике нельзя разделить на теорию и решение задач. Невозможно без решения задач усвоить теорию. Цель не в том, чтобы ученик решил задачу (т.е. получил ответ), а в том чтобы получил от этой задачи пользу, т.е. продвинулся на одну ступеньку по длинной лестнице овладения математикой. Цель не в ответе, а в процессе решения. Решая задачи учащийся приобретает новые знания и навыки, развивает в себе настойчивость, приобщается к математическому творчеству.
Наиболее эффективно и результативно развитие математического творчества проявляется при составлении математических задач преподавателем и учащимися, где отражается систематическое применение материалов по специальности, элементов производственного процесса. Математическое творчество прослеживается на всех этапах составления задач по математике. Целесообразно давать учащимся задания на составление задач, связанных с той или другой специальностью, чтобы при их решении нужно было использовать изучаемый на уроках материал. Например, предлагаются для групп по специальности “повар,кондитер” задачи на нахождение процентного содержания вещества, расчет наибольшего и наименьшего значения количества материала. Для групп по специальности “экономика и бухгалтерский учет” предлагаются задачи на определение величины дохода и возвращаемого займа, расчет прибыли, общей суммы дохода предприятия и т. д. После решения подобных задач учащиеся более подробно узнают об особенностях и значимости выбранной профессии, о трудностях в работе, об оплате.
Основным исходным положением, затрагивающим профессиональную направленность курса математики, является прикладная значимость знаний в практической деятельности. Прикладная направленность математических знаний означает осуществление реализации профессиональной подготовки. К основным направлениям этой работы в процессе обучения математике можно отнести следующие:
- усиление в аспекте прикладной ориентации взаимосвязи математики и других смежных дисциплин;
- сближение методов решения учебных задач с методами, применяемыми на практике;
- раскрытие своеобразия отражения математикой законов действительности;
- формирования у учащихся умений строить математические модели;
- изучение впечатлений учащихся, сложившихся в результате наблюдения трудового процесса, и учет обобщенных результатов при объяснении нового материала; превращение материалов наблюдения в средство повышения эффективности уроков математики;
- систематическое использование на уроках математики материала по специальности, элементов производительного процесса;
- ознакомление учащихся средствами математики с особенностями выбранной ими специальности;
Каждая решаемая задача имеет методическую цель. Поэтому преподаватель должен стремиться не к тому, чтобы задача была решена быстро и безошибочно или только на развитие тренировки, а к тому, чтобы она была решена творчески и чтобы из нее выжить как можно больше пользы для математического развития ученика.
Под составлением задачи по математике надо понимать не простую репродукцию задачи из сборника или учебного пособия, а самостоятельную постановку и решение проблемы учащимися, которая в общем случае решается с помощью логических умозаключений, математических действий на основе законов и методов математики.
Понимание взаимосвязи решения и составления задач позволит преподавателю добиться повышения эффективности и результативности составления и решения задач.
Последовательность операций в процессе составления задач сводится к следующим:
- обнаружение и наличие математической задачной ситуации;
- выявление и анализ элементов задачной ситуации (первичная модель задачи);
- краткая запись условия задачи с выполнением рисунка, чертежа, графика или схемы;
- вторичный анализ условия с выделением теории и законов, описывающих задачную ситуацию;
- упрощение условия, дополнение условия недостающими данными, постоянными;
- выбор методов, приемов, способов решения задачи;
- выделение звеньев (уравнений, выводов и т. д.);
- нахождение и осуществления решения в общем виде;
- анализ модели задачи, ее точная формулировка и корректирование;
- проверка и оценка условия задачи;
- исследование задачи, ее окончательная редакция, обсуждение, выделение и постановка новых задачных ситуаций;
Для составления и решения математических задач служат основой именно факты из практической деятельности человека для удовлетворения человеческих потребностей. Мировоззренческая направленность задачного подхода к математическому образованию требует:
- целостного видения предмета математики на каждом этапе с углублением картины математической реальности от этапа к этапу;
- “соразмерность” человеку, его потребностям, эмоциональной и интеллектуальной сферам;
- отражение мировоззренческих идей и выводов;
Можно выделить следующие виды заданий на составление задач:
- на установление аналогичных задач;
- на отыскание, составление подзадач;
- на дополнение данных по неполной ситуации;
- с другими численными данными;
- по схеме условия в общем виде;
- на отыскание, составление обратных задач;
- на отбор данных по избыточной ситуации;
- на постановку вопроса к условию;
- по схеме-решения в общем виде;
Предлагаемые учащимся преподавателем задания на составление по ситуациям в учебном материале:
- по рисункам учебника, пособия, задачника и т.д.;
- по тексту учебника, пособия;
- по материалам по профилю специальности;
- итоговое по теме, по материалам экзаменационных билетов;
- по графикам и схемам учебника, пособия задачника;
- по данной задачной ситуации;
В обучении и решении математических задач в среднем специальном заведении схемы “преподаватель-ученик”, “преподаватель-задача”, “ученик-задача” выступают в качестве составных взаимосвязанных и взаимообусловленных элементов современной концепции обучения математики: преподавания, учения и содержания изучаемого. Выделенные схемы включают в себя как прямые, так и обратные связи. Традиционное обучение решению математических задач в колледже предусматривает целенаправленное воздействие преподавателя на ученика непосредственно (“преподаватель-ученик”) или через задачу (“преподаватель–задача–ученик”). Составление математических задач позволяет осуществить эффективные и результативные обратные связи не только на уровне схемы, но и в рамках общей схемы “преподаватель-ученик-задача – преподаватель”. При этом по заданию преподавателя учащийся составляет задачу и предъявляет ее снова преподавателю. Так, в идеальном случае, ученик по требованию преподавателя составляет и решает задачу под его контролем. Но, самостоятельное, творческое составление математических задач достигается постепенным овладением всего процесса составления в ходе выполнения специальных заданий. Знания о задачах, приемах их постановки, формулировки и решения, актуализированными заданиями на составление задач, представляют собой содержание обучения составлению. Это содержание, вместе с преподаванием и учением, определяют структуру обучения составлению математических задач. Преподаватель ставит задание перед учащимися с требованием составить (полностью или частично) и решить задачу; ученик составляет и решает задачу, а саму задачу и ее решение предоставляет преподавателю для проверки с возможным последующим включением в учебно-воспитательный процесс по традиционной схеме.
В перспективе, при овладении учащимися достаточно высокого уровня в составлении математических задач, по требованию преподавателя ученик сам выбирает задачную ситуацию, составляет, решает ее, а преподаватель проверяет и осуществляет отбор для дальнейшего использования.
В процессе обучения математике в школе у учащихся формируются способности к воспроизведению знаний, а также их творческие способности. Одни сведения из курса математики должны быть усвоены прочно всеми учащимися, изучение других сведений служит целям развития. Важное значение в достижении всех этих целей имеет обучение решению задач.
Лучшему пониманию содержания задач и способов их решения содействует самостоятельное составление (придумывание) детьми задач изучаемых видов по аналогии с ранее решенной задачей: по сообщенным учителем числовым данным, по вопросу, по заданию – составить задачу, похожую на ту, которую решали, но с другими числами и о других предметах.
При организации такой работы активность учащихся проявляется с особой силой, так как им приходится самостоятельно подбирать конкретный материал, уметь использовать соответствующее правило, формулу, уравнение, которые выступают в качестве «орудия» мыслительной деятельности.
О роли самостоятельного составления задач учащимися М.Н. Скаткин писал: «Самостоятельная работа учащихся по составлению задач, выполняемая ими по заданиям различного характера и разной степени трудности, содействует закреплению умений решать задачи, формированию математических понятий, развитию мышления и укреплению связи обучения математики с жизнью» [3].
В современных учебниках редко встречаются задания, подобные следующим:
– решено иррациональное уравнение; составить аналогичное уравнение с корнями x1=–5, x2=2.
– составить тригонометрическое уравнение вида asinx–b=0, так, чтобы его решение было равно x=(–1)kπ4+πk.
– составить геометрическую прогрессию такую, чтобы сумма ее членов была равна 20.
Для успешного конструирования заданий следует:
а) изучить известные задачи и продумать способы составления аналогичных задач;
б) выяснить, каким образом могут быть реализованы общие методы составления задач применительно к изучаемой теме;
в) выявить методы составления задач, которые специфичны для изучаемой темы.
Приведем пример составления задачи по теме «Системы уравнений».
Составить и решить систему двух уравнений с двумя неизвестными, одно из которых второй степени, а другое первой, имеющую данное решение: x=-2, y=1.
Надо составить систему вида: ax2+bxy+cy2+dx+ey+f=0,mx+ny+k=0.
Составляем два тождества с учетом значений неизвестных (при произвольных коэффициентах):
(–2)2+2∙–2∙1+0∙12+0∙(–2)+3∙1=3,3∙–2+2∙1=–4.
Преобразуем: x2+2xy+3y=3,3x+2y=–4.
Решение проводится как обычно.
Самостоятельное составление учащимися задач – один из способов развития умения решать задачи, способности к творческой самостоятельности и изобретательности. Задания подобного рода становятся для учащихся стимулом показать свои знания не только в математике, но и во многих других аспектах жизни.
Литература
1. Кожухов С.К. Составление задач школьниками // Математика в школе. – 1995. – №2. – С.4-6.
2. Панина Т.С. Современные способы активизации обучения. – М.: Академия, 2008. – 176 с.
3. Скаткин М.Н. Обучение решению простых арифметических задач. – М.: Учеб. пед. изд-во, 1954, 87 с.
4. Фридман Л.М. Психолого-педагогические основы обучения математике в школе. – М.: Просвещение, 1983. – 160 с.
5. Эрдниев П.М. Методика упражнений по арифметике и алгебре. – М.: Просвещение, 1965, 327 с.
Качественное образование:
ТРИЗ-педагогика, метод создания задач по математике
В одной из книг известный журналист С. Соловейчик поделился, как рассказывая однажды маленькому мальчику сказку, обратил внимание, что ребенок не столько следит за сюжетом, сколько пытается повторить движения рук взрослого: «Я думал, что учу его сопереживать героям сказки, а на самом деле он учился жестикулировать»…
Т.е. воспитание, впрочем, как и обучение, бывает «видимое», когда мы ставим перед собой конкретные цели и надеемся на их достижение, и «невидимое», когда на самом деле мы достигаем чего-то другого. И нередко эти незаметные, неосознаваемые нами уроки оказываются не только более результативными, но порой могут свести на нет все сознательные усилия.
Например, мы говорим о гендерном равенстве, а ученики на уроке математики решают задачи о том, как «мама испекла 16 пирожков», «мама посадила 18 кустов малины», «бабушка приготовила 50 вареников», «мама подоила Буренку», «мама купила 3 пакета муки», «мама принесла из теплицы огурцы», «мама заготовила 15 л компота», «бабушка высушила 15 кг яблок», «мама купила детям костюмы» и т.д. и т.п.
А где же сильная половина? «Папа с сыновьями катался на трехколесных велосипедах», «папа пошел с сыном в цирк», «папа раздал детям абрикосы»… Нет, конечно, за четыре года обучения школьники могут однажды встретить задачу про то, как «папа принес из магазина 6 кг картофеля», и узнать о том, что «папа с сыном пилили дрова» или «ловили рыбу»…
А как вам такая задача: «Две девочки и мальчик пропололи 18 рядов капусты. Девочки пропололи по 7 рядов. Сколько рядов прополол мальчик?».
Но кроме этого ответа очень хочется узнать, а почему мальчик сделал гораздо меньше девочек?..
Вот и получается, что будущие мужчины с детства привыкают к тому, что домашняя работа не для них…(И может корни проблемы разводов надо искать в школьных учебниках?..)
Мы учим детей быть экономными и хозяйственными, ответственными и добросовестными, активными и любознательными. А на уроке решаем задачи про то, как «поезд опоздал на 70 минут», как «у продавца были 5 спелых и 4 неспелых арбуза», как «по телевизору показали 60 серий фильма и осталось показать еще 40»…
А еще, к сожалению, иногда мы учим по принципу: «Зачем думать, решать нужно!». К примеру: «Велосипедист за 5 часов проехал 70 км. За какое время он проедет 140 км?» (10 часов в седле без остановки — это реально?), «Для ремонта квартиры купили 3 банки краски» (это была квартира кума Тыквы?), «На зиму в сельской школе заготовили 994 кг угля» (речь о современной школе 21 века?)..
Грустно. И совсем непросто потом красивыми и правильными словами из планов воспитательной работы, которые говорятся напрямую в лоб, изменить то, что сформировалось косвенно, изнутри, за пределами нашего педагогического внимания.
Очень хочется надеяться, что новые учебники математики, кото-рых с нетерпением ждут наши школы, смогут избежать подобного рассогласования, когда вслух учим одному, а на самом деле — другому.
Но пока многие учителя выход видят в том, чтобы придумывать задачи самостоятельно. Очень часто в качестве содержания берутся сюжеты из детской литературы, ведь тогда можно «убить двух зайцев»: и задачу интересную решить и книжку еще раз напомнить.
Более того, процесс придумывания представляется довольно легким занятием: берешь сказочных героев, добавляешь числа — и задача готова! Но так ли все просто на самом деле?
Итак, какие типичные ошибки и недочеты можно выявить в «самодельных» задачах:
несоответствие сюжета задачи сказочной основе:
— Кролик три кочана отдал Винни-Пуху…
— Дюймовочка испекла 5 тортов…
— Крошечка-Хаврошечка играла в шахматы…
— вместе с Буратино в автобусе ехало 8 пассажиров…
— у бабы-Яги было 12 банок с вареньем…
— младший брат Элизы читал книгу 7 дней…
несоответствие чисел реальности:
— за три дня белка разгрызла 2835 орешков… (при восьмичасовом рабочем дне это больше ста в час…)
— бесенок бежит со скоростью 280 км/ч… (это средняя скорость пассажирского самолета…)
— сколько попугаев длиной 50 см может проглотить удав длиной 12 м?.. (и от кончика хвоста они в ряд так и укладываются…)
— Белоснежка собрала 128 ромашек, а колокольчиков в три раза больше… (и как она несла такую охапку, и вообще, зачем столько цветов?..)
несоответствие сюжета ценностным ориентирам:
— Соловей-Разбойник 12 богатырей погубил и 9 — покалечил…
— волк сначала съел трех козлят, а потом еще столько же…
— жадной старухе прислуживали 28 дворян, а бояр в 2 раза меньше…
— гуси ущипнули гадкого утенка 12 раз, а куры — на 4 раза больше…
— ведьма варила кости своей дочери 2 часа…
— Карлсон забрал у Малыша 6 булочек и 10 конфет…
— царевна откусила одну четвертую отравленного яблочка…
Пожалуй, довольно.
Вывод однозначный: чтобы придумать интересную задачу со сказочным содержанием нужно знать и соблюдать определенные правила, одного желания недостаточно.
Прежде всего, сюжет сказочной задачи должен соответствовать содержанию сказки-прототипа.
Даже при составлении «обычных» задач, когда ситуация, действия героев, предметы и т.д. задаются, казалось бы, совершенно произвольно, выполняются требования согласования: в магазине делают покупки, а не едят пирожки; при сочинении задачи на движение вряд ли местом действия может быть выбрана библиотека, в школьном дворе ученики сажают березы, а не кактусы и т.д.
Поэтому первым шагом при сочинении задачи на литературной (сказочной) основе будет выделение главных героев произведения и их наиболее характерных действий и признаков.
Например:
«Колобок»:
герои: бабушка, дедушка, Колобок, лиса…
Колобок: убежал, пел песни, встречал зверей…
«Красная шапочка»:
герои: девочка, бабушка, волк, охотники…
Красная шапочка: несла пирожки, собирала цветы, шла по тропинке, разговаривала с волком…
«Незнайка»:
герои: Незнайка, Знайка, коротышки…
Незнайка: сочинял, рисовал, ездил на автомобиле, играл…
Знайка: размышлял, выступал, руководил…
«Снежная Королева»:
герои: Герда, Кай, Снежная королева, принцесса, разбойница…
Герда: искала Кая, была в плену, помогала животным…
Кай: катался на санках, попал во дворец, выкладывал слово…
«Гостья из будущего»:
Герои: Алиса Селезнева, Коля Гераскин, школьники, космические пираты…
Алиса: понимала язык животных, много знала, быстро бегала…
Коля: побывал в будущем, прятался, разоблачал пиратов…
«Гарри Поттер»:
герои: Гарри Поттер, Гермиона, Рони, преподаватели…
Гарри Поттер: имел сову, летал на метле, сражался с Волан-де-Мортом…
Гермиона: старательно училась, любила читать, помогала друзьям…
При этом уже на данном этапе выбор героев и их действий происходит через призму воспитывающего характера обучения: мы не сочиняем задачи, сколько времени нужно Лисе, чтобы съесть Колобка; по какой дорожке волку лучше бежать к дому бабушки, сколько коротышек обидел Незнайка своими стихами, на сколько осколков тролли разбили злое зеркало, сколько раз пираты перевоплощались, на сколько больше подарков получил Дадли, чем Гарри и т.д. То есть сразу же обозначается, на чьей стороне будут ученики и кому они могли бы помогать, сопереживать, подражать…
Далее «гармонию» следует наполнить «алгеброй»: представить сказочный сюжет в виде условия задачи определенного типа.
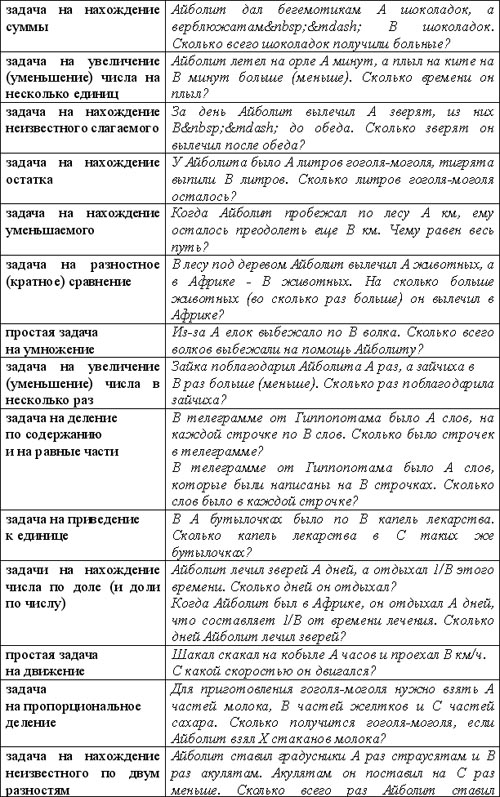
Как это можно сделать, покажем на примере сказки «Доктор Айболит»:
Легко заметить, что представлены не все типы задач, изучаемые в начальных классах (и речь идет не о составных задачах, которые получаются из объединения простых). Не были представлены задачи таких типов как «цена, количество, стоимость», «нахождение площади и периметра», «встречное (обратное, противоположное) движение» и некоторых других.
И это не случайно, ведь сюжет диктует свои правила и ограниче-ния. Если придумать задачу о том, как Айболит совершал покупки или измерял стороны прямоугольников, то это уже будет не сказочная задача, а искусственная, которая вызывает справедливую реакцию детей: «В сказке такого не было!». И в подобных случаях мы получаем не задачу на основе литературного сюжета, а задачу с использованием имен литературных героев (только возникают вопросы: «Зачем, для чего это нужно? Что это дает?»).
Поэтому сказки выбираются не произвольно, а исходя из соответствия их содержания смыслу математических действий. Например: задачи с использованием понятий «цена, количество, стоимость» можно придумывать по сказкам «Сказка о попе и его работнике Балде», «Вот какой Рассеянный»,
«Пеппи Длинныйчулок», «Старик Хоттабыч», «Приключения капитана Врунгеля»; задачи про различные виды движения могут быть придуманы по сказкам «Федорино горе», «Бременские музыканты», «Приключения Нильса с дикими гусями», «Приключения барона Мюнхаузена», «Маугли»; задачи с геометрическим содержанием можно встроить в сюжеты таких сказок, как «Три медведя», «Вершки и корешки», «Волшебник Изумрудного города», «Приключения Гулливера» и др.
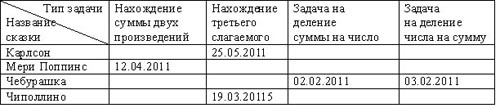
Но здесь возникает следующая проблема: если в 4 классе можно давать практически любой сказочный сюжет и он будет знаком учащимся, то круг чтения первоклассника ограничен как скоростью чтения, так и возрастными особенностями. Для решения данной проблемы рекомендуется использовать таблицу, по одной оси которой откладываются названия известных произведений, а по другой — изучаемые типы задач (они ведь тоже будут отличаться в разных классах). А на пересечении осей можно отмечать, какие задачи уже были составлены.
Пример фрагмента таблицы:
При этом не забываем, что хорошая задача отличается не только соответствием сюжета модели решения, но и «правдоподобностью» используемых числовых данных, которые не всегда определяются соответствующим концерном.
Например, Принцесса на горошине могла спать на 22 перинах, а не на 88 (хотя оба числа в пределах 100), старуха могла захотеть новое корыто длиной 1м 4 дм, а, наоборот, 4 м 1 дм — вряд ли, скорость хромой Серой шейки не может быть больше скорости зайца или лисы и т.д. То есть после того, как задача составлена, необходимо окинуть ее беспристрастным взглядом…
Все? Алгоритм пройден?
Нет. Если мы говорим о творческом процессе, то радость созидания будет гораздо полнее, когда творчество и труд превращаются в сотворчество и сотрудничество.
Уже с первого класса совместно с ребятами можно анализировать сюжет сказки и выбирать, какие из сюжетных линий могли бы стать основой задачи. Также следует обращать внимание учащихся на то, что можно «считать» в рассматриваемом сюжете.
Далее не обязательно предлагать придумывать задачи определенного типа, а можно предложить схему условия или числовое выражение, которое является решением задачи…
Можно проводить конкурсы, кто больше придумает различных задач по одной сказке или кто использует больше сказок, чтобы придумать задачи на одну тему…
Можно «издавать» сборники детских задач и использовать их во время самостоятельных работ…
Можно в качестве домашнего задания дать сочинение задач по прочитанной книге…
Можно проводить комбинированные уроки «внеклассное чтение + математика»…
А наградой за все наши усилия будет восторг класса, перефразировавшего слова поэта: «Что за прелесть эти задачи! Давайте скорее их решать!».