Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

Содержание
- История и современное применение
- Квадрат нечётного порядка
- Одинарная чётность
- Вычисление магической константы
- Дальнейшие действия
- Двойной порядок
История и современное применение
Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.
В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.
С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.
Квадрат нечётного порядка
Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:


Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.
Одинарная чётность
Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.
Вычисление магической константы
Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.
Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.
Дальнейшие действия
Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.
Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.
Алгоритм действий:

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.
Двойной порядок
Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.
Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:
Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.
Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:
По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.
Предыдущая
МатематикаАлгоритм Евклида – формулы, правила и примеры решения задач
Следующая
МатематикаМинор матрицы – способы, порядок и примеры вычисления
16
Существует несколько различных классификаций магических квадратов
пятого порядка, призванных хоть как-то их систематизировать. В книге
Мартина Гарднера [ГМ90, сс. 244-345] описан один из таких способов –
по числу в центральном квадрате. Способ любопытный, но не более того.
Сколько существует квадратов шестого порядка, до сих пор неизвестно, но их примерно 1.77 х 1019. Число огромное, поэтому нет никаких надежд пересчитать их с помощью полного перебора, а вот формулы для подсчёта магических квадратов никто придумать не смог.
Как составить магический квадрат?
Придумано очень много способов построения магических квадратов. Проще всего составлять магические квадраты нечётного порядка. Мы воспользуемся методом, который предложил французский учёный XVII века А. де ла Лубер (De La Loubère). Он основан на пяти правилах, действие которых мы рассмотрим на самом простом магическом квадрате 3 х 3 клетки.
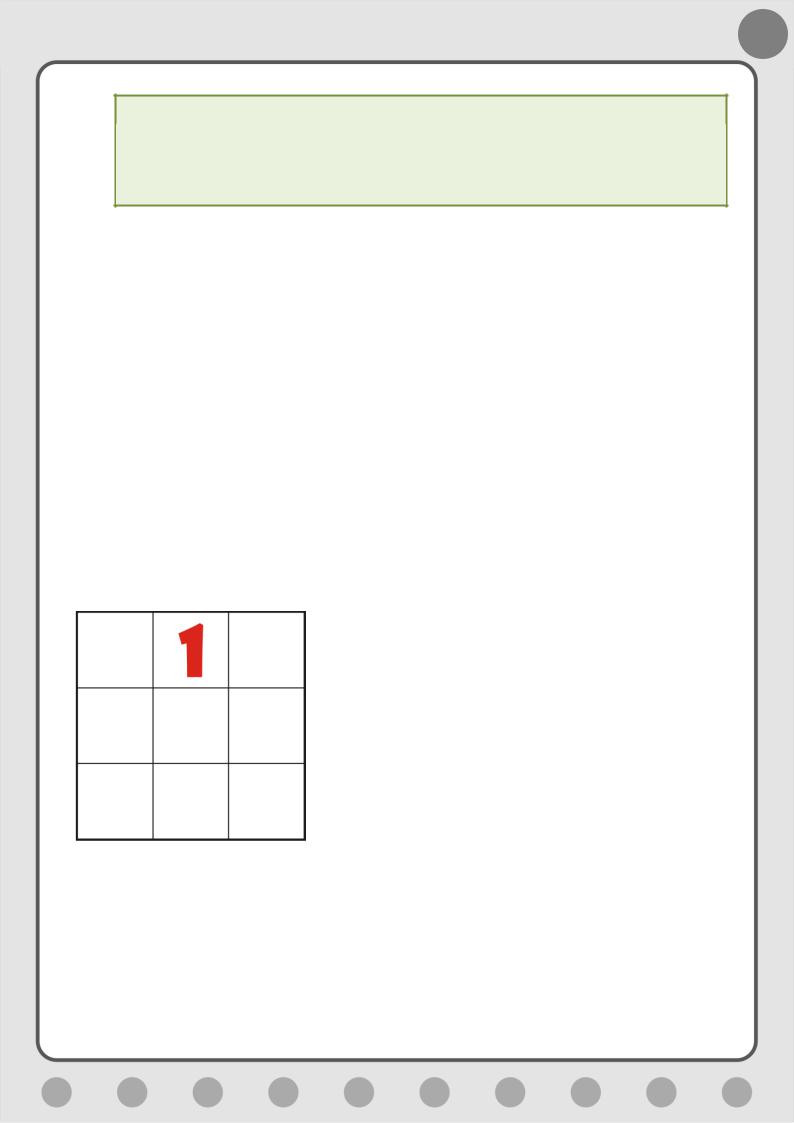
Правило 1. Поставьте 1 в среднюю колонку первой строки (Рис. 5.7).
Рис. 5.7. Первое число
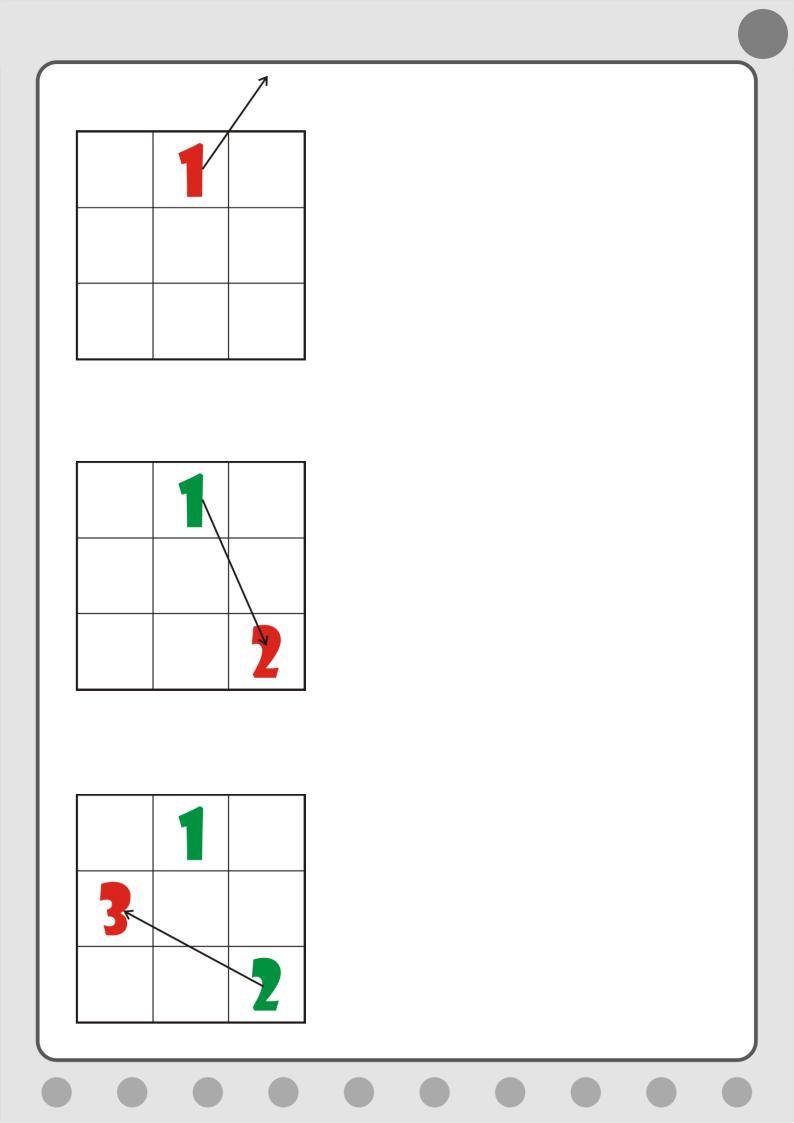
Правило 2. Следующее число поставьте, если возможно в клетку, соседнюю с текущей по диагонали правее и выше (Рис. 5.8).
17
Рис. 5.8. Пытаемся поставить второе число
Правило 3. Если новая клетка выходит за пределы квадрата сверху, то запишите число в самую нижнюю строку и в следующую колонку (Рис. 5.9).
Рис. 5.9. Ставим второе число
Правило 4. Если клетка выходит за пределы квадрата справа, то запишите число в самую первую колонку и в предыдущую строку (Рис. 5.10).
Рис. 5.10. Ставим третье число
18
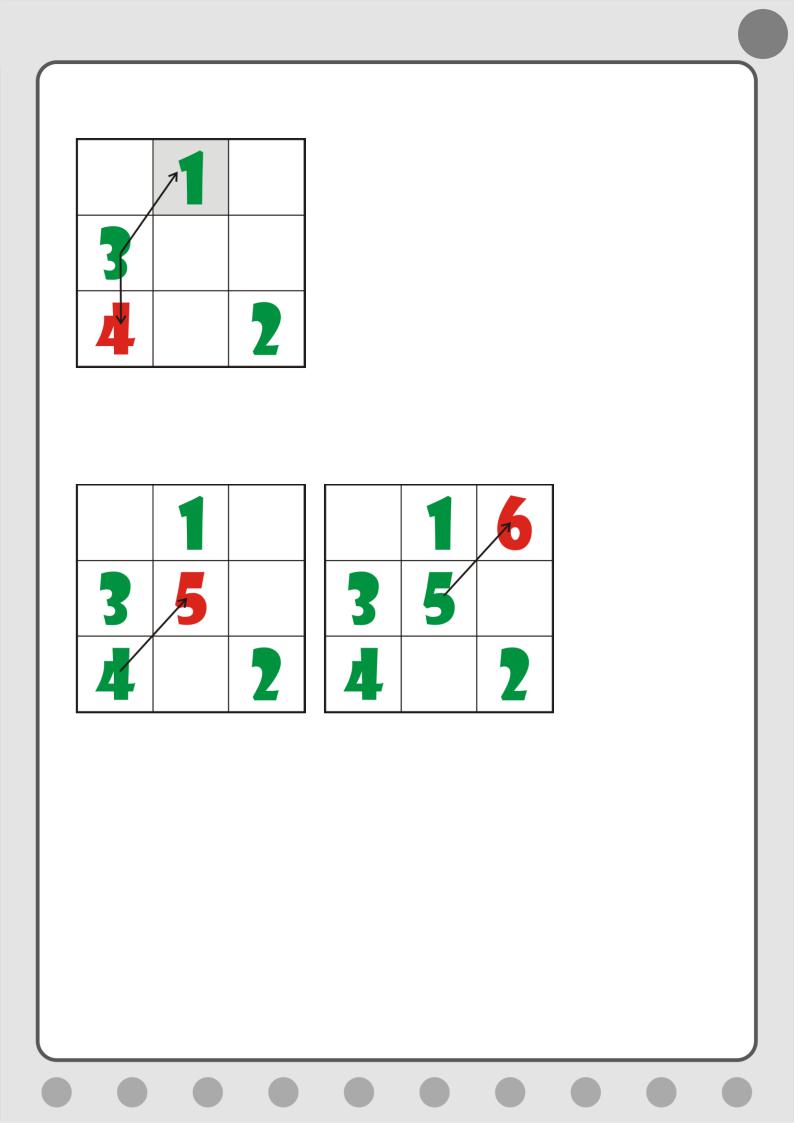
Правило 5. Если в клетке уже занята, то очередное число запишите под текущей клеткой (Рис. 5.11).
Рис. 5.11. Ставим четвёртое число
Далее переходите к Правилу 2 (Рис. 5.12).
Рис. 5.12. Ставим пятое и шестое число
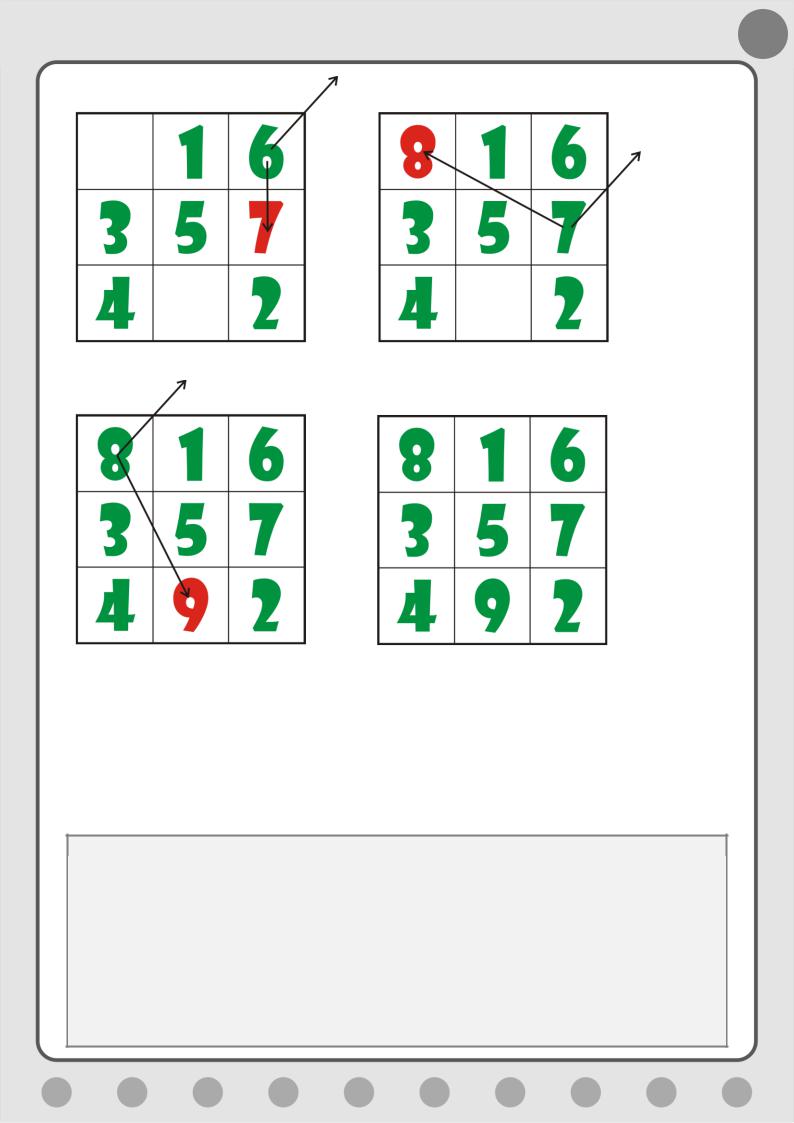
Снова выполняйте Правила 3, 4, 5, пока не составите весь квадрат (Рис.
5.13).
Не правда ли, правила очень простые и понятные, но всё равно довольно утомительно расставлять даже 9 чисел. Однако, зная алгоритм построения магических квадратов, мы сможем легко перепоручить компьютеру всю рутинную работу, оставив себе только творческую, то есть написание программы.
19
Рис. 5.13. Заполняем квадрат следующими числами
Проект Магические квадраты (Magic)
Набор полей для программы Магические квадраты совершенно очевиден:
//ПРОГРАММА ДЛЯ ГЕНЕРИРОВАНИЯ
//НЕЧЕТНЫХ МАГИЧЕСКИХ КВАДРАТОВ
//ПО МЕТОДУ ДЕ ЛА ЛУБЕРА
public partial class Form1 : Form
{
//макс. размеры квадрата: const int MAX_SIZE = 27; //var
int n=0; // порядок квадрата int [,] mq; // магический квадрат
int number=0;// текущее число для записи в квадрат

20
int col=0; // текущая колонка int row=0; // текущая строка
Метод де ла Лубера годится для составления нечётных квадратов любого размера, поэтому мы можем предоставить пользователю возможность самостоятельно выбирать порядок квадрата, разумно ограничив при этом свободу выбора 27-ью клетками.
После того как пользователь нажмёт заветную кнопку btnGen Генерировать!, метод btnGen_Click создаёт массив для хранения чисел и переходит в метод generate:
//НАЖИМАЕМ КНОПКУ “ГЕНЕРИРОВАТЬ”
private void btnGen_Click(object sender, EventArgs e)
{
//порядок квадрата:
n = (int)udNum.Value;
//создаем массив:
mq = new int[n+1, n+1];
//генерируем магический квадрат: generate();
lstRes.TopIndex = lstRes.Items.Count-27;
}
Здесь мы начинаем действовать по правилам де ла Лубера и записываем первое число – единицу – в среднюю клетку первой строки квадрата (или массива, если угодно):
//Генерируем магический квадрат void generate(){
//первое число: number=1;
rule1:
//колонка для первого числа – средняя: col = n / 2 + 1;
//строка для первого числа – первая: row=1;
//заносим его в квадрат: mq[row,col]= number;
Теперь мы последовательно пристраиваем по клеткам остальные числа – от двойки до n * n:
//переходим к следующему числу:
21
nextNumber:
number++;
Запоминаем на всякий случай координаты актуальной клетки
int tc=col; int tr = row;
и переходим в следующую клетку по диагонали:
col++; row–;
Проверяем выполнение третьего правила:
rule3:
if (row < 1) row= n;
А затем четвёртого:
rule4:
if (col > n) { col=1;
goto rule3;
}
И пятого:
rule5:
if (mq[row,col] != 0) { col=tc;
row=tr+1; goto rule3;
}
Как мы узнаем, что в клетке квадрата уже находится число? – Очень просто: мы предусмотрительно записали во все клетки нули, а числа в готовом квадрате больше нуля. Значит, по значению элемента массива мы сразу же определим, пустая клетка или уже с числом! Обратите внимание, что здесь нам понадобятся те координаты клетки, которые мы запомнили перед поиском клетки для следующего числа.
Рано или поздно мы найдём подходящую клетку для числа и запишем его в соответствующую ячейку массива:

22
//заносим его в квадрат: mq[row, col] = number;
Попробуйте иначе организовать проверку допустимости перехода в но-
вую клетку!
Если это число было последним, то программа свои обязанности выполнила, иначе она добровольно переходит к обеспечению клеткой следующего числа:
//если выставлены не все числа, то if (number < n*n)
//переходим к следующему числу: goto nextNumber;
И вот квадрат готов! Вычисляем его магическую сумму и распечатываем на экране:
//построение квадрата закончено: writeMQ();
} //generate()
Напечатать элементы массива очень просто, но важно учесть выравнивание чисел разной «длины», ведь в квадрате могут быть одно-, дву- и трёхзначные числа:
//Печатаем магический квадрат void writeMQ()
{
lstRes.ForeColor = Color.Black;
string s = “Магическая сумма = ” + (n*n*n +n)/2; lstRes.Items.Add(s);
lstRes.Items.Add(“”);
// печатаем магический квадрат: for (int i= 1; i<= n; ++i){
s=“”;
for (int j= 1; j <= n; ++j){
if (n*n > 10 && mq[i,j] < 10) s += ” “; if (n*n > 100 && mq[i,j] < 100) s += ” “; s= s + mq[i,j] + ” “;
}
lstRes.Items.Add(s);
}
lstRes.Items.Add(“”); }//writeMQ()
23
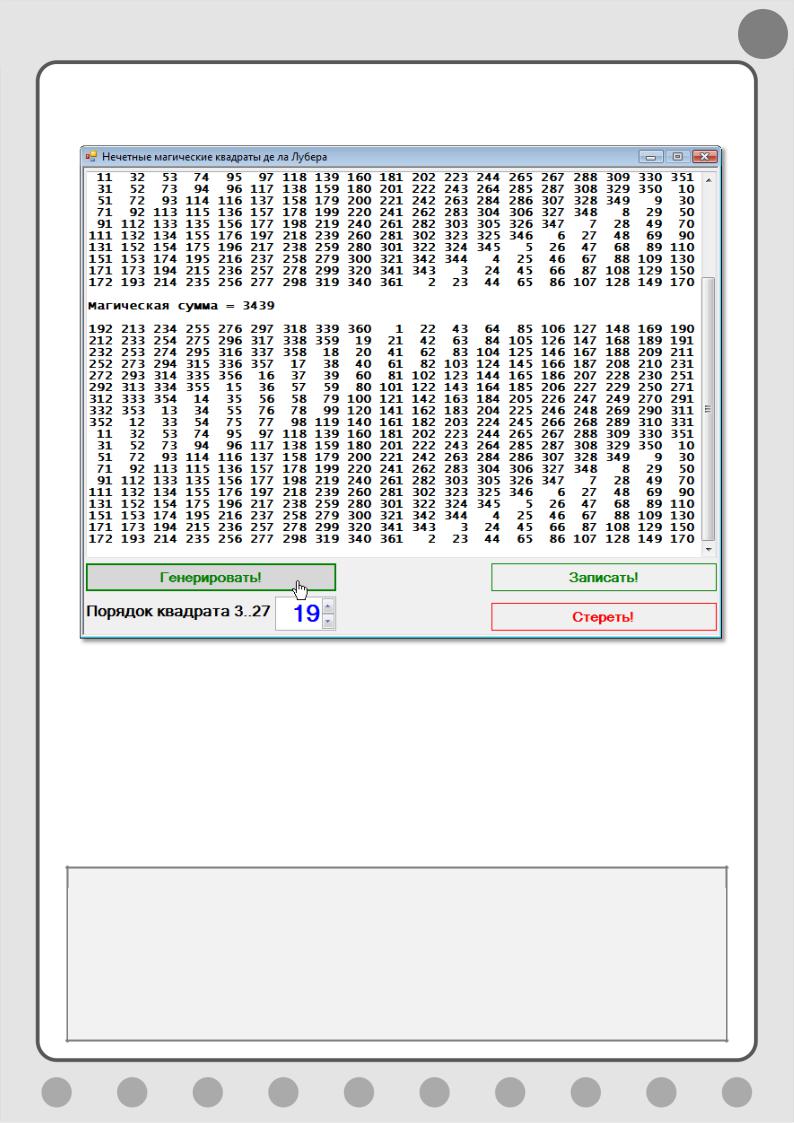
Запускаем программу – квадраты получаются быстро и на загляденье (Рис.
5.14).
Рис. 5.14. Изрядный квадратище!
В книге С.Гудман, С.Хидетниеми Введение в разработку и анализ алгорит-
мов, на страницах 297-299 мы отыщем тот же самый алгоритм, но в «сокращённом» изложении. Он не столь «прозрачен», как наша версия, но работает верно.
Добавим кнопку btnGen2 Генерировать 2! и запишем алгоритм на языке
Си-шарп в метод btnGen2_Click:
//Algorithm ODDMS
private void btnGen2_Click(object sender, EventArgs e)
{
//порядок квадрата: n = (int)udNum.Value;
//создаем массив:
mq = new int[n + 1, n + 1];
//генерируем магический квадрат: int row = 1;
24
int col = (n+1)/2;
for (int i = 1; i <= n * n; ++i)
{
mq[row, col] = i; if (i % n == 0)
{
++row;
}
else
{
if (row == 1) row = n;
else
–row;
if (col == n) col = 1;
else
++col;
}
}
//построение квадрата закончено: writeMQ();
lstRes.TopIndex = lstRes.Items.Count – 27;
}
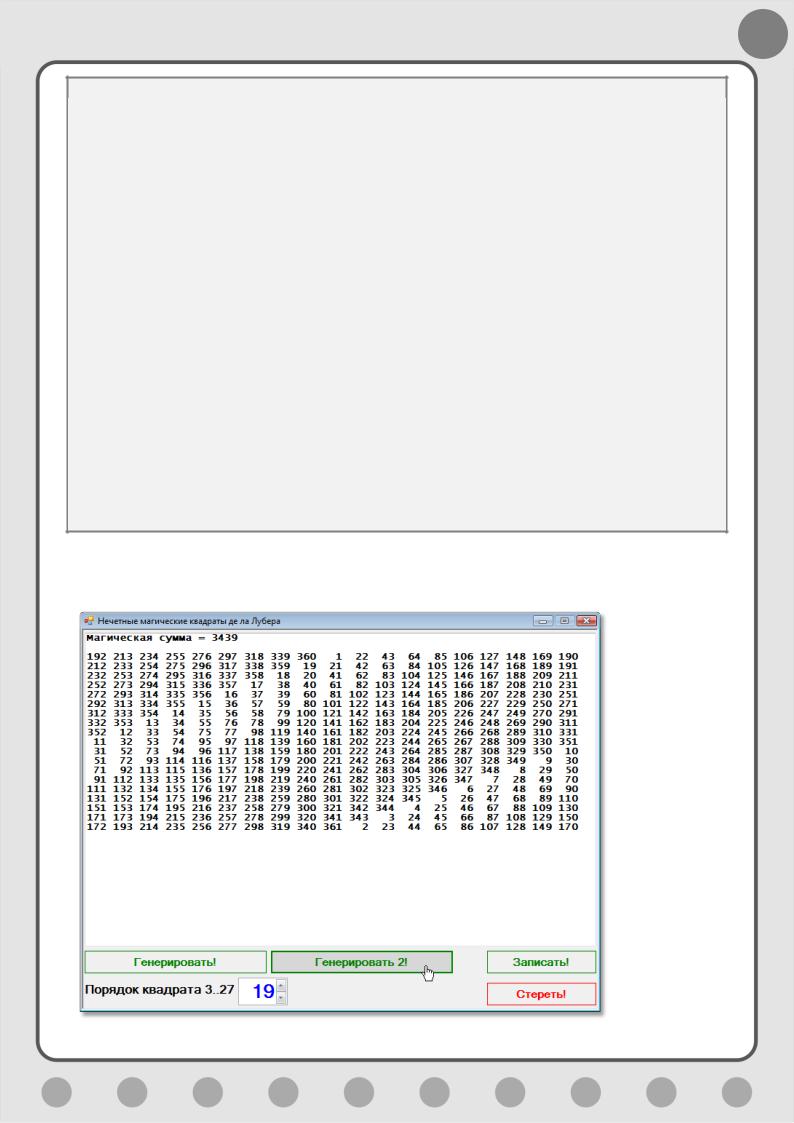
Кликаем кнопку и убеждаемся, что генерируются «наши» квадраты (Рис.
5.15).
Рис. 5.15. Старый алгоритм в новом обличии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Магические квадраты
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Коцай Е.Д. 1
1ГБОУ СОШ с.Кошки
Беспалова О.П. 1
1ГБОУ СОШ с.Кошки
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
«Математика-это дверь и ключ к наукам».
(Роджер Бэкон )
Слово « математика» пришло к нам из древнегреческого, означает «учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком”. Математика нужна всем! Математика учит нас учиться приобретать знания. А многообразие математических тем, которые можно рассмотреть, завораживает, поэтому выбор темы становится одним из этапов исследования, то есть приобретения новых знаний. Мой выбор пал на «Магические квадраты». Само понятие «магические квадраты» содержит тайну, загадку, а после знакомства с историей и некоторыми свойствами этих квадратов, возникает желание продолжать исследование.
Актуальность
Почему я выбрал такую тему? В наше время популярный вид досуга – решение судоку, головоломок с числами (в том числе и компьютерные головоломки), которые напрямую связаны со свойствами магических квадратов.
Изучение магических квадратов, их свойств может помочь в развитии:
интереса к предмету математики
её истории
любознательности
логического мышления
А так же решение задач, связанных с магическими квадратами:
улучшает память
предотвращает заболевания, связанные с нарушением работы головного мозга.
Проблема
Можно ли, используя методы математики, научиться быстро решать судоку, головоломки с числами?
Цель
изучение истории появления магических квадратов и способов их заполнения
Задачи
познакомиться с магическими квадратами
узнать историю возникновения квадратов
изучить правила составления и заполнения магические квадраты
научиться правильно и быстро строить магические квадраты
рассмотреть разновидности магических квадратов
узнать, знакомы ли мои одноклассники с чудесными квадратами
провести эксперимент
сделать выводы
предположить пути дальнейшего исследования
Гипотеза
Для заполнения магических квадратов должны существовать специальные способы, которые позволяют сделать это быстро.
Методы исследования
изучение специальной литературы;
поиск информации в сети Интернет;
опрос одноклассников;
эксперимент
анализ и обобщение.
Основная часть:
Глава 1.Теоретическая часть:
1.1. Из истории возникновения магических квадратов.
Магический квадрат один из наиболее древних головоломок – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы . Эти знаки известны под названием ло-шу и равносильны магическому квадрату. Ло-шу (Приложение 1) использовали в магических обрядах при заклинаниях.
В 11 в. о магических квадратах узнали в Индии, а затем в Японии.
Из Индии сведения о магических квадратах перешли к арабам. Арабы были знакомы с квадратом третьего порядка в VIII веке, а в XII веке его описал в своих сочинениях Ибн Эзра. Мусульмане очень благоговейно относились к квадратам пятого порядка с цифрой 1 в середине, считая это изображение символом единства Аллаха.
Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос, живший в Константинополе .
Первым квадратом, придуманным европейцем, считается квадрат (Приложение 2)немецкого художника Альбрехта Дюрера (1471 – 1528), выпустивший в 1514 году гравюру «Меланхолия», на которой в правом верхнем углу есть изображение магического квадрата четвёртого порядка. Причём два числа в середине нижней строки указывают на год создания гравюры -1514. Этот факт говорит об умении в то время составлять магические квадраты с определённым расположением некоторых чисел. Говорят, что гравюра А. Дюрера послужила толчком для знаменитых пророчеств его современника Мишеля Нострадамуса (1503- 1566).
В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет – Сатурном, Юпитером, Марсом, Солнцем, Венерой, Меркурием, и Луной. (Приложение 3)
В Западной Европе в средние века магические квадраты были достоянием представителей алхимии и астрологии. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы.
От суеверных представителей древних китайцев, индусов, европейских алхимиков и астрологов эти числовые квадраты и получали своё необычное для математики название – «магические» квадраты. Иногда по отношению к ним употребляется слово «волшебные», но значительно реже, чем «магические». Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты. А любителям математики составление квадратов служило хорошей гимнастикой ума и одно время столь же процветало, как увлечение кроссвордами в наши дни.
В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
1.2 . Разновидности магических квадратов.
Квадрат Ло Шу
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
Данный магический квадрат был известен ещё в древнем Китае. Такой магический квадрат был у древних китайцев символом огромного значения. Цифра 5 в середине означала землю, а вокруг неё в строгом равновесии располагались огонь (2 и 7), вода (1 и 6), дерево (3 и 8), металл (4 и 9). Этот квадрат – нормальный магический квадрат, заполненный числами от 1 до n2. Он так же ассоциативный или симметричный, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Квадрат, найденный в Кхаджурахо
|
7 |
12 |
1 |
14 |
|
2 |
13 |
8 |
11 |
|
16 |
3 |
10 |
5 |
|
9 |
6 |
15 |
4 |
Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо. Это первый магический квадрат, относящийся к разновидности так называемых «дьявольских» квадратов.
Дьявольский (пандиагональный) магический квадрат – такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата S(n)=n(n2+1)/2
|
1 |
8 |
13 |
12 |
|
14 |
11 |
2 |
7 |
|
4 |
5 |
16 |
9 |
|
15 |
10 |
3 |
6 |
Магический квадрат Ян Хуэя(Китай)
|
27 |
29 |
2 |
4 |
13 |
36 |
|
9 |
11 |
20 |
22 |
31 |
18 |
|
32 |
25 |
7 |
3 |
21 |
23 |
|
14 |
16 |
34 |
30 |
12 |
5 |
|
28 |
6 |
15 |
17 |
26 |
19 |
|
1 |
24 |
33 |
35 |
8 |
10 |
В XIII веке математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего порядка, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила их построения. Он сумел построить магический квадрат 6-го порядка. Этот магический квадрат почти ассоциативный – в нем только две пары центрально противолежащих чисел не дают сумму 37.
Квадрат Альбрехта Дюрера
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
8 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
Магический квадрат 4х4, изображённый на гравюре Альбрехта Дюрера «Меланхолия», считается самым ранним в европейском искусстве. Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2х2, в центральном квадрате, в квадрате из угловых клеток, в квадратах, построенных «ходом коня», в прямоугольниках, образованных парами средних клеток на противоположных сторонах.
10+11+6+7=34; 16+13+4+1=34; 2+8+9+15=34 и 3+5+12+14=34; 3+2+15+14=34 и 5+8+9+12=34.
Этот магический квадрат тоже входит в группу ассоциативных магических квадратов.
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона
Квадрат Дьюдени Квадрат Джонсона
|
3 |
61 |
19 |
37 |
|
43 |
31 |
5 |
41 |
|
7 |
11 |
73 |
29 |
|
67 |
17 |
23 |
13 |
|
67 |
1 |
43 |
|
13 |
37 |
61 |
|
31 |
73 |
7 |
Если в квадратную таблицу n x n заносится не строго натуральный ряд чисел, то данный магический квадрат – нетрадиционный. Эти два квадрата заполнены в основном простыми числами. Первый имеет порядок 3, второй – 4. Оба они были разработаны в начале двадцатого столетия.
Судоку или латинский квадрат
Эту игру, также известную как магический квадрат придумал в 1783году
швейцарский математик Леонард Эйлер.Латинским квадратом называется квадрат n х n клеток, в которых написаны числа 1, 2,…, n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу.
1.3. Свойства магических квадратов.
Магический квадрат – квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Каждый элемент магического квадрата называется клеткой.
Квадрат, сторона которого состоит из n клеток, содержит n2 клеток и называется квадратом n-го порядка. В большинстве магических квадратов используются первые n последовательных натуральных чисел.
Сумма S чисел, стоящих в каждой строке, каждом столбце и на любой диагонали, называется постоянной квадрата и равна S = n(n2 + 1)/2.
Две диагонали, проходящие через центр квадрата, называются главными диагоналями.
Ломаной называется диагональ, которая, дойдя до края квадрата, продолжается параллельно первому отрезку от противоположного края (такую диагональ образуют заштрихованные клетки на рис.).
Клетки, симметричные относительно центра квадрата, называются кососимметричными. Таковы, например, клетки a и b на рис.1
рис.1
Среди множества магических квадратов некоторые выделяются особыми свойствами: числа, из которых они составлены, удовлетворяют различным дополнительным условиям.
Правило. Составляя магический квадрат, достаточно сначала составить его из простейших чисел, т.е. из чисел натурального ряда: 1, 2, 3, 4, 5, …, а затем путем умножения, деления, увеличения или же уменьшения этих чисел можно получить бесконечное число магических квадратов с самыми разнообразными магическими суммами.
Основные свойства:
Суммы чисел в любой строке, любом столбце и любой из двух главных диагоналей равны одному и тому же числу.
Магический квадрат останется магическим, если все числа, входящие в его состав, увеличить или уменьшить на одно и то же число.
Магический квадрат останется магическим, если умножить или разделить все его числа на одно и то же число.
Из двух магических квадратов можно получить третий, складывая числа, расположенные в соответствующих полях. Магическая сумма такого квадрата равна сумме магических сумм обоих слагаемых.
Квадрат не утратит своих магических свойств, если переставить его столбцы и ряды, расположенные симметрично относительно центра квадрата.
1.4. Методы составления и заполнения МК
Изучая литературу по теме, установил, что с увеличением размеров квадрата быстро растет количество возможных магических квадратов. Так, например,
для 3 порядка – единственный
для 4 – 880
для 5 – приближается к четверти миллиона.
Универсального способа заполнения магических квадратов нет.
Способ заполнения магического квадрата зависит от его порядка
Для каждого магического квадрата определенного порядка существуют различные способы заполнения.
Рассмотрим подробно 2 метода.
Метод террас.
Этот метод предложен Баше де Мезириаком и поэтому называется ещё методом Баше.
Начну с построения магического квадрата пятого порядка. С четырёх сторон к исходному квадрату 5х5 добавляются террасы так, чтобы получился зубчатый квадрат того же порядка, что и исходный (рис. 1 и рис. 2).
|
5 |
1 |
|||||||||||||||||
|
4 |
10 |
6 |
2 |
|||||||||||||||
|
3 |
9 |
15 |
11 |
7 |
3 |
|||||||||||||
|
2 |
8 |
14 |
20 |
16 |
12 |
8 |
4 |
|||||||||||
|
1 |
7 |
13 |
19 |
25 |
21 |
17 |
13 |
9 |
5 |
|||||||||
|
6 |
12 |
18 |
24 |
22 |
18 |
14 |
10 |
|||||||||||
|
11 |
17 |
23 |
23 |
19 |
15 |
|||||||||||||
|
16 |
22 |
24 |
20 |
|||||||||||||||
|
21 |
25 |
рис.1 рис.2
В полученной фигуре располагают числа от 1 до 25 в естественном порядке косыми (диагональными) рядами снизу вверх (рис. 1) или сверху вниз (рис. 2). Числа в террасах, не попавшие в квадрат, перемещаются как бы вместе с террасами внутрь него так, чтобы они примкнули к противоположным сторонам квадрата, как показано на рис. 1а и рис. 2а.
|
5 |
1 |
|||||||||||||||||
|
4 |
10 |
6 |
2 |
|||||||||||||||
|
3 |
16 |
9 |
22 |
15 |
11 |
24 |
7 |
20 |
3 |
|||||||||
|
2 |
20 |
8 |
21 |
14 |
2 |
20 |
16 |
4 |
12 |
25 |
8 |
16 |
4 |
|||||
|
1 |
7 |
25 |
13 |
1 |
19 |
25 |
21 |
17 |
5 |
13 |
21 |
9 |
5 |
|||||
|
6 |
24 |
12 |
5 |
18 |
6 |
24 |
22 |
10 |
18 |
1 |
14 |
22 |
10 |
|||||
|
11 |
4 |
17 |
10 |
23 |
23 |
6 |
19 |
2 |
15 |
|||||||||
|
16 |
22 |
24 |
20 |
|||||||||||||||
|
21 |
25 |
рис.1а рис.2а
На рис. 3 и 4 изображены готовые магические квадраты, эти квадраты эквивалентны, один получается из другого поворотом на 90 градусов относительно центра квадрата.
|
3 |
16 |
9 |
22 |
15 |
11 |
24 |
7 |
20 |
3 |
|
|
20 |
8 |
21 |
14 |
2 |
4 |
12 |
25 |
8 |
16 |
|
|
7 |
25 |
13 |
1 |
19 |
17 |
5 |
13 |
21 |
9 |
|
|
24 |
12 |
5 |
18 |
6 |
10 |
18 |
1 |
14 |
22 |
|
|
11 |
4 |
17 |
10 |
23 |
23 |
6 |
19 |
2 |
15 |
рис.3 рис.4
Метод Рауз -Болла.
Метод Рауз-Болла состоит в следующем: в данный квадрат чётно-чётного порядка вписываются числа в их естественном порядке, начиная с левой верхней ячейки. Затем в квадрате проводятся диагонали
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
|
9 |
10 |
11 |
12 |
|
13 |
14 |
15 |
16 |
рис.1
Числа, расположенные во взаимно симметричных ячейках (относительно центра квадрата), через которые прошли диагонали, меняются местами, а числа, через которые диагонали не прошли, остаются на месте.
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
|
9 |
10 |
11 |
12 |
|
13 |
14 |
15 |
16 |
рис.2
Так, на рис. 2 диагонали пересекли восемь чисел, надо поменять местами взаимно симметричные: 1-16, 6-11, 13-4, 10-7. Готовый магический квадрат изображён на рис.3.
|
16 |
2 |
3 |
13 |
|
5 |
11 |
10 |
8 |
|
9 |
7 |
6 |
12 |
|
4 |
14 |
15 |
1 |
рис.3
Можно поступить наоборот: оставить на месте числа, через которые прошли диагонали, а поменять местами числа, не попавшие на диагонали и симметрично расположенные относительно центра квадрата. На рис.4 показан квадрат, построенный таким образом. Сравнив его с квадратом на рис.3, вы видите, что это тот же квадрат, повёрнутый на 180 градусов вокруг центра квадрата.
|
1 |
15 |
14 |
4 |
|
12 |
6 |
7 |
9 |
|
8 |
10 |
11 |
5 |
|
13 |
3 |
2 |
16 |
рис.4
Глава 2. Практическая часть:
2.1.Область применения магических квадратов.
Защита информации.
Сегодня очень актуальна проблема защиты информации. С помощью магического квадрата можно закодировать информацию. Например, (рис. 25) получится: «буду в семь».
С помощью магических квадратов так же можно закодировать информацию. Например, зашифровать текст. Расположив буквы согласно числам магического квадрата, получаем фразу «БУДУ В СЕМЬ» или «КЛЮЧИ ПОД КОВРИКОМ».
Судоку – Мудрость Востока.
Считается, что популярная игра «судоку» берет свое начало именно из магического квадрата. Игровое поле sudoku состоит из квадрата 9х9 клеток, разделенного на меньшие квадраты 3х3 клеток. У головоломки всего одно правило: игроку необходимо заполнить клетки цифрами от 1 до 9, таким образом, чтобы в каждой строке, в каждом столбце и каждом квадрате 3х3 каждая цифра встречалась только один раз.
Ключ к решению головоломки – это логика и внимание.
В середине ХХ века такие головоломки стали популярны в США, где их называли Number place, а из Америки они попали в Японию, получив название sudoku (от «су»- число, цифра и «доку»- позиция, место).
Настоящую популярность sudoku обрела в 80х годах ХХ века, когда японские
журналы начали публиковать эту головоломку на своих страницах. В 2005году английские газеты также стали печатать sudoku, и это стало началом ее триумфального шествия по всей Европе.
Она помогает нам развивать логическое мышление и вычислительные навыки. В настоящее время много газет печатают эти головоломки вместе с кроссвордами и другими логическими задачами. Не меньшую популярность завоевали судоку и в сети Интернет.
В нумерологии.
Еще великий ученый Пифагор, считал, что всем на свете управляют числа. Поэтому сущность человека заключается тоже в числе – дате его рождения. Он создал метод построения квадрата, по которому можно познать характер человека, состояние его здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и тем самым выявить, что следует предпринять для его совершенствования. Во времена Пифагора магические квадраты на каждого человека создавались индивидуально. Сейчас есть специальная программа, где вводится дата рождения человека, а на экран выводится, готовый магический квадрат. Безусловно, не следует слепо верить всему магическому. Возможно, некоторые черты характера и заложены в дате рождения человека, но человек всегда может найти способы что-то изменить в своей судьбе.
2.2. Опрос одноклассников.
Я провел опрос (Приложение 4) одноклассников. В опросе приняли участие – 20 человек. Результаты опроса представлены на диаграмме.
2.3. Эксперимент.
Я решил провести эксперимент, чтобы выяснить насколько быстро и правильно они справятся с заданиями. Предложил ребятам 3 задания с построением магических квадратов и 1 судоку (Приложение 5).
Результат эксперимента на диаграмме:
Затем я объяснил ребятам один из методов построения магических квадратов – метод «террас». Предложил вновь эти же задания сделать.
Результат на диаграмме:
Заключение:
Вывод.
Занимаясь этой темой, я узнал много интересного и познавательного. Выполнил все поставленные перед собой задачи:
познакомился с магическими квадратами
узнал их историю появления
изучил правила заполнения и составления волшебных квадратов
научился правильно и быстро строить эти квадраты
провел опрос и эксперимент
сделал выводы и предположил пути дальнейшего исследования.
В ходе проведенного исследования выяснил, что 75% одноклассников не слышали даже термин «магические квадраты», даже модные судоку решают только 10% ребят. Это очень печально!
Гипотеза.
Выполнив все задачи моего исследования, можно сказать, что моя гипотеза подтвердилась: для заполнения магических квадратов существуют специальные способы, которые позволяют сделать это быстро.
Перспектива моей дальнейшей деятельности:
узнав много полезного и интересного, поделиться с друзьями;
продолжить изучение других способов построения магических квадратов;
научиться строить квадраты более высоких порядков;
осваивать другие виды головоломок.
Список литературы:
http://www.razlib.ru/matematika/matematicheskie_golovolomki_i_razvlechenija/p29.php
http://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/
https://ru.wikipedia.org/wiki/
http://le-savchen.ucoz.ru/publ/1-1-0-16
http://hijos.ru/2014/01/24/matematika-v-aforizmax/#more-13148
http://ilib.mccme.ru/djvu/istoria/school.htm
http://dic.academic.ru/dic.nsf/ruwiki/851327
http://narod.ru/disk/5834353000/Magic_squares.pdf.html
История математики с древнейших времен до начала XIX столетия. Том 1. С древнейших времён до начала нового времени / Под ред. А.П. Юшкевича. – М.: Наука, 1970
Энциклопедия элементарной математики. Книга первая. Арифметика /Под ред. П.С. Александрова. – М.: Государственное издательство технико-теоретической литературы,1951
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Вопросы для учащихся:
Увлекаешься ли ты головоломками?
Слышал(а) ли ты термин «магический квадрат»?
Что такое «судоку»?
Приложение 5
Задания для учащихся:
Задание 1: Вставьте в пустые клетки квадрата числа 3,4,5,6,7,8,9 так, чтобы квадрат стал «магическим».
|
10 |
||
|
7 |
||
|
11 |
Задание 2:Заполни пустые клетки квадрата 3х3 числами 1,2,3,4,5,6.7,8.9 так, чтобы квадрат стал «магическим».
Задание 3: В клетках квадрата переставьте числа так, чтобы по любой вертикали, горизонтали и диагонали их суммы были равны между собой
|
20 |
30 |
40 |
|
50 |
60 |
70 |
|
80 |
90 |
100 |
Судоку:
|
6 |
2 |
8 |
7 |
|||||
|
2 |
1 |
5 |
6 |
|||||
|
9 |
4 |
6 |
1 |
|||||
|
7 |
5 |
3 |
1 |
|||||
|
8 |
6 |
5 |
4 |
|||||
|
5 |
4 |
8 |
7 |
|||||
|
4 |
8 |
7 |
3 |
|||||
|
2 |
7 |
3 |
9 |
|||||
|
7 |
3 |
1 |
5 |
Ответ:
|
6 |
4 |
9 |
3 |
1 |
2 |
8 |
5 |
7 |
|
2 |
1 |
5 |
8 |
7 |
6 |
3 |
9 |
4 |
|
8 |
3 |
7 |
5 |
9 |
4 |
6 |
2 |
1 |
|
9 |
7 |
4 |
6 |
5 |
3 |
2 |
1 |
8 |
|
1 |
8 |
6 |
9 |
2 |
7 |
5 |
4 |
3 |
|
3 |
5 |
2 |
4 |
8 |
1 |
9 |
7 |
6 |
|
4 |
9 |
8 |
7 |
3 |
5 |
1 |
6 |
2 |
|
5 |
6 |
1 |
2 |
4 |
8 |
7 |
3 |
9 |
|
7 |
2 |
3 |
1 |
6 |
9 |
4 |
8 |
5 |
Содержание:
Введение.
Основная часть:
Глава 1.Теоретическая часть:
1.1. Из истории возникновения магических квадратов.
1.2 . Разновидности магических квадратов.
1.3. Свойства магических квадратов.
1.4. Методы составления и заполнения магических квадратов
Глава 2. Практическая часть:
2.1.Область применения магических квадратов.
2.2. Опрос одноклассников.
2.3. Эксперимент.
Заключение:
Вывод.
Перспектива дальнейшей деятельности.
Список литературы.
Просмотров работы: 5533
