Как составить аддитивную модель по приведенным данным – Сайт, где вы сможете решить свои вопросы

Построение аддитивной модели временного ряда.

Рассчитаем компоненты аддитивной модели
временного ряда.

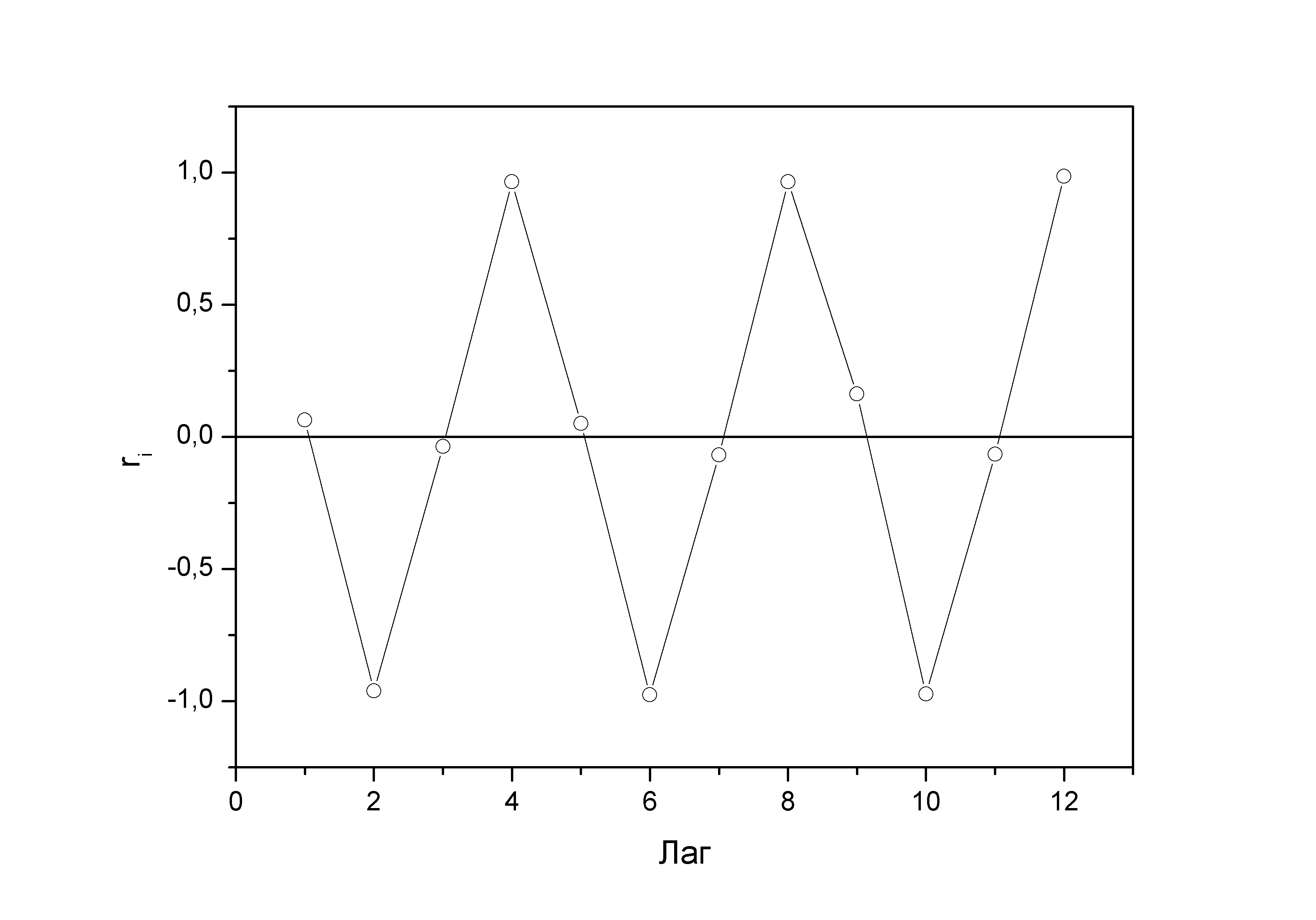
Коррелограмма

Шаг 1.
Выравнивание исходных уровней ряда
методом скользящей средней:

просуммируем
уровни ряда последовательно за каждые
четыре квартала со сдвигом на один
момент времени и определим условные
годовые объемы потребления электроэнергии
(табл. 4.5);
разделив
полученные суммы на 4, найдем скользящие
средние (гр. 4
табл. 4).
Полученные значения уже не содержат
сезонной компоненты;
приведем
эти значения в соответствие с фактическими
моментами времени –через центрированные
скользящие средние (табл. 4).

Таблица 4

№ квартала,	Количество правонарушений,	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	375	–	–	–	–
2	371	2630	657,5	–	–
3	869	2612	653	655,25	213,75
4	1015	2712	678	665,5	349,5
5	357	2835	708,75	693,75	-336,75
6	471	2840	710	709,375	-238,375
7	992	2873	718,25	714,125	277,875
8	1020	2757	689,25	703,75	316,25
9	390	2757	689,25	689,25	-299,25
10	355	2642	660,5	674,875	-319,875
11	992	2713	678,25	669,375	322,625
12	905	2812	703	690,625	214,375
13	461	2740	685	694	-233
14	454	2762	690,5	687,75	-233,75
15	920	–	–	–	–
16	927	–	–	–	–

Шаг 2.
Оценки сезонной компоненты – разность
между фактическими уровнями ряда и
центрированными скользящими средними
(табл. 4). Рассчитаем значения сезонной
компоненты
(табл. 5). Для этого найдем средние за
каждый квартал (по всем годам) оценки
сезонной компоненты.
Сезонные воздействия за период
взаимопогашаются. Для аддитивной модели
– сумма значений сезонной компоненты
по всем кварталам равна нулю.

Для данной модели
имеем:

Корректирующий
коэффициент:

Скорректированные
значения сезонной компоненты ()
(табл. 5.).

Таблица 5

Показатели	Год	№ квартала,
I	II	III	IV
1999	–	–	213,75	349,5
2000	-336,75	-238,375	277,875	316,25
2001	-299,25	-319,875	322,625	214,375
2002	-233	-233,75	–	–
Всего за i–й квартал		-869	-792	814,25	880,125
Средняя оценка сезонной компоненты для i-го квартала,		-289,667	-264	271,417	293,375
Скорректированная сезонная компонента,		-292,448	-266,781	268,636	290,593

Шаг 3.
Исключим влияние сезонной компоненты,
вычитая ее значение из каждого уровня
исходного временного ряда. Получим
величины
(табл. 6). Эти значения рассчитываются
за каждый момент времени и содержат
только тенденцию и случайную компоненту.

Таблица 6

t	y_t	S_i	y_t-S_i	T	T+S	E=y_t-(T+S)	E²
1	375	-292,448	667,448	672,700	380,252	-5,252	27,584
2	371	-266,781	637,781	673,624	406,843	-35,843	1284,721
3	869	268,636	600,364	674,547	943,183	-74,183	5503,117
4	1015	290,593	724,407	675,470	966,063	48,937	2394,830
5	357	-292,448	649,448	676,394	383,946	-26,946	726,087
6	471	-266,781	737,781	677,317	410,536	60,464	3655,895
7	992	268,636	723,364	678,240	946,876	45,124	2036,175
8	1020	290,593	729,407	679,163	969,756	50,244	2524,460
9	390	-292,448	682,448	680,087	387,639	2,361	5,574
10	355	-266,781	621,781	681,010	414,229	-59,229	3508,074
11	992	268,636	723,364	681,933	950,569	41,431	1716,528
12	905	290,593	614,407	682,857	973,450	-68,450	4685,403
13	461	-292,448	753,448	683,780	391,332	69,668	4853,630
14	454	-266,781	720,781	684,703	417,922	36,078	1301,622
15	920	268,636	651,364	685,627	954,263	-34,263	1173,953
16	927	290,593	636,407	686,550	977,143	-50,143	2514,320

Шаг 4.
Определим компоненту
данной модели через аналитическое
выравнивание ряда ()
с помощью линейного тренда:

Подставляя
значения
,
найдем уровнидля каждого момента времени (табл. 6).

Шаг 5.
Найдем значения уровней ряда, прибавим
к уровням
значения сезонной компоненты для
соответствующих кварталов (табл. 6).

График содержит
фактические значения уровней временного
ряда и теоретические.

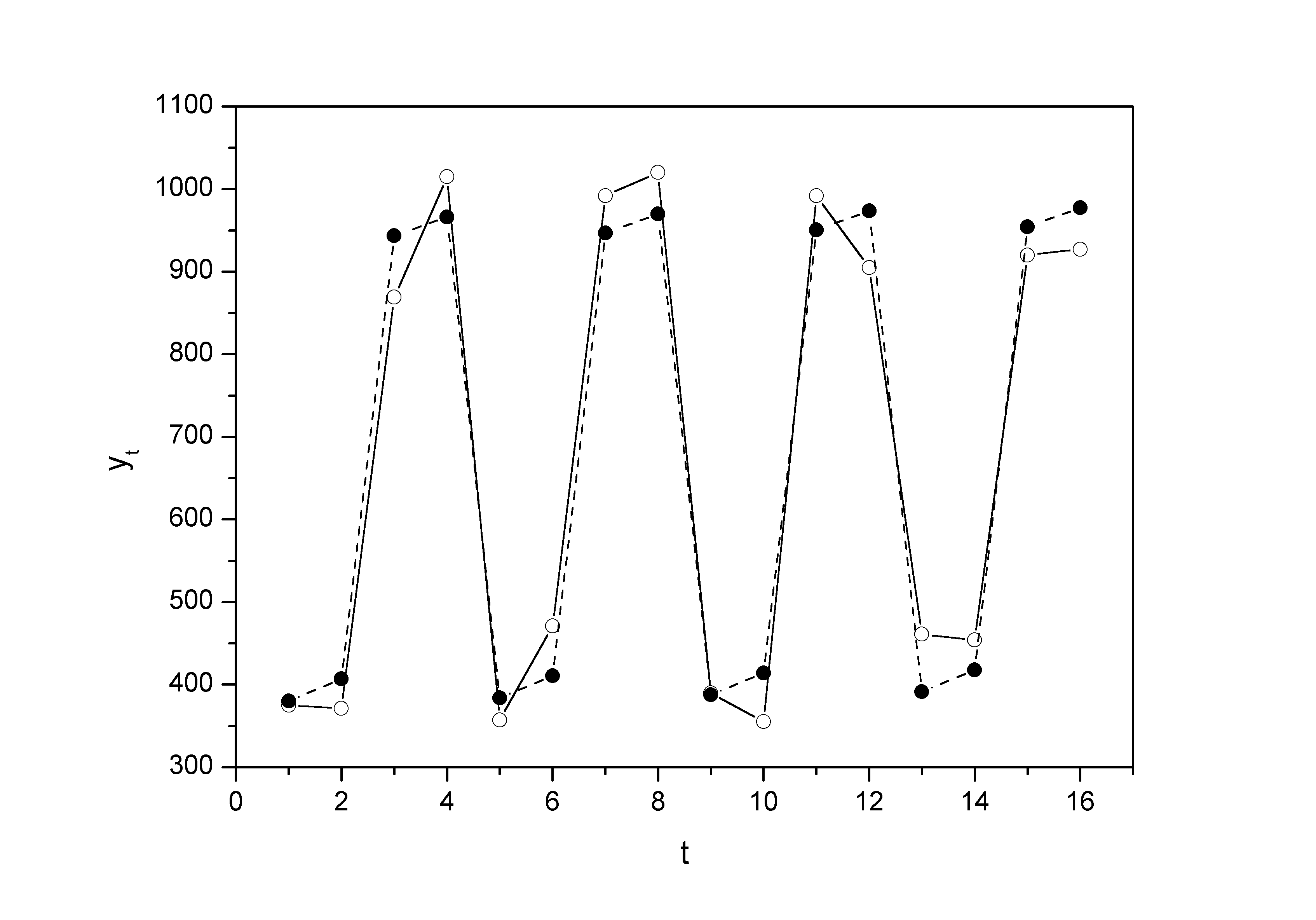
Оценка качества
модели производится через сумму квадратов
абсолютных ошибок.

Аддитивная модель
объясняет 97% общей вариации уровней
временного ряда.

Шаг 6.
Прогнозирование по аддитивной модели.
Нужно дать прогноз об общем объеме
правонарушений на I
и II
кварталы 2010 года.
Прогнозное значение
уровня временного ряда в аддитивной
модели – сумма трендовой и сезонной
компонент. Трендовая компонента:

Получим

То
есть в первые два квартала 2010 г.
следовало ожидать порядка 395 и
422 правонарушений
соответственно.

Построение
мультипликативной модели рассмотрим
на данных предыдущего примера.

Шаг 1.
Методика, применяемая на этом шаге,
полностью совпадает с методикой
построения аддитивной модели.

Таблица 7

№ квартала,	Количество правонарушений,	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
1	375	–	–	–	–
2	371	2630	657,5	–	–
3	869	2612	653	655,25	1,3262
4	1015	2712	678	665,5	1,5252
5	357	2835	708,75	693,75	0,5146
6	471	2840	710	709,375	0,6640
7	992	2873	718,25	714,125	1,3891
8	1020	2757	689,25	703,75	1,4494
9	390	2757	689,25	689,25	0,5658
10	355	2642	660,5	674,875	0,5260
11	992	2713	678,25	669,375	1,4820
12	905	2812	703	690,625	1,3104
13	461	2740	685	694	0,6643
14	454	2762	690,5	687,75	0,6601
15	920	–	–	–	–
16	927	–	–	–	–

Шаг 2.
Оценки сезонной компоненты – частное
от деления фактических уровней ряда на
центрированные скользящие средние
(табл. 7).
Эти оценки используются для расчета
сезонной компоненты
(табл. 8).
Для этого найдем средние за каждый
квартал оценки сезонной компоненты
.
Сезонные воздействия за период
взаимопогашаются. В мультипликативной
модели сумма значений сезонной компоненты
по всем кварталам равняется числу
периодов в цикле (в нашем случае – 4).

Таблица 8

Показатели	Год	№ квартала,
I	II	III	IV
1999	–	–	1,3262	1,5252
2000	0,5146	0,6640	1,3891	1,4494
2001	0,5658	0,5260	1,4820	1,3104
2002	0,6643	0,6601	–	–
Всего за i–й квартал		1,7447	1,8501	4,1973	4,2850
Средняя оценка сезонной компоненты для i-го квартала,		0,5816	0,6167	1,3991	1,4283
Скорректированная сезонная компонента,		0,5779	0,6128	1,3901	1,4192

Корректирующий
коэффициент:

Скорректированные
значения сезонной компоненты
– произведение средней оценкина корректирующий коэффициент.

Сумма
значений сезонной компоненты:

Шаг 3.
Делим уровни исходного ряда на
соответствующие значения сезонной
компоненты. Получаем
(табл. 9) – только тенденция и случайная
компонента.

Таблица 9

t	y_t	S_i	y_t/S_i	T	T·S	E=y_t/(T·S)
1	2	3	4	5	6	7
1	375	0,5779	648,9012	654,9173	378,4767	0,9908
2	371	0,6128	605,4178	658,1982	403,3439	0,9198
3	869	1,3901	625,1349	661,4791	919,5221	0,9451
4	1015	1,4192	715,1917	664,7600	943,4274	1,0759
5	357	0,5779	617,7539	668,0409	386,0608	0,9247
6	471	0,6128	768,6031	671,3218	411,3860	1,1449
7	992	1,3901	713,6177	674,6027	937,7652	1,0578
8	1020	1,4192	718,7148	677,8836	962,0524	1,0602
9	390	0,5779	674,8572	681,1645	393,6450	0,9907
10	355	0,6128	579,3081	684,4454	419,4281	0,8464
11	992	1,3901	713,6177	687,7263	956,0083	1,0377
12	905	1,4192	637,6832	691,0072	980,6774	0,9228
13	461	0,5779	797,7159	694,2881	401,2291	1,1490
14	454	0,6128	740,8616	697,5690	427,4703	1,0621
15	920	1,3901	661,8229	700,8499	974,2515	0,9443
16	927	1,4192	653,1849	704,1308	999,3024	0,9277

Шаг 4.
Компонента
в мультипликативной модели получается
через параметры линейного тренда,
используя уровни.
Уравнение тренда:

Подставляя
значения
,
найдем уровнидля каждого момента времени (табл. 9).

аг 5.
Умножаем значения
на соответствующие значения сезонной
компоненты (уровни ряда) (табл. 9). На
одном графике откладываем фактические
значения уровней временного ряда и
теоретические.

Расчет
ошибки в мультипликативной модели:

Для
сравнения моделей временного ряда можно
использовать сумму квадратов абсолютных
ошибок
:

По показателям
детерминации аддитивной и мультипликативной
моделей видно, что они примерно одинаково
аппроксимируют исходные данные.

Шаг 6.
Прогнозирование по мультипликативной
модели. Нужно дать прогноз об общем
объеме правонарушений на I
и II кварталы
2010 года. Прогнозное значение F_t
уровня временного ряда в модели –
произведение трендовой и сезонной
компонент. Трендовая компонента:

Сезонные
компоненты:
и.

В первые два
квартала 2003 г. следует ожидать порядка
409 и 436 правонарушений.

Аддитивная и
мультипликативная модели дают примерно
одинаковый прогноз.

Проверим гипотезу о наличии автокорреляции
в остатках для аддитивной модели нашего
временного ряда. Исходные данные и
промежуточные расчеты (табл.10):

Таблица 10

t	y_t	ε_t=E	ε_t_-1	(ε_t – ε_t_-1)²
1	2	3	4	5	6
1	375	-5,252	–	–	27,584
2	371	-35,843	-5,252	935,8093	1284,7
3	869	-74,183	-35,843	1469,956	5503,1
4	1015	48,937	-74,183	15158,53	2394,8
5	357	-26,946	48,937	5758,23	726,09
6	471	60,464	-26,946	7640,508	3655,9
7	992	45,124	60,464	235,3156	2036,2
8	1020	50,244	45,124	26,2144	2524,5
9	390	2,361	50,244	2292,782	5,574
10	355	-59,229	2,361	3793,328	3508,1
11	992	41,431	-59,229	10132,44	1716,5
12	905	-68,450	41,431	12073,83	4685,4
1	2	3	4	5	6
13	461	69,668	-68,45	19076,58	4853,6
14	454	36,078	69,668	1128,288	1301,6
15	920	-34,263	36,078	4947,856	1174
16	927	-50,143	-34,263	252,1744	2514,3
Сумма	-0,002	50,141	84921,85	37911,97

Фактическое значение критерия
Дарбина-Уотсона для данной модели
составляет:

Сформулируем гипотезы:
–
в остатках нет автокорреляции;–
в остатках положительная автокорреляция;–
в остатках отрицательная автокорреляция.
Уровень значимости.
По таблице значений критерия Дарбина-Уотсона
(для числа наблюденийи числа независимых параметров модели)
(зависимость только от времени)
критические значенияи.
Фактическое значение критерия
Дарбина-Уотсона в интервале(1,37<2,24<2,63).
Нет основания отклонять гипотезуоб отсутствии автокорреляции в остатках.

Приложение 5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Составить аддитивную модель по приведенным данным. Первоначальная стоимость основных фондов на начало II квартала года составила 560400 тыс. руб., ввод основных фондов во II и III кварталах соответственно – 32500 тыс. руб. и 21000 тыс. руб., выбытие – 56000 тыс. руб. и 63000 тыс. руб. Составить таблицу и проанализировать балансовым методом влияние факторов на изменение результативного показателя – первоначальной стоимости основных фондов на конец II и III кварталов.

Аддитивная модель имеет вид:
ОФкп = ОФнп + ОФввод – ОФвыб,
где ОФкп – первоначальная стоимость основных фондов на конец периода,
ОФнп – первоначальная стоимость основных фондов на начало периода,
ОФввод – стоимость введенных основных фондов,
ОФвыб – стоимость выбывших основных фондов.
Показатель II квартал III квартал Изменения
Стоимость основных фондов на начало периода 560 400 536 900 – 23 500
Стоимость введенных основных фондов 32 500 21 000 – 11 500
Стоимость выбывших основных фондов 56 000 63 000 7 000
Стоимость основных фондов на конец периода 536 900 494 900 – 42 000
ОФкп 2 кв. = 560 400 + 32 500 – 56 000 = 536 900 тыс.руб.
ОФкп 3 кв. = 536 900 + 21 000 – 63 000 = 494 900 тыс.руб.
ΔОФкп = ΔОФнп + ΔОФввод – ΔОФвыб
–42 000 = –23 500 – 11 500 – 7 000
За счет изменения стоимости введенных основных фондов стоимость основных фондов на конец периода снизилась на 11 500 тыс.руб., за счет изменения стоимости выбывших основных фондов стоимость основных фондов на конец периода снизилась на 7 000 тыс.руб., за счет изменения стоимости основных фондов на начало периода стоимость основных фондов на конец периода снизилась на 23 500 тыс.руб

. Совместное влияние факторов привело к снижению стоимости основных фондов на конец периода на 42 000 тыс.руб.
Определить стоимость израсходованного материала. В предыдущем и отчетном году количество выпущенных изделий составляло соответственно 1520 штуки и 1630 штук, расход материала на одно изделие 10,2 кг и 10,9 кг, цена 1-го кг материала 7,8 и 7,7 руб

Источник

Составить аддитивную модель по приведенным данным. Оборотные активы организации сформированы за счет собственных средств, краткосрочной кредиторской задолженности и краткосрочного кредита банка.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Задача №1.

Составить аддитивную модель по приведенным данным. Оборотные активы организации сформированы за счет собственных средств, краткосрочной кредиторской задолженности и краткосрочного кредита банка. По данным на конец года кредиторская задолженность и кредиты банка составили соответственно в предыдущем году 1018 тыс. руб., и 680 тыс. руб., в отчетном году – 1200 тыс. руб. и 720 тыс. руб. Определить величину собственных средств, направленных на формирование оборотных активов, если оборотные активы по балансу были равны в предыдущем году 2450 тыс. руб., в отчетном году – 2600 тыс. руб. Какие факторы повлияли на изменение величины собственных источников формирования оборотных активов? Составить таблицу и проанализировать балансовым методом влияние факторов на изменение результативного показателя – собственных средств как источника формирования оборотных активов.

Решение:

Аддитивные модели могут быть определены как алгебраическая сумма отдельных показателей.

Составим аддитивную модель – собственных средств организации:

СС=ОА-КЗ-К,

где ОА – оборотные активы;

КЗ – кредиторская задолженность;

К – кредиты банка.

СС₀=2450-1018-680=752 тыс.руб.

Определить фондоотдачу по следующим данным предыдущего и отчетного года: объем продаж составляет 123456 руб. и 134560 руб., стоимость основных фондов – 12000 руб. и 12400 руб.
Рентабельность продаж (как отношение чистой прибыли к объему продаж) снизилась в отчетном году по сравнению с предыдущим на 0,8 процентных пункта и составила 12%.
Определить: 1) индекс цены переменного состава; 2) индекс цены постоянного состава; 3) индекс структурных сдвигов. Сорт бумаги Цена за 1 тонну, руб Объем продажи, т Период Период базисный отчетный
По данным о производстве электроэнергии в Хабаровском крае за 1999 – 2004 гг. определить: за каждый год: 1) абсолютный прирост (базисный и цепной); 2) темп роста (базисный и цепной); 3) темп прироста

Источник

таблица (когда отправляю все съезжает – первоечисло база, второе отчет, третье абсолютное отклонение)
показатель база отчет абсол отклонение
приб от прод 48340 49360 +1020

фин рез-т от -190 80 +270
прочей операц деят-ти

фин рез-т от -1986 34 +2020
внерализ опера

Прибыль до 46164 49474 +3310
налогооблож

Приб до налогообл=Приб от продаж+фин рез от прочей опер деят+фин рез внереализ операций
Приб до налогообл база=48340-190-1986=46164
Приб до налогообл отчет=49360+80+34=49474

Вывод: в анализируемом периоде прибыль до наллогоообл увеличилсь на 3310 руб, это произошло под влиянием след факторов:
1) увеличение прибыли от продаж на 1020 руб
2) увеличение фин результата от прочей …на 270 руб
3) увеличение фин рез от внереализ. . на 2020 руб.
Таким образом наибольший вклад в увеличение прибыли до налогообложения внес фактор увеличение фин результата от внереализ.. .

ну у вас и теория бухучета))))))) мы такое по теории экономического анализа решали))) ) (

Источник

Построение аддитивной модели временного ряда.

Описание и исходные данные задания, 50% решения + фотография:

Вам также может понравиться

Как найти площадь квадрата дома

Как найти папку games на телефоне

Как найти длину радиуса окружности 2 класс

Добавить комментарий Отменить ответ