Текстовая
задача – это словесная модель некоторого
явления (ситуации, процесса). Чтобы
решить такую задачу, надо перевести ее
на язык математических действий, т.е.
построить математическую
модель.
Вообще,
математическая
модель – это описание какого-либо
реального процесса на математическом
языке.
Математической
моделью текстовой задачи является
выражение
(либо запись по действиям), если задача
решается арифметическим методом, и
уравнение
(либо система уравнений), если задача
решается алгебраическим методом.
В
процессе решения задачи четко выделяются
три этапа математического моделирования:
1
этап
– это перевод условий задачи на
математический язык; при этом выделяются
необходимые для решения данные и искомые
и математическими способами описываются
связи между ними;
2
этап
– внутримодельное решение (т.е. нахождение
значения выражения, выполнение действий,
решение уравнения);
3
этап
– интерпретация, т.е. перевод полученного
решения на тот язык, на котором была
сформулирована задача.
Проиллюстрируем
сказанное на примере решения алгебраическим
методом следующей задачи: «В одном
вагоне электропоезда было пассажиров
в 2 раза больше, чем в другом. Когда из
первого вагона вышли 3 человека, а во
второй вагон вошли 7 человек, то в обоих
вагонах пассажиров стало поровну.
Сколько пассажиров было в каждом вагоне
первоначально?»
Обозначим
через х первоначальное число пассажиров
во втором вагоне. Тогда число пассажиров
в первом вагоне – 2х. Когда из первого
вагона вышли 3 человека, в нем осталось
2х – 3 пассажира. Во второй вагон вошли
7 человек, значит, в нем стало х + 7
пассажиров. Так как в обоих вагонах
пассажиров стало поровну, то можно
записать, что 2х – 3 = х + 7. Получили
уравнение – это математическая модель
данной задачи.
Следующий
этап – решение полученного уравнения
вне зависимости от того, что в нем
обозначает переменная х: переносим в
левую часть члены уравнения, содержащие
х, а в правую – не содержащие х, причем
у переносимых членов знаки меняем на
противоположные: 2х – х = 7 + 3. Приводим
подобные члены и получаем, что х = 10.
Последний,
третий этап – используем полученное
решение, чтобы ответить на вопрос задачи:
во втором вагоне было первоначально 10
человек, а в первом – 20 (10·2=20).
Наибольшую
сложность в процессе решения текстовой
задачи представляет перевод текста с
естественного языка на математический,
т.е. 1 этап математического моделирования.
Чтобы облегчить эту процедуру, строят
вспомогательные модели – схемы, таблицы
и др. Тогда процесс решения задачи можно
рассматривать как переход от одной
модели к другой: от словесной модели
реальной ситуации, представленной в
задаче, к вспомогательной (схемы, таблицы,
рисунки и т.д.); от нее – к математической,
на которой и происходит решение задачи.
Такой
подход к процессу решения задачи
разделяют и психологи. Они считают, что
процесс решения задачи есть сложный
процесс поиска системы моделей и
определенной последовательности
перехода от одного уровня моделирования
к другому, более обобщенному, что решение
задачи человеком есть процесс ее
переформулирования. При этом используется
такая операция мышления, как анализ
через синтез, когда объект в процессе
мышления включается во все новые связи
и в силу этого выступает во все новых
качествах. Главным средством
переформулирования является моделирование.
Прием
моделирования заключается в том, что
для исследования какого-либо объекта
(в нашем случае текстовой задачи) выбирают
(или строят) другой объект, в каком-то
отношении подобный тому, который
исследуют. Построенный новый объект
изучают, с его помощью решают
исследовательские задачи, а затем
результат переносят на первоначальный
объект.
Модели
бывают разные, и поскольку в литературе
нет единообразия в их названиях, уточним
терминологию, которую будем использовать
в дальнейшем.
Все
модели можно разделить на схематизированные
и знаковые
по видам
средств, используемых для построения.
Схематизированные
модели,
в свою очередь, делятся на вещественные
и графические
в
зависимости от того, какое действие они
обеспечивают.
Вещественные
(или
предметные) модели текстовых задач
обеспечивают физическое действие с
предметами.
Они могут строиться из каких – либо
предметов (пуговиц, спичек, бумажных
полосок и т. д.), они могут быть представлены
разного рада инсценировками сюжета
задач. К этому виду моделей причисляют
и мысленное воссоздание реальной
ситуации, описанной в задаче, в виде
представлений.
Графические
модели используются, как правило, для
обобщенного,
схематического
воссоздания ситуации задачи.
К графическим следует отнести следующие
виды моделей:
-
рисунок;
-
условный
рисунок; -
чертеж;
-
схематичный
чертеж (или просто схема).
Разъясним
суть этих моделей на примере задачи:
«Лида нарисовала 4 домика, а Вова на 3
домика больше. Сколько домиков нарисовал
Вова?»
Рисунок
в качестве графической
модели
этой задачи имеет вид:
 Л.
Л.
В.
?
Условный
рисунок
может быть таким, как на рисунке:
 Л.
Л.
В.
?
Чертеж
как графическая модель выполняется при
помощи чертежных инструментов с
соблюдением заданных отношений.
 Л.
Л.
1д.
В.
?
Схематический
чертеж (схема) может выполнятся от руки,
на нем указываются все данные и искомые.
4 д.
Л .
.
3 д.
В.
?
Знаковые
модели могут быть выполнены как на
естественном, так и на математическом
языке. К знаковым моделям, выполненным
на естественном языке, можно отнести
краткую запись задачи, таблицы. Например,
краткая
запись задачи
о домиках Лиды и Вовы может быть такой:
 Л.
Л.
– 4 д.
В.
– ?, на 3 д. больше, чем
Таблица
как вид знаковой модели используется
главным образом тогда, когда в задаче
имеется несколько взаимосвязанных
величин, каждая из которых задана одним
или несколькими значениями. Пример
такой таблицы мы уже рассматривали.
Знаковыми
моделями текстовых задач, выполненных
на математическом языке, являются:
выражение, уравнение, система уравнений,
запись решения по действиям. Поскольку
на этих моделях происходит решение
задачи, их называют решающими
моделями.
Остальные модели, все схематизированные
и знаковые, выполненные на естественном
языке, – это вспомогательные
модели,
которые обеспечивают переход от текста
задачи к математической модели.
Не
следует думать, что всякая краткая
запись или чертеж, выполненные для
данной задачи, являются ее моделями.
Так как модель – это своеобразная копия
задачи, то на ней должны быть представлены
все ее объекты, все отношения между
ними, указаны требования. Для
большинства текстовых задач приходится
строить различные вспомогательные
модели. С одной стороны, эти модели
представляют собой результат анализа
задачи, но с другой – построение таких
моделей организует и направляет детальный
и глубокий анализ задачи.
Рассмотрим
процесс решения арифметическим методом
текстовой задачи о пассажирах в двух
вагонах.
Предварительный
анализ задачи позволяет выделить ее
объекты – это пассажиры в двух вагонах
поезда. О них известно, что: 1) В первом
вагоне в 2 раза больше пассажиров, чем
во втором. 2) Из первого вагона вышли 3
пассажира. 3) Во второй вошли 7 пассажиров.
4) В первом и втором вагонах пассажиров
стало поровну.
В
задаче два требования: 1) Сколько
пассажиров было первоначально в первом
вагоне? 2) Сколько пассажиров было
первоначально во втором вагоне?
Построим
графическую модель данной задачи в виде
схематического чертежа:
3 ч.
I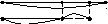
?
7 ч.
II
?
По
схеме сразу видно, что математическая
модель данной задачи имеет вид:
7+
3 – это число пассажиров во втором
вагоне, а (7 + 3) · 2 – это число пассажиров
в первом вагоне.
Произведя
вычисления, получаем ответ на вопрос
задачи: во втором вагоне было 10 пассажиров,
а в первом – 20 пассажиров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- § 1 Способы решения текстовых задач
- § 2 Этапы решения текстовых задач алгебраическим способом
- § 3 Подробное решение текстовой задачи алгебраическим способом
§ 1 Способы решения текстовых задач
Существует несколько способов решения текстовых задач:
• арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;
• алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;
• геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;
• схематический способ – это способ решения текстовой задачи с помощью схем;
• графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.
Каждый из этих способов предполагает перевод условий задачи на язык математики. Это действие математики называют математическим моделированием. Результат этого действия называют математической моделью. При применении различных способов решения получаются различные математические модели.
В арифметическом способе математической моделью является числовое выражение, то есть числовой пример с несколькими действиями, а конечный результат вычислений будет решением задачи.
В алгебраическом способе математической моделью чаще всего является уравнение, а решение уравнения даёт решение задачи.
В геометрическом способе математической моделью является геометрическая фигура, а решение задачи – это один из найденных элементов этой фигуры.
В схематическом способе математической моделью является схема, с помощью которой находят решение задачи.
В графическом способе математической моделью является график, построенный по условию задачи. При этом способе решением задачи являются координаты определённых точек графиков.
На этом занятии более подробно будет рассмотрен алгебраический способ решения задачи.
§ 2 Этапы решения текстовых задач алгебраическим способом
Решить текстовую задачу алгебраическим способом означает:
1. Ввести удобную переменную выразить через неё неизвестные величины.
2. По явным условиям, описанным в задаче, составить уравнение или неравенство.
3. Решить уравнение или неравенство
4. Выбрать из всех найденных решений те, которые подходят по смыслу задачи, то есть удовлетворяют неявным условиям задачи и, таким образом, найти ответ на главный вопрос задачи. Рассмотрим методику алгебраического способа решения текстовых задач с помощью уравнений и неравенств.
1 этап. Арифметическая краткая запись условий задачи.
Цель этого этапа: осмысление задачи.
Форма записи: схематический чертёж или таблица всех известных и неизвестных данных задачи.
Важнопомнить следующее:
• этот этап может отсутствовать, если решение задачи элементарно или она не особо усложнена условиями;
• на этом этапе решения задачи происходит понимание или осмысление её текста. Намного облегчает этот процесс умение правильно «увязать» все известные и неизвестные величины в таблицу данных задачи или составить чертёж; неизвестные величины удобно обозначать знаком «?», а «главный вопрос» задачи для того, чтобы потом на последних этапах не запутаться и правильно найти «Ответ», так как в некоторых задачах, содержащих неявный вопрос искомую величину приходится довычислять;
• все единицы измерения перевести в единые;
• значительно облегчает решение и делает задачу более понятной введение обозначений, общепринятых в физике, химии, геометрии, алгебре, экономике и так далее. Например: V,t,s-скорость, время, расстояние (длина пути или отрезка); р,V,m-плотность вещества, объём тела, масса тела; W,t,V–производительность, время работы, объём работы; a,b,P,S–две стороны прямоугольника, его периметр, его площадь; А0,р,n,An-первоначальная величина, процент её увеличения, количество увеличений, конечная величина после увеличения А0 на р процентов n раз; MА,СА,M–масса вещества А в растворе или в смеси, концентрация вещества А в растворе или смеси (доля), масса раствора или смеси; mn=10m+n–запись двузначного числа, где m,n–цифры;
• Большую помощь в задачах «на движение» оказывает схематический чертёж. Он позволяет увидеть динамику движения, а также учесть все характерные ситуации–встречи, остановки, повороты и тому подобное.
2 этап. «Легенда» или алгебраическая краткая запись условий задачи.
Цель этого этапа: удачно выбрать переменную и выразить все неизвестные величины задачи через неё.
Форма записи: такая, как и на 1этапе, но только вместо знаков «?» везде надо записать выражения с переменной.
Важно помнить:
• обычно этот этап в оформлении задачи начинается с фразы «Пусть х ед.-…,тогда…»;
• не следует пытаться обойтись небольшим числом неизвестных; наоборот, чем больше неизвестных, тем легче составлять уравнения или неравенства;
• выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи; точнее, набор переменных представляет собой список параметров, определяющих эту модель, поэтому все они должны быть независимы, и все соотношения должны следовать лишь из конкретных условий задачи;
• при введении переменных следует руководствоваться принципом наибольшего удобства математической записи условий задачи, при этом искомая величина может не входить в их число. В большинстве задач «главный вопрос» подсказывает выбор переменной.
3 этап. Составление и решение уравнения или неравенства (системы уравнений или неравенств).
Цель этого этапа: опираясь на условия задачи составить уравнение или неравенство ( систему уравнений или неравенств ) и найти его (её) решение.
Важно помнить:
• обычно этот этап в оформлении задачи начинается словами «По условию задачи (выписать условия из текста задачи), значит,…(запись уравнения или неравенства).»;
• необходимо учитывать Область Допустимых Значений переменной или переменных помня условия существования уравнения или неравенства (системы уравнений или неравенств);
• для составления уравнения или неравенства (системы уравнений или неравенств) из текста задачи выбираем условие (условия), которое позволяет увязать известные и неизвестные данные задачи в формулы: S=vt-вычисление длины пути, пройденного телом; m=pV-вычисление массы тела; V=Wt-вычисление объёма работы;S=ab–вычисление площади прямоугольника; MА=САM-вычисление массы вещества А в смеси или растворе; An=A0(1±p)n или An=A0(1±p1) … (1±pn) вычисление сложных процентов;
• если неизвестных следует брать столько, сколько потребуется, то уравнений будет cтолько, сколько получится; в простейших ситуациях мы получаем уравнение (неравенство) с одной переменной или систему уравнений (неравенств), в которой число уравнений (неравенств) совпадает с числом неизвестных.
4 этап. Анализ решения уравнения или неравенства (системы уравнений или неравенств).
Цель: из всех найденных решений уравнений или неравенств (систем уравнений или неравенств) выбрать те, которые подходят по смыслу задачи и, по мере необходимости, довычислить искомую величину.
Важно помнить:
обычно этот этап в оформлении задачи начинается фразой «По смыслу задачи х должна быть величиной… (натуральной, положительной, целой, принадлежащей промежутку и так далее), и, если смысловое условие не выполнено, то найденную величину называют посторонним решением, а , если смысловое условие выполнено, то записывают единицы измерения и пояснение к найденной величине.
• т.о., не каждое решение уравнения может являться решением задачи; особенности отбора значений переменных в различных типовых задачах будут рассмотрены ниже;
• для всякой текстовой задачи полезно провести проверку её решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям.
5 этап. Ответ.
Цель этого этапа: записать правильный ответ, удовлетворяющий всем описанным условиям задачи и отвечающий на её «главный вопрос».
§ 3 Подробное решение текстовой задачи алгебраическим способом
Рассмотрим полное решение задачи по указанной схеме.
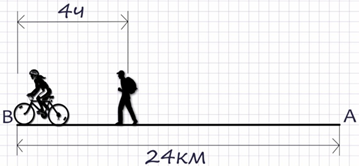
Задача. Из пункта А в пункт В, расположенный в 24км от А, одновременно отправились пешеход и велосипедист. Велосипедист прибыл в пункт В на 4часа раньше пешехода. Известно, что если бы велосипедист ехал с меньшей на 4км/ч скоростью, то на путь из А в В он затратил бы вдвое меньше времени, чем пешеход. Найти скорость пешехода.
Решение.
1 этап. Арифметическая краткая запись.

По условию задачи надо определить скорость пешехода, значит, это и является «Главным вопросом» задачи.
2 этап. «Легенда» или алгебраическая краткая запись. Поскольку путь от А до В известен, то неизвестные величины–скорости пешехода и велосипедиста и время их движения. Т.к. «главный вопрос» задачи–скорость пешехода, то обозначим за переменные скорости, а время выразим через введенные неизвестные. Пусть х км/ч–скорость пешехода, у км/ч–скорость велосипедиста, тогда

В задаче описаны два условия движения пешехода и велосипедиста, значит, получим два уравнения «увязанные» с изменением времени движения.
3 этап. Составление и решение системы уравнений.


24(х + 2) – 12х – 4х(х + 2) = 0, х(х + 2)≠ 0 – ОДЗ. х2-х-12=0; По теореме Виета х1 х2=-12, х1+х2=1. Получаем два решения первого уравнения системы: х1=4![]() ДЗ,
ДЗ,
х2=-3![]() ОДЗ. Оба решения удовлетворяют неравенству системы, т.е. ОДЗ дробно–рационального уравнения.
ОДЗ. Оба решения удовлетворяют неравенству системы, т.е. ОДЗ дробно–рационального уравнения.
4 этап. Анализ решения системы уравнений.
По смыслу задачи х–положительное число, х=-3<0 => постороннее решение,
х=4>0 =>4км/ч скорость движения пешехода.
Проверка решения задачи.
Она часто бывает полезна, но не обязательна. В задаче поставлены четыре условия существования искомой величины–скорости пешехода: 1условие–расстояние между пунктами А и В 24км; 2условие–время движения велосипедиста меньше времени движения пешехода на 4часа; 3условие–изменённая скорость велосипедиста на 4км/ч меньше фактической скорости; 4условие–изменённое время движения велосипедиста в 2раза меньше времени движения пешехода. Для проверки достоверности решения допустим выполнение двух из них при найденном решении задачи. Если два других условия при этом выполнятся, то будем считать, что задача решена верно. Если два других условия не выполнятся, то решение найдено неверно.
24км:4км/ч = 6ч – время движения пешехода; (использовали 1 условие)
6ч – 4ч = 2ч – время движения велосипедиста; (использовали 2 условие)
24км:2ч = 12км/ч – скорость движения велосипедиста;
12км/ч – 4км/ч = 8км/ч – изменённая скорость велосипедиста;
24км:8км/ч = 3ч – изменённое время движения велосипедиста; (выполнено 3 условие)
6ч:3ч = 2(раза) – отношение времени движения пешехода и велосипедиста; (выполнено 4 условие)
Все условия задачи выполнены =>скорость пешехода 4км/ч найдена верно.
5 этап. Ответ. Ответ: 4км/ч.
Таким образом, на этом занятии мы познакомились с алгебраическим способом решения текстовой задачи и разобрали методику её решения на примере задачи «на движение».
Список рекомендованной литературы:
- Г.Н. Тимофеев Математика для поступающих в вузы. Учебное пособие. Текстовые задачи.– Йошкар-Ола: Мар. гос. ун-т, 2006г.
- В. Булынин Применение графических методов при решении текстовых задач. – Еженедельная учебно-методическая газета «Математика», №14, 2005г.
- Н.И. Попов, А.Н. Марасанов Задачи на составление уравнений. Учебное пособие. Йошкар-Ола: Мар. гос. ун-т, 2003г.
- http://festival.1september.ru/articles/310281/ Н.А. Зарипова Программа элективного курса “Текстовые задачи”.
- http://festival.1september.ru/articles/415044/ Н.А. Зарипова Методика решения задач группы vts. Материалы к проведению элективного курса “Решение текстовых задач”
Тема: Составление алгоритма алгебраического
способа решения задач.
Цель.
Исследование алгебраического
способа решения задач и составление алгоритма.
Формирование действия моделирования.
Развитие компонентов УД.
Оборудование:
1. Карточки:
арифметический способ решения;
алгебраический способ решения;
задача.
2. Фломастеры, мелки, чистые листы, магниты,
компьютеры.
3. Учебные принадлежности.
Ход урока.
Организационный момент
Чему учимся на уроке математики?
Что уже знаем хорошо?
Чему надо учиться?
Тему урока сформулируем позже.
Откроем тетради, оформим начало работы.
Актуализация
1.Вспомним некоторые умения,
которые помогут в дальнейшем.
Индивидуальная работа
Составить по схеме уравнения и записать их.
(3· х+5·
2+20=72)
Все остальные учащиеся выполняют любое из этих заданий:
Запиши уравнения и реши их.
1.Число 40 увеличили на произведение числа 6 и
неизвестного и получили 76.
2.Составьте уравнение и решите задачи.
В классе 28 учеников. Сколько мальчиков в
классе, если девочек 13?
В трех вазах 27 гвоздик. В первой вазе на 3
гвоздики меньше, чем во второй вазе, и на 6 гвоздик
больше, чем в третьей. Сколько гвоздик в третьей
вазе?
1.187 * (33467 : 49 – 362)
Что мы должны знать об уравнении?
Для чего нужны уравнения?
2.Построение моделей к
уравнениям выполняем неплохо.
Вспомним, как они решаются.
Нам поможет компьютер.
Сели за компьютер. Задания выполняем в уме.
Порядок работы:
Прочитай информацию.
Подумай, а потом выполняй.
Какие инструменты нам необходимы:
экран
мышка
калькулятор
резинка
в конце посмотреть результаты, сравнить с
прошлым.
(Даются 11 заданий: сложные уравнения на : и х в пределах 100)
Кто закончил на черновике, составляет
уравнения с числами а, 8, 32, 4.
3. Нам необходимо еще
вспомнить одно умение.
(арифметический способ решения задач на
листочках.)
Задача. В трех одинаковых ящиках 21 кг
апельсинов. Сколько апельсинов в 8 таких же
ящиках?
Работаем в паре.
Модель, решение. (Можно записать выражением,
можно по действиям.)
Проверяем.
Чем пользовались?
Составление алгоритма алгебраического способа
решения задач.
Постановка учебной задачи.
Скажите, а можно было решить эту задачу другим
способом?
Что нужно иметь для решения алгебраическим
способом?
А он есть у нас?
А может ли его составить?
Да, мы с вами уже решали задачи таким способом.
Скажите, а есть ли подсказка к составлению
алгоритма?
Составляем алгоритм, записываем на листочках.
Работаем в группах.
Определите, кто будет записывать, кто
рассказывать.
Кто закончит, прикрепляем алгоритм на доску.
Вместе будем выбирать пункты алгоритма.
Идет самостоятельная работа по составлению
алгоритма.
Проверка работы.
Алгоритм:
Чтение задачи.
Выделение известных и неизвестных величин.
Установление связи между условием и вопросом.
Моделирование.
Введение неизвестного.
Выражение через это неизвестное других
величин.
Установление равенства.
Составление уравнения.
Решение уравнения.
Формулировка ответа.
Проверка.
Решение задачи способом уравнения.
Вернемся к нашей задаче, решим ее уравнением.
Х кг – в 8 ящиках
(21 : 3) кг – масса одного ящика из 3
(Х : 8) кг – масса одного ящика из 8
Уравнение: 21 : 3 = Х : 8
Упрощаем: Х : 8 = 7
Х = 56 (кг)
Ответ: 56 кг в 8 ящиках.
Какая тема урока сегодня?
(Составление алгоритма алгебраического
способа решения задач).
Поступил заказ.
Учительница по труду попросила, чтобы ученики
составили чертеж выкройки прямоугольной повязки
для дежурства. Она сказала: “Периметр повязки –
22 см, а длина на 3 см больше, чем ширина”.
Поможем?
Будем строить на компьютере. (не можем)
Почему не можем? (необходимо найти ширину и
длину).
Построим задачу.
Чего не хватает в данном тексте? (должен быть
вопрос).
Задача: Периметр прямоугольника равен 22 см,
длина на 3 см больше, чем ширина. Чему равна ширина
и длина прямоугольника?
Работаем в паре. Каким способом решаем?
Модель:

Строим на компьютере.
Работаем в паре.
Итог урока.
Обучение решению задач.
( из опыта работы учителя начальных
классов по программе и учебникам Н.Б.Истоминой )
Задачи (в широком смысле этого слова)
играют огромную роль в жизни человека. Задачи,
которые ставит перед собой человек, и задачи,
которые ставят перед ним другие люди и
обстоятельства жизни, направляют всю его
деятельность, всю жизнь.
Мышление человека главным образом
состоит из постановки и решения задач.
Перефразируя Декарта, можно сказать: жить –
значит ставить и решать задачи.
Особую
большую роль играют задачи в обучении младших
школьников математике. Решение задач выступает и
как цель, и как средство.
В гимназии № 1 г. Нерюнгри в начальной
школе в одном из классов обучение математике
ведется по программе и учебникам Н.Б. Истоминой,
которые реализуют задачи развивающего обучения,
так как целенаправленно и непрерывно формируют
приемы умственной деятельности: анализ, синтез,
сравнение, классификацию, аналогию, обобщение в
процессе усвоения математического содержания.
Активное включение приемов умственной
деятельности в процессе усвоения математических
знаний, умений и вычислительных навыков
позволяет рассматривать:
- способы организации учебной деятельности
гимназистов, - способы познавательной деятельности
школьников, - способы включения в познавательную
деятельность различных типов памяти, - вопросы преемственности со средним звеном,
-
вопросы повышения качества знаний
учащихся.
Выбор программы Н. Б Истоминой нами
обоснован. Автор этого курса не стремится
наполнить его новыми понятиями, а в основном
ориентируется на объем стабильной программы и
возрастные особенности младших школьников. Тем
не менее, направленность курса на формирование
приемов умственной деятельности потребовала
усиление содержательной линии курса, которая
связана с формированием у младших школьников
системы понятий и общих способов действий. Это
усиление нашло отражение в тематическом
построении курса, что особенно связывает эту
программу с программами развивающего обучения.
В отличие от стабильного курса, в
которой текстовая задача рассматривается как
средство формирования математических понятий и
деятельность учащихся направлена на овладение
умением решать определенные типы текстовых
задач, в математике Н. Б. Истоминой дети
приступают решению задач только после того, как у
них сформированы все необходимые для этого
знания и умения, усвоен смысл математических
понятий, сформировано умение переводить
предметные действия и их словесные описания на
язык схем и математических символов. Это
позволяет в теме “Задача” направить
деятельность учащихся на овладение общими
умениями решать задачи арифметическим способом:
умения читать задачу, выделять известные и
неизвестные величины, устанавливать связь между
условием и вопросом, выбирать арифметическое
действие для ее решения, активно используя при
этом приемы умственных действий. Авторами этой
программы изданы тетради для решения задач, в
которых детям предлагается помощь при
составлении схем, установлении зависимости
между величинами, поиска способа действий. Очень важным, на наш
взгляд, в учебниках этого автора, что рассуждать
детям помогают их сверстники – герои учебника
Миша и Маша.
В формировании навыка решения задач
арифметическим путем способствуют уроки,
проводимые в компьютерном классе. При проведении
таких уроков нами активно используется
программа “Семейный наставник” и
“Презентации”.
Особой популярностью в нашем классе
пользуются задания по диагностике,
тренировочные упражнения в решении задач,
контроль и работа над ошибками. Компьютер
используется на уроке в 3 классе в течение 10 – 15
минут 1 – 2 раза в неделю на различных этапах
урока. Уроки с компьютерной поддержкой позволяют
решать на уроке следующие задачи: повышение
интереса к предмету, осуществление
дифференцированного подхода, увеличение возможности
проведения тренировочных и коррекционных
заданий, увеличение объема проверяемого
материала, облегчение процесс контроля и оценки
знаний.
Программа Н. Б. Истоминой знакомит и
учит решать задачи алгебраическим способом, то
есть способом составления уравнения. В
компьютерной программе для начальной школы
“Семейный наставник” существует подборка
задач для решения их алгебраическим способом. В
них пошагово отрабатываются все этапы алгоритма
этого способа: введение неизвестного, выражение
через это неизвестное величин, о которых
говорится в задаче, составление уравнения,
решение его, осмысление результата и
формулировка ответа.
Эта программа нами используется постоянно, так
как помогает в мониторинге качества знаний
учащихся по математике. Дополнительно на каждого
ученика нами заводится диагностическая карта по
решению задач, в которой фиксируется успешность
ученика в умении решать задачи, недочеты на
каждом этапе решения, как в алгебраическом, так и
в арифметическом способе решения задач.
Приложение №1-2.
К сожалению, ни одна компьютерная программа не
предлагает заданий на графическое моделирование
текстовых задач, т.к. компьютерные программы
ориентированы в большей степени на традиционную
программу. Моделирование (в обучении – по
Истоминой) как психологическая проблема имеет
два аспекта: как содержание, как способ познания
и как одно из основных учебных действий, которое
является составным компонентом учебной
деятельности. Сегодня мы говорим о моделировании
как о средстве представления текста задачи и как
о средстве поиска решения задачи. На графическое
моделирование текстовых задач на уроке
выделяется достаточно много времени (для этого
не надо жалеть времени). Третьеклассники
составляют свою программу для компьютера по
моделированию.
Предлагаемый урок – исследование
алгебраического способа решения задач в 3 класс,
составление алгоритма этого способа. Дети должны
на уроке для себя открыть этот способ и составить
его алгоритм Формы работы: коллективные, парные,
групповые и индивидуальные. Урок проводится в
компьютерном классе с использованием программы
“Семейный наставник”. Дети с самого начала
урока разделены на группы по привязанности друг
к другу. На партах находятся необходимые учебные
принадлежности, фломастеры и четвертая часть
листа ватмана для записи алгоритма
алгебраического способа решения, памятка с
арифметическим способом решения задачи.
Выработанная нами система работы с задачей,
проведение уроков с компьютерной поддержкой
дают положительные результаты: стабильно
высокое качество знаний по математике в 96%, “5” у
40%учащихся, минимум ошибок при решении задач,
первые и призовые места в гимназических,
городских и республиканских олимпиадах (3 место
по математике во второй дистанционной республиканской олимпиаде для
учащихся начальной школы).
Л.П.
Виноградова, учитель начальных классов
гимназии № г.Нерюнгри

РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ
Лиханова В.Е., учитель математики МБОУ «СОШ №12» г. Ноябрьск, ЯНАО
Наряду с арифметическим, практическим методами решения задач ученики 5 класса знакомятся и с алгебраическим методом. Многие ученики сначала не будут принимать новый метод, поэтому роль учителя на данном этапе должна заключаться в том, чтобы показать преимущества данного метода, но ни в коем случае не навязывать его. С этой целью необходимо предлагать задачи, которые арифметически решить трудно.
Особенностями алгебраического метода является введение переменной величины, что позволяет действовать с ней как с явной. Выполняется анализ основных зависимостей между явными и неявными значениями величин, производится моделирование условия задачи в виде уравнения. Если при выборе действий опираемся на сюжетные особенности, то такой метод решения называется алгебраическим. Следует отметить, что в учебнике «Математика 5» авторского коллектива: Г.В.Дорофеев, И.Ф. Шарыгин, Е.А. Бунимович, Л.В. Кузнецова существуют определенные недостатки по обучению решению задач алгебраическим методом. Самым главным из них является недостаточность системы упражнений, готовящих детей к усвоению данного метода, а именно на составление различных выражений по сюжету задач и выяснение их сюжетного смысла.
Необходимые базовые знания для решения задач алгебраическим методом:
- усвоение понятия переменной величины;
- умение решать простые и составные уравнения;
- умение составлять по тексту задачи простые и составные выражения и определять их сюжетный смысл;
- находить выражения с одинаковым сюжетным смыслом.
Основные этапы формирования умения решать задачи алгебраическим методом:
- Подготовительный.
- Этап ознакомления с алгоритмом рассуждения и записью решения задачи.
- Закрепление, выработка умения.
На первом этапе учитель должен познакомить учащихся с понятием «сюжетный смысл выражения», научить составлять всевозможные выражения по тексту задачи, определять их сюжетный смысл. Это можно сделать через следующую систему упражнений:
- Дать текст с числами. Составить по этому тексту несколько выражений, записать их смысл.
- Дать текст. Учитель составляет по этому тексту выражения, а ученики объясняют их смысл по тексту.
- Предложить задание, подобное предыдущему, но среди выражений должны быть такие, которые не имеют сюжетного смысла по данному тексту.
- По предложенному тексту с числами дети сами составляют выражения и определяют их смысл. В заключение находят выражения с одинаковым сюжетным смыслом.
- Дать задачу, показать способ обозначения величины, которую требуется найти в вопросе задачи через х, показать способ составления выражений по задаче с использованием этой неизвестной величины как с известной. Определить сюжетный смысл выражений по тексту задачи.
- По предложенному тексту учитель показывает сюжетный смысл одного из выражений. Детям предлагается составить выражение с тем же сюжетным смыслом.
У пруда росли липы, осины, березы и ели. Лип росло 12, осин – в 3 раза больше, чем лип, несколько елей, берез – на 5 меньше, чем елей. Составь различные выражения и объясни, что они обозначают.
Решение.
Учитель предлагает обозначить число елей буквой х, работать с ней как с обыкновенным числом. Можно составить следующие выражения:
12·3 – количество осин,
х-5 – количество берез,
12+х – количество лип и елей,
12+(х-5) – количество лип и берез,
12·3+(х-5)+х –общее количество осин, берез, елей.
Основная задача второго этапа – введение понятия «основание для составления уравнения», введение алгоритма рассуждения и развернутой формы записи решения задачи алгебраическим методом. Деятельность учителя может быть организована следующим образом.
- Дать текст задачи. Решить ее арифметическим методом.
- Предложить обозначить через х неизвестную величину, значение которой требуется найти.
- Составить ряд выражений по тексту и определить их сюжетный смысл.
- Найти выражения с одинаковым сюжетным смыслом. Сообщить детям, что если выражения имеют одинаковый смысл, то они равны.
- Составить равенство из двух выражений, в одно из которых входит переменная.
- Вместе с детьми определить, что данная запись является уравнением.
- Решить его и установить, что значение х и есть ответ.
- Сообщить учащимся, что сюжетный смысл выражений, которые мы использовали для составления уравнения, будем называть основанием для составления уравнения, а метод решения задачи – алгебраическим.
- Решить еще одну задачу таким же методом. Запомнить алгоритм рассуждений и полную форму записи решения задачи.
- Решив другую задачу, учитель предлагает проверить правильность решения задачи. Для этого необходимо вспомнить все известные способы проверки правильности решения, которые использовали ранее.
- Сообщить детям новый способ проверки. Для этого надо составить уравнение по другому основанию. Сделать вывод.
- Сопоставляя решения первой и второй задачи, учитель в процессе фронтальной беседы составляет алгоритм решения задачи алгебраическим методом.
Алгоритм решения задачи алгебраическим методом.
- Обозначить буквой неизвестную величину.
- Составить выражения.
- Выбрать основание.
- Составить уравнение.
- Решить уравнение.
6. Проверить правильность решения.
Знакомство с новым методом решения задачи можно начать:
- с простой задачи;
- сразу с составной.
В первом случае работа будет выполняться достаточно быстро, но учащиеся не увидят преимущества данного метода (ведь задача и так решена !).
Рассмотрим задачу. Ученики изготовили 135 елочных украшений, из них фонариков на 5 больше, чем хлопушек, а снежинок в 3 раза больше, чем снежинок. Сколько хлопушек изготовили дети?
Необходимо показать, что задача решается с помощью уравнения. Для этого надо ввести переменную величину. Обозначить буквой можно как число хлопушек, так и число фонариков, так и число снежинок (проще – число хлопушек). Составляем выражения с переменной.
Хлопушки- ? штук
Фонарики-?, на 5 штук больше 135 штук
Снежинки-?, в 3 раза больше
Пусть х штук хлопушек сделали дети, тогда они изготовили (х+5) штук фонариков, 3х штук снежинок. Всего было сделано (х+(х+5)+3х) штук украшений, а это – 135 штук украшений. Выражения ( х+(х+5)+3х) и 135 имеют один и тот же сюжетный смысл, значит, их можно приравнять. Требуется подчеркнуть, чту уравнивать можно только выражения, имеющие одинаковый сюжетный смысл. Получится уравнение:
х+(х+5)+3х=135. Обратить внимание, что в уравнении наименования не пишутся. Решим уравнение
х+х+5+3х=135
5х=135-5
5х=130
х=130:5
х=26.
.
Итак, 26 хлопушек сделали дети.
Предложить решить задачу арифметическим методом. Без вспомогательной модели это сделать трудно. Составим схематический чертеж.
Хл.
Ф. 5 ш. 135 ш.
Сн. .
Решение.
Все украшения можно разделить на 5 равных частей, если бы не было5 штук фонариков. Уберем их, при этом общее количество уменьшится на 5.
1) 135-5=130 (шт.) – украшений всего.
- 130:5=26 (шт.) – в одной части , т.е. столько хлопушек сделали дети.
В задачах с пропорциональными величинами желательно использовать таблицу не только для краткой записи содержания, но и для проведения рассуждений при составлении уравнения. Сначала в таблице записывается содержание задачи, а затем (желательно другим цветом) заполняются все пустые графы выражениями с переменной величиной.
Из двух городов, расстояние между которыми 1620 км вышли одновременно навстречу друг другу два поезда, скорость одного на 10 км/ч больше скорости другого и через 18 часов они встретились. Какова скорость каждого поезда?
Скорость |
Время |
Расстояние |
|
(х+10)км/ч На 10 км/ч больше |
18 ч |
(х+10) ·18км |
|
х км/ч |
18 ч |
18х км 1 620 км |
Пусть х км/ч – скорость одного поезда, тогда скорость другого – (х+10) км/ч. До встречи один прошел расстояние 18х км, а другой – (х+10)·18 км.
Вместе они прошли расстояние (18х+(х+10) ·18) км или 1620 км.
18х+(х+10) ·18=1620
18х+18х+180=1620
36х=1620-180
36х=1440
х=1440:36
х=40
Скорость одного поезда 40 км/ч, а другого50 км/ч.
Прим. Если х км/ч – большая скорость, то можно составить такое уравнение: 18х+(х-10) ·18=1620.
Мы рассмотрели некоторые виды текстовых задач, встречающиеся в учебнике математики для 5-х классов. Несмотря на кажущуюся простоту установления связи между алгебраическим и арифметическим методами, этот прием все же требует тщательной отработки с учащимися на практических занятиях и кропотливой работы учителя в ходе самоподготовки к уроку.
Список литературы
1. Математика. 5 класс: учеб. для общеобразоват. организаций/М34/ Г.В Дорофеев, И.Ф. Шарыгин. Рос акад. наук, Рос. акад. образования, изд-во «Просвещение». – 4-е изд. – М.: Просвещение, 2016.
2. Математика. Дидактические материала. 5 класс /М 34 / Г.В Дорофеев, Л.В. Кузнецова, С.С. Минаев, С.Б. Суворова/ Рос. акад. образования, изд-во «Просвещение». – 12-е изд. – М.: Просвещение, 2015.
- Захарова, А.Е. Как помочь школьникам преодолеть некоторые затруднения в овладении решением текстовых задач. А. Захарова / Сборник научных трудов математического факультета МГПУ. М.: МГПУ, 2005. – С. 119-124.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ТЕКСТОВЫХ ЗАДАЧАХ.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Суслова Д.А. 1
1МОУ “Темповская средняя общеобразовательная школа Ртищевского района Саратовской области”
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение.
Текстовые задачи – одни из самых сложных задач в школьном курсе математики. Алгебраический метод решения не всегда бывает удобным для решения задач подобного типа – нередко бывает сложным выбрать нужную неизвестную величину так, чтобы решение было максимально простым и понятным.
С каждым годом текстовые задачи в школьном курсе математики усложняются, причем времени на совершенствование решений этих задач практически не выделяется. И если раньше их решение не вызывало особых затруднений, то теперь с этим могут возникнуть некоторые трудности. Поэтому решить задачу стандартным способом вряд ли получится. Решая одну из текстовых задач, я решила обратиться к математическому моделированию.
Для того чтобы устранить эти трудности, я решила рассмотреть другие возможные методы решения этих задач, а в частности задач на движение по окружности. Предметом моего исследования является математическое моделирование, как процесс, без которого, на мой взгляд, решение подобных задач будет наиболее трудоемким или даже невозможным.
Цель моей работы – рассмотреть основные виды математических моделей, применяемых к решению математических задач, и выбрать наиболее оптимальные к конкретной из них. К постановке этой цели меня привела следующая проблема: в современном мире, насыщенном информацией, необходимо умение представлять информацию в доступном (упрощенном) виде с целью достижения результата (решения задачи).
Исходя из цели, были поставлены следующие задачи:
-
Проанализировать научно-учебную литературу по теме работы.
-
Рассмотреть процесс математического моделирования и этапы создания модели для конкретной задачи.
-
Рассмотреть этапы создания математической модели.
-
Научиться составлять математические модели различного типа.
-
Выявить оптимальный метод математического моделирования для решения конкретной задачи (подобрать оптимальные модели для решения определённого типа задач).
Гипотеза: Существует универсальная математическая модель, с помощью которой можно решить любую текстовую задачу.
Объект исследования: текстовые задачи различного типа.
Методы исследования: анализ, аналогия, обобщение, прогнозирование, эксперимент.
Основная часть.
Глава I. Что такое математическая модель?
1.1 Краткая теоретическая справка.
Заинтересовавшись математическим моделированием, я проанализировала литературу, подробно описывающую данный метод. Существуют различные трактовки и классификации этого понятия. Я остановилась на учебном пособии [1] И.А. Печерских и А.Г. Семенова, которые дают следующее определение математической модели:
Математическая модель представляет собой формализованное описание системы на некотором абстрактном языке, например, в виде совокупности математических соотношений, т. е. такое математическое описание, которое обеспечивает имитацию работы систем или устройств на уровне, достаточно близком к их реальному поведению. Любая математическая модель описывает реальный объект, явление или процесс с некоторой степенью приближения к действительности. Целью математического моделирования является анализ реальных процессов математическими методами.
1.2 Этапы математического моделирования.
-
Постановка задачи.
На этом этапе требуется четкое понимание поставленной задачи.
-
Изучение теоретических основ и сбор информации об объекте оригинала.
На этом этапе подбирается или разрабатывается подходящая теория
-
Формализация.
Заключается в выборе системы условных обозначений.
-
Выбор метода решения.
На этом этапе устанавливаются окончательные параметры моделей с учетом условия функционирования объекта.
-
Реализация модели.
Выполнятся построение математической модели (строится график, таблица, рисунок или эскиз, граф) и решается задача исходя из новых условий.
-
Анализ полученной информации.
Сопоставляется полученное и предполагаемое решение.
7. Проверка адекватности реальному объекту.
Результаты, полученные по модели, сопоставляются с условиями исходной задачи.
Глава II. Применение моделирования к решению задачи.
Для достижения поставленной цели я составила несколько математических моделей, и постаралась к решению одной задачи (на движение по окружности) применить этот метод.
Задача.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 18 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости другого?
Данную задачу решим с помощью математических моделей:
1. Таблица.
2. «Математический маятник».
3. Графическая модель.
2.1 Таблица – математическая модель, которая помогает упорядочить все данные в задаче для более удобного восприятия.
(Приложение 1. Таблица. Стр. 14.)
Решение.
Пусть x кмч – скорость первого мотоциклиста, тогда скорость 2-го мотоциклиста (x + 25) км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый (то есть второй ) должен преодолеть изначально разделяющее их расстояние, равное половине длины всей трассы ( т.к. мотоциклисты расположены в диаметрально противоположных точках )
( x + 25 )t – xt = 9
tx + 25t – tx = 9
25t = 9
t = 21,6 (минут)
Ответ: 21,6 минут.
2.2 «Математический маятник».
Математическим маятником [2] называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Математический маятник имеет следующие характеристики: период, частота колебаний, количество колебаний и длина нити, но для решения этой задачи я остановилась на двух из них: период частота. Если связать эти величины со скоростью, временем и расстоянием, то задачу на движение по окружности можно будет решать с помощью формул, которые свойственны математическому маятнику.
T – период – это время, затраченное на один круг.
ʋ – частота колебаний – это величина обратная периоду.
Составим математическую модель.
(Приложение 2. «Математический маятник». Стр.14).
Пусть х км/ч – скорость первого мотоциклиста, тогда скорость второго мотоциклиста (х+25) км/ч. Длина всей трассы 18 км.
Т1 = время, затраченное 1-ым мотоциклистом на прохождение полного круга (период).
Т2 = время, затраченное 2-ым мотоциклистом на прохождение полного круга (период).
Для того чтобы мотоциклисты поравнялись в первый раз их частоты должны совпасть, значит:
– частота первого мотоциклиста.
– частота второго мотоциклиста.
Тогда разность – частота с которой будут происходить встречи при старте из одной точки.
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
Тогда (ч) = 21,6 (мин.)
Ответ: 21,6 мин.
2.3 Графическая модель.
Графики законов, которые описывают зависимость S от t, строятся в системе координат SOt. Поскольку t > 0 и S > О, то построения выполняются в первой координатной четверти.
График движения тела по окружности можно заменить графиком движения по прямой. Обход телом окружности и возвращение в исходную точку равносильны достижению телом на прямой точки, удаленной от начальной на расстояние S0, равное длине окружности.
Изобразим схематически в системе SOt движение мотоциклистов.
Так как все величины положительны, то достаточно рассмотреть графики в первой четверти.
Пусть x ч – время, за которое первый мотоциклист догнал второго, y км – путь, пройденный вторым мотоциклистом до момента встречи с первым. Решение сводится к решению геометрической задачи.
(Приложение 3. Графическая модель. Стр. 15)
Ответ: 21, 6 минуты.
На примере решения данной задачи были выявлены следующие преимущества решения задач с помощью геометрической модели: наглядность, оперативность, простота решения.
Глава 3. Выявление оптимальных моделей для решения конкретных
задач.
3.1 Задачи на совместную работу.
Задачи подобного типа удобнее всего решать с помощью таблицы, потому что производительность, объем работы и время на выполнение всей работы можно легко связать со скоростью, временем и расстоянием. Роль скорости выполняет производительность труда, роль расстояния – вся работа, время выполняет свою роль.
Задача.
Двое рабочих, работая вместе, могут выполнить производственное задание за 40 дней. За сколько дней может выполнить задание каждый из них, работая самостоятельно, если одному из них для этого надо на 18 дней больше, чем другому?
Решение:
Примем весь объем работы за единицу. Пусть 2-ой рабочий, работая самостоятельно, может выполнить все задание за x дней, тогда 1-ый — за (x+18) дней.
(Приложение 4. Таблица. Стр. 15)
Вместе за 1 день рабочие выполняют задания. За 40 дней рабочие выполнят всю работу. Составим уравнение:
40× ( ) = 1
→
→
Второй корень не подходит по смыслу задачи (так как время не может быть отрицательным числом). Значит, 2-ой рабочий, работая самостоятельно, может выполнить всю работу за 10 дней, а 1-ый — за 10+9=19 дней.
Ответ: 10 дней, 19 дней.
3.2 Задачи на движение.
Задачи на движение по прямой удобнее всего решать с помощью графической модели.
Задача: Два пешехода вышли одновременно из своих сел W и C навстречу друг другу. После встречи первый шел 25 минут до села C, а второй шел 16 минут до села W. Сколько минут они шли до встречи?
(Приложение 5. Графическая модель. Стр. 16)
Решение:
Пусть ОЕ расстояние между сёлами W и C. OD – график движения первого пешехода ( который шёл медленнее), а EF – график движения второго. М – место встречи.
1) ∆ MND~∆MPO,
2) ∆MNE~∆MPF,
3)
4) => что t = 20 (мин.)
Ответ: 20 мин.
3.3 Задачи на движение по окружности.
Два велосипедиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение:
Используя модель «математического маятника», описанного выше, задача решается практически устно.- частота с которой будут происходить встречи при старте из одной точки.
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
Тогда (ч) = (ч) = 20 (мин.)
Ответ: через 20 минут.
С помощью этой модели можно также быстро решать задачи, в которых отставание составляет не половину трассы, а конкретное расстояние. Решим эту же задачу, изменив в ней условие.
Два велосипедиста стартуют одновременно в одном направлении из двух точек круговой трассы, расстояние между которыми равно 3 км. Длина трассы равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение: Задача будет иметь 2 решения в зависимости от направления
движения по круговой трассе.
Составим математическую модель (для данной задачи их будет две).
(Приложение 6. «Математический маятник». Стр. 16)
В первом случае решение будет таким:
– частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда
∙ = 7; тогда Т = (ч).
Во втором случае
– частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда
=∙ = ; тогда Т = (ч).
Ответ: через часа; или через часа.
Таким образом, модель «Математический маятник» подходит для решения задач на движение по окружности. Применение такого способа решения значительно сокращает время на решение задачи, что позволит при выполнении контрольных работ и на экзамене увеличить время на решение более трудных задач.
Заключение.
В результате исследования были получены следующие результаты:
-
Был изучен процесс математического моделирования и этапы создания модели для конкретной задачи.
-
В ходе исследования была опровергнута гипотеза, о существовании универсальной математической модели для решения всех типов задач.
-
Я научилась составлять математические модели различного типа.
-
Были выявлены оптимальные математические модели для решения конкретной задачи.
Я думаю, что за моделированием – будущее. Умение составлять математические модели сможет помочь в решении задач из различных отраслей науки, а также жизненных задач. Хочется отметить, что решение задач с применением моделирования активизирует мыслительную деятельность, помогает лучше понять задачу, самостоятельно найти рациональный путь ее решения, установить подходящий способ проверки, определить условия, при которых задача имеет (или не имеет) решения. Работа с моделью позволяет яснее увидеть зависимости между данными и искомыми величинами, оценить задачу в целом, продемонстрировать разные варианты решения.
Библиографический список.
1. Рецензенты Черкасов В.С., кандидат физ.-мат. наук, доцент;
Чуешев А.В., кандидат физ.-мат. наук, доцент; Печерских, И.А. П 31 Математические модели в экономике: учебное пособие / И.А. Печерских, А.Г. Семенов; Кемеровский технологический институт пищевой промышленности. – Кемерово, 2011. – 191 с.
2. Перышкин, А. В.
П27 Физика. 9 кл. : учебник для общеобразоват. учреждений / А. В.
Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М. : Дрофа, 2009, – 300,
с, : ил, ; 1 л, цв. Вкл.
3. http://www.pedsovet.info/info/pages/referats/inf_00002.htm
Приложения
Приложение 1. Таблица
|
V (км/ч) |
t (ч) |
S (км) |
|
|
1-ый мотоциклист |
X |
t |
xt |
|
2-ой мотоциклист |
(х+25) |
t |
( x + 25 )t |
Приложение 2. «Математический маятник».
Приложение 3. Графическая модель.
18
A
O
y
D
9
C
t
x
Приложение 4. Таблица.
|
Производительность труда |
Время работы |
Работа |
|
|
1-ый рабочий |
ч/день |
(x+18) дней |
1часть |
|
2-ой рабочий |
ч/день |
1часть |
Приложение 5. Графическая модель.
25 минут
Приложение 6. «Математический маятник».
1) 2)
х
х
х+21
х+21
25
Просмотров работы: 9076
