Циклы со счетчиком
В
циклах такого типа известно число
повторений цикла, т.е. оно является
фиксированным числом. В этом случае
переменная, которая считает количество
повторений (шагов) цикла, называется
счетчиком
цикла (или
параметром
цикла, или
управляющей
переменной
цикла).
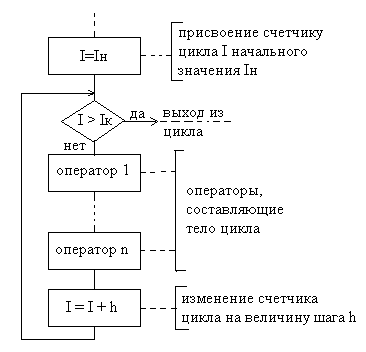
Блок-схема
циклического алгоритма в этом случае
выглядит так:
Такая
блок-схема хорошо иллюстрирует работу
цикла со счетчиком. Перед выполнением
первого шага цикла счетчику цикла должно
быть присвоено начальное значение –
любое число в зависимости от алгоритма.
Если величина счетчика цикла не превышает
конечное значение, то далее будет
выполняться группа действий, составляющих
тело цикла. После выполнения тела цикла
счетчик цикла изменяется на определенную
величину – шаг изменения счетчика цикла
h.
Если полученное значение счетчика цикла
не превысит конечное значение, то цикл
продолжится до тех пор, пока счетчик
цикла не станет больше конечного значения
– тогда управление передается действию,
следующему за циклом.
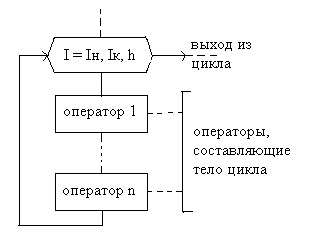
В
дальнейшем мы будем использовать в
блок-схемах для изображения цикла со
счетчиком блок «Подготовка». В блоке
«Подготовка» записывается счетчик
цикла (I),
далее последовательно указываются
начальное значение (Iн),
конечное значение (Iк)
счетчика цикла и шаг его изменения (h).
Если шаг изменения h
равен 1, его можно не записывать.
Желательно, чтобы линия потока входила
в блок сверху, линия потока к телу цикла
выходила снизу, слева (или справа) входила
линия потока перехода к следующему шагу
цикла, а справа (или слева) выходила
линия потока – выход из цикла.
При
использовании цикла со счетчиком
необходимо соблюдать некоторые
требования:
-
в
теле цикла нельзя принудительно
изменять значение счетчика цикла; -
не
разрешается передавать управление
оператору
тела цикла
извне, т.е. вход в цикл допускается
только через начало цикла.
Циклы с предусловием
Циклы
с предусловием чаще всего используют
тогда, когда неизвестно число повторений
цикла. Циклы
с предусловием
– это такие циклы, в которых до начала
выполнения тела цикла проверяется
условие выполнения следующего шага
цикла. Если значение этого условия
истинно (т.е. условие выполняется), то
выполняется тело цикла. В теле цикла
должно изменяться значение по крайней
мере одной переменной, которая влияет
на значение условия (иначе произойдет
«зацикливание»). Далее опять проверяется
условие выполнения цикла, и если значение
условия ложно, то осуществляется выход
из цикла.
Можно
использовать и еще один вариант этого
цикла, когда проверяется не истинность
значения условия, а ложность. В этом
случае выход из цикла происходит, когда
значение условия цикла становится
истинным. Тот или иной вариант цикла
используется в зависимости от того,
какое условие в данном алгоритме
программисту удобнее использовать.
Особенность
этого типа цикла в том, что тело цикла
может не выполниться ни разу, если
условие первоначально ложно в первом
варианте (или истинно во втором).
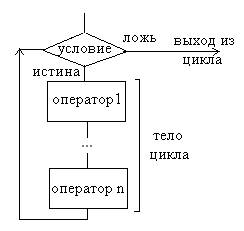
На
блок-схеме такой цикл реализуется
следующей конструкцией:
Циклы с постусловием
Этот
тип цикла также используется при
неизвестном заранее количестве повторений
цикла, но в отличие от цикла с предусловием
здесь условие на выход из цикла проверяется
после того, как выполнились операторы
тела цикла, поэтому хотя бы один раз
тело цикла будет обязательно выполнено.
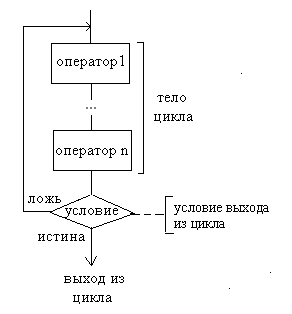
На блок-схеме этот
тип цикла изображается следующим
образом:
Сложные циклы
Циклы,
которые содержат внутри себя (в теле
цикла) один или несколько других циклов,
называются сложными
или
вложенными циклами.
При этом циклы,
охватывающие другие циклы, называются
внешними,
а циклы, входящие во внешние, – внутренними
циклами.
На каждом шаге
внешнего цикла внутренний цикл
«прокручивается» полностью.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье будет рассмотрена работа циклического алгоритма — что это, как он работает, какие виды существуют. Также будут рассмотрены примеры циклических алгоритмов в разных языках программирования.
Прежде чем приступить к основной теме статьи, следует прояснить терминологию вопроса и рассмотреть основные определения:
— цикл — вид управляющей конструкции в языках программирования. Он позволяет организовать многократное исполнение определённого набора инструкций (последовательность действий, при котором выполняется тело цикла);
— тело цикла — последовательность инструкций, обеспечивающая их многократное исполнение;
— итерация — однократное исполнение тела цикла;
— условие выхода (условие окончания) — выражение, которое определяет, станет ли в очередной раз выполняться итерация либо произойдёт завершение цикла;
— счётчик цикла — переменная, которая сохраняет номер итерации.
Счётчик не обязательно должен содержаться в цикле и счётчик совсем не обязательно должен быть один, то есть условие выхода порой зависит от нескольких изменяемых переменных. Вдобавок к этому, условие выхода иногда зависит от внешних условий (как пример — наступление определённого времени).
Работа любого цикла вне зависимости от его вида включает в себя:
— первоначальную инициализацию циклических переменных;
— проверку условия выхода из цикла;
— выполнение тела;
— обновление циклической переменной на каждой итерации.
Многие языки программирования предоставляют разработчику средства, обеспечивающие досрочное завершение цикла (выход из него вне зависимости от истинности условия выхода).
Виды циклических алгоритмов
Безусловные циклы
В некоторых программах и линейных алгоритмах на компьютерах выход из циклов не предусмотрен логикой. Эти циклы называются безусловными (другое название — бесконечные). При написании таких алгоритмов для решения поставленных задач специальных синтаксических средств не используют (они часто и не предусмотрены). На практике вполне достаточно конструкций, которые предназначены для формирования обычных (условных) циклов. Чтобы обеспечить бесконечное повторение, проверка условия или исключается (LOOP…END LOOP, язык программирования Ада), или заменяется константным значением (while true do …, Pascal).
Теперь следует рассмотреть группу циклов с условием.
Циклический алгоритм с предусловием
При наличии предусловия цикл выполняется до тех пор, пока истинно определённое условие, которое указано перед началом. Данное условие проверяется ещё до выполнения тела, в результате чего тело алгоритма может вообще ни разу не выполнится (пример такой ситуации с нулевым количеством итераций — условие изначально ложно). Что касается применения и реализации, то во многих процедурных языках программирования такой алгоритм реализуется с помощью оператора while.
Циклический алгоритм с постусловием
В данном случае проверка условия происходит уже после выполнения тела. Это означает, что тело цикла хотя бы раз, да выполнится. В Pascal такой алгоритм реализуется посредством оператора repeat..until, в языке программирования Си — с помощью do…while.
В зависимости от языка, трактовка условий бывает разной. В том же Pascal речь идёт об условии выхода (работа линейного алгоритма завершится, когда условие истинно; «цикл до»), а в вышеупомянутом Си можно говорить об условии продолжения (цикл завершится, когда условие ложно; «цикл пока»).
Циклический алгоритм с выходом из середины
Это самая общая форма условного линейного алгоритма. Синтаксически оформляется посредством 3-х конструкций:
— начало цикла,
— конец,
— команда выхода.
Конструкция начала обеспечивает маркировку программной точки, где начинается тело, конструкция конца — где тело заканчивается. Внутри циклического алгоритма присутствует команда, обеспечивающая выход — цикл оканчивается, а управление передаётся оператору, следующему за конструкцией конца.
Если сравнивать этот алгоритм с вышеупомянутыми, то он имеет особенность: часть тела, которая расположена после начала и до команды выхода, выполнится всегда, а часть тела, расположенная после команды выхода, при последней итерации не выполнится.
Чтобы организовать выход из середины, в некоторых языках программирования необходимо использовать специальные конструкции. В Ада это LOOP…END LOOP и команда EXIT либо EXIT WHEN:
Внутри этого алгоритма может находиться любое число команд выхода обоих типов — как EXIT WHEN (используется, если проверяется лишь условие выхода), так и просто EXIT (используется, если выход осуществляется в одной из вариаций сложного условного оператора).
В некоторых языках специальные конструкции для выхода из середины отсутствуют. В таких случаях смоделировать выход можно, используя любой условный цикл и оператор досрочного выхода (тот же break в Си) или goto — оператор безусловного перехода.
Циклический алгоритм cо счётчиком
При реализации этого алгоритма на компьютере определённая переменная меняет своё значение с некоторым шагом (она имеет заданное начальное и конечное значения), причём для каждого значения переменной тело цикла выполнится хотя бы раз. Во многих процедурных языках программирования алгоритм со счётчиком реализуется с помощью оператора for. В нём указывается счётчик (его ещё называют переменной цикла), определённое число проходов (граничное значение счётчика) и, в некоторых случаях, шаг изменения счётчика. В качестве примера — циклический алгоритм со счётчиком в языке программирования Оберон-2:
Хотите знать про алгоритмы больше? Записывайтесь на специализированные курсы в OTUS!
Источник — https://dic.academic.ru/dic.nsf/ruwiki/1188296.
Циклический алгоритм со счетчиком примеры
Циклический алгоритм и его составление в информатике: примеры, решение
Содержание:
Алгоритм является классической совокупностью четко установленных норм для поиска решения задачи. Класс задач – произвольный. В структуру может входить последовательность действий, список инструментария, необходимый для поиска ответа на исходный вопрос задания.
Циклом называют некоторое повторение действия, вычисления.
Цикличный алгоритм, примеры которого можно встретить в повседневной жизни, описывает действия. Они повторяются до момента решения поставленной задачи. Иногда число повторений – обязательное условие задания. Информатика разделяет все структуры повторения на три вида:
- Циклический алгоритм со счетчиком. Конкретная работа должна быть выполнена установленное количество раз. В таких видах конструкций условие уже содержит параметр, указывающий число повторных операций. Простой пример циклического алгоритма со счетчиком: требуется распечатать задание на контрольную на весь класс. В классе 21 ученик. Действие повторится 21 раз;
- Циклический конструктив с условиями. Вычисление или процесс выполняется до того момента, пока не будет сделана работа. После наступит окончание проекта. Данный вид используют в ситуациях, когда число повторений, необходимых для достижения цели, неизвестно. Если рассматривать условный алгоритм с циклом, примеры найти не составит труда. Садовнику необходимо посадить дерево. Он должен выкопать яму. Заранее неизвестно, сколько движений лопатой ему нужно сделать. Он ориентируется на результат;
- Повторение с предварительным условием. Исполнитель изначально проверяет заданные параметры, после приступает к осуществлению действия;
- Цикл с последующим условием. Задача выполняется один раз, после проводится проверка ее параметров.
Составление циклических алгоритмов – информатика и программирование
Главное правило составления конструктивов – конечность. Процесс должен осуществляться до определенного момента. Если окончание не наступает – структуру называют зацикленной. Состав структур с повторениями:
- Название процедуры. Исполнитель указывает основные условия. Они определяют, сколько раз повторится операция;
- Тело алгоритма. Это оператор, он может быть составным или простым. Повторяется в ходе процесса. Допускается содержание разных операторов. Они отвечают за ввод, вывод, присваивание. Отдельная группа условных операций и других. Все операторы, находящиеся внутри системы, – это вложенные конструкции.
Часто встречается задание: приведите пример циклического алгоритма. Чтобы справиться с этой задачей, рекомендуется следовать принципам последовательности составления конструктивов:
- Выявление последовательностей, требующих повторения.
- Определение количества циклических оборотов до начала его работы.
- Использование системы со счетчиком, если количество повторов уже задано.
- Использование структуры с последующим условием при минимум одном исполнении процесса.
- При отсутствии данной информации или возможности нулевого цикла применяется система с предварительным условием.
- Определение пределов для вида со счетчиком.
- Выявление параметров повторов, окончания для последовательностей с условиями.
- Поиск известных переменных до старта. Крайне важны коэффициенты, находящиеся в оперативном условии, если есть предварительные параметры.
- Запись операторов, вычисляющих, выводящих переменные.
- Создание алгоритмической схемы.
- Выбор данных, которыми можно воспользоваться для теста программного продукта.
Циклический алгоритм примеры – информатика
- Укажите процесс, который демонстрирует работу циклического алгоритма.
Рассмотрим пример классической структуры с повторами. Она состоит из четырех частей:
- Присвоение начального обозначения параметру;
- Выполнение основных операций, повторяющихся на цикличных витках;
- Ввод величины шага, проведение соответствующих изменений;
- Ввод условия для окончания или повторного проведения операций;
- Проверка итогов.
Сумма рассчитывается с помощью данной системы. Рассмотрим процесс на примере i-1nxiyi. Действуем по следующей схеме:
- Устанавливается стартовое значение для суммы – нулевое;
- Исследуется первый параметр i, равный единице;
- Выводится xi, yi для вычисления СУММ=СУММ+Xi x Y i;
- Суммирование проводится циклично. Следующее действие i=i+1;
- Повторение выполняется до того, как будет получено нужное значение. Его необходимо вывести.
- Приведите пример циклического алгоритма из жизни.
На уроке физики ученики должны использовать одинаковую формулу до того момента, пока выражение не станет верным. Без этого они не получат нужный результат.
Циклы со счетчиком
В циклах такого типа известно число повторений цикла, т.е. оно является фиксированным числом. В этом случае переменная, которая считает количество повторений (шагов) цикла, называется счетчиком цикла (или параметром цикла, или управляющей переменной цикла).
Блок-схема циклического алгоритма в этом случае выглядит так:
Такая блок-схема хорошо иллюстрирует работу цикла со счетчиком. Перед выполнением первого шага цикла счетчику цикла должно быть присвоено начальное значение – любое число в зависимости от алгоритма. Если величина счетчика цикла не превышает конечное значение, то далее будет выполняться группа действий, составляющих тело цикла. После выполнения тела цикла счетчик цикла изменяется на определенную величину – шаг изменения счетчика цикла h. Если полученное значение счетчика цикла не превысит конечное значение, то цикл продолжится до тех пор, пока счетчик цикла не станет больше конечного значения – тогда управление передается действию, следующему за циклом.
В дальнейшем мы будем использовать в блок-схемах для изображения цикла со счетчиком блок «Подготовка». В блоке «Подготовка» записывается счетчик цикла (I), далее последовательно указываются начальное значение (Iн), конечное значение (Iк) счетчика цикла и шаг его изменения (h). Если шаг изменения h равен 1, его можно не записывать. Желательно, чтобы линия потока входила в блок сверху, линия потока к телу цикла выходила снизу, слева (или справа) входила линия потока перехода к следующему шагу цикла, а справа (или слева) выходила линия потока – выход из цикла.
При использовании цикла со счетчиком необходимо соблюдать некоторые требования:
в теле цикла нельзя принудительно изменять значение счетчика цикла;
не разрешается передавать управление оператору тела цикла извне, т.е. вход в цикл допускается только через начало цикла.
Циклы с предусловием
Циклы с предусловием чаще всего используют тогда, когда неизвестно число повторений цикла. Циклы с предусловием – это такие циклы, в которых до начала выполнения тела цикла проверяется условие выполнения следующего шага цикла. Если значение этого условия истинно (т.е. условие выполняется), то выполняется тело цикла. В теле цикла должно изменяться значение по крайней мере одной переменной, которая влияет на значение условия (иначе произойдет «зацикливание»). Далее опять проверяется условие выполнения цикла, и если значение условия ложно, то осуществляется выход из цикла.
Можно использовать и еще один вариант этого цикла, когда проверяется не истинность значения условия, а ложность. В этом случае выход из цикла происходит, когда значение условия цикла становится истинным. Тот или иной вариант цикла используется в зависимости от того, какое условие в данном алгоритме программисту удобнее использовать.
Особенность этого типа цикла в том, что тело цикла может не выполниться ни разу, если условие первоначально ложно в первом варианте (или истинно во втором).
На блок-схеме такой цикл реализуется следующей конструкцией:
Циклы с постусловием
Этот тип цикла также используется при неизвестном заранее количестве повторений цикла, но в отличие от цикла с предусловием здесь условие на выход из цикла проверяется после того, как выполнились операторы тела цикла, поэтому хотя бы один раз тело цикла будет обязательно выполнено.
На блок-схеме этот тип цикла изображается следующим образом:
Циклы, которые содержат внутри себя (в теле цикла) один или несколько других циклов, называются сложными или вложенными циклами.
При этом циклы, охватывающие другие циклы, называются внешними, а циклы, входящие во внешние, – внутренними циклами.
На каждом шаге внешнего цикла внутренний цикл «прокручивается» полностью.
Алгоритмическая структура «цикл». Циклы со счетчиком и циклы по условию
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Алгоритмическая структура «цикл». Циклы со счетчиком и циклы по условию.
Лучшее качества компьютеров проявляются не тогда, когда они рассчитывают значения сложных выражений, а когда многократно, с незначительными изменениями, повторяют сравнительно простые операции. Даже очень простые расчеты могут поставить человека в тупик, если их надо повторить тысячи раз, а повторять операции миллионы раз человек совершенно не способен.
С необходимостью повторяющихся вычислений программисты сталкиваются постоянно. Например, если надо подсчитать, сколько раз буква «о» встречается в тексте необходимо перебрать все буквы. При всей простоте этой программы исполнить ее человеку очень трудно, а для компьютера это задача на несколько секунд.
Циклический алгоритм — описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие.
Перечень повторяющихся действий называют телом цикла.
Например, на уроке физкультуры вы должны пробежать некоторое количество кругов вокруг стадиона.
Такие циклы называются — циклы со счетчиком .
На языке Basic они записываются следующим образом:
FOR Счетчик=НачЗнач TO КонЗнач [STEP шаг]
тело цикла
NEXT [Счетчик]
Параметры указанные в квадратных скобках являются не обязательными (их можно не записывать). По умолчанию шаг цикла равен одному, т.е. каждый раз после прохождения тела цикла счетчик увеличивается на единицу.
Пример: Вывести на экран все числа от 1 до 100. Для этого можно было бы написать следующую программу:
REM Вывод чисел от 1 до 100
PRINT 1
PRINT 2
PRINT 3
PRINT 4
PRINT 5
PRINT 6
PRINT 7
.
PRINT 98
PRINT 99
PRINT 100
END
Всего каких-то 102 строчки ;-). Хотя эту же программу можно написать намного короче:
REM Вывод чисел от 1 до 100
FOR I=1 TO 100
PRINT I
NEXT
END
Немного исправив программу можно сделать, чтобы она выводила все числа от a до b.
REM Вывод чисел от a до b
a=55
b=107
FOR I=a TO b
PRINT I
NEXT
END
В этом случае счетчик при первом прохождении цикла принимает значение переменной a, после чего выполняются операторы до ключевого слова NEXT. После этого счетчик увеличивается на единицу и сравнивается со значение переменной b, если счетчик меньше, то цикл выполняется еще.
Легко сделать чтобы программа выводила числа в обратном порядке. Для этого шаг цикла должен быть равен -1 (минус один). В этом случае значение счетчика каждый раз после прохождения цикла будет уменьшено на единицу.
REM Вывод чисел от b до a
a=55
b=107
FOR I=b TO a STEP -1
PRINT I
NEXT
END
Пример: Вычислить сумму двухзначных натуральных чисел.
REM Вычислить сумму двухзначных натуральных чисел
FOR I=10 TO 99
s=s+I
NEXT
PRINT «Результат = «,s
END
Программа перебирает числа от 10 до 99 каждый раз выполняя действия s=s+I . С точки зрения математики это совершенно бессмысленная запись, но рассмотрим её внимательней.
Процесс решения вычислительной задачи — это процесс последовательного изменения значений переменных. В итоге — в определенных переменных получается результат. Переменная получает определенное значение в результате присваивания . Вы помните, что присваивание — это занесение в ячейку, отведенную под переменную, определенного значения в результате выполнения команды.
В результате операции а=5 переменная а получает значение 5.
В результате операции с=a+b переменная с получает значение равное сумме значений переменной а и b .
В результате операции s=s+I переменная s получает значение равное сумме предыдущего значения переменной s и значения переменной I . Т.е., если до операции присваивания значение s было равно 5, а переменной I равно 3, то после операции значение переменной s будет равно 8 (5+3, старое значение s + значение I ).
Значит после выполнения нашей программы в переменной s будет хранится сумма всех двузначных чисел от 10 до 99.
Пример: вычислить факториал числа а (записывается так: а!). Факториал — это произведение чисел от 1 до а. Например, 5! (факториал пяти) — это 5!=1*2*3*4*5.
REM Вычислить факториал числа
a=5
f=1
FOR I=1 TO a
f=f*I
NEXT
PRINT f
END
Вы, конечно, заметили, что до начала цикла мы присвоили переменной f значение равное единице. Иначе бы мы получили в результате ноль.
В субботу вечером вы смотрите телевизор. Время от времени поглядываете на часы и если время меньше полуночи, то продолжаете смотреть телевизор, если это не так, то вы прекращаете просмотр телепередач.
Циклы такого вида называют — циклы с предусловием .
На языке Basic они записываются следующим образом:
DO WHILE условие
Тело цикла
LOOP
В этом цикле проверяется условие и если оно выполняется (ИСТИНА), то выполняется тело цикла до ключевого слова LOOP, затем условие проверяется снова . и так до тех пор пока условие истино.
DO UNTIL условие
Тело цикла
LOOP
Этот цикл отличается от предыдущего только тем, что он выполняется до тех пор пока условие не истинно (т.е. совсем наоборот).
Пример: Вывести все натуральные числа меньше данного.
REM Вывод всех чисел меньше данного
a=0
chislo=10
DO WHILE a может быть не выполнен ни разу (если условие первоначально не истинно, например, a =5, а chislo =4). И наоборот, если условие будет истинно при любых значениях переменный, то цикл будет выполнятся бесконечное число раз (произойдет зацикливание ).
Пример цикла, который будет выполнятся бесконечное число раз:
REM зацикливание
DO WHILE a=a
PRINT «Это сообщение будет выводится на экран постоянно»
LOOP
PRINT «А это сообщение вы не увидите никогда»
END
Вам надо поточить все карандаши в коробке. Вы точите один карандаш и откладываете его в сторону. Затем проверяете, остались ли карандаши в коробке. Если условие ложно, то снова выполняется действие ‘заточить карандаш’. Как только условие становится истинным, то цикл прекращается.
Циклы такого вида называют — циклы с постусловием .
На языке Basic они записываются следующим образом:
DO
Тело цикла
LOOP WHILE условие
DO
Тело цикла
LOOP UNTIL условие
Циклы такого рода отличаются тем, что хоть один раз, но тело цикла будет выполнено вне зависимости от условия. Условие проверяется после первого выполнения тела цикла.
Пример: Вычислите сумму цифр в числе.
REM Сумма цифр числа
DIM a, chislo, s AS INTEGER
INPUT «Введите число: «, chislo
a=chislo
DO
s=s+a MOD 10
a=a/10
a=INT(a)
LOOP UNTIL a=0
PRINT «Сумма цифр числа «,chislo ,» равна: «, s
END
Переменную s используем для хранения суммы цифр. До начала цикла в переменную a заносим значение переменной chislo . Все дальнейшие преобразования осуществляем с переменной а . В цикле берем остаток от деления на 10 (последняя цифра числа) и прибавляем к тому, что уже есть в переменной s ; делим значение переменной а на 10, берем целую часть (т.е. отбрасываем последнюю цифру числа) и заносим в а . Цикл продолжается до тех пор пока значение переменной а не окажется равным нулю (перебрали все цифры числа). Результат выводим на экран.
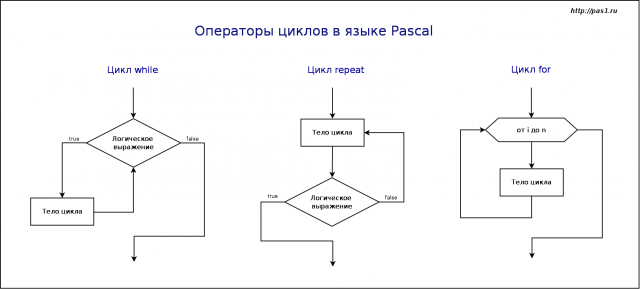
Циклы в Паскале
При решении задач может возникнуть необходимость повторить одни и те же действия несколько или множество раз. В программировании блоки кода, которые требуется повторять не единожды, оборачиваются в специальные конструкции – циклы. У циклов выделяют заголовок и тело. Заголовок определяет, до каких пор или сколько раз тело цикла будет выполняться. Тело содержит выражения, которые выполняются, если в заголовке цикла выражение вернуло логическую истину (True, не ноль). После того как достигнута последняя инструкция тела, поток выполнения снова возвращается к заголовку цикла. Снова проверяется условие выполнения цикла. В зависимости от результата тело цикла либо повторяется, либо поток выполнения переходит к следующему выражению после всего цикла.
В языке программирования Паскаль существует три вида циклических конструкций.
Цикл for
Часто цикл for называют циклом со счетчиком. Этот цикл используется, когда число повторений не связано с тем, что происходит в теле цикла. Т.е. количество повторений может быть вычислено заранее (хотя оно не вычисляется).
В заголовке цикла указываются два значения. Первое значение присваивается так называемой переменной-счетчику, от этого значения начинается отсчет количества итераций (повторений). Отсчет идет всегда с шагом равным единице. Второе значение указывает, при каком значении счетчика цикл должен остановиться. Другими словами, количество итераций цикла определяется разностью между вторым и первым значением плюс единица. В Pascal тело цикла не должно содержать выражений, изменяющих счетчик.
Цикл for существует в двух формах:
Счетчик – это переменная любого из перечисляемых типов (целого, булевого, символьного, диапазонного, перечисления). Начальные и конечные значения могут быть представлены не только значениями, но и выражениями, возвращающими совместимые с типом счетчика типы данных. Если между начальным и конечным выражением указано служебное слово to, то на каждом шаге цикла значение параметра будет увеличиваться на единицу. Если же указано downto, то значение параметра будет уменьшаться на единицу.
Количество итераций цикла for известно именно до его выполнения, но не до выполнения всей программы. Так в примере ниже, количество выполнений цикла определяется пользователем. Значение присваивается переменной, а затем используется в заголовке цикла. Но когда оно используется, циклу уже точно известно, сколько раз надо выполниться.
Цикл while
Цикл while является циклом с предусловием. В заголовке цикла находится логическое выражение. Если оно возвращает true, то тело цикла выполняется, если false – то нет.
Когда тело цикла было выполнено, то ход программы снова возвращается в заголовок цикла. Условие выполнения тела снова проверяется (находится значение логического выражения). Тело цикла выполнится столько раз, сколько раз логическое выражение вернет true. Поэтому очень важно в теле цикла предусмотреть изменение переменной, фигурирующей в заголовке цикла, таким образом, чтобы когда-нибудь обязательно наступала ситуация false. Иначе произойдет так называемое зацикливание, одна из самых неприятных ошибок в программировании.
Цикл repeat
Цикл while может не выполниться ни разу, если логическое выражение в заголовке сразу вернуло false. Однако такая ситуация не всегда может быть приемлемой. Бывает, что тело цикла должно выполниться хотя бы один раз, не зависимо оттого, что вернет логическое выражение. В таком случае используется цикл repeat – цикл с постусловием.
В цикле repeat логическое выражение стоит после тела цикла. Причем, в отличие от цикла while, здесь всё наоборот: в случае true происходит выход из цикла, в случае false – его повторение.
В примере, даже если n будет равно 0, одна звездочка все равно будет напечатана.
11. Типовые алгоритмы табулирования
функций, вычисления количества, суммы и произведения
Итак, основное назначение циклов — обработка большого
объема данных. Математически эта обработка зачастую сводится к поиску, выбору и
статистической обработке нужных величин. Практически в любой реальной задаче мы
ищем максимальные и минимальные значения в наборе данных, суммируем или перемножаем
требуемые данные, определяем арифметическое среднее или количество элементов, отвечающих
условию. Для решения всех этих распространенных задач существуют типовые алгоритмы,
задающие правила выполнения соответствующих расчетов. Изучением этих алгоритмов
мы займемся в гл. 11 и 12.
Разумеется, настоящие задачи, встающие перед программистами,
значительно сложнее, чем приведенные далее примеры, но из типовых алгоритмов, как
из кирпичиков, строится здание любой сложной программы.
11.1. Алгоритм табулирования
Применяется для составления всевозможных таблиц, которыми
могут быть как абстрактная таблица значений математической функции, так и конкретная
таблица стоимости товара или платежей, совершенных абонентом сотового оператора.
В общем виде алгоритм можно описать так:
1.
до цикла задается начальное значение
управляющей переменной, условием выхода из цикла служит достижение управляющей переменной
конечного значения;
2.
в теле цикла на каждом шаге вычисляется
очередное значение функции, зависящее от управляющей переменной, затем формируется
строка таблицы;
3.
в конце шага цикла значение управляющей
переменной (обозначим ее x) изменяется оператором вида x:=x+d;, где d — заданный шаг по управляющей
переменной.
В качестве примера составим таблицу синусов в пределах
от 0 до π с шагом по аргументу 0.25. Обозначим аргумент как x, значение синуса от x обозначим
как y. В простейшем случае программа табулирования может выглядеть
так:
var x,y:real;
begin
writeln(‘x’:10,’sin(x)’:10);
{печать заголовка таблицы до
цикла}
x:=0; {начальное значение аргумента}
while x<=pi+1e-6 do begin
y:=sin(x); {вычисление функции}
writeln (x:10:2, y:10:2);
{печать строки таблицы}
x:=x+0.25; {шаг по x}
end;
end.
“Расширим” задачу за счет использования произвольных
границ изменения аргумента и произвольного шага, а также выполнения всех необходимых
проверок корректности. Пусть, например, требуется составить таблицу значений следующей
функции:
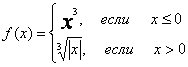
значения
a, b вводятся пользователем.
Напишем текст программы, сопроводив его соответствующими
комментариями.
var x,f,a,b,dx:real;
n:integer; {счетчик выведенных
строк}
begin
repeat {Цикл ввода с контролем
правильности значений: a,dx,b должны быть
числами, dx>0, a+dx должно быть меньше b}
writeln (‘Введите a,dx,b:’);
{$I-}read (a,dx,b);{$I+}
if IoResult <> 0 then
begin
writeln (‘Вы не ввели 3 числовых ‘,
‘значения, попробуем еще раз’);
continue;
end;
if (dx<=0) or (a+dx>=b)
then begin
writeln (‘Вы не ввели допустимые
‘,
‘данные, попробуем еще раз’);
continue;
end
else break;
until false;
{Печать заголовка таблицы}
writeln;
writeln (‘x’:10,’f(x)’:10);
x:=a;
n:=2; {2 строки уже использованы}
while x<=b+1e-6 do begin
{в условии цикла учитываем возможную
погрешность работы с real!}
if x<=0 then f:=sqr(x)*x
else f:=exp(1/3*ln(abs(x)));
{корень 3 степени взяли через
exp и ln}
writeln (x:10:2,f:10:2);
n:=n+1;
if n=24 then begin
{На экране консоли по умолчанию 25 строк}
write (‘Нажмите Enter…’);
reset (input); readln;
n:=1;
end;
x:=x+dx;
end;
writeln (‘Таблица выведена‘);
reset (input); readln;
end.
Как видно из примера, основной порядок действий — такой
же, как в предыдущей задаче. Так как экран консоли по умолчанию содержит всего 25 строк, с помощью
переменной n мы дополнительно
контролируем число уже выведенных строк и делаем по заполнении экрана паузу до нажатия
пользователем клавиши Enter.
Разумеется, другие изученные нами виды циклов также могут
применяться при табулировании. Рассмотрим в качестве примера следующую задачу.
Известна стоимость единицы товара. Составить таблицу стоимости
1, 2, …, K единиц товара, значение
K вводится.
Так как число единиц товара — заведомо целое, при программировании задачи будет удобен
цикл for:
var t:real;
i,k:integer;
begin
writeln;
writeln (‘Стоимость единицы
товара:’);
read (t);
writeln (‘Количество единиц
товара:’);
read (k);
writeln (‘Единиц’:10,’Стоимость’:10);
for i:=1 to k do
writeln (i:10,(i*t):10:2);
end.
Здесь для простоты мы исключили сделанные в предыдущем
примере проверки. Стоимость единицы товара обозначена t, переменная i необходима для
перебора возможных значений единиц товара в цикле for. Поскольку счетчик цикла for автоматически меняется с шагом 1, а оператором writeln можно выводить не только значения переменных, но и выражения,
основной цикл программы состоит из одного оператора и не нуждается в операторных
скобках.
11.2. Алгоритм организации счетчика
Этот алгоритм применяется, когда требуется подсчитать количество
элементов данных, отвечающих какому-либо условию или условиям. В общем виде алгоритм
описывается следующим образом:
1.
в разделе var описать переменную целочисленного типа, с помощью которой
будет вестись подсчет;
2.
до цикла присвоить ей начальное значение
0;
3.
в теле цикла, если очередной элемент
данных отвечает условию подсчета, увеличить эту переменную на 1 оператором вида k:=k+1;.
Необходимость присваивания начальных значений на шаге 2
этого и последующих алгоритмов связана с тем, что после описания в разделе var значение переменной еще не определено. “Пока мы не
начали подсчитывать количество, оно равно нулю” — этот очевидный для человека
факт не очевиден для компьютера! Поэтому любой переменной, которая может изменяться
в теле цикла, необходимо присвоить до цикла начальное значение, что и делает оператор
вида k:=0;.
Рассматриваемый нами алгоритм очень часто встречается в
самых различных задачах, поэтому для “быстрой” записи операции по увеличению
счетчика (она называется инкремент) или его уменьшению (декремент)
существуют специальные стандартные процедуры:
Inc(X,N); — увеличивает значение переменной.
Здесь параметр X — переменная порядкового типа, а N — переменная или выражение целочисленного типа. Значение
X увеличивается
на 1, если параметр N не определен, или
на N, если параметр N определен, то есть
Inc(X); соответствует X:=X+1;, а Inc(X,N); соответствует X:=X+N;.
Dec(X,N); — уменьшает значение переменной.
Параметр X — также
переменная порядкового типа, N — целочисленное
значение или выражение. Значение X уменьшается на 1, если параметр
N не определен,
или на N, если параметр N определен, то есть
Dec(X); соответствует X:=X-1;, а Dec(X,N); соответствует X:=X–N;.
С помощью Inc и Dec генерируется более
оптимизированный код, особенно полезный в сложных циклах. Возможно, мы будем использовать
их не во всех примерах, но вам советую о них не забывать.
В качестве примера реализации алгоритма рассмотрим следующую
задачу.
Последовательность z(i) задана
соотношениями 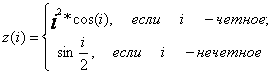
i=1,2,…,100. Найти количество элементов последовательности,
больших значения 0.5.
Обозначив искомое количество за k, составим программу:
var z:real;
i,k:integer;
begin
k:=0;
for i:=1 to 100 do
begin
if i mod 2 = 0 then
z:=sqr(i)*cos(i)
else z:=sin(i/2);
if z>0.5 then
inc(k);
end;
writeln (‘Количество=’,k);
end.
Так как шаг по переменной i равен 1, в программе
использован цикл for, для проверки того, является ли значение i четным, использована операция mod.
В следующей задаче займемся обработкой данных по мере их
ввода пользователем.
Известны оценки за экзамен по информатике для группы из
n студентов, 2≤n≤25.
Оценить количественную и качественную успеваемость группы по формулам:
,
, где k1 — количество
“троек”, “четверок” и “пятерок”, k2 —
количество только “четверок” и “пятерок”.
Для ввода текущей оценки используем целочисленную переменную
a, в качестве счетчика цикла for введем переменную i (“номер
студента”), остальные величины описаны в условии задачи. При вводе значения
n и очередного значения a для простоты
не будем контролировать корректность вводимых данных.
var a,i,n,k1,k2:integer;
ykol,ykach:real;
begin
writeln;
writeln (‘Введите количество
студентов:’);
read (n);
k1:=0;
k2:=0;
for i:=1 to n do
begin
write (‘Введите оценку ‘,i,’
студента:’);
read (a);
if a>2 then begin
inc(k1);
if a>3 then
inc(k2);
end;
end;
ykol:=k1/n*100;
ykach:=k2/n*100;
writeln
(‘Количественная успеваемость=’,ykol:6:2);
writeln
(‘Качественная успеваемость
=’,ykach:6:2);
reset (input); readln;
end.
11.3. Алгоритмы накопления суммы и произведения
Данные алгоритмы применяются, когда требуется сложить или
перемножить выбранные данные. В общем виде эти широко применяемые алгоритмы можно
описать так:
1.
для подсчета каждой суммы или произведения
описать по одной переменной того же типа, что суммируемые или перемножаемые данные;
2.
до цикла переменной-сумме присвоить
начальное значение 0, а произведению — значение 1;
3.
в теле цикла, если очередной элемент
данных t отвечает условию суммирования или перемножения, сумма накапливается
оператором вида s:=s+t;, а произведение — оператором вида p:=p*t;
Очевидно, почему начальное значение произведения — 1, а не 0. После оператора
p:=0; оператор p:=p*t;, расположенный в теле цикла, будет возвращать только нули.
Рассмотрим типовую задачу. Для функции 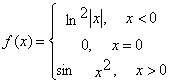
найти арифметическое среднее ее положительных
значений и произведение ненулевых значений.
Для поиска арифметического среднего необходимо сначала
найти сумму s и количество k положительных
значений функции. Составим следующую программу:
var x,f,s,p:real;
k:integer;
begin
s:=0; k:=0; p:=1;
x:=-5;
while x<=5+1e-6
do begin
if x<0 then f:=sqr(ln(abs(x)))
else if x>0 then
f:=sin(sqr(x))
else f:=0;
if f>0 then begin
s:=s+f;
k:=k+1;
end;
if f<>0 then
p:=p*f;
x:=x+0.5;
end;
s:=s/k; {теперь в s – искомое
среднее}
writeln
(‘Среднее положительных =’,s:10:6);
writeln
(‘Произведение ненулевых=’,p:10:6);
reset (input); readln;
end.
В следующей задаче также применяется алгоритм накопления
суммы.
Требуется написать программу, имитирующую работу кассового
аппарата: пользователь в цикле вводит цену очередного товара или 0 для завершения
ввода, программа суммирует цены. По завершении цикла ввода программа начисляет скидку
с общей стоимости товара по правилам: скидки нет, если общая стоимость покупки
— менее 10000 руб.; скидка равна 5%, если общая стоимость — от 10000 до 20000
руб.; скидка равна 7%, если общая стоимость — свыше 20000 руб. После начисления
скидки выводится окончательная стоимость покупки.
Обозначив общую стоимость покупки s, а цену очередного товара — t, напишем следующую программу:
var s,t:real;
begin
writeln;
s:=0; {начальное значение суммы!}
repeat
writeln (‘Введите стоимость
товара или ‘
‘0 для завершения ввода:’);
{$I-}read(t);{$I+}
if (IoResult<>0)
or (t<0) then begin
writeln (‘Ошибка! Повторите ввод’);
continue;
end;
if t=0 then break;
{Округляем t до 2 знаков после
запятой –
на случай, если есть копейки}
t:=round (t*100) / 100;
s:=s+t; {накопление суммы}
until false;
{Начисление скидки и вывод ответа}
writeln (‘Стоимость без скидки:’,s:8:2);
if s>20000 then s:=s-s*0.07
else if s>10000
then s:=s-s*0.05;
writeln (‘Стоимость со скидкой:’,s:8:2);
writeln (‘Спасибо за покупку!’);
reset (input); readln;
end.
Тип данных real выбран для s и t не случайно — выбор integer ограничил бы диапазон обрабатываемых значений и не позволил
в удобном виде ввести копейки. Проверки корректности ввода, делаемые программой,
знакомы по предыдущим примерам и поэтому не закомментированы.
Здравствуйте. Хочу поделиться алгоритмом и программной реализацией счетчика времени наработки изделия на микроконтроллере 1986BE92QI на языке Си.
Очень часто появляется необходимость отсчитывать время, отработанное некоторым устройством. Для ведения счетчика наработки необходимо периодически с определенным интервалом времени, например каждую минуту, обновлять значение, хранящееся в ячейке энергонезависимой памяти EEPROM. К сожалению, ресурс циклов записи и стирания этих ячеек памяти обычно мал и составляет около 10.000 циклов (по оценке производителя). Значит, если стирать и перезаписывать значение в одну и туже ячейку памяти с интервалом в 1 минуту, то ресурс ячейки будет израсходован примерно за неделю. Для увеличения этого времени можно использовать не одну ячейку, а все ячейки некоторой, свободной страницы памяти, например последней. Это даст нам 1024 * 10.000 запас циклов записи и стирания, что эквивалентно, примерно 19 годам при ежеминутной перезаписи значений счетчика. Или использовать даже две страницы, в зависимости от требований. В микроконтроллере 1986BE92QI доступны 32 страницы энергонезависимой памяти для записи программы и 1 страница информационной энергонезависимой памяти по 4 кбайт. Каждая страница поделена на 4 сектора (SECTOR_A, SECTOR_B, SECTOR_C, SECTOR_D). Разбитие страницы на сектора дает возможность стирать данные страницы не целиком, а поблочно по 256 четырех байтных слова в четыре этапа.
Итак, для ведения счетчика наработки можно использовать следующий алгоритм. Значение счетчика записывается в первую ячейку первого сектора (SECTOR_A). Через минуту происходит инкремент счетчика и его значение записывается во вторую ячейку первого сектора и так до конца сектора. Затем осуществляется переход на следующий сектор (SECTOR_B), но перед записью значений происходит стирание этого сектора и выполняется запись значения в первую ячейку сектора B, затем во вторую ячейку и так далее до конца страницы. Заполнение всей страницы данными происходит за 1024 минуты. Когда вся страница заполнена осуществляется переход на первый сектор SECTOR_A, он предварительно очищается, т.к. сохранившиеся там данные нам уже не нужны, ведь самые актуальные значения находятся в секторе D. И продолжается запись данных уже в первый сектор.
Каждое записываемое в ячейку памяти значение состоит из четырех байт. В первых трех байтах находится само значение счетчика минут. В четвертом байте 8 битная, посчитанная для этих трех байт контрольная сумма CRC8. Эта контрольная сумма позволяет определять испорченность записанных данных. Ниже приведена структура записываемого в память значения счетчика с тремя байтами данных uint8_t val[3] и байтом контрольной суммы uint8_t crc.
typedef struct
{
union
{
struct
{
uint8_t val[3];
uint8_t crc;
};
uint32_t value;
};
} counter_value_t;Если записанная контрольная сумма не будет совпадать с подсчитанной контрольной суммой, то это означает, что данные в данной ячейке испорчены и их использовать нельзя и необходимо взять предыдущее значение минут. Потеря одной-двух минут не будет критичной, если надо подсчитать несколько лет наработки.
Испортить записываемое значение также возможно, если произойдет отключение питания микроконтроллера во время записи в ячейку EEPROM. Наличие контрольной суммы также позволяет определять испорченные значения при записи.
При первом запуске микроконтроллер проходится последовательно по каждой ячейке памяти страницы, считывает значение счетчика и ищется максимальное не испорченное значение. С адреса следующего за этим значением продолжится ведение записи счетчика в память.
В листинге ниже представлен код на языке Си для реализации описанного алгоритма.
#include <MDR32Fx.h>
#include <stdlib.h>
#include <crc8.h>
#include <MDR32F9Qx_eeprom.h>
#include <stdint.h>
#include <MDR32F9Qx_config.h>
#include <MDR32F9Qx_eeprom.h>
// Стартовый адрес страницы для записи.
#define PAGE 0x0801F000
#define SECTORA (PAGE)
#define SECTORB (PAGE + 0x04)
#define SECTORC (PAGE + 0x08)
#define SECTORD (PAGE + 0x0C)
// Кол-во секторов в странице
#define SECTORS 4
// Кол-во 32 битных слов в странице
#define WORDS 256
// EEPROM Bank Selector
#define BANK_SELECT EEPROM_Main_Bank_Select
#define EEPROM_REG_ACCESS_KEY ((uint32_t)0x8AAA5551)
#define DELAY_LOOP_CYCLES (8UL)
#define GET_US_LOOPS(N) ((uint32_t)((float)(N) * FLASH_PROG_FREQ_MHZ / DELAY_LOOP_CYCLES))
#pragma anon_unions
typedef struct
{
union
{
struct
{
uint8_t val[3]; // Значение счетчика
uint8_t crc; // Контрольная сумма
};
uint32_t value;
};
} counter_value_t;
typedef enum {
RC_OK = 0,
RC_EMPTY = 1,
RC_CRCERR = 2
}rc_mem_t;
const uint32_t sectors[4]={
SECTORA,
SECTORB,
SECTORC,
SECTORD
};
uint32_t last_eeprom_word = 0; // Последнее прочитанное значение
uint32_t eeprom_word = 0; // Текущее прочитанное значение
uint32_t sector = 0; // Текущий сектор
uint32_t position = 0; // Текущая позиция в секторе
/**----------------------------------------------------------------------------
* @brief Program delay.
* @param loops: Number of the loops.
* @retval None.
*/
__RAMFUNC static void ProgramDelay(uint32_t loops)
{
volatile uint32_t i = loops;
for (; i > 0; i--)
{
}
}
/**-----------------------------------------------------------------------------
* @brief Стирание одного сектора.
* @param adress: начальный адрес сектора.
* @param bankSelector: выбранный банк памяти.
* @retval None.
*/
__RAMFUNC void EEPROM_EraseSector(uint32_t address, uint32_t bankSelector)
{
uint32_t Command;
assert_param(IS_EEPROM_BANK_SELECTOR(BankSelector));
MDR_EEPROM->KEY = EEPROM_REG_ACCESS_KEY;
Command = (MDR_EEPROM->CMD & EEPROM_CMD_DELAY_Msk) | EEPROM_CMD_CON;
Command |= (bankSelector == EEPROM_Info_Bank_Select) ? EEPROM_CMD_IFREN : 0;
MDR_EEPROM->CMD = Command;
MDR_EEPROM->ADR = address; // Page Address
MDR_EEPROM->DI = 0;
Command |= EEPROM_CMD_XE | EEPROM_CMD_ERASE;
MDR_EEPROM->CMD = Command;
ProgramDelay(GET_US_LOOPS(5)); // Wait for 5 us
Command |= EEPROM_CMD_NVSTR;
MDR_EEPROM->CMD = Command;
ProgramDelay(GET_US_LOOPS(40000)); // Wait for 40 ms
Command &= ~EEPROM_CMD_ERASE;
MDR_EEPROM->CMD = Command;
ProgramDelay(GET_US_LOOPS(5)); // Wait for 5 us
Command &= ~(EEPROM_CMD_XE | EEPROM_CMD_NVSTR);
MDR_EEPROM->CMD = Command;
ProgramDelay(GET_US_LOOPS(1)); // Wait for 1 us
Command &= EEPROM_CMD_DELAY_Msk;
MDR_EEPROM->CMD = Command;
MDR_EEPROM->KEY = 0;
}
/**-----------------------------------------------------------------------------
* @brief Получение значения.
* @param adress: адресс ячеки для чтения.
* @param bankSelector: выбранный банк памяти.
* @param value: указатель на переменную для чтения значения из памяти.
* @retval Результат операции.
*/
rc_mem_t GetWord(uint32_t address, uint32_t bankSelector, uint32_t * value)
{
rc_mem_t ret = 0;
counter_value_t count;
uint8_t crc = 0;
address -= address % 4;
__disable_irq();
count.value = EEPROM_ReadWord (address, bankSelector);
__enable_irq();
crc = getCRC8byTable( count.val, 3);
if (count.value == 0xFFFFFFFF)
ret = RC_EMPTY;
else if (count.crc != crc)
ret = RC_CRCERR;
else
{
ret = RC_OK;
*value = count.value & 0x00FFFFFF;
}
return ret;
}
/**-----------------------------------------------------------------------------
* @brief Запись значения в память.
* @param adress: адресс ячеки для записи.
* @param bankSelector: выбранный банк памяти.
* @param value: значение для записи в ячейку памяти.
* @retval Результат операции.
*/
void SetWord(uint32_t address, uint32_t bankSelector, uint32_t value)
{
counter_value_t count;
address -= address%4;
memcpy( count.val, &value, 3);
count.crc = getCRC8byTable( count.val, 3);
__disable_irq();
EEPROM_ProgramWord ( address, bankSelector, count.value);
__enable_irq();
}
/**-----------------------------------------------------------------------------
* @brief Ведение счетчика.
* @param Нет.
* @retval Нет.
*/
void Moto()
{
static uint8_t isFirst = 1;
uint32_t i = 0;
rc_mem_t ret = 0;
// поиск текущего сектора
for (i = sector, last_eeprom_word = 0; i < 4; i++)
{
ret = GetWord(sectors[i], BANK_SELECT, &eeprom_word);
if ( ret == RC_EMPTY || ret == RC_CRCERR || eeprom_word < last_eeprom_word)
break;
else
{
sector = i;
last_eeprom_word = eeprom_word;
}
}
// поиск текущей позиции в секторе
for (i = 0; i < WORDS; i++)
{
ret = GetWord(sectors[sector] + i * 16, BANK_SELECT, &eeprom_word);
if (ret == RC_EMPTY)
break;
else if (ret != RC_EMPTY)
last_eeprom_word = eeprom_word + 1;
}
position = i;
if (isFirst)
{
isFirst = 0;
return;
}
// стираем следующий сектор, если начинать сначала
if (position == WORDS)
{
position = 0;
sector++;
if(sector == SECTORS )
sector = 0;
__disable_irq();
EEPROM_EraseSector(sectors[sector], BANK_SELECT);
__enable_irq();
}
// записываем значение + 1
SetWord(sectors[sector] + position * 16, BANK_SELECT, last_eeprom_word);
}
/**----------------------------------------------------------------------------
* @brief Получение значения.
* @param Нет.
* @retval Значение счетчика.
*/
uint32_t GetMoto()
{
return last_eeprom_word;
}
/**-----------------------------------------------------------------------------
* @brief Установка значения счетчика.
* @param value: Значение счетчика.
* @retval Нет.
*/
void SetMoto(uint32_t value)
{
__disable_irq();
EEPROM_ErasePage (PAGE, BANK_SELECT);
__enable_irq();
sector = 0;
position = 0;
last_eeprom_word = value;
SetWord(sectors[sector] + position * 16, BANK_SELECT, value);
}
Стоит обратить внимание, что при записи в EEPROM блокируются прерывания. Это может быть довольно критичным недостатком для приложений, в которых реализованы различные защиты на других прерываниях, например, прерываниях по компаратору.
Данная реализация счетчика содержит только минимальный необходимый набор проверок и контроля ошибок и не претендует на максимальную полноту охвата решаемой проблемы. Можно придумать и добавить дополнительные проверки, например, проверку сохраненного значения в памяти непосредственно после записи и т.д.
И, на всякий случай, реализация алгоритма вычисления контрольной суммы CRC8 табличным методом.
#include <stdint.h>
const uint8_t crc8tab[256] =
{
0x00, 0x31, 0x62, 0x53, 0xC4, 0xF5, 0xA6, 0x97,
0xB9, 0x88, 0xDB, 0xEA, 0x7D, 0x4C, 0x1F, 0x2E,
0x43, 0x72, 0x21, 0x10, 0x87, 0xB6, 0xE5, 0xD4,
0xFA, 0xCB, 0x98, 0xA9, 0x3E, 0x0F, 0x5C, 0x6D,
0x86, 0xB7, 0xE4, 0xD5, 0x42, 0x73, 0x20, 0x11,
0x3F, 0x0E, 0x5D, 0x6C, 0xFB, 0xCA, 0x99, 0xA8,
0xC5, 0xF4, 0xA7, 0x96, 0x01, 0x30, 0x63, 0x52,
0x7C, 0x4D, 0x1E, 0x2F, 0xB8, 0x89, 0xDA, 0xEB,
0x3D, 0x0C, 0x5F, 0x6E, 0xF9, 0xC8, 0x9B, 0xAA,
0x84, 0xB5, 0xE6, 0xD7, 0x40, 0x71, 0x22, 0x13,
0x7E, 0x4F, 0x1C, 0x2D, 0xBA, 0x8B, 0xD8, 0xE9,
0xC7, 0xF6, 0xA5, 0x94, 0x03, 0x32, 0x61, 0x50,
0xBB, 0x8A, 0xD9, 0xE8, 0x7F, 0x4E, 0x1D, 0x2C,
0x02, 0x33, 0x60, 0x51, 0xC6, 0xF7, 0xA4, 0x95,
0xF8, 0xC9, 0x9A, 0xAB, 0x3C, 0x0D, 0x5E, 0x6F,
0x41, 0x70, 0x23, 0x12, 0x85, 0xB4, 0xE7, 0xD6,
0x7A, 0x4B, 0x18, 0x29, 0xBE, 0x8F, 0xDC, 0xED,
0xC3, 0xF2, 0xA1, 0x90, 0x07, 0x36, 0x65, 0x54,
0x39, 0x08, 0x5B, 0x6A, 0xFD, 0xCC, 0x9F, 0xAE,
0x80, 0xB1, 0xE2, 0xD3, 0x44, 0x75, 0x26, 0x17,
0xFC, 0xCD, 0x9E, 0xAF, 0x38, 0x09, 0x5A, 0x6B,
0x45, 0x74, 0x27, 0x16, 0x81, 0xB0, 0xE3, 0xD2,
0xBF, 0x8E, 0xDD, 0xEC, 0x7B, 0x4A, 0x19, 0x28,
0x06, 0x37, 0x64, 0x55, 0xC2, 0xF3, 0xA0, 0x91,
0x47, 0x76, 0x25, 0x14, 0x83, 0xB2, 0xE1, 0xD0,
0xFE, 0xCF, 0x9C, 0xAD, 0x3A, 0x0B, 0x58, 0x69,
0x04, 0x35, 0x66, 0x57, 0xC0, 0xF1, 0xA2, 0x93,
0xBD, 0x8C, 0xDF, 0xEE, 0x79, 0x48, 0x1B, 0x2A,
0xC1, 0xF0, 0xA3, 0x92, 0x05, 0x34, 0x67, 0x56,
0x78, 0x49, 0x1A, 0x2B, 0xBC, 0x8D, 0xDE, 0xEF,
0x82, 0xB3, 0xE0, 0xD1, 0x46, 0x77, 0x24, 0x15,
0x3B, 0x0A, 0x59, 0x68, 0xFF, 0xCE, 0x9D, 0xAC
};
//-----------------------------------------------------------------------------
//
// getCRC8byTable
//
// Calculation of the CRC-8
//
// Parametric model of CRC-8 algorithm:
// Name : CRC-8
// Poly : 0x31 x^8 + x^5 + x^4 + 1
// Init : 0xFF
// Revert: false
// XorOut: 0x00
// Check : 0xF7 ("123456789")
// MaxLen: 15 bytes(127 bits) - detection of single, dual,
// triple and all odd errors
//
uint8_t getCRC8byTable( uint8_t* arr, uint16_t len )
{
uint8_t crc8 = 0xff;
unsigned int i;
for( i = 0; i< len; i++)
{
crc8 = crc8tab[ crc8 ^ arr[i] ];
}
return crc8;
}
//-----------------------------------------------------------------------------
//
// getCRC8
//
// calculation of the CRC directly
//
// Parametric model of CRC-8 algorithm:
// Name : CRC-8
// Poly : 0x31 x^8 + x^5 + x^4 + 1
// Init : 0xFF
// Revert: false
// XorOut: 0x00
// Check : 0xF7 ("123456789")
// MaxLen: 15 bytes(127 bits) - detection of single, dual,
// triple and all odd errors
//
uint8_t getCRC8(uint8_t *pcBlock, uint16_t len )
{
uint8_t crc = 0xff;
unsigned int i;
while (len--)
{
crc ^= *pcBlock++;
for (i = 0; i < 8; i++)
crc = crc & 0x80 ? (crc << 1) ^ 0x31 : crc << 1;
}
return crc;
}