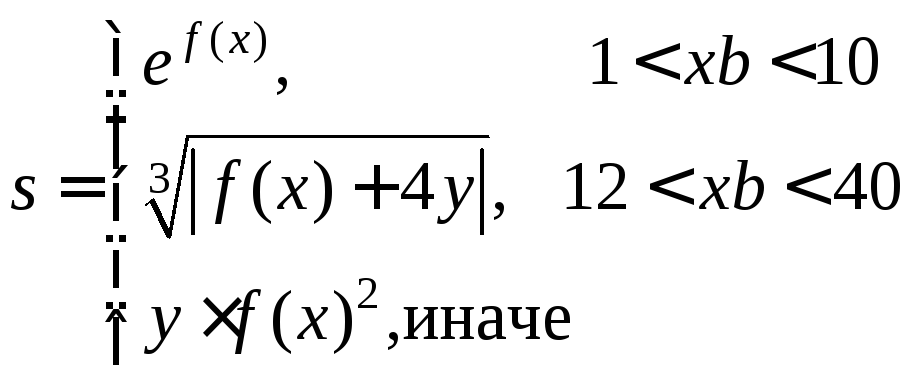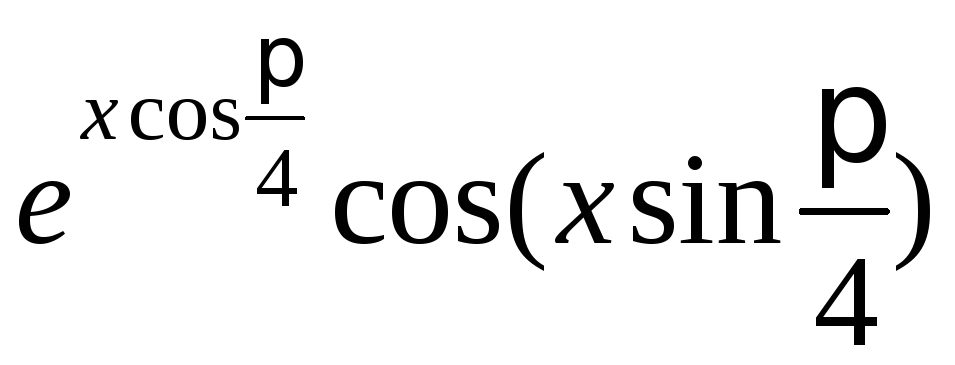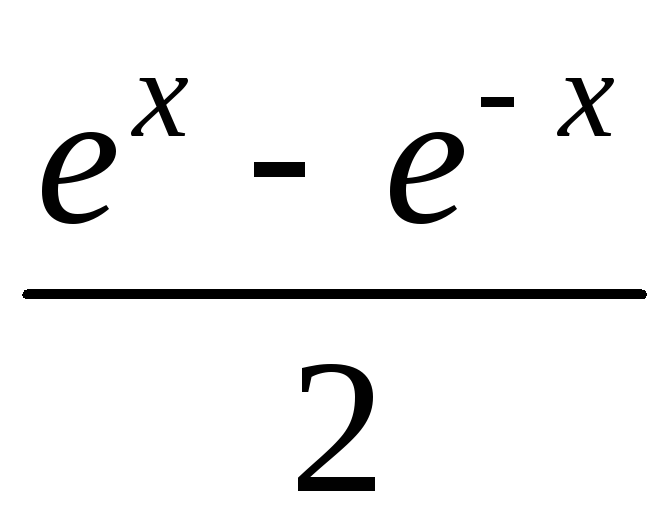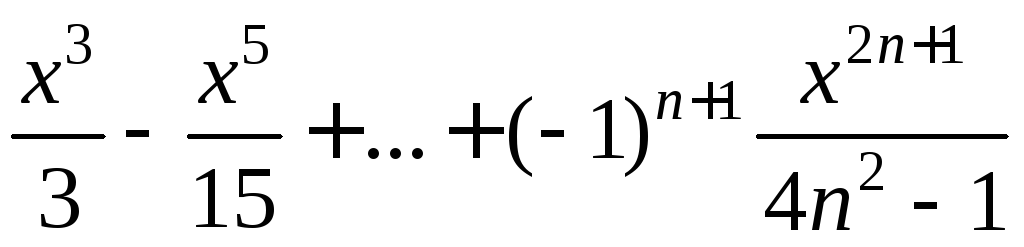Примеры составления блок-схемы алгоритма
Пример 1.
Составить схему алгоритма вычисления
значения :
![]()
Для
начала для построения блок –схемы
алгоритма опишем последовательность
действий, необходимых для решения данной
задачи:
-
начало
-
ввод
чисел a,b -
вычисление
х -
вычисление
z -
вывод
результата -
конец
Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.

Пример
2. Составить
схему алгоритма вычисления значения:
x=a+b
при a>b,
x=a*b,
при a<=b.

Пример 3. Составить схему алгоритма вычисления значения:
![]()
Для начала для
построения блок –схемы алгоритма опишем
последовательность действий, необходимых
для решения данной задачи:
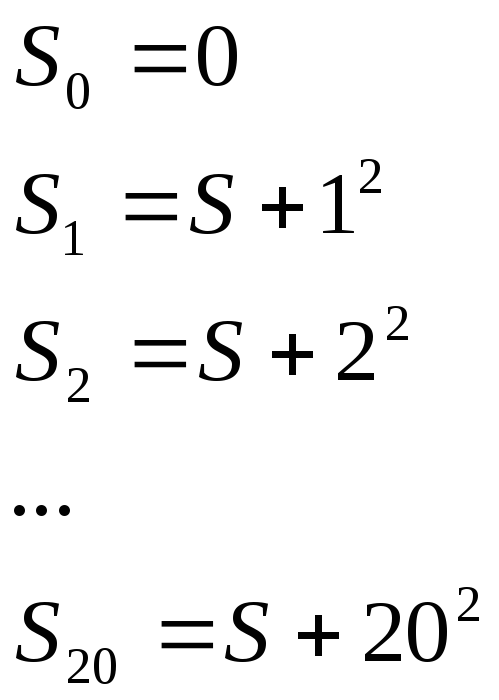
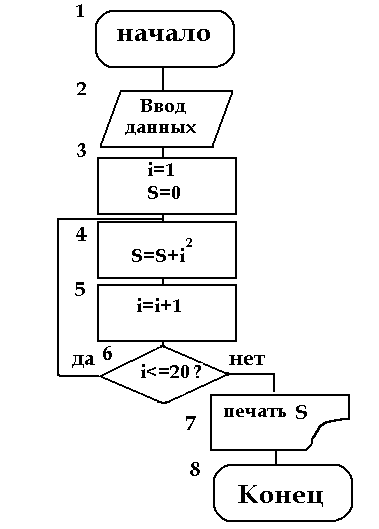
Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.
Порядок выполнения работы
-
Изучить
теоретические сведения по теме
”Построение блок-схем алгоритмов”. -
Получить
у преподавателя индивидуальное задание
и нарисовать блок-схему алгоритма
согласно заданному варианту. -
Ответить
на контрольные вопросы. -
Сформулировать
выводы.
Контрольные вопросы
-
Основные
этапы решения задач на компьютере. -
Свойства алгоритма.
Типы вычислительных процессов. -
Блок схемы. Понятие
и правила построения. -
Примеры построения
блок-схем алгоритмов.
Задание
№1: Разработайте
алгоритм и представьте его в графическом
виде (блок-схемы) для следующих задач:
Задание 1.1
Вычислить значение выражения при
заданных исходных данных.
Указание.
Для упрощения выражений введите
промежуточные переменные.
Сравнить полученное
значение с указанным правильным
результатом.
1.

При
x = 14.26;
y = – 1.22;
z = 3.5![]() ответs
ответs
= 0.749155.
2.

При
x = –4.5; y = 0.75![]() ;
;
z = –0.845![]() ответs
ответs
= –3.23765.
3.

При
x = 3.74![]() ;
;
y=–0.825; z = 0.16![]() ответs
ответs
= 1.05534.
4.

При
x = 0.4![]() ;
;
y = –0.875; z = –0.475![]() ответ
ответ
s = 1.98727.
5.

При
x = –15.246; y = 4.642![]() ;
;
z = 21 ответ
s = –182.038.
6.
![]()
При
x = 16.55![]() ;
;
y = –2.75; z = 0.15
ответ s
= –40.6307.
7.

При
x = 0.1722; y = 6.33; z = 3.25![]() ответ
ответ
s = –205.306.
8.

При
x = –2.235![]() ;
;
y = 2.23; z = 15.221
ответ s
= 39.3741.
9.

При
x = 1.825![]() ;
;
y = 18.225; z = –3.298![]() ответ
ответ
s = 1.21308.
10.
![]()
При
x = 3.981![]() ;
;
y = –1.625![]() ;
;
z = 0.512
ответ s
= 1.26185.
11.

При
x = 6.251; y = 0.827; z = 25.001
ответ
s = 0.712122.
12.
При
x
= 3.251; y
= 0.325; z
= 0.466![]()
ответ s
= 4.23655.
13.
 .
.
При
x
= 17.421; y
= 10.365![]() ;
;
z
= 0.828![]()
ответ s
= 0.330564.
14.
 .
.
При
x
= 12.3![]() ;
;
y
= 15.4; z
= 0.252![]()
ответ s
= 82.8256.
15.
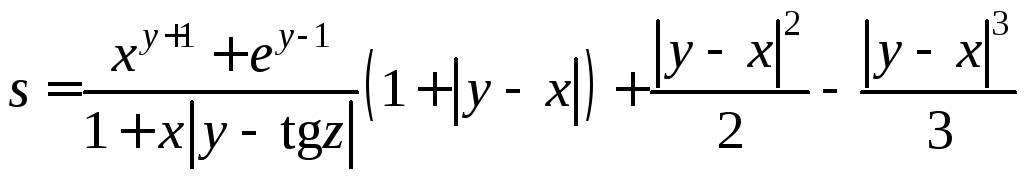 .
.
При
x
= 2.444; y
= 0.869![]() ;
;
z
= –0.13![]()
ответ s
= –0.498707.
Задание
1.2 Вычислить
значение выражения при заданных исходных
данных. Предусмотреть вывод информации
о выбранной ветви вычислений.
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
Задание
1.3 Вывести
на экран таблицу значений функции Y(x)
и ее разложения в ряд S(x)
для x,
изменяющегося от a
до b
с шагом h
= (b –
a)/10,
табл. 1.
Таблица 1.
|
№ |
a |
b |
S(x) |
n |
Y(x) |
|
1 |
0.1 |
1 |
|
160 |
|
|
2 |
0.1 |
1 |
|
100 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
3 |
0.1 |
1 |
|
120 |
|
|
4 |
0.1 |
1 |
|
80 |
|
|
5 |
0.1 |
1 |
|
140 |
|
|
6 |
0.1 |
1 |
|
80 |
|
|
7 |
0.1 |
1 |
|
120 |
|
|
8 |
0.1 |
1 |
|
100 |
|
|
9 |
0.1 |
1 |
|
140 |
|
|
10 |
0.1 |
0.5 |
|
150 |
|
|
11 |
0.1 |
1 |
|
100 |
|
|
12 |
0.1 |
1 |
|
80 |
|
|
13 |
–2 |
–0.1 |
|
160 |
|
|
14 |
0.2 |
0.8 |
|
120 |
|
|
15 |
0.1 |
0.8 |
|
180 |
|
Задание
№2:
Решите представленные ниже задачи,
указав номер задачи и полученный ответ.
Задача
2.1
Определите
результаты работы блок-схемы алгоритма
при
![]()
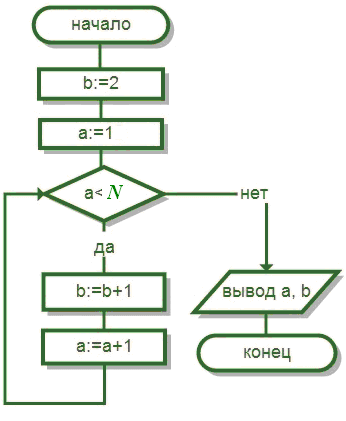
Задача
2.2
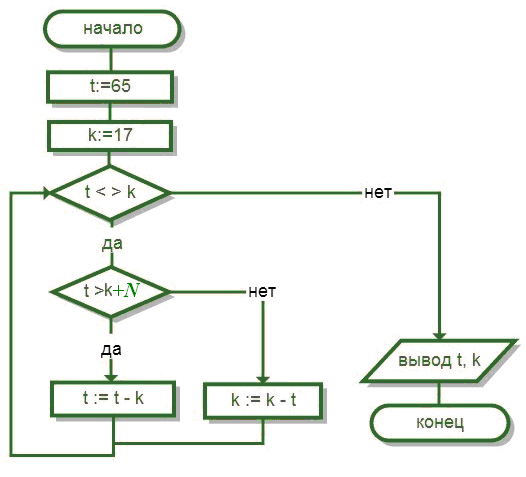
Какие
значения примут t и k в
результате работы фрагмента блок-схемы
алгоритма?
Задача
2.3.
Определите
значения
элементов
массива А2,
А4,
А6,
А8
при N=8
в результате работы фрагмента алгоритма

Содержание
- Линейный алгоритм
- Структура программы на языке Паскаль
- Заголовок программы
- Раздел описания переменных
- Тело программы
- Команды в Паскаль для ввода и вывода данных
- Команда Read
- Команда Write
- Примеры программ на паскале — задания на линейные алгоритмы
Линейный алгоритм
Линейным называется алгоритм, в котором команды выполняются последовательно друг за другом. Это самая простая конструкция. Программирование линейных алгоритмов освоить очень легко. Для написания простых программ на паскале разберем основные правила записи кода, основные команды и операторы Паскаль.
Структура программы на языке Паскаль
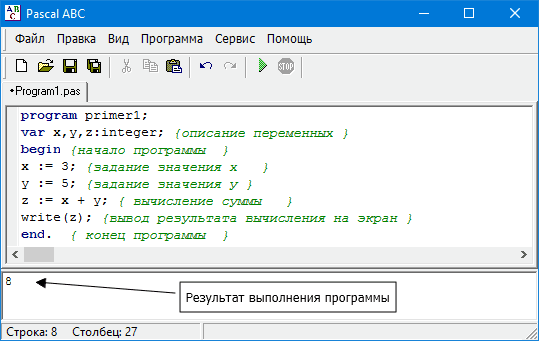
Прежде чем самостоятельно писать программы, разберем ее структуру на примере. Ниже приведен код программы, которая вычисляет сумму двух чисел и выводит ее на экран.
program primer1; var х,у,z:integer; { описание переменных } begin { начало программы } х := 3; { установка значения х } у := 5; { установка значения у } z := х + у; { вычисление суммы } write(z); {вывод результата вычисления на экран } end. { конец программы }
Заголовок программы
Текст программы начинается со слова program. После него записывается имя программы. Данная строка носит информативный характер и ее можно не писать.
Раздел подключения модулей начинается со служебного слова uses, за которым следует список имен модулей, перечисляемых через запятую.
Раздел описаний может включать разделы описания переменных, констант, меток, типов, процедур и функций, которые следуют друг за другом в произвольном порядке. Раздел подключения модулей и раздел описаний меток, констант и др. могут отсутствовать.
Раздел описания переменных
Раздел программы, обозначенный служебным словом var, содержит описание переменных с указанием их типов. Они используются для хранения исходных данных, результатов вычисления и промежуточных результатов.
Комментарии в программе можно записывать внутри фигурных скобок. Они игнорируются во время выполнения программы. Эти пояснения вы пишите только для себя.
В нашем примере переменные с именами X и Y используются для хранения исходных данных. Переменная с именем Z используется для хранения результата вычислений.
Имя переменной может записываться большими или маленькими латинскими буквами. Имя может содержать цифры, знак подчеркивания и не должно начинаться с цифры. Прописные и строчные символы считаются одинаковыми. В качестве имени нельзя использовать служебное слово языка Pascal.
Переменные одного типа можно указать в одной строке через запятую. После ставится двоеточие и указывается тип, к которому принадлежат переменные. Тип определяет допустимый диапазон значений.
Принадлежность переменной к типу integer означает, что она может хранить только целые числа. Если требуется хранить действительные (дробные) числа, тогда используется тип real.
Тело программы
Все что находится между служебными словами Begin и end — тело программы. Здесь записываются основные команды.
Оператор присваивания значений переменным имеет следующую структуру: переменная := выражение
Значок : = (двоеточие, равно) читается как «присвоить».
Умножение обозначается символом * (звездочка), деление — символом / (слеш).
Вывод результата выполняет команда write или print.
Каждая строка содержащая команду на языке Паскаль обязательно заканчивается символом «точка с запятой«.
Команды в Паскаль для ввода и вывода данных
Команда Read
В первом примере мы присвоили значения переменным непосредственно в тексте программы. Но так как программа пишется для решения множества однотипных задач, то удобнее задавать значения переменным во время ее работы. Для этого применяется команда read, которая позволяет ввести текстовые или числовые данные с клавиатуры.
Модифицируем код программы из примера выше.
program primer1; var х,у,z:integer; { описание переменных } begin { начало программы } read(x,y); { ввод значений х и y с клавиатуры } z := х + у; { вычисление суммы } write(z); {вывод результата вычисления на экран } end. { конец программы }
Теперь ввод значений переменных Х и У будет осуществляться по запросу работающей программы. В этот момент нужно будет с клавиатуры ввести два числа через пробел и нажать клавишу Enter, чтобы продолжить выполнение программы.
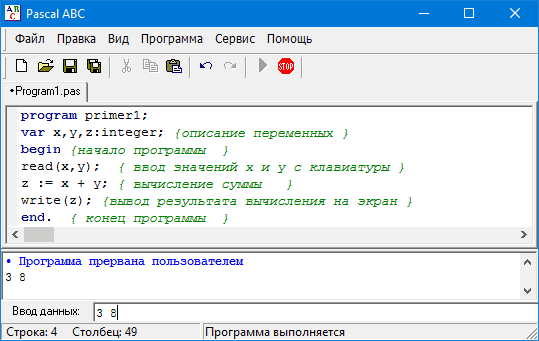
При работающей программе в системе программирования PascalABC появится строка ввода данных. Там и пишутся значения переменных.
Команда Write
В предыдущем примере, при работе программы, не совсем понятно, что нужно вводить и что за числа появляются на экране по завершению работы программы. Поэтому изменим код программы, чтобы у нее появился минимальный пользовательский интерфейс. Для этого задействуем уже знакомую нам команду Write.
program primer1; var х,у,z:integer; { описание переменных } begin { начало программы } writeln('Вычисление суммы двух чисел'); write('Введите два целых числа через пробел'); readln(x,y); { ввод значений х и y с клавиатуры } z := х + у; { вычисление суммы } write('Сумма = ',z); {вывод результата вычисления на экран } end. { конец программы }
Теперь посмотрите, как добавленные строки повлияли на работу программы.
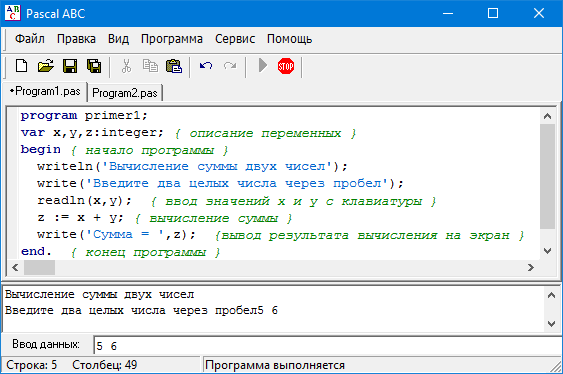
У нас появились подсказки. Посмотрите на команду write. В качестве ее аргумента был использован текст, заключенный в апострофы. И еще, появилось окончание ln у оператора write. Именно оно заставляет последующий вывод информации делать с новой строки. Это же окончание можно использовать совместно с оператором read.
Readln и Writeln в паскале — это модифицированные команды Read и Write. В командах добавлено окончание ln (line new — новая строка). Такая форма операторов делает последующий вывод информации, при работе программы, с новой строки.
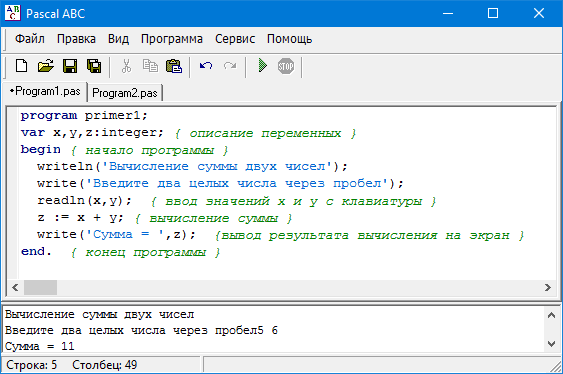
Также поменялся вывод результата. Здесь тоже появилась подсказка.
Примеры программ на паскале — задания на линейные алгоритмы
Задание 1. Модифицировать программу так, чтобы она вычисляла и выводила на экран сумму и произведение трех целых чисел.
Решение:
program zadanie1; var х,у,k,z,p:integer; { описание переменных } begin { начало программы } writeln('Вычисление суммы и произведения трех чисел'); write('Введите три целых числа через пробел'); readln(x,y,k); { ввод значений х,y,k с клавиатуры } z := x + y + k; { вычисление суммы } p := x * y * k; { вычисление произведения } write('Сумма = ',z); {вывод результата сложения на экран } write('Произведение = ',p); {вывод результата произведения на экран } end. { конец программы }
Задание 2. Дана длина ребра куба а. Найти объем куба V=a3 и площадь его поверхности S=6a2.
Решение:
program zadanie2; var a,v,s:real; { описание переменных } begin { начало программы } writeln('Вычисление объема и площади поверхности куба'); write('Введите длину ребра куба'); readln(a); { ввод значения a с клавиатуры } v := a * a * a; { вычисление объема } s := 6 * a * a; { вычисление площади } write('Объем куба = ',v); {вывод результата объем куба } write('Площадь поверхности = ',s); {вывод результата площадь поверхности } end. { конец программы }
Посмотрите еще примеры линейных алгоритмов.
Дополнительные задания:
Lin1 Введите значения для двух переменных. Обменяйте их значения, используя третью (буферную) переменную.
![]()
Хотите подробнее узнать о системе PascalABC и начать писать в ней свои первые программы, тогда статья «Знакомство с PascalABC» для вас.
Следующая тема для изучения Условный оператор
Тест “Линейный алгоритм”
Проверь свои знания по теме «Линейный алгоритм»
Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
![]() ,
,
где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.
|
Разветвляющиеся алгоритмы
Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример
ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.
Этап 1. Математическое описание решения задачи.
Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения чисел x и y. Выходным данными являются:
- наибольшее число
- любое из чисел, если числа равны
Для решения задачи нам необходимо знать значения x и y.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
|
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма
В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:
- первая: это элементы 1, 2, 3, 4, 8.
- вторая: это элементы 1, 2, 3, 5, 6, 8
- третья: это элементы 1, 2, 3, 5, 7, 8.
Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.
Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.
Циклические алгоритмы
Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.
При разработке алгоритма циклической структуры выделяют следующие понятия:
- параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
- начальное и конечное значения параметров цикла;
- шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:
- начальные значения цикла;
- конечные значения цикла;
- шаг цикла.
В тело цикла входят:
- многократно повторяющиеся действия для вычисления искомых величин;
- подготовка следующего значения параметра цикла;
- подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.
Пример
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1. Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
![]()
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.
Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
- начальное значение параметра цикла равно 1,
- конечное значение параметра цикла равно n,
- шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
S=S+i; I=I+1;
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Этап 3. Разработка алгоритма решения задачи.
Введем обозначения: S – сумма последовательности, i – значение натурального числа.
Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма. Номера элементов соответствуют номерам шагов словесного описания алгоритма.
|