Как составить алгоритм генератора

Генератор псевдослучайных чисел и генератор случайных чисел

Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.

Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.

Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.

Энтропия?—?это мера беспорядка. Информационная энтропия?—?мера неопределённости или непредсказуемости информации.

Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()

ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ?—?это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.

Придумываем свой алгоритм ГПСЧ

Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG)?—?алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:

function* rand() {
  const n = 100;
  const mod = 2;
  let i = 0;
  while (true) {
    yield i % mod;
    if (i++ > n) i = 0;
  }
}
let i = 0;
for (let x of rand()) {
 if (i++ > 100) break;
  console.log(x);
}

Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.

А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:

const vector = [...Math.PI.toFixed(48).replace('.','')];
function* rand() {
 for (let i=3; i<1000; i++) {
   if (i > 99) i = 2;
    for (let n=0; n<vector.length; n++) {
      yield (vector[n] % i);
    }
  }
}

Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9.

Мы получили генератор чисел от 0 до 9, но распределение очень неравномерное и каждый раз он будет генерировать одну и ту же последовательность.

Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:

function* rand() {
 let newNumVector = () => [...(+new Date)+''].reverse();
 let vector = newNumVector();
 let i=2;
 while (true) {
    if (i++ > 99) i = 2;
    let n=-1;
    while (++n < vector.length) yield (vector[n] % i);
    vector = newNumVector();
  }
}

// TEST:
let i = 0;
for (let x of rand()) {
  if (i++ > 100) break;
  console.log(x)
}

Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random()?—?это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.

Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них?—?это Линейный конгруэнтный ГПСЧ(LCPRNG).

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG)?—?это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой формулой. Получаемая последовательность зависит от выбора стартового числа?—?т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

const a = 45;
const c = 21;
const m = 67;
var seed = 2;
const rand = () => seed = (a * seed + c) % m;
for(let i=0; i<30; i++)
  console.log( rand() )

Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).

Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ?—?это проблема. Если говорить про другие задачи, то эти свойства?—?могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.

Еще одно свойство?—?воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.

Как устроен Math.random()

Метод Math.random() возвращает псевдослучайное число с плавающей запятой из диапазона [0, 1), то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.

Как устроен алгоритм Math.random()?—?интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:

uint32_t state0 = 1;
uint32_t state1 = 2;
uint32_t mwc1616() {
   state0 = 18030 * (state0 & 0xffff) + (state0 >> 16);
   state1 = 30903 * (state1 & 0xffff) + (state1 >> 16);
   return (state0 << 16) + (state1 & 0xffff);
}

Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.

Предсказываем Math.random()

Чем это было чревато? Есть такой квест: alf.nu/ReturnTrue

В нем есть задача:

{
	let rand = Math.random();
	function random4(x) {
	    return rand === x;
	}
}

random4(???)

Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:

random4(function(){var A=18030,B=36969,F=65535,Z=16,M=Math,I=M.imul,c=M.random,M=M.pow(2,32),k,d,g=c()*M,h=c()*M;for(k=0;F^k&&(c=I(A,g>>>Z)+k++)&F^h>>>Z;);for(k=0;F^k&&(d=I(B,g&F)+k++)&F^h&F;);for(k=2;k—;g=c<<Z|d&F)c=c/A|c%A<<Z,d=d/B|d%B<<Z;return(g<0?g+M:g)/M}())

Этот код работал в 70% случаев для Chrome < 49 и Node.js < 5. Рома Дворнов, как всегда, показал чудеса магии, которая не что иное, как глубокое понимание внутренних механизмов браузеров. Я все жду, когда Роман сделает доклад на основе этих событий или напишет более подробную статью.

Что здесь происходит? Все дело в том, что алгоритм можно предсказать. Чтобы это было нагляднее, можно сгенерировать картинку случайных пикселей. На сайте есть такой генератор. Вот что было, когда в браузере был алгоритм MWC1616:

Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие?—?числа можно предсказать.

Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.

Новый алгоритм выглядит так:

uint64_t state0 = 1;
uint64_t state1 = 2;
uint64_t xorshift128plus() {
   uint64_t s1 = state0;
   uint64_t s0 = state1;
   state0 = s0;
   s1 ^= s1 << 23;
   s1 ^= s1 >> 17;
   s1 ^= s0;
   s1 ^= s0 >> 26;
   state1 = s1;
   return state0 + state1;
}

Его все так же можно будет просчитать и предсказать. Но пока у нас нет “длинной математики” в JS. Можно попробовать через TypedArray сделать или использовать специальные библиотеки. Возможно кто-то однажды снова напишет предсказатель. Возможно это будешь ты, читатель. Кто знает 😉

Сrypto Random Values

Метод Math.random() не предоставляет криптографически стойкие случайные числа. Не используйте его ни для чего, связанного с безопасностью. Вместо него используйте Web Crypto API (API криптографии в вебе) и более точный метод window.crypto.getRandomValues().

Пример генерации случайного числа:

let [rvalue] = crypto.getRandomValues(new Uint8Array(1));
console.log( rvalue )

Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).

Я работаю программистом в игровой студии IT Territory, а с недавних пор перешел на направление экспериментальных проектов, где мы проверяем на прототипах различные геймплейные гипотезы. И работая над одним из прототипов мы столкнулись с задачей генерации случайных чисел. Я хотел бы поделиться с вами полученным опытом: расскажу о псевдогенераторах случайных чисел, об альтернативе в виде хеш-функции, покажу, как её можно оптимизировать, и опишу комбинированные подходы, которые мы применяли в проекте.

Случайными числами пользовались с самого зарождения математики. Сегодня их применяют во всевозможных научных изысканиях, при проверке математических теорем, в статистике и т.д. Также случайные числа широко используются в игровой индустрии для генерирования 3D-моделей, текстур и целых миров. Их применяют для создания вариативности поведения в играх и приложениях. 

Есть разные способы получения случайных чисел. Самый простой и понятный — это словари: мы предварительно собираем и сохраняем набор чисел и по мере надобности берём их по очереди. 

К первым техническим способам получения случайных чисел можно отнести различные генераторы с использованием энтропии. Это устройства, основанные на физических свойствах, например, емкости конденсатора, шуме радиоволн, длительности нажатия на кнопку и так далее. Хоть такие числа действительно будут случайными, у таких способов отсутствует важный критерий — повторяемость.

Сегодня мы с вами поговорим о генераторах псевдослучайных чисел — вычисляемых функциях. К ним предъявляются следующие требования:

• Длинный период. Любой генератор рано или поздно начинает повторяться, и чем позже это случится, тем лучше, тем непредсказуемее будет результат.

• Портируемость алгоритма на различные системы. 

• Скорость получения последовательности. Чем быстрее, тем лучше. 

• Повторяемость результата. Это очень важный показатель. От него зависят все компьютерные игры, которые используют генераторы миров и различные системы с аналогичной функциональностью. Воспроизводимость даёт нам общий контент для всех, то есть мы можем генерировать на отдельных клиентах одинаковое содержимое. Также мы можем генерировать контент на лету в зависимости от входных данных, например, от местоположения игрока в мире. Ещё повторяемость случайных чисел используется для сохранения конкретного контента в виде зерна. То есть мы можем держать у себя только какое-то число или массив чисел, на основе которых будут генерироваться нужные нам параметры для заранее отобранного контента.

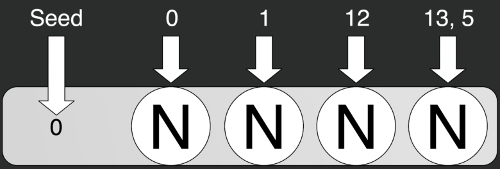
Зерно

Зерно — это основа генерирования. Оно представляет собой число или вектор чисел, который мы отправляем при инициализации генератора. 

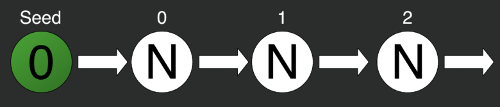
var random = new Random(0);
var rn0 = random.Next();
var rn1 = random.Next();
var rn2 = random.Next();

На иллюстрации просто инициализирован стандартный генератор случайных чисел из стандартной библиотеки C#. При инициализации отправляем в него некоторое число — seed (зерно), — в данном случае это 0. Затем по очереди берём по одному числу методом Next. Но тут мы столкнёмся с первой проблемой: генерирование всегда будет последовательным. Мы не можем получить сразу i-тый элемент последовательности. Для получения второго элемента последовательности необходимо сначала задать зерно, потом вычислить нулевой элемент, за ним первый и только потом уже второй, третий и i-й. 

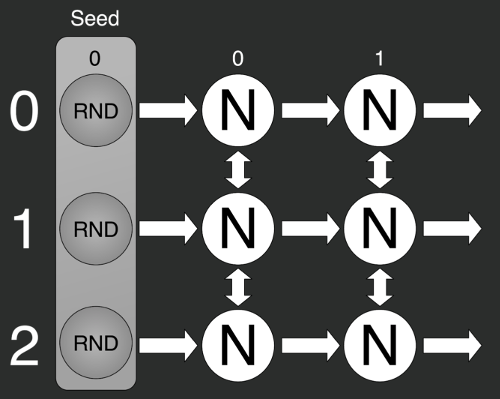
Решить эту проблему можно будет с помощью разделения одного генератора на несколько отдельных. 

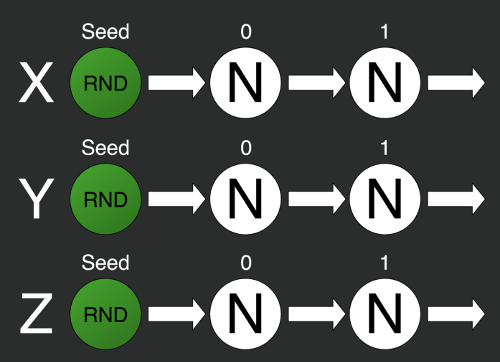
var X = 0;
var Y = 1;
var Z = 2;

var rs0 = new Random(X);
var rs1 = new Random(Y);
var rs2 = new Random(Z);

То есть берём несколько генераторов и задаём им разные зёрна. Но тут мы можем столкнуться со второй проблемой: нельзя гарантировать случайность i-тых элементов разных последовательностей с разными зёрнами. 

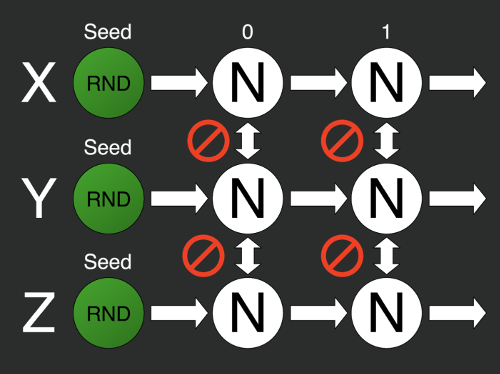
На иллюстрации изображён результат генерирования нулевого элемента последовательности с помощью стандартной библиотекой C#. Мы постепенно меняли зерно от 0 до N. 

Качество генератора

Предлагаю оценивать качество генератора с помощью изображений разного типа. Первый тип — это просто сгенерированная последовательность, который мы визуализируем с помощью первых трёх байтов полученного числа, конвертированных в RGB-представление. 

private static uint GetBytePart(uint i, int byteIndex)
{
   return ((i >> (8 * byteIndex)) % 256 + 256) % 256;
}

public static Color GetColor(uint i)
{
   float r = GetBytePart(i, 0) / 255f;
   float g = GetBytePart(i, 1) / 255f;
   float b = GetBytePart(i, 2) / 255f;
   return new Color(r, g, b);
}

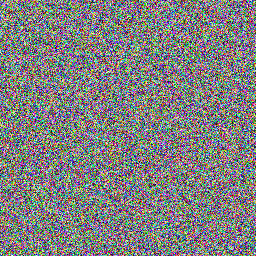
Второй тип изображений — это пространственная интерпретация сгенерированной последовательности. Мы берём первые два бита числа (Х и Y), затем считаем количество попаданий в заданные точки и при визуализации вычитаем из 1 отношение количества попаданий в конкретный пиксель к максимальному количеству попаданий в какой-то другой пиксель. Черные пиксели — это точка, куда мы попадаем чаще всего, а белые — куда мы либо почти, либо совсем не попали. 

var max = 0;
for (var i = 0; i < ints.Length; i += 2)
{
   var x = GetBytePart(ints[i], ByteIndex);
   var y = GetBytePart(ints[i + 1], ByteIndex);
   var value = coords[x, y];
   value++;
   max = Mathf.Max(value, max);
   coords[x, y] = value;
}

Сравнение генераторов

Стандартные средства C#

Ниже я сравнил стандартный генератор из библиотеки С# и линейную последовательность. Первый столбец слева — это случайная последовательность от 0 до N в рамках одного зерна. В центре вверху показаны нулевые элементы случайных последовательностей при разных зёрнах от 0 до N. Вторая линейная последовательность — это числа от 0 до N, которые я визуализировал нашим алгоритмом. 

В рамках одного зерна генератор действительно создаёт случайное число. Но при этом для i-тых элементов последовательностей с разным зерном прослеживается паттерн, который схож с паттерном линейной последовательности. 

Линейный конгруэнтный генератор (LCG)

Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом. 

const long randMax = 4294967296;
state = 214013 * state + 2531011;
state ^= state >> 15;
return (uint) (state % randMax);

При генерировании с одним зерном паттерн нигде не образуется. Но при использовании i-тых элементов в последовательностях с различными зёрнами паттерн начинает прослеживаться. Причём его вид будет зависеть исключительно от коэффициентов, которые мы подобрали для генератора. Например, есть частный случай линейного конгруэнтного генератора — Randu. 

const long randMax = 2147483648;
state = 65539 * state + 0;
return (uint) (state % randMax);

Этот генератор страшен тем, что умножает одно большое число на другое и берёт остаток от деления на 2³¹. В результате формируется вот такая красивая картинка. 

XorShift

Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.

state ^= state << 13;
state ^= state >> 17;
state ^= state << 5;
return state;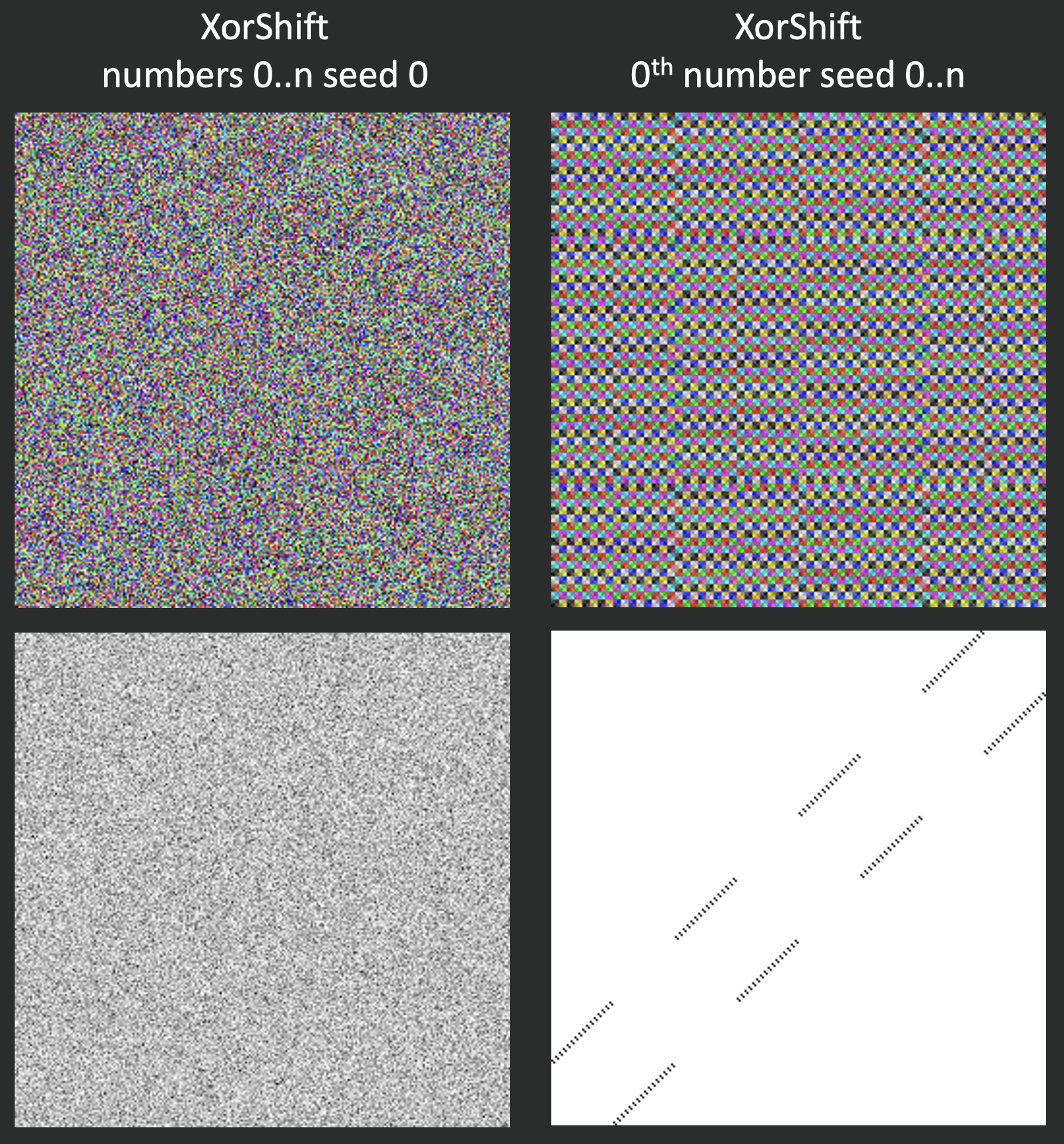

Вихрь Мерсенна

Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно. Однако и сложность этого алгоритма достаточно велика, в двух словах его не объяснить.

ulong x;
 if (mti >= NN)
 {
  // generate NN words at one time
  for (var i = 0; i < NN - MM; i++)
  {
   x = (mt[i] & UM) | (mt[i + 1] & LM);
   mt[i] = mt[i + MM] 
           ^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
  }
  for (var i = NN - MM; i < NN - 1; i++)
  {
   x = (mt[i] & UM) | (mt[i + 1] & LM);
   mt[i] = mt[i + (MM - NN)] 
           ^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
  }
  x = (mt[NN - 1] & UM) | (mt[0] & LM);
  mt[NN - 1] = mt[MM - 1] 
               ^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
  mti = 0;
 }
 x = mt[mti++];
 x ^= (x >> 29) & 0x5555555555555555L;
 x ^= (x << 17) & 0x71d67fffeda60000L;
 x ^= (x << 37) & 0xfff7eee000000000L;
 x ^= x >> 43;
 return x;

Unity — Random

Из других разработок стоит упомянуть генератор от компании Unity — Random, который используется в наборе стандартных библиотек для работы с Unity. При использовании первых элементов последовательности для разных зёрен у него будет прослеживаться паттерн, но при увеличении индекса паттерн исчезает и получается действительно случайная последовательность. 

Перемешанный конгруэнтный генератор (PCG)

Противоположностью юнитёвского Random’a является перемешанный конгруэнтный генератор. Его особенность в том, что для первых элементов с различными зёрнами отсутствует ярко выраженный паттерн. Но при увеличении индекса он всё же возникает.

Длительность последовательного генерирования

Это важная характеристика генераторов. В таблице приведена длительность для алгоритмов в миллисекундах. Замеры проводились на моём MacBook Pro 2019 года. 

Вихрь Мерсенна работает дольше всего, но даёт качественный результат. Стандартный генератор Random из библиотеки C# подходит для задач, в которых случайность вторична и не имеет какой-то значимой роли, то есть его можно использовать в рамках одного зерна. LCG (линейный конгруэнтный генератор) — это уже более серьёзный алгоритм, но требуется время на подбор нужных коэффициентов, чтобы получить адекватный паттерн. XorShift — самый быстрый алгоритм из всех рассмотренных. Его можно использовать там, где нужно быстро получить случайное значение, но помните про ярко выраженный паттерн с повторяющимся значением. Unity Random и PCG (перемешанный конгруэнтный генератор) сопоставимы по длительности работы, поэтому в разных ситуациях мы можем менять их местами: для длительных последовательностей использовать Unity, а для коротких — PCG.

Альтернатива генераторам — хеш-функции

Хеш-функции (функции свёртки) по определённому алгоритму преобразуют массив входных данных произвольной длины в строку заданной длины. Они позволяют быстрее искать данные, это свойство используется в хеш-таблицах. Также для хеш-функций характерна равномерность распределения, так называемый лавинный эффект. Это означает, что изменение малого количества битов во входном тексте приведёт к лавинообразному и сильному изменению значений выходного массива битов. То есть все выходные биты зависят от каждого входного бита.

Требования к генераторам на основе хеш-функций предъявляются те же самые, что и к простым генераторам, кроме длительности получения последовательности. Дело в том, что такому генератору можно отправить на вход одновременно зерно и требуемое состояние, потому что хеш-функции принимают на вход массивы данных. 

Вот пример использования хеш-функции: можно либо создать конкретный класс, отправить туда зерно и постепенно запрашивать только конкретные состояния, либо написать статичную функцию, и отправить туда сразу и зерно, и конкретное состояние. Слева показан алгоритм работы MD5 из стандартной библиотеки C#. 

var hash = new Hash(0);
var rn0 = hash.GetHash(0);
var rn1 = hash.GetHash(1);
var rn2 = hash.GetHash(12);
var rn3 = hash.GetHash(13, 5);

var rn4 = Hash.GetHash(0, 0);
var rn5 = Hash.GetHash(0, 1);
var rn6 = Hash.GetHash(0, 12);
var rn7 = Hash.GetHash(0, 13, 5);

Сделать генератор на основе хеш-функции можно так. Непосредственно при инициализации генератора задаём зерно, увеличиваем счётчик на 1 при запросе следующего значения и выводим результат хеша по зерну и счётчику. 

class HashRandom
{ 
	private int seed; 
	private int counter;  
	public HashRandom(int seed) 
{  
	this.seed = seed; 
	} 
	public uint Next() 
	{  
	return Hash.GetHash(seed, counter++); 
	}
}

Одни из самых популярных хеш-функций — это MurMur3 и WangHash.

MurMur3 не создаёт паттернов при использованиии i-тых элементов разных последовательностей при разных зёрнах. У WangHash статистические показатели образуют заметный паттерн. Но любую функцию можно прогнать через себя два раза и получить улучшенные показатели, как это показано в правом крайнем столбце WangDoubleHash. 

Также сегодня активно развивается и набирает популярность алгоритм xxHash.

Забегая вперёд, скажу, что мы выбрали этот генератор для наших проектов и активно его используем. 

Длительность последовательного генерирования у всех хеш-функций примерно одинакова. Однако у MD5 эта характеристика заметно отличается, но не потому, что алгоритм плохой, а потому что в стандартной реализации MD5 много разных состояний, которые влияют на быстродействие алгоритма. 

Оптимизация хеш-функций

Этот инструмент создавался для других целей — свёртки целых сообщений, поэтому на вход они принимают массивы данных. Лучше оптимизировать хеш-функции для задач генерирования случайных чисел, ведь нам достаточно подать два простых числа — зерно и счётчик. 

Что нужно сделать для оптимизации:

1. Убрать функцию включения хвоста. Это операция вставки недостающих элементов в конец массива для хеш-функции. Если его длина меньше требуемой для хеширования, недостающие элементы заполняются определёнными значениями, обычно нулями. 

2. Перевести обработку данных с типа byte на тип int.

3. Избавиться от конвертирования массива byte в одно число int.

Мы можем взять такую реализацию алгоритма xxHash:

uint h32;
var index = 0;
var len = buf.Length;

if (len >= 16)
{ 
	var limit = len - 16; 
	var v1 = seed + P1 + P2; 
	var v2 = seed + P2; 
	var v3 = seed + 0; 
	var v4 = seed - P1; 

	do 
	{  
		v1 = SubHash(v1, buf, index);  
		index += 4;  
		v2 = SubHash(v2, buf, index);  
		index += 4;  
		v3 = SubHash(v3, buf, index);  
		index += 4;  
		v4 = SubHash(v4, buf, index);  index += 4; 
	} while (index <= limit); 

	h32 = Rot32(v1, 1) + Rot32(v2, 7) + Rot32(v3, 12) + Rot32(v4, 18);
}
else
{ 
	h32 = seed + P5;
}
h32 += (uint) len;

while (index <= len — 4)
{ 
	h32 += BitConverter.ToUInt32(buf, index) * P3; 
	h32 = Rot32(h32, 17) * P4; 
	index += 4;
}

while (index < len)
{ 
	h32 += buf[index] * P5; 
	h32 = Rot32(h32, 11) * P1; 
	index++;
}
h32 ^= h32 >> 15;
h32 *= P2;
h32 ^= h32 >> 13;
h32 *= P3;
h32 ^= h32 >> 16;

return h32;

И уменьшить до такой:

public static uint GetHash(int buf, uint seed)
{ 
	var h32 = seed + P5; 
	h32 += 4U; 
	h32 += (uint) buf * P3; 
	h32 = Rot32(h32, 17) * P4; 
	h32 ^= h32 >> 15; 
	h32 *= P2; 
	h32 ^= h32 >> 13; 
	h32 *= P3; 
	h32 ^= h32 >> 16; 
	return h32;
}

Здесь Р1, Р2, Р3, Р4, Р5 — стандартные коэффициенты алгоритма xxHash. 

Комбинированные подходы

Комбинированные подходы бывают двух типов:

1. Сочетание хеш-функции и генератора случайных чисел. 

2. Иерархические генераторы. 

С первым всё предельно просто: берём хеш-функцию и получаем с её помощью зёрна, которые отправляем в другие генераторы. Слева показан результат работы комбинации стандартного Random из библиотеки C#, зёрна которому мы создавали с помощью хеш-функций. 

Второй подход гораздо интереснее. Мы его используем в ситуациях, когда нам необходимо генерировать группы последовательностей, например, ботов для тестирования. 

Сначала генерируем зёрна, а затем отправляем их в генераторы ботов. Первое число, полученное из генератора, мы используем как индекс для массива из ников игроков. Второе число будет зерном для генерирования истории матчей. Третье у нас используется для генерирования истории турнира. И т.п.

В этой иерархии могут применяться разные генераторы. Например, когда нам необходимо создать какую-то короткую последовательность, мы использовали перемешанный конгруэнтный генератор. А когда нам нужно было создать длинную историю матча, то использовали генератор Unity.

Мы разобрали наиболее популярные алгоритмы генераторов псевдослучайных чисел, рассмотрели альтернативу в виде хеш-функций, узнали, как их оптимизировать и прошлись по комбинированным подходам к генерированию псевдослучайных чисел. Надеюсь, что вам это было полезно!

Алгоритм
работы и управляющая программа генератора
разрабатываются на основе решений,
принятых при анализе технического
задания и создании электрической схемы
устройства. На этом этапе разработчик
должен учитывать особенности архитектуры
микроконтроллера и его возможности.

Пример.

Согласно заданию
программируемый генератор формирует
дискретные сигналы, соответствующие
последовательности символов
*ПРИМЕР*.
Предусмотрено несколько
режимов работы устройства, сопровождающихся
соответствующей индикацией. Блок-схема
алгоритма работы генератора приведена
на рисунке 5.1.

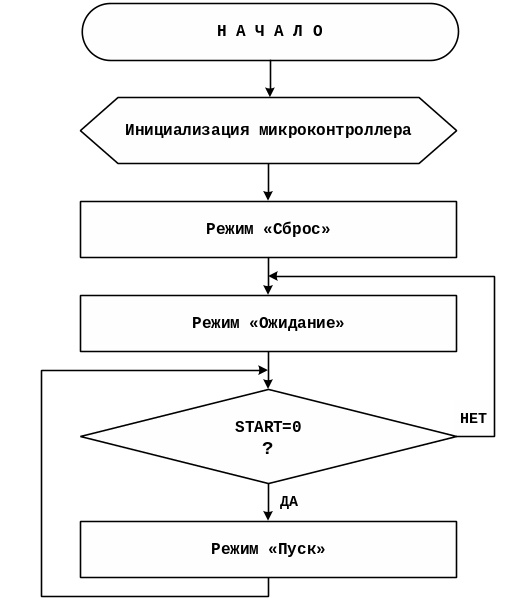
Рисунок 5.1 –
Блок-схема алгоритма работы генератора
сигналов

Микроконтроллер
выполняет управляющую программу,
размещенную во
внешней памяти программ.
Так как область младших адресов памяти
программ отведена под обработку
прерываний, основная программа размещается
по адресу 40h.

Пример
блок-схемы алгоритма работы управляющей
программы генератора приведен на рисунке
5.2.

При получении
сигнала «Reset»
генератор переходит в режим «Сброс».
Производится инициализация микроконтроллера:
загрузка начальных значений
регистров-указателей и счетчиков,
настройка системы прерываний и таймеров.
Индикация режима производится
светодиодами, подключенными к линиям
Р1.2
и
Р1.3,
поочередно зажигающимися на 0,4
с

в течение 1,6
с. Таким образом, всего
осуществляется
4
цикла
индикации, для подсчета которых
используется регистр R2.

Затем генератор
переходит в режим «Ожидание», производится
опрос сигнала «Start»,
подаваемого на линию Р1.1
микроконтроллера. Индикация режима
производится светодиодом, подключенным
к линии
Р1.4.

Если на линию Р1.1
подается уровень логического
нуля
генератор переводится в режим
«Пуск», включается таймер Т0
и начинается формирование
дискретных сигналов Q1-Q8.

Если на линии Р1.1
устанавливается уровень
логической единицы, таймер
выключается, формирование выходных
сигналов прекращается и генератор снова
переводится в режим «Ожидание».

В каждом цикле
выдачи дискретных сигналов в порт вывода
последовательно записываются 8
кодовых комбинаций.
Кодовая таблица сигналов
хранится во внешней
памяти данных
по адресу 9000h.

Кодовые комбинации
на входах порта вывода обновляются
каждые 0,1
мс.
Для обеспечения заданной длительности
используется таймер/счетчик Т0,
работающий в режиме восьмиразрядного
таймера с автоперезагрузкой. Перед
первым пуском таймера в регистр TH0
записывается число 38h,
которое автоматически
перезагружается в регистр TL0 при
переполнении таймера.
Для выбора режима работы таймера
в регистре TMOD устанавливаются
соответствующие значения битов C/T,
М0 и М1. Для включения таймера
в регистре TCON устанавливается
бит TR0.

Чтение кодовых
комбинаций из памяти, их запись в порт
вывода и организация нового цикла выдачи
сигналов выполняются при обработке
запроса прерывания от таймера Т0.
Для разрешения прерывания от таймера
Т0
необходимо
в регистре IE
установить бит ЕТ0
и снять блокировку всех прерываний,
установив бит ЕА.

Для обслуживания
прерывания таймера Т0
в ячейку памяти программ с адресом 0Вh
записывается код команды безусловного
перехода к подпрограмме обработки
прерывания
TIMER.

Чтение
кодовой таблицы производится с
использованием косвенной адресации
через регистр-указатель данных DPTR.
Регистр общего назначения R3
используется
как счетчик, для контроля
количества
кодовых комбинаций, записанных в порт
вывода. После
выдачи последней кодовой комбинации
регистр-указатель DPTR
и
регистр-счетчик
R3
загружаются
начальными значениями.

Адрес порта вывода
дискретных сигналов AB00h
принадлежит внешней памяти данных.
Запись в порт вывода текущей кодовой
комбинации производится с использованием
косвенной адресации. Порт Р2
используется для адресации старшего
байта адреса, а
регистр R0,
как регистр-указатель младшего
байта адреса.

Пример
блок-схемы алгоритма работы подпрограммы
обработки прерывания таймера приведен
на рисунке 5.3.

На
рисунке 5.4 приведены примеры блок-схем
алгоритмов работы подпрограмм формирования
временных интервалов 400, 100 и 1 мс.

В
качестве пояснения к программе укажите
в специальной таблице имена переменных,
их назначение, а так же специализацию
регистров общего назначения. Для примера
см. таблицу 5.1.

Создание
и отладка рабочей программы генератора
производится при помощи интегрированной
среды разработки программного обеспечения
Keil
mVision.

Таблица 5.1 –
Назначение переменных, меток и регистров,
используемых в программе

После
проверки работоспособности программы
и ее соответствия заданию в пояснительной
записке приводятся:

• листинг
  программы,
  содержащий результаты компиляции

(см.
файл *.lst

в
директории
проекта);

• загрузочный
  файл
  программы
  (см. файл *.hex
  
  в
  директории
  проекта).

Рисунок
5.2 – Блок-схема алгоритма работы управляющей
программы генератора

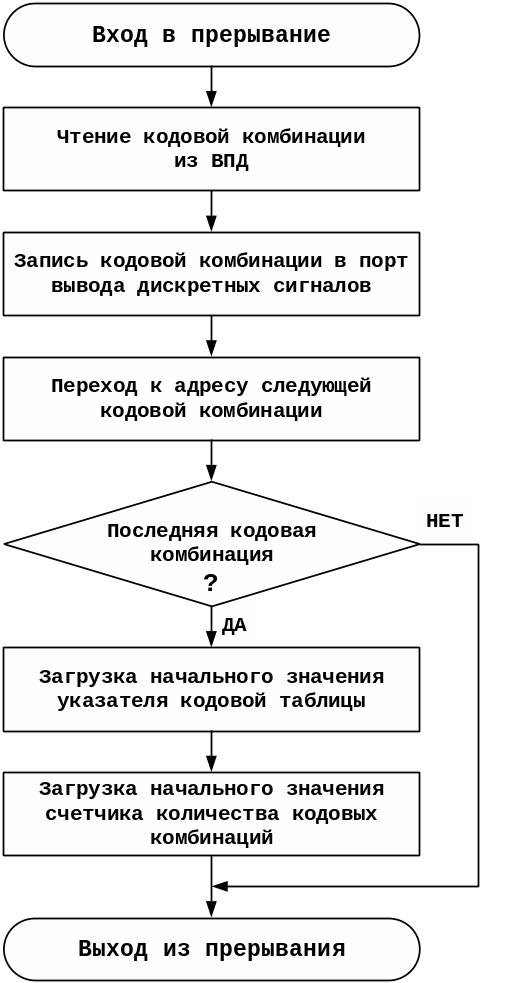
Рисунок 5.3 –
Блок-схема алгоритма работы подпрограммы
обработки прерывания таймера

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании?—?напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать?

Меня очень увлекают различные IT головоломки и задачки и генератор случайных чисел — одна из таких задачек. Обычно в своем телеграм канале я разбираю всякие головоломки и разные задачи с собеседований. Задача про генератор случайных чисел набрала большую популярность и мне захотелось увековечить ее в недрах одного из авторитетных источников информации — то бишь здесь, на Хабре.

Данный материал будет полезен всем тем фронтендерам и Node.js разработчикам, кто на острие технологий и хочет попасть в блокчейн проект/стартап, где вопросы про безопасность и криптографию, хотя бы на базовом уровне, спрашивают даже у фронтендеров.

Генератор псевдослучайных чисел и генератор случайных чисел

Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.

Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.

Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.

Энтропия?—?это мера беспорядка. Информационная энтропия?—?мера неопределённости или непредсказуемости информации.

Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()

ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ?—?это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.

Придумываем свой алгоритм ГПСЧ

Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG)?—?алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:

Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.

А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:

Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9.

Мы получили генератор чисел от 0 до 9, но распределение очень неравномерное и каждый раз он будет генерировать одну и ту же последовательность.

Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:

Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random()?—?это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.

Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них?—?это Линейный конгруэнтный ГПСЧ(LCPRNG).

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG)?—?это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой формулой. Получаемая последовательность зависит от выбора стартового числа?—?т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).

Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ?—?это проблема. Если говорить про другие задачи, то эти свойства?—?могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.

Еще одно свойство?—?воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.

Как устроен Math.random()

Метод Math.random() возвращает псевдослучайное число с плавающей запятой из диапазона [0, 1), то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.

Как устроен алгоритм Math.random()?—?интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:

Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.

Предсказываем Math.random()

Чем это было чревато? Есть такой квест: alf.nu/ReturnTrue

В нем есть задача:

Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:

Этот код работал в 70% случаев для Chrome

Введение

Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:

• Генераторы сессий(PHPSESSID)
• Генерация текста для капчи
• Шифрование
• Генерация соли для хранения паролей в необратимом виде
• Генератор паролей
• Порядок раздачи карт в интернет казино

Как отличить случайную последовательность чисел от неслучайной?

Пусть есть последовательность чисел: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Является ли она случайной? Есть строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Но оно не помогает ответить на наш вопрос, так как нам не хватает информации для ответа. Теперь скажем, что данные числа получились набором одной из верхних строк клавиатуры. «Конечно не случайная» — воскликните Вы и тут же назовете следующие число и будете абсолютно правы. Последовательность будет случайной только если между символами, нету зависимости. Например, если бы данные символы появились в результате вытягивания бочонков в лото, то последовательность была бы случайной.

Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.

Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)

Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.

Уязвимости ГПСЧ

• Предсказуемая зависимость между числами.
• Предсказуемое начальное значение генератора.
• Малая длина периода генерируемой последовательности случайных чисел, после которой генератор зацикливается.

Линейный конгруэнтный ГПСЧ(LCPRNG)

Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

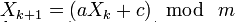
где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.

Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].

Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.

Предсказание результатов линейно-конгруэнтного метода

Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.

Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.

Взлом встроенного генератора случайных чисел в Java

Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код(jdk1.7) данного класса можно увидеть используемые константы

Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)

Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).

Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:

до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так

Вывод данной программы будет примерно таким:

Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.

И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));

И всё, мы успешно взломали ГПСЧ в Java.

Взлом ГПСЧ Mersenne twister в PHP

Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.

Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:

10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor

Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так

Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.

Область для взлома

Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.

Задание распределения для генератора псевдослучайных чисел

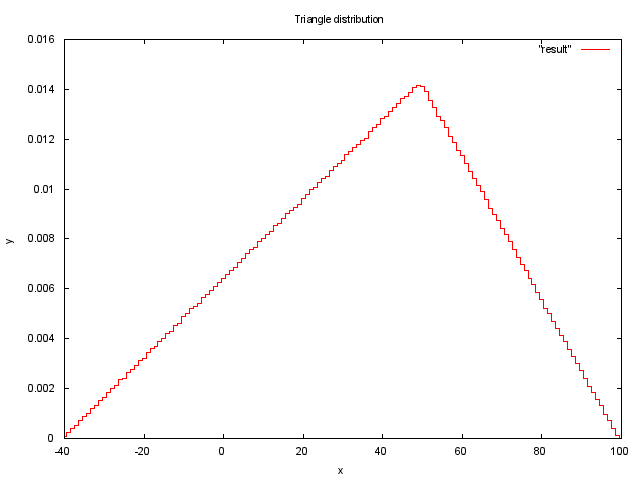
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.

Треугольное распределение

Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.

В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так

Экспоненциальное распределение

Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).

Тесты ГПСЧ

Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.

Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.

В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.

Случайные числа используются во многих алгоритма х машинного обучения. Например, распространенной задачей является выбор случайной строки матрицы. В C# код может выглядеть так:

В этой статье я покажу, как генерировать случайные числа с помощью четырех разных алгоритмов: алгоритма Лемера (Lehmer), линейного конгруэнтного алгоритма ( linear congruential algorithm), алгоритма Вичмана-Хилла (Wichmann-Hill) и алгоритма Фибоначчи с запаздываниями (lagged Fibonacci algorithm).

Но зачем обременять себя созданием собственного генератора случайных чисел (random number generator, RNG), когда в Microsoft .NET Framework уже есть эффективный и простой в использовании класс Random? Существует два сценария, где вам может понадобиться создать свой RNG. Во-первых, в разные языки программирования встроены разные алгоритмы генерации случайных чисел, а значит, если вы пишете код, который будет переноситься на несколько языков, можно создать собственный RNG, чтобы реализовать его во всех нужных вам языках. Во-вторых, некоторые языки, в частности R, имеют лишь глобальный RNG, поэтому, если вы захотите создать несколько генераторов, вам придется писать свой RNG.

Хороший способ получить представление о том, куда я клоню в этой статье, — взглянуть на демонстрационную программу на рис. 1. Демонстрационная программа начинает с создания очень простого RNGЮ используя алгоритм Лемера. Затем с помощью RNG генерируется 1000 случайных целых чисел между 0 и 9 включительно. За кулисами записываются счетчики для каждого из сгенерированных целых чисел, которые потом отображаются на экране. Этот процесс повторяется для линейного конгруэнтного алгоритма, алгоритма Вичмана-Хилла и алгоритм Фибоначчи с запаздываниями.

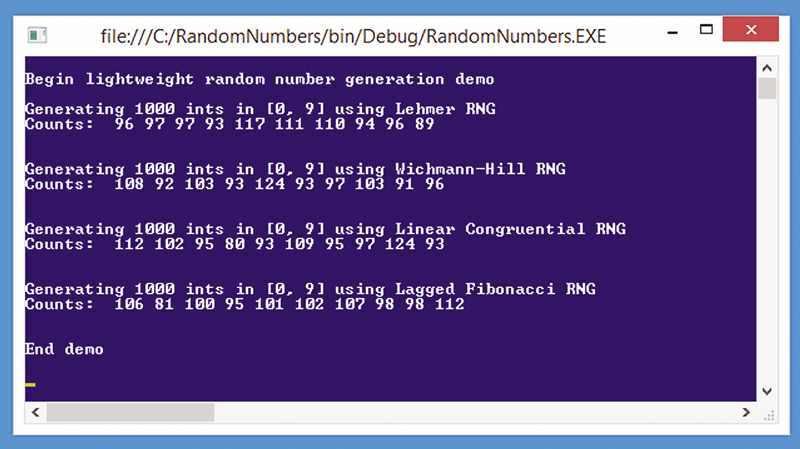
Рис. 1. Демонстрация упрощенной генерации случайных чисел

В этой статье предполагается, что вы умеете программировать хотя бы на среднем уровне, но ничего не знаете о генерации случайных чисел. Демонстрационная программа написана на C#, но, поскольку один из основных случаев использования собственной генерации случайных чисел — написание портируемого кода, эта программа разработана так, чтобы ее можно было легко транслировать на другие языки.

Алгоритм Лемера

Самый простой приемлемый метод генерации случайных чисел — алгоритм Лемера. (Для простоты я использую термин «генерация случайных чисел» вместо более точного термина «генерация псевдослучайных чисел».) Выраженный в символьном виде, алгоритм Лемера представляет собой следующее:

На словах это звучит так: «новое случайное число является старым случайным числом, умножаемым на константу a, после чего над результатом выполняется операция по модулю константы m». Например, предположим, что в некий момент текущее случайное число равно 104, a = 3 и m = 100. Тогда новое случайное число будет равно 3 * 104 mod 100 = 312 mod 100 = 12. Вроде бы просто, но в реализации этого алгоритма много хитроумных деталей.

Чтобы создать демонстрационную программу, я запустил Visual Studio, выбрал шаблон C# Console Application и назвал проект RandomNumbers. В этой программе нет значимых зависимостей от .NET Framework, поэтому подойдет любая версия Visual Studio.

После загрузки кода шаблона в окно редактора я переименовал в окне Solution Explorer файл Program.cs в более описательный RandomNumbersProgram.cs, и Visual Studio автоматически переименовала класс Program за меня. В начале кода я удалил все лишние выражения using, оставив только ссылки на пространства имен верхнего уровня System и Collections.Generic.

Затем я добавил класс с именем LehmerRng для реализации RNG-алгоритма Лемера. Код показан на рис. 2. Версия алгоритма Лемера за 1988 год использует a = 16807 и m = 2147483647 (которое является int.MaxValue). Позднее, в 1993 году Лемер предложил другую версию, где a = 48271 как чуть более качественную альтернативу. Эти значения берутся из математической теории. Демонстрационный код основан на знаменитой статье С. К. Парка (S. K. Park) и К. У. Миллера (K. W. Miller) «Random Number Generators: Good Ones Are Hard to Find».

Рис. 2. Реализация алгоритма Лемера

Проблема реализации в том, чтобы предотвращать арифметическое переполнение. Алгоритм Лемера использует ловкий алгебраический трюк. Значение q является результатом m / a (целочисленное деление), а значение r равно m % a (m по модулю a).

При инициализации RNG Лемера начальным (зародышевым) значением можно использовать любое целое число в диапазоне [1, int.MaxValue – 1]. Многие RNG имеют конструктор без параметров, который получает системные дату и время, преобразует их в целое число и использует в качестве начального значения.

RNG Лемера вызывается в методе Main демонстрационной программы:

Каждый вызов метода Next возвращает значение в диапазоне [0.0, 1.0) — больше или равно 0.0 и строго меньше 1.0. Шаблон (int)(hi – lo) * Next + lo) будет возвращать целое число в диапазоне [lo, hi–1].

Алгоритм Лемера весьма эффективен, и в простых сценариях я обычно выбираю именно его. Но заметьте, что ни один алгоритм из представленных в этой статье не обладает надежностью криптографического уровня и что их следует применять только в ситуациях, где не требуется статической строгости (statistical rigor).

Алгоритм Вичмана-Хилла

Этот алгоритм датируется 1982 годом. Идея Вичмана-Хилла заключается в генерации трех предварительных результатов и последующего их объединения в один финальный результат. Код, реализующий алгоритм Вичмана-Хилла, представлен на рис. 3. Демонстрационный код основан на статье Б. А. Вичмана (B. A. Wichmann) и А. Д. Хилла (I. D. Hill) «Algorithm AS 183: An Efficient and Portable Pseudo-Random Number Generator».

Рис. 3. Реализация алгоритма Вичмана-Хилла

Поскольку алгоритм Вичмана-Хилла использует три разных генерирующих уравнения, он требует трех начальных значений. В этом алгоритме три m-значения равны 30269, 30307 и 30323, поэтому вам понадобятся три начальных значения в диапазоне [1, 30000]. Вы могли бы написать конструктор, принимающий эти три значения, но тогда вы получили бы несколько раздражающий программный интерфейс. В демонстрации применяется параметр с одним начальным значением, генерирующим три рабочих зародыша.

Вызов RNG Вичмана-Хилла осуществляется по тому же шаблону, что и других демонстрационных RNG:

Алгоритм Вичмана-Хилла лишь немного труднее в реализации, чем алгоритм Лемера. Преимущество первого над вторым в том, что алгоритм Вичмана-Хилла генерирует более длинную последовательность (более 6 000 000 000 000 значений) до того, как начнет повторяться.

Линейный конгруэнтный алгоритм

Оказывается, и алгоритм Лемера, и алгоритм Вичмана-Хилла можно считать особыми случаями так называемого линейного конгруэнтного алгоритма (linear congruential, LC). Выраженный в виде уравнения, LC выглядит так:

Это точно соответствует алгоритму Лемера с добавлением дополнительной константы c. Включение c придает универсальному LC-алгоритму несколько лучшие статистические свойства по сравнению с алгоритмом Лемера. Демонстрационная реализация LC-алгоритма показана на рис. 4. Код основан на стандарте POSIX (Portable Operating System Interface).

Рис. 4. Реализация линейного конгруэнтного алгоритма

LC-алгоритм использует несколько битовых операций. Здесь идея в том, чтобы в базовых математических типах работать не с целым типом (32 бита), а с длинным целым (64 бита). По окончании 32 из этих битов (с 16-го по 47-й включительно) извлекаются и преобразуются в целое число. Этот подход дает более качественные результаты, чем при использовании просто 32 младших или старших битов, но за счет некоторого усложнения кодирования.

В демонстрации генератор случайных чисел LC вызывается так:

Заметьте, что в отличие от генераторов Лемера и Вичмана-Хилла генератор LC может принимать начальное значение 0. Конструктор в демонстрации LC копирует значение входного параметра seed непосредственно в член класса — поле seed. Многие распространенные реализации LC выполняют предварительные манипуляции над входным начальным значением, чтобы избежать генерации хорошо известных серий начальных значений.

Алгоритм Фибоначчи с запаздываниями

Этот алгоритм, выраженный уравнением, выглядит так:

Если на словах, то новое случайное число является тем, которое было сгенерировано 7 раз назад, плюс случайное число, сгенерированное 10 раз назад, и деленное по модулю на большое значение m. Значения (7, 10) можно изменять, как я вскоре поясню.

Допустим, что в некий момент времени последовательность сгенерированных чисел следующая:

где 561 — самое последнее из сгенерированных значений. Если m = 100, то следующим случайным числом будет:

Заметьте, что в любой момент вам всегда нужны 10 самых последних сгенерированных значений. Поэтому ключевая задача в алгоритме Фибоначчи с запаздываниями состоит в генерации начальных значений, необходимых для запуска процесса. Демонстрационная реализация алгоритма Фибоначчи с запаздываниями приведена на рис. 5.

Рис. 5. Реализация алгоритма Фибоначчи с запаздываниями

Демонстрационный код использует предыдущие случайные числа X(i–7) и X(i–10) для генерации следующего случайного числа. В научно-исследовательской литературе по этой тематике значения (7, 10) обычно обозначаются (j, k). Существуют другие пары (j, k), которые можно применять для алгоритма Фибоначчи с запаздываниями. Несколько значений, рекомендованных в хорошо известной книге «Art of Computer Programming» (Addison-Wesley, 1968), — (24,55), (38,89), (37,100), (30,127), (83,258), (107,378).

Чтобы инициализировать (j, k) в RNG Фибоначчи с запаздываниями, вы должны предварительно заполнить список значениями k. Это можно сделать несколькими способами. Однако наименьшее из начальных значений k обязательно должно быть нечетным. В демонстрации применяется грубый метод копирования значения параметра seed для всех начальных значений k с последующим удалением первой 1000 сгенерированных значений. Если значение параметра seed четное, тогда первое из значений k выставляется равным 11 (произвольному нечетному числу).

Чтобы предотвратить арифметическое переполнение, метод Next использует тип long для вычислений и математическое свойство: (a + b) mod n = [(a mod n) + (b mod n)] mod n.

Заключение

Позвольте мне подчеркнуть, что все четыре RNG, представленные в этой статье, предназначены только для некритичных случаев применения. С учетом этого я прогнал все RNG через набор хорошо известных базовых тестов на степень случайности, и они прошли эти тесты. Но даже при этом коварство RNG всем хорошо известно, и время от времени даже в стандартных RNG обнаруживаются дефекты, иногда лишь спустя годы их использования. Например, в 1960-х годах IBM распространяла реализацию линейного конгруэнтного алгоритма под названием RANDU, которая, как оказалось, обладала невероятно плохими качествами. А в Microsoft Excel 2008 была выявлена ужасно проблемная реализация алгоритма Вичмана-Хилла.

Нынешний фаворит в генерации случайных чисел — алгоритм Фортуна (Fortuna) (названный в честь римской богини удачи). Алгоритм Фортуна был опубликован в 2003 году и основан на математической энтропии плюс сложных шифровальных методах, таких как AES (Advanced Encryption System).

Джеймс Маккафри (Dr. James McCaffrey) — работает на Microsoft Research в Редмонде (штат Вашингтон). Принимал участие в создании нескольких продуктов Microsoft, в том числе Internet Explorer и Bing. С ним можно связаться по адресу [email protected]

Выражаю благодарность за рецензирование статьи экспертам Microsoft Крису Ли (Chris Lee) и Кирку Олинику (Kirk Olynyk).

В прошлый раз мы разбирались с теорией про цепи Маркова. Вот основные тезисы:

Сегодня попробуем это в деле и напишем самый простой генератор текста на цепях Маркова. Это будет похоже на работу нейросети, но на самом деле никаких «нейро» там нет — просто сети, которые сделаны на алгоритме цепей Маркова. А сеть — это просто таблица со связями между элементами. 

Короче: никакого искусственного интеллекта, просто озверевшие алгоритмы вслепую дёргают слова. 

Логика проекта

Код будем писать на Python, потому что от отлично подходит под задачи такого плана — обработка текста и построение моделей со сложными связями.

Логика будет такой:

Сделаем всё по шагам, как обычно.

Проверяем, что у нас есть Python

Python не так-то просто запустить, поэтому, если вы ещё ничего не делали на Python, прочитайте нашу статью в тему. Там всё описано по шагам. 

Разбиваем исходный текст

Для тренировки мы взяли восьмой том полного собрания сочинений Чехова — повести и рассказы. В нём примерно 150 тысяч слов, поэтому должно получиться разнообразно. Этот файл нужно сохранить как che.txt и положить в ту же папку, что и код программы.

👉 Чтобы быстро работать с большими массивами данных, будем использовать библиотеку numpy — она написана специально для биг-даты, работы с нейросетями и обработки больших матриц. Для установки можно использовать команду pip3 install numpy:

# подключаем библиотеку numpy
import numpy as np

# отправляем в переменную всё содержимое текстового файла
text = open('che.txt', encoding='utf8').read()

# разбиваем текст на отдельные слова (знаки препинания останутся рядом со своими словами)
corpus = text.split()

Генерируем пары

Для этого используем специальную команду-генератор: yield. В функциях она работает как return — возвращает какое-то значение, а нам она нужна из-за особенностей своей работы. Дело в том, что yield не хранит и не запоминает никакие значения — она просто генерирует что-то, тут же про это забывает и переходит к следующему. Именно так и работают цепи Маркова — они не запоминают все предыдущие состояния, а работают только с конкретными парами в данный момент.

👉 Мы разберём генераторы более подробно в отдельной статье, а пока просто используем их в нашем коде.

# делаем новую функцию-генератор, которая определит пары слов
def make_pairs(corpus):
    # перебираем все слова в корпусе, кроме последнего
    for i in range(len(corpus)-1):
        # генерируем новую пару и возвращаем её как результат работы функции
        yield (corpus[i], corpus[i+1])
        
# вызываем генератор и получаем все пары слов
pairs = make_pairs(corpus)

В результате мы получаем все пары слов, которые идут друг за другом — с повторениями и в том порядке, как они расположены в исходном тексте. Теперь можно составлять словарь для цепочек.

Составляем словарь

Пойдём по самому простому пути: не будем высчитывать вероятности продолжения для каждого слова, а просто укажем вторым элементом в паре все слова, которые могут быть продолжением. Например, у нас в переменной pairs  есть такие пары:

привет → это

привет → друг

привет → как

привет → друг

привет → друг

Видно, что «друг» встречается в 3 раза чаще остальных слов, поэтому вероятность его появления — ⅗. Но чтобы не считать вероятности, мы сделаем так:

👉 Это, конечно, не так изящно, как в серьёзных алгоритмах с матрицами и вероятностями, зато работает точно так же и более просто в реализации.

Вот блок с этим кодом на Python:

# словарь, на старте пока пустой
word_dict = {}

# перебираем все слова попарно из нашего списка пар
for word_1, word_2 in pairs:
    # если первое слово уже есть в словаре
    if word_1 in word_dict.keys():
        # то добавляем второе слово как возможное продолжение первого
        word_dict[word_1].append(word_2)
    # если же первого слова у нас в словаре не было
    else:
        # создаём новую запись в словаре и указываем второе слово как продолжение первого
        word_dict[word_1] = [word_2]

Выбираем слово для старта

Чтобы было совсем непредсказуемо, начальное слово тоже будем выбирать случайным образом. Главное требование к начальному слову — первая заглавная буква. Выполним это условие так:

# случайно выбираем первое слово для старта
first_word = np.random.choice(corpus)

# если в нашем первом слове нет больших букв 
while first_word.islower():
    # то выбираем новое слово случайным образом
    # и так до тех пор, пока не найдём слово с большой буквой
    first_word = np.random.choice(corpus)

Запускаем алгоритм

У нас почти всё готово для запуска. Единственное, что нам осталось сделать — установить количество слов в готовом тексте. После этого наш алгоритм возьмёт первое слово, добавит в цепочку, потом выберет для этого слова случайное продолжение, потом выберет случайное продолжение уже для второго слова и так далее. Так он будет делать, пока не наберёт нужное количество слов, после чего остановится.

# делаем наше первое слово первым звеном
chain = [first_word]

# сколько слов будет в готовом тексте
n_words = 100

# делаем цикл с нашим количеством слов
for i in range(n_words):
    # на каждом шаге добавляем следующее слово из словаря, выбирая его случайным образом из доступных вариантов
    chain.append(np.random.choice(word_dict[chain[-1]]))

# выводим результат
print(' '.join(chain))

Результат

После обработки Чехова наш алгоритм выдал такое:

В октябре 1894 г. Текст статьи, написанные за вечерним чаем сидела за ивы. Они понятия о равнодушии к себе в целом — бич божий! Егор Семеныч и боялась. В повести пассивности, пессимизма, равнодушия («формализма») писали это она отвечала она не застав его лоб. Он пишет, что сам Песоцкий впервые явилась мысль о ненормальностях брака. Поймите мои руки; он, — а женщин небось поставил крест на о. Сахалине (см.: М. — Нет, вы тоже, согласитесь, сытость есть две ночи и белые, пухлые руки и мог не содержащем единой и не заслуживает «ни закрепления, ни мне не знаю, для меня с 50 рисунками

Здесь нет смысла, хотя все слова связаны друг с другом. Чтобы результат был более читабельным, нам нужно увеличить количество слов в парах и оптимизировать алгоритм. Это сделаем в другой раз, на сегодня пока всё.

Неправильно ты, Дядя Фёдор, на Питоне кодишь

Опытные питонисты абсолютно справедливо сделают нам замечание: нужно не писать новый алгоритм для обработки цепей Маркова, а использовать какую-нибудь готовую библиотеку типа Markovify. 

Всецело поддерживаем. В рабочих проектах, где вам нужно будет быстро получить правильный и предсказуемый результат, нужно не изобретать алгоритмы с нуля, а использовать опыт предыдущих поколений. 

Но нам было интересно сделать собственный алгоритм. А когда человеку интересно, ничто не должно стоять на его пути. 

Но в другой раз сделаем на библиотеке, окей.

# подключаем библиотеку numpy
import numpy as np

# отправляем в переменную всё содержимое текстового файла
text = open('che.txt', encoding='utf8').read()

# разбиваем текст на отдельные слова (знаки препинания останутся рядом со своими словами)
corpus = text.split()

# делаем новую функцию-генератор, которая определит пары слов
def make_pairs(corpus):
    # перебираем все слова в корпусе, кроме последнего
    for i in range(len(corpus)-1):
        # генерируем новую пару и возвращаем её как результат работы функции
        yield (corpus[i], corpus[i+1])
        
# вызываем генератор и получаем все пары слов
pairs = make_pairs(corpus)

# словарь, на старте пока пустой
word_dict = {}

# перебираем все слова попарно из нашего списка пар
for word_1, word_2 in pairs:
    # если первое слово уже есть в словаре
    if word_1 in word_dict.keys():
        # то добавляем второе слово как возможное продолжение первого
        word_dict[word_1].append(word_2)
    # если же первого слова у нас в словаре не было
    else:
        # создаём новую запись в словаре и указываем второе слово как продолжение первого
        word_dict[word_1] = [word_2]
 
# случайно выбираем первое слово для старта
first_word = np.random.choice(corpus)

# если в нашем первом слове нет больших букв 
while first_word.islower():
    # то выбираем новое слово случайным образом
    # и так до тех пор, пока не найдём слово с большой буквой
    first_word = np.random.choice(corpus)

# делаем наше первое слово первым звеном
chain = [first_word]

# сколько слов будет в готовом тексте
n_words = 100

# делаем цикл с нашим количеством слов
for i in range(n_words):
    # на каждом шаге добавляем следующее слово из словаря, выбирая его случайным образом из доступных вариантов
    chain.append(np.random.choice(word_dict[chain[-1]]))

# выводим результат
print(' '.join(chain))