Как составить алгоритм линейной структуры

Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.

Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.

Алгоритмический язык

Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает:
— разбиение на этапы;
— разработку алгоритма;
— составление программы решения на алгоритмическом языке;
— ввод данных;
— отладку программы (возможны ошибки — их надо исправить);
— выполнение на ПК;
— анализ результатов.

Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.

Свойства алгоритма

Их несколько:
— конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов;
— однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия;
— результативность. Итог работы — результат, полученный за конечное число шагов;
— универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.

Линейная структура

Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.

Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.

Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим:
— принести пылесос к месту уборки;
— включить;
— пропылесосить;
— выключить;
— унести пылесос.

И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.

Теперь поговорим про графическую форму представления.

Блок-схема

Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.

Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.

Блок начала-конца:

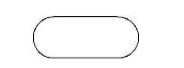
Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):

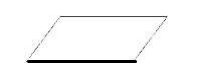
Арифметический блок (отображает арифметическую операцию/группу операций):

Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:

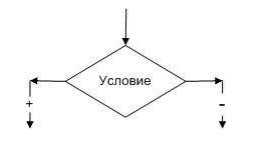
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:

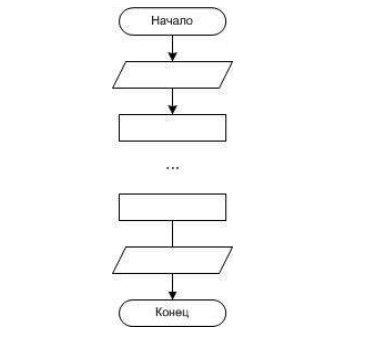
А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.

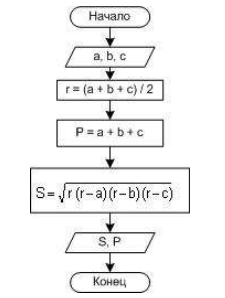
Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.

Примеры линейных алгоритмов

Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:

И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:

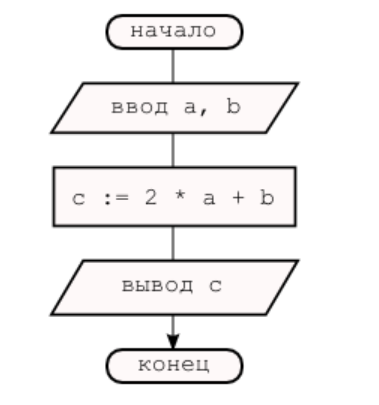
Как составить программу линейной структуры?

Порядок следующий:
— определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных;
— определите, каков тип данных будет у искомого результата, выберите название переменных (переменной);
— определите, какие математические формулы связывают результат и исходные данные;
— если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена;
— опишите все используемые переменные;
— запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.

На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!

Источники:
• https://inep.sfedu.ru/wp-content/uploads/2018/05/25/lection_27.pdf;
• https://www.sites.google.com/site/415ict/textbooks/prog-9/02-linejnyj-algoritm.

Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.

Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.

Алгоритмический язык

Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает: — разбиение на этапы;

— разработку алгоритма;

— составление программы решения на алгоритмическом языке;

— ввод данных;

— отладку программы (возможны ошибки — их надо исправить);

— выполнение на ПК;

— анализ результатов.

Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.

Свойства алгоритма

Их несколько:

— конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов;

— однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия;

— результативность. Итог работы — результат, полученный за конечное число шагов;

— универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.

Линейная структура

Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.

Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.

Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим:

— принести пылесос к месту уборки;

— включить;

— пропылесосить;

— выключить;

— унести пылесос.

И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.

Теперь поговорим про графическую форму представления.

Блок-схема

Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.

Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.

Блок начала-конца:

Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):

Арифметический блок (отображает арифметическую операцию/группу операций):

Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:

Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:

А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.

Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.

Примеры линейных алгоритмов

Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:

И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:

Как составить программу линейной структуры?

Порядок следующий: — определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных; — определите, каков тип данных будет у искомого результата, выберите название переменных (переменной); — определите, какие математические формулы связывают результат и исходные данные; — если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена; — опишите все используемые переменные; — запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.

На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!

Источники:

• https://inep.sfedu.ru/wp-content/uploads/2018/05/25/lection_27.pdf;

• https://www.sites.google.com/site/415ict/textbooks/prog-9/02-linejnyj-algoritm.

Как работает пирамидальная сортировка выбором? Разберемся в этом 20 июля на открытом уроке в OTUS с Евгением Волосатовым, программистом с 20-летним опытом. Сортировка выбором — один из самых простых алгоритмов сортировки. Ее можно значительно ускорить, если использовать структуру данных «куча» для поиска максимального элемента за О(1) константное время. В результате получится алгоритм пирамидальной сортировки HeapSort. На этом открытом уроке мы расскажем идею алгоритма и наглядно продемонстрируем его работу на визуальных примерах с конкретными числами. Вебинар пройдет в рамках онлайн-курса «Алгоритмы и структуры данных» и позволит познакомиться с преподавателем.

1. Алгоритмы линейной структуры

Линейные
алгоритмы предполагают последовательное
выполнение действий в порядке, заданном
схемой, без их повторения или пропуска
некоторых действий. Алгоритм линейной
структуры изображается линейной
последовательностью связанных друг с
другом блоков (рис. 9.8). Такой
порядок выполнения действий называется
естественным. Поэтому в схемах алгоритмов
линейной структуры нет блока «Решение».

Рис. 9.25. Алгоритм линейной
структуры

В
тестовом задании ниже представлен
линейный вычислительный процесс.
Фрагмент данного алгоритма записан в
словесно-формульном виде.

Тестовое
задание 9.7.

Чему
равны значения переменных аиbпосле выполнения следующего фрагмента
алгоритма:

1)
а =
3;

2)
b = 7;

3)
b = a;

4)
a = b;

5)
b = b*2

Ответы:

1. a= 3;b= 6

2. a= 14;b= 7

3. a= 7;b= 14

4. a= 6;b= 3

5. a= 3;b= 14

Решение.Выполняем алгоритм последовательно по
шагам:

1) а
=3;

2) b =
7;

3) b
= a; знак равенства
«=» в этом случае трактуется как знак
присваивания «=:», следовательно,
переменнойbприсваивается
значение переменнойа=3; т.е. переменнаяbпримет значениеb=3;

4) a=b;
переменнойаприсваивается
значение переменнойb=3;
следовательно, переменнаяапримет
значениеа =3;

5) b=b*2;
переменнойbприсваивается значениеb*2
(к этому моменту переменнаяbимеет значениеb=3); следовательно,
переменнаяbпримет
значениеb= b·2=3·2=6.

Таким
образом, в результате выполнения
алгоритма переменные аиb
примут значения a = 3;b = 6.

Визуальное
представление данного фрагмента
алгоритма в виде блок-схемы представлено
на рисунке 9.9.

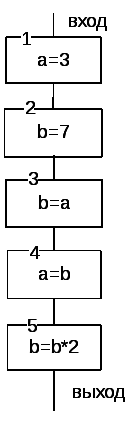
Рис. 9.26. Визуальное
представление фрагмента линейного
алгоритма

1. Алгоритмы ветвящейся структуры

В
отличие от линейных
алгоритмов, в которых
команды выполняются последовательно
одна за другой, в разветвляющиеся
алгоритмы входит условие, в зависимости
от выполнения или невыполнения которого
выполняется та или иная последовательность
операций, групп операций или базовая
управляющая структура.Каждая такая
последовательность действий называетсяветвьюалгоритма.

Таким
образом, алгоритм ветвящейся структуры
содержит только структуры «Следование»
и «Ветвление» (рис. 9.2, 9.3 и 9.4).

Структура
«Ветвление» описывает следующий процесс:
если B
– ИСТИНА (TRUE) (не равно
нулю), то выполняется структураS1;
еслиB– ЛОЖЬ (FALSE)
– структураS2. При
этом происходит разветвление алгоритма
(рис. 9.3).

Следует иметь в виду, что, хотя на схеме
алгоритма должны быть показаны все
возможные направления вычислений в
зависимости от выполнения определённого
условия (или условий), при однократном
прохождении программы процесс реализуется
только по одной ветви, а остальные
исключаются. Любая ветвь, по которой
осуществляются вычисления, должна
приводить к завершению вычислительного
процесса.

Пример.Рассмотрим пример
ветвящегося вычислительного процесса.
Определить и вывести на экран монитора
сведения о положении точки (Х,Y)
в указанной области (рис. 9.10). Координаты
точки вводятся с клавиатуры по запросу
пользователя. Примечание: прямая,
уравнение которойх= 2 принадлежит
области В.

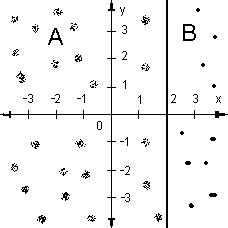
Рис. 9.27. Рисунок,
иллюстрирующий условие примера

Визуальное
представление алгоритма в виде блок-схемы
представлено на рисунке 9.11.

Рис. 9.28. Визуальное
представление простого ветвящегося
алгоритма решения задачи в виде блок-схемы

Если сравнить схему на рисунке 9.11 со
схемами на рисунках 9.2 и 9.3, то видно, что
данный алгоритм содержит базовые
управляющие структуры – «Следование»
и «Ветвление». При x≥ 2 блоки выполняются в следующей
последовательности: 1, 2, 3, 4, 5, 7.
Следовательно, еслиx≥ 2, в блоке 5 на мониторе будет выведено
«точкаX,Yв области В».Если
x
< 2,
последовательность
выполнения блоковследующая: 1, 2, 3,
4, 6, 7, т.е. на экран в блоке 6 будет выведено
«точкаX,Yв области А». Данный результат соответствует
условию задачи.

В
тестовом задании 9.2 представлен фрагмент
данного ветвящегося алгоритма, записанный
в словесно-формульном виде.

Тестовое задание 9.8

Определите значение
переменной z
после выполнения фрагмента алгоритма,
представленного на рисунке 9.12:

Рис. 9.29. Рисунок к заданию
9.8

Решение.

Блок 1. Присваиваем значения х= 7 иy= 5.

Блок 2. Выполняем проверку x>y, результат –
«истина», следовательно, после блока 2
выполняем блок 3.

Блок 3. Вычисляем значение переменной
z=x+y
= 7+5 = 12.

Блок 5. Выводим значение переменной zна экран монитора.

Соседние файлы в папке Информатика_ЗФ

• #
• #
• #
• #
• #
• #

Конспект

Составление линейных алгоритмов

 На предыдущих уроках мы узнали, что такое алгоритм, какие бывают виды алгоритмов, и кто их исполняет.

Сегодня мы попрактикуемся в составлении алгоритмов. Это очень важные навыки. Мы уже неоднократно отмечали, что составить алгоритм, то есть объяснить другому, как выполнять те или иные задачи так, чтобы это было понятно каждому, – очень тяжело. Наша задача – научиться составлять алгоритмы для различных примеров, чтобы впоследствии, когда вы столкнётесь с необходимостью составлять алгоритмы для написания различных программ, это не составляло для вас особого труда.

 Начнём мы с самых простых алгоритмов – линейных. Их составление, обычно, не вызывает особого труда. Однако, навыки составления таких алгоритмов чрезвычайно важны.

Пример 1. Составить алгоритм запуска программы Paint в ОС Windows 7.

Решение:

Вспомним из курса информатики 5 класса порядок действий для запуска программы Paint.

1. Войти в меню «Пуск».
2. Войти в пункт «Все программы».
3. Войти в пункт «Стандартные».
4. Выбрать программу «Paint».

Данный алгоритм в виде блок-схемы имеет следующий вид:

 

Рис. 1. Блок-схема к примеру 1.

Составление алгоритмов с ветвлениями

Рассмотрим пример на составление алгоритмов с ветвлениями.

 Пример 2. Составьте алгоритм для перехода дороги на светофоре.

Рис. 2. Светофор (Источник).

Решение:

Возможны следующие ситуации: в тот момент, когда мы подошли к дороге горел красный или зелёный свет. Если горел зелёный свет, то можно переходить дорогу. Если же горел красный свет, то необходимо дождаться зелёного – и уже тогда переходить дорогу.

Таким образом, алгоритм имеет следующий вид:

1. Подойти к светофору.
2. Посмотреть на его свет.
3. Если горит зелёный, то перейти дорогу.
4. Если горит красный, то подождать, пока загорится зелёный, и уже тогда перейти дорогу.

Блок-схема данного алгоритма имеет вид:

Рис. 3. Блок-схема к примеру 2.

Составление циклических алгоритмов

Рассмотрим пример на составление циклического алгоритма. Мы уже несколько раз обсуждали перевод чисел из десятичной системы в двоичную. Теперь пришло время чётко сформулировать этот алгоритм.

Напомним, что его принцип состоит в делении числа на 2 и записей остатков, получающихся при делении.

Пример 3. Составить алгоритм перевода чисел из десятичной системы в двоичную.

Решение:

То есть, алгоритм будет выглядеть так:

1. Если число равно 0 или 1, то это и будет его двоичное представление.
2. Если число больше 1, то мы делим его на 2.
3. Полученный остаток от деления записываем в последний разряд двоичного представления числа.
4. Если полученное частное равно 1, то его дописываем в первый разряд двоичного представления числа и прекращаем вычисления.
5. Если же полученное частное больше 1, то мы заменяем исходное число на него и возвращаемся в пункт 2).

Блок-схема этого алгоритма выглядит следующим образом:

Рис. 4. Блок-схема к примеру 3.

Примечание: подумайте, можно ли как-то упростить приведенную блок-схему.

«Чтение» алгоритмов

Пример 4. По заданной блок-схеме выполнить действия алгоритма для числа 23.

Рис. 5. Блок-схема к примеру 4.

Решение:

1. a=23
2. 23+5=28
3. 28<35
4. 28+5=33
5. 33<35
6. 33+5=38
7. 38>35
8. 
9. 76 – двузначное число
10. 76-50=26.

Ответ: 26.

На этом уроке мы разобрали примеры составления алгоритмов, а также пример «чтения алгоритма» по готовой блок-схеме.

На следующем уроке мы обсудим игры и выигрышные стратегии.

Как убить Кощея?

Наверное, все помнят из детства сказку, в которой рассказывается о местонахождении смерти Кощея Бессмертного: «Смерть моя – на конце иглы, которая в яйце, яйцо – в утке, утка – в зайце, заяц в сундуке сидит, сундук на крепкий замок закрыт и закопан под самым большим дубом на острове Буяне, посреди моря-океяна …»

Рис. 6. Кощей Бессмертный и Василиса Премудрая (Источник).

Предположим, вместо Ивана-царевича бороться с Кощеем был брошен Иван-дурак. Давайте поможем Василисе Премудрой составить такой алгоритм, чтобы даже Иван-дурак смог убить Кощея.

1. Конечно же, сначала необходимо разыскать остров Буян (на такие вещи, будем считать, Иван-дурак способен).
2. Поскольку сундук закопан под самым большим дубом, то сначала необходимо найти самый большой дуб на острове.
3. Затем нужно выкопать сам сундук.
4. Прежде чем доставать зайца, необходимо сломать крепкий замок.
5. Теперь уже можно достать зайца.
6. Из зайца нужно достать утку.
7. Из утки достать яйцо.
8. Разбить яйцо и достать иголку.
9. Иголку поломать.

Это тоже линейный алгоритм, хотя и более длинный, чем алгоритм запуска программы Paint.

Его блок-схема выглядит так:

Рис. 7. Блок-схема.

На распутье…

И снова обратимся к сказочным персонажам в поисках примеров различных алгоритмов. Когда речь идёт об алгоритмах с ветвлениями, то, конечно, нельзя не вспомнить о богатыре, стоящем на распутье возле камня.

Рис. 8. Богатырь на распутье (Источник).

На камне написано:

«Направо пойдёшь – коня потеряешь, себя спасёшь; налево пойдёшь – себя потеряешь, коня спасёшь; прямо пойдёшь – и себя и коня потеряешь».

Попробуем составить алгоритм действий, который составил автор надписи на камне для путников?

1. Если мы пойдём направо, то потеряем коня. Если же мы не пойдём направо, то у нас остаётся два варианта (мы считаем, что назад возвращаться путник не будет): пойти прямо и налево.
2. В случае, если мы пойдём налево, то потеряем себя, а коня спасём.
3. Если же мы пойдём прямо, то потеряем и себя, и коня.

Блок-схема этого алгоритма выглядит так:

Рис. 9. Блок-схема.

Репка

Русские народные сказки не оставили нас и без циклического алгоритма. И, как ни странно, спрятался он в одной из самых незамысловатых сказок – «Репке».

Рис. 10. Репка.

Вспомним сюжет сказки: дед тянет-потянет – вытянуть не может. Затем на помощь к деду по очереди подходят новые персонажи – и так до тех пор, пока не приходит мышка.

Попытаемся составить алгоритм действий всех персонажей сказки для того, чтобы они всё-таки смогли вытянуть Репку.

1. Изначально к Репке подошёл дед и попытался вытянуть.
2. Поскольку вытянуть Репку не получилось, то понадобилась помощь следующего персонажа.
3. И так происходит до тех пор, пока не появилась мышка (или, другими словами, до тех пор, пока Репку не вытащили).

В виде блок-схемы этот алгоритм выглядит следующим образом:

Рис. 11. Блок-схема.

Список рекомендованной литературы

1. Босова Л.Л. Информатика и ИКТ: Учебник для 6 класса. – М.: БИНОМ. Лаборатория знаний, 2012
2. Босова Л.Л. Информатика: Рабочая тетрадь для 6 класса. – М.: БИНОМ. Лаборатория знаний, 2010.
3. Босова Л.Л., Босова А.Ю. Уроки информатики в 5-6 классах: Методическое пособие. – М.: БИНОМ. Лаборатория знаний, 2010.

 Рекомендованные ссылки на ресурсы интернет

1. Интернет портал «Сообщество взаимопомощи учителей» (Источник).
2. Интернет портал «Nsportal.ru» (Источник).
3. Интернет портал «Фестиваль педагогических идей» (Источник).

 Рекомендованное домашнее задание

1. §3.3, 3.4 (Босова Л.Л. Информатика и ИКТ: Учебник для 6 класса);
2. Постарайся самостоятельно составить линейный алгоритм из 5-6 фигур;
3. Составь блок-схему циклического алгоритма выполнения домашнего задания;